1 Introduction

The heterogeneity of rock mass makes it quite a complex system, and the mechanical behavior and deformation mechanism of rock or rock mass is one of the most concerning problems in the geotechnical field [1]. Since the concept of rock entire stress–strain curve was proposed [2], scholars and experts at home and abroad began to study rock constitutive models other than the classical elastoplastic model [3]. Whereafter, those popular rock constitutive models, such as Drucker–Prager criterion [4], Mohr–Coulomb criterion [5], Hoek–Brown criterion [6] and so on, were rapidly developed in scientific researches and engineering applications.

Rock is a kind of brittle material with original damage and defects. Numerous researches have shown that rock failure showed progressive characteristics [7,8,9]. The strength of rock gradually decays to residual strength with the continuous development of deformation when the external load exceeds its compressive strength, causing strain softening performances. From the microscopic perspective, the macroscopic nonlinear mechanical behavior of rock can be regarded as the superposition effect of inhomogeneous microscopic damage, while such inhomogeneity can be described by certain probability distributions. In this case, the concept of rock statistical damage constitutive was put forward by combining continuous damage theory and statistical strength theory on the basis of effective stress concept and strain equivalence hypothesis [10]. Therefore, the establishment of rock constitutive models based on the random distribution of internal defects in rock has become an effective approach to studying the rock stress–strain relationships and reproducing the entire process of rock deformation and failure, which has attracted the worldwide research attentions.

On the basis of strain strength theory, Tang [11] took the axial strain as the statistical distribution variable and conducted a damage study on the rock failure process. Chen [12] established a damage constitutive model effectively reflecting the residual strength in the post-peak stage of rock failure. Liu et al. [13] proposed a damage model in the form of logistic equation to simulate the stress–strain relation of rocks based on the uniaxial compression tests of three types of rock. Cao et al. [14,15,16,17] proposed the concept of rock microelement strength and the corresponding measuring method, which can reasonably embody the influence of complex stress state, providing a new research approach for the establishment of the statistical damage evolution equation of rocks. According to the current published literatures, the adopted failure criterion types describing the rock microelements strength are mostly the maximum tensile strain criterion [13], Mohr–Coulomb criterion [18], or Drucker–Prager criterion [19] due to their simple expressions. However, Shi et al. [20] stated that the axial strain cannot accurately represent the rock microelement strength, causing certain application limitations to the strain-based damage constitutive models. Besides, assuming the microelement failure conforms to Drucker–Prager criterion lacks rationality since the results by Drucker–Prager criterion is conservative [21]. While Mohr–Coulomb criterion fails to describe the rock strength in low-stress or tensile-stress zone. In addition, its linear relation expression does not agree well with the parabolic shape of the rock failure envelope [22].

To avoid the deficiencies caused by above rock failure criteria and manifest the mechanical performances and the deformation characteristics of rock materials as accurately as possible, this study investigated the combination of Hoek–Brown criterion and damage statistical distribution theory to predict the entire stress–strain curve in conventional triaxial test. It was assumed that the strength characteristics of rock microelements follows the statistical law of Weibull distribution, and the Hoek–Brown criterion was considered as the statistical distribution variable of these microelements. Then, based on the effective stress principle, the statistical constitutive model of rock damage under the confining stress was derived by strict mathematical deduction, which was subsequently verified by comparing with the triaxial test data of representative rock materials.

2 A brief review to Hoek–Brown criterion

In 1980, Hoek and Brown established the Hoek–Brown criterion by means of statistical analyses of hundreds of rock triaxial test data and numerous rock mass field test results and combining theoretical research and practical test results of rock properties [6, 23], which considers the low-stress and tensile-stress areas as well as the influence of the confining pressure on rock strength, and well embodies the nonlinear behavior of rock failure. Since then, this criterion has become the most widely used and influential criterion in the field of rock mechanics [24, 25]. The Hoek–Brown criterion can be expressed as:

$$\sigma_{1} - \sigma_{3} = \sigma_{ci} \left( {m_{i} \frac{{\sigma_{3} }}{{\sigma_{ci} }} + 1} \right)^{0.5} ,$$
(1)

where σ1 and σ3 are the maximum and minimum principal stresses, respectively, (MPa), σci is the unconfined compressive strength (MPa), and mi is a material constant that reflect the hardness of intact rocks. According to Hoek and Brown [22], σci is the dominant parameter that sets the scale of the rock mass failure curve on the σ1 versus σ3 plot. Using the experience of engineering geologists from laboratories and engineering field as a guide, Hoek et al. [26] presented a relatively comprehensive and detailed method for determining the specific value of mi, which covers the texture and mineral composition of various rock materials.

Subsequently, Hoek [27] improved the original Hoek–Brown criterion so that it can be applied to different rocks and rock masses, and proposed the generalized Hoek–Brown rock mass criterion, which can be defined as:

$$\sigma_{1} - \sigma_{3} = \sigma_{c} \left( {m_{b} \frac{{\sigma_{3} }}{{\sigma_{c} }} + s} \right)^{a} ,$$
(2)

where mb, s, and a are empirical parameters that reflect rock mass characteristics; Among them, mb and a are related to rock mass classification, whereas s represents the fragmentation degree of rock mass. The value of s ranges within 0.0 ~ 1.0, wherein s = 1.0 signifies intact rock mass.

To quantify these empirical parameters, Hoek [28] introduced the disturbance parameter D to take the blast effects and stress release into consideration and proposed a new method for determining the values of mb, s, and a based on the geological strength index (GSI), a system of rock mass characterization that was developed to link the failure criterion of rock mass to engineering geology observations from the views of the structure and the surface quality in the field, as presented by the following equations.

$$m_{b} = \exp \left( {\frac{GSI - 100}{{28 - 14D}}} \right)m_{i} ,$$
(3)
$$s = \exp \left( {\frac{GSI - 100}{{9 - 3D}}} \right),$$
(4)
$$a = \frac{1}{2} + \frac{1}{6}\left[ {\exp \left( { - GSI/15} \right) - \exp \left( { - 20/3} \right)} \right],$$
(5)

where GSI ranges from approximately 10 (for extremely fractured rock mass) to 100 (for intact rock mass); D is dependent on engineering experience, and D = 1 for completely disturbed rock mass while D = 0 for undisturbed rock mass. Obviously, mb and s are closely associated with GSI and D, while a is merely dependent on GSI.

The generalized Hoek–Brown rock mass strength criterion defined s and a on the basis of the original criterion so that they can be applied to low-quality rock masses (fractured rock mass), especially under the condition of low confining stress. As a result, it has gained wide acceptance as a tool for estimating the strength characteristics of fractured rock mass, which was adopted by the rock mechanics community because of the lack of suitable alternatives. While, in general, it has been found to provide satisfactory estimates, there are several questions on the limits of its applicability. Except for the service limit of GSI system, the Hoek–Brown criterion is only applicable for confining stresses within the range defined by σ3 = 0 and the transition from shear to ductile failure [29], at which point σ1 = 4.0σ3 [30] or σ1 = 3.4σ3 [31]. Besides, it is inapplicable when massive rock is in a state of relatively high confinement [32], or in massive to moderately jointed hard rock having high values of GSI [33].

3 Establishment of the statistical damage constitutive model

As previously implied, the randomly distributed micro defects in rocks are the main factors that cause rock damage and nonlinear mechanical behavior in the triaxial compression process (Fig. 1) [34]. For simplifications, the anisotropic rock material was regarded as an isotropic material, and its damages were considered as isotropic damages [34, 35]. According to Lemaitre strain equivalence theory and the concept of effective stress [36], the relationship between the nominal maximum principal stress σ1 and the effective maximum principal stress σ1* of isotropic damage can be expressed as:

$$\sigma_{1} = \sigma_{1}^{*} \left( {1 - D_{rock} } \right).$$
(6)
Fig. 1
figure 1

Progressive failure of rock

Full size image

From Eq. 6, it can be inferred that σ1 = 0 when Drock = 1. This result indicates that the rock fails to bear loads in completely damaged state. However, laboratory tests demonstrated that rock materials at the post-peak stage of the stress–strain curve usually have reserved certain bearing capacity (residual stress σr) due to the influence of friction and confining pressure, which is an important finding in the stability assessment of rock engineering. On this basis, the nominal maximum principal stress σ1 can be divided into two parts: the effective maximum principal stress σ1* provided by undamaged rock component and residual stress σr provided by damaged rock component [37]. Equation 6 should be modified into:

$$\sigma_{1} = \sigma_{1}^{*} \left( {1 - D_{rock} } \right) + \sigma_{r} D_{rock} .$$
(7)

Because of the particularity of triaxial test equipment, the direct measuring result of laboratory triaxial compression test is generally deviatoric stress–strain curve [38]. In this case, the deviatoric stress–strain curve was chosen as the research object to avoid unnecessary errors. Therefore, Eq. (7) can be rewritten as:

$$\sigma_{{1}} { - }\sigma_{{3}} { = }\left( {\sigma_{{1}}^{*} { - }\sigma_{{3}}^{*} } \right)\left( {{1 - }D_{rock} } \right){ + }\left( {\sigma_{r} { - }\sigma_{{3}}^{*} } \right)D_{rock}$$
(8)

Drock is the ratio of damaged microelements (Ndam) to the total number of microelements (Ntol) (Eq. 9).

$$D_{rock} { = }\frac{{N_{dam} }}{{N_{tol} }}$$
(9)

To establish the model, a series of assumptions of the rock microelements must be made clearly in advance for better understanding:

(1) The rock material is homogenous, continuous and brittle [39].

(2) The undamaged microelements conform to the linear elastic constitutive law before the failure.

The rock material is divided into infinite microelements, and the microdefects can be regarded as the damaged microelements, in which case the compaction stage will not be taken into account and the undamaged microelements show linear elastic properties directly at the initiation of loading. In accordance with Hooke’s law, Eq. 10 can be obtained:

$$\left( {\sigma_{1}^{*} - \sigma_{3}^{*} } \right) = E\varepsilon_{1}^{*} ,$$
(10)

where E is the elastic modulus of the rock material and ε1* is the effective strain of the elastic part of the rock material.

(3) The failure of undamaged microelement is instantaneous, and the yield satisfies the Hoek–Brown criterion (Eq. 1).

(4) The statistical law of the microelements strength is assumed to follow the Weibull distribution [40] (Eq. 11).

$$N_{dam} = \int_{0}^{{f_{HB} }} {N_{tol} \frac{\gamma }{\beta }} \left( {\frac{x}{\beta }} \right)^{\gamma - 1} \exp \left[ { - \left( {\frac{x}{\beta }} \right)^{\gamma } } \right]dx$$
(11)

The failure of rock materials is probabilistic due to the random distribution and growth of various scale defects, and the number of damaged microelements can be quantified by the statistical damage mechanics theory [41]. In the researches on the damage and fracture of rock and concrete, literature [42] shows that Weibull distribution, underpinned by statistical theory of brittle failure, is applicable to the fracture process of materials. Besides, through comparing the damage constitutive models of different distributions, Li et al. [43] have pointed out that Weibull distribution-based statistical constitutive model was the most suitable one to reflect the stress–strain relation for brittle rocks. By the same method, Chen et al. [44] also believed that using Weibull distribution to describe the microelement strength was more reasonable. Thus, Drock can be expressed as Eq. 12 by substituting Eq. 9 to Eq. 11.

$$D_{rock} = 1 - \exp \left[ { - \left( {\frac{{f_{HB} \left( {\sigma^{*} } \right)}}{\beta }} \right)^{\gamma } } \right]$$
(12)

where β and γ are both the Weibull distribution parameters.

The coordination relationship between the damage of the rock microelement and the deformation of the undamaged part indicates that the effective strain equals to the axial strain (\(\varepsilon_{{1}}^{*} { = }\varepsilon_{{1}}\)). Since rock damage mainly occurs in the axial direction with few lateral damages, it can be considered that \(\sigma_{2}^{*} = \sigma_{2}\) and \(\sigma_{3}^{*} = \sigma_{3}\). By combining with Eqs. 10 and 12, Eq. 8 can be rewritten as:

$$\left( {\sigma_{1} - \sigma_{3} } \right) = \left[ {E\varepsilon_{1} - \left( {\sigma_{r} - \sigma_{3} } \right)} \right]\exp \left[ { - \left( {\frac{{f_{HB} \left( {\sigma^{*} } \right)}}{\beta }} \right)^{\gamma } } \right] + \left( {\sigma_{r} - \sigma_{3} } \right).$$
(13)

The Hoek–Brown criterion can be expressed in the form of the effective stress invariant [45].

$$f_{HB} \left( {\sigma^{*} } \right) = m_{i} \sigma_{ci} \frac{{I_{1}^{*} }}{3} + 4J_{2}^{*} \cos^{2} \theta_{\sigma } + m_{i} \sigma_{ci} \sqrt {J_{2}^{*} } \left( {\cos \theta_{\sigma } + \frac{{\sin \theta_{\sigma } }}{\sqrt 3 }} \right),$$
(14)

where I1* is the first invariant of the effective stress (\(I_{1}^{*} = \sigma_{1}^{*} + \sigma_{2}^{*} + \sigma_{3}^{*}\)), J2* is the second invariant of the effective stress deviation (\(J_{2}^{*} = \frac{{\left[ {\left( {\sigma_{1}^{*} - \sigma_{2}^{*} } \right)^{2} + \left( {\sigma_{2}^{*} - \sigma_{3}^{*} } \right)^{2} + \left( {\sigma_{3}^{*} - \sigma_{1} } \right)^{2} } \right]}}{6}\)), and θσ is the Lode angle. In conventional triaxial compression tests, \(\sigma_{2}^{*} = \sigma_{3}^{*}\) and θσ = 30°. Consequently, fHB(σ*) can be calculated as:

$$f_{HB} \left( {\sigma^{*} } \right) = m_{i} \sigma_{ci} E\varepsilon_{1} + \left( {E\varepsilon_{1} - \sigma_{3} } \right)^{2} .$$
(15)

For the conventional triaxial test for intact rocks, Eq. 1 can be rewritten as:

$$\left( {\sigma_{1} - \sigma_{3} } \right)^{2} = \sigma_{ci} m_{i} \sigma_{3} + \sigma_{ci}^{2} .$$
(16)

Let y = (σ1−σ3)2 and x = σ3, and the specific values of σci and mi can be fitted using the least squares method.

The geometric conditions of the rock deviatoric stress–strain curve indicate that the derivative of the curve at the peak is zero. By calculating the derivative of Eq. 13, inputting the peak coordinate, and setting the derivative equal to zero, the following relationship can be obtained:

$$\left( {\frac{{f_{HB} \left( {\sigma_{p}^{*} } \right)}}{\beta }} \right)^{\gamma } = \frac{{f_{HB} \left( {\sigma_{p}^{*} } \right)}}{{\gamma \left[ {E\varepsilon_{p} - \left( {\sigma_{r} - \sigma_{3} } \right)} \right]\left( {m_{i} \sigma_{ci} + 2E\varepsilon_{p} + 4\nu \sigma_{3} - 2\sigma_{3} } \right)}}.$$
(17)

By substituting Eq. 17 into Eq. 13, β and γ can be determined:

$$\gamma = \frac{{f\left( {\sigma_{p}^{*} } \right)}}{{\ln \frac{{E\varepsilon_{p} - \left( {\sigma_{r} - \sigma_{3} } \right)}}{{\sigma_{p} - \sigma_{r} }}\left[ {E\varepsilon_{p} - \left( {\sigma_{r} - \sigma_{3} } \right)} \right]\left( {m_{i} \sigma_{ci} + 2E\varepsilon_{p} + 4\nu \sigma_{3} - 2\sigma_{3} } \right)}},$$
(18)
$$\beta = \frac{{f\left( {\sigma_{p}^{*} } \right)}}{{\left( {\ln \frac{{E\varepsilon_{p} - \left( {\sigma_{r} - \sigma_{3} } \right)}}{{\sigma_{p} - \sigma_{r} }}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \gamma }}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$\gamma $}}}} }}.$$
(19)

At the same time, it should be emphasized that the established model also has its limitations. The most obvious one is the application limitation of Hoek–Brown criterion which was previously mentioned. Second, a series of assumptions and simplifications were made during the model establishment, thus it can only be applied when rock materials satisfy those. Finally, according to the mathematical expression of the model, it is closely related to the elasticity modulus E and residual strength σr of rock materials. As a result, to obtain an expectant result, it is suggested to be utilized to describe the test data which have obvious linear stage and residual stage.

4 Verification

The triaxial test results presented in existing literatures were used to validate the rationality of the statistical damage constitutive model based on Hoek–Brown criterion. Considering the nonlinearity of stress–strain curves, the image observation method should not be used as the only criterion to evaluate the matching effect between the predicted values and test values, which is subjective. Therefore, the correlation factor δ was introduced [46].

$$\delta = 1 - \frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {\frac{{\left| {\sigma_{\left( i \right)} - \sigma_{i} } \right|}}{{\sigma_{i} }}} \right)} ,$$
(20)

where σ(i) and σi are the respective maximum principal stresses of the predicted and observed samples and n is the number of the samples included in the evaluation. Evaluation criteria were established on the basis of the different values of δ to evaluate the matching effect (Table 1).

Table 1 Evaluation standard of the correlation factor δ in the matching effect
Full size table

(1) Triaxial test results of sandstone presented in literature [47]

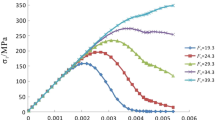
The deviatoric stress–strain curves of sandstone are plotted in Fig. 2. The Hoek–Brown parameters σci (57.59 MPa) and mi (9.94) were obtained by fitting the test values of σ1–σ3 and σ3 in accordance with Eq. 16 (Fig. 3), and the specific values of β and γ were then calculated. Table 2 lists the relevant equation parameters for different values of σ3 (0, 5, 10, 15, 25, and 35 MPa). The predicted deviatoric stress–strain curve under the specific confining pressure can be obtained through the previously enumerated steps. Figure 4 illustrates the comparison of the predicted curves and test results. The predicted curves conform well with the test results in Fig. 4, and the values of δ in Table 3 indicate that the two have a relatively good agreement. However, the agreement is relatively weaker when σ3 = 0 MPa, in which case the test result has a distinct compaction stage. This finding suggests that the damage constitutive equation can accurately simulate the entire deviatoric stress–strain response during the failure process of sandstone in the triaxial test to some extent.

Fig. 2
figure 2

Deviatoric stress–strain curves of sandstone (Wang)

Full size image
Fig. 3
figure 3

Fitting result of σci and mi

Full size image
Table 2 Equation parameters of the triaxial tests on sandstone
Full size table
Fig. 4
figure 4

Comparison of the predicted curves and test data: a σ3 = 0 MPa; b σ3 = 5 MPa; c σ3 = 10 MPa; d σ3 = 15 MPa; e σ3 = 25 MPa; f σ3 = 35 MPa

Full size image
Table 3 The evaluation of the predicted curves and the test results
Full size table

(2) Triaxial test results of sandstone presented in literature [48]

Similarly, the deviatoric stress–strain curves of sandstone (Fig. 5) were selected to demonstrate the validity of the proposed model. The necessary parameters were substituted to Eqs. 13, 15, 16, 18, and 19 to obtain the predicted curves, and the evaluation results calculated using Eq. 18 are summarized in Table 4. Figure 5 and Table 4 imply the good agreement between the test results and the predicted curves, thereby confirming the rationality and feasibility of the proposed model. However, only the test data under three confining pressures were included in this analysis, which may make it relatively inaccurate in determining the specific values of mi and σci, and ultimately, causing worse evaluations of the correlation between the test results and predicted curves by the value of δ.

Fig. 5
figure 5

Comparison of the predicted curves and test data: a σ3 = 3 MPa; b σ3 = 5 MPa; c σ3 = 7 MPa

Full size image
Table 4 The evaluation results of the triaxial tests on sandstone
Full size table

(3) Triaxial test results of rock-like materials presented in literature [49]

To verify the applicability of the proposed model to other kinds of rock materials, part of triaxial test results of cemented sand under different confining stresses (σ3 = 0.2, 0.3, and 0.4 MPa) were also employed to analyze and compare with theoretical curves. The execution steps were similar to that of sandstone. The comparison and evaluation results are presented in Fig. 6 and Table 5. Figure 6 indicates that the predicted curves coincide well with the test results. The value of δ is approximately 0.85–0.9 (Table 5) corresponding to the evaluation standard of qualified correlation and nice correlation and, therefore, confirms the rationality and applicability of the proposed model. The relatively small value of δ can be ascribed to the obvious nonlinear deformation in the initial compaction stage, which causes the predicted curve to locate above the test results. Equation 20 indicates that the calculated value of δ will be small because the value of xi is smaller than that of x(i).

Fig. 6
figure 6

Comparison of the predicted curves and test data: a σ3 = 0.2 MPa; b σ3 = 0.3 MPa; c σ3 = 0.4 MPa

Full size image
Table 5 The evaluation results of the triaxial tests on rock-like material
Full size table

5 Conclusion

(1) Given that the existing statistical damage constitutive models rarely consider the Hoek–Brown criterion, the present study assumed that the statistical law of rock microelement strength follows Weibull distribution and rock microelement yields obeying Hoek–Brown criterion to establish a new statistical damage constitutive model which considers the rock softening and reflects the entire stress–strain relationship, and is simple in terms of expression.

(2) The conventional triaxial test results of representative rock materials were compared with the theoretical curves obtained using the proposed model. In addition, the correlation factor evaluation method was utilized to evaluate the consistency. The results revealed that the new model can effectively reproduce the deviatoric stress–strain response during the failure process of tested rocks.

(3) Hoek–Brown criterion not only applies to intact rocks, but also can describe the strength characteristics of rock mass relatively accurately. Therefore, the model in this paper may be further applied to the stress–strain relation of rock mass, which reflects a wide applicability.