1 Introduction

With the advantages of high efficiency, high torque-to-inertia ratio, the permanent magnet synchronous motor (PMSM) has been widely used in mechanical arms, integrated chip packaging equipment, etc. [1]. Thus, it is of great importance to improve the dynamic performance and motion control accuracy of PMSM drive systems.

First, the typical single motor position control usually uses a position loop-speed loop-current loop three-loop control structure, and the regulator parameters in [2, 3]. Commonly used methods include the P-PI-PI and PI-P-PI control structures. When tracking the slope input signal under the P-PI-PI structure, there are steady state errors. Thus, a feedforward control link was adopted to compensate the corresponding velocity component to the given velocity, namely the P-PI-PI with feedforward control [4]. However, excessive differential action was likely to result in system oscillation. In addition, there is a response delay and a great deal of quantization noise during the speed measurement under PI-P-PI control. To obtain better motion control performance, the authors of [5] proposed a double closed-loop structure, where the speed loop was removed, a phase leading link and a high-order low-pass filtering link were added, and the PI-Lead position controller was born [6]. However, these vector control-based structures have a number of limitations. (1) The cascaded PI control limits the system dynamic response, and even affects the system position tracking performance. (2) The cascaded PI control needs to adjust multiple parameters, and is usually used to control errors that have occurred, due to its inability to control errors in advance.

Model predictive control is used to obtain the optimal control input through minimization of the cost function based on the current output of the controlled object [7]. Finite control set model predictive control (FCS-MPC), as a major classification of model predictive control, is widely used in motor control due to its advantages of high control flexibility and no need for pulse width modulation. FCS-MPC mainly includes predictive current (torque) control [8], predictive speed control [9], and predictive position control [10] in PMSM applications. The cost function in the predictive position control proposed in [11, 12] contains both current, speed, and position information, as well as a nonlinear function that limits the current and speed. The control targets may interfere with each other, and the effect of each control target needs to be reflected by the weight coefficient. Thus, at least three weight coefficients need to be adjusted. In addition, the effect of the weight coefficient adjustment on the system performance is not clear, and the tuning method is limited to the empirical method or the trial-and-error method, which has the problems of relying on manual experience and consuming a great deal of time.

To explore a more effective weight coefficient tuning method, researchers have looked into predictive torque and speed control. In [13, 14], the torque and flux linkage were unified into the stator flux linkage vector. Thus, the cost function only contains a control target, which eliminates the need for weight coefficient settings. The authors of [15] converted torque and flux linkage control into relative error rate control, which eliminated the weight coefficient. In [16], by introducing a fuzzy method and a sorting method, the importance of torque and flux linkage was balanced, and the weight coefficient was omitted. The authors of [17] proposed a PMSM three-vector predictive torque control based on the rapid screening of voltage vectors. The authors of [18] proposed a PMSM fast speed predictive control based on expected voltage vector that selected alternative voltage vectors through partial sectors, which reduces the calculation steps and eliminates the adjustment of the weight coefficients. The authors of [19, 20] proposed direct predictive speed control and predictive torque control strategies without weighting coefficients through the direct selection method of alternative voltage vectors. In addition, the voltage vector is corrected by the current limit circle to ensure that the current limit is not exceeded. However, for predictive position control, the current limit and the speed limit must be considered. The authors of [21] proposed a new method to limit both the current and the speed based on the voltage boundary, which analyzes the voltage rectangular region corresponding to the current and speed constraints, and further modifies the voltage duty ratio. However, the ergodic method is still used in selecting the voltage vectors.

To solve the problems of weight coefficient adjustment and low efficiency in voltage vector selection, this paper proposes a fast position predictive control (FPPC) strategy for PMSM systems. First, the prediction of reference voltage vectors with current, speed, and position information is performed. To solve the problem in [12] that the weight coefficient of the traditional cost function is difficult to adjust, and to shorten the number of calculations, the cost function is uniformly transformed into the voltage dimension, and the optimization selection of the alternative voltage vector and cost function are performed based on the reference position angle. Thus, the number of alternative voltage vectors is reduced to 3. Then, to consider both the current limit and the speed limit, unlike the voltage rectangular area proposed in [21], a current limit circle and a speed limit rectangle are established, and the position relationship between the two areas is analyzed to achieve double the current and speed limit to meet the needs of actual users.

2 Fast position predictive control strategy

2.1 Reference voltage vector prediction

The mathematical modeling of a PMSM refers to [22]. After delay compensation, the predicted voltage vector equation at the time k + 1 is:

$$ \left\{ \begin{gathered} u_{d} (k + 1) = L_{s} \frac{{i_{d} (k + 2) - i_{d} (k + 1)}}{{T_{s} }} + \hfill \\ R_{s} i_{d} (k + 1) - L_{s} \omega_{e} (t)i_{q} (k + 1) \hfill \\ u_{q} (k + 1) = L_{s} \frac{{i_{q} (k + 2) - i_{q} (k + 1)}}{{T_{s} }} + \hfill \\ L_{s} \omega_{e} (t)i_{d} (k + 1) + \omega_{e} (t)\psi_{f} + R_{s} i_{q} (k + 1) \hfill \\ \end{gathered} \right., $$
(1)

where ud and id are the d axis stator voltage and current; Rs and Ls are the stator resistance and inductance; uq and iq are the q axis stator voltage and current; ψf is the flux linkage; ωe is the electrical angular velocity; and Ts is the current sampling period.

From the motion equation of PMSM, it can be seen that:

$$ i_{q} (k + 2) = \frac{1}{{K_{t} }}\left[ {J\frac{\omega (t + 1) - \omega (t)}{{T_{sm} }} + T_{L} + B\omega (t)} \right], $$
(2)
$$ \omega (t + 1) = \frac{\theta (l + 1) - \theta (l)}{{T_{pm} }}, $$
(3)

where Kt is the torque constant, J is the moment of inertia, TL is the load torque, B is the friction coefficient, θ and ω are the mechanical position angle and angular velocity, Tsm, Tpm, t, and l are the speed and position sampling period and sampling time, respectively.

By substituting Eqs. (2) and (3) into Eq. (1), the following can be obtained:

$$ \begin{aligned} u_{q} (k + 1) & = \frac{{L_{s} J\left[ {\theta (l + 1) - \theta (l) - T_{pm} \omega (t)} \right] + L_{s} T_{L} T_{pm} T_{sm} }}{{K_{t} T_{s} T_{pm} T_{sm} }} \\ & + \frac{{L_{s} B\omega (t)}}{{K_{t} T_{s} }} - \frac{{L_{s} i_{q} (k + 1)}}{{T_{s} }} + L_{s} \omega_{e} (t)i_{d} (k + 1), \\ & + \omega_{e} (t)\psi_{f} + R_{s} i_{q} (k + 1) \\ \end{aligned} $$
(4)

Selecting the predicted position θ(l + 1) as the reference position \(\theta (l + 1) = \theta^{*}\), it can be obtained that:

$$ \begin{aligned} u_{q}^{*} & = \frac{{L_{s} J\left[ {\theta^{*} - \theta (l) - T_{pm} \omega (t)} \right] + L_{s} T_{L} T_{pm} T_{sm} }}{{K_{t} T_{s} T_{pm} T_{sm} }} \\ & + \frac{{L_{s} B\omega (t)}}{{K_{t} T_{s} }} - \frac{{L_{s} i_{q} (k + 1)}}{{T_{s} }} + L_{s} \omega_{e} (t)i_{d} (k + 1), \\ & + \omega_{e} (t)\psi_{f} + Ri_{q} (k + 1) \\ \end{aligned} $$
(5)

Selecting the predicted d-axis current id(k + 2) in Eq. (1) as the reference current \(i_{{\text{d}}}^{*}\), it can be seen that:

$$ \begin{aligned} u_{d}^{*} & = L\frac{{i_{d}^{*} - i_{d} (k + 1)}}{{T_{s} }} + Ri_{d} (k + 1) \\ & - L\omega_{e} (t)i_{q} (k + 1) \\ \end{aligned} $$
(6)

It can be known from Eqs. (5) and (6) that the d-axis and q-axis components of the reference voltage vector \(u_{q}^{ * }\) and \(u_{d}^{ * }\) can be determined through the position and d-axis current given values.

2.2 Improved cost function

The traditional cost function is:

$$ \begin{aligned} J & = \underbrace {{\lambda_{e} (\theta^{ * } - \theta (k + 1))^{2} }}_{(a)} + \underbrace {{\lambda_{\omega } \omega^{2} (k + 1)}}_{(b)} + \underbrace {{\lambda_{d} i_{d}^{2} (k + 1)}}_{(c)} \\ & + \underbrace {{\hat{f}_{1} (\omega (k + 1))}}_{(d)} + \underbrace {{\hat{f}_{2} (i_{d} (k + 1),i_{q} (k + 1))}}_{(e)}, \\ \end{aligned} $$
(7)

J usually contains five terms: (a) the position tracking error term; (b) the optimal speed term; (c) the id = 0 term; (d) the maximum speed limit term; and (e) the maximum current limit term. At the same time, J needs to adjust λe, λω, and λd simultaneously, and the algorithm complexity increases accordingly. This paper selects the following improved cost function:

$$ J_{opt} = \left| {u_{d}^{*} - u_{d}^{j} } \right| + \left| {u_{q}^{*} - u_{q}^{j} } \right|, $$
(8)

where uj represents the alternative voltage vector, j = 0, 1, 2, 3, 4, 5, 6, 7.

From Eq. (8), Jopt only includes the voltage tracking error. Thus, the weight coefficient can be omitted and the complexity of the algorithm can be reduced.

By substituting Eqs. (1), (5), and Eq. (6) into Eq. (8), the following can be obtained:

$$ J = \frac{L}{{T_{s} }}\left| {i_{d}^{ * } - i_{d} (k + 2)} \right| + \frac{L}{{T_{s} }}\left| {\frac{J}{{K_{t} T_{pm} T_{sm} }}\left[ {\theta^{ * } - \theta (l + 1)} \right]} \right| $$
(9)

2.3 Alternative voltage vectors selection

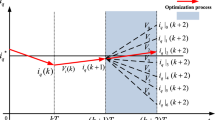
Figure 1 shows a partition structure diagram of a 2-level voltage source inverter (VSI), which includes 6 effective vectors V1 ~ V6 + 2 zero vectors V0 and V7.

Fig. 1
figure 1

Partition structure diagram of a 2-level VSI

Full size image

The eight-vector algorithm is used to select the optimal vector from these 8 vectors. At this time, it is necessary to calculate 7 times on Eq. (1) including the id, and iq items, and Eqs. (2), (3), and (9), respectively. In addition, one time delay compensation on Eq. (1) including the id and iq items, then 6 times comparative calculation of the cost function were carried out. Finally, a total of 43 calculations were performed. It can be seen that the calculation number is relatively large, which is not conducive to the improvement of calculation efficiency in practical applications.

To improve the computational efficiency of the strategy, \(u_{q}^{*} (k + 1)\) and \(u_{d}^{ * } (k + 1)\) are converted to the α-β axis as:

$$ \left[ \begin{gathered} u_{\alpha }^{*} (k + 1) \hfill \\ u_{\beta }^{*} (k + 1) \hfill \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}c} {\cos \theta_{e} } & { - \sin \theta_{e} } \\ {\sin \theta_{e} } & {\cos \theta_{e} } \\ \end{array} } \right]\left[ \begin{gathered} u_{d}^{*} (k + 1) \hfill \\ u_{q}^{*} (k + 1) \hfill \\ \end{gathered} \right], $$
(10)
$$ \theta_{ref} \,\, = \,\,\arctan \frac{{u_{\beta }^{*} (k + 1)}}{{u_{\alpha }^{*} (k + 1)}} $$
(11)

where θref is the reference position angle.

With Eq. (11), the candidate voltage vector distribution corresponding to the reference vector falling into the sector can be defined, as shown in Table 1.

Table 1 Alternative voltage vector distribution
Full size table

The selection of V0 and V7 is based on the minimum number of switching times.

Through the above improvements, it is only necessary to perform 3 times calculations on Eq. (1) including the id and iq items, Eqs. (2), (3), and (9), respectively. In addition, one time delay compensation on Eq. (5) including the id and iq items, then one time for Eqs. (5–6) and (10–11) are calculated. After that, the comparison calculation of the cost function is carried out twice. Finally, a total of 23 calculations are needed. It can be seen that the calculation efficiency can be greatly improved.

2.4 Current and speed limit modules

Limited by the rated output current along with the PMSM maximum voltage and current [22], the current limit in the actual system is:

$$ \begin{gathered} \left[ {u_{\alpha } (k + 1) + \Gamma_{1} } \right]^{2} + \left[ {u_{\beta } (k + 1) + \Gamma_{2} } \right]^{2} \le ({{L_{s} } \mathord{\left/ {\vphantom {{L_{s} } {T_{s} }}} \right. \kern-0pt} {T_{s} }} \cdot I_{\max } )^{2} \hfill \\ {\text{and}}\left\{ \begin{gathered} \Gamma_{1} = \left( {\frac{{L_{s} }}{{T_{s} }} - R_{s} } \right)i_{\alpha } (k + 1) + \omega_{e} \psi_{f} \sin \theta_{e} \hfill \\ \Gamma_{2} = \left( {\frac{{L_{s} }}{{T_{s} }} - R_{s} } \right)\left. {i_{\beta } (k + 1) - \omega_{e} \psi_{f} \cos \theta_{e} } \right] \hfill \\ \end{gathered} \right., \hfill \\ \end{gathered} $$
(12)

From Eq. (12), the voltage limit circle should be satisfied, as shown in Fig. 2.

Fig. 2
figure 2

Current limit

Full size image

In practical applications, the motor is often required to track the reference position trajectory at a changing speed. Thus, in addition to the current limit, it is also necessary to meet the speed limit conditions:

$$ \omega^{2} (t + 1) \le \omega_{\max }^{2} , $$
(13)

It can be obtained from Eq. (2) that:

$$ \begin{aligned} \omega (t + 1) & = \Lambda_{1} \left[ { - \sin \theta_{e} u_{\alpha } (k + 1) + \cos \theta_{e} u_{\beta } (k + 1)} \right] + \Lambda_{2} \\ {\text{and }}\Lambda_{1} & = \frac{{T_{s} T_{sm} K_{t} }}{{L_{s} J}} \\ \Lambda_{2} & = \frac{{T_{sm} K_{t} }}{J}\left( {1 - \frac{{T_{s} R_{s} }}{{L_{s} }}} \right)\left[ { - \sin \theta_{e} i_{\alpha } (k + 1) + \cos \theta_{e} i_{\beta } (k + 1)} \right] \\ & - \frac{{T_{s} T_{sm} K_{t} }}{{L_{s} J_{eq} }}p\omega (t)\psi_{f} - \frac{{T_{sm} T_{L} }}{J} + \left( {1 - \frac{{T_{sm} B}}{J}} \right)\omega (t) \\ \end{aligned} $$
(14)

Substituting Eq. (14) into Eq. (13), it can be seen that the speed limit in the α-β coordinates can be regarded as an area surrounded by two parallel straight lines, as can be seen in Fig. 3.

Fig. 3
figure 3

Speed limit

Full size image

Since the relationship between the dual constraints of current and speed is uncertain, if the system current limit and speed limit are considered simultaneously, they should be classified and discussed, as shown in Fig. 4.

Fig. 4
figure 4

Speed limit and current limit relationship

Full size image

When the relationship in Fig. 4a is satisfied, the speed limit is satisfied. Thus, only the current limit needs to be considered. Depending on the location of the voltage circle, four cases are discussed, as shown in Fig. 5.

Fig. 5
figure 5

Current limit 1

Full size image

① Determine whether the start and end points of the voltage vector are within the circle. If they are in the circle, they do not intersect. This is Case1, where the current limit is met, and no additional adjustments are required.

② If one point is inside the circle and the other point is outside the circle, and they intersect. This is Case2. At this time, the adjustment time of the effective voltage vector is determined according to the intersecting point, as shown in Table 2.where \(\Pi_{1} = 16r^{2} - 12\Gamma_{1}^{2} - 4\Gamma_{2}^{2} + 8\sqrt 3 \Gamma_{1} \Gamma_{2}\), \(\Pi_{2} = 16r^{2} - 12\Gamma_{1}^{2} - 4\Gamma_{2}^{2} - 8\sqrt 3 \Gamma_{1} \Gamma_{2}\), u = 2/3udc, \({{r = L_{s} } \mathord{\left/ {\vphantom {{r = L_{s} } {T_{s} }}} \right. \kern-0pt} {T_{s} }} \cdot I_{\max }\).

Table 2 Adjustment times corresponding to effective voltage vectors under a current limit
Full size table

③ If both points are outside the circle, further judgment is required.

  1. a)

    The distance equation is used to judge whether the distance from the center of the current limit circle to the voltage vector line segment is greater than the radius. If so, they do not intersect. This is Case4, in which the current limit is not satisfied, and the zero vector is selected.

  2. b)

    The cosine theorem is used to judge whether ∠O'OP and ∠O'PO are both acute angles. If they are acute angles, they intersect; otherwise, they do not intersect. This is Case3. When they intersect, the adjustment time of the effective voltage vector is determined according to the larger intersection. The method is the same as ②. When they do not intersect, the zero vector is used.

When the relationship in Fig. 4b is satisfied, the speed limit and the current limit need to be considered at the same time. Thus, according to the position of the voltage circle, four cases are discussed, as shown in Fig. 6.

Fig. 6
figure 6

Current limit 2

Full size image

Case1': When Eq. (12) holds, the selected optimal vector falls within the voltage circle, this is the green circle. At this time, the current limit is satisfied, and only the speed limit needs to be considered. The intersection with the selected optimal vector is determined through the speed limit, and the adjustment time of the effective voltage vector is determined according to the intersecting point, as shown in Table 3.where \(\Omega_{1} = - \sin \theta_{e} + \sqrt 3 \cos \theta_{e}\) and \(\Omega_{2} = - \sin \theta_{e} - \sqrt 3 \cos \theta_{e}\).

Table 3 Adjustment times corresponding to effective voltage vectors under a speed limit
Full size table

When Eq. (12) does not hold, it can be divided into three cases:

Case2': When the circle is outside the rectangular frame, this is the blue circle. At this point, the intersection with the selected optimal vector is determined by the speed limit, and the optimal voltage vector at the intersection is used to replace the optimal voltage vector, while satisfying \(t_{opt} = t_{m1} \cap t_{n1}\).

Case3': When the circle is inside the rectangular frame, this is the pink circle. At this time, the intersection with the selected optimal vector is determined by the current limit, and the vector at the intersection replaces the optimal vector, while satisfying \(t_{opt} = t_{m1} \cap t_{n1}\).

Case4': At this moment, the selected optimal effective vector has no intersection with the voltage circle. The zero vector is acted on the entire control cycle.

When the relationship in Fig. 4c is satisfied, the speed limit is not satisfied. Regardless of the position of the voltage circle, the zero vector is acted on the entire control cycle.

3 Control system structure and robustness analysis

3.1 Control system structure

A structure diagram of the proposed FPPC for PMSM systems includes one-step delay compensation, reference voltage vector prediction, an improved cost function, alternative voltage vector selection, a load observer, and current and speed limit modules, as shown in Fig. 7.

Fig. 7
figure 7

Block diagram of FPPC for a PMSM system

Full size image

From Eq. (5) and Fig. 7, the load torque needs to be used in the reference voltage vector prediction. However, the load torque is generally unknown and needs to be observed. Thus, the error feedback correction method is used to design the load observer as:

$$ \left\{ \begin{aligned} \dot{\hat{\theta }} & = \hat{\omega } + a_{1} (\theta - \hat{\theta }) \\ \dot{\hat{\omega }} & = \frac{{K_{t} }}{J}i_{q} - \frac{B}{J}\hat{\omega } - \frac{{\hat{T}_{L} }}{J} + a_{2} (\theta - \hat{\theta }) \\ \dot{\hat{T}}_{L} & = a_{3} (\theta - \hat{\theta }) \\ \end{aligned} \right. $$
(15)

where \(\hat{T}_{L}\), \(\hat{\omega }\), \(\hat{\theta }\) represent the observed values of the observer, and a1, a2, a3 represent the observer coefficients. In addition, for the selection method of a1, a2, a3 refer to [18].

3.2 Parameter variation robustness analysis

Considering the motor parameter variations, according to Eq. (1), the predicted current used for the one-step delay compensation is:

$$ \begin{gathered} i_{de} (k + 1) = \left[ {1 - \frac{{T_{s} (R + \Delta R)}}{L + \Delta L}} \right]i_{d} (k) + \hfill \\ T_{s} \omega_{e} (t)i_{q} (k) + \frac{{T_{s} }}{L + \Delta L}u_{d} (k), \hfill \\ i_{qe} (k + 1) = \left[ {1 - \frac{{T_{s} (R + \Delta R)}}{L + \Delta L}} \right] \cdot i_{q} (k) - \hfill \\ T_{s} \omega_{e} (t)i_{d} (k) + \frac{{T_{s} }}{L + \Delta L}u_{q} (k) - \frac{{T_{s} \omega_{e} (t)\psi_{f} }}{L + \Delta L} \hfill \\ \end{gathered} $$
(16)

where \(\Delta R\) and \(\Delta L\) represent the errors between the nominal parameters and the actual parameters in the motor model.

Equation (16) is substituted into Eqs. (6) and (5), and subtracted from Eqs. (6) and (5), respectively. It can be obtained that:

$$ \begin{aligned} D_{d} & = u_{de}^{ * } (k + 1) - u_{d}^{ * } (k + 1) = \frac{\Delta L}{{T_{s} }} \cdot i_{d}^{ * } + \Delta a(k + 1) \\ D_{q} & = u_{qe}^{ * } (k + 1) - u_{q}^{ * } (k + 1) = \frac{1}{{T_{s} }}\left[ {(L + \Delta L)V_{qe}^{ * } - LV_{q}^{ * } } \right] + \Delta b(k + 1), \\ \end{aligned} $$
(17)

\(\begin{aligned} {\text{where}}\;\Delta a(k + 1) & = \left( {\Delta R - \frac{\Delta L}{{T_{s} }}} \right) \cdot i_{d} (k + 1) - \omega_{e} (t)[(\Delta L)i_{q} (k + 1) \\ & + (L + \Delta L)E_{q} ] + (R + \Delta R)E_{d} - \frac{L + \Delta L}{{T_{s} }}E_{d} , \\ \end{aligned}\) \(\begin{aligned} \Delta b(k + 1) & = \left( {\Delta R - \frac{\Delta L}{{T_{s} }}} \right) \cdot i_{q} (k + 1) + (R + \Delta R)E_{q} - \\ & \frac{L + \Delta L}{{T_{s} }}E_{q} + \omega_{e} (t)\left[ {\Delta Li_{d} (k + 1) + (L + \Delta L)E_{d} } \right], \\ \end{aligned}\) \(\begin{aligned} V_{qe}^{ * } & = \frac{{(J + \Delta J)\left[ {\theta^{ * } - \theta (l) - T_{pm} \omega (t)} \right]}}{{K_{t} T_{pm} T_{sm} }} + \frac{{T_{L} }}{{K_{t} }} + \frac{(B + \Delta B)\omega (t)}{{K_{t} }}, \\ V_{q}^{ * } & = \frac{{J\left[ {\theta^{ * } - \theta (l) - T_{pm} \omega (t)} \right]}}{{k_{t} T_{pm} T_{sm} }} + \frac{{T_{L} }}{{K_{t} }} + \frac{B\omega (t)}{{K_{t} }}. \\ \end{aligned}\) \(D_{d} ,D_{q}\)\(D_{d}\), \(D_{q}\) represent the d-axis and q-axis reference voltage errors.

The impact of \(\frac{\Delta R}{R},\frac{\Delta L}{L},\frac{\Delta J}{J},\frac{\Delta B}{B}\) on \(D_{d}\) and \(D_{q}\) is analyzed to display the independent relationship between parameter variations and the reference voltage error more intuitively. The values of the parameters under steady state operation when tracking the slope signal are \(i_{d}^{ * } = i_{d} = 0,\,\,i_{q}^{ * } = i_{q} = 1.8A,\,\,T_{L} = 0.1N \cdot m,\,\,\theta^{ * } = \theta = 4rad,\) \(\omega = 40rad/s,\,\,u_{d} = - 0.026V,\,\,u_{q} = 0.972V.\)

  1. 1)

    When only R changes, there are the following:

    $$ \begin{aligned} D_{d} & = \omega_{e} T_{s} \Delta Ri_{q} , \\ D_{q} & = - \left( {R + \Delta R} \right) \cdot \frac{{T_{s} \Delta R}}{L}i_{q} \\ \end{aligned} $$
    (18)
  2. 2)

    When only L changes, there are the following:

    $$ \begin{aligned} D_{d} & = - \frac{{RT_{s} \Delta L}}{L(L + \Delta L)}u_{d} + \frac{\Delta L}{L}u_{d} - \omega_{e} \Delta Li_{q} - \\ & \frac{{\omega_{e} T_{s} R\Delta Li_{q} }}{L} + \frac{{\omega_{e} T_{s} \Delta Lu_{q} }}{L} + \omega_{e}^{2} T_{s} \Delta L\psi_{f} , \\ D_{q} & = - \frac{\Delta L}{{T_{s} }}i_{q} - \frac{R\Delta L}{L}i_{q} + \frac{\Delta L}{L}u_{q} + \Delta L\omega_{e} \psi_{f} + \\ & \frac{{\Delta L\omega_{e} T_{s} }}{L}u_{d} + \frac{{T_{s} R^{2} \Delta L}}{L(L + \Delta L)}i_{q} - \frac{{T_{s} R\Delta L}}{L(L + \Delta L)}u_{q} \\ & - \frac{{R\Delta LT_{s} \omega_{e} \psi_{f} }}{L + \Delta L} + \frac{\Delta L}{{T_{s} }} \cdot \left( { - \frac{J\omega }{{K_{t} T_{sm} }} + \frac{{T_{L} }}{{K_{t} }} + \frac{B\omega }{{K_{t} }}} \right) \\ \end{aligned} $$
    (19)
  3. 3)

    When only J changes, there are the following:

    $$ \begin{aligned} D_{d} & = 0 \\ D_{q} & = - \frac{L\Delta J\omega }{{T_{s} K_{t} T_{sm} }}, \\ \end{aligned} $$
    (20)
  4. 4)

    When only B changes, there are the following:

    $$ \begin{aligned} D_{d} & = 0 \\ D_{q} & = \frac{L\Delta B\omega }{{T_{s} K_{t} }} \\ \end{aligned} $$
    (21)

The influence of parameter variations on \(D_{d}\) and \(D_{q}\) is drawn in Fig. 8.

Fig. 8
figure 8

Influence of parameter variations on \(D_{d}\) and \(D_{q}\)

Full size image

It can be seen that \(D_{d}\) and \(D_{q}\) are not greatly affected by changes of R and B. In addition, \(D_{d}\) is not greatly affected by changes of L and J. However, \(D_{q}\) is affected by changes of L and J.

4 Experiment validation

4.1 Experimental system

To realize the verification of the FPPC strategy on a PMSM system, an experimental platform was established as shown in Fig. 9. The main control DSP adopts a TMS320F28379 TI processor, with a main frequency of 200 MHz, and a control period of 50 μs. The parameters of the surface-mount PMSM are shown in Table 4.

Fig. 9
figure 9

PMSM system experimental platform

Full size image
Table 4 PMSM parameters
Full size table

4.2 Observer verification

To verify the effect of the observer in the proposed FPPC control algorithm, a simulation study was carried out in MATLAB, where a PMSM was made to track a broken line trajectory, and a 0.1 N‧m load was suddenly applied at 0.4 s. Figure 10 shows simulation waveform.

Fig. 10
figure 10

Observed waveform diagram

Full size image

From Fig. 10, it can be seen that the proposed observer in this paper can better observe the position, speed, and load torque.

4.3 Motion trajectory tracking test

To verify the control effect of the proposed FPPC control algorithm when tracking a polyline motion trajectory, the PMSM system is made to track a broken line trajectory under load. Figure 11 shows experimental waveforms with the traditional cost function PPC strategy [12], the model predictive direct position control (MP-DPC) [21], the proposed PPC (eight voltage vector, 8VV) strategy, and the FPPC (three voltage vector, 3VV) strategy.

Fig. 11
figure 11

Experimental waveforms when tracking a polyline trajectory: a traditional PPC, b MP-DPC, c 8VV, d FPPC

Full size image

In addition, Table 5 shows a comparison of the calculation times between the 8VV and the proposed 3VV algorithms.

Table 5 Computation time comparison
Full size table

From Fig. 11, it can be seen that when compared with the traditional cost function PPC strategy, the proposed control strategy and the MP-DPC can achieve a better tracking effect when compared with that of the traditional strategy. In addition, it does not need to adjust the weight coefficient, saving the workload of adjusting the coefficient by manual trials and increasing practicability. At the same time, the proposed FPPC strategy can achieve a similar tracking effect when compared with the 8VV and the MP-DPC strategy. However, the computational efficiency can be significantly improved, while the position steady-state performance may be slightly reduced.

To verify the control effect of the proposed FPPC control algorithm when tracking a curve motion trajectory, the PMSM system is made to track a sine curve trajectory under load. Figure 12 shows experimental waveforms in the proposed FPPC strategy.

Fig. 12
figure 12

Waveforms when tracking a sine curve trajectory

Full size image

From Fig. 12, it can be seen that the FPPC strategy can track the linear motion trajectory well. It can also track the curve motion trajectory.

4.4 Robustness experiment

To verify the control effect of the proposed FPPC control algorithm when loaded, the PMSM system is made to track an oblique motion trajectory. The PI + predictive speed control (PSC) [9], the traditional cost function PPC [12], the MP-DPC [21], and the proposed FPPC are used to observe waveform changes when a sudden resistor load 3.5Ω is added, as shown in Fig. 13. Table 6 summarizes the dynamic performance comparison of the four algorithms.

Fig. 13
figure 13

Experimental waveforms when the load is added

Full size image
Table 6 Comparison of the dynamic responses of four algorithms
Full size table

From Fig. 13 and Table 6, when compared with the PI + PSC strategy, the PCC strategy has a smaller tracking error when loading. In addition, the adjustment speed is faster. When compared with the traditional PPC strategy, the proposed FPPC and the MP-DPC strategy have fewer tracking errors and a quicker dynamic adjustment speed, without the need for tuning the weights, and the algorithm complexity can be reduced. When compared with MP-DPC strategy, the FPPC strategy has similar tracking errors and dynamic performance. However, the computational efficiency can be improved since the MP-DPC selects the voltage vector from six active vectors.

To verify the parameter robustness of the proposed FPPC strategy when the parameters are changed, when R, L, J, and B are changed by plus or minus 30%, the PMSM system is tracks the polyline trajectory. Figure 14 shows experimental waveforms.

Fig. 14
figure 14

Experimental waveforms when R, L, J, and B change

Full size image

From Fig. 14, when R and B change by plus or minus 30%, the position, speed, and current of the PMSM system when tracking the polyline trajectory do not change much, which indicates that the FPPC algorithm has certain parameter robustness. When J change by plus or minus 30%, the position error at the inflection point is larger, which indicates that the position response is more sensitive to J when compared with other motor parameters. When L change by plus or minus 30%, the current steady error of the PMSM system is larger, which indicates that the current response is more sensitive to L when compared with the other motor parameters.

4.5 Current and speed limit verification

To realize the verification of the speed and current limit module, the speed limit ωmax is set to 300 rad/s, and the current limit Imax is set to 6.5 A. Figure 15 shows starting signal waveforms.

Fig. 15
figure 15

Motor starting signal waveforms

Full size image

From Fig. 15, it can be seen that when the current and speed limit module is used, the current and speed of the motor can be effectively limited when starting, which avoids overcurrent and overspeed.

5 Conclusion

The FPPC strategy for PMSM systems without weight coefficients has a number of advantages.

  1. 1)

    Based on the FCS-MPC architecture, the system dynamic response performance and motion control accuracy when loading can be improved.

  2. 2)

    By adopting an improved cost function and converting the traditional cost function into voltage dimensions, the weight coefficient can be omitted and the algorithm can be simplified.

  3. 3)

    The current and speed limits are integrated into the selection of alternative vectors to improve the selected optimal vector, which can meet actual system requirements.

  4. 4)

    Based on the sector distribution of the reference voltage vector, the proposed strategy can shorten the number of calculations and improve the calculation efficiency.