1 Introduction

Field oriented control (FOC) is one of the most popular control algorithms for improving the dynamic performance of PMSM drives [1, 2]. FOC with proportional and integral (PI) controllers are widely used in industrial applications of PMSM drives due to low ripples in the stator flux and torque and low stator current THD. The use of a PI controller results in a few limitations. (i) A slow dynamic response, since the inner controller regulates the motor currents [3]. (ii) The gains of the PI controller affect the performance of the drive. (iii) The nonlinear effects of the motor and drive system must be neglected for precise tuning of the PI controller gains. (iv) The optimal tuning of PI controllers is time consuming.

To overcome these disadvantages, recent research on AC drives has focused on various controllers like the sliding mode controller (SMC) [4,5,6], model reference adaptive system (MRAS) [7], indirect FOC [8,9,10], etc. Model predictive controllers (MPCs) [11,12,13,14,15,16], are one of the most popular controllers among them. In MPC, a mathematical model of the motor is developed to predict the performance of the motor based on the motor parameters, and an objective function is optimized to choose the BVV. The selected voltage vector is applied to the motor during the next control cycle. This process is repeated for every control cycle [17].

Generally, MPCs are categorized based on their input sets [18] or available voltage vectors [19] into continuous control set-MPCs (CCS-MPCs) and finite control set-MPCs (FCS-MPCs) [20]. In FCS-MPCs limited voltage-vectors are used to control the motor without the use of modulation techniques [21,22,23]. However, in CCS-MPCs, space vector modulation (SVM) is normally used to control the motor, due to which any required voltage vector can be produced [24,25,26]. Thus, the phase and magnitude of the voltage-vector can be regulated to any required value. Two reported applications of MPC methods include the model predictive current control (MPCC) method [27] and the model predictive torque control (MPTC) method [28].

In the traditional FCS-MPC, the selected voltage vector is applied to the motor for the entire duration of the control cycle. As a result, the performance variables cannot be controlled with precision, and significant errors exist between the controlled variables and their commanded values. To overcome this drawback, the selected voltage vector is applied to the motor only for a portion of the control cycle [29,30,31,32,33]. This is achieved by defining the cost function in terms of the error in the stator current and optimizing it to determine the BVV, which is applied as the active voltage vector to the inverter. The duty ratio of the selected BVV is evaluated in such a way that the stator current is controlled according to DB control theory. Thus, only one BVV and one ZVV are applied to the motor. The performance of the controller can be improved by applying two BVVs with one ZVV. However, the computational complexity, computation time and parameter dependence increase since each BVV has to be determined separately. This limitation can be overcome by using an MPCC algorithm based on the current track circle [27] instead of a cost function.

In this paper, an advanced predictive current controller (APCC) based on DB control theory is presented. To avoid the complexity associated with selecting two BVVs and the calculation of two different time durations, the APCC synthesizes each of the voltage vectors through space vector pulse width modulation (SVPWM) using two voltage components along with one ZVV. The proposed technique reduces the computational complexity and improves the motor performance. The APCC technique is able to achieve improved performance of the PMSM drive under steady state and transient state operations with reduced computational complexity.

In the steady state, the root mean square (RMS) value of the stator current error is computed and used to derive the optimal voltage vector components along with the duration for which it has to be applied during the duty cycle. In the transient condition, the voltage vector having largest magnitude is applied for the entire duration of the control cycle. Furthermore, the phase of the voltage vector is precisely tuned to control the components of the stator current in the DB mode. The MTPA algorithm is used in the proposed APCC for the generation of the reference stator current. This improves the motor efficiency by: (a) reducing the copper losses; (b) reducing ripples in the torque and stator current under the steady state; and (c) achieving a fast-dynamic response during the transient state.

In addition to the Introduction and Conclusion, this paper has four more sections, viz, proposed APCC based on DB control theory in Sect. 2, implementation of the APCC based on DB control theory in Sect. 3, comparison of the proposed APCC with recent current controllers in Sect. 4, and results and discussions in Sect. 5.

2 Proposed APCC based on DB control theory

The main objectives of the proposed APCC based on DB control theory is to: (a) reduce the ripples in the stator current and torque under steady state operation and (b) achieve a fast-dynamic response during transient conditions. To effectively implement this technique, it is necessary to obtain the optimum voltage vector components of the BVV along with the duration for which it has to be applied during a control cycle.

2.1 Steady-state operation of a PMSM drive

The modeling equations of the PMSM in the rotor reference frame are

$${v}_{\mathrm{sd}}={R}_{s}{i}_{\mathrm{sd}}+{L}_{d}\frac{d}{dt}{i}_{\mathrm{sd}}-{\omega }_{r}{L}_{q}{i}_{\mathrm{sq}},$$
(1)
$${v}_{\mathrm{sq}}={R}_{s}{i}_{\mathrm{sq}}+{L}_{q}\frac{d}{dt}{i}_{\mathrm{sq}}+{\omega }_{r}({L}_{d}{i}_{\mathrm{sd}}+{\psi }_{m}),$$
(2)

where \({v}_{\mathrm{sd}}\) and \({v}_{\mathrm{sq}}\) are stator voltage vectors in the d–q axes, \({i}_{\mathrm{sd}}\) and \({i}_{\mathrm{sq}}\) are stator current vectors in the d–q axes, \({R}_{s}\) is stator resistance, \({L}_{d}\) and \({L}_{q}\) are the stator inductances in the d–q axes, \({\omega }_{r}\) is the rotor speed, and \({\psi }_{m}\) is the magnitude of the permanent magnet (PM) flux. The stator current components are derived from Eqs. (1) and (2) as

$${L}_{d}\frac{d}{dt}{i}_{\mathrm{sd}}={{v}_{\mathrm{sd}}-R}_{s}{i}_{\mathrm{sd}}+{\omega }_{r}{L}_{q}{i}_{\mathrm{sq}},$$
(3)
$${L}_{q}\frac{d}{dt}{i}_{\mathrm{sq}}={v}_{\mathrm{sq}}-{R}_{s}{i}_{\mathrm{sq}}-{\omega }_{r}({L}_{d}{i}_{\mathrm{sd}}+{\psi }_{m}).$$
(4)
  1. i.

    Representation of the stator current components in the discrete time mode:

    The stator current components are expressed in the discrete time mode for the digital implementation of the proposed controller as

    $$\Delta {i}_{\mathrm{sd}}=\frac{\Delta T}{{L}_{d}}({v}_{\mathrm{sd}}-{R}_{s}{i}_{\mathrm{sd}}+{\omega }_{r}{L}_{q}{i}_{\mathrm{sq}}),$$
    (5)
    $$\Delta {i}_{\mathrm{sq}}=\frac{\Delta T}{{L}_{q}}\left({v}_{\mathrm{sq}}-{R}_{s}{i}_{\mathrm{sq}}-{\omega }_{r}\left({L}_{d}{i}_{\mathrm{sd}}+{\psi }_{m}\right)\right).$$
    (6)

    Since \({i}_{\mathrm{sd}}\), \({i}_{\mathrm{sq}}\) and \({\omega }_{r}\) are measured for every cycle by controlling \({v}_{\mathrm{sd}}\) and \({v}_{\mathrm{sq}}\) in accordance with Eqs. (5) and (6), precise control of the stator current components is possible under the following assumptions. (a) \({T}_{s}\) is the control cycle period. (b) An arbitrary non zero voltage vector \(\overrightarrow{{v}_{s}^{*}}\) is applied to the motor for \({T}_{k}^{*}\), where \(\left({T}_{k}^{*} \le {T}_{s}\right)\) and (c) is a ZVV applied to the motor in the remaining control cycle. The stator current components of the motor are modified by applying \(\overrightarrow{{v}_{s}^{*}}\) and ZVV, and they are expressed as

    $$\Delta {i}_{\mathrm{sd}0} ={ S}_{d0}({T}_{s}-{T}_{k}^{*}),$$
    (7)
    $$\Delta {i}_{\mathrm{sq}0}={S}_{q0}({T}_{s}-{T}_{k}^{*}),$$
    (8)
    $$\Delta {i}_{\mathrm{sd}1}={\frac{{T}_{k}^{*}}{{L}_{d}}{v}_{\mathrm{sd}}^{*}+S}_{d0}{T}_{k}^{*},$$
    (9)
    $$\Delta {i}_{\mathrm{sq}1}= {\frac{{T}_{k}^{*}}{{L}_{q}}{v}_{\mathrm{sq}}^{*}+S}_{q0}{T}_{k}^{*},$$
    (10)
    $${S}_{d0}=\frac{1}{{L}_{d}}(-{R}_{s}{i}_{\mathrm{sd}}+{\omega }_{r}{L}_{q}{i}_{\mathrm{sq}}),$$
    (11)
    $${S}_{q0}=\frac{1}{{L}_{q}}\left(-{R}_{s}{i}_{\mathrm{sq}}-{\omega }_{r}\left({L}_{d}{i}_{\mathrm{sd}}+{\psi }_{m}\right)\right),$$
    (12)

    where \(\Delta {i}_{\mathrm{sd}0}\), \(\Delta {i}_{\mathrm{sq}0}\) and \(\Delta {i}_{\mathrm{sd}1}\), \(\Delta {i}_{\mathrm{sq}1}\) are the modified d–q axes current components when ZVV and \(\overrightarrow{{v}_{s}^{*}}\) are applied, respectively. For \({T}_{s}=\) 50 μs, all of the machine parameters remain constant. Hence, the slopes \({S}_{d0}\) and \({S}_{q0}\) are invariant within one control cycle. Accordingly, the modified stator current in every control cycle is derived as

    $${i}_{\mathrm{sd}}=\left\{\begin{array}{c}{i}_{\mathrm{sd}}\left(k\right)+\left(\frac{1}{{L}_{d}}{v}_{\mathrm{sd}}^{*}+{S}_{d0}\right)t 0\le t\le {T}_{k}^{*}\\ {i}_{\mathrm{sd}}\left(k\right)+\frac{{T}_{k}^{*}}{{L}_{d}}{v}_{\mathrm{sd}}^{*}+{S}_{d0}t {T}_{k}^{*}<t\le {T}_{s}\end{array}\right.,$$
    (13)
    $${i}_{\mathrm{sq}}=\left\{\begin{array}{c}{i}_{\mathrm{sq}}\left(k\right)+\left(\frac{1}{{L}_{q}}{v}_{\mathrm{sq}}^{*}+{S}_{q0}\right)t 0\le t\le {T}_{k}^{*}\\ {i}_{\mathrm{sq}}\left(k\right)+\frac{{T}_{k}^{*}}{{L}_{q}}{v}_{\mathrm{sq}}^{*}+{S}_{q0}t {T}_{k}^{*}<t\le {T}_{s}\end{array}\right.,$$
    (14)

    where \({i}_{\mathrm{sd}}\left(k\right)\) and \({i}_{\mathrm{sq}}\left(k\right)\) are the d–q axes stator current components in the kth control cycle.

  2. ii.

    Minimization of ripples in the stator current components:

    Generally, the performance of any signal that varies from its reference value is calculated using a RMS function [34]. The RMS value of the stator current error, \({i}_{{s}_{\mathrm{err}\left(\mathrm{RMS}\right)}}\), over one control cycle is expressed as

    $${\left|{i}_{{s}_{\mathrm{err}\left(\mathrm{RMS}\right)}}\right|}^{2}=\frac{1}{{T}_{s}}\underset{0}{\overset{{T}_{s}}{\int }}\left\{{\left({i}_{\mathrm{sd}}^{*}-{i}_{\mathrm{sd}}\right)}^{2}+{\left({i}_{\mathrm{sq}}^{*}-{i}_{\mathrm{sq}}\right)}^{2}\right\}dt,$$
    (15)

    where \({i}_{\mathrm{sd}}^{*}\) and \({i}_{\mathrm{sq}}^{*}\) are the reference stator currents in the d–q axes. Using Eqs. (13), (14) and (15) can be expressed as

    $${\left|{i}_{{s}_{\mathrm{err}\left(\mathrm{RMS}\right)}}\right|}^{2}= \frac{1}{{T}_{s}}\underset{0}{\overset{{T}_{k}}{\int }}\left\{{\left({i}_{{\mathrm{sd}}_{\mathrm{err}}}-\left(\frac{{v}_{\mathrm{sd}}^{*}}{{L}_{d}}+{S}_{d0}\right)t\right)}^{2}+{\left({i}_{{\mathrm{sq}}_{\mathrm{err}}}-\left(\frac{{v}_{\mathrm{sq}}^{*}}{{L}_{d}}+{S}_{q0}\right)t\right)}^{2}\right\}dt +\frac{1}{{T}_{s}}\underset{{T}_{k}}{\overset{{T}_{s}}{\int }}\left\{{\left({i}_{{\mathrm{sd}}_{\mathrm{err}}}-\frac{{T}_{k}^{*}}{{L}_{d}}{v}_{\mathrm{sd}}^{*}-{S}_{d0}t\right)}^{2}+{\left({i}_{{\mathrm{sq}}_{\mathrm{err}}}-\frac{{T}_{k}^{*}}{{L}_{d}}{v}_{\mathrm{sq}}^{*}-{S}_{q0}t\right)}^{2}\right\}dt,$$
    (16)

    where

    $${i}_{\mathrm{sd}\_\mathrm{err}}={i}_{\mathrm{sd}}^{*}-{i}_{\mathrm{sd}}(k),$$
    (17)
    $${i}_{\mathrm{sq}\_\mathrm{err}}={i}_{\mathrm{sq}}^{*}-{i}_{\mathrm{sq}}(k).$$
    (18)

    \({\left|{i}_{s\_\mathrm{err}(\mathrm{RMS})}\right|}^{2}\) is used as the objective function with the variables \({T}_{k}^{*}\), \({v}_{\mathrm{sd}}^{*}\), and \({v}_{\mathrm{sq}}^{*}\). An unconstrained optimization problem is introduced in Eq. (16) to reduce stator current ripples. It is solved to obtain the optimal voltage vector components and the optimal time duration as

    $${v}_{\mathrm{sd}}^{*}=\frac{{L}_{d}({i}_{\mathrm{s}{\mathrm{d}\_}_{\mathrm{err}}}-{S}_{d0}{T}_{s})}{{T}_{s}},$$
    (19)
    $${v}_{\mathrm{sq}}^{*}=\frac{{L}_{q}({i}_{\mathrm{s}{\mathrm{q}\_}_{\mathrm{err}}}-{S}_{q0}{T}_{s})}{{T}_{s}},$$
    (20)
    $${T}_{k}^{*}=\frac{{i}_{\mathrm{s}{\mathrm{d}\_}_{\mathrm{err}}}-{S}_{d0}{T}_{s}}{2{S}_{q1}-{S}_{q0}}+\frac{{i}_{\mathrm{s}{\mathrm{q}\_}_{\mathrm{err}}}-{S}_{q0}{T}_{s}}{2{S}_{d1}-{S}_{d0}},$$
    (21)

    where

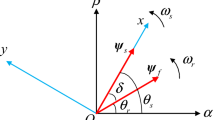
    $${S}_{d1}=\frac{1}{{L}_{d}}\left({v}_{\mathrm{sd}}^{*}-{R}_{s}{i}_{\mathrm{sd}}+{\omega }_{r}{L}_{q}{i}_{\mathrm{sq}}\right),$$
    (22)
    $${S}_{q1}=\frac{1}{{L}_{q}}\left({v}_{\mathrm{sq}}^{*}-{R}_{s}{i}_{\mathrm{sq}}+{\omega }_{r}{L}_{d}{i}_{\mathrm{sd}}\right).$$
    (23)

    These calculated values of \({v}_{\mathrm{sd}}^{*}\) and \({v}_{\mathrm{sq}}^{*}\) are transformed into the stationary reference frame, i.e. into the α–β axes, to obtain the voltage vectors components \({v}_{s\alpha }^{*}\) and \({v}_{s\beta }^{*}\). These voltage vector components and \({T}_{k}^{*}\) are applied to the SVPWM block, which computes the BVV that is applied to the motor for the duration \({T}_{k}^{*}\). The ZVV is applied for the remaining period of the control cycle.

2.2 Transient operation of the PMSM drive

In the transient state, the principle of the DB control theory is employed, which results in a fast dynamic response of the PMSM. At the end of each control cycle, the calculated stator current components of the motor track their commanded values. Accordingly, the optimal voltage vector components are obtained by solving

$$\left.\begin{array}{c}{{i}_{\mathrm{sd}}\left(k+1\right)=i}_{\mathrm{sd}}^{*}={i}_{\mathrm{sd}}\left(k\right)+\frac{{T}_{k}^{*}}{{L}_{d}}{v}_{\mathrm{sd}}^{*}+{S}_{d0}{T}_{s}\\ {i}_{\mathrm{sq}}\left(k+1\right)={i}_{\mathrm{sq}}^{*}={i}_{\mathrm{sq}}\left(k\right)+\frac{{T}_{k}^{*}}{{L}_{q}}{v}_{\mathrm{sq}}^{*}+{S}_{q0}{T}_{s}\end{array}\right\}.$$
(24)

Using Eq. (24) the optimal voltage vector components are expressed as

$${v}_{\mathrm{sd}}^{*}=\frac{{L}_{d}}{{T}_{k}^{*}}({i}_{{\mathrm{sd}}_{\mathrm{err}}}-{S}_{d0}{T}_{s}),$$
(25)
$${v}_{\mathrm{sq}}^{*}=\frac{{L}_{q}}{{T}_{k}^{*}}({i}_{{\mathrm{sq}}_{\mathrm{err}}}-{S}_{q0}{T}_{s}).$$
(26)

A fast dynamic response under the transient state is achieved when voltage vector having the largest magnitude computed using Eqs. (25) and (26) is applied to the motor for the entire duration of the control cycle. In other words, \({T}_{k}^{*}\) and \(\overrightarrow{{v}_{s}^{*}}\) must be adjusted to \({T}_{s}\) and \({V}_{\mathrm{max}}\), respectively, where \({V}_{\mathrm{max}}\) is the voltage vector with the largest magnitude in the linear region of SVPWM. The phase of the voltage vector with respect to the d-axis of the rotor reference frame is obtained from Eqs. (25) and (26) as

$${\theta }_{s}^{*}={\mathrm{tan}}^{-1}\left(\frac{{L}_{q}\left({i}_{\mathrm{sd}\_\mathrm{err}}-{S}_{d0}{T}_{s}\right)}{{L}_{d}\left({i}_{\mathrm{sq}\_\mathrm{err}}-{S}_{q0}{T}_{s}\right)}\right).$$
(27)

Applying this voltage vector for the entire duration of the control cycle appreciably improves the dynamic response of the motor.

3 Implementation of the APCC based on DB control theory

The proposed APCC is implemented on a PMSM with the specifications given in Table 1. Even though the implementation of over modulation is simpler and it allows for better utilization of the DC input voltage, it results in a highly distorted non-sinusoidal output voltage and its associated high stator current harmonics. Therefore, the operation of the SVPWM in the over modulation region has been avoided in the proposed APCC.

Table 1 Technical specifications of a 3.4 kW PMSM drive
Full size table

To avoid operation in the over modulation region, the magnitude of the voltage vector has to be restricted to \({v}_{\mathrm{max}}\), and \({T}_{k}^{*}\) has to be restricted to \({T}_{s}\). For the steady state

$$\frac{{T}_{k}^{*}\left|\overrightarrow{{v}_{s}^{*}}\right|}{{T}_{s}}\le {v}_{\mathrm{max}},$$
(28)

and for the transient state:

$$\frac{{T}_{k}^{*}\left|\overrightarrow{{v}_{s}^{*}}\right|}{{T}_{s}}>{v}_{\mathrm{max}}.$$
(29)

Figures 1 and 2 show the flow chart and the block diagram of the proposed APCC, respectively. A PI controller is used to obtain the torque command, \({T}_{e}^{*}\), which is used by the MTPA block to generate the quadrature and direct axes stator currents, i.e. \({i}_{\mathrm{sd}}^{*}\) and \({i}_{\mathrm{sq}}^{*}\), using the rotor speed.

Fig. 1
figure 1

Flow chart of the proposed APCC

Full size image
Fig. 2
figure 2

Block diagram of the proposed APCC

Full size image

These current components are processed in the APCC to obtain the optimum voltage vector components, \({v}_{\mathrm{sd}}^{*}\) and \({v}_{\mathrm{sq}}^{*}\), which are then transformed to the stationery reference frame before being fed into the SVPWM to produce the required gating pulses for the inverter. A MTPA algorithm is used to generate stator reference currents in the d–q axes. The maximum torque can be achieved in a surface mounted PMSM by using the zero d-axis current and q-axis stator current, which are computed using

$${i}_{\mathrm{sd}\_\mathrm{mtpa}}=0,$$
(30)
$${i}_{\mathrm{sq}\_\mathrm{mtpa}}=\frac{{T}^{*}}{\frac{3}{2}.P.{\psi }_{m}},$$
(31)
$${i}_{\mathrm{sd}\_\mathrm{sat}}={i}_{\mathrm{sd}\_\mathrm{mtpa}}=0,$$
(32)
$${i}_{\mathrm{sq}\_\mathrm{sat}}=\mathrm{sat}({i}_{{\mathrm{sq}}_{\mathrm{mtpa}}}, {i}_{\mathrm{max}}),$$
(33)
$${i}_{\mathrm{max}}\ge \sqrt{{i}_{\mathrm{sd}}^{2}+{i}_{\mathrm{sq}}^{2}},$$
(34)

where \({i}_{\mathrm{sd}\_\mathrm{mtpa}}\) and \({i}_{\mathrm{sq}\_\mathrm{mtpa}}\) are the d–q axes currents corresponding to the MTPA, \({i}_{\mathrm{sd}\_\mathrm{sat}}\, { \mathrm{and}\, i}_{\mathrm{sq}\_\mathrm{sat}}\) are the d–q axes saturation currents, \({i}_{\mathrm{max}}\) is the maximum phase current, and \({i}_{\mathrm{sd}}^{*}\, \mathrm{and }\,{i}_{\mathrm{sq}}^{*}\) are the reference currents corresponding to the reference torque T*. The stator reference currents in the d–q axes are

$${i}_{\mathrm{sd}}^{*}={i}_{\mathrm{sd}\_\mathrm{sat}},$$
(35)
$${i}_{\mathrm{sq}}^{*}={i}_{\mathrm{sq}\_\mathrm{sat}}.$$
(36)

4 Comparison of the proposed APCC with recent current controllers

The merits and demerits of the proposed controller in comparison with the controllers implemented in [24] and [30] are briefly discussed in this section.

4.1 Comparison of the APCC with hysteresis-based direct current controller (DCC)

In DCC [24], the cost function is defined by a RMS function of the torque ripples and the control of the stator flux is considered to be a constraint. The optimization problem to find the optimal voltage vector components is solved using the Lagrange–Multiplier method. Table 2 summarizes a comparison between the controller implemented in [24] and the APCC.

Table 2 Comparison between the DCC and the proposed APCC
Full size table

4.2 Comparison of the APCC with the duty MPCC

In the duty MPCC [30], a BVV and a ZVV are applied to a PMSM in each control cycle. In this technique the BVV is selected by applying two approaches. In the first approach, the cost value of all the accessible voltage vectors is defined to find the lowest value voltage vector, and the DB control of the stator current is attained by defining the time duration for the selected voltage vector.

In the second approach, the theoretical optimum voltage vector is selected through DB control of the stator current, and the voltage vector closest to the theoretical optimal voltage vector is selected as the BVV. The error of the selected BVV and theoretical optimum voltage vector are minimized by calculating the time period of the voltage vector. Table 3 shows a comparison between the duty MPCC and the proposed APCC.

Table 3 Comparison between the duty MPCC and the proposed APCC
Full size table

5 Results and discussion

The performance of the PMSM drive, with the specifications given in Table 1, is investigated using the APCC under different operating conditions through simulation studies. The performance of a motor using the proposed controller is also compared with the performance of the traditional hysteresis-based DCC and the duty MPCC. The sampling time for the APCC is set at 50 μs. In the hysteresis based DCC, the bandwidth of the hysteresis controller is adjusted to zero to achieve the minimum stator current ripples. Only the important characteristics of the control algorithms are considered in the comparative analysis by neglecting non-idealities such as dead time in the inverter switches, saturation in the motor-core, etc.

5.1 Starting response of a PMSM for rated speed operation

The starting responses of a PMSM drive under no load and the rated speed are shown in Fig. 3 using the DCC, the duty MPCC and the APCC. Since a PI controller is used to regulate the speed of the PMSM, there is no overshoot. It is observed that the speed, torque and stator current response for the three controllers are similar without any appreciable steady state error or overshoot in the motor speed or torque. The torque response of the drive under rated torque operation is given in Fig. 4. It is observed that the dynamic response of the APCC method is faster than that of the other two methods having minimum settling and rise times as presented in Table 4.

Fig. 3
figure 3

No load speed, torque and current characteristics of a PMSM: a DCC; b duty MPCC; c APCC

Full size image
Fig. 4
figure 4

Torque characteristics of a PMSM under rated-torque operation: a DCC; b duty MPCC; c APCC

Full size image
Table 4 Settling and rising times of the torque response
Full size table

5.2 Total harmonic distortion (THD) in stator currents

Figures 5 and 6 represent the harmonic spectrum of the stator currents at 3000 rpm and 300 rpm, respectively. The stator current ripples and THD are lower if the switching frequency is high. The average switching frequency for all of the methods are kept the same for the comparative analysis. In the simulation analysis, the average switching frequencies of the DCC, the duty MPCC and the proposed APCC are kept constant at 7.5 kHz for operating speeds of 3000 rpm and 300 rpm. The THD is analyzed up to 6 kHz.

Fig. 5
figure 5

Harmonic spectrum at 3000 rpm: a DCC; b duty MPCC; c APCC

Full size image
Fig. 6
figure 6

Harmonic spectrum at 300 rpm: a DCC; b duty MPCC; c APCC

Full size image

Figure 7 shows the THD in the stator current of a PMSM using the DCC, the duty MPCC and the APCC at different operating speeds of the motor, i.e. 300 rpm and 3000 rpm. It is observed that the THD in the stator current with the APCC is the lowest when compared with the DCC and the duty MPCC.

Fig. 7
figure 7

Comparison of the THD in the stator current with the DCC, the duty MPCC, and the APCC

Full size image

5.3 Steady-state performance of a PMSM

The zoomed steady state performance of the motor under its rated speed and rated torque operation is shown in Fig. 8. The stator current ripples are 0.28%, 0.14% and 0.07% in the DCC, the Duty MPCC and the APCC, respectively. In addition, the torque ripples are 0.27%, 0.13% and 0.09% in the DCC, the Duty MPCC and the APCC, respectively. The lowest torque and stator current ripples are achieved with the APCC. The ripples in stator current and motor torque are calculated as a percentage of the difference between the maximum value \({X}_{\mathrm{max}}\) and the minimum value \({X}_{\mathrm{min}}\) when compared to the average value \({X}_{\mathrm{avg}}\). Where X can be the stator current or the motor torque. Figure 9 shows a comparison of the ripples in the stator current and torque in a PMSM with the DCC, the duty MPCC and the APCC. It is noted that the APCC has the lowest stator current and torque ripples.

Fig. 8
figure 8

Torque and stator current of the PMSM at its rated-speed and rated-torque operation: a DCC; b duty MPCC; c APCC

Full size image
Fig. 9
figure 9

Stator current and torque ripples in a PMSM with the DCC, the duty MPCC, and the APCC

Full size image

6 Conclusion

In this paper, an advanced predictive current controller based on DB control theory is presented, which reduces the ripples in the stator current and torque by optimization of the voltage vector components and the time for applying this voltage vector to the PMSM drive. An unconstrained optimization problem is solved, which reduces the computational complexity.

The proposed method employs a novel approach to calculate the stator current references of a PMSM using MTPA control, which reduces the copper loss. During the transient state, the voltage vector with the largest value is applied to the motor for the complete duration of the control cycle. The stator current components are controlled in a deadbeat manner. Thus, at the end of each control cycle, the phase of the voltage vector component is adjusted in such a way that the stator current error is reduced to zero.

Both the steady state and transient operations of the proposed APCC based on DB control theory are analyzed through simulation studies using MATLAB/Simulink. It is observed that when compared to some of the recently reported predictive current controllers, the proposed APCC controller has several advantages. (a) It provides better torque dynamics; (b) has significantly less THD in the stator current; (c) has less ripples in the stator current and torque; and (d) reduces the computational complexity. Thus, he proposed APCC controller based on DB control theory is a useful alternative to other contemporary predictive current controllers.