Geometry of spaces of homogeneous trinomials on ${\mathbb {R}}^2$

Abstract

For each pair of numbers $m,n\in {{\mathbb {N}}}$ with $m>n$, we consider the norm on ${{\mathbb {R}}}^3$ given by $\Vert (a,b,c)\Vert _{m,n}=\sup \{|ax^m+bx^{m-n}y^n+cy^m|:x,y\in [-1,1]\}$ for every $(a,b,c)\in {{\mathbb {R}}}^3$. We investigate some geometrical properties of these norms. We provide an explicit formula for $\Vert \cdot \Vert _{m,n}$, a full description of the extreme points of the corresponding unit balls and a parametrization and a plot of their unit spheres for certain values of m and n.

1 Introduction and notation

The Krein–Milman Theorem is a fundamental result in Functional Analysis. Essentially, the Krein–Milman Theorem states that any convex body (a compact, convex, nonempty set) in a Banach space can be characterized by its extreme points. Let us recall that, given a convex body C in a Banach space, a point $e \in C$ is said to be extreme if $x, y \in C$ and $\lambda x + (1 - \lambda ) y = e$, for some $0< \lambda < 1$, entails $x=y=e$. Equivalently, $e \in C$ is extreme if and only if $C {\setminus} \{e\}$ is convex.

In the last few years a considerable effort has been made in order to determine the extreme points of the unit ball of several polynomial spaces (see for instance [5,6,7,8,9,10, 12,13,14,15,16,17,18,19, 22,23,24, 26,27,29, 31, 32, 36, 37]). A particularly interesting work as far as this paper is concerned is [36], where the authors study the geometry of the spaces of trinomials on the real line with independent term. Being more specific, if ${{\mathcal {P}}}_{m,n}({{\mathbb {R}}})$ denotes the 3-dimensional space of polynomials of the form $ax^m+bx^n+c$ with $m,n\in {{\mathbb {N}}}$, $m>n$ and $a,b,c\in {{\mathbb {R}}}$, in [36] the authors give a full characterization of the extreme points of the unit ball of ${{\mathcal {P}}}_{m,n}({{\mathbb {R}}})$ endowed with the sup norm on the unit interval $[-1,1]$. All possible choices of $m,n\in {{\mathbb {N}}}$ with $m>n$ are studied. Using the natural identification of ${{\mathcal {P}}}_{m,n}({{\mathbb {R}}})$ with ${{\mathbb {R}}}^3$ through the mapping ${{\mathcal {P}}}_{m,n}({{\mathbb {R}}})\ni ax^m+bx^n+c\mapsto (a,b,c)\in {{\mathbb {R}}}^3$, what we have in fact is a geometrical problem in ${{\mathbb {R}}}^3$, namely, the characterization of the extreme points of the unit ball of ${{\mathbb {R}}}^3$ with the norm $\Vert \cdot \Vert _{m,n}$ ($m>n$), where

$$\begin{aligned} \Vert (a,b,c)\Vert _{m,n}{:}{=}\sup \{|ax^m+bx^n+c|:x\in [-1,1]\}. \end{aligned}$$

Observe that the norm $\Vert \cdot \Vert _{m,n}$ with $m=2$ and $n=1$ had already been studied by Aron and Klimek in [5], providing a full description of the extreme points in the unit ball of $\Vert \cdot \Vert _{2,1}$, among other interesting results. In [5] the norm $\Vert \cdot \Vert _{2,1}$ is denoted by $\Vert \cdot \Vert _{{\mathbb {R}}}$. Aron and Klimek also studied the norm in ${{\mathbb {R}}}^3$ defined by

$$\begin{aligned} \Vert (a,b,c)\Vert _{{\mathbb {C}}}=\sup \{|az^2+bz+c|:z\in {{\mathbb {D}}}\}, \end{aligned}$$

where ${{\mathbb {D}}}$ is the unit disk in ${{\mathbb {C}}}$ and $a,b,c\in {{\mathbb {R}}}$.

The study of non-absolute norms in ${{\mathbb {R}}}^3$ is among the motivations of Aron and Klimek’s work. Recall that a norm $\Vert \cdot \Vert$ in ${{\mathbb {R}}}^3$ is absolute if the following two conditions are satisfied:

• 1. $\Vert (a,b,c)\Vert =\Vert (|a|,|b|,|c|)\Vert$ for all $(a,b,c)\in {{\mathbb {R}}}^3$.

• 2. If $|a_1|\le |a_2|$, $|b_1|\le |b_2|$ and $|c_1|\le |c_2|$, then $\Vert (a_1,b_1,c_1)\Vert \le \Vert (a_2,b_2,c_2)\Vert$.

Whereas the classical $\ell _p$-norms are clearly absolute in ${{\mathbb {R}}}^3$, it can be proved that the norms $\Vert \cdot \Vert _{{\mathbb {R}}}$ and $\Vert \cdot \Vert _{{\mathbb {C}}}$ are not absolute [5].

In this paper we present a highly non-trivial extension of the results obtained in [5, 36] to study the geometry of the space of homogeneous trinomials defined on ${{\mathbb {R}}}^2$ endowed with the supremum norm over the unit square $[-1,1]^2$. We represent this space by ${{\mathcal {P}}}_{m,n}({{\mathbb {R}}}^2)$ with $m,n\in {{\mathbb {N}}}$ and $m>n$. Observe that a typical element P of ${{\mathcal {P}}}_{m,n}({{\mathbb {R}}}^2)$ has the form

$$\begin{aligned} P(x,y)= ax^m+bx^{m-n}y^n+cy^m, \end{aligned}$$

and its norm is given by

$$\begin{aligned} {\left| \!\left| \!\left| P \right| \!\right| \!\right| }_{m,n}=\sup \{|P(x,y)|:(x,y)\in [-1,1]^2\}. \end{aligned}$$

We will mainly use the representation of P as an element of ${{\mathbb {R}}}^3$ given by the coordinates of P in the basis $\{x^m,x^{m-n}y^n,y^m\}$, that is (a, b, c). Therefore we will study the geometry of the unit ball of ${{\mathbb {R}}}^3$ endowed with the norm

$$\begin{aligned} {\left| \!\left| \!\left| (a,b,c) \right| \!\right| \!\right| }_{m,n}=\sup \{|ax^m+bx^{m-n}y^n+cy^m|:(x,y)\in [-1,1]^2\}. \end{aligned}$$

Notice that the norms $\Vert \cdot \Vert _{m,n}$ and ${\left| \!\left| \!\left| \cdot \right| \!\right| \!\right| }_{m,n}$ are just a modification of Aron and Klimek’s norm $\Vert \cdot \Vert _{{\mathbb {R}}}$. Hence, it is no wonder they are not absolute either.

In [36] the authors denoted the unit sphere and unit ball of $({\mathbb {R}}^3,\Vert \cdot \Vert _{m,n})$ by ${\mathsf {S}}_{m,n}$ and ${\mathsf {B}}_{m,n}$ respectively. In order to be consistent with this notation, in this paper ${\mathsf {S}}^h_{m,n}$ and ${\mathsf {B}}^h_{m,n}$ will denote, respectively, the unit sphere and the unit ball of the space $({\mathbb {R}}^3,{\left| \!\left| \!\left| \cdot \right| \!\right| \!\right| }_{m,n})$ (observe that h stands here for homogeneity).

The study of the geometry of ${{\mathsf {B}}}_{m,n}$ depends strongly on whether m and n are even or odd. As a matter of fact, each of the four possible choices of the parity of m and n requires a specific treatment (see [36]). Notice that, by homogeneity and symmetry, the elements of ${{\mathcal {P}}}_{m,n}({{\mathbb {R}}}^2)$ attain their norm on the set $\{(1,y),(x,1):x,y\in [-1,1]\}$. Hence

$$\begin{aligned} {\left| \!\left| \!\left| (a,b,c) \right| \!\right| \!\right| }_{m,n}=\max \{\Vert (a,b,c)\Vert _{m,m-n},\Vert (c,b,a)\Vert _{m,n}\}, \end{aligned}$$

for every $(a,b,c)\in {{\mathbb {R}}}^3$. Using the previous identity, a moment’s thought reveals that

$$\begin{aligned} {\left| \!\left| \!\left| (a,b,c) \right| \!\right| \!\right| }_{m,n}={\left| \!\left| \!\left| (c,b,a) \right| \!\right| \!\right| }_{m,m-n}, \end{aligned}$$

(1)

for all $(a,b,c)\in {{\mathbb {R}}}^3$. The identity (1) allows us to simplify the casuistic of the study of the geometry of ${{\mathsf {B}}}^h_{m,n}$, at least when m is odd since the case m and n odd can be reduced to the case m odd and n even by swapping a and c on the one hand, and n and $m-n$ on the other.

If C is a convex body, ${{\mathrm{ext}}}\,(C)$ will denote the set of extreme points of C. Also, $\pi _{ab}$ (respectively $\pi _{ac}$) will denote the linear projection given by $\pi _{ab}(a,b,c)=(a,b)$ (respectively $\pi _{ac}(a,b,c)=(a,c)$), for every $(a,b,c)\in {{\mathbb {R}}}^3$. The plots of the unit spheres and their projections appearing in this paper were produced using MATLAB. All graphs presented here are scaled.

The geometrical structure of the unit ball of a polynomial space, and more particularly, the extreme points of its unit ball, have been used systematically in the past in order to obtain sharp polynomial inequalities. Indeed, an elementary application of the Krein–Milman Theorem together with a full description of the extreme points of the unit ball of a Banach space of polynomials may produce sharp Bernstein–Markov type inequalities [2, 4, 21, 33,34,35], sharp polynomial Bohnenblust–Hille inequalities [11, 20, 30], exact values of polarization constants and unconditional constants [19, 25, 32] and many other polynomial inequalities of interest (see for instance [1, 3]).

The rest of the paper is arranged as follows: Sect. 2 is devoted to the study of the geometry of ${{\mathsf {B}}}_{m,n}^h$ for m even. This case is particularly difficult to study for most choices of n since it often requires solving polynomial equations of arbitrary degree with no explicit solution. However it is possible to give an explicit description of the geometry of ${{\mathsf {B}}}_{m,n}^h$ if $m=2n$. The study of ${{\mathsf {B}}}_{2n,n}^h$ when n is odd is tightly related to the spaces ${{\mathcal {P}}}(^2\ell _1^2)$ and ${{\mathcal {P}}}(^2\ell _\infty ^2)$, whose geometry has been already characterized in [10]. The case when $m=2n$ and n is even is also closely related to the space of 2-homogeneous polynomials in ${{\mathbb {R}}}^2$ endowed with the sup norm over the square $[0,1]^2$, or simply ${{\mathcal {P}}}(^2\square )$. The latter space has already been studied in [12]. In Sect. 3 we study ${\mathsf B}_{m,n}^h$ for m odd. In this case an explicit description of both ${{\mathsf {S}}}_{m,n}^h$ and the extreme points of ${\mathsf B}_{m,n}^h$ can be obtained for all choices of n. Whether n is even or odd is not really relevant in our study. However, the cases $m/2<2$ and $m/n>2$ do require a slightly different approach.

2 The geometry of the spaces ${{\mathcal {P}}}(^2\ell _1^2)$, ${{\mathcal {P}}}(^2\ell _\infty ^2)$ and ${{\mathcal {P}}}_{2n,n}({\mathbb {R}}^2)$ for arbitrary n

In general it will not be possible to describe explicitly the extreme points of ${{\mathsf {B}}}_{m,n}^h$ when m is even. However a wise choice of m and n may allow us to obtain explicit results. In this section we will consider the case $m=2n$ for $n\in {\mathbb N}$. Observe that ${{\mathcal {P}}}_{2,1}({{\mathbb {R}}}^2)$ is nothing but ${{\mathcal {P}}}(^2\ell _\infty ^2)$. On the other hand, the latter space has essentially been studied in [10], where the authors characterized the polynomials P that belong to the unit sphere of ${\mathcal {P}}(^2 \ell _1^2)$ and also the polynomials P that are extreme in ${{\mathsf {B}}}_{{{\mathcal {P}}}(^2\ell ^2_1)}$.

Theorem 2.1

[10] A polynomial $P(x,y)=ax^2+bxy+cy^2$ belongs to ${\mathsf {S}}_{\mathcal P(^2 \ell _1^2)}$ if and only if P satisfies one of the following conditions:

• (a) If $|b|\le 2,$ then $|a|=1$ or $|c|=1$.

• (b) If $|a|<1,$ $|c|<1$ and $2<|b|\le 4,$ then $4|b|-b^2=2(|a+c|-ac)$.

Furthermore, P is an extreme point if and only if $|a|=|c|=1$ and $|b|=2$ or $a=-c,$ $2<|b|\le 4$ and $4a^2=4|b|-b^2$.

Using the fact that the real versions of $\ell _1^2$ and $\ell _\infty ^2$ are isometric it follows straightforwardly that ${{\mathcal {P}}}(^2\ell _1^2)$ and ${{\mathcal {P}}}(^2\ell _\infty ^2)$ are isometric as well. The reader can check as a simple exercise that the matrix

$$\begin{aligned} \Upsilon =\left( \begin{array}{rrr} 1&{}1&{}1\\ -2&{}0&{}2\\ 1&{}-1&{}1 \end{array} \right) , \end{aligned}$$

defines an isometry between ${{\mathcal {P}}}(^2\ell _1^2)$ and ${{\mathcal {P}}}(^2\ell _\infty ^2)$, which combined with Theorem 2.1 yields the following characterization of the extreme points of ${{\mathsf {B}}}_{{{\mathcal {P}}}(^2\ell ^2_\infty )}$:

Theorem 2.2

[7] The extreme points of ${{\mathsf {B}}}_{{{\mathcal {P}}}(^2\ell ^2_\infty )}$ are

$$\begin{aligned} \pm x^2,\ \pm y^2\text{ and } \pm \left( ax^2-ay^2\pm 2\sqrt{a(1-a)}xy\right) \quad \text{for } a\in [1/2,1]. \end{aligned}$$

A parametrization of ${{\mathsf {S}}}_{{{\mathcal {P}}}(^2\ell _1^2)}$ is provided below omitting the easy proofs. First notice that the projection of ${{\mathsf {S}}}_{{{\mathcal {P}}}(^2\ell _1^2)}$ over the ac-plane is given by

$$\begin{aligned} \pi _{ac}({{\mathsf {S}}}_{{{\mathcal {P}}}(^2\ell _1^2)})=J\cup K=[-1,1]^2, \end{aligned}$$

(2)

where

$$\begin{aligned} J&= \left\{ (x,y)\in [-1,1]^2 : y\le -x \right\} ,\\ K&= \left\{ (x,y)\in [-1,1]^2 : y\ge -x \right\} . \end{aligned}$$

Also, define

$$\begin{aligned} H(a,c)={\left\{ \begin{array}{ll} 2\left( 1+\sqrt{(1+a)(1+c)} \right) &{} \text{if } (a,c)\in J,\\ 2\left( 1+\sqrt{(1-a)(1-c)} \right) &{} \text{if } (a,c)\in K, \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} \Omega =\left\{ (a,b,c)\in {\mathbb {R}}^3 : ((|a|=1 \text{ and } |c|\le 1) \text{ or } (|c|=1 \text{ and } |a|\le 1))\ \text{and}\ |b|\le 2 \right\} . \end{aligned}$$

Then

$$\begin{aligned} {\mathsf {S}}_{{\mathcal {P}}(^2 \ell _1^2)}={{\,\mathrm{graph\,\!}\,}}(H)\cup {{\,\mathrm{graph\,\!}\,}}(-H)\cup \Omega . \end{aligned}$$

(3)

A sketch of ${\mathsf {S}}_{{\mathcal {P}}(^2 \ell _1^2)}$ can be seen in Fig. 1.

Fig. 1

Sketch of ${{\mathsf {S}}}_{{{\mathcal {P}}}(^2\ell _1^2)}$. The extreme points appear with a thicker line or big dots. The surfaces that form ${{\mathsf {S}}}_{{{\mathcal {P}}}(^2\ell _1^2)}$ are delimited by thin lines

2.1 ${{\mathcal {P}}}_{2n,n}({{\mathbb {R}}}^2)$ when n is odd

Observe that

$$\begin{aligned}{}[-1,1]^2\ni (x,y)\mapsto R(x,y)=(x^n,y^n)\in [-1,1]^2 \end{aligned}$$

(4)

is a bijection. Thus, for every $ax^{2n}+bx^ny^n+cy^{2n}\in {\mathcal {P}}_{2n,n}({{\mathbb {R}}}^2)$ we have

$$\begin{aligned} {\left| \!\left| \!\left| ax^{2n}+bx^ny^n+cy^{2n} \right| \!\right| \!\right| }_{2n,n}={\left| \!\left| \!\left| ax^{2}+bxy+cy^{2} \right| \!\right| \!\right| }_{2,1}. \end{aligned}$$

In other words, whenever n is odd, ${{\mathcal {P}}}_{2n,n}({{\mathbb {R}}}^2)$ is nothing but ${{\mathcal {P}}}_{2,1}({{\mathbb {R}}}^2)={\mathcal {P}}(^2\ell _\infty ^2)$. Using the previous comments and the isometry existing between ${{\mathcal {P}}}(^2\ell _1^2)$ and ${\mathcal {P}}(^2\ell _\infty ^2)$, it is just a simple exercise to obtain a characterization of the extreme points in ${{\mathsf {B}}}^h_{2n,n}$ whenever n is odd. We can even provide a parametrization of ${{\mathsf {S}}}^h_{2n,n}$, for which some definitions will be helpful. Consider the sets A, B, C, D and E defined by:

$$\begin{aligned} A&=\left\{ (a,c)\in {\mathbb {R}}^2 : 0<-a\le c\le 1\text{ and } c>a+1 \right\} ,\\ B&=\left\{ (a,c)\in {\mathbb {R}}^2 : a+1<c<-a\le 1 \right\} ,\\ C&=\left\{ (a,c)\in {\mathbb {R}}^2 : c\le a+1,\ c\le 1-a,\ c\ge -1-a \text{ and } c\ge a-1 \right\} ,\\ D&=\left\{ (a,c)\in {\mathbb {R}}^2 : -1<-a<c<a-1 \right\} ,\\ E&=\left\{ (a,c)\in {\mathbb {R}}^2 : -1\le c<a-1 \text{ and } c\le -a \right\} . \end{aligned}$$

Now, applying $\Upsilon$ to (2) and (3) we have:

Theorem 2.3

$\pi _{ac}({\mathsf {B}}_{2n,n}^h)=A\cup B\cup C\cup D\cup E$ (see Fig. 2).

Fig. 2

Projection of the unit ball of ${{\mathcal {P}}}_{2n,n}({\mathbb {R}}^2)$ for $n\in {\mathbb {N}}$ odd over the ac-plane

Theorem 2.4

Let F be the mapping defined on $\pi _{ac}({{\mathsf {B}}}_{2n,n}^h)$ by

$$\begin{aligned} F(a,c)=\left\{ \begin{array}{ll} 2\sqrt{a(c-1)}&{}\quad \text{if }(a,c)\in A,\\ 2\sqrt{c(a+1)}&{}\quad \text{if }(a,c)\in B,\\ 1-|a+c|&{}\quad \text{if }(a,c)\in C,\\ 2\sqrt{c(a-1)}&{}\quad \text{if }(a,c)\in D,\\ 2\sqrt{a(c+1)}&{}\quad \text{if }(a,c)\in E. \end{array}\right. \end{aligned}$$

Then,

• (a) ${{\mathsf {S}}}_{2n,n}^h={{\,\mathrm{graph\,\!}\,}}(F)\cup {{\,\mathrm{graph\,\!}\,}}(-F)$ (see Fig. 3for a sketch of ${{\mathsf {S}}}_{2n,n}^h).$

• (b)
  $$\begin{aligned} {{\,\mathrm{ext\,\!}\,}}\left( {{\mathsf {B}}}^h_{2n,n}\right)&=\left\{ \pm \left( t,\pm 2\sqrt{t(1-t)},-t\right) :t\in \left[ -1,-\frac{1}{2}\right] \right\} \\ &\quad \cup \{\left( \pm 1,0,0\right) ,\left( 0,0,\pm 1\right) \}. \end{aligned}$$

The proofs of Theorems 2.3 and 2.4 may be tedious, but are quite mechanical, for which reason we spare the details.

Fig. 3

Sketch of the unit sphere of ${{\mathcal {P}}}_{2n,n}({\mathbb {R}}^2)$ for $n\in {\mathbb {N}}$ odd. The extreme points appear with a thicker line or big dots. The surfaces that form ${\mathcal {P}}_{2n,n}({\mathbb {R}}^2)$ are delimited by thin lines

2.2 ${{\mathcal {P}}}_{2n,n}({{\mathbb {R}}}^2)$ when n is even

The function R considered in (4) is no longer a bijection if n is even. In fact R maps $[-1,1]^2$ onto $[0,1]^2$ whenever n is even. Thus

$$\begin{aligned} {\left| \!\left| \!\left| (a,b,c) \right| \!\right| \!\right| }_{2n,n}&=\sup \{|ax^{2n}+bx^ny^n+cy^{2n}|:(x,y)\in [-1,1]^2\}\\ &=\sup \{|ax^{2}+bxy+cy^{2}|:(x,y)\in [0,1]^2\}. \end{aligned}$$

In other words, ${{\mathcal {P}}}_{2n,n}({{\mathbb {R}}}^2)$ coincides with the space ${\mathcal {P}}(^2 \square )$ of the 2-homogeneous polynomials on ${{\mathbb {R}}}^2$ endowed with the sup-norm on the square $\square =[0,1]^2$. The geometry of the space ${\mathcal {P}}(^2 \square )$ has already been studied in [12]. We will just reproduce the main results in [12] for the sake of completeness.

Fig. 4

Projection of the unit ball of ${{\mathcal {P}}}(\square ^2)$ over the ac-plane

Theorem 2.5

[12] If for every $(a,c)\in [-1,1]^2$ we define the mappings

$$\begin{aligned} F_s(a,c)&=\left\{ \begin{array}{ll} 2\sqrt{ac+|a|}&{}\quad \text{if }(a,c)\in A_s,\\ 2\sqrt{ac+|c|}&{}\quad \text{if }(a,c)\in C_s,\\ 1-a-c &{} \quad \text{if }(a,c)\in B_s, \end{array}\right. \\ G_s(a,c)&=-F_s(-a,-c), \end{aligned}$$

where $A_s,$ $B_s$ and $C_s$ are as in Fig. 4and the set

$$\begin{aligned} H_s=\{(a,b,c)\in {{\mathbb {R}}}^3:(a,c)\in \partial [-1,1]^2\text{ and } G_s(a,c)\le b\le F_s(a,c)\}, \end{aligned}$$

then

• (a) ${{\mathsf {S}}}_\square ={{\,\mathrm{graph\,\!}\,}}(F_s)\cup {{\,\mathrm{graph\,\!}\,}}(G_s)\cup H_s$ (see Fig. 5).

• (b) The extreme points of ${{\mathsf {B}}}_\square$ have the form

  $$\begin{aligned} \pm \left(t,2\sqrt{1-t},-1\right)\quad \text{and}\quad \pm \left(-1,2\sqrt{1-t},t\right)\qquad \text{with}\ t\in [0,1] \end{aligned}$$

  or

  $$\begin{aligned} \pm (1,-1,1),\ \pm (1-3,1),\ \pm (1,0,0),\ \pm (0,0,1). \end{aligned}$$

Fig. 5

Sketch of ${{\mathsf {S}}}_{2n,n}^h$ with n even. The extreme points are depicted with a thicker line, or isolated dots. The different surfaces that form ${{\mathsf {S}}}_{2n,n}^h$ are delimited by thin lines

3 The geometry of the space $({{\mathbb {R}}}^3,{\left| \!\left| \!\left| \cdot \right| \!\right| \!\right| }_{m,n})$ for m odd

It was pointed out in the introduction that the case m and n odd can be reduced to the case m odd and n even by applying (1). This allows us to focus our attention on the case m odd and n even. First, for completeness we reproduce a technical result that appears in [36]:

Lemma 3.1

If $m,n\in {{\mathbb {N}}}$ are such that $m>n$ then the equation

$$\begin{aligned} |n+mx|=(m-n)|x|^\frac{m}{m-n} \end{aligned}$$

has only three roots, one at $x=-1,$ another one at a point $\lambda _0\in (-\frac{n}{m},0)$ and a third one at a point $\lambda _1>0$. In addition to that we have

$$\begin{aligned} |n+mx|< (m-n)|x|^\frac{m}{m-n}, \end{aligned}$$

(5)

if and only if $x<\lambda _0$ or $x > \lambda _1$.

Remark 3.2

The dependence of $\lambda _0$ on m and n justifies the notation $\lambda _0(m,n)$ to represent $\lambda _0$. The value of $\lambda _0(m,m-n)$ for every odd number m and every even number n with $m>n$ will play an important role in the results of this section. For short we put $\mu _0(m,n)=\lambda _0(m,m-n)$, or simply $\mu _0=\mu _0(m,n)$. Some values for $\mu _0$ can be obtained using numerical calculus. For completeness, we reproduce some values of $\mu _0$ provided in [36]. For instance $\mu _0=-\frac{1}{4}$ when $m=3$ and $n=2$, and $\mu _0=\frac{4+\root 3 \of {10}-2\root 3 \of {100}}{6}$ when $m=5$ and $n=2$. More values for $\mu _0$ can be obtained numerically. The reader can find below a table with 15 values for $\mu _0$ with an accuracy of 5 decimal digits.

$\mu _0$	$m=3$	$m=5$	$m=7$	$m=9$	$m=11$
$n=2$	$-0.25000$	$-0.52145$	$-0.65076$	$-0.72537$	$-0.77380$
$n=4$	–	$-0.13471$	$-0.34142$	$-0.47306$	$-0.56186$
$n=6$	–	–	$-0.09072$	$-0.25000$	$-0.36750$
$n=8$	–	–	–	$-0.06795$	$-0.19558$
$n=10$	–	–	–	–	$-0.05414$

In order to proceed, an explicit formula for $\Vert \cdot \Vert _{m,n}$ whenever m is odd will be fundamental in this section. Such formula can be found in [36]. We reproduce, for completeness, the required result:

Lemma 3.3

[36, Theorems 2.3 and 3.2] Let $m,n\in {{\mathbb {N}}}$ be such that $m>n$ and m is odd. If n is odd as well, then

$$\begin{aligned} \Vert (a,b,c)\Vert _{m,n} = \left\{ \begin{array}{ll} \frac{(m-n)|a|}{n}\cdot \left| \frac{nb}{ma}\right| ^\frac{m}{m-n} + |c| &{} \quad \text{if}\ a\ne 0\ \text{and}\ -1< \frac{nb}{ma} < \lambda _0,\\ |a+b|+|c| &{}\quad \text{otherwise}, \end{array}\right. \end{aligned}$$

where $\lambda _0$ is the number in $(-\frac{n}{m},0)$ given by Lemma 3.1. If n is even, then

$$\begin{aligned} \Vert (a,b,c)\Vert _{m,n} =\max \{|c|,|a|+|b+c|\}. \end{aligned}$$

Theorem 3.4

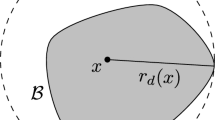
Let $m,n\in {{\mathbb {N}}}$ with $m>n,$ m odd and n even. Consider the number $K_{m,n}=\frac{n}{m-n}\left( \frac{m-n}{m}\right) ^\frac{m}{n},$ the interval $I_{m,n}=[\eta _1,\eta _2],$ where $\eta _1=-\frac{m}{m-n},$ $\eta _2=\frac{m}{m-n}\mu _0$ and $\mu _0=\mu _0(m,n)$ is the number in $(-\frac{m-n}{m},0)$ introduced in Remark 3.2 (see also Lemma 3.1), and the sets $A_{m,n},$ $F_{m,n},$ $B_{m,n}$ and ${{\mathcal {B}}}$ (see Figs. 6and 7) given by

$$\begin{aligned} A_{m,n}&=\left\{ (x,y)\in {{\mathbb {R}}}^2:x\in I_{m,n}\text{ and } |y|\ge 1-K_{m,n}|x|^\frac{m}{n}\right\} ,\\ F_{m,n}&=\{(x,y)\in {{\mathbb {R}}}^2:x\in I_{m,n}\text{ and } 1-K_{m,n}|x|^\frac{m}{n}<|y|< 1-|1+x|\},\\ {{\mathcal {B}}}&=B_{\ell _1^2}((-1,0),1)=\{(x,y)\in {{\mathbb {R}}}^2:|x+1|+|y|<1\},\\ B_{m,n}&={{\mathcal {B}}}{\setminus} F_{m,n}. \end{aligned}$$

Then,

$$\begin{aligned} {\left| \!\left| \!\left| (a,b,c) \right| \!\right| \!\right| }_{m,n} = \left\{ \begin{array}{ll} \frac{n|a|}{m-n}\cdot \left| \frac{(m-n)b}{ma}\right| ^\frac{m}{n} + |c|&{}\quad \text{if}\ a\ne 0\ \text{and}\ \left( \frac{b}{a},\frac{c}{a}\right) \in A_{m,n},\\ |a| &{}\quad \text{if}\ a\ne 0\ \text{and}\ \left( \frac{b}{a},\frac{c}{a}\right) \in B_{m,n},\\ |a+b|+|c| &{}\quad \text{otherwise}. \end{array}\right. \end{aligned}$$

(6)

Proof

It is straightforward to prove that ${\left| \!\left| \!\left| (0,b,c) \right| \!\right| \!\right| }_{m,n}=|b|+|c|$ for every choice of m and n in ${{\mathbb {N}}}$, so (6) is satisfied when $a=0$.

Now assume that $a\ne 0$. Then

$$\begin{aligned} {\left| \!\left| \!\left| (a,b,c) \right| \!\right| \!\right| }_{m,n}&=|a|\cdot {\left| \!\left| \!\left| (1,b/a,c/a) \right| \!\right| \!\right| }_{m,n} \\ &=|a|\cdot \max \{\Vert (1,b/a,c/a)\Vert _{m,m-n},\Vert (c/a,b/a,1)\Vert _{m,n}\}. \end{aligned}$$

(7)

To handle the maximum in (7) it will be easier to consider the change of variables $b\leftrightarrow b/a$ and $c\leftrightarrow c/a$. Since $m-n$ is odd and n is even, by Lemma 3.3 and the fact that we have defined $\mu _0=\lambda _0(m,m-n)$, we have

$$\begin{aligned} \Vert (1,b,c)\Vert _{m,m-n}&=\left\{ \begin{array}{ll} \frac{n}{m-n}\cdot \left| \frac{m-n}{m}b\right| ^\frac{m}{n} + |c| &{} \quad \text{if}\ -\frac{m}{m-n}< b< \frac{m}{m-n}\mu _0,\\ |1+b|+|c| &{}\quad \text{otherwise}. \end{array}\right. \\&= \left\{ \begin{array}{ll} K_{m-n}|b|^\frac{m}{n} + |c| &{}\quad \text{if}\ \eta _1< b < \eta _2,\\ |1+b|+|c| &{}\quad \text{otherwise}. \end{array}\right. \\ \Vert (c,b,1)\Vert _{m,n}&=\max \{1,|1+b|+|c|\}. \end{aligned}$$

Hence it all amounts to compare the functions $f(b,c)=K_{m,n}|b|^\frac{m}{n} + |c|$, $g(b,c)=|1+b|+|c|$ and $h(b,c)=1$. Obviously, $f(b,c)=g(b,c)$ is equivalent to $K_{m-n}|b|^\frac{m}{n}=|1+b|$ which, using Lemma 3.1, can be proved to have only two solutions, namely $\eta _1$ and $\eta _2$. From the latter it is straightforward to deduce that $f(b,c)>g(b,c)$ if and only if $\eta _1< b < \eta _2$. On the other hand, $g(b,c)<h(b,c)=1$ if and only if $(b,c)\in B_{\ell _1^2}((-1,0),1)$. Finally, the functions f and h agree along the curves $c=\pm (1-K_{m,n}|b|^\frac{m}{n})$. Actually, it is easy to see that $f(b,c)<h(b,c)=1$ in the region of the bc-plane bounded by the graphs of $c=\pm (1-K_{m,n}|b|^\frac{m}{n})$. It is important to remark that the curves $c=\pm (1-K_{m,n}|b|^\frac{m}{n})$ meet the boundary of $B_{\ell _1^2}((-1,0),1)$ at $\eta _1$ and $\eta _2$ if $\frac{m}{n}>2$ (see Fig. 7) and at $\eta _2$ if $\frac{m}{n}<2$ (see Fig. 6). Putting all these ideas together we arrive at the fact that $\max \{\Vert (1,b,c)\Vert _{m,m-n},\Vert (c,b,1)\Vert _{m,n}\}$ is given by

$$\begin{aligned} \left\{ \begin{array}{ll} K_{m-n}|b|^\frac{m}{n} + |c| &{}\quad \text{if}\ (b,c)\in A_{m,n},\\ 1 &{} \quad \text{if}\ (b,c)\in B_{m,n},\\ |c|+|1+b|&{}\quad \text{otherwise}. \end{array}\right. \end{aligned}$$

Undoing the change of variables $b\leftrightarrow b/a$ and $c\leftrightarrow c/a$ in the latter estimate in combination with (7) yield (6), which concludes the proof. $\square$

Fig. 6

Regions appearing in the definition of ${\left| \!\left| \!\left| \cdot \right| \!\right| \!\right| }_{m,n}$ when m is odd, n is even and $m/n<2$. The case considered in the picture corresponds to the choice $m=3$ and $n=2$

Fig. 7

Regions appearing in the definition of ${\left| \!\left| \!\left| \cdot \right| \!\right| \!\right| }_{m,n}$ when m is odd, n is even and $m/n>2$. The case considered in the picture corresponds to the choice $m=5$ and $n=2$

Formula (6) allows us to obtain a parametrization of ${{\mathsf {S}}}^h_{m,n}$. First, it is convenient to determine the projection of ${{\mathsf {B}}}^h_{m,n}$ onto the ab-plane.

Theorem 3.5

Let $m,n\in {{\mathbb {N}}}$ be such that $m>n,$ m is odd and n is even. Consider the numbers $a_0=\frac{m-n}{n},$ $L_{m,n}=\frac{m}{m-n}\left( \frac{m-n}{n}\right) ^\frac{n}{m}$ and $\eta _1$ and $\eta _2$ as in Theorem 3.4. Now define the sets $R_{m,n},$ $S_{m,n},$ $U_{m,n}$ and $V_{m,n}$ as follows:

If $\frac{m}{n}<2,$ then

$$\begin{aligned} R_{m,n}&=\left\{ (a,b)\in {{\mathbb {R}}}^2:\ -1\le a\le 0\text{ and } \eta _2a< b< \min \left\{ \eta _1a,L_{m,n}|a|^\frac{m-n}{m}\right\} \right\} ,\\ U_{m,n}&=\left\{ (a,b)\in {{\mathbb {R}}}^2:\ -a_0\le a\le 1\text{ and }\max \{\eta _1a,\eta _2a\} \le b\le 1-a\right\} ,\\ S_{m,n}&=-R_{m,n},\\ V_{m,n}&=-U_{m,n}. \end{aligned}$$

If $\frac{m}{n}>2,$ then

$$\begin{aligned} R_{m,n}&=\left\{ (a,b)\in {{\mathbb {R}}}^2:\ -1\le a\le 0\text{ and } \eta _2a< b< \eta _1 a\right\} ,\\ U_{m,n}&=\left\{ (a,b)\in {{\mathbb {R}}}^2:\ -1\le a\le 1\text{ and }\max \left\{ \eta _1a,\eta _2a\right\} \le b\le 1-a\right\} ,\\ S_{m,n}&=-R_{m,n},\\ V_{m,n}&=-U_{m,n}. \end{aligned}$$

Then, $\pi _{ab}({{\mathsf {B}}}^h_{m,n})=R_{m,n}\cup S_{m,n}\cup U_{m,n}\cup V_{m,n}$ (see Figs. 8and 9).

Proof

Observe that according to (6) we have that

$$\begin{aligned} {\left| \!\left| \!\left| (a,b,c) \right| \!\right| \!\right| }_{m,n}={\left| \!\left| \!\left| (a,b,-c) \right| \!\right| \!\right| }_{m,n} \end{aligned}$$

for all $(a,b,c)\in {{\mathbb {R}}}^3$. From the symmetry with respect to the ab-plane it follows that

$$\begin{aligned} \pi _{ab}({{\mathsf {B}}}^h_{m,n})=\{(a,b)\in {{\mathbb {R}}}^2:{\left| \!\left| \!\left| (a,b,0) \right| \!\right| \!\right| }_{m,n}\le 1\}. \end{aligned}$$

A point of the form (a, b, 0) satisfies one of the following conditions:

• (a) $a\ne 0$ and $(b/a,0)\in A_{m,n}$.

• (b) $a\ne 0$ and $(b/a,0)\in B_{m,n}$.

• (c) $a=0$ or $a\ne 0$ and $(b/a,0)\notin A_{m,n}\cup B_{m,n}$.

Let us examine first the case $\frac{m}{n}<2$. In the following, it will be of much help to keep an eye on Fig. 8. For technical reasons, it will be useful to consider the sets $R^\pm _{m,n}$, $S^\pm _{m,n}$, $U^{+,1}_{m,n}$, $U^{+,2}_{m,n}$, $U^-_{m,n}$, $V^+_{m,n}$, $V_{m,n}^{-,1}$, $V_{m,n}^{-,2}$, defined as in Fig. 8.

The fact that (a, b, 0) satisfies (a) together with ${\left| \!\left| \!\left| (a,b,0) \right| \!\right| \!\right| }_{m,n}\le 1$ are equivalent to $a\ne 0$, $(b/a,0)\in A_{m,n}$ and

$$\begin{aligned} \frac{n|a|}{m-n}\cdot \left| \frac{(m-n)b}{ma}\right| ^\frac{m}{n}={\left| \!\left| \!\left| (a,b,0) \right| \!\right| \!\right| }_{m,n}\le 1. \end{aligned}$$

(8)

We have that $(b/a,0)\in A_{m,n}$ is equivalent to $\eta _1\le \frac{b}{a}\le -L_{m,n}$ (see Fig. 8), whereas (8) is equivalent to $|b|\le L_{m,n} |a|^\frac{m-n}{m}$. The combination of the last two conditions is equivalent to $(a,b)\in R^+_{m,n}\cup S^-_{m,n}$. Now, that (a, b, 0) satisfies (b) and ${\left| \!\left| \!\left| (a,b,0) \right| \!\right| \!\right| }_{m,n}\le 1$ are equivalent to $a\ne 0$, $(b/a,0)\in B_{m,n}$ and

$$\begin{aligned} |a|={\left| \!\left| \!\left| (a,b,0) \right| \!\right| \!\right| }_{m,n}\le 1. \end{aligned}$$

(9)

The condition $(b/a,0)\in B_{m,n}$ with $a\ne 0$ is equivalent to $-L_{m,n}\le \frac{b}{a}\le 0$ (see Fig. 8). The latter together with (9) are equivalent to

$$\begin{aligned} (a,b)\in V_{m,n}^+\cup R_{m,n}^-\cup U_{m,n}^-\cup S_{m,n}^+. \end{aligned}$$

Finally, let us assume that (a, b, 0) satisfies (c) and ${\left| \!\left| \!\left| (a,b,0) \right| \!\right| \!\right| }_{m,n}\le 1$. Satisfying (c) means that either $a=0$ or $a\ne 0$ and $(b/a,0)\notin A_{m,n}\cup B_{m,n}$. The combination $a=0$ and ${\left| \!\left| \!\left| (0,b,0) \right| \!\right| \!\right| }_{m,n}\le 1$ is equivalent to $|b|={\left| \!\left| \!\left| (0,b,0) \right| \!\right| \!\right| }_{m,n}\le 1$. It is quite obvious that the vertical segment $\{(0,b)\in {{\mathbb {R}}}^2:|b|\le 1\}$ is contained in $U_{m,n}\cup V_{m,n}$. If $a\ne 0$ and $(b/a,0)\notin A_{m,n}\cup B_{m,n}$, then either $b/a\le \eta _1$ or $b/a\ge 0$. Observe that the combination $b/a\le \eta _1$ ($a\ne 0$) with $|a+b|={\left| \!\left| \!\left| (a,b,0) \right| \!\right| \!\right| }_{m,n}\le 1$ is equivalent to $(a,b)\in U^{+,1}_{m,n}\cup V^{-,2}_{m,n}$ (recall that $\eta _1<0$). In the remaining case we have $b/a\ge 0$ and $|a+b|\le 1$, which is equivalent to $(a,b)\in U_{m,n}^{+,2}\cup V_{m,n}^{-,1}$.

We conclude that

$$\begin{aligned} \pi _{ab}({{\mathsf {B}}}^h_{m,n})&=\{(a,b)\in {{\mathbb {R}}}^2:{\left| \!\left| \!\left| (a,b,0) \right| \!\right| \!\right| }_{m,n}\le 1\}\\ &=R^\pm _{m,n}\cup S^\pm _{m,n}\cup U_{m,n}^-\cup U_{m,n}^{+,1}\cup U_{m,n}^{+,2} \cup V_{m,n}^+\cup V_{m,n}^{-,1}\cup V_{m,n}^{-,2}\\ &=R_{m,n}\cup S_{m,n}\cup U_{m,n}\cup V_{m,n}. \end{aligned}$$

The case $\frac{m}{n}>2$ is somewhat simpler and similar to the previous case. Now it is Fig. 9 that we should take into consideration. Also, for technical reasons the following sets will be used: $U^{+,1}_{m,n}$, $U^{+,2}_{m,n}$, $U^{+,3}_{m,n}$, $U^-_{m,n}$, $V^+_{m,n}$, $V_{m,n}^{-,1}$, $V_{m,n}^{-,2}$, $V_{m,n}^{-,3}$, defined as in Fig. 9.

First observe that no point of the form (a, b, 0) satisfies (a). Now assume that (a, b, 0) satisfies (b) and ${\left| \!\left| \!\left| (a,b,0) \right| \!\right| \!\right| }_{m,n}\le 1$ or, equivalently, $a\ne 0$, $-2\le b/a\le 0$ and $|a|= {\left| \!\left| \!\left| (a,b,0) \right| \!\right| \!\right| }_{m,n}\le 1$. All that is equivalent to

$$\begin{aligned} (a,b)\in U^{+,1}_{m,n}\cup R_{m,n}\cup V^+_{m,n}\cup U_{m,n}^-\cup S_{m,n}\cup V^{-,3}_{m,n}. \end{aligned}$$

Finally, suppose that (a, b, 0) satisfies (c) and ${\left| \!\left| \!\left| (a,b,0) \right| \!\right| \!\right| }_{m,n}\le 1$. The fact that (a, b, 0) satisfies (c) is equivalent to $a=0$ on the one hand or $a\ne 0$ and $b/a\notin [-2,0]$ on the other. First, if $a=0$, then $|b|={\left| \!\left| \!\left| (0,b,0) \right| \!\right| \!\right| }_{m,n}\le 1$. As in the previous case, the vertical segment $\{(0,b)\in {{\mathbb {R}}}^2:|b|\le 1\}$ is contained in $U_{m,n}\cup V_{m,n}$. Now, that $a\ne 0$, $b/a<-2$ and $|a+b|={\left| \!\left| \!\left| (a,b,0) \right| \!\right| \!\right| }_{m,n}\le 1$ are equivalent to $(a,b)\in U^{+,2}_{m,n}\cup V^{-,2}_{m,n}$. In the remaining case $a\ne 0$, $b/a>0$ and $|a+b|={\left| \!\left| \!\left| (a,b,0) \right| \!\right| \!\right| }_{m,n}\le 1$, which are equivalent to $(a,b)\in U^{+,3}_{m,n}\cup V_{m,n}^{-,1}$. This concludes the proof. $\square$

Fig. 8

Projection of ${{\mathsf {B}}}^h_{m,n}$ over the ab-plane with $\frac{m}{n}<2$. The picture corresponds with the choice $m=5$, $n=4$

Fig. 9

Projection of ${{\mathsf {B}}}^h_{m,n}$ over the ab-plane with $\frac{m}{n}>2$. The picture corresponds with the choice $m=5$, $n=2$

Theorem 3.6

Let $m,n\in {{\mathbb {N}}}$ be such that $m>n,$ m is odd and n is even and suppose that $K_{m,n},$ $L_{m,n},$ $a_0,$ $\eta _1$ and $\eta _2$ are as in Theorems 3.4and 3.5. Define

$$\begin{aligned} G_{m,n}(a,b)=\left\{ \begin{array}{ll} 1-K_{m,n}|a|\left| \frac{b}{a}\right| ^\frac{m}{n}&{}\quad \text{if }(a,b)\in R_{m,n}\cup S_{m,n},\\ 1-|a+b|&{}\quad \text{if }(a,b)\in U_{m,n}\cup V_{m,n}, \end{array}\right. \end{aligned}$$

and

$$\begin{aligned} \Gamma _{m,n}= \left\{ \begin{array}{ll} \{(-1,b,c)\in {{\mathbb {R}}}^3:0\le b\le L_{m,n}\text{ and } |c|\le G_{m,n}(-1,b)\}&{}\quad \text{if }\frac{m}{n}<2,\\ \{(-1,b,c)\in {{\mathbb {R}}}^3:0\le b\le 2\text{ and } |c|\le G_{m,n}(-1,b)\}&{}\quad \text{if }\frac{m}{n}>2. \end{array}\right. \end{aligned}$$

Then,

• (a) ${{\mathsf {S}}}^h_{m,n}={{\,\mathrm{graph\,\!}\,}}(G_{m,n})\cup {{\,\mathrm{graph\,\!}\,}}(-G_{m,n}) \cup \Gamma _{m,n}\cup (-\Gamma _{m,n})$.

• (b) If $\frac{m}{n}<2,$ then

  $$\begin{aligned} {{\,\mathrm{ext\,\!}\,}}({{\mathsf {B}}}^h_{m,n})&=\left\{ \pm \left( -1,t, \pm (1-K_{m,n}|t|^\frac{m}{n})\right) :t\in [-\eta _2,L_{m,n}]\right\} \\ &\quad \cup \left\{ \pm (0,s,L_{m,n}|s|^\frac{m}{n}):s\in [-1,-a_0]\right\} \\ &\quad \cup \{(\pm 1,0,0),(0,0\pm 1)\}. \end{aligned}$$

  If $\frac{m}{n}>2,$ then

  $$\begin{aligned} {{\,\mathrm{ext\,\!}\,}}({{\mathsf {B}}}^h_{m,n})&=\left\{ \pm \left( -1,t, \pm (1-K_{m,n}|t|^\frac{m}{n})\right) :t\in [-\eta _2,-\eta _1]\right\} \\ &\quad \cup \{(\pm 1,0,0),(0,0\pm 1),\pm (1,-2,0)\}. \end{aligned}$$

Fig. 10

Sketch of ${{\mathsf {S}}}^h_{m,n}$ with $\frac{m}{n}<2$. The picture corresponds with the choice $m=5$, $n=4$. The extreme points appear with a thicker line or big dots. The surfaces that form ${{\mathsf {S}}}_{m,n}^h$ are delimited by thin lines

Fig. 11

Sketch of ${{\mathsf {S}}}^h_{m,n}$ with $\frac{m}{n}>2$. The picture corresponds with the choice $m=5$, $n=2$. The extreme points appear with a thicker line or big dots. The surfaces that form ${{\mathsf {S}}^h}_{m,n}$ are delimited by thin lines

Proof

We restrict our attention to the case $\frac{m}{n}<2$. The case $\frac{m}{n}>2$ is similar and, as a matter of fact, simpler (Fig. 11). Observe that any two norms $\Vert \cdot \Vert _a$ and $\Vert \cdot \Vert _b$ coincide on a linear space if and only if $\Vert x\Vert _a=1$ for every $x\in {\mathsf S}_{\Vert \cdot \Vert _b}$. Since $G_{m,n}$ can be easily proved to be convex using elementary differential calculus, the set

$$\begin{aligned} {\mathsf S}_{m,n}^*={{\,\mathrm{graph\,\!}\,}}(G_{m,n})\cup {{\,\mathrm{graph\,\!}\,}}(-G_{m,n})\cup \Gamma _{m,n}\cup (-\Gamma _{m,n}) \end{aligned}$$

is the unit sphere of a norm in ${{\mathbb {R}}}^3$. Hence, in order to prove part (a) we just need to show that ${{\mathsf {S}}}^*_{m,n}\subset {{\mathsf {S}}}^h_{m,n}$. Using the fact that $R_{m,n}$ and $S_{m,n}$ on the one hand, and $U_{m,n}$ and $V_{m,n}$ on the other are symmetric with respect to the origin, together with the symmetry of ${\mathsf S}^h_{m,n}$, it is enough to prove that

$$\begin{aligned} {{\,\mathrm{graph\,\!}\,}}(G_{m,n}|_{R_{m,n}\cup U_{m,n}})\cup \Gamma _{m,n}\subset {{\mathsf {S}}}^h_{m,n}. \end{aligned}$$

Let us take $(a,b)\in R_{m,n}$ and show that $(a,b,G_{m,n}(a,b))\in {{\mathsf {S}}}_{m,n}^h$. From $(a,b)\in R_{m,n}$ it follows that

$$\begin{aligned} -1\le a\le 0\quad \text{and}\quad \eta _2a\le b\le \min \left\{ \eta _1 a, L_{m,n} |a|^\frac{m-n}{m}\right\} . \end{aligned}$$

The case $a=0$ is fairly simple and left to the reader, so in the rest of the proof we assume that $a\ne 0$. If $-1\le a<0$ then, dividing by a and taking into consideration that a is negative,

$$\begin{aligned} \max \left\{ \eta _1,-L_{m,n}|a|^{-\frac{n}{m}}\right\} \le \frac{b}{a}\le \eta _2. \end{aligned}$$

Hence $\eta _1\le \frac{b}{a}\le \eta _2$. On the other hand

$$\begin{aligned} \frac{G_{m,n}(a,b)}{a}=\frac{1}{a}+K_{m,n}\left| \frac{b}{a}\right| ^{\frac{m}{n}}\le -1+K_{m,n}\left| \frac{b}{a}\right| ^{\frac{m}{n}}=-\left( 1-K_{m,n}\left| \frac{b}{a}\right| ^{\frac{m}{n}}\right) . \end{aligned}$$

Therefore $(b/a,G_{m,n}(a,b)/a)\in A_{m,n}$ (see Fig. 6), which, according to (3.4) yields

$$\begin{aligned} {\left| \!\left| \!\left| (a,b,G_{m,n}(a,b)) \right| \!\right| \!\right| }_{m,n}&=K_{m,n}|a| \left| \frac{b}{a}\right| ^\frac{m}{n} +|G_{m,n}|\\&=K_{m,n}|a| \left| \frac{b}{a}\right| ^\frac{m}{n}+\left| 1-K_{m,n}|a|\left| \frac{b}{a}\right| ^\frac{m}{n}\right| =1. \end{aligned}$$

Observe that the last identity follows from the fact that $\left| \frac{b}{a}\right| \le |\eta _1|$. Thus, for $-1\le a<0$ we have

$$\begin{aligned} K_{m,n}|a|\left| \frac{b}{a}\right| ^\frac{m}{n}\le K_{m,n}\left| \frac{b}{a}\right| ^\frac{m}{n}\le K_{m,n}|\eta _1|^\frac{m}{n}=\left( \frac{n}{m}\right) ^\frac{m}{n}<1. \end{aligned}$$

We conclude that $(a,b,G_{m,n}(a,b))\in {{\mathsf {S}}}_{m,n}^h$. Now take $(a,b)\in U_{m,n}$. We have that $G_{m,n}(a,b)=1-|a+b|$ and we have to prove that

$$\begin{aligned} {\left| \!\left| \!\left| (a,b,G_{m,n}(a,b) \right| \!\right| \!\right| }_{m,n}={\left| \!\left| \!\left| (a,b,1-|a+b|) \right| \!\right| \!\right| }_{m,n}=1. \end{aligned}$$

Since $(a,b)\in U_{m,n}$ we have

$$\begin{aligned} \max \{\eta _1a,\eta _2a\}\le b\le 1-a, \end{aligned}$$

(10)

for $-a_0\le a<1$. If $-a_0\le a<0$, then dividing by a in (10) we have

$$\begin{aligned} \frac{1}{a}-1\le \frac{b}{a}\le \min \{\eta _1,\eta _2\}=\eta _1. \end{aligned}$$

Hence $\left( \frac{b}{a},\frac{G_{m,n}(a,b)}{a}\right)$ satisfies the third condition in (3.4), and since $|a+b|\le 1$ for all $(a,b)\in U_{m,n}$, from (3.4) it follows that

$$\begin{aligned} {\left| \!\left| \!\left| (a,b,1-|a+b|) \right| \!\right| \!\right| }_{m,n}=|a+b|+\left| 1-|a+b|\right| =1. \end{aligned}$$

(11)

If now $0<a<1$, dividing by a in (10) we arrive at

$$\begin{aligned} \eta _2=\max \{\eta _1,\eta _2\}\le \frac{b}{a}\le \frac{1}{a}-1. \end{aligned}$$

If $\frac{b}{a}$ were positive, then $\left( \frac{b}{a},\frac{G_{m,n}(a,b)}{a}\right) \notin A_{m,n}\cup B_{m,n}$, and therefore, as in (11) it follows that ${\left| \!\left| \!\left| (a,b,G_{m,n}(a,b)) \right| \!\right| \!\right| }_{m,n}=1$. There remains to consider the case where $\eta _2\le \frac{b}{a}\le 0$ with $0<a\le 1$. Then

$$\begin{aligned} \frac{G_{m,n}(a,b)}{a}=\frac{1}{a}-\left| 1+\frac{b}{a}\right| >1-\left| 1+\frac{b}{a}\right| =-\frac{b}{a}. \end{aligned}$$

We deduce once again that $\left( \frac{b}{a},\frac{G_{m,n}(a,b)}{a}\right) \notin A_{m,n}\cup B_{m,n}$, from which, as in (11) we have ${\left| \!\left| \!\left| (a,b,G_{m,n}(a,b)) \right| \!\right| \!\right| }_{m,n}=1$.

To finish the proof of part (a) we still have to show that $\Gamma _{m,n}\subset {{\mathsf {S}}}_{m,n}$. If $(-1,b,c)\in \Gamma _{m,n}$, then $0\le b\le L_{m,n}$ and $|c|\le G_{m,n}(-1,b)$. Then b satisfies either $0\le b\le -\eta _2$ or $-\eta _2<b\le L_{m,n}$. In the first case we have that $\eta _2\le -b\le 0$ and since $(-1,b)\in V_{m,n}$,

$$\begin{aligned} |-c|=|c|\le G_{m,n}(-1,b)=1-|-1+b|=b. \end{aligned}$$

Thus $(-b,-c)\in B_{m,n}$, from which, using (3.4), we have ${\left| \!\left| \!\left| (-1,b,c) \right| \!\right| \!\right| }_{m,n}=1$. If now $-\eta _2<b\le L_{m,n}$, then $-L_{m,n}<-b\le \eta _2$ and, since $(-1,b)\in R_{m,n}$,

$$\begin{aligned} |-c|=|c|\le G_{m,n}=1-K_{m,n}|b|^\frac{m}{n}. \end{aligned}$$

Therefore $(-b,-c)\in B_{m,n}$, from which, using (3.4), we have ${\left| \!\left| \!\left| (-1,b,c) \right| \!\right| \!\right| }_{m,n}=1$.

As for part (b) of the statement, it is crucial to observe that $c=G_{m,n}(a,b)$ defines a ruled surface on $R_{m,n}$, i.e., it is affine on the rays $\{(a,\lambda a):a\le 0\}$ (with $\eta _1\le \lambda \le \eta _2$). Indeed, $G_{m,n}(a,\lambda a)=1+K_{m,n} \lambda ^\frac{m}{n} a$ for all $a\le 0$ and $\eta _1\le \lambda \le \eta _2$. By symmetry, $G_{m,n}$ also defines a ruled surface when restricted to $S_{m,n}$. On the other hand, it is obvious that the rest of ${{\mathsf {S}}}_{m,n}^h$ is formed by flat faces, such as $\pm \Gamma _{m,n}$, ${{\,\mathrm{graph\,\!}\,}}(\pm G_{m,n}|_{U_{m,n}})$ or ${{\,\mathrm{graph\,\!}\,}}(\pm G_{m,n}|_{V_{m,n}})$. Therefore, extreme points can only occur under the following three circumstances (we recommend to visualize Fig. 10):

• 1. The intersection of the flat surfaces $\pm \Gamma _{m,n}$ and the non-flat ruled surfaces ${{\,\mathrm{graph\,\!}\,}}(\pm G_{m,n}|_{R_{m,n}})$ or ${{\,\mathrm{graph\,\!}\,}}(\pm G_{m,n}|_{S_{m,n}})$:

  $$\begin{aligned} {{\,\mathrm{graph\,\!}\,}}(\pm G_{m,n}|_{R_{m,n}})\cap \Gamma _{m,n}&=\left\{ \left( -1,t,\pm (1-K_{m,n}|t|^\frac{m}{n})\right) :t\in [-\eta _2,L_{m,n}]\right\} ,\\ {{\,\mathrm{graph\,\!}\,}}(\pm G_{m,n}|_{S_{m,n}})\cap (-\Gamma _{m,n})&=\left\{ \left( 1,t,\pm (1-K_{m,n}|t|^\frac{m}{n})\right) :t\in [-\eta _2,L_{m,n}]\right\} . \end{aligned}$$

• 2. The intersection of two non-flat ruled surfaces ${{\,\mathrm{graph\,\!}\,}}(\pm G_{m,n}|_{R_{m,n}})$ and ${{\,\mathrm{graph\,\!}\,}}(\pm G_{m,n}|_{S_{m,n}})$:

  $$\begin{aligned} {{\,\mathrm{graph\,\!}\,}}(G_{m,n}|_{R_{m,n}})\cap {{\,\mathrm{graph\,\!}\,}}(- G_{m,n}|_{R_{m,n}})&=\left\{ (0,s,L_{m,n}|s|^\frac{m}{n}):s\in [-1,-a_0]\right\} ,\\ {{\,\mathrm{graph\,\!}\,}}(G_{m,n}|_{S_{m,n}})\cap {{\,\mathrm{graph\,\!}\,}}(- G_{m,n}|_{S_{m,n}})&=\left\{ (0,s,-L_{m,n}|s|^\frac{m}{n}):s\in [a_0,1]\right\} . \end{aligned}$$

• 3. The end points of the segments that result of the intersection of two sets among ${{\,\mathrm{graph\,\!}\,}}(\pm G_{m,n}|_{U_{m,n}})$, ${{\,\mathrm{graph\,\!}\,}}(\pm G_{m,n}|_{V_{m,n}})$, ${{\,\mathrm{graph\,\!}\,}}(\pm G_{m,n}|_{R_{m,n}})$ and ${{\,\mathrm{graph\,\!}\,}}(\pm G_{m,n}|_{S_{m,n}})$. The reader can check easily that only four points satisfy the latter condition, namely $(\pm 1,0,0)$ and $(0,0,\pm 1)$.

All the points obtained in 1. 2. and 3. are indeed extreme. The construction of a supporting hyperplane is left to the reader. $\square$