Introduction

Due to the advantages of high efficiency, high power density and wide speed range, permanent magnet synchronous motor (PMSM) has been an attractive selection for wind power generation [1] and electric vehicle [2]. However, the main weakness of PMSM is the need of a more complex controller because of its nonlinear and strong coupling characteristics [3]. Therefore, direct torque control [4] and field-orientation mechanism [5] are used in motor control system, where, the field-orientation mechanism is usually employed in the practical applications by cascade configuration of proportional plus integral (PI) controllers. Although PI controller has a simple structure, it may still fail to meet the practical requirement for applications with the dynamically changeable working conditions and the disturbance. To meet the high-performance requirement and strong robustness of PMSM drive system, until now, various nonlinear control techniques have been widely applied in PMSM, such as, model predictive control [5], backstepping control [6], active disturbance rejection control [7], sliding mode control [8] and intelligent control [9], which enhance the motor control performance in different aspects.

Among these new control methods, backstepping control is a systematic and recursive design approach for the nonlinear system. By using variable virtual control laws, the control procedure of the original high order system is simplified. It can not only guarantee global stability but also have excellent tracking performance in practical implementation. Thus, it is particularly adapted for the speed or servo control of PMSM, and an enhanced dynamic behavior of the motor can be accomplished. However, the controller requires full knowledge of the machine parameters and operating conditions. If the machine parameters are known, backstepping can achieve the precise control. The fact that PMSM drive system faces inevitable disturbance, such as parameter variations, model uncertainties and external load torque. Thus, the key of the backstepping controller is to reject the disturbance. To improve the robustness for the uncertainties in PMSM, the adaptive backstepping control strategy is studied in the literatures [10,11,12,13,14]. The performance is significantly improved by estimating the uncertain parameters in the process of backstepping controller. However, it is difficult to estimate all the uncertain parameters in the system, and complicated computation is necessary. What’s more, the speed of convergence of the unknown parameters as well as the lumped disturbance to the true values is always a concern, which may lead to slow convergence [15]. Besides the above research, a backstepping control method by using integral actions in each step of the original algorithm is proposed in [16], meanwhile, a nonlinear observer is implemented experimentally to estimate the rotor resistance and the load torque, and the robustness is improved effectively. In [17,18,19], the adaptive backstepping sliding mode control methods are studied for the motor drive system, but the chattering problem of the sliding mode controller cannot be neglected. In [5, 20, 21], the backstepping controllers are designed by combining with intelligent control methods, such as neural network control and fuzzy control, which employ a neural network or a fuzzy logic system to approximate the uncertainties of the motor. They provide the satisfactory approximation accuracy, but these methods have the highly online computational burden, which are not conducive to the practical application.

For the uncertain system, an alternative is the disturbance estimation and attenuation technology, which is designed to estimate the disturbances and corresponding compensation is then generated by making use of the estimate [22]. Meanwhile, it proves that disturbance estimation and attenuation technology have a different but complementary mechanism to widely used robust control and adaptive control [23]. Up to now, various disturbance estimation and attenuation technologies have been proposed, among which, nonlinear disturbance observer [24, 25] and extended state observer [26, 27] have evoked considerable research in the field of PMSM drive. But the designed observers above are only applicable for the matched uncertainties, which mean that the uncertainties exist in the same channel as that of the control input. In fact, the matched disturbance and mismatched disturbance are collectively existed in PMSM, thus this method cannot completely eliminate the lump disturbance of PMSM drive system, which improves the difficulty for inhibiting the lump disturbance. In [28, 29], a composite backstepping control method based on adaptive disturbance observer is proposed for the nonlinear system, which can effectively deal with the matched and mismatched disturbance. It is found that the disturbance observer can provide excelling tracking performance for the disturbance of the system. It provides a new way for the robust speed control of PMSM drive system. In [30], a disturbance observer based on backstepping control is proposed for PMSM, but the designed observer also cannot estimate all disturbance in PMSM drive system. Only partial motor parameters are estimated. In addition, the designed observer is complicated.

Aiming at the speed control problem of PMSM, this paper presents and validates a novel robust control method that synthesizes backstepping control technique and nonlinear disturbance observer, which considers the influence of both matched and mismatched disturbance. Firstly, the backstepping control method is employed to the speed control system of PMSM with single-loop control structure. The controller is derived systematically through recursive design and suitable Lyapunov functions. To improve the disturbance rejection performance of backstepping control, a nonlinear observer is designed to estimate the disturbance, and it is especially applicable for systems which cannot satisfy matching conditions. Then, a feedforward compensation part for disturbance is introduced to the controller besides the backstepping feedback part. The designed controller has the advantage of simple structure, easy adjustment of parameters, strong practicability and so on. The contributions of the paper are (1) the nonlinear disturbance observer is introduced to the backstepping control of PMSM, instead of the traditional adaptive backstepping control. (2) The controller has the strong disturbance rejection ability for all of the uncertain parameters and load torque. (3) Compared with the adaptive backstepping control method, the designed controller is simple and the controller parameters are easy to be regulated. In the end, the simulation and experimental verification based on the dSPACE are completed. The results show that the designed controller has fast response and robustness under various conditions.

This paper is organized as follows. In second section, the mathematical model of PMSM is introduced. In third section, the backstepping controller is constructed. In fourth section, the nonlinear disturbance observer is studied. Simulation and experiment are demonstrated in fifth section, which is followed by conclusion in sixth section.

Mathematical Model of PMSM

According to rotor field-oriented method, the mathematical model of the PMSM in the dq-axes rotor reference frame can be expressed as

$$\left\{ \begin{aligned} \frac{{{\text{d}}i_{d} }}{{{\text{d}}t}} & = \frac{{ - R_{s} i_{d} + n_{p} \omega L_{q} i_{q} }}{{L_{d} }} + \frac{1}{{L_{d} }}u_{d} + f_{d} \\ \frac{{{\text{d}}i_{q} }}{{{\text{d}}t}} & = \frac{{ - R_{s} i_{q} - n_{p} \omega L_{d} i_{d} - n_{p} \omega \varPhi }}{{L_{q} }} + \frac{1}{{L_{q} }}u_{q} + f_{q} \\ \frac{d\omega }{dt} & = \frac{{n_{p} \left[ {(L_{d} - L_{q} )i_{d} i_{q} + \varPhi i_{q} } \right] - B\omega }}{{J_{m} }} + f_{w} \\ \end{aligned} \right.,$$
(1)

where \(L_{d}\) and \(L_{q}\) represent d-axes and q-axes stator inductances, \(i_{d}\) and \(i_{q}\) are the stator current, \(u_{d}\) and \(u_{q}\) are the stator input voltage in dq-axes reference frame, \(R_{s}\) is the per-phase stator resistance, \(n_{p}\) is the number of pole pairs, \(\omega\) is the mechanical angular speed of the rotor, \(\varPhi\) is the rotor flux, \(J_{m}\) is the moment of inertia, \(B\) is the viscous friction coefficient, \(f_{d}\), \(f_{q}\) and \(f_{w}\) represent the disturbance caused by the parameter variations and external load torque, and they are given by

$$\left\{ \begin{aligned} f_{d} & = - \frac{1}{{L_{d} }}\left( {\Delta R_{s} i_{d} - \Delta L_{q} n_{p} \omega i_{q} + \Delta L_{d} \frac{{{\text{d}}i_{d} }}{{{\text{d}}t}}} \right) \\ f_{q} & = - \frac{1}{{L_{q} }}\left( {\Delta R_{s} i_{q} + \Delta L_{d} n_{p} \omega i_{d} + \Delta \varPhi n_{p} \omega + \Delta L_{q} \frac{{{\text{d}}i_{q} }}{{{\text{d}}t}}} \right) \\ f_{w} & = - \frac{1}{{J_{m} }}\left( {\Delta J_{m} \frac{d\omega }{dt} + \Delta B\omega + \tau_{L} - n_{p} (\Delta L_{d} - \Delta L_{q} )i_{d} i_{q} - n_{p} \Delta \varPhi i_{q} } \right) \\ \end{aligned} \right.,$$
(2)

where \(\tau_{L}\) is the load torque, \(\Delta R_{s} = R_{st} - R_{s}\), \(\Delta L_{d} = L_{dt} - L_{d},\)\(\Delta L_{q} = L_{qt} - L_{q},\)\(\Delta \varPhi = \varPhi_{t} - \varPhi,\)\(\Delta J_{m} = J_{mt} - J_{m},\)\(\Delta B = B_{t} - B,\) in which \(R_{s},\)\(L_{d},\)\(L_{q},\)\(\varPhi\), \(J_{m}\) and \(B\) denote the nominal parameter values. \(R_{st}\), \(L_{dt}\), \(L_{qt}\), \(\varPhi_{t}\), \(J_{mt}\) and \(B_{t}\) are the actual parameter values. The disturbance is assumed to be bounded and changed slowly in the system, thus

$$\frac{{df_{d} }}{dt} = \frac{{df_{q} }}{dt} = \frac{{df_{w} }}{dt} = 0.$$
(3)

Thus, the motor model (1) can be considered as a nonlinear system with the state variables \(x = (\begin{array}{*{20}c} {x_{1} } & {x_{2} } & {x_{3} } \\ \end{array} )^{T} = (\begin{array}{*{20}c} {i_{d} } & {i_{q} } & \omega \\ \end{array} )^{T},\) the input variables \(u = (\begin{array}{*{20}c} {u_{d} } & {u_{q} } \\ \end{array} )^{T},\) and the output variables \(y = (\begin{array}{*{20}c} {y_{1} } & {y_{2} } \\ \end{array} )^{T} = (\begin{array}{*{20}c} {i_{d} } & \omega \\ \end{array} )^{T}\). Meanwhile, the system has the disturbance \(d = (\begin{array}{*{20}c} {f_{d} } & {f_{q} } & {f_{w} } \\ \end{array} )^{T}\).

Given the PMSM system model (1), the paper attempts to devise a robust feedback control law scheme which allows for the accurate tracking of the given reference speed by using backstepping control and nonlinear disturbance observer.

Design of Backstepping Controller For PMSM

The control task is to find a controller that adjusts the stator voltage to realize the fast speed and current tracking

regulation of PMSM drive. Simultaneously the controller has the ability of rejecting the disturbance, such as parameter variations, model uncertainties and the load torque disturbance. Thus an improved backstepping controller with nonlinear disturbance observer is proposed in this paper.

This section introduces the main design steps of the backstepping method for PMSM. The variables to be controlled are the components of the output speed and current. The task is to find the input action to realize the speed and current tracking control.

The backstepping controller is completed by the recursive design. The design procedure starts from determining the fictitious control input for the motor speed.

Firstly, define \(e = \omega^{*} - \omega\), where \(\omega^{*}\) is the reference speed of the motor. The reference d-axes current \(i_{d}^{*}\) is usually set to be zero to maintain a constant flux operating condition. Then the motor model given by (1) can be modified to

$$\frac{d\omega }{dt} = \frac{{n_{p} \varPhi i_{q} - B\omega }}{{J_{m} }} + f_{w} .$$
(4)

Then

$$\dot{e} = \dot{\omega }^{*} - \dot{\omega } = \dot{\omega }^{*} - \frac{{n_{p} \varPhi i_{q} }}{{J_{m} }}{ + }\frac{B\omega }{{J_{m} }} - f_{w} .$$
(5)

The next step is to consider the reference q-axes current \(i_{q}^{*}\) as a virtual control input to the output speed, and then choose the Lyapunov function as \(V_{1} = \frac{1}{2}e^{2}\). The time derivative of \(V_{1}\) is

$$\begin{aligned}\dot{V}_{1} & = e\dot{e} = e\dot{\omega }^{*} - \frac{{n_{p} \varPhi i_{q} }}{{J_{m} }}e + \frac{B\omega }{{J_{m} }}e - f_{w} e \\ & = - k_{s} e^{2} - \frac{e}{{J_{m} }}\left( {n_{p} \varPhi i_{q} - B\omega + J_{m} f_{w} - J_{m} \dot{\omega }^{*} - k_{s} J_{m} e} \right), \\ \end{aligned}$$
(6)

where \(k_{s}\) is a positive constant.

Therefore, to force (6) become negative definite, the virtual control input can be designed as

$$i_{q}^{*} = \frac{1}{{n_{p} \varPhi }}\left( {B\omega - J_{m} f_{w} + J_{m} \dot{\omega }^{*} + k_{s} J_{m} e} \right).$$
(7)

Then, substitute (7) into (6), \(\dot{V}_{1} = - k_{s} e^{2} \le 0\) can be guaranteed.

Continuing with the backstepping control, for stabilizing the current components, the dq-axes current tracking error can be defined as

$$e_{d} = i_{d}^{*} - i_{d} ,e_{q} = i_{q}^{*} - i_{q} .$$
(8)

Substitute (1), (4), (7) into (8), the time derivative of \(e_{d}\) and \(e_{q}\) is

$$\dot{e}_{d} = \dot{i}_{d}^{*} - \dot{i}_{d} = \frac{{R_{s} i_{d} - n_{p} \omega L_{q} i_{q} }}{{L_{d} }} - \frac{1}{{L_{d} }}u_{d} - f_{d} - k_{d} e_{d} + k_{d} e_{d} ,$$
(9)
$$\begin{aligned} \dot{e}_{q} & = \dot{i}_{q}^{*} - \dot{i}_{q} \\ & = \frac{1}{{n_{p} \varPhi }}(B\dot{\omega } - J_{m} \dot{f}_{w} + J_{m} \ddot{\omega }^{*} + k_{s} J_{m} \dot{e}) - \dot{i}_{q} \\ & = \frac{1}{{n_{p} \varPhi }}\left[ {B\left( {\frac{{n_{p} \varPhi i_{q} - B\omega }}{{J_{m} }} + f_{w} } \right) + J_{m} \ddot{\omega }^{*} + k_{s} (J_{m} \dot{\omega }^{*} - n_{p} \varPhi i_{q} + B\omega - J_{m} f_{w} )} \right] - \dot{i}_{q} \\ & = \frac{1}{{n_{p} \varPhi }}\left[ {B\left( {\frac{{n_{p} \varPhi i_{q} - B\omega }}{{J_{m} }} + f_{w} } \right) + J_{m} \ddot{\omega }^{*} + k_{s} (J_{m} \dot{\omega }^{*} - n_{p} \varPhi i_{q} + B\omega - J_{m} f_{w} } \right] \\ & \quad + \frac{{R_{s} i_{q} + n_{p} \omega L_{d} i_{d} + n_{p} \omega \varPhi }}{{L_{q} }} - \frac{1}{{L_{q} }}u_{q} - f_{q} - k_{q} e_{q} + k_{q} e_{q} , \\ \end{aligned}$$
(10)

where \(k_{d} > 0\), \(k_{q} > 0\).

Define a new Lyapunov function be \(V_{2} = \frac{1}{2}e^{2} + \frac{1}{2}e_{d}^{2} + \frac{1}{2}e_{q}^{2}\), then \(\dot{V}_{2} = e\dot{e} + e_{d} \dot{e}_{d} + e_{q} \dot{e}_{q}\). From (9) and (10), the dq-axes current tracking error dynamics can be stabilized if the control inputs are designed as

$$u_{d} = L_{d} \left( {\frac{{R_{s} i_{d} - n_{p} \omega L_{q} i_{q} }}{{L_{d} }} - f_{d} + k_{d} e_{d} } \right),$$
(11)
$$\begin{aligned} u_{q} & = \frac{{L_{q} }}{{n_{p} \varPhi }}\left[ \begin{aligned} B\left( {\frac{{n_{p} \varPhi i_{q} - B\omega }}{{J_{m} }} + f_{w} } \right) + J_{m} \ddot{\omega }^{*} + k_{s} (J_{m} \dot{\omega }^{*} - n_{p} \varPhi i_{q} \hfill \\ + B\omega - J_{m} f_{w} \hfill \\ \end{aligned} \right] \\ & \quad + R_{s} i_{q} + n_{p} \omega L_{d} i_{d} + n_{p} \omega \varPhi - L_{q} f_{q} + k_{q} e_{q} . \\ \end{aligned}$$
(12)

Therefore, \(\dot{V}_{2} = - k_{s} e^{2} - k_{d} e_{d}^{2} - k_{q} e_{q}^{2} \le 0\), and the closed-loop system is asymptotically stable, and the objective of speed and current control is attained when the controller are designed as (11) and (12). However, it can be seen that the disturbance \(f_{d}\), \(f_{q}\) and \(f_{w}\) are included in the controller. The speed and current tracking performance may be affected significantly by the various disturbance. For this reason, its necessary to consider the disturbance to strength the robustness of the backstepping controller.

Design of Nonlinear Disturbance Observer For PMSM

In practical PMSM control system, the disturbance is unavoidable and undetectable. To strengthen the robust performance of the backstepping controller, a nonlinear disturbance observer [31,32,33] is designed to estimate the lump disturbance, which includes the matched and mismatched disturbance. The observer design process is as follows.

According to the model of PMSM in (1), define

$$f(x) = \left[ {\begin{array}{*{20}c} {f_{1} (x)} \\ {f_{2} (x)} \\ {f_{3} (x)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\frac{{ - R_{s} i_{d} + n_{p} \omega L_{q} i_{q} }}{{L_{d} }}} \\ {\frac{{ - R_{s} i_{q} - n_{p} \omega L_{d} i_{d} - n_{p} \omega \varPhi }}{{L_{q} }}} \\ {\frac{{n_{p} \left[ {(L_{d} - L_{q} )i_{d} i_{q} + \varPhi i_{q} } \right] - B\omega }}{{J_{m} }}} \\ \end{array} } \right],\quad g_{1} (x) = \left[ {\begin{array}{*{20}c} {\frac{1}{{L_{d} }}} & 0 & 0 \\ 0 & {\frac{1}{{L_{q} }}} & 0 \\ \end{array} } \right]^{T} .$$

Then, a nonlinear disturbance observer is designed as

$$\left\{ \begin{aligned} \dot{z}_{d} & = - l(x)z_{d} - l(x)(\lambda (x){ + }f(x) + g_{1} (x)u) \\ \hat{d} & = z_{d} + \lambda (x) \\ \end{aligned} \right.,$$
(13)

where \(\hat{d} = \left[ {\begin{array}{*{20}c} {\hat{f}_{d} } & {\hat{f}_{q} } & {\hat{f}_{w} } \\ \end{array} } \right]^{T}\) is the estimated disturbance, \(z_{d}\) is the internal state variable of the observer, \(\lambda (x)\) is a nonlinear function designed for the observer, \(l(x)\) is the observer gain, and

$$l(x) = \frac{\partial \lambda (x)}{\partial x}.$$
(14)

Define the disturbance error \(\tilde{d} = d - \hat{d}\), the following can be derived as

$$\dot{\tilde{d}} = - l(x)\tilde{d} + \dot{d}.$$
(15)

Replace the disturbance terms in (7), (11) and (12) by the estimated values, then submit the backstepping controller (7), (13), (14) into (1) and (4), the following can be derived as

$$\dot{z} = Az + B\tilde{d},$$
(16)

where

$$z = \left[ {\begin{array}{*{20}c} {i_{d} - i_{d}^{*} } \\ {\omega - \omega^{*} } \\ {\dot{\omega } - \dot{\omega }^{*} } \\ \end{array} } \right],\quad A = \left[ {\begin{array}{*{20}c} { - k_{d} } & 0 & 0 \\ 0 & 0 & 1 \\ 0 & { - \frac{{k_{q} k_{s} }}{{L_{q} }}} & { - k_{s} - \frac{{k_{q} }}{{L_{q} }}} \\ \end{array} } \right],\quad B = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & { \frac{{n_{p} \varPhi }}{{J_{m} }}} & {k_{s} + \frac{{k_{q} }}{{L_{q} }} - \frac{B}{{J_{m} }}} \\ \end{array} } \right].$$

From (15) and (16),

$$\left[ {\begin{array}{*{20}c} {\dot{z}} \\ {\dot{\tilde{d}}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} A & B \\ 0 & { - l(x)} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} z \\ {\tilde{d}} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} 0 \\ {\dot{d}} \\ \end{array} } \right].$$
(17)

Then choose \(l(x)\) and make \(\left[ {\begin{array}{*{20}c} A & B \\ 0 & { - l(x)} \\ \end{array} } \right]\) to be Hurwtiz, the asymptotic stability of (17) can be ensured.

Thus, the final designed controller can be derived as

$$u_{d} = L_{d} \left( {\frac{{R_{s} i_{d} - n_{p} \omega L_{q} i_{q} }}{{L_{d} }} - \hat{f}_{d} + k_{d} e_{d} } \right),$$
(18)
$$\begin{aligned} u_{q} & = \frac{{L_{q} }}{{n_{p} \varPhi }}\left[ \begin{aligned} B\left( {\frac{{n_{p} \varPhi i_{q} - B\omega }}{{J_{m} }} + \hat{f}_{w} } \right) + J_{m} \ddot{\omega }^{*} + k_{s} (J_{m} \dot{\omega }^{*} - n_{p} \varPhi i_{q} \hfill \\ + B\omega - J_{m} \hat{f}_{w} \hfill \\ \end{aligned} \right] \\ & \quad + R_{s} i_{q} + n_{p} \omega L_{d} i_{d} + n_{p} \omega \varPhi - L_{q} \hat{f}_{q} + k_{q} e_{q} . \\ \end{aligned}$$
(19)

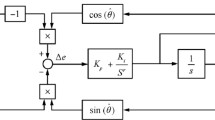
To verify the speed and current control performance of PMSM, a single-loop controller based on backstepping control and nonlinear disturbance observer is designed instead of the traditional cascade control structure including a speed loop and two current loops. Compared with the traditional method, the novel controller parameters are more convenient to be adjusted. The PMSM drive system structure investigated in this work is shown in Fig. 1. The control system includes an interior PMSM, an inverter, a pulse width modulation (PWM) module, two coordinate transformation modules and the designed motor controller. As seen in Fig. 1, the rotor angular speed and the rotor position can be obtained from the sensor. The dq-axes current can be calculated from the phase current by Clarke and Park transformation.

Fig. 1
figure 1

Block diagram of PMSM control system

Full size image

Simulation and Experiment

Simulation and Analysis

The simulation based Matlab/Simulink for the PMSM drive system is completed to demonstrate the effectiveness of the proposed novel motor control method. The motor parameters are given in Table 1. In the simulation, the PMSM system under two speed control schemes, i.e., the proposed backstepping control with disturbance observer and PI control, are compared. The parameters in the backstepping controller are designed as \(k_{s} = 5000\), \(k_{d} = 3000\), \(k_{q} = 3000\), and the observer gain is set as \(l(x) = diag(\begin{array}{*{20}c} {100} & {100} & {100} \\ \end{array} )\). The sample time in the controller is \(T_{s} = 0.05ms\).To have a fair comparison, the parameters of the PI controller are obtained by trial and error so as to achieve satisfactory performance. In order to ensure the smoothness of the reference speed, the reference speed is passed through a second order linear filter as \(F(s) = \frac{{\omega_{n}^{2} }}{{s^{2} + 2\xi \omega_{n} s + \omega_{n}^{2} }}\), where \(\xi = 1\), \(\omega_{n} = 100\).

Table 1 Parameters of PMSM
Full size table

The reference speed is given as 1000r/min. The speed response waveforms of two methods are shown in Fig. 2a, the dq-axes current waveforms of the proposed method are shown in Fig. 2b. Then a disturbance torque \(\tau_{L} = 1\,{\text{N}}\,{\text{m}}\) is added at t = 0.5 s, the comparison simulation results are shown in Fig. 3. Figure 3a is the speed variation waveforms of two methods. Figure 3b is the current variation waveforms of the proposed method. As seen in the figures, when the motor is started, the proposed backstepping control with disturbance observer has the faster transient response and the smaller overshoot. When the load torque is changed, both the controllers have proved to be effective regarding disturbance rejection, but a large speed error during transients is observed with PI controller and a long time is needed to recover to the reference speed.

Fig. 2
figure 2

Simulation results of two methods when the motor is started

Full size image
Fig. 3
figure 3

Simulation results of two methods with load disturbance

Full size image

The robustness of the designed controller is verified while the motor parameters have perturbation. Firstly, the electrical parameters are changed. The values of rotor-flux linkage, armature resistance, and dq-axes inductance are changed to 80, 200 and 150% of the normal values in the motor, respectively. Similarly, the load disturbance \(\tau_{L} = 1\,{\text{N}}\,{\text{m}}\) is added to the motor at t = 0.5 s. The simulation results are shown in Fig. 4. Then, the mechanical parameters are changed in the motor. The values of the moment of inertia and the viscous friction coefficient are turned to two times of the normal values. The simulation results are shown in Fig. 5.

Fig. 4
figure 4

Simulation results of the proposed method with electrical parameter variations

Full size image
Fig. 5
figure 5

Simulation results of the proposed method with mechanical parameter variations

Full size image

It can be seen in Figs. 4 and 5 that the designed controller could eliminate the steady-state error between the actual speed and the reference speed when the parameters have disturbance, and the speed could track the reference speed quickly. Meanwhile, the motor still has the good transient response and the strong robustness for the disturbance torque.

Experiment and Analysis

The experimental platform is shown in Fig. 6, which consists of a six-pole 0.72 kW PMSM coupled to a dynamometer, and an IPM based on inverter with dSPACE as a controller. dSPACE is powerful processor. For the reason that it can automatically implement the Simulink models on the real-time hardware, it is very convenient to test the new control strategy in a real environment quickly and without barriers for motor drive system. The system adopts single-phase rectification supplied by AC 220 V. For the reason that the rated voltage of motor is 330 V, the motor cannot reach the condition of rated operation under the supply voltage in the experiment. The phase current is measured by the Hall-effect sensors. A resolver is used to measure the rotor speed and absolute rotor position. In the experiment, the load torque is provided by hysteresis dynamometer. The experimental results are shown in Figs. 7, 8, 9, 10, 11.

Fig. 6
figure 6

Experimental platform of PMSM control system

Full size image
Fig. 7
figure 7

Experimental results of two methods when the motor is started

Full size image
Fig. 8
figure 8

Experimental results of two methods with load disturbance

Full size image
Fig. 9
figure 9

Experimental results of the proposed method with speed variation

Full size image
Fig. 10
figure 10

Experimental results of the proposed method with electrical parameter variations

Full size image
Fig. 11
figure 11

Experimental results of the proposed method with mechanical parameter variations

Full size image

Firstly, the reference speed is given as 1000 r/min, and the motor is started with no-load. When the motor is running at a steady state of 1000 r/min, the load torque \(\tau_{L} = 1\,{\text{N}}\,{\text{m}}\) is suddenly added to the system. The experimental comparison between backstepping control with nonlinear disturbance observer and PI control is completed. Figure 7a is the speed response waveforms of two different methods when the motor is started. Figure 7b is the dq-axes current waveforms based on the proposed controller. Figure 8a is the speed variation waveforms of two methods when the load disturbance is added. Figure 8b is the dq-axes current variation waveforms based on the proposed controller. Figure 9 shows the speed and current response waveforms with the proposed controller when the reference speed is changed to 1500 r/min.

As seen in the experimental results, compared with the PI controller, the motor speed with the proposed controller has the faster transient response and the smaller overshoot. The dq-axes current can quickly converge to the stable values and the d-axis current is maintained at zero. When the load torque is added, both controllers can restrain the disturbance effectively. But compared with PI controller, the novel controller has less speed fluctuations and shorter recovering time. Meanwhile, the d-axes current is still equal to zero. For the reason that the identification of motor parameters have slightly error and the load torque added in the experiment by the hysteresis dynamometer are not completely accurate, thus, the q-axes current have the difference in the simulation and experimental results. When the motor speed is changed, it can be seen that the speed can quickly track the reference value with small overshoot also.

Tests have also been performed to verify the robustness of the proposed control scheme with respect to the parameter variations. The experiment includes two parts. (1) The electrical parameters are changed in the controller. The value of rotor-flux linkage is increased by 50%, the value of armature resistance is decreased by 50%, and the values of the dq-axes inductance is decreased by 25%. (2) The mechanical parameters are changed in the controller. The values of the moment of inertia and the viscous friction coefficient are decreased by 50%. Figures 10 and 11 show the results in both cases. As shown in the Figs. 10 and 11, the speed and current waveforms are almost not affected because the observer can modify the control to cancel the offset caused by the parameter variations. The precise speed and current tracking control is achieved in the experiment.

Conclusion

This paper studies a novel speed and current single-loop control method for PMSM drive system based on backstepping control theory. The lump disturbance including the parameter perturbation, model uncertainties and external load disturbance is considered in the backstepping controller. To improve the robustness, a nonlinear disturbance observer method is adopted to estimate the lump disturbance in the system, which is used to the feed-forward compensation control. The controller combines the merit of both backstepping control and disturbance observer. Simulation and experiment results prove that the designed controller has excellent transient speed response and strong robustness. The controller parameters are easy to be regulated, so it provides an effective approach for the engineering application.