1 Introduction

The limited supply of conventional fossil fuels cannot cope with the ever-growing energy demands. Thus, there is a growing interest in search of alternative systems, harnessing the full potential of renewable energy sources. Hydrogen is an abundant, renewable, and clean-burning fuel that produces only water upon its combustion. It has the highest energy density per unit mass (between 120 and 142 MJ/kg) and can provide high on-demand power [1, 2]. The application scope of hydrogen fuel cells (HFCs) is vast, particularly in transportation (such as cars, buses, and forklift trucks) and HFC-based backup power [3,4,5]; the space industry is widely using hydrogen as a fuel in rocket propulsion systems. Even though with these exceptional qualities, HFCs are still not fully commercialized due to the low-volumetric density of hydrogen gas, which makes it very challenging for onboard storage.

A robust and reliable hydrogen storage system that is compact, portable, safe, cost-efficient, and provides faster kinetics could be functional for a sustainable hydrogen economy. There are two general methods for hydrogen storage: (i) physical storage based on utilizing high pressures and cryogenic temperatures, and (ii) material storage based on chemisorption and physisorption [6,7,8,9,10]. Physisorption is the result of weak van der Waals force of attractions due to fluctuating dipole moments on the interacting adsorbate and adsorbent. For transportation purposes, hydrogen storage by material-based physisorption is an attractive method as there is no chemical dissociation of molecules and no fuel contamination [11]. On the other hand, it provides faster kinetics for discharging and refueling than reactive hydrogen storage [12]. For the year 2020, the US Department of Energy (DOE) has set a goal for a storage system that delivers hydrogen at a gravimetric and volumetric capacity of 4.5 wt % hydrogen and 0.030 kg hydrogen/L, respectively [13].

Graphene [14], a single layer that is made of hexagonally arranged carbon atoms, demonstrates excellent mechanical strength [15, 16], thermal stability [17], and possesses a high-specific surface area (SSA) of ~ 2630 m2g−1 [18]. In addition to these remarkable properties, graphene has good reversibility, faster adsorption, and desorption kinetics [19]. Graphene also has potential application in nanocomposites as a reinforcement agent [20], gas barrier [21], and nanoelectromechanical systems [22]. For solid-state hydrogen storage, SSA plays a vital role in achieving high-gravimetric density for hydrogen storage [23, 24]. Various chemical reactions can also be used to tune graphene properties and their interlayer spacing [25], thus enhancing the adsorption properties.

Several experimental investigations and simulation studies based on density functional theory (DFT) and grand canonical Monte Carlo (GCMC) simulations have been reported for hydrogen storage on graphene sheets [26,27,28,29,30,31]. Wang and Johnson [32] performed GCMC simulations on graphitic nanofibers and hydrogen atoms in an attempt to explain the solid–fluid behavior at the nanoscale level as reported by Chambers et al. [33]. They concluded that no realistic potential could account for the high hydrogen adsorption reported by Chambers et al. [33]. The studies of Jhi [34] and Torres et al. [35] on chemically activated nanostructured carbon to investigate hydrogen storage reveal that hydrogen sorption can be controlled by modifying the structure and chemistry of pores. They reported high adsorption energy of about 0.301 eV and a gravimetric density of 2.7% for nanostructured-activated carbon. Ma et al. [24] measured 0.4 wt% and < 0.2 wt% hydrogen uptakes of graphene at cryogenic and room temperature, respectively, with a BET surface area of 156 m2g−1. Their investigations suggest that low SSA is responsible for the small gravimetric uptake. López-Corral et al. [36] computationally observed hydrogen adsorption on palladium (Pd)-decorated graphene sheets using the tight-binding model and reported a strong C–Pd and Pd–H bonds, which promote dissociation of hydrogen molecules and bonding between atomic hydrogen and carbon surface. Huang et al. [37] experimentally investigated graphene samples decorated with Pd and platinum (Pt) for hydrogen storage at 303 K temperature and up to a 5.7 MPa pressure. They concluded that the decoration of Pd or Pt metals doubles the adsorption capacity and supports the existence of spillover effect. Recently, a review article [31] reports the hydrogen storage capabilities of chemically altered graphene composites and discusses the promising techniques to control the binding energy of H2 molecules such as surface chemical modifications and metal catalyst dispersion. They concluded that structural and chemical modifications might introduce new materials that may elevate the current storage capabilities. Shiraz and Tavakoli [26] reviewed the graphene-based nanomaterials for hydrogen storage. They reported that doping of graphene with alkali or transition metals shows an increase in gravimetric hydrogen density and validated this using density functional theory [38]. Their ab initio study confirmed that hydrogen favors hollow sites and revealed that graphene-like boron nitride heterostructure shows advanced adsorption behavior compared with its counterparts i.e., graphene. Feng et al. [39] studied hydrogen adsorption on carbon nanostructures such as graphene, multi-walled CNT, and activated carbon with varying SSA at cryogenic temperatures. They reported that graphene sheets have high potential as a hydrogen storage media with isosteric heat of adsorption about 4.01–5.88 kJ/mol and also revealed that adsorbent with fold structure is more beneficial than pore structure.

A literature survey over the two decades suggests that numerous experimental and theoretical studies were performed on CNTs, CNFs, graphene, and metal hydrides for hydrogen storage. These works of literature lack a detailed computational and analytical study of the effect of temperature and pressure on the hydrogen adsorption capacity of a graphene sheet. Therefore, it is of great significance to investigate hydrogen adsorption behavior on graphene to analyze the gravimetric density and adsorption energy of hydrogen. Low temperature and high pressures are the extreme optimum conditions where a high gravimetric density can be achieved with a low-cost volumetric setup. For instance, hydrogen is transported in the cryogenic vessels in large quantities and at high pressures in composite pressure vessels at high gravimetric density [8,9,10]. To the best of current authors’ knowledge, no single MDS study is performed to study the effect of temperature and pressure on graphene sheets’ hydrogen adsorption capacity. Keeping in mind the practical application aspects related to hydrogen storage process at low temperature (77–300 K) and pressures in the range of 1–10 MPa, we investigated hydrogen adsorption behavior of graphene under varied conditions using a novel energy-centered method. To accomplish this, an innovative framework is needed to be developed to improve the conceptual knowledge of graphene adsorption properties. The present work attempts to simulate hydrogen adsorption on monolayer graphene using MDS and introduce a pathway for creating novel materials based on computational techniques that can hold hydrogen at ambient conditions through physisorption. The obtained isotherms at different temperatures are fitted over the available isotherm models.

2 Methodology

MDS allow studying the mechanisms and behaviors of nanomaterials which no other simulation methods can perform in a computationally efficient manner. MDS carried out in this study uses the Large Scale Atomic/Molecular Massively Parallel Simulator (LAMMPS), an open-source package developed by Sandia National laboratories [40]. To study the influence of graphene sheet size, square sheets with edge lengths ranging from 50 to 200 Å were considered. The results of MDS were fitted over different analytical adsorption equations.

2.1 Molecular dynamics simulations

To carry out MDS, first, a graphene sheet surrounded by hydrogen molecules was modeled. Perfect graphene lattices were modeled separately using VESTA [41] and then imported into the simulation box. The modeled graphene sheet structures were relaxed to achieve stress-free sheets at a given temperature, and then H2 molecules were randomly added surrounding the graphene sheet.

In all MD calculations, periodic boundary conditions were applied in the in-plane directions of graphene sheet to eliminate the free-edge effects, and out-of-plane direction was applied with periodic boundary conditions with large dimensions to avoid any interlayer interactions. Figure 1a illustrates the relaxed graphene sheet placed in the middle of the simulation box and hydrogen molecules randomly surrounding the sheet. The interatomic interactions of the carbon atoms in the graphene sheet were modeled using Tersoff potential [42] as it has been successfully applied to predict the properties of graphene [43,44,45,46].

Fig. 1
figure 1

System configuration of graphene sheet and H2 molecules: a initial system configuration with relaxed graphene sheet, b system at simulation time 1 ns, and c adsorbed H2 molecules around graphene

Full size image

In Tersoff potential, the potential energy (E) of an atomic configuration is a function of the distance rij between two neighbouring atoms i and j:

$$E = \mathop \sum \limits_{i} E_{i} = \frac{1}{2}\mathop \sum \limits_{i \ne j} V_{ij} ,$$
(1)

where,

$$V_{ij} = f_{c} \left( {r_{ij} } \right)\left[ {f_{R} \left( {r_{ij} } \right) + b_{ij} f_{A} \left( {r_{ij} } \right)} \right],$$
(2)
$$f_{R} \left( r \right) = A {\text{exp}}\left( { - \lambda_{1} r} \right),$$
(3)
$$f_{A} \left( r \right) = - B{\text{ exp}}\left( { - \lambda_{2} r} \right),$$
(4)
$$f_{c} \left( r \right) = \left\{ {\begin{array}{ll} {1,} & {r < R - D} \\ {\frac{1}{2} - \frac{1}{2}{\text{sin}}\left( {\frac{\pi }{2} \frac{r - R}{D}} \right), } & {R - D < r_{ij} < R + D} \\ {0,} & {r_{ij} > R + D} \\ \end{array} } \right. ,$$
(5)
$$b_{ij} = \left( {1 + \beta^{n} \zeta_{ij}^{n} } \right)^{{ - \frac{1}{2n}}} ,$$
(6)
$$\zeta_{ij} = \mathop \sum \limits_{k \ne i,j} f_{c} \left( {r_{ik} } \right) g\left( {\theta_{ijk} } \right) exp\left[ {\lambda_{3}^{m} \left( {r_{ij} - r_{ik} } \right)^{m} } \right],$$
(7)
$$g\left( \theta \right) = \gamma_{ijk} \left( {1 + \frac{{c^{2} }}{{d^{2} }} - \frac{{c^{2} }}{{\left[ {d^{2} + \left( {\cos \theta - \cos \theta_{0} } \right)^{2} } \right]}}} \right),$$
(8)

where Vij is the potential energy of the pair, fR and fA are the repulsive and attractive pair potentials with fc as a cut-off function. Also, fR is a two-body term, and fA includes three-body interactions. The summations in the formula are overall neighbors J and K of an atom I within a cut-off distance equal to R + D. bij term is the many-body parameter that describes how the bond formation energy is affected due to the presence of neighboring atoms. A physisorption based interaction between H2 molecules and carbon atoms was modeled using Lennard–Jones (LJ) 12–6 potential

$$u_{ij} = 4\varepsilon_{ij} \left[ {\left( {\frac{{\sigma_{ij} }}{r}} \right)^{12} - \left( {\frac{{\sigma_{ij} }}{r}} \right)^{6} } \right],$$
(9)

where \({u}_{ij}\) is the pairwise interaction energy, and \({\varepsilon }_{ij}\) and \({\sigma }_{ij}\) are the well-depth energy and the distance at which pair interaction energy goes to zero, respectively. The cut-off distance of 12 Å was chosen for LJ interactions. Table 1 describes the LJ potential parameters used in this work reported by Cracknell [47]. Carbon atoms and H2 molecules interactions were obtained using Lorentz-Berthelot mixing rules:

$$\varepsilon_{ij} = \sqrt {\varepsilon_{ii} \varepsilon_{jj} }\, \sigma_{ij} = \frac{{\sigma_{ii} + \sigma_{jj} }}{2},$$
(10)
Table 1 LJ interaction parameters for carbon atoms and hydrogen molecules
Full size table

Initially, carbon atoms were arranged according to the ideal graphene atomic configuration at 0 K with a lattice constant of 0.148 nm. For all simulations, a timestep of 1.0 fs was considered to encapsulate the adsorption dynamics. The conjugate gradient method was applied with an energy convergence of 10–10 kcal mol−1 [48] to obtain an energy minimized graphene sheet. After energy minimization, the system was equilibrated for 250 ps under isothermal and isobaric conditions to achieve a stress-free and equilibrated sheet in planar directions. H2 molecules were added randomly in the simulation box above and below the relaxed graphene sheet. The number of H2 molecules added to the system was arbitrarily chosen to be about six molecules of H2 per carbon atom in the graphene sheet. A long equilibration step of 15 ns was performed to ensure an equilibrated system with a uniform distribution, as shown in Fig. 2. It can be seen that the system gets equilibrated after 2 ns, so to save the computational time, all subsequent MDS runs were conducted for 4 ns. In all MDS, the system ran for 250 ps to achieve the desired system temperature and pressure. After that, an equilibration run of 4 ns was performed under the isothermal and isobaric conditions. Nosé–Hoover thermostat and barostat were used for controlling the temperature and pressure of the system, respectively. The above simulation steps were performed multiple times for each set of pressure and temperature to obtain reliable results.

Fig. 2
figure 2

a Time evolution of the system at 77 K and 1 MPa, respectively, and b variation of potential energy of the system and adsorption of H2 molecules with the time

Full size image

The amount of hydrogen adsorbed was calculated by observing the distribution of potential energy of each particle, discussed in detail in Sect. 3. The gravimetric density (wt%) was calculated by

$$\delta \left( {{\text{wt}}\% } \right) = \frac{{w_{{\text{H2-adsorbed}}} }}{{w_{{\text{H2-adsorbed}}} + w_{{\text{c-Graphene}}} }},$$
(11)

where, \(w_{{\text{H2-adsorbed}}}\) is the weight of adsorbed hydrogen molecules and \(w_{{\text{c-Graphene}}}\) is the weight percentage of the graphene sheet. The adsorption energy was calculated by

$$E_{{{\text{adsorption}}}} = E_{{\text{Graphene + H2}}} - \left( {E_{{{\text{Graphene}}}} + E_{{{\text{H2}}}} } \right),$$
(12)

where, \({E}_{\mathrm{Graphene}}\) is the potential energy of graphene sheet, \({E}_{\mathrm{H}2}\) is the potential energy of one hydrogen molecule and \({E}_{\mathrm{Graphene}+\mathrm{H}2}\) is the potential energy of the graphene sheet with adsorbed hydrogen molecules.

2.2 Adsorption isotherms

To explain the adsorption behavior between adsorbate (hydrogen) and adsorbent (graphene) at different pressures, various analytical expressions of adsorption isotherms are used in this work. These equations define the adsorption capacity (q) of the adsorbent as a function of pressure (p) for a specific temperature.

2.2.1 Langmuir isotherm

The Langmuir theory [49] assumes that the adsorbate adheres to the adsorbent and covers the surface forming a monolayer of the adsorbate. It also assumes the adsorption to be homogeneous, i.e., all adsorption sites are equal. At low pressures, this dense state allows higher volumes to be stored by sorption than is possible by compression

$$q = \frac{{q_{mL} K_{L} p}}{{1 + K_{L} p}},$$
(13)

where q is the amount of adsorbate on the surface adsorbent at a pressure p. qmL is the constant reflecting theoretical monolayer capacity, and KL is the affinity constant or Langmuir constant, which indicates the strength of adsorption.

2.2.2 Freundlich isotherm

Freundlich isotherm [50] defines the surface heterogeneity and the exponential distribution of active sites and their energies. Its expression applies to heterogeneous adsorption, and the expression is given by

$$q = K_{L} p^{{n_{F} }} ,$$
(14)

where KF is the Freundlich constant, and nF is the heterogeneity factor.

2.2.3 Sips (Langmuir–Freundlich) isotherm

The Sips isotherm [51] is a combination of the Langmuir and Freundlich isotherms. Its general expression is

$$q = \frac{{q_{mS} K_{S} p^{{n_{S} }} }}{{1 + K_{S} p^{{n_{S} }} }},$$
(15)

where qmS is the maximum adsorption capacity at a particular temperature, KS is the Sips constant, and nS is the heterogeneity factor. If nS is equal to 1, the Sips equation is reduced to the Langmuir equation, and the surface is homogeneous.

2.2.4 Toth isotherm

Toth isotherm [52] is another modification of Langmuir isotherm with an aim to reduce the actual and predicted data differences. It is also applicable to heterogeneous adsorption. Most sites have adsorption energy lower than the maximum. The Toth equation assumes the asymmetrical quasi-Gaussian distribution of site energies

$$q = \frac{{q_{mT} K_{T} p}}{{\left( {1 + \left( {K_{T} p} \right)^{{n_{T} }} } \right)^{{1/n_{T} }} }},$$
(16)

where qmT is the constant reflecting maximum adsorption capacity, KT is the Toth constant, and nT is the heterogeneity factor, 0 < nT ≤ 1, For homogeneous adsorption nT = 1 and the Toth equation reduces to the Langmuir equation.

2.2.5 Fritz–Schlunder isotherm

The Fritz–Schlunder isotherm [53] expression is described as follows:

$$q = \frac{{q_{mFS} K_{FS} p}}{{1 + q_{mFS} p^{{n_{FS} }} }},$$
(17)

where qmFS is a constant reflecting maximum adsorption capacity (mg g−1), KFS is the Fritz–Schlunder equilibrium constant, and nFS is the Fritz–Schlunder model exponent.

2.3 Error functions

Accuracy of linear fits is described by Pearson correlation coefficient, R. The R describes the strength of the linear relationship between two variables. To carry out a curve fitting for the above isotherms, non-linear fitting methods are required. Unlike linear regression, non-linear regression requires the minimization of an objective function using the iterative methods. Here, the objective function is the error function. The minimization of the error function between the actual and predicted data leads to a converged solution. Thus, an accurate set of parameters can be obtained for the adsorption isotherm models. Five different error functions are used in this work.

2.3.1 The Sum of the squares of the errors

The sum of the squares of the errors (SSE) is the most widely used error function:

$${\text{SSE}} = \mathop \sum \limits_{i = 1}^{n} \left( {q_{p} - q_{a} } \right)_{i}^{2} ,$$
(18)

where qp is the adsorption capacity predicted, qa is the adsorption capacity obtained from MDS, and n is the number of data points in the adsorption isotherm obtained from MDS. The major drawback is that it provides a better fit for high-pressure ranges only. As iterations proceed, the square of the errors becomes very small for the high-pressure values the minimization converges.

2.3.2 The hybrid fractional error function

The hybrid fractional error function (HYBRID) was developed to improve the fitting of SSE at low-pressure ranges:

$${\text{HYBRID}} = \frac{100}{{n - p}}\mathop \sum \limits_{i = 1}^{n} \left[ {\frac{{\left( {q_{p} - q_{a} } \right)^{2} }}{{q_{a} }}} \right]_{i} ,$$
(19)

where p is the number of parameters that are free to evolve with iterations, i.e., denotes the degree of freedom for the minimization. Each sum of the squares of the error values is divided by the actual adsorption values.

2.3.3 The average relative error function

The average relative error (ARE) is a function developed for minimizing the fractional error distribution across the entire range of pressures. Its expression is given by

$${\text{ARE}} = \frac{100}{n}\mathop \sum \limits_{i = 1}^{n} \left| {\frac{{q_{p} - q_{a} }}{{q_{a} }}} \right|_{i} ,$$
(20)

The number of experimental points is included as a divisor.

2.3.4 The Marquardt’s percent standard deviation

The Marquardt’s percent standard deviation (MPSD) is expressed as

$${\text{MPSD}} = 100\sqrt {\frac{1}{n - p}\mathop \sum \limits_{i = 1}^{n} \left( {\frac{{q_{p} - q_{a} }}{{q_{a} }}} \right)_{i}^{2} } ,$$
(21)

and is similar to a geometric mean error distribution modified according to the number of degrees of freedom of the system.

2.3.5 The sum of the absolute errors function

The sum of the absolute errors (SAE) is similar to the SSE. The expression is given by

$${\text{SAE}} = \mathop \sum \limits_{i = 1}^{n} \left| {q_{p} - q_{a} } \right|_{i} ,$$
(22)

Thus, the parameters obtained from this fit also has the same limitation of providing a better fit at only high-pressure ranges.

2.4 Accuracy of the fit

The level of accuracy or the goodness of the fit depends upon the thorough interpretations of the adsorption isotherms. Meaningful comparisons of the set of obtained parameters can be made using the sum of the normalized errors (SNE) described by Porter et al. [54], standard error (SE), and Correlation index or the coefficient of determination (R2). To calculate SNE, the errors obtained from each isotherm fitting equation for each error function were normalized with the maximum value and summed. The standard error (SE) of y values is defined as

$${\text{SE}} = \sqrt {\frac{{\sum \left( {y_{a} - y_{p} } \right)^{2} }}{n - p}} ,$$
(23)

\({\text{and}}\), Correlation index or the coefficient of determination (R2) determined by the relation

$$R^{2} = 1 - \frac{{\sum \left( {y_{a} - y_{p} } \right)^{2} }}{{\sum \left( {y_{a} - y_{{{\text{mean}}}} } \right)^{2} }}.$$
(24)

The above relation is used for determining the goodness of fit; it determines the strength of the relation between the dependent and independent variables. In non-linear models, a high correlation can exist even if the model differs from the actual data. So, an examination of the residuals is also performed.

3 Results and discussions

Temperature and pressure are critical parameters for gas adsorption and desorption phenomena as well as application point of view. For example, consider a boiler of the central heating system of building which can be considered as energetically excellent as almost all the energy content of oil fuel/natural gas is converted to heat. Exergetically, the boiler is not a good idea because it exergo-thermodynamically generates flame temperatures up to 1000 °C for achieving the objective of supplying room radiator temperatures of some 60–70 °C. If a hydrogen-fueled low-temperature fuel cell is installed then it first generates electricity from 35–40% of the fuel’s energy, with the remaining heat still sufficing to warm the building over most of the year [55]. Another low-temperature energetic use includes the space industry and submersibles, which could have been non-existent without the highly energetic hydrogen, where low-temperature high-efficiency hydrogen fuel cells can guarantee their extended travel [55]. Keeping in mind such practical applications, the simulations were performed at lower temperatures in the pressure range of 1–10 MPa to store hydrogen, resulting in a significant amount of hydrogen adsorption (illustrated in Fig. 1 (b) and (c)). We also validated current simulations in the same range of temperatures and pressures. To simulate an accurate adsorption molecular dynamics, an equilibrated system should be achieved. A system with equilibrated potential energy, temperature, and pressure indicates a stable system. Figure 2a shows the time evolution of the system properties at temperature and pressure of 77 K and 1 MPa, respectively, for 15 ns. It can be observed that the system was stable and equilibrated throughout the simulation after raising it to the desired temperature and pressure. This is due to the thermodynamic controls that keep the system to the desired temperature and pressure during the simulation and then a relaxation of the system achieving an equilibrated system. Figure 2b shows that the initial potential energy and weight percentage value gradually reaches an equilibrium after increasing temperature and pressure. In all MDS, a runtime of 4 ns was chosen to save the computational time as the system equilibrates after 2 ns. The system is controlled to be in thermodynamics equilibrium, and the intermolecular interaction of the H2 molecules repels each other as more and more hydrogen attaches itself to the graphene sheet. Gradually, H2 molecules adhere to low-potential energy sites, thus bringing the whole system to an equilibrium.

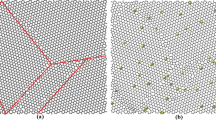
To calculate the hydrogen adsorption percentage, potential energy distribution patterns of H2 molecules were observed. It was found that H2 molecules adsorbed around the graphene sheet had lower potential energy as compared to free H2 molecules, setting the basis for adsorption percentage estimation. Figure 3 shows the potential energy distribution of each H2 molecules around the graphene sheet at 77 K and 1 MPa with a probabilistic curve-fitting. It can be observed from Fig. 3 that a local minima point exists in the energy distribution, and below this minimum point, adsorbed H2 molecules lie, as shown in Fig. 3 (a). For validation of the estimation method, the H2 molecules belonging to the adsorbed potential energy were segregated and can be observed to be surrounded around the sheet as visualized in Fig. 3b. Graphene sheet was kept hidden in the figure for clarity. Then, the number of adsorbed H2 molecules were counted, and adsorption weight percentage (wt%) was calculated using Eq. (1). An average of wt% for the last few timesteps of the equilibrated system was calculated to get an approximate adsorption value. To the best of current authors’ knowledge, no other study has used such novel method to observe adsorption phenomena using MDS.

Fig. 3
figure 3

a Potential energy distribution (PED) of hydrogen molecules, and b front and top views of H2 molecules at 77 K and 1 MPa

Full size image

Using the above method for estimating adsorption wt%, the hydrogen adsorption phenomenon was studied on multiple systems of graphene sheets and H2 molecules. The adsorption energy (Ea) of the hydrogen molecules was also calculated using Eq. (2). It should be noted that the adsorption energies calculated are negative values which signifies the strength of the attraction between H2 molecules and graphene sheet. A higher value signifies a stronger attractive force between the adsorbate (hydrogen) and adsorbent (graphene layer).

It is a well-known fact that MDS with small systems tends to be very unstable, and produce false results, and large systems require a lot of computational resources. So, we considered graphene sheets of edge lengths 50 Å, 60 Å, 70 Å, 80 Å, 90 Å, 100 Å, 150 Å and 200 Å to study the influence of graphene sheet size on the adsorption energy and weight percentage of H2 molecules. Table 2 shows the results of the simulations performed on these sheet sizes at 77 K and 1 MPa. It can be observed that the graphene sheet size variation has an influence on hydrogen adsorption up to a sheet-edge length of 90 Å. After that, sheet size has no significant impact on the adsorption energy and wt% of small systems in MDS impose problems while controlling the temperature and pressure fluctuations. Thus, a square sheet with an edge length of 100 Å was considered for subsequent simulations to study the adsorption phenomena.

Table 2 The influence of sheet edge length on hydrogen adsorption at 77 K and 1 MPa
Full size table

From Fig. 2b and Table 2, it can be seen that a pristine graphene sheet of 100 Å with a SSA of ~ 2630 m2/g at 77 K and 1 MPa can hold hydrogen molecules with 4.9 wt%. Current results agree well with the experimental results obtained by Klechikov et al. [23]. The adsorption energy of the H2 molecule on the graphene sheet was found to be 0.0202 eV. The low-adsorption energy of the H2 molecule indicates that a graphene-based system is physisorption-based adsorption phenomenon, which agrees with previous literature.

Figure 4a illustrates the adsorption energy of H2 molecules adhering to the graphene sheet up to a pressure of 10 MPa at 77 K, 100 K, 200 K, and 300 K. It is observed that as the pressure increases the adsorption energy reduces to a more negative value indicating stronger adsorption between the graphene sheet and H2 molecules. At higher temperatures, an increase in adsorption energy is observed, indicating a weaker adsorption strength. Adsorption isotherms up to a pressure of 10 MPa at 77 K, 100 K, 200 K, and 300 K are shown in Fig. 4b. It can be seen that the gravimetric hydrogen density increases as the pressure rises. A higher density of H2 molecules adheres to the adsorbent upon increasing the pressure.

Fig. 4
figure 4

a Variation of adsorption energy with pressure, and b adsorption isotherms at 77 K, 100 K, 200 K, and 300 K

Full size image

At 77 K temperature, the gravimetric density increases 2.07, 2.73, 3.16, and 3.38 times as the pressure increases from 0.2 MPa to 0.6, 1.5, 5, and 10 MPa, respectively. At lower temperatures, the gravimetric density increases rapidly with the pressure, but after a certain pressure value, it reaches a saturation level. As the temperature increases, the gravimetric density of H2 molecules largely reduces. As H2 molecules are weakly bonded with graphene sheet, the kinetic energy of the system increases at higher temperatures, and as a result, the adsorbed H2 molecules are desorbed, which is in agreement with previous works [56, 57]. At 10 MPa pressure, the gravimetric density increases 1.96, 5.11, and 6.26 times as the temperature is lowered from 300 to 200 K, 100 K, and 77 K. It can be seen that Fig. 4b shows the characteristics of type I adsorption isotherms out of the five characteristic isotherms described by Brunauer, Emmett, and Teller (BET) [58]. The adsorption isotherms resulted from MDS at 77 K are used for determining the best fitting analytical model amongst the Langmuir, Freundlich, Sips, Toth, and Fritz–Schlunder models described in Sect. 2.2. These models describe the behavior of type I adsorption isotherms. The parameters for the isotherm models were determined by minimizing the error functions described in Sect. 2.3. Each isotherm model was fitted against the adsorption isotherm at 77 K for each error function.

Table 3 shows the comparison of SNE, SE, R2, and thereby the isotherm parameters for each model that provides the closest fit to the MDS isotherm data. Similar values of SNE, SE, and R2 can be observed for the SSE and HYBRID error functions. For a good fit, the values of SNE and SE should be the lower, and the value of R2 should be higher. It can be seen that the Freundlich isotherm model has the highest SNE and SE values and lowest R2 value for about all error functions. The minimum values of SNE and SE are found to be 0.195 and ~ 0.0099, respectively, for Langmuir, Sips, and Toth isotherm models with the SSE and HYBRID error functions. The SSE and HYBRID error functions also provide the maximum value of the correlation index (R2) of magnitude 0.9953 for Langmuir, Sips, and Toth isotherms. This indicates that the Langmuir, Sips, and Toth isotherm models fit well with the provided adsorption isotherms. A more detailed analysis is provided in Fig. 5. Figure 5a depicts the non-linear fitting of the adsorption isotherm at 77 K obtained from MDS and Fig. 5b illustrates the error residuals of the five isotherm models at 15 data points obtained with the minimization of the HYBRID error function. Curve-fitting and residual analysis of all five models are shown in both figures, and it is observed that the Freundlich and Fritz–Schlunder isotherms show poor-fitting compared to the other models. The Langmuir, Sips, and Toth isotherm models show almost equal residuals at all data points and provide an equally good curve-fitting at high-pressure regions. From Fig. 3a it can be observed that the potential energy of adsorbed hydrogen molecules is a Gaussian distribution, and the Toth isotherm model assumes an asymmetrical quasi-Gaussian distribution.

Table 3 A comparison of the sum of normalized errors (SNE), standard error (SE) and coefficient of determination (R2)
Full size table
Fig. 5
figure 5

a Non-linear fitting, and b error residuals of the isotherm from MDS at 77 K

Full size image

Thus, the Toth isotherm model is considered the best-fitting model. Table 4 shows the parameters of Toth isotherms fitted for the isotherms at 77 K, 100 K, 200 K, and 300 K. The heterogeneity factor (nT) is equal to 1 at all temperatures, thus indicating a homogenous surface. The Toth constant KL values are found to be decreasing rapidly with increasing temperatures. Thus, indicating a firm relation of adsorption energy with temperatures. The maximum adsorption capacity or gravimetric density predicted from the Toth isotherms also decreases as the temperature increases.

Table 4 The parameters obtained from Toth isotherm models at different temperatures using the HYBRID error function
Full size table

4 Conclusions

MDS simulations were performed to investigate the hydrogen adsorption phenomena on monolayer graphene sheets. A new method based on potential energy distributions (PEDs) was developed to study the adsorption dynamics of hydrogen on graphene sheets at varied temperature and pressure. PEDs in conjunction with MDS used in this article provide an accurate description of the number of adsorbed hydrogen molecules on graphene sheet. To the best of current authors’ knowledge, no existing study employed such novel method for the estimation of gravimetric density. The effect of temperature and pressure on gravimetric density and adsorption energy of H2 molecules on the graphene sheet was analysed in detail. The adsorption energies observed are far less than required for hydrogen storage systems. Due to the weak attraction between the H2 molecule and the graphene sheet, the gravimetric density is high at only low temperatures. The H2 molecules are desorbed at higher temperatures due to the increase in the kinetic energies. Low temperature and high pressure favors the adsorption of H2 molecules on the graphene sheet. The adsorption isotherms obtained from MDS at different temperatures were modeled and evaluated using five existing adsorption isotherms. A thorough comparison of non-linear fit by minimizing five different error functions was performed on the basis of three attributes belonging to each isotherm model SNE, SE, and R2. The order of the goodness of adsorption isotherm models is as follows: \(\mathrm{Toth}>\mathrm{Langmuir}>\mathrm{Sips}>\mathrm{Fritz}-\mathrm{Schlunder}>\mathrm{Freundlich}\). The Toth isotherm was found to be the best fit model over the MDS isotherms and provides best predictions. On the basis of Toth model, the maximum adsorption capacity (wt%) values were found to be 6.956, 6.384, 4.520, 3.403 at 77 K, 100 K, 200 K, and 300 K.