Introduction

Currently the applications of fibre-reinforced composites (FRP) in industries have been increased in manifolds. Dynamic investigation of FRP beam has significance in structural work of modern manufacturing industries since it has higher strength and light weight.

FRP beam may fail by the presence of a mini crack. Therefore, diagnosis of fault location and its depth is experimentation for investigators.

Different types of solid elements application in finite element modelling have been explained in help site of ANSYS1 [1]. Altun and Dirikgil [2] have investigated consequence on behaviour of polypropylene fibre beam at high temperature using fuzzy, neural network and ANFIS non-destructive techniques. Cao et al. [3] have considered beam modes using wavelet approaches for identifying the multicrack positions in a cracked beam. Dash and Parhi [4] have prepared a fuzzy neuro hybrid inverse technique and employed to detect faults in beam (non-composite type) structures. Fang et al. [5] have investigated neural network technique for identifying the fault clamp-free beams. Ghoneam [6] has studied vibration behaviour of laminated composite cracked beam. Hagan et al. [7] have analysed neural network (back propagation) techniques and designed and illustrated various problems by considering various input layer, hidden layer and output layer data. The mixture rule mechanics of unidirectional and bidirectional (woven) fibre composite have been derived by Jones [8]. Knibbs and Morris [9] have observed the variation of material properties by varying the fibre orientation. Majumdar et al. [10] have taken natural frequency as well as optimised a method established with an ant colony technique to find damage in a damaged (pre-cracked) beam. The compliance matrix of unidirectional FRP beam type structures has been derived from Nikpur et al. [11]. Nguyen et al. [12] have studied mix method (fuzzy neuro) for surveying crack position of beam. Rafiee et al. [13] have introduced genetic algorithm method and optimised for detecting damage in faulty gearbox arrangement. Sekhar [14] has studied vibration character on multicracked rotor. Suresh et al. [15] have calculated damage position and its depth in a clamped–free beam using radial network technique. Tada et al. [16] have studied and derived the flexibility influence coefficient matrix using Castigliano’s theorem in line of the elasticity array of the beam material. Vinson et al. [17] have expressed how to calculate the natural frequency of the composite beam. They have ignored shear as well as rotary inertia. Xue et al. [18] have calculated modal curvature of beam by applying wave model. Zheng et al. [19] have studied neural radial basis network to establish delamination position of laminated beam. They have first examined by finite element method and followed into reverse technique (radial basis network) to forecast the delaminating position and size in laminated beam. Zhu et al. [20] have considered a hybrid neuro-fuzzy model for calculating crack with failure time cycle of plate-like structure.

The aim of the current research paper is to establish the dynamical parameters (subjected to the free vibration) of fabricated FRP beam with a pre-transverse crack. The fibres orientation consequences on the dynamical parameters of pre-cracked as well as intact FRP beam are observed. The FRP beams are modelled using three kind approaches as; mathematical method, FEA, neural network (non-destructive) techniques. Clamped–free FRP beam is analysed using all the three analysis methods. The dynamical parameters (modal curvatures and frequencies) of FRP beams are found by applying each method. These parameters are then matched by the actual experimentation executed with experimental setup (FFT) on FRP composite beam manufactured in the laboratory. Therefore, a research work has been completed to observe the variations in mode shapes as well as corresponding relative frequency caused by presence of pre-transverse crack in FRP composite beam by changing fibre orientation. An excellent agreement has been examined between the outcomes of mathematical method, FEA, experimentation and neural network techniques.

Mathematical Method

In this present study, an FRP composite cracked and un-cracked beam with Clamped–free end conditions has been considered for analysis. Since the stress intensity factor for beam can be derived using Castigliano’s theorem within linear elastic range, the derivation of a stiffness matrix is given below.

Local Stiffness Matrix

As per Castigliano’s principle [16], the extra dislodgment along the direction of Pi can be given by:

$$u_{i} = \frac{{\partial U_{\text{c}} }}{{\partial P_{i} }};\quad {\text{where }}U_{\text{c}} \;{\text{is}}\;{\text{strain}}\;{\text{energy}}.$$
(1)

The strain energy (Uc) can be related to release rate of strain energy (Jc) as:

$$U_{\text{c}} = \int\limits_{0}^{{h_{1} }} {\frac{{\partial U_{\text{c}} }}{\partial h}} {\text{d}}h = \int\limits_{0}^{{h_{1} }} {J_{\text{c}} (h){\text{d}}h} ;\quad w{\text{here}},\;J_{\text{C}} = \frac{{\partial U_{\text{c}} }}{\partial h}.$$
(2)

As of Eqs. (1) and (2), one may have:

$$u_{i} = \frac{\partial }{{\partial P_{i} }}\left[ {\int\limits_{0}^{{h_{1} }} {J_{\text{c}} (h){\text{d}}h} } \right].$$
(3)

Integrating over the breadth ‘W’, the final flexibility influences co-efficient Cij, obtained [11] as:

$$\begin{aligned} C_{ij} & = \frac{{\partial u_{i} }}{{\partial P_{j} }} \\ & = \frac{{\partial^{2} }}{{\partial P_{i} \partial P_{j} }}\int\limits_{ - W/2}^{ + W/2} {\int\limits_{0}^{{h_{1} }} {\left\{ {\varUpsilon_{1} \left( {\sum\limits_{i = 1}^{6} {K_{Ii} } } \right)^{2} + \varUpsilon_{2} \left( {\sum\limits_{n = 1}^{6} {K_{IIi} } } \right)^{2} + \varUpsilon_{3} \sum\limits_{i}^{6} {K_{Ii} } \sum\limits_{i = 1}^{6} {K_{IIi} } + \varUpsilon_{4} \left( {\sum\limits_{i = 1}^{6} {K_{IIIi} } } \right)^{2} } \right\}} }\; {\text{d}}h{\text{d}}z, \\ \end{aligned}$$
(4)

where \(\begin{aligned} \varUpsilon_{1} = - 0.5\bar{\delta }_{22} \text{Im} \left( {\frac{{g_{1} + g_{2} }}{{g_{1} g_{2} }}} \right);\varUpsilon_{2} = \bar{\delta }_{11} \text{Im} \left( {g_{1} g_{2} } \right); \hfill \\ \varUpsilon_{3} = 0.5\bar{\delta }_{11} \text{Im} \left( {g_{1} + g_{2} } \right);\varUpsilon_{4} = \frac{1}{2}\sqrt {\delta_{44} \delta_{55} } . \hfill \\ \end{aligned}\)

The constants \(\bar{\delta }_{ij}\) are calculated from the relations [11]:

$$\begin{aligned} \bar{\delta }_{11} & = \delta_{11} m^{4} - (2\delta_{12} + \delta_{66} )m^{2} n^{2} + \delta_{22} n^{4} ,\bar{\delta }_{22} = \delta_{11} n^{4} - (2\delta_{12} + \delta_{66} )m^{2} n^{2} + \delta_{22} m^{4} ; \\ \bar{\delta }_{12} & = (\delta_{11} + \delta_{22} - \delta_{66} )m^{2} n^{2} + \delta_{12} (m^{4} + n^{4} ),\bar{\delta }_{16} = (2\delta_{11} + 2\delta_{12} + \delta_{66} )m^{3} n + (2\delta_{22} - 2\delta_{12} - \delta_{66} )mn^{3} ; \\ \bar{\delta }_{26} & = ( - 2\delta_{11} + 2\delta_{12} + \delta_{66} )mn^{3} + (2\delta_{22} - 2\delta_{12} - \delta_{66} )m^{3} n,\bar{\delta }_{66} = 2(2\delta_{11} - 4\delta_{12} + 2\delta_{22} )m^{2} n^{2} + \delta_{66} (m^{4} + n^{4} ); \\ \end{aligned}$$

where \(m = \cos \alpha \,{\text{and}}\,n = \sin \alpha\), α indicates angle in geometrical axis \(xy\) of FRP beam.

The terms \(\delta_{ij}\) correspond to the position where the geometrical axis of FRP beam concurs by principal axis of material. This is associated with the properties of FRP beam obtained [8, 11] as:

$$\delta_{11} = \frac{1}{{E_{xx} }}\left( {1 - \frac{{E_{yy} }}{{E_{xx} }}\nu_{xy}^{2} } \right),\delta_{22} = \frac{1}{{E_{yy} }}(1 - \nu_{yz}^{2} ),\delta_{12} = \frac{{ - \nu_{xy} }}{{E_{xx} }}(1 + \nu_{yz} ),\delta_{66} = \frac{1}{{G_{xy} }},\delta_{44} = \frac{1}{{G_{yz} }},\delta_{55} = \delta_{66} ,$$

where as the properties of the FRP composite \(\begin{aligned} \hfill \\ E_{xx} ,E_{yy} ,\nu_{xy} ,\nu_{yz} ,G_{xy} ,G_{yz} \,\,and\rho_{c} \hfill \\ \hfill \\ \end{aligned}\) are given in Table 5. \(K_{Ii} ,K_{IIi} \,{\text{and}}\,K_{IIIi}\) relevant to loads \(P_{i}\) input assumed at crack locality. Stress concentrations are given in Table 1 [11].

Table 1 \(K_{Ii} ,K_{IIi} \,{\text{and}}\,K_{IIIi}\) values
Full size table

Vibration Characters of Pre-cracked FRP Beams by Analytical Methods

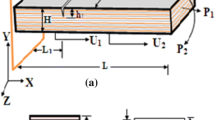
Figure 1 is showing FRP composite beam with dimensions \(L \times W \times H\) having a fault of intensity h1 by place L1 from clamped end. Let \(U_{1} \left( {x, \, t} \right); \, U_{2} \left( {x, \, t} \right)\) be the amplitudes of longitudinal vibration of the sections before and after the crack, respectively, and \(Y_{1} \left( {x, \, t} \right); \, Y_{2} \left( {x, \, t} \right)\) be the corresponding amplitudes of bending vibration of respective section. The usual function of the arrangement is as follows:

$$u_{1} (\bar{x}) = A_{1} \cos (\bar{K}_{\text{u}} \bar{x}) + A_{2} \sin (\bar{K}_{\text{u}} \bar{x}),$$
(8)
$$\bar{u}_{2} (\bar{x}) = A_{3} \cos (\bar{K}_{\text{u}} \bar{x}) + A_{4} \sin (\bar{K}_{\text{u}} \bar{x}),$$
(9)
$$\bar{y}_{1} (\bar{x}) = A_{5} \cosh (\bar{K}_{\text{y}} \bar{x}) + A_{6} \sinh (\bar{K}_{\text{y}} \bar{x}) + A_{7} \cos (\bar{K}_{\text{y}} \bar{x}) + A_{8} \sin (\bar{K}_{\text{y}} \bar{x}),$$
(10)
$$\bar{y}_{2} (\bar{x}) = A_{9} \cosh (\bar{K}_{\text{y}} \bar{x}) + A_{10} \sinh (\bar{K}_{\text{y}} \bar{x}) + A_{11} \cos (\bar{K}_{\text{y}} \bar{x}) + A_{12} \sin (\bar{K}_{\text{y}} \bar{x}),$$
(11)

where \(\bar{u} = \frac{u}{L}\), \(\bar{x} = \frac{x}{L}\), \(\bar{y} = \frac{y}{L}\), \(\chi = \,\frac{{L_{1} }}{L}\), \(\bar{K}_{\text{u}} = \frac{\omega L}{{C_{\text{u}} }}\), \(\bar{K}_{\text{y}} = \left( {\frac{{\omega L^{2} }}{{C_{\text{y}} }}} \right)^{1/2}\), \(C_{\text{u}} = \left( {\frac{E}{\rho }} \right)^{1/2}\), \(C_{\text{y}} = \left( {\frac{EI}{\mu }} \right)^{1/2}\), \(\mu = A\rho_{\text{C}}\); Ai (i = 1, 12) is evaluated using end conditions. End conditions (clamped–free) are calculated \(\bar{u}_{1} (0) = 0\); \(\bar{y}_{1} (0) = 0\); \(\bar{y}^{\prime}_{1} (0) = 0\); \(\bar{u}^{\prime}_{2} (1) = 0\); \(\bar{y}_{2}^{\prime \prime } (1) = 0\); \(\bar{y}_{2}^{\prime \prime \prime } (1) = 0\).

Fig. 1
figure 1

FRP beam a clamped–free, b transverse sectional view of C–F beam, c clamped–clamped with crack depth h1, d transverse sectional view of C–C beam

Full size image

For the case of a transverse crack in a beam and by applying the compatibility conditions, we write: \(\bar{u}_{1} (\chi ) = \bar{u}_{2} (\chi )\); \(\bar{y}_{1} (\chi ) = \bar{y}_{2} (\chi )\); \(\overline{y}_{1}^{\prime \prime } (\chi ) = \overline{y}_{2}^{\prime \prime } (\chi )\); \(\overline{y}_{1}^{\prime \prime \prime } (\chi ) = \overline{y}_{2}^{\prime \prime \prime } (\chi )\).

Pre-crack distance L1 from fixed end of clamp-free composite beam, one gets:

$${\text{AE}}\frac{{{\text{d}}u_{1} (L_{1} )}}{{{\text{d}}x}} = K_{11} (u_{2} (L_{1} ) - u_{1} (L_{1} )) + K_{12} \left( {\frac{{{\text{d}}y_{2} (L_{1} )}}{{{\text{d}}x}} - \frac{{{\text{d}}y_{1} (L_{1} )}}{{{\text{d}}x}}} \right),$$
(12)

\(\frac{\text{AE}}{{LK_{11} K_{12} }}\) is multiplied with Eq. (11):

$$M_{1} M_{2} \bar{u}^{\prime}(\chi ) = M_{2} (\bar{u}_{2} (\chi ) - \bar{u}_{1} (\chi )) + M_{1} (\bar{y}^{\prime}_{2} (\chi ) - \bar{y}^{\prime}_{1} (\chi )),$$
(13)
$${\text{Similarly}},\;{\text{EI}}\frac{{{\text{d}}^{2} y_{1} (L_{1} )}}{{{\text{d}}x^{2} }} = K_{21} (u_{2} (L_{1} ) - u_{1} (L_{1} )) + K_{22} \left( {\frac{{{\text{d}}y_{2} (L_{1} )}}{{{\text{d}}x}} - \frac{{{\text{d}}y_{1} (L_{1} )}}{{{\text{d}}x}}} \right),$$
(14)

\(\frac{\text{EI}}{{L^{2} K_{22} K_{21} }}\) is multiplied in Eq. (13) and resulting equation:

$$M_{3} M_{4} \overline{y}_{1}^{\prime \prime } (\chi ) = M_{3} (\bar{u}_{2} (\chi ) - \bar{u}_{1} (\chi )) + M_{4} (\bar{y}^{\prime}_{2} (\chi ) - \bar{y}^{\prime}_{1} (\chi )),$$
(15)

where \(M_{1} = \frac{\text{AE}}{{LK_{11} }}\), \(M_{2} = \frac{\text{AE}}{{K_{12} }}\), \(M_{3} = \frac{\text{EI}}{{LK_{22} }}\), \(M_{4} = \frac{\text{EI}}{{L^{2} K_{21} }}\).

Using functions in “Eqs. (8)–(11)” for end conditions, the Eq. (7) stated above is yielded the characteristic equation of the structure as:

$$\left| K \right| = 0;\quad {\text{where order of }}K = 12 \times 12.$$
(16)

Equation (16) is expressed by ωn, the χ, K are expressed by the ψ.

FEA (ANSYS)

In addition to above analytical approach, finite element approach (FEA) is used in the current investigation using ANSYS1. The proposed FEA modelling is used to find out natural frequencies and mode shapes of FRP composite beam due to the presence and absence of crack under clamped–free boundary condition. The dimension of the FRP composite beam is taken as 640 mm × 50 mm × 6 mm. The FRP beam is composed 13 layers of woven fibres (E-glass) with different orientation and epoxy, and volume ratio is 40:60. Crack severity, location, fibre orientation are varied in a logical way for the current investigation. 20 nodded (solid element 186) is considered and applied for modelling FRP beam. Using mixture rule and from the laboratory test, FRP beam properties are tabulated (Table 5). The processes are stated in Sect. 5. Proposed model is meshed and end conditions are applied as per the problem stated. Fibres by altering orientations (0°/7.5°/15°/22.5°/30°/37.5°/45°) for individual FRP beam (13 layers) are designed via lay-up processes. The results are analysed for studying the dynamics of the FRP beam.

Diagnosis of Fault Using Neural Network Techniques (NNT)

Back Propagation

The design and architecture of neural network is consisting of four numbers of layers. The first layer with four neurons is used as an input layer. Then for adjusting the neuron weight, three concealed layers are used to overcome difficulties for particular error limit. Empirically, 8 neurons are given to first concealed layer, 16 neurons for second concealed layer and 6 neurons for third concealed layer. Subsequently two neurons are used in the fourth layer of output for RCL and RCD, respectively.

Back propagation method is implemented for reducing the erroneousness by optimizing the inputs (RFNF, RSNF, RTNF and Theta) and for achieving the objective RCL and RCD. Neurons are made from the training data. The errors are converged during training for minimising threshold error that governs the RCL and RCD. Empirically, the neural network is trained via 20,000 training patterns.

Neural Network Techniques (NNT)

The inputs are RFNF = ∇1; RSNF = ∇2; RTNF = ∇3; and orientation of fibre = Theta = β; the outputs are RCL = \(\chi\) and RCD = \(\psi\).

The neural network input data consists of the following mechanism.

Figure. 4 presents the fundamental function of a particular neuron. The relation (Figs. 3, 4) in input–output is integrated as nonlinear with a layer of transfer function f(1–3), and linear as output f4 obtained [4, 7] as:

$$a^{1} = f^{1} (w^{1} \varGamma + b^{1} ),$$
(17)
$$a^{2} = f^{2} (w^{2} a^{1} + b^{2} ) = f^{2} \left\{ {w^{2} [f^{1} (w^{1} \varGamma + b^{1} )] + b^{2} } \right\},$$
(18)
$$a^{3} = f^{3} (w^{3} a^{2} + b^{3} ) = f^{3} \{ w^{3} \{ f^{2} \{ w^{2} [f^{1} (w^{1} \varGamma + b^{1} )] + b^{2} \} \} + b^{3} \} ,$$
(19)
$$a^{4} = f^{4} (w^{4} a^{3} + b^{4} ) = f^{4} \{ f^{3} \{ w^{3} \{ f^{2} \{ w^{2} [f^{1} (w^{1} \varGamma + b^{1} )] + b^{2} \} \} + b^{3} \} + b^{4} \} ,$$
(20)

where the weighted (wi) input and bias \((b^{j} )\) are present in the hidden neuron.

The sigmoid; hyperbolic tangent sigmoid and logistic sigmoid functions are mainly employed as activation functions. In the present analysis, \(f^{1} ,f^{2} \,{\text{and}}\,f^{3}\) are sigmoid functions used in layers 1–3 and purelin function (Eq. 22) is used in layer number 4. The sigmoid functions (Eq. 21) have three distinct (well bounded, differentiable and continuous) characters. The layer functions are:

$$f^{i} (n) = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {1 + (e)^{ - n} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${1 + (e)^{ - n} }$}};\quad {\text{where}}\,(i = 1,2,3),$$
(21)
$$f^{4} (n) = n.$$
(22)

Experimentation

So as to study the crack influence of a FRP composite beam, various methods like mathematical, FEA and neural network techniques are discussed in above three sections. Above three method’s results are compared and validated with experimental results. The experimentation details are given below.

Procedure

E-glass (woven) and epoxy FRP sheets (each 13 layers), volume ratio 40:60, dimensions 3000 mm × 720 mm × 6 mm are fabricated with hand lay-up process [8, 9, 11]. From the fabricated FRP sheets, intact beams with dimensions 720 mm × 60 mm × 6 mm and angles 0°/7.5°/15°/22.5°/30°/37.5°/45° are cut with taking reference from the axis of fabricated FRP sheets. The more size 80 mm of FRP beam is taken for holding of FFT holder that is required during the time of experimental verification. Final practical dimensions of the each FRP beams are 640 mm × 50 mm × 6 mm considered during the FFT study. Material properties are obtained by considering mixture rule (Table 3). Further these properties values are validated using actual laboratory testing machine (Table 4).The pre-transverse crack in the FRP beam is done in the different places (i.e. RCL = 0.1, 0.2, 0.3, 0.4, 0.5, 0.6) with varying crack depth (RCD = 0.1, 0.2, 0.3, 0.4, 0.5) of FRP.

Experiments are performed on FRP intact and pre-cracked beams (altering fibre orientations) by considering two end conditions as clamped–clamped, clamped–free. However, RCL and RCD ratios are kept constant for all these cases. Other sets of pre-cracked FRP beams are produced by different RCL maintaining constant fibre orientation and RCD. Experiment setup (Fig. 5) is operated to observe natural frequencies and corresponding mode shapes. Initially, excitation is developed for free vibration using a power hammer. The vibration signatures of FRP beam captured using accelerometer (instrument no. 7) are communicated to analyser (instrument no. 2) as input and is incorporated with the PULSE LITE Software interfaced in PC. The amplitudes of the vibration signatures, resonance frequencies on varying crack locality in length and varying crack depth in height are verified.

Results and Discussion

The present article is focused on the vibrant performance of FRP beams with a pre-crack under the free vibration and compared with the performance of intact FRP beams. The effect of altering fibres (woven) orientations in dynamical performance of the both pre-cracked and intact FRP beams is observed. In current research analytical, finite element (ANSYS), neural network and experimental investigations of FRP (woven fibre)-cracked beams are carried out. Pre-cracked FRP beam classical model (clamped–free) is shown in Fig. 1. Solid 186 element 20 nodded is considered in FEA analysis (ANSYS). The FRP beam meshed model with sectional views is shown in Fig. 2a. FEA (ANSYS) is implemented for studying FRP beam dynamic parameters (natural frequency, mode shape). FEA results are compared and validated by the results of both experimentation and mathematical methods. Figure 2b–d presents the first, second and third mode shapes and corresponding frequency of clamped–free (C–F) FRP un-cracked beam. Figure 3 shows the NNT Controller consisting of four numbers input, two numbers output. Figure 4 shows sigmoid functions and purelin function, respectively. Figure 5 shows the setup used in experimentation studies. RNFs are observed by altering RCD as well as RCL. The variations of dynamic parameters are observed by altering fibres (woven) orientation. Typical illustrations are given in Table 2 for both clamped–clamped and clamped–free end conditions using neural network technique. Table 3 presents the properties using mixture rule. These properties are compared and verified with experimentation (Table 4). The results of three approaches (analytical, FEA, neural technique) are compared with experimental results under the both end condition and given in Table 5.

Fig. 2
figure 2

a Meshed model with sectional view, b first mode with frequency, c second mode with frequency, d third mode with frequency

Full size image
Fig. 3
figure 3

Four inputs, four hidden layers transfer function and two outputs

Full size image
Fig. 4
figure 4

Transfer function (i) a = logsigmoid(n); (ii) a = purelin(n); (iii) a = sigmoid function

Full size image
Fig. 5
figure 5

Experimentation setup. 1—FRP beam; 2—vibration analyser; 3—PC interface PULSE LITE software; 4—power supply; 5—function generator; 6—amplifier; 7—accelerometer; 8—clamp

Full size image
Table 2 Illustration of neural network training
Full size table
Table 3 Material properties of proposed FRP by applying mixture rule
Full size table
Table 4 Fabricated FRP beam properties are compared that are got by mixture rules, experimentations
Full size table
Table 5 Analytical, ANSYS, neural network methods are compared and certified in experimentation
Full size table

It is experimented from all the first, second and third mode of vibration that RNF decreases by altering orientation from 0° to 45° for a fixed RCD and RCL that are presented in Fig. 6a–c. The slopes are more signified in the range 20°–45° and represent unexpected changes in RNF. That specifies FRP beam stiffness is decreased by range of fibres orientation increased. Deviation in RNF is noted for altering the RCL for a given RCD and orientation. Figures 7a–c and 8a–c present that in first, second and third mode of FRP beam vibrations the RNF is increasing by the changing RCL from clamped end to free end of FRP beam. In other words, it is précised as FRP beam flexibility is decreasing to increase RCL, and therefore RNFs values are increasing. RNF deviance is outlined for changing RCD at a fixed RCL as well as orientation. From the first, second and third mode of FRP beam vibration, RNF is decreased by increasing RCD. It is shown in Fig. 9a–c that RNF is varied by altering RCD and keeping RCL = 0.1 and orientation = 0°. The curve shows that FRP beam stiffness is reducing to increase RCD so as to decrease the RNF values. Here is exciting to message that the closeness of the shape of the curves of all three methods (analytical, ANSYS and experimentation) is shown in Figs. 6a–c, 7a–c, 8a–c and 9a–c. Results in Figs. 7a–c and 8a–c show considerable variations with experiment. The first three mode shapes are compared with the methods of analytical and experiment (clamped–clamped end condition), and it is presented in Fig. 10a–c. From the mode shape, it indicates that the curvature of the graph largely deviates from position of the crack. From the study, it is also found that with the increase in RCD from 0 to 0.5 the deviation of curve increases. Figure 11a presents the best performance vs. mean squared error by neural network technique (NNT). Figure 11b shows targets vs. output by neural network technique (NNT). Figure 11c shows gradients vs. gradient by neural network technique (NNT). From the results (Table 5), it has been observed that the results differ from 0.0 to 5.7% which is a good agreement.

Fig. 6
figure 6

a Orientation vs. RFNF on RCD = 0.3 RCL = 0. 1. b Orientation vs. RSNF on RCD = 0.1, RCL = 0. 1. c Orientation vs. RTNF on RCD = 0.3, RCL = 0. 1

Full size image
Fig. 7
figure 7

a RCL vs. RFNF on first mode vibration. b RCL vs. RSNF on second mode vibration. c RCL vs. RTNF on third mode vibration

Full size image
Fig. 8
figure 8

a RCL vs. RFNF on first mode vibration. b RCL vs. RSNF on second mode vibration. c RCL vs. RTNF on third mode vibration

Full size image
Fig. 9
figure 9

a RCD vs. RFNF on first mode vibration. b RCD vs. RSNF on second mode vibration. c RCD vs. RTNF on third mode vibration

Full size image
Fig. 10
figure 10

a Relative length vs. transverse deflection (compared with un-crack and crack of FRP beam, RCL = 0.3 and RCD = 0.5 in first mode shape). b Relative distance vs. transverse deflection (compared with un-crack and crack of FRP beam of RCL = 0.3 and RCD = 0.5 in first mode shape). c Relative distance vs. transverse deflection (compared with un-crack and crack of FRP beam of RCL = 0.3 and RCD = 0.5 in first mode shape)

Full size image
Fig. 11
figure 11

a Best performance vs. mean squared error by neural network technique (NNT). b Targets vs. output by neural network technique (NNT). c Gradients vs. gradient by neural network technique (NNT)

Full size image

Putting clamped–clamped boundary conditions; at, \(x = 0,\left\{ \begin{aligned} y = 0 \hfill \\ \frac{{{\text{d}}y}}{{{\text{d}}x}} = 0 \hfill \\ \end{aligned} \right.\) at, by putting boundary conditions as; \((\beta_{1} l)^{2} = 22.4,(\beta_{2} l)^{2} = 61.7,(\beta_{3} l)^{2} = 121\), and mode shapes are compared with amongst analytical and experiment.

Conclusion

The alterations in FRP beam mode and frequency instigated with presence of pre-crack by altering orientation (woven fibre) are calculated in the present investigation. An excellent agreement (within 6% deviation) has been experimented amongst the four methods (mathematical, finite element method, neural network techniques (NNT) and experiments with following concluding points.

(1) When the RCD amplified, the stiffness is reduced as an effect RNF value decreases. (2) By increasing RCL, the RNF decreases. Likewise, RNF is decreasing after increasing RCD, RCL as well as orientations (from 0° to 45°). (3) Presence of crack has indicated considerable variation in mode shapes. (4) As the fibre orientation increased from 0° to 45°, the stiffness was going down, therefore RNF was lessened. (5) Bidirectional (woven) FRP beam with 0° direction is best amongst all other orientations in aspect of good stiffness and higher RNF. (6) As the deviation of the results is within 6%, the neural network (NN) can be applied to identify the crack and its severity as a non-destructive technique.