1 Introduction

As well known, the maximum flight speed of a conventional single main rotor configuration is approximately 278–315 km/h [1], due to the limitation of shock wave on the advancing blade tips and dynamic stall on the retreating side. Combined with the advancing blade concept (ABC) [2], rigid coaxial rotor compound helicopter offers a solution for the speed limit of single rotor configuration. At high speed, the retreating blades are offloaded, and the rotor speed is slowed down to avoid high tip Mach number. The X2 Technology Demonstrator aircraft has achieved a speed of 463 km/h in steady level flight [3]. At the same time, there are complex aerodynamic interactions between the upper and lower rotors, which can result in vibration loads on the blades and hub as well as special acoustic characteristics. So it is necessary to study the unsteady aerodynamic loads of high-speed coaxial rotor.

At present, experimental researches on high-speed coaxial rotor are rather limited, while there are many experiments on traditional coaxial rotor. Harrington [4] examined the hover performance data of two full-scale traditional coaxial rotors. The blade of the first coaxial rotor was tapered both in thickness and chordwise, recognized as Harrington rotor-1. Another was Harrington rotor-2 and only tapered in thickness. Dingeldein [5] performed a further test on the performance of Harrington rotor-1 in hover and forward flight. Ramasamy [6] conducted a series of experiments on the hover performance characteristic of a small-scale coaxial rotor system compared with the tandem and tilt-rotor systems and summarized the hover experiments on traditional coaxial rotor. Cameron et al. [7] tested the hover performance of a Mach-scale coaxial rotor, providing the individual upper and lower rotor loads. However, experiments on high advance ratio single rotor are sufficient. The UH-60A slowed rotor test [8, 9] conducted in the US Air Force National Full-Scale Aerodynamics Complex (NFAC) provided valuable sectional loads and performance of UH-60A rotor at high advance ratio.

Analysis of coaxial rotor has been carried out by many researchers. The blade element momentum theory (BEMT) had been introduced to investigate the performance of coaxial rotor [10, 11]. Recently, some new efforts were made to develop inflow model for coaxial rotor [12, 13]. Vortex method was also applied to coaxial rotor [14,15,16,17,18,19] for aerodynamic performance prediction and wake simulation. Among these, Schmaus and Chopra [18, 19] expanded the comprehensive analysis model University of Maryland Advanced Rotor Code (UMARC), where the rotor interactions were captured by a free wake model, with trim routines for the coaxial rotor in hover and forward flight. These methods are more efficient than computational fluid dynamics (CFD) method. However, CFD method has its obvious advantages on the simulation of detailed flow field and blade motions. Lakshminarayan and Baeder [20] used the compressible RANS solver OVERTURNS and sliding meshes to study the interaction characteristics of Harington rotor-2 in hover. In their research, loads of the upper and lower rotors showed opposite impulsive behavior when blades meet. Barbely et al. [21, 22] investigated coaxial rotor wakes and blade–blade aerodynamic interactions using Rotor Unstructured Navier–Stokes (RotUNS) CFD method. However, the blades were modeled by lifting-line theory; the fidelity of blade geometry could not be ensured. Researchers at University of Maryland [23, 24] conducted some analysis on the aerodynamic interaction of X2 in forward flight using CFD and free wake coupled with computational structural dynamics (CSD). It was found that the low-fidelity (free wake) model provided accurate performance estimation, but could not precisely predict the vibratory loads of the coaxial rotor, while CFD solutions were significantly better. So CFD method is adopted in the present paper to compute the flow field and to capture the unsteady loads of high-speed coaxial rotor.

To achieve torque balance and correctly simulate the lift offset (LOS) in forward flight, trim is necessary for coaxial rotor. Kim and Park [25] combined Newton iteration method with a CFD solver for a single rotor trim, and the control settings were updated by the CFD solver, and thus the efficiency is low. Zhao and He [26] applied the “delta method” to single rotor trim in coupled CFD/CSD calculation. Ye et al. [27] expanded the “delta method” to build a high-efficiency trim strategy for single rotor CFD simulation. In Ref. [20], Lakshminarayan and Baeder coupled the Jacobian matrix from a vortex filament code for a traditional coaxial rotor trim, but their trim model was limited to hover state. Qi et al. [28] developed a trim model for coaxial rotor based on the “delta method”, which was also just for hover.

Inspired by the previous researches, the goal of this paper is to build a CFD method based on RANS equations to provide a better understanding of the interaction aerodynamics and unsteady loads of a high-speed coaxial rotor. Different from the traditional coaxial rotor, the trim of high-speed coaxial rotor is hard to achieve required LOS. Thus, an efficiency trim model for coaxial rotor in forward flight is established to get appropriate rotor control settings, by applying the “delta method”. The CFD method for coaxial rotor is developed based on the method for single rotor configuration built by our research group [29, 30] at Nanjing University of Aeronautics and Astronautics. In this paper, a model rotor with no twist and taper is used for numerical examples. Cases in three advance ratios are simulated: one is 0.15 (low advance ratio) and the other two are 0.4 and 0.6 (high advance ratios). Through the analysis of temporal blade loads and flow field, some special unsteady interaction features are captured in high-speed flight states.

2 Methodology

2.1 Numerical Method

The Navier–Stokes equations are used as governing equations for predicting the flowfield, as shown below:

$$ \frac{\partial }{\partial t}\iiint\limits_{\partial V} {\varvec{W}{\text{d}}V + \mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\limits_{\partial S} {(\varvec{F}_{\text{c}} - \varvec{F}_{\text{v}} ) \cdot \varvec{n}{\text{d}}S} } = 0, $$
(1)

where W represents the vector of conservation variables, Fc is the vector of the convective flux, and Fv viscous flux. S is the boundary of control volume, and V is the volume of control volume.

For spatial discretization, Roe scheme [31] is used to compute the convective flux terms. Dual time-stepping method is employed for temporal discretization. The one-equation Spalart–Allmaras turbulence model [32] is used to compute the turbulent viscosity for the closure of RANS equations.

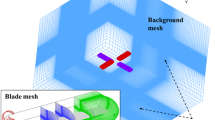
Moving overset meshes are adopted to simulate the motions of coaxial rotor blades in forward flight. The viscous blade meshes are generated in structured C–O type, as shown in Fig. 1. A Cartesian background mesh is used to capture the far-field flow, as shown in Fig. 2. For the coaxial rotor model used in current work, each blade mesh has 221 × 87 × 101 points in the stream-wise, normal and spanwise directions, respectively. The background Cartesian mesh has 245 × 210 × 218 points in the x, y and z directions, respectively. The background mesh is refined in the region of rotor wake. Near the rotor disk, the refined mesh spacing of background is about 0.05 c.

Fig. 1
figure 1

C–O blade mesh for the coaxial rotor model

Full size image
Fig. 2
figure 2

Moving overset mesh system for the coaxial rotor model

Full size image

2.2 Trim Model

The blade pitch of a rotor for the coaxial system can be expressed as:

$$ \theta (\psi ) = \theta_{0} + \theta_{1s} \sin (\psi ) + \theta_{1c} \cos (\psi ) + \cdots , $$
(2)

where \( \psi \) represents azimuth angle, \( \theta_{0} \) is the collective pitch angle, \( \theta_{1s} \) and \( \theta_{1c} \) denote longitudinal and lateral cyclic pitches, respectively.

The control settings (input vector) and target variables (response vector) are as shown below:

$$\varvec{x} = \{ \theta_{0U} ,\theta_{1sU} ,\theta_{1cU} ,\theta_{0L} ,\theta_{1sL} ,\theta_{1cL} \}^{\text{T}}, \varvec{y} = \{ C_{\text{T}} ,C_{\text{Q}} ,LOS,C_{\text{MU}} ,C_{\text{L}} ,C_{\text{ML}} \}^{\text{T}} , $$
(3)
$$ {\text{LOS}} = {{\left( {C_{\text{LU}} - C_{\text{LL}} } \right)} \mathord{\left/ {\vphantom {{\left( {C_{\text{LU}} - C_{\text{LL}} } \right)} {C_{\text{T}} }}} \right. \kern-0pt} {C_{\text{T}} }},\;C_{\text{L}} = C_{\text{LU}} + C_{\text{LL}} , $$
(4)

where CT and CQ represent the total thrust and torque coefficients of the coaxial system, and CL and CM are the coefficients of rotor rolling and pitching moment. The subscripts of U and L indicate the upper rotor and the lower rotor, respectively. The positive directions of CLU and CLL are opposite in the global coordinate system. Since thrusts of the upper and lower rotors are often different due to rotor interactions, the average lateral lift offset [19] of dual rotors is adopted in this paper, as shown in Eq. (4).

The relationship between the input vector and response one can be expressed by

$$ \varvec{y} = f(\varvec{x}). $$
(5)

The function can be carried out by Taylor expansion to the first order at x0 as follows:

$$ \varvec{y} = f(\varvec{x}_{0} ) + \frac{\partial y}{\partial x}x = x_{0} \cdot (\varvec{x} - \varvec{x}_{0} ) + \ldots $$
(6)

Neglecting the higher order terms, the expression for the change of the input vector x can be written as:

$$ \Delta \varvec{x} = (\varvec{x} - \varvec{x}_{0} ) = \varvec{J}^{ - 1} (f(\varvec{x}_{0} + \Delta \varvec{x}) - f(\varvec{x}_{0} )) = \varvec{J}^{ - 1} \cdot \Delta \varvec{y}\text{,} $$
(7)

where J represents the Jacobian matrix given by

$$ \varvec{J} = \left[ {\begin{array}{*{20}c} {\frac{{\partial C_{\text{T}} }}{{\partial \theta_{0U} }}} & {\frac{{\partial C_{\text{T}} }}{{\partial \theta_{1sU} }}} & {\frac{{\partial C_{\text{T}} }}{{\partial \theta_{1cU} }}} & {\frac{{\partial C_{\text{T}} }}{{\partial \theta_{0L} }}} & {\frac{{\partial C_{\text{T}} }}{{\partial \theta_{1sL} }}} & {\frac{{\partial C_{\text{T}} }}{{\partial \theta_{1cL} }}} \\ {\frac{{\partial C_{\text{Q}} }}{{\partial \theta_{0U} }}} & {\frac{{\partial C_{\text{Q}} }}{{\partial \theta_{1sU} }}} & {\frac{{\partial C_{\text{Q}} }}{{\partial \theta_{1cU} }}} & {\frac{{\partial C_{\text{Q}} }}{{\partial \theta_{0L} }}} & {\frac{{\partial C_{\text{Q}} }}{{\partial \theta_{1sL} }}} & {\frac{{\partial C_{\text{Q}} }}{{\partial \theta_{1cL} }}} \\ {\frac{{\partial {\text{LOS}}}}{{\partial \theta_{0U} }}} & {\frac{{\partial {\text{LOS}}}}{{\partial \theta_{1sU} }}} & {\frac{{\partial {\text{LOS}}}}{{\partial \theta_{1cU} }}} & {\frac{{\partial {\text{LOS}}}}{{\partial \theta_{0L} }}} & {\frac{{\partial {\text{LOS}}}}{{\partial \theta_{1sL} }}} & {\frac{{\partial {\text{LOS}}}}{{\partial \theta_{1cL} }}} \\ {\frac{{\partial C_{\text{MU}} }}{{\partial \theta_{0U} }}} & {\frac{{\partial C_{\text{MU}} }}{{\partial \theta_{1sU} }}} & {\frac{{\partial C_{\text{MU}} }}{{\partial \theta_{1cU} }}} & {\frac{{\partial C_{\text{MU}} }}{{\partial \theta_{0L} }}} & {\frac{{\partial C_{\text{MU}} }}{{\partial \theta_{1sL} }}} & {\frac{{\partial C_{\text{MU}} }}{{\partial \theta_{1cL} }}} \\ {\frac{{\partial C_{\text{L}} }}{{\partial \theta_{0U} }}} & {\frac{{\partial C_{\text{L}} }}{{\partial \theta_{1sU} }}} & {\frac{{\partial C_{\text{L}} }}{{\partial \theta_{1cU} }}} & {\frac{{\partial C_{\text{L}} }}{{\partial \theta_{0L} }}} & {\frac{{\partial C_{\text{L}} }}{{\partial \theta_{1sL} }}} & {\frac{{\partial C_{\text{L}} }}{{\partial \theta_{1cL} }}} \\ {\frac{{\partial C_{\text{ML}} }}{{\partial \theta_{0U} }}} & {\frac{{\partial C_{\text{ML}} }}{{\partial \theta_{1sU} }}} & {\frac{{\partial C_{\text{ML}} }}{{\partial \theta_{1cU} }}} & {\frac{{\partial C_{\text{ML}} }}{{\partial \theta_{0L} }}} & {\frac{{\partial C_{\text{ML}} }}{{\partial \theta_{1sL} }}} & {\frac{{\partial C_{\text{ML}} }}{{\partial \theta_{1cL} }}} \\ \end{array} } \right]. $$
(8)

The input vector is updated by adding the variation calculated by the difference between current values and target values to the current value, as follows:

$$ \Delta \varvec{x}^{(n)} = \varvec{J}^{{(n)^{ - 1} }} \cdot (\varvec{y}^{(n)} - \varvec{y}^{\text{target}} ),\;\varvec{x}^{(n + 1)} = \varvec{x}^{(n)} + \Delta \varvec{x}^{(n)} . $$
(9)

In this way, the iteration is continued until the relative error (\( \varepsilon \)) meets the convergence criterion given by

$$\begin{aligned} & \varepsilon= (\varepsilon_{\text{T}} ,\varepsilon_{\text{Q}} ,\varepsilon_{\text{LOS}} ,\varepsilon_{\text{MU}} ,\varepsilon_{\text{L}} ,\varepsilon_{\text{ML}} )^{\text{T}} \\ & \varepsilon_{\text{T}}= {{\left| {C_{\text{TU}} + C_{\text{TL}} } \right|} \mathord{\left/ {\vphantom {{\left| {C_{\text{TU}} + C_{\text{TL}} } \right|} {\left| {C_{\text{T}}^{\text{target}} } \right|}}} \right. \kern-0pt} {\left| {C_{\text{T}}^{\text{target}} } \right|}},\, \varepsilon_{\text{Q}} = \left| {C_{\text{QU}} + C_{\text{QL}} } \right|,\\ &\varepsilon_{\text{LOS}} = \left| {{\text{LOS}} - {\text{LOS}}^{\text{Target}} } \right|, \\ & \varepsilon_{\text{MU}} = \left| {C_{\text{MU}} } \right|,\;\varepsilon_{\text{L}} = \left| {C_{\text{L}} } \right|,\;\varepsilon_{\text{ML}} = \left| {C_{\text{ML}} } \right| \\ & \left\{ {\begin{array}{*{20}l} {\varepsilon_{\text{T}} ,\varepsilon_{\text{LOS}} < 1 \times 10^{ - 2} \, } \hfill \\ {\varepsilon_{\text{Q}} ,\varepsilon_{\text{MU}} ,\varepsilon_{\text{L}} ,\varepsilon_{\text{ML}} < 1 \times 10^{ - 6} } \hfill \\ \end{array} } \right.. \end{aligned} $$
(10)

The trim model for coaxial rotor in forward flight is developed based on the hover trim model built by our research group [28]. In the trim model, the “delta method” [26] is employed to improve the efficiency. The BEMT model for coaxial rotor developed by Valkov [33] and the Newton iteration method are adopted as the simplified trim model [27]. The CFD solver above is used to modify the rotor performance (y) calculated by BEMT to guarantee the accuracy.

In the process of trim, the initial input vector x0 is obtained through Newton iteration by setting the target y of BEMT trim model \( \varvec{y}_{\text{BEMT}}^{{{\text{target}}(0)}} = y^{\text{target}} \). Then, the initial rotor performance (\( \varvec{y}_{\text{CFD}}^{(0)} \)) is obtained by running CFD solver for three revolutions with the initial pitches (x0) to get the convergence of the flow field. After this, \( \varvec{y}_{\text{BEMT}}^{\text{target}} \) are updated by the difference between \( \varvec{y}_{\text{CFD}} \) and \( \varvec{y}^{\text{target}} \), as given by

$$ \varvec{y}_{\text{BEMT}}^{{{\text{target}}(n + 1)}} = y_{\text{BEMT}}^{{{\text{target}}(n)}} + (\varvec{y}^{\text{target}} - \varvec{y}^{(n)} ). $$
(11)

In this way, new x is gotten by BEMT trim model and then provided for CFD solver to get new y. Here, the CFD solver is run for only one revolution to improve the efficiency. The input vector is updated until the relative error (\( \varepsilon \)) of CFD results satisfies the convergence criterion as shown in Eq. (10). If full-CFD trim method is used, six more revolutions of CFD solver are needed in each trim step to get the Jacobi matrix. For the coaxial rotor model in current work, the CFD solver costs about 20 h for each revolution, which is very time consuming. Thus, 120 h are saved for each trim step using current trim method, and the trim efficiency is greatly improved, correspondingly.

2.3 Validations


Figures 3 and 4 compare the computed rotor performance of the present work and experimental data of Harrington coaxial rotor-1 [5] in hover and forward flight. Relative errors of CQ between present work and experiment for coaxial rotor are also given in Fig. 4. Results of CAMRAD II in Ref. [21] are also given in forward flight. For hover cases, a series of thrust coefficient levels are computed using the trimmed collective pitches for torque balance of the coaxial rotor. For forward flight cases, the trimmed pitches are achieved by setting the target CT as 0.0048 and keeping torque balanced. As shown in the figure, the results of single rotor demonstrate good agreement with the experimental data in hover and forward flight. For the coaxial rotor, there are some errors in reasonable range. This may be because of the complex interaction of coaxial rotor and the regardless of rotor hub in calculation. In forward flight, the maximum relative error happens at μ = 0.24, which is 7.77%.

Fig. 3
figure 3

Comparison of hover performance of Harrington coaxial rotor-1

Full size image
Fig. 4
figure 4

Comparison of forward flight performance of Harrington coaxial rotor-1

Full size image

The trimmed pitches for Harrington coaxial rotor-1 are given in Table 1, compared with the results of CAMRAD II given by Ref. [21]. The rotor shaft tilt angles are set same as CAMRAD II data. It can be seen that results are close, except that \( \theta_{1c}^{{}} \) of current results are larger than CARMD II. For the present trimmed results, \( \theta_{1cL}^{{}} \) is larger than \( \theta_{1cU}^{{}} \) when μ = 0.12, and their difference turns small when μ = 0.24. This may be because the wake of upper rotor acts on the rear of the lower rotor, which enhances the longitudinal asymmetry of the flow field in the lower rotor disk, and such wake interaction turns weaker at higher advance ratio.

Table 1 Trimmed pitches for Harrington coaxial rotor-1 compared with CAMRAD II results
Full size table

3 Results and Discussion

3.1 Cases Setup and Trim Results

The main parameters of the coaxial rotor model used in this paper are listed in Table 2. The blades have no twist, with constant chord and thickness. The solidity of one rotor is about 0.07. The rotor tip Mach number is set as 0.587 for μ < 0.4, and it is reduced to 0.47 for μ ≥ 0.4, with a consideration to limit tip Mach numbers to 0.9 or less [24]. The upper rotor rotates anti-clockwise and the lower rotor rotates clockwise, from top view. It should be noticed that the y-axis heads down.

Table 2 Summary of the coaxial rotor model parameters
Full size table

In trim process, the target CT is set as 0.01 for the coaxial rotor model in this paper. The single rotor, which means the isolated upper rotor, adopts same pitches with the upper rotor. The trim convergence criterion can be reached in seven iteration steps for all cases in current work. Figure 5 and Table 3 give the trim history of pitches and relative error for case of μ < 0.15, LOS = 0, as an example. Figure 6 gives the trimmed rotor pitches for different states. It can be seen that at low speed (μ < 0.25), the lateral cyclic pitches (\( \theta_{1c} \)) of dual rotors have obvious differences, due to the strong rotor wake interaction. At higher speed (μ ≥ 0.25), the rotor interaction turns weak, and pitches of coaxial rotor are rather close. So it is sufficient to let the pitches of upper and lower rotors share same values in the process of trim, at high speeds. With the increase of LOS, \( \theta_{0} \) drops down, while \( \theta_{1s} \) rises up, and changes of \( \theta_{0} \) and \( \theta_{1s} \) are larger than \( \theta_{1c} \).

Fig. 5
figure 5

Trim history of pitches for the coaxial rotor model

Full size image
Table 3 Trim history of relative errors for the coaxial rotor model (μ = 0.15, LOS = 0)
Full size table
Fig. 6
figure 6

Trimmed rotor pitches for different advance ratios

Full size image

3.2 Low Advance Ratio Cases

Figure 7 gives the temporal CT variation of blades over one revolution with different LOS at μ = 0.15. To make a further insight into the interaction of blade and tip vortex, the temporal variations of sectional lift at 0.8R are given in Fig. 8. The key features of blade load fluctuations can be seen as follows.

Fig. 7
figure 7

Temporal variations of blade CT (μ = 0.15)

Full size image
Fig. 8
figure 8

Temporal sectional lift variations at 0.8R (μ = 0.15)

Full size image

3.2.1 Periodic Fluctuations Shared by U1 and L1

The thrusts of U1 and L1 share a tendency of gradually rising and sharply dropping in a period of 90°, as the dual rotors meet each other every other 90°. This is similar to the phenomenon in hover caused by the interaction of rotor wake in the research of Lakshminarayan [20], as upper and lower blades meeting and leaving periodically. However, this is not as obvious as hover cases, which is just significantly shown in 90°–180° region in forward flight.

3.2.2 Impulsive Fluctuations Around Blade-Meeting Azimuths

There are pulse-type fluctuations of U1 and L1 around the blade-meeting azimuths. For the upper blade, the thrust spikes down, but for the lower blade it spikes up. Meanwhile, the pulse amplitude of the upper blade is much larger than that of the lower one, especially at 0° and 270°. The change of LOS has little influence on the impulsive fluctuation, at 0° and 180°. However, the change amplitudes of L1 at 90° and L1 at 270° both have an obvious increase at LOS = 0.3. This will be discussed in detail later in Fig. 9.

Fig. 9
figure 9

Cp contours in different sections at 0° and 90° azimuths (μ = 0.15)

Full size image

3.2.3 Load Reductions Over the Rear of the Coaxial Rotor Disks

The blade loads over the rear of the upper and lower disks have a reduction compared with the single rotor. Here, the rear of rotor disk is corresponding to regions of 0°–90° and 270°–360° in Fig. 7. For LOS = 0 the reduction can be obviously seen. For LOS = 0.3, the blade loads have significant increase on the advancing side (0°–180°).

3.2.4 Blade–Vortex Interaction

The temporal sectional lift variations at 0.8R of U1, L1 and S1 with different LOS are shown in Fig. 8. On the advancing side, there are two Blade–vortex interaction (BVI) events, marked as #1 and #2. At #1, the lift fluctuations caused by BVI are mainly presented on L1. At #2, the sectional lifts of three blades are all evidently influenced by the BVI and exhibit similar waveform. On the retreating side, the BVI mainly occurs on L1 and S1 around 270°, marked as #3. Compared with LOS = 0, the BVI of LOS = 0.3 turns weaker at #1 and #3 and stronger at #2. That is reasonable, as loads increase with LOS on the advancing side and decrease on the retreating side. The detailed flowfield insight of the BVI events will be given in the following part.

To make a further study on the impulsive fluctuations of blade thrust around blade-meeting azimuths. The Cp contours in different spanwise sections at 0° and 90° are shown in Fig. 9. At the blade-meeting time, the upper rotor enters the low-pressure region induced by the lower rotor. However, the high-pressure region below the upper rotor is evidently weaker than the low-pressure region above it. It corresponds to the larger amplitude of U1 as mentioned above, compared with that of L1. Additionally, at 0°, the pressure distribution varies little with LOS. So the impulsive amplitudes of lift fluctuations are similar between LOS = 0 and LOS = 0.3. At 90°, for LOS = 0.2, there is a high-pressure region between U1 (90°) and L2 (270°), due to the high load of U1 and low load of L2. At the same time, on the retreating side of upper rotor (see U2, at 270°) the pressure field is dominated by the high-load blade L1 (at 90°). Thus, for U1 at 90° and L1 at 270° the impulsive amplitudes are both enlarged and for L1 it is more evident.

Figure 10 shows the induced velocity in y-axis direction (Vy) contours in longitudinal sections at 0°, when μ = 0.15. The induced velocity is normalized by the rotor tip speed (Vtip) and the y-axis heads down. On the one hand, the Vy around S1 (U1, L1) at 0° is larger than that around S2 (U2, L2) at 180° due to the forward flight flow. On the other hand, the wakes interaction of coaxial system mainly takes place on the rear of rotor disk. Thus, the Vy around U1 and L1 is larger than that around S1 due to the interaction of dual rotors, especially near the blade tips.

Fig. 10
figure 10

Vy contours in longitudinal section (μ = 0.15, LOS = 0, \( \psi = 0^{ \circ } \))

Full size image

Figure 11 shows the iso-surface of vorticity magnitude (Vor) of the coaxial system and single rotor. The iso-surfaces are colored by Vy/Vtip. The BVI events marked in Fig. 8 are also pointed out here. For the single rotor, it is obvious to see two BVI events. One is #2 interaction S1 and blade tip vortex S2 on the advancing side, the other is #3 interaction between S2 and blade tip vortex of S1 on the retreating side. For the coaxial system, the wake structures are complicated. It is obvious to see the blade tip vortex of U1 acts on L1 rather than U2 after a vortex age of 180°, which is different with the single rotor. That is because the wake of upper rotor moves down faster than that of the single rotor, due to the interaction of coaxial rotor.

Fig. 11
figure 11

Iso-surface of vorticity magnitude for q = 0.2 (μ = 0.15, LOS = 0, \( \psi = 90^{ \circ } \))

Full size image

The vorticity magnitude contours of sections A and B with different LOS are given in Fig. 12. In section A of LOS = 0, BVI events happen around U1 and L2 blade sections, which correspond to #2 and #3 BVI events marked in Fig. 8. As seen in section B of LOS = 0, there is no BVI event around U2, while there are two BVI events (#1 and #2) around L1. The interaction #1 takes place before 90°, and #2 takes place after 90°. For LOS = 0.3, the BVI events are obviously severer than that of LOS = 0 on advancing sides. Interactions #3 and #1 are weaker, as the blade tip vortexes located on retreating sides are weaker.

Fig. 12
figure 12

Vorticity magnitude contours in different sections (μ = 0.15, \( \psi = 90^{ \circ } \))

Full size image

Figure 13 shows the sectional lift distribution (clMa2) for the coaxial system and single rotor. The impulsive fluctuations around blade-meeting azimuths for upper and lower rotors are clearly shown. The main BVI events are marked in the figures, which correspond to those in Fig. 8. The upper rotor wake acts on the lower rotor, leading to a low-load region on the lower rotor around 300°, which is obviously shown when LOS = 0.3.

Fig. 13
figure 13

Sectional lift distributions (clMa2) for the coaxial and single rotors (μ = 0.15)

Full size image

3.3 High Advance Ratio Cases

Figure 14 gives the temporal CT variation of blades over one revolution with LOS for μ = 0.4, as well as the temporal variation of sectional lift at 0.8R. The impulsive fluctuations around blade-meeting azimuths are still clearly shown for U1 around 270°. The amplitude increases with advance ratio and LOS. That is because the flowfield is dominated by the advancing blade with higher loads. However, for L1 blade the impulsive fluctuation is still not obvious. Meanwhile, the loads reduction between 270° and 360° is still severer for larger LOS, similar to the cases of μ = 0.15. However, the difference between S1 and U1 (L1) is smaller at higher advance ratio, because wakes of coaxial rotor travel fast backward and have little interaction in rotor disk.

Fig. 14
figure 14

Temporal loads variation with different LOS (μ = 0.4)

Full size image

Two BVI events are marked in Fig. 14b. Interaction #2 is similar to the #2 marked in μ = 0.15 cases. However, the BVI event on the retreating side disappears, because the wake moves faster backward far away from reaching the retreating blade, as shown in Fig. 15. Moreover, at 90° the wake of U1 reaches L1 at about 0.5R rather than 0.8R as shown in μ = 0.15 cases.

Fig. 15
figure 15

Iso-surface of vorticity magnitude for q = 0.2 (μ = 0.4, LOS = 0.1)

Full size image

Another BVI event is marked as #1 in Fig. 14, which is not as strong as BVI #2. Figure 16 shows the vorticity magnitude contours in the upper rotor plane at different azimuths. At the current advance ratio, the tip vortex of U1 starts to reach the root of itself at 345°, but there is no significant BVI. At 15°, the root vortex of U2 lies almost parallel to the root of U1, forming BVI #1. Furthermore, BVI #1 is stronger around the root of U1, compared with the tip of it.

Fig. 16
figure 16

Vorticity magnitude contours in upper rotor plane (μ = 0.4, LOS = 0.1)

Full size image

Figure 17 shows the sectional lift distribution for μ = 0.4. The impulsive fluctuations caused by blade-meeting are only shown around 270°. The two BVI events in Fig. 14 are marked only for the single rotor, because the BVI characteristics of coaxial system are similar to it. In fact, the lift distribution of single rotor and coaxial system has little difference at high advance ratio. BVI #2 is stronger at the tip region, while BVI #1 is stronger at the root region, which is coincident with Fig. 16.

Fig. 17
figure 17

Sectional lift distributions (clMa2) for the coaxial and single rotors (μ = 0.4)

Full size image

Figure 18 gives the blade loads variation with LOS for μ = 0.6. The impulsive fluctuations around blade-meeting azimuths are still clearly shown on U1. Three BVI events are identified, as marked in the figure. BVI #2 is the interaction between the advancing blade and tip vortex of retreating blade, which is stronger with the increase of LOS.

Fig. 18
figure 18

Temporal loads variation with different LOS (μ = 0.6)

Full size image

The vorticity magnitude contours in the plane of single rotor are given in Fig. 19 to show the BVI events of #1 and #3. The #1 BVI is recognized as parallel interactions because the leading edge of U1 is nearly parallel to the vortex filament, as shown in the Fig. 19a. Moreover, the interaction is stronger near the root of U1 than the tip. The #3 BVI is complex as there are two vortices acting on the blade. One is the tip vortex and the other is the root vortex as marked in Fig. 19b. This interaction mainly takes place near the tip of U1.

Fig. 19
figure 19

Vorticity magnitude contours in the plane of single rotor (μ = 0.6, LOS = 0.3)

Full size image

Figure 20 shows the sectional lift distribution for the single rotor for μ = 0.6. As shown in the figures, complicated lift fluctuations occur near the BVI locations. The lift fluctuations caused by the #1 BVI are stronger on the inside of spanwise than on the outside. The lift fluctuations caused by the #3 BVI is only observed on the outside of spanwise.

Fig. 20
figure 20

Sectional lift distributions (clMa2) for the single rotor (μ = 0.6)

Full size image

4 Conclusions

A CFD solver based on RANS equations and a high-efficiency trim model are established to simulate the aerodynamics of a coaxial rotor model in forward flight. The goal of this work is to study the unsteady aerodynamic loads of coaxial rotor. Based on cases at different advance ratios in this paper, the following conclusions can be drawn.

  1. 1.

    At low advance ratio (μ ≤ 0.25, for current cases), the lateral and longitudinal cyclic pitches of coaxial rotor have obvious differences between the upper and lower rotors, due to the interaction of rotor wakes. At higher advance ratio (μ > 0.25), the interaction is weak and, thus, pitches of the upper and lower rotors are rather close.

  2. 2.

    There are obvious wake interactions for coaxial rotor at low speed (such as μ = 0.15). The thrusts of upper and lower blades share a tendency of gradually rising and sharply dropping in every 90° period, which is more significant in the region of 90°–180°. Meanwhile, there are load reductions over the rear of coaxial rotor disks, because the interactions mainly take place on the rear area due to the forward flight flow. The interactions turn weak with the increase of advance ratio.

  3. 3.

    The impulsive thrust fluctuations caused by blade-meeting are obviously exhibited around 270° for upper blades, and the strengths increase with LOS and advance ratio. Such interaction exerts greater impact on the loads of upper rotor, compared with the lower rotor.

  4. 4.

    With the increase of advance ratio, the BVI location of the advancing blade gradually moves toward the root at 90°. For the advance ratio of μ = 0.15, the tip vortex of advancing upper blade reaches the retreating lower blade, forming special BVI of coaxial rotor. In higher speed, the BVI located on the retreating side disappears, as the tip vortex moves backward fast due to the forward flight flow.

  5. 5.

    At high speed (μ ≥ 0.4), two new kinds of BVI start to appear. One is the parallel BVI between the root vortex of the front blade and the rear blade shown around 15°, at μ = 0.4 and 0.6. The other is the complex interaction among the tip vortex, root vortex and the rear blade around 345°, at μ = 0.6.