1 Introduction

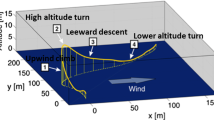
The operational deployment of small unmanned air vehicles (sUAVs) is always challenging due to their endurance and range limitations. Efforts in the form of enhancing aerodynamic efficiency, swarming technology and battery performance improvement through solar or fuel cells are typically adopted. Another emerging area to improve range and endurance of these platforms is the usage of biologically inspired aerodynamic maneuvers (Fig. 1),which are classified into two broad categories. The first one does not cater for atmospheric wind shears and can be executed anywhere. These include transitions between hover and cruise [1, 2], perching [3,4,5] and in-flight morphing [6, 7] strategies. The second class is primarily dependent on soaring strategies [8,9,10]. The soaring maneuvers belong to the domain of active maneuvers, as they are dependent on atmospheric currents and wind shears. Among soaring, dynamic soaring [11] is of profound importance, as it enables UAV to perform powerless flight by actively acquiring energy available in atmospheric vertical wind gradients. It is potentially of greater utility than static and gust soaring, as the wind gradients are more predictable and are present whenever there is wind. Additionally, it is robust with respect to weather and its primary advantage is in picking up speed, in contrast to static soaring, which is mere harnessing of lift.

Fig. 1
figure 1

Broad classification of biologically inspired maneuvers

Full size image

The seminal work on dynamic soaring can be traced back to Lord Rayleigh in 1883 [12]. Subsequent research for decades focused on understanding the basics of flight of soaring birds. This understanding improved drastically with the emergence of digital technology. Alberstam [13] and Weimerskirch [14] tracked albatross by satellite and other measurement devices and reported useful information in ascertaining the flight performance parameters of soaring flight. Since dynamic soaring is dependent upon wind shear, geographical regions in which sufficient wind shear exists to facilitate dynamic soaring were also identified [15, 16]. Data given by Idrac [17] and Sachs [18] refer to a wind speed of 5 m/s close to the sea surface as the lowest permissible value for dynamic soaring. For full-scale aircraft, Sachs and Da Costa [16] showed that dynamic soaring by full-size sailplanes is possible with values of wind shear found near mountain ridges. Gordan [19] carried out a detailed search on extending dynamic soaring to full-sized planes and ascertained that full-size sailplanes could extract energy from horizontal wind shears, although the utility of the energy extraction could be marginal depending on the flight conditions and the type of sailplane used. Zhao [20] analyzed different optimal dynamic soaring patterns (loiter, travel and basic modes) of a glider by incorporating optimal control techniques and effects of wind gradient slope and profile nonlinearity. Zhao and Qi [21] examined minimum fuel-powered dynamic soaring of UAV (both propeller-driven and jet-driven) assuming a linear wind gradient profile and a three-dimensional point-mass UAV model.

In all cases, however, the base line model utilized for dynamic soaring have always been a fixed configuration [10, 11, 22,23,24,25] in which the platform cannot change its configuration. However, soaring birds such as albatross, can morph their wings during different phases of flight to enhance their maneuver potential [26]. They can effectively vary wing sweep, wing span, wing twist, wing dihedral as well as wing anhedral with the shoulder lock fixed-wing flying [9, 27]. As soaring birds while performing dynamic soaring acquires optimum energy from atmosphere under morphing condition, a biologically inspired morphable platform with the ability to vary its planform parameters is envisaged to efficiently optimize the energy gain from the atmosphere.

Morphing has a significant impact on aerodynamic characteristics of the flying vehicle and remarkable improvement in the flight regime is achieved by employing different morphing techniques [28, 29]. Although there is a lot of versatility in morphing schemes, such as wing [30], fuselage [31], tail [32] or engine [33] morphing, altering wing parameters (such as wing planform, airfoil shape and so on) have the most powerful and influential impact on the performance parameters [34]. For span variation, inflatable telescopic wing design is normally a preferred choice as it has the ability to undergo a 114% change [35] in aspect ratio while supporting aerodynamic loads. Similarly, increase/ decrease in sweep angles [36] causes corresponding changes in parameters such as critical mach number, dihedral effect, high-speed drag and maximum lift coefficient \(C_{L_\mathrm{max}}\). Wings with higher sweep angle are more advantageous in attaining the highest maximum speed (dash), while the smaller wing sweep angle is more suitable for higher range and endurance for loiter / reconnaissance missions. Similarly, wing dihedral [37] variation affects rolling moment \(C_{l_\mathrm{max}}\) and lateral stability. Amongst these available morphing techniques, the technique most suitable for dynamic soaring is therefore to be identified for ascertaining the platform configurations during different phases of the maneuver.

As demonstrated by soaring birds, different planform configurations are required during the dynamic soaring maneuver to ensure maximum energy extract from the atmospheric wind shear [27]. It is ,however, noticeable that a planform configuration suitable for achieving desired performance during a particular stage of the maneuver may adversely effect the performance parameters in the other phase [38]. As an example, for enhanced forward length distance of the energy neutral dynamic soaring cycle, wings with lower span, higher sweep and dihedral configurations are preferred for speedy climb with higher velocity and more rolling stability [28, 39]. However, wings with extended span and minimum sweep angle are desired during the descent phase to achieve higher cruise distance [26, 40]. Also, high directional stability is required during climb and descent phases of the soaring flight to avoid unnecessary control effort [41, 42]. However, the same is not desirable during high and low altitude turn phases of the maneuver [43, 44], as considerably large control effort will be required to overcome this directional stability.

In this research, the impact of sweep variation on dynamic soaring is investigated. Detailed analysis for integrating dynamic soaring trajectories under morphing conditions is performed for a UAV capable of performing sweep variations. After selecting a generic UAV platform, its aerodynamic model is generated through empirical formulas readily available in literature. The trajectory generation problem is modeled as a nonlinear-constrained optimization problem with objective function, constraints on aircraft states and controls, and point-mass dynamic model with nonlinear wind shear model [11, 20, 21]. The algorithm used for trajectory optimization is based on Guass pseudospectral technique, commercially available as GPOPS-II [45]. In results and discussion section, comparison of advantages between fixed and sweep capable configuration is made. Comparisons are made in the form of state and control variables and performance parameters that include cycle time, maximum achievable velocity, minimum required wind shear, maximum altitude gain, distances covered in the east/north direction, aerodynamic forces and so on.

2 Problem Setup

2.1 Aircraft Model Description

The aircraft model considered consists of a conventional radio controlled (RC) standard wing–tail configuration as shown in Fig. 2. The dimensions of the aircraft include fuselage length of 1 m, wing span of 1.5 m, mean aerodynamic chord of 0.4640 m, aspect ratio of 3.232, nominal wing sweep of \(0^{\circ }\), wing area of 0.696 \(\mathrm{m}^2\), taper ratio of 1 and aerodynamic surfaces are constructed from NACA 0012 airfoil. The recommended all up weight (AUW) for enhanced performance is about 1.6 kg. The wing is assumed to have an internal mechanism with sweep capability up to \(50^{\circ }\).

Fig. 2
figure 2

Oblique and side views of the morphing UAV considered in this study

Full size image

The moment of inertias are calculated by assuming body to be rigid at a particular orientation. The symmetrical inertia tensor at \(0^{\circ }\) sweep angle and origin at centre of gravity is defined in Eq. (1)

$$\begin{aligned} \varvec{I}= & {} \begin{bmatrix} I_{xx}&-I_{xy}&-I_{xz}\\ -I_{xy}&I_{yy}&-I_{yz}\\ -I_{xz}&-I_{yz}&I_{zz}\\ \end{bmatrix}\nonumber \\= & {} \begin{bmatrix} 5377694.89&-3859.41&-6807.93\\ -3859.41&24885559.95&-3209.00\\ -6807.93&-3209.00&23093644.43\\ \end{bmatrix} \,\mathrm{g}~\mathrm{mm}^2.\nonumber \\ \end{aligned}$$
(1)

2.2 Nonlinear flight dynamic modeling

The equations of motion considered to model the flight dynamics of the aircraft are coupled and nonlinear in nature. It is assumed that the three-dimensional point-mass model considered in the study will represent the qualitative behavior of the aircraft dynamics and elaborate model may not be required to assess the macro level contribution of sweep effect on dynamic soaring trajectories. The dynamic modeling utilized in this study is aligned with other studies [20, 21, 46] for describing system dynamics and elaborated in Eq. (2)

$$\begin{aligned} \begin{aligned} \dot{V}&= \frac{1}{m}[-D-mg\sin \gamma -m\dot{V}_W\cos \gamma \sin \psi ] \\ \dot{\psi }&=\frac{1}{mV_t\cos \gamma }[L\sin \phi -m \dot{V}_W\cos \psi ] \\ \dot{\gamma }&=\frac{1}{mV_t}[L\cos \phi -m g\cos \gamma +m\dot{V}_W\sin \psi \sin \gamma ]\\ \dot{x}&= V\cos \gamma \sin \psi +V_W\\ \dot{y}&= V\cos \gamma \cos \psi \\ \dot{h}&=V\sin \gamma \\ \end{aligned} \end{aligned}$$
(2)

where V is the UAV velocity, \(V_W\) is the wind velocity, \(\gamma \) is the flight path angle, \(\psi \) is the heading angle, \(\phi \) is the bank angle, L is the lift, D is drag, m is the mass of the UAV, and x,y,h are the position vectors in the direction of inertial north, east, and down, respectively. In this model, the speed of UAV is modeled in a wind relative reference frame and the position of UAV is modeled in an earth-fixed frame (North, east, down) as shown in Fig. 3

Fig. 3
figure 3

UAV orientation during the dynamic soaring maneuver

Full size image

Typically, wind shear estimation during dynamic soaring maneuver is done either through some known model once the wind conditions are known or online estimation of wind shear in unknown wind conditions. In this study, the wind shear velocity \(V_W\) is approximated with well-established nonlinear logarithmic wind shear model [11, 18] model. The logarithmic relation between wind velocity (\(V_W\)) and height above the surface (h) is given by Eq. (3)

$$\begin{aligned} V_W=V_{w_\mathrm{ref}} \frac{\ln (h/h_0)}{\ln ({h_\mathrm{ref}}/h_0)}, \end{aligned}$$
(3)

where \(V_{w_\mathrm{ref}}\) represents the strength of the wind shear velocity at reference altitude \(h_\mathrm{ref}\). Also, \(h_0\) is the surface correctness factor that determines the distribution of the wind gradient with varying altitude, reflecting the surface properties, such as irregularity, roughness and drag. The values \(h_\mathrm{ref}=10\) m and \(h_{0}=0.03\) m are chosen in this study [18]. The minimum reference wind speed value at this altitude, which still permits dynamic soaring is ascertained through the optimization process.

The wind shear gradient is represented by Eq. (4):

$$\begin{aligned} \dot{V}_W=V_{w_\mathrm{ref}} \frac{1}{h\ln (h_\mathrm{ref}/h_0)}\dot{h}, \end{aligned}$$
(4)

where \(\dot{h}\) is the rate of change in the altitude.

The lift and drag forces acting on the UAV vary with varying sweep angle and angle of attack through the following empirical relation

$$\begin{aligned} L=0.5\rho V^2 S C_L \,\,\, \mathrm{and} \,\,\,D=0.5\rho V^2 S C_D \end{aligned}$$
(5)

where \(\rho \) is the density of the air and S is the wing area. The lift and drag are the functions of the angle of attack and sweep angle and are determined through empirical techniques. The lift coefficient is determined using the relationship

$$\begin{aligned} C_L=C_{L_{\alpha }}(\alpha -\alpha _{L=0}) \end{aligned}$$
(6)

where \(C_{L_{\alpha }}\) is the lift curve slope of the wing, \(\alpha \) is the angle of attack and \(\alpha _{L=0}\) is the angle of attack at zero lift. The lift curve slope of the wing is determined utilizing the empirical relationship [47]

$$\begin{aligned} C_{L_{\alpha }}=\frac{c_{L_{\alpha }}\cos \varLambda }{\sqrt{(1+c_{L_{\alpha }}K\cos \varLambda )^2}+c_{l_{\alpha }}K \cos \varLambda } \end{aligned}$$
(7)

where \(c_{L_{\alpha }}\) is the lift curve slope of the cross-section. The induced drag factor (K) is defined as

$$\begin{aligned} K=\frac{1}{\pi e \mathrm{AR}} \end{aligned}$$
(8)

where e is the span efficiency factor having a value of 0.8. Also, AR is the wing aspect ratio and is calculated using the relationship

$$\begin{aligned} \mathrm{AR}=b_\mathrm{eff}^2/S_\mathrm{eff} \end{aligned}$$
(9)

where \(b_\mathrm{eff}\) is the effective wing span and \(S_\mathrm{eff}\) is the effective wing area. The effective wing span and the effective wing area (in case of leading edge sweep) are related to the nominal wing span \(b_\mathrm{nom}\) and nominal area \(S_\mathrm{nom}\) through sweep angle. This is governed by Eq. (10)

$$\begin{aligned} b_\mathrm{eff}=b_\mathrm{nom} \cos \varLambda , \,\,\,\,\,\,\, S_\mathrm{eff}=S_\mathrm{nom}-\varDelta S \end{aligned}$$
(10)

where \(\varDelta S\) is the change in wing area due to sweep variation and is given as

$$\begin{aligned} \varDelta S=0.5c_\mathrm{nom}^2\tan \varLambda \end{aligned}$$
(11)

where \(c_\mathrm{nom}\) is the nominal wing chord. The parabolic drag coefficient is given by Eq. (12)

$$\begin{aligned} C_D=C_{D_{0}}+KC_L^2 \end{aligned}$$
(12)

where \(C_{D_{0}}\) is the zero lift drag coefficient.

Fig. 4
figure 4

Operational flow chart of GPOPS– II [45]

Full size image

2.3 Trajectory Optimization Setup

The optimal optimization evaluation is done using a commercially available algorithm GPOPS-II [45] integrated with Matlab®. The algorithm is based on state-of-the-art hp-adaptive version of the Legendre–Gauss–Radau (LGR) orthogonal collocation method. This algorithm has been rigorously tested in different studies [24, 48,49,50,51,52,53]. The operational functionality [45] of the GPOPS-II is demonstrated in Fig. 4. The flow chart explains the intermediate steps adopted in the algorithm starting from the user-provided input data for the optimal control problem to the computation of the optimal solution.

Table 1 Path constraints and numeric bounds for implementing loiter maneuver
Full size table

The flight model described by Eq. (2) with nonlinear wind profile Eq. (3) is configured as a nonlinear system of the form specified in Eq. (13):

$$\begin{aligned} \dot{\varvec{x}}= F(\varvec{x}(t),\varvec{u}(t)). \end{aligned}$$
(13)

The flight dynamics model includes six states variables (which are function of a time period t), as defined in Eq. (14):

$$\begin{aligned} \varvec{x}(t)= [V, \,\, \psi \,\,\gamma , \,\, x, \,\, y, \,\,h]^T, \,\,\,\varvec{x}(t) \in \mathbb {R}^6 \end{aligned}$$
(14)

Control vector for fixed (non-morphing) configuration is defined in Eq. (15)

$$\begin{aligned} \varvec{u}(t)= [\alpha , \,\,\phi ]^T, \,\,\, \varvec{u} \in \mathbb {R}^2 \end{aligned}$$
(15)

where \(\phi \) is the bank angle.

Control vector \(\varvec{u}(t)\) for sweep morphology is defined as

$$\begin{aligned} \varvec{u}(t)= [\varLambda ,\,\, \,\,\alpha , \,\,\phi ]^T, \,\,\, \varvec{u} \in \mathbb {R}^3 \end{aligned}$$
(16)

where \(\varLambda \) denotes the wing sweep angle.

Dynamic soaring flight is then formulated as a nonlinear optimal control problem to find a control \(\varvec{u}(t)\) that optimizes performance function specified in Eq. (17) [9, 23] subject to the dynamic constraints in Eqs. (2), and satisfying path and boundary constraints.

$$\begin{aligned} J= \mathrm{min}[V_{w,\mathrm{ref}}] \end{aligned}$$
(17)

where \(V_{w,\mathrm{ref}}\) (wind velocity at reference altitude) is the parameter to be minimized by the optimization algorithm. Different modes of dynamic soaring (basic, loiter, and forward flight modes) are implemented through boundary constraints [20]. Boundary conditions for implementing loiter mode of dynamic soaring is depicted at Eq. (18):

$$\begin{aligned} V_{t_{f}}= & {} V_{t_0}, \psi _{t_{f}}= \psi _{t_0}, \gamma _{t_{f}}= \gamma _{t_0},, x_{t_{f}}= x_{t_0}, \nonumber \\ y_{t_{f}}= & {} y_{t_0}, h_{t_{f}}= h_{t_0}, \end{aligned}$$
(18)

where \(V_{t_{0}}, \psi _{t_{0}}, \gamma _{t_{0}}, x_{t_0} , y_{t_0},\) and \(h_{t_0}\) represents the state vector at initial time \(t_{0}\) and \(V_{t_{f}}, \psi _{t_{f}}, \gamma _{t_{f}}, x_{t_f} , y_{t_f},\) and \(h_{t_f}\) represents the state vector at final time \(t_{f}\).

Path constraints and numerical bounds for the states and control during the dynamic soaring maneuver are depicted in Table 1. Since dynamic soaring is a high maneuvering cycle, which generates high accelerations, an additional path constraint of load factor (n) is included, which gives a global measure of the load to which the aircraft structure is subjected to.

In this problem, the initial orientation that is [x, y, h] is kept constrained at \([x_0,y_0,h_0]\) (value within the permissible range depicted in Table 1). A value of \([x_0,y_0,h_0]=[0,0,0]\) was chosen as the initial point of the maneuver. The initial airspeed, flight path angle and heading angle \([V_\mathrm{init}, \gamma _\mathrm{init},\psi _\mathrm{init}]\) are however left unconstrained (within the permissible range). This allows the optimization process to determine their optimal values for sustainable soaring flights.

3 Results and Discussion

Fig. 5
figure 5

UAV-optimized trajectories during the loiter maneuver

Full size image
Fig. 6
figure 6

UAV states during the loiter maneuver

Full size image

This section deals with the quantification of benefits achieved through wing sweep morphing over fixed-wing configuration. To conduct intelligence, surveillance and reconnaisance (ISR) missions, UAVs are desired to loiter over a certain area for extended time periods. A representative case of the optimized dynamic soaring trajectories in loiter mode are compared in Fig. 5 under same atmospheric conditions. It can be seen that the morphing platform outperformed fixed configuration in terms of altitude gain and area coverage under similar wind shear and allied flight conditions. An approximate increase of 29%, 28% and 25% are observed in altitude gain, distance traveled along the east and north directions, respectively. By incorporating variable-sweep phenomena, aerodynamic advantages are harnessed from the atmosphere thereby expanding the flight performance envelope of the dynamic soaring maneuver.

Fig. 7
figure 7

UAV controls during four different phases of the loiter maneuver

Full size image

An elaborate analysis of the state histories for both morphing and fixed configurations is presented in Fig. 6. The velocity decreases during the windward climb phase of the maneuver and approaches zero at the highest point. Subsequently, the UAV picks up the speed after high altitude turn in which it experiences tailwind. The decrease in altitude results in converting potential energy to kinetic energy. Both UAVs start from the same point in the space. For variable-sweep case, an approximate increase of 13% in the maximum velocity attained during the maneuver is observed.

As shown in Eq. (2), to have powerless flight, the velocity added by wind shear (third term) must be greater than or at least even with that consumed by drag (first term).

$$\begin{aligned} \dot{V} = \frac{1}{m}[-D-mg\sin \gamma -m\dot{V}_W\cos \gamma \sin \psi ] \end{aligned}$$
(19)

From Eq. (4)

$$\begin{aligned} \dot{V}_W=V_{w_\mathrm{ref}} \frac{1}{h\ln (h_\mathrm{ref}/h_0)}\dot{h}. \end{aligned}$$
(20)

And from Eq. (2),

$$\begin{aligned} \dot{h}=V \mathrm{sin} \gamma . \end{aligned}$$
(21)

So Eq. (19) transforms to Eq. (22):

$$\begin{aligned} \begin{aligned} \dot{V}&= \frac{1}{m}\Bigg [-\varvec{D}-mg \mathrm{sin} \gamma \\&\quad - m V_{w_\mathrm{ref}} \frac{1}{hln(h_\mathrm{ref}/h_0)}\mathrm{sin}\gamma \mathrm{cos}\gamma \mathrm{sin}\psi \Bigg ]. \end{aligned} \end{aligned}$$
(22)

This requires that estimates (23) must be satisfied for sustained powerless flight.

$$\begin{aligned} \begin{aligned} \mathrm{sin}\gamma \, \mathrm{cos}\gamma \, \mathrm{sin}\psi <0. \end{aligned} \end{aligned}$$
(23)

This can be achieved through windward climb and tailwind descend. During the windward climb phase, estimate (24) holds.

$$ \begin{aligned} \begin{aligned}&0<\gamma< \pi /2 \Rightarrow \mathrm{sin}\gamma \, \& \,\mathrm{cos} \gamma >0, \\&\pi< \psi<2\pi \quad \mathrm{or}\, \, -\pi< \psi<0, \Rightarrow \mathrm{sin}\psi<0, \\&\mathrm{so}\,\, \mathrm{overall}, \,\,\mathrm{sin}\gamma \, \mathrm{cos}\gamma \, \mathrm{sin}\psi <0. \end{aligned} \end{aligned}$$
(24)

And during the decent phase, estimate (25) holds.

$$ \begin{aligned} \begin{aligned}&-\pi /2<\gamma< 0 \Rightarrow \mathrm{sin}\gamma<0, \ \& \,\mathrm{cos} \gamma>0, \\&0< \psi<\pi \quad or\, \, -\pi< \psi<-2\pi , \Rightarrow \mathrm{sin}\psi >0, \\&\mathrm{so}\,\, \mathrm{overall}, \,\,\mathrm{sin}\gamma \, \mathrm{cos}\gamma \, \mathrm{sin}\psi <0. \end{aligned} \end{aligned}$$
(25)

UAV can therefore extract energy from the atmosphere, during both the climb and descent phases. The optimized trajectories of flight path angle and heading angles (Fig. 6) reflects that the constraints imposed by estimate (24) and estimate (25) are completely satisfied.

The results can be further corroborated with the control vector history plotted in Fig. 7. The fixed configuration retains zero sweep during the complete maneuver. For morphing configuration, the wings sweep back to \(50^{\circ }\) during windward climb and tailwind descent phases. The associated angle of attack requirement is also less thereby suggesting towards low drag desirability during these phases. At higher altitude, drag penalty is finished due to reduced velocity. At this moment, the morphing wing goes to minimum sweep condition, that is \(0^{\circ }\). In this phase, the aircraft wants to extract maximum lift from its aerodynamic surfaces. This suggest that the aircraft is trying to circumvent the stall conditions.

The UAV maintains the lower sweep configuration throughout the high altitude turn phase. During the tailwind descent, the wings sweep back to \(50^{\circ }\), low drag configuration, after crossing the threshold velocity of 10.62 m/s (refer Fig. 8). Another important observation made from the state and control histories is increase in overall loiter time per cycle with morphing. This is also a desirable attribute in enhancing loiter performance. The algorithm performs rapid optimization of the sweep during various phases within the permissible range. In real-world conditions, a rate limiter can be incorporated to ensure that the change in the sweep variations is not beyond admissible rates for the wing actuators.

Fig. 8
figure 8

Sweep variation during the loiter maneuver

Full size image

The history of aerodynamic coefficients is shown in Fig. 9. Coefficient of lift and drag requirement are low during the beginning of the maneuver as the dynamic pressure is significant to generate desired aerodynamic forces. However, with the increase of altitude and velocity reduction, the coefficients spike to overcome the dynamic pressure deficiency. This particularly holds for the change from windward climb to tailwind descent turning phase. Unsteady aerodynamic effects are generally present for non-smooth temporal behavior of aerodynamic coefficients. In Fig. 9, overall behavior of aerodynamic coefficients is smooth in nature thereby suggesting minimum effect of unsteady phenomena. However, couple of minor kinks in the drag behavior are observed during the turning phase that may be assumed to have negligible effect. Therefore, the simulation results are adequate to suggest potential benefits of morphing during loiter mode of dynamic soaring maneuvers.

Fig. 9
figure 9

Aerodynamic coefficients during four different phases of the loiter maneuver

Full size image

Comparison of aerodynamic coefficient (\(C_L\)) calculated through empirical technique was duly verified through vortex lattice method (VLM) methodology. Fig. 10 depicts variation in lift coefficient with respect to varying sweep angle for different angles of attack. Results from both the empirical and VLM methodologies are superimposed for analysis purpose. It is evident that both the methodologies follow a similar pattern, which shows the accuracy of the empirical technique utilized in this study for predicting the aerodynamic forces.

Fig. 10
figure 10

Aerodynamic coefficient comparison : empirical Vs VLM techniques

Full size image

The objective of the trajectory optimization formulation is to reduce the overall wind shear requirement. It can be clearly seen from Fig. 11 that the minimum shear wind strength required for dynamic soaring maneuver with fixed configuration is 11.8 m/s and 9.8 m/s with morphing feature at an altitude of 10 m above ground level. The advantage increases with the increase in altitude suggesting morphing to be more effective at high altitudes. Reduction in the wind shear requirements is the fundamental challenge in executing dynamic soaring maneuvers. These results strongly support the utility of morphing to execute dynamic soaring maneuvers in low wind conditions typically found in urban areas. Operations such as area surveillance/ reconnaissance, medical support, search and rescue and various types of other missions are frequently required in such urban areas. In this study, the morphing configuration reduces minimum wind shear requirements by approximately 24% at different altitudes (10 m, 20 m and 30 m). This substantiates the fact that a morphing capable UAV could perform dynamic soaring in areas where wind shear is not of the magnitude that could support dynamic soaring for a fixed planform UAV.

Fig. 11
figure 11

Optimal trajectories for minimum required wind shear

Full size image
Fig. 12
figure 12

Normalized energy during four different phases of the loiter maneuver

Full size image
Table 2 Comparative analysis: Morphing vs. fixed configuration
Full size table

Likewise, the normalized energies (total, potential and kinetic energies) are also higher in the case of morphing configuration (Fig. 12). Approximately, 34% increase in the total normalized energy is achieved by morphing UAV in comparison with the fixed-wing configuration. The kinetic energy is exchanged for the potential energy as the UAV gains height. After reaching maximum altitude, the UAV takes the high altitude turn and start its downwind flight where the potential energy is traded for the kinetic energy. The overall energy at the start and end of the maneuver remains constant which ensures an energy neutral cycle.

The entire results of this section are summarized and collected in Table 2. In Table 2, all conducted comparisons between the sweep morphology and the fixed configuration are presented. It is noticeable that sweep morphology is better then fixed configuration in the results of achieving higher velocities, greater area coverage, higher altitude gains, lesser required minimum wind shear, low drag generations at low angles of attack (lower altitudes), and high lift generation at high angles of attack (higher altitude).

4 Conclusions

This paper proposed the idea of implementing dynamic soaring maneuver for a morphing capable platform. As a test case, impact of morphing was investigated for a platform capable of performing sweep variation (\(0^{\circ }\)–\(50^{\circ }\)) during the soaring maneuver. Utilizing nonlinear logarithmic wind shear model and a three-dimensional point-mass model, an optimal control problem was formulated and solved numerically utilizing Guass pseudospectral-based optimization solver GPOPS-II. Analysis revealed striking results as the morphing platform outclassed the fixed configuration platform in all aspects during the dynamic soaring loiter maneuver. Approximately, \(24\%\) lesser wind shear was required by the morphing platform in comparison to the fixed counterpart. This reflects that morphing platform could perform dynamic soaring in areas where fixed configurations might not possibly perform because of the presence of lesser wind shear. This will be of significant importance in applications where UAV is required to perform surveillance over urban areas where wind shear is lesser in magnitude due to surrounding interferences. Apart from this, the morphing platform showed approximately 29%, 28% and 25% improvement in the altitude, east and north distances, respectively. Also, considerable decrease in drag (20%) and lift requirement (10%) was demonstrated by the morphing platform. Approximately, \(34 \%\) increased normalized energy and \(13 \% \) increased velocity during the maneuver showed the effectiveness of the proposed integration. Through the results achieved, the idea of integrating dynamic soaring and morphology is highly supported. It is envisaged that this study will open a new avenue for researchers where the impact of various other morphologies (such as but not limited to wing twist, wing dihedral, span variation) on dynamic soaring heuristics can be analyzed to determine the configuration most suitable for dynamic soaring during different phases of the maneuver.