1 Introduction

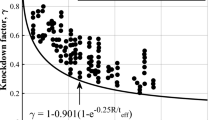
Most space launch vehicles use thin cylinders as their main structural elements. However, the cylindrical structures are seriously weak in buckling under compressive loads. Thus, the structural design of space launch vehicles often considers the buckling load as the primary design criterion. The buckling load of a cylinder in a test is usually lower than the predicted value from a linear buckling analysis for a geometrically perfect cylinder. The initial imperfection of a cylindrical structure causes this large difference between the measured and calculated buckling loads. Therefore, the shell knockdown factor is used for the buckling design of launch vehicle structures so that the analytical buckling load is reduced (knocked down) appropriately. Current buckling designs of space launch vehicle structures usually use the knockdown factor provided by the NASA space vehicle design criteria ([1], Fig. 1). In Fig. 1, the lower knockdown factor means that the amount of imperfection of the cylinder is more.

Fig. 1
figure 1

Lower bound of knockdown factor [1]

Full size image

NASA’s lower bound of knockdown factors [1] was derived using test data collected from the 1930s to the 1960s. Thus, NASA’s buckling design criteria [1] allow the launch vehicle structures to be designed over-conservatively, that is, to be over-weighted since they do not consider advanced structural concepts, precise manufacturing techniques, and modern materials [2]. Two recent projects, SBKF (Shell Buckling Knockdown Factor [3]) and DESICOS (New Robust DESign Guideline for Imperfection Sensitive Composite Launcher Structures [4]), were conducted to redevelop the shell knockdown factor to design lightweight launch vehicles. Intensive computational studies [5,6,7] were conducted along with buckling tests in both projects.

In numerical analyses for investigations of buckling behavior of shell structures, the SPLA (single perturbation load approach [8], Fig. 2) was used to model the geometrical imperfection of a cylinder. The single buckle is considered as the worst case of imperfection of thin-walled structures, and a radial perturbation load applied to the cylinder normally can represent well the single buckle [8]. The SPLA, using a single perturbation load, has been considered one of the best methods for representing the initial imperfection of shell structures. The multiple perturbation load approach (MPLA [7], Fig. 3), which considers several perturbations, may provide the worst geometrical imperfection than the SPLA. However, the more perturbation loads for the MPLA are used, the more unrealistically the cylinder’s imperfection is represented [7].

Fig. 2
figure 2

SPLA (single perturbation load approach) for the initial imperfection modeling

Full size image
Fig. 3
figure 3

Multiple perturbation load approach (MPLA)

Full size image

Although the load–displacement curves of the postbuckling analyses using the MPLA were given in a previous work [7], the shell knockdown factors were not derived, and they were not compared with the values given by NASA’s buckling design criteria [1]. Therefore, the work did not investigate whether the analysis-based buckling design using the MPLA was less conservative than NASA’s buckling design criteria [1] and the buckling design using the SPLA. Furthermore, most previous postbuckling analyses did not consider various shell-thickness ratios (ratio of radius to thickness) to derive the knockdown factor of cylindrical structures; thus, the knockdown factor variation was not investigated for different shell-thickness ratios.

Therefore, this work conducts postbuckling analyses of cylindrical structures using two different imperfection models (SPLA and MPLA) and derives the shell knockdown factors using the obtained analysis results. The derived knockdown factors using the SPLA and MPLA are compared to each other and to NASA’s knockdown factor [1], and the knockdown factor variation is investigated with increasing numbers of lateral perturbation loads. In addition, the knockdown factor variation is studied as the cylinder’s thickness changes when the SPLA is used to model the initial imperfection.

For the present study, a simple isotropic cylinder without stiffeners is considered and a commercial nonlinear finite element analysis code, ABAQUS, is used. Four-node shell elements with reduced integration (S4R elements) are used for the finite element modeling of a cylinder. The Newton–Raphson method with a displacement control scheme is used to analyze the postbuckling of the cylinder. Additionally, artificial damping is applied to stabilize unstable quasi-static analyses. Local and global instabilities are investigated in the postbuckling analyses. Finally, using the predicted global buckling loads, the shell knockdown factors are derived with different imperfection models and various shell-thickness ratios. All the derived knockdown factors are compared with the corresponding values of NASA’s knockdown factor [1].

2 Analytical Methods

2.1 Analysis Models

In this work, the cylinder model to derive the shell knockdown factor is based on NASA’s test article given in the Ref. [10]. The cylinder does not have stiffeners and it was constructed using aluminum alloy sheets. Two straps were used in order to bond the sheets into a circular shape. The schematic diagram of the cylinder is given in Fig. 4, and its radius (R), length (L), and thickness (t) are 0.229, 0.787, and 0.001 m, respectively. The elastic modulus (E) and Poisson’s ratio (ν) of aluminum are 70 GPa and 0.3, respectively. A further detailed description, e.g., boundary conditions, is given in the Ref. [10]. When the shell-thickness ratio (R/t) is changed in the present study, the radius (R) of the cylinder is fixed and the thickness (t) is changed.

Fig. 4
figure 4

Schematic diagram of the cylinder [10]

Full size image

2.2 Initial Imperfection Models

Two different methods, SPLA and MPLA, are used to represent the geometrically initial imperfection of a cylinder. As previously indicated in Figs. 2 and 3, the SPLA uses one lateral perturbation load, but the MPLA uses one or more lateral perturbation loads. In the present work, the MPLA considers two, three, and four perturbation loads with the same magnitude and an equal interval between perturbation loads along the circumferential direction (Fig. 3).

In the numerical analyses using ABAQUS, the SPLA and MPLA are both modeled through the following process. First, the lateral perturbation load(s) in the radial direction is applied at the middle(s) of the cylinder to model the initial imperfection of a cylinder. In this step, the deformed shape of a cylinder subject to the lateral perturbation load(s) is determined by a nonlinear static analysis. Second, the deformed configuration from the previous step is introduced to the perfect cylinder by modifying the nodal coordinate values of its ABAQUS model. This step represents the cylinder with the initial imperfection but in a stress-free condition [11]. Finally, the axial displacement at the edges of the cylinder is applied to the cylinder obtained from the second step. In this step, a nonlinear static postbuckling analysis using the displacement control is conducted to predict the relation between the axial load and the axial displacement of the cylinder (Fig. 5). This step continues until the global instability converges as the perturbation load(s) increases. When the perturbation load(s) of the SPLA or MPLA is higher than a certain value of the perturbation load, Q1, for the convergence of the global buckling load, as shown in Fig. 6, a small and sudden drop may appear in the curve of the axial load and displacement, as seen in Fig. 7. This small drop represents the local buckling of the cylinder.

Fig. 5
figure 5

Load–displacement curve of the postbuckling analysis

Full size image
Fig. 6
figure 6

Global buckling load in terms of perturbation load

Full size image
Fig. 7
figure 7

Global and local instabilities

Full size image

2.3 Modeling and Analysis Techniques for ABAQUS

To derive the shell knockdown factor, using numerical analysis results without any test data, nonlinear static postbuckling analyses are conducted for the cylinder described in the previous sections. In this postbuckling analysis, the behavior of the axial load and the shortening of a cylinder is investigated as the lateral perturbation load increases, and the global and local buckling loads are determined. ABAQUS is used for the present nonlinear postbuckling analyses with the Newton–Raphson method. A displacement control scheme is used for the Newton–Raphson method and artificial damping is applied to stabilize the nonlinear static analyses for local instabilities, because the artificial damping may dissipate the released strain energy when a local instability occurs [12].

S4R shell elements are used for the finite element modeling using ABAQUS. The strap is not modeled in this work except the example (given in Fig. 9) to validate the postbuckling analysis using the SPLA and artificial damping. This is because the postbuckling analysis without the strap is also reasonably good which will be shown in Fig. 9 and it is easier to model the cylinder without the strap when the different initial imperfection modeling schemes and various shell-thickness ratios are considered. This will be explained in detail in Sect. 3.1, again. All the nodes at each end of the cylinder are coupled with a control node using the kinematic coupling (Fig. 8) for application of a uniform displacement condition. For the displacement control method, the axial displacement is enforced, instead of the axial load, to the control node. A nonlinear analysis using a displacement control method can investigate the local instability as well as the global instability of a cylinder, as shown in Figs. 5 and 7.

Fig. 8
figure 8

Schematic diagram for rigid links and a control node

Full size image

2.4 Derivation of Shell Knockdown Factors

As given in Eq. (1), the shell knockdown factor, γ, is defined as the ratio between two global buckling loads of a cylinder, with and without the initial imperfection, (Ncr)imperfect and (Ncr)perfect, respectively. The two global buckling loads are determined from the postbuckling analyses; thus, the shell knockdown factor can be derived using numerical analysis results without test results.

$$ \gamma = \frac{{(N_{\text{cr}} )_{\text{imperfect}} }}{{(N_{\text{cr}} )_{\text{perfect}} }} $$
(1)

In addition, Eq. (2) calculates the shell knockdown factor of an isotropic cylinder, γ, using NASA’s buckling design criteria [1], as follows:

$$ \gamma = 1 - 0.901(1 - {\text{e}}^{ - \varphi } ) $$
(2)
$$ \varphi = \frac{1}{29.8}\frac{R}{t} $$
(3)

3 Results and Discussion

3.1 Comparison of Knockdown Factors Using SPLA and MPLA

Postbuckling analyses using two different imperfection methods, the SPLA and the MPLA, are conducted for NASA’s test article without strap (R/t = 225). Then, the knockdown factors are derived using Eq. (1) and compared with the corresponding values of NASA’s buckling design criteria ([1], Eq. (2)).

Figure 9 validates the postbuckling analyses with and without the strap for the NASA’s test article. The local buckling load (A) and the global buckling load (B) are observed clearly in the curves. For the cylinder model with the strap, the global and local buckling loads are predicted excellently, as compared to the previous NASA’s prediction [10]. The present analysis considering the strap and the previous NASA’s analysis [10] predict the global buckling loads without the initial imperfection as 289 and 288 kN, respectively. But, when the initial imperfection of the cylinder is considered, the global buckling loads are converged to 174.1 and 173.5 kN by the present analysis with the strap and the previous NASA’s prediction [10], respectively, when the value of the lateral perturbation load (Q) exceeds 110 N for the SPLA. Although the present calculation and the NASA’s prediction use different analyses’ techniques, the correlation between the two predictions is good. Thus, the present modeling and analysis techniques using the SPLA and artificial damping are validated excellently. When the strap is not modeled for the perfect cylinder without the initial imperfection, the global buckling load is calculated as 272.2 kN, which is lower than the present analysis considering the strap by only 5.88%. The converged global buckling load for the cylinder without the strap is predicted as 167 kN when the initial imperfection is considered using the SPLA. The relative error of the present analysis without the strap with respect to the present result with the strap is − 4.08%. Therefore, it is believed that the postbuckling analysis without the strap for the NASA’s test article is also quite reasonable. In addition, when the effects of the different initial imperfection modeling schemes and various shell-thickness ratios are investigated on the shell knockdown factor, which will be given in later, it is more appropriate to use the cylinder model without the strap. Therefore, the cylinder model without the strap is used for the remaining analyses in this study.

Fig. 9
figure 9

Validation of postbuckling analyses using SPLA (R/t = 225 and num. of perturbation loads: 1)

Full size image

The deformed shapes of a cylinder with a perturbation load of 90 N are given in Fig. 10. Note that the scaling factors to plot clearly the deformations of the cylinder are different for the two figures. The derived knockdown factor of 0.602 is much higher than 0.45, the corresponding NASA’s knockdown factor (Eq. (2)), by 33.89%. Therefore, the present analysis-based buckling design using the SPLA provides a lighter weight design for launch vehicle structures than the design using the previous design criteria [1].

Fig. 10
figure 10

Deformed shapes of the cylinder (num. of perturbation loads: 1 and perturbation load: 90 N)

Full size image

Figure 11 shows the relation between the axial load and the shortening of a cylinder (R/t = 225) when the MPLA with two perturbation loads is used. Similar to the previous case using the SPLA, the local instability (A) and global instability (B) are shown definitely in the curve. As the magnitude of the perturbation loads increases, the global buckling load converges to 148.4 kN. Because the global buckling load of a perfect cylinder without the initial imperfection is 272.2 kN, the knockdown factor using the MPLA with two perturbation loads is derived as 0.545. This value is lower than the knockdown factor derived using the SPLA by 9.51%, but is higher than the corresponding value using NASA’s buckling design criteria [1] by 21.15%.

Fig. 11
figure 11

Load–displacement curve of the cylinder (R/t = 225 and num. of perturbation loads: 2)

Full size image

The deformed configurations are shown in Fig. 12. As compared to the results with the SPLA given in Fig. 10, the buckling waves spread farther in the circumferential direction when the global buckling occurs. In addition, local bucklings are observed at two locations where the perturbation loads are applied.

Fig. 12
figure 12

Deformed shapes of the cylinder (num. of perturbation loads: 2 and perturbation load: 90 N)

Full size image

The postbuckling analysis results are given in Fig. 13 for the MPLA with three perturbation loads. Similar to the previous cases, the local buckling load (A) and the global buckling load (B) can be determined easily in the axial load and displacement curve. Since the global buckling loads are predicted as 125.5 kN for the cylinder with three perturbation loads, the knockdown factor is derived as 0.461, which is lower than the results using the SPLA and the MPLA with two perturbation loads by 23.48 and 15.43%, respectively. However, the derived knockdown factor using three perturbation loads is similar to the corresponding NASA’s knockdown factor [1] of 0.45 with a relative error of 2.46%. Figure 14 shows the deformed shapes of a cylinder using three perturbation loads when the magnitude of the perturbation loads is 90 N.

Fig. 13
figure 13

Load–displacement curve of the cylinder (R/t = 225 and num. of perturbation loads: 3)

Full size image
Fig. 14
figure 14

Deformed shapes of the cylinder (num. of perturbation loads: 3 and perturbation load: 90 N)

Full size image

The curve of the axial load and the shortening of the cylinder is given in Fig. 15 for the MPLA with four perturbation loads. As the magnitude of the perturbation loads increases, the global buckling load (B) converges to 111.3 kN; therefore, the knockdown factor is calculated as 0.409. This derived knockdown factor is lower than the previous results using the SPLA and the MPLA with two and three perturbation loads by 32.13, 25.00, and 11.32%, respectively. In addition, it is lower than the corresponding value using NASA’s buckling design criteria [1] by 9.14%. The deformed configurations of a cylinder with four perturbation loads are shown in Fig. 16.

Fig. 15
figure 15

Load–displacement curve of the cylinder (R/t = 225 and num. of perturbation loads: 4)

Full size image
Fig. 16
figure 16

Deformed shapes of the cylinder (num. of perturbation loads: 4 and perturbation load: 90 N)

Full size image

Figure 17 represents the convergence of the knockdown factors using the SPLA and the MPLA with two, three, and four perturbation loads. As shown in the figure, all the knockdown factors converge well when the magnitude of the perturbation load(s) exceeds about 90 N. Figure 18 compares the derived knockdown factors with the corresponding value using NASA’s buckling design criteria [1]. The SPLA and the MPLA with two perturbation loads provide higher knockdown factors than NASA’s knockdown factor [1]; however, the MPLA with three perturbation loads gives a knockdown factor similar to NASA’s knockdown factor [1] and the knockdown factor derived by the MPLA using four perturbation loads is lower than NASA’s knockdown factor [1]. Therefore, the SPLA in this work does not represent the worst initial imperfection of a cylinder as similar to the previous result [7]; i.e., it does not guarantee the lower bound of the knockdown factors. However, as the number of MPLA perturbation loads increases, the imperfection of a cylinder becomes unrealistic but the SPLA was validated successfully for the realistic, worst, and simulating imperfection [7, 11]. In addition, it is known that the knockdown factor derived by the SPLA is similar to that by another imperfection model such as the single dimple imperfection approach [7]. Furthermore, there has been no guideline to determine the number of perturbation loads for the MPLA, which provides the realistic and worst imperfection modeling of thin shell structures. Therefore, the SPLA has been more widely used for the realistic modeling of the initial imperfection of a cylindrical structure than the MPLA, although the MPLA may provide the lower knockdown factor, as compared to the SPLA.

Fig. 17
figure 17

Knockdown factor in terms of perturbation load with different imperfection models

Full size image
Fig. 18
figure 18

Knockdown factors of the cylinder different initial imperfection models

Full size image

3.2 Knockdown Factors for the Different Shell-Thickness Ratios

Most previous works to derive numerically shell knockdown factors did not consider the various shell-thickness ratios (R/t) of the cylinder [2,3,4,5,6,7, 9, 10]. However, the various shell-thickness ratios should be considered to establish newly the buckling design criteria for a cylinder. Therefore, three different thickness ratios (including the thickness ratio of 225 used in Sect. 3.1) are considered in this section. The SPLA is used to model the initial imperfection of a cylinder. As previously described, to vary the shell-thickness (R/t), thickness (t) of a cylinder is changed while the radius (R) is fixed as 0.229 m.

Figure 19 shows the axial load and displacement curve for a cylinder with the thickness ratio of 400. The global buckling load converges to the value of 54 kN as the perturbation load increases; thus, the knockdown factor is derived as 0.628 because the global buckling load is calculated as 86 kN for the perfect cylinder without the initial imperfection. This derived knockdown factor is higher than the corresponding NASA’s knockdown factor [1] of 0.36 by 74.42%.

Fig. 19
figure 19

Load–displacement curve of the cylinder (R/t = 400)

Full size image

The postbuckling analysis result for the cylinder with the thickness ratio of 600 is given in Fig. 20. The converged global buckling load is calculated as 24.5 kN; however, the global buckling load for the perfect cylinder is predicted as about 39 kN. Thus, the knockdown factor is derived as 0.628, which is higher than 0.29, the corresponding value using NASA’s buckling design criteria [1], by 116.6%.

Fig. 20
figure 20

Load–displacement curve of the cylinder (R/t = 600)

Full size image

Figure 21 shows the convergences of the knockdown factors as the perturbation load increases. As seen in the figure, the higher the shell-thickness ratio, the lower the value of Q1. Figure 22 compares the variation of the derived knockdown factors with NASA’s knockdown factor [1] for the different shell-thickness ratios. The variation of the present knockdown factors is not sensitive to the change of a cylinder’s thickness ratio, while the knockdown factor using NASA’s buckling design criteria [1] is seriously reduced as the shell-thickness ratio increases.

Fig. 21
figure 21

Knockdown factor in terms of perturbation load with various shell-thickness ratios

Full size image
Fig. 22
figure 22

Knockdown factor of the cylinder in terms of the shell-thickness ratio

Full size image

4 Conclusion

This study conducted postbuckling analyses of a cylinder under compressive loads and derived the shell knockdown factors using obtained numerical results for the structural design of lightweight launch vehicles. A nonlinear finite element analysis code, ABAQUS, was used for the numerical studies. The knockdown factors were derived using two different imperfection models, SPLA and MPLA, and they were compared to each other as well as to the corresponding NASA’s knockdown factors. As the number of lateral perturbation loads increased, the knockdown factor was reduced.

The derived knockdown factors using the SPLA and the MPLA with two perturbation loads were higher than NASA’s knockdown factor. However, the MPLA using three perturbation loads provided a value similar to NASA’s knockdown factor and the MPLA with four perturbation loads produced a lower knockdown factor, as compared to NASA’s knockdown factor. Furthermore, the knockdown factor variation derived by the SPLA was investigated for changing shell-thickness ratios (ratio of radius to thickness). For the three different shell-thickness ratios of 225, 400, and 600, the derived knockdown factor in this study was not sensitive to the change of the shell-thickness ratio and they were all higher than NASA’s knockdown factor.