1 Introduction

Wind energy is the one of most renewable energy sources that is widely used in the world. It is almost universally recognized as the main promising source of energy to generate clean electricity in short and medium terms. It has numerous advantages such as contributing to environmental preservation [1] and generating no waste nor greenhouse gases from the obtained power because its generation system does not pollute the atmosphere, soil, or water [2]. Finally, the derivation of this source is not ephemeral and is always available in nature [3].

Two types of wind conversion systems may be considered. First, the conversion system is provided from the fixed wind speed. Therefore, the generator is directly connected to the grid, from which a poor quality of power energy is derived in the grid when the wind varies [4]. Second, the conversion system is provided through the variable wind speed, from which the generator is equipped with a power electronic converter and then connected to the grid.

Compared to the first conversion system, the second one has many advantages such as good maximum power point tracking (MPPT) performance, a robust decoupling system between generation and grid frequency, as well as good flexibility between them in terms of control and optimal operation [5], and better efficiency to control mechanical stress with reduced cost [6]. For these reasons, variable speed wind turbines are currently the most important and fastest growing application of wind generation systems [6, 7].

In terms of the type of generators for wind energy conversion systems (WECS), several configurations are widely used for the variation speed wide. Among them is the electrical generator, which is either a synchronous generator with external field excitation and a permanent magnet synchronous generator (PMSG) or a doubly fed induction generator with a squirrel cage [8, 9] equipped with a front-end AC–AC power electronic converter [10, 11].

Recently, induction generator systems are becoming more commonly used for several reasons such as their modeling simplicity, their reliability, and their allowing maximum power extraction over a large range of wind speeds. Furthermore, their active and reactive power controls are fully decoupled by independent control of the rotor currents [12].

The objective control of the variable speed of a WECS consists of maximizing the extracted power. Therefore, a considerable amount of MPPT techniques has been presented in the literature. Such techniques can be basically categorized into four groups: tip-speed ratio (TSR) control, optimal torque control (OTC), power signal feedback (PSF) control, and hill-climb search (HCS) control.

The first algorithm is required to maintain the optimal value of the TSR at which the extracted power is maximized by regulating the rotational speed [13, 14].In the OTC algorithm [15, 16], the torque of the generator is tuned to obtain the optimum torque reference curve according to the maximum power of the wind turbine. The PSF method requires knowledge of the maximum power curve of the wind turbine to find the optimal value of the power rotation speed with various wind speeds [17, 18]. Finally, HCS control is a mathematical optimization used to locate the local maximum point of a given function [12, 19]. This algorithm brings the operating point around the maximum power coefficient by increasing or decreasing the rotational speed using a step.

In the past several years, many researchers have focused on the variable speed control of wind turbines in the literature. These studies have started with classical controllers such as the proportional integral (PI) controller for controlling the generator torque [20] and the linear quadratic Gaussian (LQG) controller for ensuring an optimal dynamic behavior of the WECS around the operating point [21] and have continued with some modern controllers such as the generalized predictive control (GPC) controller for maximizing the generated power of the WECS [22, 23],sliding mode control [24], and implementation of the reference model for a doubly fed induction generator (DFIG) based upon the WECS presented in [25]. Unfortunately, the above control strategies required a linear model in which robustness against plant uncertainties cannot be guaranteed owing to the strong nonlinear dynamics of WECSs.

In this regard, synthesis controllers based upon the on–off control strategy have been suggested to avoid the above disadvantages. The obtained controllers have the ability to maximize as much as possible the power of the induction generator while superimposing tracking of the optimal torque value [26]. However, a common drawback of these strategies appears in the definition step of the switching component, which is followed by the sign of the TSR error and therefore yields a discontinuous sign function.

Lin et al. [27] proposed a sliding mode controller combined with a fuzzy inference mechanism for the PMSG speed control in a wind generation system. The main contribution of this paper is to introduce a fuzzy logic control (FLC) strategy in the alternate component of the on–off controller to maximize the extracted power and to eliminate the chattering phenomenon caused by mechanical stress, such that the performances of the standard on–off control are enhanced and the obtained power energy is therefore increased. A plant model in which strong non-stationarities are considered is proposed to model the dynamic behavior of the wind turbine. Furthermore, a robust controller synthesized from combining fuzzy logic and on–off control strategies is proposed to maximize the power captured by the WECS. The controller can drive the conversion system to the optimal operating point by which the switching component problem is resolved in the synthesis controller step.

The present paper is organized as follows. In Sect. 2, a brief description of the proposed system with variable wind speed will be presented. In Sect. 3, the modeling steps of the wind energy system will be given. In Sect. 4, a fuzzy on–off control strategy of the WECS and a robustness analysis will be discussed in detail. In Sect. 5, simulation results will be proved. Finally, we end with a conclusion and numerical data of the proposed system.

2 Description of the WECS Equipped with an Induction Generator

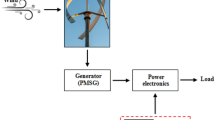
The system to be controlled consists of the WECS based upon an induction generator. The stator winding is connected to the electrical grid. However, the rotor, which is driven by the wind turbine, is connected back-to-back to an AC–DC–AC voltage source converter (see Fig. 1). The power captured by the wind turbine is converted into an electrical form by the induction generator and is transmitted to the grid via the stator winding. The produced power must have the same quality when it reaches the electrical network, i.e., 220 V amplitude and 50 Hz frequency. Its harmonics must be kept at a low level, despite changes of both wind speed and consumed electrical energy, which may be either active or reactive. The variable speed regime is achieved by torque control to maximize the power captured by the WECS. References such as [2, 5] give the requirement details of wind turbines.

Fig. 1
figure 1

Schematic diagram of the WECS equipped with the induction generator

Full size image

3 WECS Modeling Steps

3.1 Modeling of the Wind Turbine Connected with MPPT

The kinetic energy of the wind can be converted into electrical energy that can be expressed as

$$E_{k} = \frac{1}{2}mv^{2}$$
(1)

where \(v\)is the wind speed and \(m\) is the air mass that passes through a disk in time unit, defined by

$$m = \rho Sd$$
(2)

where \(\uprho\), \(S,\) and \(d\) denote, respectively, the air density, the area swept by the rotor blades, and the distance traveled by the wind. The power available from the turbine is defined by [28]

$$P_{\text{w}} = \frac{1}{2}\uprho \uppi R^{2} v^{3}$$
(3)

From Betz’s theory, the mechanical power harvested by the wind turbine is given by [29]

$$P_{\text{m}} = \frac{1}{2}\uprho \uppi R^{2} v^{3} C_{p} \left( {\uplambda,\upbeta} \right)$$
(4)

where \(R\), \(\uplambda\), \(\upbeta\) and \(C_{p}\) are, respectively, the blade radius, the tip-speed ratio, the pitch angle, and the energy coefficient. The tip-speed ratio is defined by

$$\uplambda = \left( {\frac{R}{v}} \right)\varOmega_{\text{t}}$$
(5)

where \(\varOmega_{\text{t}}\) denotes the rotor speed of the wind turbine. The power coefficient \(C_{p} \left( {\uplambda,\upbeta} \right)\) depends on the number of rotor blades and its geometric and aerodynamic shapes (length, profile of sections, etc.). They are designed according to the characteristics of a site, the desired power rating, the type of regulation, and the type of operation (at fixed or variable speed). \(C_{p} \left( {\uplambda,\upbeta} \right)\) is presented as a nonlinear function of \(\uplambda\) and \(\upbeta\), which are tabulated, and is described by a family of polynomials. The theoretical upper limit of the power coefficient \(C_{\text{pmax}}\) is given by Betz’s limit [30]:

$$C_{\text{pmax}} = \frac{16}{27} \approx 0.59$$
(6)

In practice, friction and the drag force reduce this value to ~ 0.5 for large wind turbines. We can also compute analytic expressions of \(C_{p} \left(\uplambda \right)\) for different values of \(\uplambda\). The analytical expression generally used is a polynomial regression [30]:

$$C_{p} \left(\uplambda \right) = \mathop \sum \limits_{l} a_{l}\uplambda^{l}$$
(7)

Figure 2 shows the C p –λ curve for \(0 \le\uplambda \le 12\).

Fig. 2
figure 2

C p –λ characteristics

Full size image

According to this figure, it is easy to see that the maximum value of the power coefficient (i.e., \(C_{\text{pmax}} = 0.498\)) is achieved when the speed ratio attains its optimal value (i.e., \(\uplambda = 7\)).

The aerodynamic torque \(\varGamma_{\text{t}}\) can be determined through the mechanical power \(P_{\text{m}}\) and the rotation speed of the blades,\(\varOmega_{t}\). It is given as follows [31]:

$$\varGamma_{\text{t}} = \frac{{P_{\text{m}} }}{{\varOmega_{\text{t}} }}$$
(8)

The mechanical torque \(\varGamma_{\text{g}}\), which is applied on the generator shaft, is defined by [29]

$$\varGamma_{\text{g}} = \left( {\frac{1}{G}} \right)\varGamma_{\text{t}}$$
(9)

where \(G\) denotes the gearbox of the generator. The mechanical generator speed \(\varOmega_{\text{m}}\) is determined by solving the following differential equation:

$$J\frac{{d\varOmega_{\text{m}} }}{dt} + f\varOmega_{\text{m}} = \varGamma_{\text{g}} - \varGamma_{\text{e}}$$
(10)

where \(f\) and \(J\) denote the friction coefficient and the system moment of inertia, respectively. Furthermore, the rotation speed \(\varOmega_{\text{t}}\) is also determined from the mechanical generator speed \(\varOmega_{\text{m}}\) as

$$\varOmega_{\text{m}} = \varOmega_{\text{t}} G$$
(11)

Figure 3 shows the connection of the mechanical parts of the wind turbine by using MPPT.

Fig. 3
figure 3

Connection of the wind turbine by using MPPT

Full size image

3.2 Modeling of the Induction Generator

The stator and rotor components that model the nonlinear induction generator behavior are defined in d–q coordinates by [32]

$$\left\{ {\begin{array}{*{20}c} {\upsilon_{ds} = R_{s} i_{ds} + \frac{{d{\varphi }_{ds} }}{dt} - \omega_{s} {\varphi }_{qs} } \\ {\upsilon_{ds} = R_{s} i_{qs} + \frac{{d{\varphi }_{ds} }}{dt} - \omega_{s} {\varphi }_{ds} } \\ {0 = R_{r} i_{dr} + \frac{{d{\varphi }_{dr} }}{dt} - \omega_{r} {\varphi }_{qr} } \\ {0 = R_{r} i_{qr} + \frac{{d{\varphi }_{qr} }}{dt} - \omega_{r} {\varphi }_{dr} } \\ \end{array} } \right.$$
(12)

and its stator and rotor fluxes are given by [33]

$$\left\{ {\begin{array}{*{20}c} {{\varphi }_{ds} = L_{s} i_{ds} + L_{m} i_{dr} } \\ {{\varphi }_{qs} = L_{s} i_{qs} + L_{m} i_{qr} } \\ {{\varphi }_{dr} = L_{r} i_{dr} + L_{m} i_{ds} } \\ {{\varphi }_{qr} = L_{r} i_{qr} + L_{m} i_{qs} } \\ \end{array} } \right.$$
(13)

where \(\upsilon_{ds} \;{\text{V}}_{\text{ds}} ,{\text{V}}_{\text{qs}} ,{\text{V}}_{\text{dr}} ,{\text{V}}_{\text{qr}} \;{\text{and}}\;\upsilon_{ds}\) are the measured stator voltage components; \({\text{I}}_{\text{ds}} ,{\text{I}}_{\text{qs}} ,{\text{I}}_{\text{qr}} ,i_{ds} ,i_{qs} ,i_{dr} ,\;{\text{and}}\;i_{qr}\) are, respectively, the components of the stator and rotor current; \(\varphi_{ds} ,\varphi_{qs} ,\varphi_{dr} ,\;{\text{and}}\;\varphi_{qr}\) \({\text{V}}_{\text{ds}} ,{\text{V}}_{\text{qs}} ,{\text{V}}_{\text{dr}} ,{\text{V}}_{\text{qr}}\) are the components of the stator and rotor flux vectors;\(R_{s} {\text{and }}R_{r}\) are the stator and rotor phase resistances;\(L_{s}\) and \(L_{r}\) are the cyclic stator and rotor inductances; and \(L_{m}\) is the cyclic mutual inductance.

The plant model of the induction generator is established from both Eqs. (12) and (13) using MATLAB/Simulink software. Its stator voltages give the plant model output, and the plant model input is given by the electromagnetic torque, which is expressed by

$$\varGamma_{\text{e}} = \frac{3}{2}p\frac{{L_{m} }}{{L_{r} }}\left( {i_{qs } {\varphi }_{dr} - i_{ds } {\varphi }_{qr} } \right)$$
(14)

In the next section, we will assume that the rotor field is oriented along the d axis. Consequently, the rotor flux \({\varphi }_{qr}\) becomes equal to zero (i.e., \({\varphi }_{qr} = 0\)) and Eq. (14) can be rewritten as

$$\varGamma_{\text{e}} = \frac{3}{2}p\frac{{L_{m} }}{{L_{r} }}i_{qs } {\varphi }_{dr}$$
(15)

The obtained electromagnetic torque will be compared to the one provided by the proposed fuzzy on–off controller wherein an optimal reference stator current can ensure a constant stator voltage with a constant frequency in the electrical grid.

In the Appendix, Table 2 summarizes the induction machine parameters and Table 3 gives the numerical data for each parameter of the wind turbine.

4 Proposed Fuzzy On–Off Design Controller

Enhancement performances of the standard on–off controller for any wind speed profile present the main contribution of this paper. This goal was achieved by using the proposed fuzzy on–off controller, which ensures an optimal reference electromagnetic torque. The proposed control strategy is shown in Fig. 4.

Fig. 4
figure 4

Conversion system based upon the proposed fuzzy on–off controller

Full size image

If the rotor flux \({\varphi }_{r}\) is constant, the generator torque \(\varGamma_{\text{e}}\) can be controlled by the stator current \(i_{ds}\), and the rotor flux \({\varphi }_{r}\) is related only to the excitation component of the stator current \(i_{ds}\), and the direction of the stator current \(i_{ds}\) along the d axis determines the direction of \({\varphi }_{r}\). In Fig. 4, we can get the rotor flux \({\varphi }_{r}\) and the slip angular velocity \(\upomega_{s}\) by using the rotor flux function and the slip function, respectively. The q axis reference current \(i_{qs}^{*}\) is proportional to the torque reference \(\varGamma_{\text{e}}^{*}\) that is generated from the fuzzy on–off based MPPT controller and varies under wind speed variations. According to Fig. 4, the three-phase line currents are compared to the three-phase reference currents applied to a hysteresis controller to generate pulse-width modulation (PWM) pulses to control the converter. Therefore, the proposed fuzzy on–off controller has the ability to generate the above mentioned torque by minimizing the discrepancy between the tip-speed ratio are its optimal value [34]. This discrepancy is given by

$$\upsigma =\uplambda_{\text{opt}} -\uplambda$$
(16)

Minimizing \(\upsigma\) requires an optimal control law. The control law obtained by using the standard on–off control strategy has two control components, the equivalent control component \(u^{\text{eq}}\) and the alternate high-frequency component \(u^{n}\). The obtained control law is expressed by

$$u = u^{\text{eq}} + u^{n}$$
(17)

The control component \(u^{\text{eq}}\) is defined by

$$u^{\text{eq}} = \left( {\frac{1}{2}\pi \rho R^{3} \frac{{C_{p} \left( {\uplambda_{\text{opt}} } \right)}}{{\uplambda_{\text{opt}} G}}} \right)v_{s}^{2}$$
(18)

where \(v_{s}\) denotes the low-frequency wind speed component. However, the control component \(u^{n}\), which alternates between \(-\upalpha\) and \(+\upalpha,\) where \(\upalpha > 0\), is defined

$$u^{n} =\upalpha{\text{sign}}\left(\upsigma \right)$$
(19)

Notice that the control component \(u^{\text{eq}}\) makes the system operate at the optimal point. In contrast, the control component \(u^{n}\) has the ability to stabilize the dynamic behavior of the system around this optimal point when it is reached. Therefore, the chattering problem appears because of the term \({\text{sign}}\left(\upsigma \right)\) given in Eq. (19).

Substituting the alternate high-frequency component \(u^{n}\) by the fuzzy control law \(u^{f}\) solves the above problem, yielding the following new control law:

$$u_{\text{new}} = {\text{u}}^{\text{eq}} + u^{f}$$
(20)

Figure 5 shows the proposed schematic diagram for determining the control law \(u_{\text{new}}\) and the optimal reference electromagnetic torque \(\varGamma_{\text{e}}^{*}\). According to Fig. 5, it is easy to see that the reference electromagnetic torque \(\varGamma_{\text{e}}^{*}\), which is given through the electromagnetic subsystem (EMS) block, is ensured by the proposed new control law \(u_{\text{new}}\). Figure 5 shows also that the low-frequency component \(v_{s}\) is extracted from the wind speed \(v\left( t \right)\) using the high-order low-pass filter (LPF). Furthermore, two zero-order sample-and-hold \(\left( {{\text{S}}\& {\text{H}}} \right)\) blocks are introduced before the proposed FLC system to limit the loop switching frequency if \(\upsigma\) and \({\dot{\sigma }}\) have large spectrums. So that, if this frequency is too large, the dynamic behavior of the electromagnetic subsystem becomes too fast, such that the control loop becomes inefficient. The \({\text{S}}\& H\) blocks are approximated as first-order low-pass filters, each given with the time constant \(T_{{{\text{S}}\& H}} = \frac{{T_{s} }}{2}\), where \(T_{s}\) denotes the sampling time chosen by the user.

Fig. 5
figure 5

Proposed fuzzy on–off control for MPPT

Full size image

Now, preventing the switching component is an important aspect in the on–off control strategy. A fuzzy system is a particular form of nonlinear mapping, from which the fuzzy system input is achieved by the variable \(\upsigma\) and its derivative \({\dot{\sigma }}\) and the fuzzy system output is given by \(u^{f}\).

Moreover, the fuzzy input–output system is linked through a rule base, which is commonly obtained from expert knowledge. It contains a collection of fuzzy conditional statements expressed as sets of “if–then” rules such as

$$R^{r} :{\text{if}}\left( {x_{1} {\text{is }}A_{1}^{r} } \right) {\text{and }}\left( {x_{2} {\text{is }}A_{2}^{r} } \right) {\text{and }} \cdots \left( {x_{n} {\text{is }}A_{n}^{r} } \right)\;{\text{then }}\left( {z {\text{is }}B^{r} } \right)$$

where \(A^{\text{r}}\) and \(B^{\text{r}}\) are fuzzy sets with membership functions \(\mu_{{A_{i}^{r} }} \left( {x_{i} } \right)\) and \(\mu_{{B_{i}^{r} }} \left( y \right),\) respectively, \(x\left( t \right) = \left[ {x_{1} , x_{2} , \ldots ,x_{n} } \right]^{\text{T}}\) are the input variables vector, \(z\) is the output variable, \(r\) is the number of rules and, \(n\) is the number of the fuzzy variables. With a singleton fuzzifier, a product inference engine, and a weighted average defuzzification, the output of the fuzzy system can be written as [35]

$$z\left( t \right) = \frac{{\mathop \sum \nolimits_{i = 1}^{{n_{r} }}\uptheta^{i} \left( t \right)\left( {\mathop \prod \nolimits_{j = 1}^{h}\upmu_{{A_{j}^{i} }} \left( {x_{j} \left( t \right)} \right)} \right)}}{{\mathop \sum \nolimits_{i = 1}^{{n_{r} }} \left( {\mathop \prod \nolimits_{j = 1}^{h}\upmu_{{A_{j}^{i} }} \left( {x_{j} \left( t \right)} \right)} \right)}} =\uptheta^{T} \left( t \right)\varPsi \left( {x\left( t \right)} \right)$$
(21)

where \(n_{r}\) is the number of total fuzzy rules, \(\uptheta^{i} \left( t \right)\) is the vector of the centers of the membership functions of \(z,\) and \(\varPsi = \left[ {\varPsi^{1} ,\varPsi^{2} , \ldots ,\varPsi^{{n_{r} }} } \right]^{T}\) is a fuzzy basis vector, where \(\varPsi^{i}\) is defined as

$$\varPsi^{i} \left( {x\left( t \right)} \right) = \frac{{\mathop \prod \nolimits_{j = 1}^{h}\upmu_{{A_{j}^{i} }} \left( {x_{j} \left( t \right)} \right)}}{{\mathop \sum \nolimits_{i = 1}^{{n_{r} }} \left( {\mathop \prod \nolimits_{j = 1}^{h}\upmu_{{A_{j}^{i} }} \left( {x_{j} \left( t \right)} \right)} \right)}}$$
(22)

In Table 1, the following fuzzy sets are used:\({\text{NB}}\): negative big, \({\text{NM}}\): negative medium, \({\text{NS}}\): negative small, \({\text{ZR}}\): zero, \({\text{PS}}\): positive small, \({\text{PM}}\): positive medium, and \({\text{PB}}\):positive big.

Table 1 Fuzzy rules
Full size table

Furthermore, the proposed fuzzy rules for the output variable \(z^{f}\) are listed in Table 1.

The fuzzy rules of the output variables are built to guarantee the stability of the system around the operating point by choosing a control law such that only \(\upsigma = 0\). In fuzzy on–off control, fuzzy logic theory is applied to compensate for the system uncertainty and reduce the effect of the chattering. The idea of extracting the fuzzy rules is similar to that of applying a saturation function. The difference is that the control gain varies along with the on–off surface all the time.

If \(\upsigma\) is NB and \({\dot{\sigma }}\) is NB then \(z^{f}\) has a large negative value. As a result, the energy of \(\upsigma\) decays fast. If \(\upsigma\) is ZR and \({\dot{\sigma }}\) is ZR then \(z^{f}\) is ZR.

If \(\upsigma\) is PB and \({\dot{\sigma }}\) is PB then the PB value of \(z^{f}\) is allowed to avoid chattering, where the desired fuzzy control law is determined by

$$u^{f} = \alpha z^{f} =\upalpha \cdot \frac{{\mathop \sum \nolimits_{i = 1}^{49} \left( {\uptheta^{i}\upmu_{{\upsigma_{i} }}\upmu_{{{\dot{\sigma }}_{i} }} } \right)}}{{\mathop \sum \nolimits_{i = 1}^{49} \left( {\upmu_{{\upsigma_{i} }}\upmu_{{{\dot{\sigma }}_{i} }} } \right)}}$$
(23)

Equation (20) can be rewritten as follows:

$$u_{\text{new}} = \left( {\frac{1}{2}\uppi \uprho R^{3} \frac{{C_{p} \left( {\lambda_{\text{opt}} } \right)}}{{\lambda_{\text{opt}} G}}} \right)v_{s}^{2} +\upalpha\frac{{\mathop \sum \nolimits_{i = 1}^{49} \left( {\theta^{i}\upmu_{{\upsigma_{i} }}\upmu_{{{\dot{\sigma }}_{i} }} } \right)}}{{\mathop \sum \nolimits_{i = 1}^{49} \left( {\mu_{{\upsigma_{i} }} \mu_{{{\dot{\sigma }}_{i} }} } \right)}}$$
(24)

Here,\(\uptheta^{i}\) is the singleton control in the \(i{\text{th}}\) rule, and \(\upmu_{{\upsigma_{i} }}\) and \(\upmu_{{{\dot{\sigma }}_{i} }}\) are, respectively, the membership functions of \(\upsigma\) and \({\dot{\sigma }}\) in the \(i^{\text{th}}\) rule. Figure 6 presents the linguistic values for \(\upsigma,{\dot{\sigma }},\) and \(z^{f}\). We define seven triangular membership functions distributed within the range [− 1, 1]. Then there are 49 rules, which are used in the simulation [36].

Fig. 6
figure 6

Membership functions used for \(\upsigma,{\dot{\sigma }},\) and \(z^{f} .\)

Full size image

5 Results and Discussion

The simulation results were obtained using MATLAB/Simulink software. The proposed fuzzy on–off controller performances were verified for various wind profiles. The wind’s speed was altered from \(5\) to \(8\)  m/s with a mean of 7 \({\text{m}}/{\text{s}}\). The time range used for the simulation was \(t \in \left[ {t_{0} , t_{ \hbox{max} } } \right] = \left[ {0 , 120} \right]\) s wherein the sampling time \(T_{S} = 0.01\) s was chosen (see Fig. 7).

Fig. 7
figure 7

Wind speed profile

Full size image

Notice that the maximum value of the energy coefficient is given by \(C_{{{\text{p}}_{ \hbox{max} } }} = 0.475\). Furthermore, Fig. 8 compares the curves of the energy coefficient given by the standard and the fuzzy on–off control strategies.

Fig. 8
figure 8

Power coefficient curves

Full size image

According to Fig. 8, it is easy to observe that the curves given by the improved on–off controller and the maximum energy coefficient are matched as close as possible are each time point. Consequently, the proposed FLC strategy has the ability to enhance the obtained performances of the standard on–off controller. To confirm this previous result, Fig. 9 compares the tip-speed ratio curves of previous controllers with the optimal value \(\uplambda_{\text{opt}}\). Figure 10 compares the obtained discrepancy by using both standard and improved on–off controllers.

Fig. 9
figure 9

Tip-speed ratio

Full size image
Fig. 10
figure 10

Tip-speed ratio error

Full size image

According to Figs. 9 and 10, the proposed controller ensures better minimization of the discrepancy. Moreover, the mean square error of \(\upsigma\) provided by the previous controllers can be expressed by

$${\text{MSE}} = \frac{1}{{n_{s} }}\mathop \sum \limits_{k = 0}^{{n_{s} }} \left( {\uplambda_{\text{opt}} -\uplambda \left( k \right)} \right)^{2}$$
(25)

where \(n_{s} = \frac{{t_{ \hbox{max} } }}{{T_{S} }}\) is the sampling number. Therefore, the proposed controller provides \(n_{s} = 0.5419.\) In contrast, the standard on–off controller provides \(n_{s} = 1.1022.\) Therefore, a 50% improvement is guaranteed by using our proposed method. Figure 11 compares the electromagnetic torques that are provided by both previous controllers; we can see that better tracking of the reference electromagnetic torque is ensured by using the improved on–off controller.

Fig. 11
figure 11

Electromagnetic torque

Full size image

Figure 12 shows the obtained performances of the WECS based upon the proposed controller.

Fig. 12
figure 12

Performance of fuzzy on–off control

Full size image

According to Fig. 12, it is easy to observe that the distribution of the operating point is given around the optimal regime characteristic (ORC) in the speed–power plane (see Fig. 12a) and that the electromagnetic torque is provided around the optimal tip-speed ratio \(\uplambda_{\text{opt}} = 7\) (see Fig. 12b). As a result, both figures confirm the effectiveness of the proposed controller wherein the operating point variance around the ORC is always satisfied.

6 Conclusions

In this paper, a fuzzy control law has been proposed to solve the chattering problem of the standard on–off design controller, thereby enhancing its performance. The proposed controller was applied to a WECS equipped with an induction generator connected to the electrical grid. It provided optimal reference electromagnetic torque in which power point tracking is maximized for the variable wind speed case. The previous electromagnetic torque was determined through the proposed FLC system. Its inputs were the discrepancy between the tip-speed ratio and its optimal value as well as the time derivative of the above discrepancy. Moreover, it generated fuzzy control law that replaces the undesired alternate high-frequency component law, thereby avoiding the chattering problem of the on–off control strategy. Afterward, the proposed fuzzy control was combined with the equivalent control in which the reference electromagnetic torque was derived. The reference electromagnetic torque improved the quality of the reference stator current, and the obtained performances given through the WECS were enhanced. The obtained simulation results demonstrate the notable improvement that the control strategy supplies. Furthermore, the proposed method can also be applied to any conventional on–off control strategy and to some other energy conversion systems.