1 Introduction

To obtain high-quality products, a precise mathematical model is important for strip shape control in the strip rolling process, of which the core is the calculation of roll deformation to achieve the setting parameters including roll bending force and roll shifting. It is widely recognized that the prediction of roll deformation of a six-high mill is much more complicated than that of a four-high mill since the six-high mill has more rolls and contact interfaces and more complex conditions of equilibrium and compatibility; as a result, more calculation time is required to achieve a reasonably accurate solution, which is unable to meet the requirements of online application. Therefore, a precise and efficient calculation method for predicting roll deformation has long been the focus of the steel rolling research area.

Over the past 40 years, two most representative methods for predicting roll deformation are the finite element method (FEM) and the influence function method (IFM). FEM has proved to be reliable and is generally used for offline calculation and analysis, for instance, four-high mill modeling [1, 2] and six-high mill simulation [3,4,5] by FEM to analyze the capability of the strip shape control of cold rolling mill. Yuan et al. [6] proposed a more accurate roll flattening model for a six-high mill based on FEM. Ma et al. [7] modeled a 12-high mill by FEM to determine the effect of the intermediate roll shifting on the strip flatness. Cho and Hwang [8] and Yu et al. [9] developed FEM models to analyze roll deformation in 20-high Sendzimir mills. However, the solution time of FEM is the most prohibitive of all and it cannot meet the requirements of online calculation of the strip shape control. Regarding to the influence function method, Shohet and Townsend [10] proposed the influence function method in 1968, and then Edwards et al. [11] and Wang [12] improved the theory and presented a matrix method to solve the beam deflection. So far, the traditional IFM has been widely studied in the analysis of roll deformation in all types of rolling mill, for instance, Jiang et al. [13, 14] used IFM to analyze the mechanics of roll edge contact in cold rolling of thin strip and ultra-thin strip. Liang [15] and Bai et al. [16] used IFM to analyze the capability of the strip shape control of six-high mills. Liu and Lee [17] used IFM to model the thin strip cold and temper rolling process. Zhou and Bai [18] calculated the rolling force for strip cold rolling based on IFM. He et al. [19] improved the division method in IFM to an advanced structure to deal with the left rolled pieces after division. Qin and Miao [20] and Zhang et al. [21] improved the IFM of 20-high mill and analyzed the strip shape control capability of 20-high mills. However, the IFM requires an iterative solution to satisfy the equilibrium and compatibility conditions, and its solution time is still too long to meet the requirements of real-time control. Therefore, in recent years, several highly efficient calculation methods for predicting roll deformation have been presented, for instance, Malik and Grandhi [22] combined Timoshenko beam finite elements with multiple coupled Winkler elastic foundations and proposed the strip profile calculation method for real-time applications. He et al. [23, 24] presented an improved IFM to predict the roll deformation of a four-high mill. Wang et al. [25] reduced the calculation time of IFM of four-high mill. However, the six-high rolling mill is the most widely applied in cold rolling and the highly efficient calculation method for predicting roll deformation of six-high mill is still few.

In the present study, a numerical iterative method is proposed to predict roll deformation of a six-high mill, where the finite difference method is employed to calculate the roll deflection and the polynomial is used to describe the relationship between roll flattening and roll contact pressure. In addition, a new variable correction strategy is proposed in the iteration process to improve the stability and efficiency of the numerical calculation. The roll center flattening and the roll flattening deviation are put forward to the iteration, both of which are corrected simultaneously according to the conditions of equilibrium and compatibility of roll. On the basis of above, a model of UCM (universal crown mill) cold rolling mill is established through C++ programming. Eventually, by the comparison with tradition methods, the proposed method proves to have sufficient accuracy and efficiency, which is suitable for the online calculation of strip shape control.

2 Traditional influence function method of six-high mill

The traditional IFM for a six-high mill is discussed briefly for better explanation, because the new method proposed in this study is based on the influence function method.

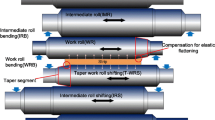
The IFM is a discrete numerical method, and there are two discrete forms according to the symmetry and asymmetry characteristics of the six-high mill, as shown in Fig. 1. One considers the roll as a simply supported beam and the roll is divided and numbered from one side to another side along the axis direction of roll to calculate asymmetry variables, such as roll contract pressure and roll deformation distribution. The other considers the roll as a cantilever beam and the roll is divided and numbered from the middle of the roll to both sides to calculate symmetrical variables, such as rolling force and strip thickness distribution. Besides, the rolling force, the roll contact pressure, and the contact pressure between work roll and strip are uniform in each element and are replaced by a concentrated load that is applied to the middle of each element.

Fig. 1
figure 1

Discretization of roll in six-high UCM mill

Full size image

In Fig. 1, FI and FW are the bending force of intermediate roll and work roll, respectively, and p is the rolling force distribution applied to work roll.

If g(i, j) is the vertical displacement of a beam at position i caused by the unit load applied to the beam at position j, the displacement of the beam at position i caused by the load distribution handled as a number of concentrated loads applied to the middle of each element, y(i), can be calculated by the following equation:

$$y(i) = \sum\limits_{j}^{N} {g(i,j)p_{j} }$$
(1)

where pj is the concentrated load applied to the middle of element j; and N is the number of discrete units. The vertical displacement y(i) represents not only the roll deflection, but also the flattening of contact zone.

The iterative solution process of the traditional IFM is illustrated in Fig. 2. In Fig. 2, ε is the set point; and WR, IR, BR are the abbreviations of work roll, intermediate roll and backup roll, respectively. It is observed that the distribution of roll contact pressure and the roll center flattening are considered to be the correction variables, and there are totally four loops in the iteration, which requires more calculation time to meet four convergence conditions. Meanwhile, the large amounts of matrix multiplication calculations are contained in the influent function method, leading to the added calculation time.

Fig. 2
figure 2

Iterative solution process of traditional influence function method of six-high mill

Full size image

3 New rapid calculation method of six-high mill

3.1 Deflection of roll

According to the beam theory of Timoshenko and Goodier [26], the deflection of a beam combines bending and shear force, and the differential equations are expressed as following equation:

$$\left\{ \begin{aligned} \frac{{{\text{d}}^{2} y_{\text{M}} }}{{{\text{d}}x^{2} }} = - \frac{M}{EI} \hfill \\ \frac{{{\text{d}}^{2} y_{\text{S}} }}{{{\text{d}}x^{2} }} = - \frac{{\alpha_{\text{s}} t}}{GA} \hfill \\ \end{aligned} \right.$$
(2)

where yM is the displacement caused by bending force; yS is the displacement caused by shear force; M is the bending moment; t is the load applied to the differential element; E is the modulus of elasticity; I is the moment of inertia; GA is the shear stiffness; and αs is the shear function.

Equation (2) can be transformed into the difference equation by using the backward difference method according to the boundary conditions; thus, the deformation of element i can be expressed as:

$$y\left( i \right) = y_{\text{M}}^{{}} \left( i \right) + y_{\text{S}}^{{}} \left( i \right) = y\left( {i - 1} \right) + \frac{{M_{1} + M_{2} + \cdots + M_{i - 1} }}{EI}\left( {\Delta x} \right)^{2} + \frac{{M_{i} }}{2EI}\left( {\Delta x} \right)^{2} + \frac{{\alpha_{\text{s}} t_{i} }}{GA}\left( {\Delta x} \right)$$
(3)

where \(y_{\text{M}}^{{}} (i)\) is the deflection caused by bending moment at element i; \(y_{\text{S}}^{{}} (i)\) is the deflection caused by shear force at element i; Δx is the width of each element; Mi is the bending moment at element i; and ti is the concentrated load applied to the middle of element i.

The bending moment of an element is obtained by the combination of concentrated load applied to that element; thus, the deformation of each roll can be calculated according to Eq. (3).

3.2 Contact flattening

Based on the study of Foppl [12], when the modulus of elasticity of contact rolls is equal, the flattening between a pair of rolls is given directly by the following equation:

$$\delta \left( i \right) = \frac{{2\left( {1 - v^{2} } \right)q\left( i \right)}}{\uppi E}\left( {\frac{2}{3} + \ln \frac{{2R_{1} }}{b\left( i \right)} + \ln \frac{{2R_{2} }}{b\left( i \right)}} \right)$$
(4)

where δ(i) is the flattening between two contact rolls at element i; v is the Poisson’s ratio of rolls; q(i) is the contact pressure at element i; R1 and R2 represent the radii of the two contact rolls, respectively; and b is half width of the roll flattening contact zone given by Hertz as following equation:

$$b\left( i \right) = \sqrt {\frac{{8\left( {1 - v^{2} } \right)q\left( i \right)}}{\uppi E} \cdot \frac{{R_{1} R_{2} }}{{R_{1} + R_{2} }}}$$
(5)

According to Eqs. (4) and (5), the relationship between the roll flattening and the roll contact pressure can be expressed by the following equation:

$$\delta \left( i \right) = \frac{{2\left( {1 - v^{2} } \right)q\left( i \right)}}{\uppi E}\left( {\ln \frac{{\uppi\sqrt[3]{{q\left( i \right)^{2} }}E}}{{4\left( {1 - v^{2} } \right)}} + \ln \left( {2R_{1} + 2R_{2} } \right) - \ln q\left( i \right)} \right)$$
(6)

It is observed in Eq. (6) that there is a nonlinear relationship between the flattening and the contact pressure. Thus, a polynomial is employed to describe Eq. (6) in order to avoid the complex calculation of the Newton’s method (an iterative numerical method generally applied to solve a nonlinear problem). The polynomial can be expressed as following equations:

$$\delta (i)= a_{0} + a_{1} q + a_{2} q^{2} + a_{3} q^{3} + a_{4} q^{4}$$
(7)
$$q (i)= b_{0} + b_{1} \delta + b_{2} \delta^{2} + b_{3} \delta^{3} + b_{4} \delta^{4}$$
(8)

where a0, …, a4 and b0, …, b4 are the polynomial coefficients, respectively. The relationship between the flattening and the contact pressure is described by Eqs. (7) and (8), and q(i) can be calculated rapidly from δ(i).

The IFM is still employed to calculate the flattening between the work roll and the strip because the work roll cannot be regarded as the semi-infinite model when it contacts with the strip, and the modified flattening model in IFM is more accurate than the Foppl equation using the present method. The flattening between the work roll and the strip is expressed as the following equation:

$$\varvec{Y}_{\text{ws}} = \varvec{G}_{\text{ws}} {\varvec{P}}$$
(9)

where Yws is the flattening matrix between the work roll and the strip; Gws is the influence function matrix composed of gws(i, j); and P are the rolling force distribution matrix. The exact forms of gws(i, j) are derived as demonstrated in Ref. [12].

3.3 Iterative solution process

The roll flattening deviation and the roll center flattening are put forward to the iterative solution process.

3.3.1 Definition and correction of roll flattening deviation

In order to simplify the correction process of the roll flattening in the iteration, the roll flattening deviation is defined to describe the distribution of the flattening between rolls Δδ(i), which is the difference between the value of the roll flattening at element i and the value of the roll center flattening (roll flattening at the middle point of the roll axis direction), as the following equation:

$$\Delta \delta \left( i \right) = \delta \left( i \right) - \delta \left( 0 \right)$$
(10)

where δ(0) is the roll center flattening.

The roll flattening deviation is corrected by means of the exponential smoothing method in the iteration, which is expressed as the following equation:

$$\Delta \delta \left( i \right)_{\text{I}}^{n} = \beta \Delta \delta \left( i \right)_{\text{C}}^{n - 1} + \left( {1 - \beta } \right)\Delta \delta \left( i \right)_{\text{I}}^{n - 1}$$
(11)

where \(\Delta \delta \left( i \right)_{\text{I}}^{n}\) is the iterative value of roll flattening deviation for the n iteration; \(\Delta \delta \left( i \right)_{\text{I}}^{n - 1}\) is the iterative value of roll flattening deviation for the (n − 1) iteration; \(\Delta \delta (i)_{\text{C}}^{n - 1}\) is the calculated value of roll flattening deviation for the (n − 1) iteration; and \(\beta\) is the smoothing function.

3.3.2 Initialization and correction of roll center flattening

The value of roll center flattening can be initialized at the first step of the iteration according to the assumption of the uniform distribution of the roll contact pressure and the relationship between flattening and contact pressure described by polynomial.

During the iteration, the value of roll center flattening for the n iteration is corrected as the following equation:

$$\delta \left( 0 \right)^{n} = \delta \left( 0 \right)^{n - 1} + \left( {\Delta \delta_{1/4}^{n - 1} - \Delta \delta_{1/4}^{n} } \right) + \Delta \delta \left( 0 \right)^{n}$$
(12)

where δ(0)n is the value of roll center flattening for the n iteration; δ(0)n−1 is the value of roll center flattening for the (n − 1) iteration; \(\Delta \delta_{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0pt} 4}}}^{n - 1}\) is the average value of the roll flattening deviation at the positions of 1/4 roll body length distance from the drive side and that from the operate side for the (n − 1) iteration, while \(\Delta \delta_{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0pt} 4}}}^{n}\) is that for the n iteration; and \(\Delta \delta \left( 0 \right)^{n}\) is the correction value of roll center flattening for the n iteration.

3.3.3 Calculation of Δδ(0)n

Whether the rolls are in contact with each other is determined by δ(i)n (the roll flattening at element i). If δ(i)n > 0, the rolls are in contact with each other and the sum length of all contact elements for the n iteration Ln and the sum of roll contact pressure for the n iteration Q nS can be calculated directly, and the correction value of roll center flattening can be calculated by the following equation:

$$\Delta \delta \left( 0 \right)^{n} = k\frac{{Q_{\text{wi/ ib}} - Q_{\text{S}}^{n} }}{{L^{n} }}$$
(13)

where k is the average slope of the fitting curve in Eq. (7); Qwi/ib is the roll contact pressure obtained by the static equilibrium conditions expressed as the following equation:

$$\left\{ {\begin{array}{*{20}l} {Q_{\text{wi}} = P + 2F_{\text{W}} } \hfill \\ {Q_{\text{ib}} = Q_{\text{wi}} + 2F_{\text{I}} } \hfill \\ \end{array} } \right.$$
(14)

where P is the sum of the rolling force; FW is the bending force of work roll on a single side; and FI is the bending force of intermediate roll on a single side.

In this step, the relationship between roll flattening and roll contact pressure is considered to be proportional and the average slope of the curve of the polynomial in Eq. (7) is adopted to rapidly calculate the roll flattening from the roll contact pressure. Meanwhile, the static equilibrium conditions are considered in the calculation of Qwi/ib, which can reduce four convergent conditions in IFM to two convergent conditions.

3.3.4 Termination conditions of iteration

Considering the accuracy and efficiency of the method, both the iterations times and the error of the roll flattening deviation are chosen as the termination conditions, and the iteration is terminated when any one of them is met.

3.3.5 Flowchart of iterative solution process

The flowchart of the iterative solution process for rapidly calculating roll deformation of the six-high mill is shown in Fig. 3. It is observed that there are only two loops in the iteration, where the roll flattening deviation and roll center flattening are corrected at the same time and the static equilibrium of rolls is considered in the correction, which reduces four convergent conditions in IFM to two convergent conditions. Meanwhile, the gray part in Fig. 3 is the correction process and has been discussed in detail in Sects. 3.3.2 and 3.3.3.

Fig. 3
figure 3

Iterative solution process of rapid calculation method of six-high mill

Full size image

4 Results and discussion

The FEM is widely used in all kinds of simulation due to its satisfactory precision; thus, the FEM is employed to model the UCM cold rolling mill to evaluate the accuracy of the new method to predict the roll deformation of a six-high mill. The parameters of the UCM rolling mill are illustrated in Table 1.

Table 1 Parameters of UCM rolling mill
Full size table

4.1 FEM model of the UCM six-high mill

The ABAQUS finite element software was employed to model the UCM six-high mill according to the parameters given in Table 1. The partial symmetry of the six-high mill roll configuration was exploited, leading to an upper half model of the mill, as shown in Fig. 4. The end contour of the intermediate roll is a circular arc curve, of which the radius is 1000 mm and the length is 50 mm at the axis direction. It can be seen from Fig. 4 that the mesh at the roll contact interface is dense while that at the other parts is sparse. All the rolls are elastic, and the rolling force is assumed as a uniformly distributed load applied to the nodes at the lower surface of work roll.

Fig. 4
figure 4

FEM model of the six-high rolling mill

Full size image

4.2 Comparison and validation

On the basis of the proposed rapid calculation method (RCM), the six-high rolling mill was also modeled by C++ programming. According to the actual production, the conditions are selected as shown in Table 2.

Table 2 Conditions of the simulation
Full size table

The FEM, IFM and RCM are employed to calculate the two conditions in Table 2, respectively. Table 3 indicates the specific difference of solution time between FEM, IFM and RCM. It is observed that the solution time of RCM on both computing platform is extremely shortened comparing with that of FEM and IFM, which proves that the new method can meet the requirement of the calculation time of real-time strip shape control.

Table 3 Average solution time of different methods on two computing platforms
Full size table

Figure 5 shows the comparison of loaded roll gap profile. Figures 6, 7 and 8 show the deflection of rolls predicted by FEM, IFM and RCM respectively under two different conditions, and Figs. 9 and 10 show the roll flattening predicted by IFM and RCM respectively under two different conditions.

Fig. 5
figure 5

Loaded roll gap profile under different conditions

Full size image
Fig. 6
figure 6

Deflection of work roll under different conditions

Full size image
Fig. 7
figure 7

Deflection of intermediate roll under different conditions

Full size image
Fig. 8
figure 8

Deflection of backup roll under different conditions

Full size image
Fig. 9
figure 9

Flattening of WR and IR under different conditions

Full size image
Fig. 10
figure 10

Flattening of IR and BR under different conditions

Full size image

It is observed that the loaded roll gap profile and the deflection predicted by RCM is in great agreement with those predicted by IFM and FEM, and the rolls exhibit consistent deformation behavior in three methods when the condition changes from condition a to b in Table 2. Meanwhile, the roll flattening calculated by IFM and RCM is also similar. In conclusion, the above calculation results demonstrated the accuracy of the proposed method, and its calculation time is perfectly suitable for online calculation.

5 Conclusions

  1. 1.

    The finite difference method is employed to handle the roll deflection and the polynomial is used to describe the nonlinear relationship between roll flattening and roll contact pressure. Furthermore, a new variable correction strategy is adopted in the iteration, which maintains good convergence and stability of the proposed method.

  2. 2.

    The results predicted by RCM is in agreement with those predicted by IFM and FEM, and the calculation time of RCM is decreased to the millisecond, which indicates that the proposed rapid calculation method is suitable for the online calculation of strip shape control.