1 Introduction

In recent years, increasing demands on traffic security, efficiency, and mobility have motivated the development of intelligent transportation means. Autonomous vehicles, with great potential in improving road safety and traffic throughput, have become an emerging research focus [1,2,3].

One of the key technologies of autonomous vehicles is path following, which refers to tracking a predefined trajectory by designing control laws. Many control schemes have been established for this issue. Gaining et al. [4] established an adaptive proportion–integral–derivative (PID) controller for lateral path tracking control, with the parameters of the PID controller tuned by a neural network. Hajjaji and Bentalba [5] presented a Takagi–Sugeno-based fuzzy path-following controller and parameterized the outcome of the fuzzy tracking control problem in terms of a linear matrix inequality (LMI) problem. To cope with the presence of slips in the path-following process, the chained systems theory was introduced by Arogeti and Berman [6], which incorporates a peak-to-peak criterion to maintain the closed-loop performance. Kapania et al. [7] proposed a feedback–feedforward steering controller that can simultaneously maintain the vehicle stability within the handling limits while minimizing the deviation of the lateral position. Wang et al. [8] designed an output-feedback triple-step controller to realize coordinated lateral and longitudinal control for autonomous vehicles without a measurement of lateral velocity. Recently, model predictive control (MPC) has been extensively studied for the path following of autonomous vehicles because of its capability to systematically deal with multiple constraints and vehicle dynamics [9, 10]. Ji et al. [11] formulated the path-following task as a multi-constrained MPC, which can accurately calculate the front steering angle to prevent the vehicle from colliding with a moving obstacle vehicle. However, although MPC has better robustness compared with most model-based controllers owing to the rolling optimization strategy, its performance is still affected by model mismatch problems to some extent. Such problems may harm the performance of MPC. Guo et al. [12] treated model mismatch as a measurable disturbance and presented a path-following scheme based on MPC that considers this measurable disturbance to improve the control precision. In Refs. [13, 14], the path-following problem was transformed into a yaw-rate tracking problem, where the desired yaw rate was designed by the backstepping method based on the path-following model, and a linear quadratic regulator controller was adopted to obtain the optimal active front steering input.

For most studies in this field, the longitudinal velocity was assumed to be constant, and the lateral and longitudinal control problems were investigated separately. In fact, strong couplings exist between the lateral and longitudinal dynamics [15], especially in some aggressive maneuvers, such as accelerating or decelerating while steering. For controllers that have not taken this factor into consideration, the control precision may be influenced. Furthermore, in some limiting path-following conditions with strong coupling effects, the vehicle would be in danger of losing stability. To this end, some studies have attempted to deal with the coupling effects in the path-following control of autonomous vehicles. Lim and Hedrick [16] proposed a combined lateral and longitudinal dynamic surface controller to compensate for the coupling effects, and the results show that the dynamic coupling compensation can significantly improve control performance. Tomizuka et al. [17] presented a systematic controller to manage the lateral and longitudinal motions of autonomous vehicles based on robust adaptive control. Rajamani et al. [18] introduced an on-board supervisor that utilizes inter-vehicle communication to coordinate the operation of the decoupled lateral and longitudinal controllers. Kumarawadu et al. [19] proposed a combined lateral and longitudinal control algorithm using an adaptive neural network, in which an online adaptive neural module acts as a dynamic compensator to counteract the coupling effects. Guo et al. [20] proposed a multi-objective hierarchical architecture used for coordinated lateral and longitudinal motion control based on the robust backstepping method. Artia et al. [21] presented heterogeneous criteria to update the longitudinal reference speed in order to improve the lateral stability for automated vehicle guidance. All the studies above attempted to deal with the coupling effects using one specific method regardless of its diversity. However, the coupling of vehicles is complex and caused by many factors with different characteristics. Thus, utilizing one specific method may not be sufficient to deal with this complex issue. Moreover, the presence of system uncertainties in the path-following control caused by the changes in operation conditions, such as road adhesions, should not be ignored. In particular, some coupling effects can also cause system uncertainties, which will be discussed in this paper. Previous studies [22,23,24] have proven that LMI theory-based robust feedback control methods can effectively deal with uncertainties. Since feedback controllers must rely on existing errors, and thus, the time lag is unavoidable. More importantly, to the best of our knowledge, most existing studies on the uncertainties in path-following control only treat system uncertainties as the indeterminacy of a single dynamic parameter, such as the tire cornering stiffness. Physical parameters, such as mass and moment inertia, are not constant values; they vary owing to many factors, such as passengers, remaining fuel, and baggage. These uncertainties will also have a significant influence on the control performance but were neglected in previous studies.

This paper proposes a novel integrated control method for the path-following control of autonomous vehicles, aiming at dealing with various types of coupling effects and system uncertainties. The main contributions of this paper lie in three aspects: (1) Different from previous studies, the coupling in the path-following control of autonomous vehicles is analyzed and classified in a systematic way, and comprehensive coping strategies for the complex coupling effects are proposed according to their respective properties. Some kinds of coupling effects are directly compensated by component feedback, whereas others can be treated as uncertainties or disturbances, which will be considered in the controller design process. For unsafe coupling effects, such as saturated tire force coupling, a safe speed profile is introduced. (2) For the lateral controller, the dynamic and physical parameters, e.g., mass and moment of inertia varying in different loading conditions, are simultaneously considered in the design of the robust controller based on the LMI theory. (3) For the longitudinal controller, considering that the accurate value of mass is unknown and disturbances are obvious, a radial basis function (RBF) neural network-based sliding mode controller is introduced, which has the ability to cope with disturbances and system uncertainties in an adaptive way.

The rest of this paper is organized as follows: The types of coupling effects are first figured out in Sect. 2, followed by their comprehensive solutions. The lateral and longitudinal robust control methods and the safe speed profile are proposed in Sect. 3. Simulations based on the CarSim–Simulink joint platform are presented in Sect. 4. Lastly, the conclusions are given in Sect. 5.

2 Coupling Analysis and Decoupling Method

The complex kinematic and dynamic relations between the longitudinal and lateral motions of a vehicle and its tires lead to the coupling effects. With the increase in velocity, the influence caused by coupling will become more serious. Owing to the complexity of the coupling effects, a combined lateral and longitudinal control scheme can improve the path-following performance by exclusively dealing with the coupling effects according to their attributes. Thus, the identification of the complex coupling effects is essential. Based on the analysis of vehicle dynamics [16, 20, 25], coupling can be classified into three types:

Kinematic coupling: This coupling appears in two ways: (1) The wheel steering angle changes the direction of tire longitudinal and lateral tire forces, which have components in longitudinal and lateral directions, and the value of yaw moment are also affected jointly. (2) Lateral velocity and yaw rate exist in the longitudinal dynamics equation; likewise, longitudinal velocity and yaw rate exist in the lateral dynamics equation. In addition, based on the feedback path-following model, the rates of lateral error from the desired path and heading error are also a function of the longitudinal velocity.

Tire force coupling: When a vehicle is moving, its tires generate longitudinal and lateral forces through a single surface where the tires are in contact with the road. Because these forces are caused by friction, given a friction coefficient, the magnitude of the resultant forces of each tire is limited by the Coulomb constraint, which is also called saturation limits. This kind of coupling can be illustrated by a well-known friction ellipse [26]. Owing to the fact that the generation of tire forces is not only according to the Coulomb theory but also based on the nonlinear relationship between the tire slip and tire force, the longitudinal and lateral slips interact with each other under a unified condition even when the tires are operating far below the saturation limit. This kind of tire force coupling can be called the unsaturated tire force coupling. Because the coexistence of the longitudinal and lateral tire forces is of common occurrence in the daily operation of vehicles, the unsaturated tire force coupling is quite frequent. Because this kind of coupling is not so fierce, it can be considered as system uncertainties, which will be handled in the controller design. However, once the tire resultant force approaches the saturation limit, the tire force coupling effects will become especially significant. Then, when the tires get saturated, the vehicle is in danger of losing stability and controllability. Thus, tire force saturation needs to be avoided as much as possible.

Load transfer coupling: Generally, the tire lateral and longitudinal forces are functions of the tire vertical load. Thus, the redistribution of the vertical load caused by longitudinal and lateral acceleration will lead to a change in the yaw plane dynamics. Similar to the unsaturated tire force coupling, it can be considered system uncertainties in the controller design process.

The above analysis implies that the coupling effects between longitudinal and lateral dynamics are complex and diverse. They have different attributes and are not isolated from each other. Thus, different handling strategies should be adopted for different coupling properties rather than handling them all by a single method. Therefore, a comprehensive handling solution is proposed, as shown in Fig. 1. The kinematic coupling caused by coupled components in dynamics relationships can be directly compensated through feedback, which was also performed by most previous related research on coupling. Compared with previous research, another type of kinetic coupling caused by the front-wheel steering angle, together with the load transfer coupling and unsaturated tire force coupling, is treated as a disturbance or system uncertainty in this research. For the lateral controller, they are handled by the proposed LMI-based robust feedback controller; for the longitudinal controller, an RBF neural network-based adaptive sliding mode controller is introduced to deal with the error caused by them. Moreover, for the saturated tire force coupling, which cannot be handled by the controller, a safe speed profile is proposed to prevent it. The specifics of these methods are proposed in Sect. 3.

Fig. 1
figure 1

Comprehensive handling strategies of coupling

Full size image

3 Robust Controller Design

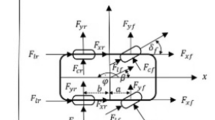
The path-following control of autonomous vehicles can be decoupled into lateral and longitudinal control. The lateral control refers to minimizing and eliminating the lateral and heading errors between the vehicle and the predefined path, whereas the longitudinal control is defined as tracking the reference longitudinal velocity. For the controller design, a simplified single-track model is introduced based on the following assumptions: (1) The steering angle of the front wheel is small, and (2) the difference of the steering angle between the left and right wheels caused by Ackermann steering geometry is neglected [27]. The schematic of the simplified single-track model is shown in Fig. 2.

Fig. 2
figure 2

Vehicle simplified single-track model

Full size image

The longitudinal motion can be formulated as

$$m\left( {\dot{v}_{x} - rv_{y} } \right) = F_{{x{\text{f}}}} + F_{{x{\text{r}}}} = F_{x}$$
(1)

The lateral motion is established as

$$m\left( {\dot{v}_{y} + rv_{x} } \right) = F_{{y{\text{f}}}} + F_{{y{\text{r}}}}$$
(2)

The yaw motion can be formed as

$$I_{z} \dot{r} = l_{{\text{f}}} F_{{y{\text{f}}}} - l_{r} F_{{y{\text{r}}}}$$
(3)

where Fxf and Fxr are the longitudinal force of the front and rear tires, respectively; Fyf and Fyr are the lateral tire force of the front and rear tires, respectively; and Fx is the total longitudinal force of the vehicle, vx, vy, r are the longitudinal velocity, lateral velocity and yaw rate, m and Iz are the mass and inertia moment of vehicle, respectively, lf and lr are the distance from the front and rear axle to the center of mass, respectively.

When the vehicle has a small steering angle δf, the side-slip angle is also small. The relationship between the tire lateral force and side-slip angle can be assumed linear under this condition. And the lateral tire forces are given by

$$\begin{aligned} & F_{{y{\text{f}}}} = C_{{\text{f}}} \alpha_{{\text{f}}} = C_{{\text{f}}} \left( {\delta_{{\text{f}}} - \frac{{v_{y} + l_{{\text{f}}} r}}{{v_{x} }}} \right) \\ & F_{{y{\text{r}}}} = C_{{\text{r}}} \alpha_{{\text{r}}} = C_{{\text{r}}} \left( { - \frac{{v_{y} - l_{{\text{r}}} r}}{{v_{x} }}} \right) \\ \end{aligned}$$
(4)

where Cf and Cr denote the cornering stiffness of the front and rear tires, respectively.

It is obvious that the proposed single-track model has some errors caused by external disturbances and model mismatches, and these factors will be considered in the controller design process. The block diagram of the lateral and longitudinal controllers is shown in Fig. 3. The whole control system consists of three parts: The lateral feedforward controller according to the curvature preview is presented in Sect. 3.1; the LMI-based robust lateral feedback controller, which considers the system uncertainties and disturbances, is proposed in Sect. 3.2; and the longitudinal controller is presented in Sect. 3.3. For the tire force saturation that cannot be handled by the controller, a safe speed profile is introduced to prevent it in Sect. 3.4.

Fig. 3
figure 3

Block diagram of the controller

Full size image

3.1 Feedforward Steering Controller

The objective of the feedforward controller is to provide an approximate value of the steering angle to traverse a predefined path with a known path curvature and longitudinal velocity. This method can help minimize the level of compensation required by the steering feedback, reducing tracking errors and allowing for less overall control effort [7]. For simplicity, the generation of the feedforward steering angle should be independent of the vehicle states and system uncertainties. Here, a feedforward steering controller based on the vehicle longitudinal velocity and path curvature is proposed.

The path-following model for feedforward control is shown in Fig. 4, where L is the preview distance, P is the preview point, ρ(s + L) is the curvature of the reference path at the preview point, and ρ(s) is the curvature at the current position of the vehicle. This model assumes that the autonomous vehicle has already tracked the reference path well. Then, the steering angle can be calculated based on the curvature of the preview point of the vehicle. By assuming steady-state cornering, the following kinematic relation holds:

$$r = \frac{{v_{x} }}{R} = v_{x} \rho$$
(5)

where R is the turning radius of cornering, which is also the reciprocal of curvature ρ.

Fig. 4
figure 4

Path-following model for feedforward control

Full size image

For a single-track model, the relationship between the yaw rate and front-wheel steering angle can be calculated as follows [26]:

$$r = \frac{{v_{x} \delta_{{\text{f}}} }}{{l_{{\text{f}}} + l_{{\text{r}}} + v_{x}^{2} G}}$$
(6)

where G = m(Crlr─Cl)/(CfCr(lf + lr)), and it’s transformation form of the steering gradient.

Clearly, given a preview time Δt, the preview distance L can be represented by vx as follows:

$$L = v_{x} \Delta t$$
(7)

According to the kinematic relation, the required yaw rate to eliminate the curvature difference between the vehicle current position and preview point is generated. Then, the steering angle can be calculated according to Eq. (6). Combining Eqs. (5)–(7), the feedforward steering angle δffw is given by

$$\delta_{{{\text{ffw}}}} = \left( {l_{{\text{f}}} + l_{{\text{r}}} + v_{x}^{2} G} \right) \cdot \int {\frac{(\rho (s + L) - \rho (s))}{{\Delta t}}}$$
(8)

Considering the steady-state limit of the yaw rate [26], the feedforward steering angle can be modified as

$$\delta_{{{\text{ffw}}}} = \min \left( {\left( {l_{{\text{f}}} + l_{{\text{r}}} + v_{x}^{2} G} \right) \cdot \int {\frac{(\rho (s + L) - \rho (s))}{{\Delta t}}} ,\frac{{\mu g(l_{{\text{f}}} + l_{{\text{r}}} + G)}}{{v_{x}^{2} }}} \right)$$
(9)

3.2 Robust Feedback Steering Controller

As mentioned above, the feedforward controller only calculates an approximate value of the steering angle to traverse a predefined path. Thus, a feedback controller is necessary to compensate for the path-following error between the autonomous vehicle and the reference path. Moreover, the uncertainties and disturbances should be taken into consideration. In this section, the path-following error model for the feedback controller is presented first, then the system uncertainties are discussed, and finally, the LMI-based feedback controller is proposed.

3.2.1 Path-Following Error Model

The path-following error model for the feedback controller is shown in Fig. 5, where ey is the lateral error from the vehicle center of gravity to the closest point d on the desired path and ρ(d) is the curvature of point d. S is the curvilinear distance along the path. Ψd is the desired heading angle, and Ψ is the actual heading angle of vehicle. Thus, the heading error can be defined as Ψ = Ψ − Ψd. The path-following error dynamics for autonomous vehicles based on the Serret–Frenet equation can be modeled as follows [28]:

$$\begin{aligned} & \dot{e}_{y} = v_{x} \sin \Delta \psi + v_{y} \cos \Delta \psi \\ & \Delta \dot{\psi } = \dot{\psi } - \dot{\psi }_{d} = r - \rho (d)v_{x} \\ \end{aligned}$$
(10)
Fig. 5
figure 5

Path-following model for feedback control

Full size image

Because the feedforward controller has given an appropriate steering angle for path following, it can be assumed that the heading error is sufficiently small. With this assumption, Eq. (10) can be modified as follows [29]:

$$\begin{aligned} & \dot{e}_{y} = v_{x} \Delta \psi + v_{y} + w_{1} \\ & \Delta \dot{\psi } = r - \rho (d)v_{x} \\ \end{aligned}$$
(11)

where w1 denotes the disturbances generated by external perturbation and modeling simplification.

Combining the error-based path-following model Eq. (11) with vehicle dynamic Eqs. (2)–(4) and considering the errors caused by the model mismatch, the following equations are obtained:

$$\begin{aligned} & \dot{e}_{y} = v_{x} \Delta \psi + v_{y} + w_{1} \\ & \Delta \dot{\psi } = r - \rho (d)v_{x} \\ & \dot{v}_{y} = - \frac{{(C_{{\text{f}}} + C_{{\text{r}}} )}}{{mv_{x} }}v_{y} + \left( { - v_{x} - \frac{{(l_{{\text{f}}} C_{{\text{f}}} - l_{{\text{r}}} C_{{\text{r}}} )}}{{mv_{x} }}} \right)r + \frac{{C_{{\text{f}}} }}{m}\delta_{{\text{f}}} + w_{2} \\ & \dot{r} = \frac{{(l_{{\text{r}}} C_{{\text{r}}} - l_{{\text{f}}} C_{{\text{f}}} )}}{{I_{z} }}v_{y} - \frac{{(C_{{\text{f}}} l_{{\text{f}}}^{2} + C_{{\text{r}}} l_{{\text{r}}}^{2} )}}{{v_{x} I_{z} }}r + \frac{{l_{{\text{f}}} C_{{\text{f}}} }}{{I_{z} }}\delta_{{\text{f}}} + w_{3} \\ \end{aligned}$$
(12)

where δf is the sum of the feedforward steering angle δffw and feedback steering angle δfb. Similar to w1, w2 and w3 denote the external disturbances and errors produced by the model mismatch. Because numerous works have been done in perception and estimation, it is assumed that the data of the states can be observed and estimated.

Equation (12) can be manipulated into a state-space form. The state vector is defined as x = [ey ΔΨvy r]T, and the control input is u(t) = δfb. Because the feedback controller is used to calculate a feedback steering angle, the presence of the feedforward controller should not be ignored. The disturbance matrix is defined as w = [w1 ρw2 w3 δffw]. The state-space form of the combined path-following–vehicle dynamic model is presented as follows:

$$\dot{{x}} = {\varvec{A}}x + {\varvec{B}}_{1} u + {\varvec{B}}_{2} w$$
(13)

where

$${\varvec{A}} = \left[ {\begin{array}{*{20}c} 0 & {v_{x} } & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & { - \frac{{C_{{\text{f}}} + C_{{\text{r}}} }}{{mv_{x} }}} & { - v_{x} - \frac{{C_{{\text{f}}} l_{{\text{f}}} - C_{{\text{r}}} l_{{\text{r}}} }}{{mv_{x} }}} \\ 0 & 0 & {\frac{{C_{{\text{r}}} l_{{\text{r}}} - C_{{\text{f}}} l_{{\text{f}}} }}{{I_{z} v_{x} }}} & { - \frac{{C_{{\text{f}}} l_{{\text{f}}}^{2} + C_{{\text{r}}} l_{{\text{r}}}^{{2}} }}{{I_{z} v_{x} }}} \\ \end{array} } \right],\;{\varvec{B}}_{1} = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {\frac{{C_{{\text{f}}} }}{m}} \\ {\frac{{C_{{\text{f}}} l_{{\text{f}}} }}{{I_{z} }}} \\ \end{array} } \right],{\varvec{B}}_{2} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 & 0 \\ 0 & {v_{x} } & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & {\frac{{C_{{\text{f}}} }}{m}} \\ 0 & 0 & 0 & 1 & {\frac{{C_{{\text{f}}} l_{{\text{f}}} }}{{I_{z} }}} \\ \end{array} } \right]$$

3.2.2 System Uncertainties

Autonomous vehicles have a complex nonlinear system with uncertainties. For lateral control, the tire cornering stiffness is the uncertainty parameter due to the change in operating conditions and coupling effects, as discussed in Sect. 2, including the unsaturated tire force coupling and load transfer coupling. Thus, the tire stiffness can be represented as

$$C_{{\text{f}}} = C_{{{\text{f0}}}} + N_{{\text{f}}} \tilde{C}_{{\text{f}}} ,\;C_{{\text{r}}} = C_{{{\text{r0}}}} + N_{{\text{r}}} \tilde{C}_{{\text{r}}}$$
(14)

where Cf0 and Cr0 are the nominal values of Cf and Cr, respectively; \(\tilde{C}_{{\text{f}}} \;{\text{and}}\;\tilde{C}_{{\text{r}}} \;\) denote the extent of uncertainties; Nf and Nr are the time-varying parameters and satisfy \(\left| {N_{{\text{f,r}}} } \right| \le 1\). Because road conditions are usually uniform to the front and rear wheels, it is assumed that Nf = Nr.

Moreover, as mentioned in the introduction, the vehicle mass m is not always a constant parameter and can be assumed to vary between its minimum value mmin and its maximum value mmax. Because m is the denominator in the system matrix, 1/m is given as [30]

$$\frac{1}{m} = \frac{1}{{m_{0} }} + N_{m} \frac{1}{{\tilde{m}}}$$
(15)

where Nm is the time-varying parameter and satisfies \(\left| {N_{m} } \right| \le 1\), \(m_{0} = \frac{{m_{\min } + m_{\max } }}{{2m_{\min } m_{\max } }}\), \(\tilde{m} = \frac{{m_{\min } - m_{\max } }}{{2m_{\min } m_{\max } }}\). The uncertainties in the moment of yaw inertia can be represented in a similar way:

$$\frac{1}{{I_{z} }} = \frac{1}{{I_{z0} }} + N_{I} \frac{1}{{\tilde{I}_{z} }}$$
(16)

where NI satisfies \(\left| {N_{I} } \right| \le 1\), \(I_{{{\text{z0}}}} = \frac{{I_{{{\text{zmin}}}} + I_{{{\text{zmax}}}} }}{{2I_{{{\text{zmin}}}} I_{{{\text{zmax}}}} }}\), \(\tilde{I}_{z} = \frac{{\tilde{I}_{{{\text{zmin}}}} - \tilde{I}_{{{\text{zmax}}}} }}{{2\tilde{I}_{{{\text{zmin}}}} \tilde{I}_{{{\text{zmax}}}} }}\), and Izmin and Izmax are the minimal and maximum values of Iz, respectively. Moreover, it is reasonable to assume that Nm = NI because the moment of inertia is proportional to the mass.

Based on the consideration of uncertainties, the system matrices in Eq. (13) can be expressed as follows:

$$\begin{aligned} & \tilde{\varvec{A}} = {\varvec{A}}_{0} + {\varvec{\tilde{A}}}N_{0} \\ & \tilde{\varvec{B}}_{1} = {\varvec{B}}_{10} + {\varvec{\tilde{B}}}_{1} N_{1} \\ & \tilde{\varvec{B}}_{2} = {\varvec{B}}_{20} + {\varvec{\tilde{B}}}_{2} N_{2} \\ \end{aligned}$$
(17)

where

$${\varvec{A}}_{0} = \left[ {\begin{array}{*{20}c} 0 & {v_{x} } & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & { - (\frac{{C_{{{\text{f}}0}} + C_{{{\text{r}}0}} }}{{m_{0} v_{x} }} + \frac{{\tilde{C}_{{\text{f}}} + \tilde{C}_{{\text{r}}} }}{{\tilde{m}v_{x} }})} & { - v_{x} - (\frac{{C_{{{\text{f0}}}} l_{{\text{f}}} - C_{{{\text{r0}}}} l_{{\text{r}}} }}{{m_{0} v_{x} }} + \frac{{\tilde{C}_{{\text{f}}} l_{{\text{f}}} - \tilde{C}_{{\text{r}}} l_{{\text{r}}} }}{{\tilde{m}v_{x} }})} \\ 0 & 0 & {(\frac{{C_{{{\text{r0}}}} l_{r} - C_{{{\text{f0}}}} l_{f} }}{{I_{z0} v_{x} }} + \frac{{\tilde{C}_{{\text{r}}} l_{{\text{r}}} - \tilde{C}_{{\text{f}}} l_{{\text{f}}} }}{{\tilde{I}_{z} v_{x} }})} & { - (\frac{{C_{{{\text{f0}}}} l_{{\text{f}}}^{{2}} + C_{{{\text{r0}}}} l_{{\text{r}}}^{{2}} }}{{I_{z0} v_{x} }} + \frac{{\tilde{C}_{{\text{f}}} l_{{\text{f}}}^{{2}} + \tilde{C}_{{\text{r}}} l_{{\text{r}}}^{{2}} }}{{\tilde{I}_{z} v_{x} }})} \\ \end{array} } \right]$$
$${\varvec{B}}_{10} = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {\frac{{C_{{{\text{f0}}}} }}{{m_{0} }} + \frac{{\tilde{C}_{{\text{f}}} }}{{\tilde{m}}}} \\ {\frac{{C_{{{\text{f0}}}} l_{{\text{f}}} }}{{I_{z0} }} + \frac{{\tilde{C}_{{\text{f}}} l_{{\text{f}}} }}{{\tilde{I}_{z} }}} \\ \end{array} } \right],{\varvec{B}}_{20} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 & 0 \\ 0 & {v_{x} } & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & {\frac{{C_{{{\text{f0}}}} }}{{m_{0} }} + \frac{{\tilde{C}_{{\text{f}}} }}{{\tilde{m}}}} \\ 0 & 0 & 0 & 1 & {\frac{{C_{{{\text{f0}}}} l_{{\text{f}}} }}{{I_{z0} }} + \frac{{\tilde{C}_{{\text{f}}} l_{{\text{f}}} }}{{\tilde{I}_{z} }}} \\ \end{array} } \right]$$
$$\tilde{{A}} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & { - (\frac{{\tilde{C}_{{\text{f}}} + \tilde{C}_{{\text{r}}} }}{{m_{0} v_{x} }} + \frac{{C_{{{\text{f0}}}} + C_{{{\text{r0}}}} }}{{\tilde{m}v_{x} }})} & { - (\frac{{\tilde{C}_{{\text{f}}} l_{{\text{f}}} - \tilde{C}_{{\text{r}}} l_{{\text{r}}} }}{{m_{0} v_{x} }} + \frac{{C_{{{\text{f0}}}} l_{{\text{f}}} - C_{{{\text{r0}}}} l_{{\text{r}}} }}{{\tilde{m}v_{x} }})} \\ 0 & 0 & {(\frac{{\tilde{C}_{{\text{r}}} l_{{\text{r}}} - \tilde{C}_{{\text{f}}} l_{{\text{f}}} }}{{I_{z0} v_{x} }} + \frac{{C_{{{\text{r0}}}} l_{{\text{r}}} - C_{{{\text{f0}}}} l_{{\text{f}}} }}{{\tilde{I}_{z} v_{x} }})} & { - (\frac{{\tilde{C}_{{\text{f}}} l_{{\text{f}}}^{2} + \tilde{C}_{{\text{r}}} l_{{\text{r}}}^{{2}} }}{{I_{z0} v_{x} }} + \frac{{C_{{{\text{f0}}}} l_{{\text{f}}}^{2} + C_{{{\text{r0}}}} l_{{\text{r}}}^{{2}} }}{{\tilde{I}_{z} v_{x} }})} \\ \end{array} } \right]$$
$$\tilde{{B}}_{1} = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {\frac{{\tilde{C}_{{\text{f}}} }}{{m_{0} }} + \frac{{C_{{{\text{f0}}}} }}{{\tilde{m}}}} \\ {\frac{{\tilde{C}_{{\text{f}}} l_{{\text{f}}} }}{{I_{z0} }} + \frac{{C_{{{\text{f0}}}} l_{{\text{f}}} }}{{\tilde{I}_{z} }}} \\ \end{array} } \right],\tilde{{B}}_{2} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {\frac{{\tilde{C}_{{\text{f}}} }}{m} + \frac{{C_{{{\text{f0}}}} }}{{\tilde{m}}}} \\ 0 & 0 & 0 & 0 & {\frac{{\tilde{C}_{{\text{f}}} l_{{\text{f}}} }}{{I_{z} }} + \frac{{C_{{{\text{f0}}}} l_{{\text{f}}} }}{{\tilde{I}_{z} }}} \\ \end{array} } \right]$$

Because \(\left| {N_{i} } \right| \le 1\), it can be obtained that \(\left| {N_{0} } \right| \le 1\),\(\left| {N_{1} } \right| \le 1\), and \(\left| {N_{2} } \right| \le 1\).

According to the coupling analysis, the lateral dynamics are affected by the longitudinal velocity vx, which is a time-varying parameter and also exists in the system matrices. Thus, the variation of longitudinal velocity should be considered in the lateral controller. Different from the cornering stiffness and physical parameters whose specific values remain unknown, the specific value of velocity is available. It is assumed that vx varies in the range of [vxmin, vxmax], so \({1 \mathord{\left/ {\vphantom {1 {v_{x} }}} \right. \kern-\nulldelimiterspace} {v_{x} }}\) varies in \(\left[ {{1 \mathord{\left/ {\vphantom {1 {v_{x\max } ,{1 \mathord{\left/ {\vphantom {1 {v_{x\min } }}} \right. \kern-\nulldelimiterspace} {v_{x\min } }}}}} \right. \kern-\nulldelimiterspace} {v_{x\max } ,{1 \mathord{\left/ {\vphantom {1 {v_{x\min } }}} \right. \kern-\nulldelimiterspace} {v_{x\min } }}}}} \right]\). Herein, a polytope with four vertices is introduced to cover all the possible situations of pair [vx, 1/vx], with its coordinates written as \(\tilde{\vartheta }_{1} = v_{x\min } ,\;\;\tilde{\vartheta }_{2} = v_{x\max } ,\;\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\vartheta }_{1} = 1/v_{x\min } ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\vartheta }_{2} = 1/v_{x\max }\).

Then, the time-varying parameters vx, 1/vx can be expressed as [31]

$$v_{x} = \sum\limits_{i = 1}^{2} {\tilde{h}_{i} \left( t \right)\tilde{\vartheta }_{i} } ,\;\frac{1}{{v_{x} }} = \sum\limits_{i = 1}^{2} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h}_{i} \left( t \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\vartheta }_{i} }$$
(18)

with the weighting factors defined as

\(\begin{aligned} & \tilde{h}_{1} = \frac{{v_{x\max } - v_{x} }}{{v_{x\max } - v_{x\min } }},\;\tilde{h}_{2} = \frac{{v_{x} - v_{x\min } }}{{v_{x\max } - v_{x\min } }},\\&\;\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h}_{1} = \frac{{{1 \mathord{\left/ {\vphantom {1 {v_{x\min } - {1 \mathord{\left/ {\vphantom {1 {v_{x} }}} \right. \kern-\nulldelimiterspace} {v_{x} }}}}} \right. \kern-\nulldelimiterspace} {v_{x\min } - {1 \mathord{\left/ {\vphantom {1 {v_{x} }}} \right. \kern-\nulldelimiterspace} {v_{x} }}}}}}{{{1 \mathord{\left/ {\vphantom {1 {v_{x\min } - {1 \mathord{\left/ {\vphantom {1 {v_{x\max } }}} \right. \kern-\nulldelimiterspace} {v_{x\max } }}}}} \right. \kern-\nulldelimiterspace} {v_{x\min } - {1 \mathord{\left/ {\vphantom {1 {v_{x\max } }}} \right. \kern-\nulldelimiterspace} {v_{x\max } }}}}}},\;\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h}_{2} = \frac{{{1 \mathord{\left/ {\vphantom {1 {v_{x} - {1 \mathord{\left/ {\vphantom {1 {v_{x\max } }}} \right. \kern-\nulldelimiterspace} {v_{x\max } }}}}} \right. \kern-\nulldelimiterspace} {v_{x} - {1 \mathord{\left/ {\vphantom {1 {v_{x\max } }}} \right. \kern-\nulldelimiterspace} {v_{x\max } }}}}}}{{{1 \mathord{\left/ {\vphantom {1 {v_{x\min } - {1 \mathord{\left/ {\vphantom {1 {v_{x\max } }}} \right. \kern-\nulldelimiterspace} {v_{x\max } }}}}} \right. \kern-\nulldelimiterspace} {v_{x\min } - {1 \mathord{\left/ {\vphantom {1 {v_{x\max } }}} \right. \kern-\nulldelimiterspace} {v_{x\max } }}}}}}\end{aligned}\).

Define h1 = h11, h2 = h12, h3 = h21, and h4 = h22, with \(h_{ij} = \tilde{h}_{i} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h}_{j} ,(i = 1,2,j = 1,2).\) According to the definition of h, it is defined that

$$\sum\limits_{i = 1}^{4} {h_{i} \left( t \right)} = 1,h_{i} \left( t \right) \ge 0$$
(19)

Based on Eqs. (17), (18), and (19), the system plant Eq. (13) can be rewritten in the polytope form as follows:

$$\begin{aligned} & \dot{{x}}(t) = \sum\limits_{i = 1}^{4} {h_{i} (t)} \left[ {({\varvec{A}}_{0i} + \tilde{{A}}_{i} N_{0} ){\varvec{x}}(t) + ({\varvec{B}}_{10i} + \tilde{{B}}_{1i} N_{1} ){\varvec{u}}(t) + ({\varvec{B}}_{20i} + \tilde{{B}}_{2i} N_{2} ){\varvec{w}}(t)} \right] \\ & {\varvec{z}}{\text{(t) = }}{\varvec{Cx}}(t) \\ \end{aligned}$$
(20)

where z = [ey ΔΨ vy]T is the control output,

$${\varvec{C}} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \end{array} } \right]$$

3.2.3 Robust Feedback Steering Controller Design

The objective of the feedback controller is to generate a control signal u(t), such that the system in Eq. (20) is asymptotically stable, which means that the path-following error can be constrained in a small range and has the following H∞ disturbance attenuation performance in the presence of external disturbance and system uncertainties:

$$\int_{0}^{t} {{\varvec{z}}^{\text{T}} \left( t \right){\varvec{z}}\left( t \right){\text{d}}t} \le \gamma^{2} \int_{0}^{t} {{\varvec{w}}^{\text{T}} \left( t \right){\varvec{w}}\left( t \right){\text{d}}t}$$
(21)

where γ is the prescribed attenuation level.

The design of the controller can be presented as

$${\varvec{u}}(t) = \sum\limits_{i = 1}^{4} {h_{i} (t){\varvec{K}}_{i} {\varvec{x}}(t)}$$
(22)

where Ki is the feedback gain matrix to be designed. Substituting Eq. (22) into Eq. (20), then

$$\begin{aligned} & \dot{{x}}(t) = \sum\limits_{i = 1}^{4} {h_{i} (t)} \left[ {(\hat{{A}} + \hat{{B}}_{1} {\varvec{K}}_{i} ){\varvec{x}}(t) + \hat{{B}}_{2} {\varvec{w}}(t)} \right] \\ & {\varvec{z}}{\text{(t) = }}{\varvec{Cx}}(t) \\ \end{aligned}$$
(23)

where \(\hat{{A}}{ = }{\varvec{A}}_{0i} + \tilde{{A}}_{i} N_{0}\), \(\hat{{B}}_{1} = {\varvec{B}}_{10} + \tilde{{B}}_{1i} N_{1}\), \(\hat{{B}}_{2} = {\varvec{B}}_{20i} + \tilde{{B}}_{2i} N_{2}\). Defining \(\overline{{A}}{ = }\hat{{A}} + \hat{{B}}_{1} {\varvec{K}}_{i}\), Eq. (23) can be rewritten as

$$\begin{aligned} & \dot{{x}}(t) = \sum\limits_{i = 1}^{4} {h_{i} (t)} \left[ {\overline{{A}}{x}(t) + \hat{{B}}_{2} {\varvec{w}}(t)} \right] \\ & {\varvec{z}}{\text{(t) = }}{\varvec{Cx}}(t) \\ \end{aligned}$$
(24)

Inspired by Ref. [23], the LMI theory is adopted for the robust feedback controller. To deal with the system uncertainties, the following lemmas are introduced:

Lemma 1

[31]. Given a positive constant scalar γ, the closed-loop system in Eq. (24) is asymptotically stable and can satisfy the H∞ performance index Eq. (21) performance for all \(w\left( t \right) \in [0,\infty )\), if and only if there exists a symmetric positive definite matrix P that satisfies the following conditions:

$$\left[ {\begin{array}{*{20}c} {{\varvec{P}}\overline{{A}} + \overline{{A}}^{{\text{T}}} {\varvec{P}}} & {{\varvec{P}}\hat{{B}}} & {{\varvec{C}}^{{\text{T}}} } \\ * & { - {\varvec{\varGamma}}^{2} I} & 0 \\ * & * & { - I} \\ \end{array} } \right]{ < }0$$
(25)

Lemma 2

[32]. Let \({\varvec{Y}} = {\varvec{Y}}^{{\text{T}}}\), \({\varvec{\varGamma}}\) and \({\varvec{\varUpsilon}}\) can be real matrices with compatible dimensions, and N satisfies \({\varvec{N}}^{{\text{T}}} {\varvec{N}} < 1\). Then, the following conditions.

$${\varvec{Y}} + {\varGamma}\varvec{N}\Upsilon +{\varvec{\varUpsilon}}^{{\text{T}}}{\varvec{N\varGamma}}^{{\text{T}}} < 0$$
(26)

holds if and only if there exists a positive scalar \(\varepsilon > 0\), such that

$$\left[ {\begin{array}{*{20}c} {\mathbf{\varvec{Y}}} & {\varepsilon{\varvec{\varGamma}}} & {{\varUpsilon}^{{\text{T}}} } \\ {\varepsilon{\varvec{\varGamma}}^{{\text{T}}} } & { - \varepsilon I} & 0 \\{\varvec{\varUpsilon}}& 0 & { - \varepsilon I} \\ \end{array} } \right] < 0$$
(27)

Now, the design method of the LMI-based robust feedback controller could be proposed.

Theorem 1.

Given a positive constant γ, a state-feedback controller exists, such that the closed-loop system in Eq. (23) can satisfy the H∞ performance index Eq. (21), if there exist scalars \(\varepsilon_{i} > 0\;(i = 1,2,3)\), a matrix H, and a symmetric positive matrix Q, such that.

$$\left[ {\begin{array}{*{20}c} {\varvec{\Theta}}_{\mathbf{i}} & {\varvec{B}}_{20i} & {\varvec{Q}}{\varvec{C}}^{\text{T}} & \varepsilon_{1} {\tilde{A}}_{i} & {\varvec{Q}} & \varepsilon_{2} {\tilde{B}}_{1i} & {\varvec{H}}^{\text{T}} & \varepsilon_{3} {\tilde{B}}_{2} & 0 \\ * & - \gamma^{2} I & 0 & 0 & 0 & 0 & 0 & 0 & I \\ * & * & - I & 0 & 0 & 0 & 0 & 0 & 0 \\ * & * & * & - \varepsilon_{1} I & 0 & 0 & 0 & 0 & 0 \\ * & * & * & * & - \varepsilon_{1} I & 0 & 0 & 0 & 0 \\ * & * & * & * & * & - \varepsilon_{2} I & 0 & 0 & 0 \\ * & * & * & * & * & * & - \varepsilon_{2} I & 0 & 0 \\ * & * & * & * & * & * & * & - \varepsilon_{3} I & 0 \\ * & * & * & * & * & * & * & * & - \varepsilon_{3} I \\ \end{array} } \right] < 0$$
(28)

where \({{\varvec{\Theta}}} = {\varvec{Q}}{\varvec{A}}_{0i}^{{\text{T}}} + {\varvec{A}}_{0i} {\varvec{Q}} + {\varvec{H}}^{{\text{T}}} {\varvec{B}}_{{{10}}}^{{\text{T}}} + {\varvec{B}}_{10} {\varvec{H}}\) and H = KQ.

Proof.

Because \(\overline{{A}}{ = }\hat{{A}} + \hat{{B}}_{1} {\varvec{K}}_{i}\) and \(\hat{{A}}{ = }{\varvec{A}}_{0i} + \tilde{{A}}_{i} {\varvec{N}}_{0}\),

$${\varvec{P}}\overline{{A}} + \overline{{A}}^{{\text{T}}} {\varvec{P}} = {\varvec{P}}(\hat{{A}} + \hat{{B}}_{1} {\varvec{K}}_{i} ) + (\hat{{A}} + \hat{{B}}_{1} {\varvec{K}}_{i} )^{{\text{T}}} {\varvec{P}} = {\varvec{P}}({\varvec{A}}_{0i} + \tilde{{A}}_{i} N_{0} + \hat{{B}}_{1} {\varvec{K}}_{i} ) + ({\varvec{A}}_{0i} + \tilde{{A}}_{i} N_{0} + \hat{{B}}_{1} {\varvec{K}}_{i} )^{{\text{T}}} {\varvec{P}}$$
(29)

Substituting Eq. (29) to Eq. (25), the left side of Eq. (25) can be rewritten as

$$\begin{aligned} & \left[ {\begin{array}{*{20}c} {{\varvec{P}}\overline{{A}} + \overline{{A}}^{{\text{T}}} {\varvec{P}}} & {{P\hat{B}}_{2} } & {{\varvec{C}}^{{\text{T}}} } \\ * & { - \gamma^{2} I} & 0 \\ * & * & { - I} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\varvec{P}}({\varvec{A}}_{0i} + \tilde{{A}}_{i} N_{0} + \hat{{B}}_{1} {\varvec{K}}_{i} ) + ({\varvec{A}}_{0i} + \tilde{{A}}_{i} N_{0} + \hat{{B}}_{1} {\varvec{K}}_{i} )^{{\text{T}}} {\varvec{P}}} & {{\varvec{P}}\hat{{B}}_{2i} } & {{\varvec{C}}^{{\text{T}}} } \\ * & { - \gamma^{2} I} & 0 \\ * & * & { - I} \\ \end{array} } \right] \\ & \quad \quad = \left[ {\begin{array}{*{20}c} {{\varvec{P}}({\varvec{A}}_{0i} + \hat{{B}}_{1} {\varvec{K}}_{i} ) + ({\varvec{A}}_{0i} + \hat{{B}}_{1} {\varvec{K}}_{i} )^{{\varvec{T}}} {\varvec{P}}} & {{\varvec{P}}\hat{{B}}_{2i} } & {{\varvec{C}}^{{\text{T}}} } \\ * & { - \gamma^{2} I} & 0 \\ * & * & { - I} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {{\varvec{P}}\tilde{{A}}_{i} } \\ 0 \\ 0 \\ \end{array} } \right]N_{0} \left[ {\begin{array}{*{20}c} I & 0 & 0 \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} I \\ 0 \\ 0 \\ \end{array} } \right]N_{0} \left[ {\begin{array}{*{20}c} {{\varvec{P}}\tilde{{A}}_{i}^{{\text{T}}} } & 0 & 0 \\ \end{array} } \right] \\ \end{aligned}$$
(30)

Based on Lemma 2, the following inequality can be derived from Eq. (30):

$$\left[ {\begin{array}{*{20}c} {{\varvec{P}}({\varvec{A}}_{0i} + \hat{{B}}_{1} {\varvec{K}}_{i} ) + ({\varvec{A}}_{0i} + \hat{{B}}_{1} {\varvec{K}}_{i} )^{{\text{T}}} {\varvec{P}}} & {{\varvec{P}}\hat{{B}}_{2} } & {{\varvec{C}}^{{\text{T}}} } & {\varepsilon_{1} {\varvec{P}}\tilde{{A}}_{i} } & I \\ * & { - \gamma^{2} I} & 0 & 0 & 0 \\ * & * & { - I} & 0 & 0 \\ * & * & * & { - \varepsilon_{1} I} & 0 \\ * & * & * & * & { - \varepsilon_{1} I} \\ \end{array} } \right] < 0$$
(31)

Then, because \(\hat{{B}}_{1} = {\varvec{B}}_{10} + \tilde{{B}}_{1i} N_{1}\), the left side of Eq. (31) can be rewritten as

$$\begin{aligned} & \left[ {\begin{array}{*{20}c} {{\varvec{P}}({\varvec{A}}_{0i} + \hat{{B}}_{1} {\varvec{K}}_{i} ) + ({\varvec{A}}_{0i} + \hat{{B}}_{1} {\varvec{K}}_{i} )^{{\text{T}}} {\varvec{P}}} & {{\varvec{P}}\hat{{B}}_{2i} } & {{\varvec{C}}^{{\text{T}}} } & {\varepsilon_{1} {\varvec{P}}\tilde{{A}}_{i} } & I \\ * & { - \gamma^{2} I} & 0 & 0 & 0 \\ * & * & { - I} & 0 & 0 \\ * & * & * & { - \varepsilon_{1} I} & 0 \\ * & * & * & * & { - \varepsilon_{1} I} \\ \end{array} } \right] \\ & \quad \quad = \left[ {\begin{array}{*{20}c} {{\varvec{P}}({\varvec{A}}_{0i} + {\varvec{B}}_{10} {\varvec{K}}_{i} ) + ({\varvec{A}}_{0i} + {\varvec{B}}_{10} {\varvec{K}}_{i} )^{{T}} {\varvec{P}}} & {{\varvec{P}}\hat{{B}}_{2i} } & {{\varvec{C}}^{{\text{T}}} } & {\varepsilon_{1} {\varvec{P}}\tilde{{A}}_{i} } & I \\ * & { - \gamma^{2} I} & 0 & 0 & 0 \\ * & * & { - I} & 0 & 0 \\ * & * & * & { - \varepsilon_{1} I} & 0 \\ * & * & * & * & { - \varepsilon_{1} I} \\ \end{array} } \right] \\ & \quad \quad + \left[ {\begin{array}{*{20}c} {{\varvec{P}}\tilde{{B}}_{1i} } \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array} } \right]N_{1} \left[ {\begin{array}{*{20}c} {{\varvec{K}}_{i} } & 0 & 0 & 0 & 0 \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {{\varvec{K}}_{i}^{{\text{T}}} } \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array} } \right]N_{1} \left[ {\begin{array}{*{20}c} {(\tilde{{B}}_{1i} {\varvec{P}})^{{\text{T}}} } & 0 & 0 & 0 & 0 \\ \end{array} } \right] \\ \end{aligned}$$
(32)

Thus, based on Lemma 2, the following inequality holds:

$$\left[ {\begin{array}{*{20}c} {{\varvec{P}}({\varvec{A}}_{0i} + {\varvec{B}}_{10} {\varvec{K}}_{i} ) + ({\varvec{A}}_{0i} + {\varvec{B}}_{10} {\varvec{K}}_{i} )^{{\text{T}}} {\varvec{P}}} & {{\varvec{P}}\hat{{B}}_{2i} } & {{\varvec{C}}^{{\text{T}}} } & {\varepsilon_{1} {\varvec{P}}\tilde{{A}}_{i} } & I & {\varepsilon_{2} {\varvec{P}}\tilde{{B}}_{1i}^{{\text{T}}} } & {{\varvec{K}}^{{\text{T}}} } \\ * & { - \gamma^{2} I} & 0 & 0 & 0 & 0 & 0 \\ * & * & { - I} & 0 & 0 & 0 & 0 \\ * & * & * & { - \varepsilon_{1} I} & 0 & 0 & 0 \\ * & * & * & * & { - \varepsilon_{1} I} & 0 & 0 \\ * & * & * & * & * & { - \varepsilon_{2} I} & 0 \\ * & * & * & * & * & * & { - \varepsilon_{2} I} \\ \end{array} } \right] < 0$$
(33)

Afterward, \(\hat{{B}}_{2} = {\varvec{B}}_{20i} + \tilde{{B}}_{2i} N_{2}\) is substituted into Eq. (33), and the left side of Eq. (33) can be rewritten as

$$\begin{aligned} & \left[ {\begin{array}{*{20}c} {{\varvec{P}}({\varvec{A}}_{0i} + {\varvec{B}}_{10} {\varvec{K}}_{i} ) + ({\varvec{A}}_{0i} + {\varvec{B}}_{10} {\varvec{K}}_{i} )^{{\text{T}}} {\varvec{P}}} & {{\varvec{P}}\hat{{B}}_{2i} } & {{\varvec{C}}^{{\text{T}}} } & {\varepsilon_{1} {\varvec{P}}\tilde{{A}}_{i} } & I & {\varepsilon_{2} {\varvec{P}}\tilde{{B}}_{1i}^{{\text{T}}} } & {{\varvec{K}}^{{\text{T}}} } \\ * & { - \gamma^{2} I} & 0 & 0 & 0 & 0 & 0 \\ * & * & { - I} & 0 & 0 & 0 & 0 \\ * & * & * & { - \varepsilon_{1} I} & 0 & 0 & 0 \\ * & * & * & * & { - \varepsilon_{1} I} & 0 & 0 \\ * & * & * & * & * & { - \varepsilon_{2} I} & 0 \\ * & * & * & * & * & * & { - \varepsilon_{2} I} \\ \end{array} } \right] \\ & \quad \quad = \left[ {\begin{array}{*{20}c} {{\varvec{P}}({\varvec{A}}_{0i} + {\varvec{B}}_{10} {\varvec{K}}_{i} ) + ({\varvec{A}}_{0i} + {\varvec{B}}_{10} {\varvec{K}}_{i} )^{{\text{T}}} {\varvec{P}}} & {{\varvec{P}}{\varvec{B}}_{20i} } & {{\varvec{C}}^{{\text{T}}} } & {\varepsilon_{1} {\varvec{P}}\tilde{{A}}_{i} } & I & {\varepsilon_{2} {\varvec{P}}\tilde{{B}}_{1i}^{{\text{T}}} } & {{\varvec{K}}^{{\text{T}}} } \\ * & { - \gamma^{2} I} & 0 & 0 & 0 & 0 & 0 \\ * & * & { - I} & 0 & 0 & 0 & 0 \\ * & * & * & { - \varepsilon_{1} I} & 0 & 0 & 0 \\ * & * & * & * & { - \varepsilon_{1} I} & 0 & 0 \\ * & * & * & * & * & { - \varepsilon_{2} I} & 0 \\ * & * & * & * & * & * & { - \varepsilon_{2} I} \\ \end{array} } \right] \\ & \quad \quad + \left[ {\begin{array}{*{20}c} {{\varvec{P}}\tilde{{B}}_{2} } \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array} } \right]N_{2} \left[ {\begin{array}{*{20}c} 0 & I & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} 0 \\ I \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array} } \right]N_{2} \left[ {\begin{array}{*{20}c} {({\varvec{P}}\tilde{{B}}_{2} )^{{\text{T}}} } & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right] \\ \end{aligned}$$
(34)

Based on Lemma 2, the following inequalities are derived:

$$\left[ {\begin{array}{*{20}c} {{\varvec{P}}({\varvec{A}}_{0i} + {\varvec{B}}_{10} {\varvec{K}}_{i} ) + ({\varvec{A}}_{0i} + {\varvec{B}}_{10} {\varvec{K}}_{i} )^{{T}} {\varvec{P}}} & {{\varvec{P}}{\varvec{B}}_{20i} } & {{\varvec{C}}^{{\text{T}}} } & {\varepsilon_{1} {\varvec{P}}\tilde{{A}}_{i} } & I & {\varepsilon_{2} {\varvec{P}}\tilde{{B}}_{1i} } & {{\varvec{K}}^{{\text{T}}} } & {\varepsilon_{3} {\varvec{P}}\tilde{{B}}_{2} } & 0 \\ * & { - \gamma^{2} I} & 0 & 0 & 0 & 0 & 0 & 0 & I \\ * & * & { - I} & 0 & 0 & 0 & 0 & 0 & 0 \\ * & * & * & { - \varepsilon_{1} I} & 0 & 0 & 0 & 0 & 0 \\ * & * & * & * & { - \varepsilon_{1} I} & 0 & 0 & 0 & 0 \\ * & * & * & * & * & { - \varepsilon_{2} I} & 0 & 0 & 0 \\ * & * & * & * & * & * & { - \varepsilon_{2} I} & 0 & 0 \\ * & * & * & * & * & * & * & { - \varepsilon_{3} I} & 0 \\ * & * & * & * & * & * & * & * & { - \varepsilon_{3} I} \\ \end{array} } \right] < 0$$
(35)

There are two unknown matrix P and Ki in Eq. (35). Hence, it is difficult to derive P and K by solving Eq. (35) directly, and Eq. (35) must be transformed to a new inequality that is easy to solve. Thus, Q = P−1 and H = KQ are defined and a congruence transformation is conducted with diag{Q, I, I, I, I, I, I, I, I, I) to the above inequalities. Consequently, the inequality Eq. (28) holds, which completes the proof.

According to Eq. (22), the feedback controller can be expressed as

$$\delta_{{{\text{fb}}}} = \sum\limits_{i = 1}^{4} {h_{i} (t){\varvec{K}}_{i} {\varvec{x}}(t)}$$
(36)

The total front steering angle is the sum of the feedforward and feedback controller:

$$\delta_{{\text{f}}} = \delta_{{{\text{ffw}}}} + \delta_{{{\text{fb}}}}$$
(37)

The maximum value of the front steering angle should be constrained by the limits of the steering system \(\delta_{{{\text{flim}}}}\). Moreover, in the path-following process, sometimes, to finish some limiting path-following tasks, such as collision avoidance, a proper and transient side slip is permitted [33]. However, rollover, which is extremely dangerous for vehicles, should be prohibited. Therefore, the front-wheel steering angle should also be constrained for rollover prevention.

According to the rollover thresholds [26] and steady-state cornering assumption, the rollover constraint \(\delta_{{{\text{frp}}}}\) for the front-wheel steering angle can be proposed as

$$\delta_{{{\text{frp}}}} = \frac{{b(l_{{\text{f}}} + l_{{\text{r}}} + (mv_{x}^{2} (C_{{\text{r}}} l_{{\text{r}}} - C_{{\text{f}}} l_{{\text{f}}} )/(C_{{\text{f}}} C_{{\text{r}}} (l_{{\text{f}}} + l_{{\text{r}}} )))}}{{2h_{{\text{g}}} v_{x}^{2} }}$$
(38)

where hg is the height of the mass center of the autonomous vehicle.

Thus, the total front steering angle can be presented as

$$\delta_{{\text{f}}} = \min (\delta_{{{\text{ffw}}}} + \delta_{{{\text{fb}}}} ,S_{{\updelta }} \delta_{{{\text{flim}}}} ,S_{{\updelta }} \delta_{{{\text{frp}}}} )$$
(39)

where \(S_{{\updelta }}\) is the safety factor of the front-wheel steering angle, which is between 0 and 1. Here, \(S_{{\updelta }} = 0.9\).

Remark: Because Lemma 1 is derived from the Lyapunov condition [31], as a corollary of Lemma 1, the stability of the proposed controller can be guaranteed.

3.3 Longitudinal Controller

As mentioned above, some errors are caused by the model mismatch and external disturbance in the single-track model. For longitudinal dynamics, the external disturbances are quite obvious, such as air drag and ramp resistance. These factors are lumped as w5. Mass uncertainties greatly influence the longitudinal control. The longitudinal dynamics Eq. (1) can be rewritten as

$$\dot{v}_{x} = \tau F_{x} + rv_{y} + w_{5}$$
(40)

where \(\tau { = }\frac{1}{m}\).

Because the specific values of \(\tau\) and w5 are unknown, the RBF neural network method is introduced [34]. The structure of the RBF is shown in Fig. 6, where the number of nodes in the hidden layer is set as 5. The two unknown terms can be approximated by

$$\begin{aligned} & \hat{w}_{5} = {\varvec{W}}^{{\text{T}}} {\varvec{h}}_{w} (x) \\ & \hat{\tau } = {\varvec{V}}^{{\text{T}}} {\varvec{h}}_{m} (x) \\ \end{aligned}$$
(41)

where \(\hat{w}_{5}\) is the estimation value of w5 and \(\hat{\tau }\) is the estimation value of \(\tau\). W = [W1, W2,…, W5] and V = [V1, V2,…, V5] are the bounded weight vectors of the network, x are the inputs of the network, and hw,m = [h1, h2,…, h5] is the regressor vector that can be defined as

$$h_{j} = \exp \left( {\frac{{\left\| {x - {\text{c}}_{j} } \right\|^{2} }}{{2b_{j}^{2} }}} \right)$$
(42)

where x is the inputs of the network, c is the central vector of the Gaussian basic function of the jth node in the hidden layer, and b is its width. Here, it is assumed that w5 and m can be approximated by

$$\begin{aligned} & w_{5} = {\varvec{W}}^{{*}{\text{T}}} {\varvec{h}}_{w} (x) + \chi_{{_{w} }} \\ & \tau = {\varvec{V}}^{{*}{\text{T}}} {\varvec{h}}_{m} (x) + \chi_{m} \\ \end{aligned}$$
(43)

where W* and V* are the desired weighting factors and χw and χm are the approximation errors of w5 and τ, respectively.The two inputs of the neural networks are defined as ex and \(\int {e_{x} }\), with ex = vxd-vx, where vxd is the desired longitudinal velocity. The sliding surface can be defined as

$$S = e_{x} + \xi \int {e_{x} }$$
(44)

where ξ is a strictly positive constant.

Fig. 6
figure 6

Structure of the RBF neural network

Full size image

The control law for the sliding surface can be defined as

$$F_{x} = \frac{1}{{\hat{\tau }}}(\dot{v}_{xd} - rv_{y} + \xi (v_{x} - v_{xd} ) + \eta {\text{sgn}} (S) + k_{{\text{s}}} S + \hat{w}_{5} )$$
(45)

where η and ks are strictly positive design scalars.

Combining Eq. (45) with the differential of the sliding surface S, then

$$\begin{aligned} & \dot{S} = \dot{e}_{x} + \xi e_{x} { = }\dot{v}_{xd} - \tau F_{x} - rv_{y} - w_{5} + \xi (v_{xd} - v_{x} ) \\ & \quad \quad = \dot{v}_{xd} - \hat{\tau }F_{x} + (\hat{\tau } - \tau )F_{x} + rv_{y} + w_{5} + \xi (v_{xd} - v_{x} ) \\ & \quad \quad = \dot{v}_{xd} - \frac{{\hat{\tau }}}{{\hat{\tau }}}(\dot{v}_{xd} - rv_{y} + \xi (v_{x} - v_{xd} ) + \eta {\text{sgn}} (S) + k_{{\text{s}}} S - \hat{w}_{5} ) \\ & \quad \quad + (\hat{\tau } - \tau )F_{x} - rv_{y} - w_{5} + \xi (v_{xd} - v_{x} ) \\ & \quad \quad = (\tilde{{V}}{h}_{{\text{m}}} (x) - \chi_{{_{m} }} )F_{x} + \tilde{{W}}{h}_{w} (x) - \chi_{{_{w} }} - \eta {\text{sgn}} (S) - k_{{\text{s}}} S \\ \end{aligned}$$
(46)

where \(\tilde{{W}}{ = }\hat{{W}} - {\varvec{W}}^{*}\), \(\tilde{{V}}{ = }\hat{{V}} - {\varvec{V}}^{*}\), and \(\begin{gathered} \tilde{w}_{5} = \hat{w}_{5} - w_{5} { = }\tilde{{W}}{h}_{{\text{w}}} (x) - \chi_{{_{w} }} \hfill \\ \tilde{\tau }{ = }\hat{\tau } - \tau = \tilde{{V}}{h}_{{\text{m}}} (x) - \chi_{{\text{m}}} \hfill \\ \end{gathered}\).

To derive the adaptive law for W and V, the Lyapunov function is designed as

$$L{ = }\frac{1}{2}S^{2} + \frac{1}{{2\sigma_{{\text{w}}} }}\tilde{{W}}^{{\text{T}}} \tilde{{W}} + \frac{1}{{2\sigma_{{\text{m}}} }}\tilde{{V}}^{{\text{T}}} \tilde{{V}}$$
(47)

where σw > 0, σm > 0.

Considering Eq. (46), then we have:

$$\begin{aligned} & \dot{L}{ = }S\dot{S} + \frac{1}{{\sigma_{{\text{w}}} }}\tilde{{W}}^{\text{T}} {\dot{\tilde{W}}} + \frac{1}{{\sigma_{m} }}\tilde{{V}}^{\text{T}} {\dot{\tilde{V}}} \\ & \quad \quad = S((\tilde{{V}}{h}_{{\text{m}}} (x) - \chi_{{_{{\text{m}}} }} )F_{x} + \tilde{{W}}{h}_{{\text{w}}} (x) - \chi_{{_{{\text{w}}} }} \\ & \quad \quad - \eta {\text{sgn}} (S) - k_{{\text{s}}} S) + \frac{1}{{\sigma_{{\text{w}}} }}\tilde{{W}}^{{\text{T}}} {\dot{\tilde{W}}} + \frac{1}{{\sigma_{{\text{m}}} }}\tilde{{V}}^{{\text{T}}} {\dot{\tilde{V}}} \\ & \quad \quad = \tilde{{W}}^{{\text{T}}} (S{\varvec{h}}_{{\text{w}}} (x){ + }\frac{1}{{\sigma_{{\text{w}}} }}{\dot{\hat{W}}}) + \tilde{{V}}^{\text{T}} (S{\varvec{h}}_{{\text{m}}} (x){ + }\frac{1}{{\sigma_{{\text{m}}} }}{\dot{\hat{V}}}) \\ & \quad \quad + S( - \chi_{{_{{\text{w}}} }} - \eta {\text{sgn}} (S) - k_{{\text{s}}} S - \chi_{{_{{\text{m}}} }} F_{x} ) \\ \end{aligned}$$
(48)

By setting the adaptive law as

$$\begin{aligned} & {\dot{\hat{W}}}{ = } - \sigma_{{\text{w}}} S{\varvec{h}}_{{\text{w}}} (x) \\ & {\dot{\hat{V}}}{ = } - \sigma_{m} S{\varvec{h}}_{m} (x) \\ \end{aligned}$$
(49)

Then,

$$\dot{L}{ = }S( - \chi_{{_{{\text{w}}} }} - \eta {\text{sgn}} (S) - \chi_{{_{{{m}}} }} F_{x} ){ = }S( - \chi_{{_{{\text{w}}} }} - \chi_{{_{{{m}}} }} F_{x} ) - \eta \left| S \right| - k_{{\text{s}}} S^{2}$$
(50)

Because the adaption error χw and χm have very small values, by setting \(\eta \ge \left| {\chi_{{{w}}} + \chi_{{{m}}} F_{x} } \right|\), \(\dot{L} < 0\). In this way, the stability of the longitudinal controller under disturbances and uncertainties can be ensured.

Once the total driving force Fx is obtained, it can be achieved by a powertrain system or directly transformed to the pedal position of the throttle or brake using look-up tables. Except for the traditional internal combustion engine vehicles with one power source, owing to the development of the innovative technology of electric vehicles in recent years, many possibilities of powertrain configurations have been proposed, such as four-wheel driving (4WD). However, because this study focuses on the common control problem of autonomous vehicles under the coupling effects, only the generalized longitudinal force Fx is calculated, and the specific implementation of Fx for the powertrain is not discussed. The longitudinal control for autonomous vehicles of one specific powertrain configuration, such as 4WD, has recently also become a research hotspot, including tire force allocation [35], slip rate control [36], and direct yaw moment control [37]. Essentially, for 4WD vehicles, the redundant control output, generated by the torque differences between left and right in-wheel motors, also known as the active yaw moment, can strongly improve vehicle cornering performance, especially under some extreme driving conditions [38, 39].

3.4 Safe Speed Profile

Although the proposed lateral and longitudinal controllers can deal with a variety of coupling effects, the coupling effects caused by tire force saturation remain to be solved. The tire force saturation always happens in some limiting driving maneuvers, such as performing large steering maneuvers in high-speed conditions. In these limiting operation conditions, vehicles commonly lose their stability and controllability, which is quite dangerous. To prevent these situations from happening, the reference longitudinal velocity should be adapted to the curvature of the path. Inspired by Ref. [21], a safe speed profile is introduced.

Figure 7 shows a sample situation when the vehicle is about to turn. In this figure, “turn-in point” denotes the point where the curvature is no longer zero, and “turn-in part” is the path where the curvature is increasing. Then, the “summit point” is where the curvature comes to the summit ρcmax. This curvature will be held for a distance, called the “summit part.” Sentry, Sin-turn, and Ssummit denote the curvilinear distance of the vehicle current position, “turn-in point,” and “summit point,” respectively. As shown in Fig. 7, when a curve appears at the reference path in front of the vehicle, the task of the safe speed profile is to generate the safe constraint of the longitudinal speed along the reference path based on the path curvature ρ and vehicle entry speed ventry to avoid tire force saturation.

Fig. 7
figure 7

Sample situation when the vehicle is about to turn. a Reference path in global coordinates; b curvature

Full size image

The vehicle longitudinal and lateral acceleration is constrained by the tire force saturation limit as [26]

$$\sqrt {a_{x}^{2} + a_{y}^{2} } \le \mu g$$
(51)

To generate the safe limit of the longitudinal velocity at the curve path, it is assumed that all the lateral tire forces are used to provide the centrifugal force under the steady-state steering condition. Then,

$$a_{y} { = }v_{x} r{ = }v_{x}^{2} \rho$$
(52)

Equation (52) is substituted into Eq. (51). Then, the maximum admissible velocity vxmax is given as

$$v_{x\max } = sf_{vx} \sqrt {\frac{{a_{y} }}{\rho }} = sf_{vx} \sqrt {\frac{\mu g}{\rho }}$$
(53)

where sfvx is the safety factor of the longitudinal velocity; here, sfvx = 0.95. The velocity at the maximum curvature vmaxcur is calculated as

$$v_{{{\text{maxcur}}}} = 0.95\sqrt {\frac{\mu g}{{\rho_{{{\text{cmax}}}} }}}$$
(54)

Then, comparisons were made between vmaxcur and the vehicle entry speed ventry. If ventry < vmaxcur, it is not necessary for the vehicle to decelerate, and the vehicle can keep its entry speed ventry during the whole turn-in process. However, if ventry > vmaxcur, the vehicle should decelerate to enable its speed below the maximum admissible speed given in Eq. (54).

When the vehicle decelerates, deceleration should also be constrained to prevent the tire forces from saturation. According to Eqs. (51) and (52), the maximum admissible deceleration can be derived as

$$a_{x\max } = sf_{ax} \sqrt {\mu^{2} g^{2} - (v_{x}^{2} \rho )^{2} }$$
(55)

where sfax is the safety factor of the longitudinal velocity; here, sfax = 0.85.

In addition, oversized or too early deceleration at the straight path far before the curve should be avoided. Thus, another criterion for deceleration is defined as

$$a_{x\max d} = \frac{{v_{x}^{2} - v_{{{\text{maxcur}}}}^{{2}} }}{{s_{{{\text{dis}}}} }}$$
(56)

where sdis is the distance between the vehicle’s current position and the “summit point.”

Thus, the criteria of the safe speed profile along the reference path when ventry > vmaxcur can be summarized as

$$\begin{aligned} & v_{x} \le 0.95\sqrt {\frac{\mu g}{\rho }} \\ & a_{x} \le \min \left( {0.85\sqrt {\mu^{2} g^{2} - (v_{x}^{2} \rho )^{2} } ,\frac{{v_{x}^{2} - v_{{{\text{maxcur}}}}^{{2}} }}{{s_{{{\text{dis}}}} }}} \right) \\ \end{aligned}$$
(57)

Moreover, the speed profile during the turn-off process can be derived in a similar way, where the vehicle should avoid tire force saturation during acceleration.

The proposed safe speed profile can also act as constraints when conducting some speed profile optimizations to minimize energy consumption or enhance driving comfort. Because this section mainly focuses on the prevention of tire force saturation, speed profile optimization is not discussed here. Accordingly, the readers can refer to Refs. [40, 41] for details.

4 Simulation and Discussion

In this section, two simulation cases with relatively fierce coupling effects are presented to verify the effectiveness of the proposed control method. One is a double-lane-change maneuver, and the other is the ramp maneuver. The simulations are based on the CarSim–Simulink platform. The controllers are constructed in Simulink, whereas CarSim provides a high-fidelity vehicle model based on experimental data. The vehicle parameters used in the simulations are presented in Table 1, and the parametric uncertainty of the cornering stiffness is assumed as 30% of the nominal value in CarSim. To reflect the uncertainties in vehicle parameters, the mass and inertial moment in controller are set as 1200 kg and 1081 kg·m2, respectively.

Table 1 Parameters used in the simulation
Full size table

To show the necessity and superiority of the proposed controller, another well-designed robust controller is proposed for comparison. For its lateral feedback controller, the cornering stiffness is considered, but the uncertainties in physical parameters are not, which is similar to what previous studies have done [22,23,24]. In the longitudinal control, a sliding mode control with an exponential approaching role is considered as follows:

$$F_{x} = m[\dot{v}_{xd} - rv_{y} + \xi (v_{xd} - v_{x} )] + \eta {\text{sgn}} (S) + k_{s} S$$
(58)

where S is the sliding surface and the approaching parameters η and ks are the same as the proposed controller.

For convenience, the controller for comparison is named as “controller 2” hereafter, and the proposed controller is referred to as “controller 1.”

4.1 Double-Lane Change

In this case, the vehicle is made to conduct a double-lane-change maneuver on a high-adhesive condition (μ = 0.75) with a constant velocity of 25 m/s. The curvature of the required path is shown in Fig. 8. This figure shows that this maneuver is quite aggressive. The tracking performance, including the velocity tracking and path tracking, is shown in Fig. 9. The longitudinal performance is shown in Fig. 9a, where the longitudinal velocity is influenced when the double-lane-change maneuver starts. Although both controllers can deal with this effect, compared with controller 2, the longitudinal velocity of controller 1 is clearly closer to the reference value during the whole maneuver. Figure 9b, c shows the lateral path-following error and heading error, respectively. By taking the uncertainties of physical parameters into consideration, controller 1 can have smaller tracking error in general. To quantitatively analyze the tracking performance, the root mean square (RMS) values of the two controllers are listed in Table 2. The table shows that the RMS values of the velocity tracking errors, lateral errors, and tracking errors of controller 1 are 44.32%, 65.74%, and 47.59% of that of controller 2, respectively, which shows a considerable improvement.

Fig. 8
figure 8

Curvature of the required path

Full size image
Fig. 9
figure 9

Tracking performance: a longitudinal velocity; b lateral error; c heading error

Full size image
Table 2 RMS values of the tracking error (double-lane change)
Full size table

The dynamics responses are shown in Fig. 10, including the yaw rate responses in Fig. 10a and the side-slip angle in Fig. 10b. Controller 1 shows better dynamics stability because the side-slip angle is smaller in general and the yaw rate varies smoother. The control inputs are shown in Fig. 11. To maintain the velocity and compensate for the coupling effects, the longitudinal forces evidently increase when the steering action starts. Moreover, controller 1 has larger longitudinal forces compared with controller 2 at the very beginning of the case. This is because the actual mass (1410 kg) is larger than the mass used in the controller (1200 kg), and the proposed controller can become adaptive to the model-mismatch problem owing to the RBF neural network. As a result, a larger value is calculated, which is appropriate to the actual mass of the vehicle, to compensate for the external disturbances in the first few seconds.

Fig. 10
figure 10

Dynamics responses: a yaw rate; b side-slip angle

Full size image
Fig. 11
figure 11

Control inputs: a steering angle; b longitudinal force

Full size image

The global trajectory is shown in Fig. 12. Although both controllers can finish the aggressive double-lane-change maneuver satisfactorily, the proposed controller clearly has better performance. This result illustrates the effectiveness and superiority of the proposed controller.

Fig. 12
figure 12

Global trajectory in double-lane change maneuver

Full size image

4.2 Ramp maneuver

To further evaluate the effectiveness and robustness of the proposed controller, the vehicle is made to conduct a ramp maneuver on a slippery road (μ = 0.35) with an initial longitudinal velocity of 15 m/s. The curvature of the path is shown in Fig. 13. The tire force saturation clearly cannot be avoided at the initial velocity. Thus, a varying reference velocity generated by the safe speed profile is introduced. The tracking performances are shown in Fig. 14. As shown in the figure, owing to the mismatch of the vehicle mass, controller 2 has a clear deviation from the reference speed after the deceleration, whereas the proposed controller can track the reference velocity very well during the whole maneuver owing to the adaptive ability brought by the RBF neural network. Figure 14b, c shows the lateral error and heading error, respectively. The lateral error of controller 1 is evidently smaller than that of controller 2. However, for the heading error, controller 1 only shows limited improvement as compared with controller 2. This is because the curvature of the reference path remains constant for a while when it comes to the “summit point.” This result presents a “steady steering” condition for the lateral controllers. The RMS value of the two controllers is shown in Table 3, and the RMS error values of controller 1 are 12.21% (velocity tracking error), 69.82% (lateral error), and 90.42% (heading error) of that of controller 2. From the perspective of the RMS lateral error value, the improvement in the lateral path tracking is similar to case 1, whereas the improvement of velocity tracking is evidently more significant than that of case 1. This result can be explained by the fact that the reference velocity is adjusted by the speed profile, and the influence caused by the mass mismatch is greater in the varying-velocity condition.

Fig. 13
figure 13

Curvature of the required path

Full size image
Fig. 14
figure 14

Tracking performance: a longitudinal velocity; b lateral error; c heading error

Full size image
Table 3 RMS values of the tracking error (Ramp)
Full size table

The yaw rate and side-slip angle are shown in Fig. 15a, b, respectively. The dynamics responses of the two controllers are similar, except that the sideslip angle of controller 1 is a little smaller than that of controller 2. The control inputs are shown in Fig. 16. The difference in the steering angle of the two controllers is subtle, whereas the longitudinal force calculated by controller 1 is larger than that of controller 2 at the beginning of the deceleration owing to the adaptive compensation ability of the RBF neural network.

Fig. 15
figure 15

Dynamics responses: a yaw rate; b side-slip angle

Full size image
Fig. 16
figure 16

Control inputs: a steering angle; b longitudinal force

Full size image

The global trajectory is shown in Fig. 17. Owing to the safe speed profile, both controllers can complete the maneuver successfully. Nevertheless, controller 1 shows better tracking performance than controller 2. The results of this case further verify the effectiveness and robustness of the proposed controller under low-adhesive conditions with strong coupling effects. These results also illustrate the importance of considering the physical parameter uncertainties in the controller design because the mass and moment of inertia often deviate from their nominal value in the controller owing to many factors, such as the number and weight of the passengers, goods in the trunk, and fuel condition.

Fig. 17
figure 17

Global trajectory in ramp maneuver

Full size image

5 Conclusions

The coupling effects and system uncertainties evidently degrade the path-following performance of autonomous vehicles, especially under some extreme conditions. These factors have multi-source complexity. Therefore, comprehensive handling strategies are proposed in the combined longitudinal and lateral control scheme for different types of coupling effects, and the uncertainties in dynamics parameters and physical parameters are considered. The simulation results show that even under strong coupling effects, the proposed controller has excellent performance owing to its exclusively designed strategies for coupling effects. Furthermore, the proposed controller can significantly improve the path-following performance under conditions with evident uncertainties, especially where the dynamics and physical parameters deviate far from their nominal values. Compared with a well-designed robust controller, the velocity tracking performance, lateral tracking performance, and heading tracking performance improve by 55.68%, 34.26%, and 52.41%, respectively, in the double-lane change maneuver, and increase by 87.79%, 30.18%, and 9.58%, respectively, in the ramp maneuver.

However, robust methods may bring conservativeness to the controller. Future focus will be put on how to reduce the conservativeness in path-following control without affecting the robustness of the system.