1 Introduction

With the evolution of nature, architected cellular materials are equipped with low density, high stiffness and high strength. The beaks and bones of birds, for example, contain highly porous, cellular core [1]. Owing to their desirable energy absorption capacity and mechanical properties, architected cellular materials have been intensively applied in the domains of vehicle, chemistry, electrical engineering, architecture, and bio-mechanics [2,3,4].

Unlike pure solid structures, both utilized material and cell topology dominate the mechanical properties of cellular material. Among this, cell topology consists of relative density, cell size,etc [5,6,7,8]. It has been research hotspots to set up relationship of cell topology and performance and realize the redesign based on practical applications [9].

Previous work has investigated the crushing behaviors of cellular materials with various cell microtopology. In a complementary study, Fleck et al. [10, 11] illustrated that the performance of sandwich panels attribute greatly to the topology and relative density. The study on the in-plane mechanical properties of honeycomb structures were conducted, various cell types were taken into account and initial yield surfaces were obtained by Wang et al. [12, 13]. In order to investigate the impact behaviors of honeycombs, experiments and numerical simulations are conducted by Papka and Kyriakides [14, 15]. Liu and Zhang [5] discussed honeycomb structures filled with equilateral triangular or quadratic cells with regular and staggered arrangements in terms of impact velocity and structural parameters.

The aforementioned pioneering work mainly paid attention to convex cells and gave less attention to concave cells, let alone the dynamic crushing analysis of re-entrant cellular materials. The present study proposes a novel re-entrant square cellular material. To explore the relationship between microtopology and macrodynamic responses, the effects of cell microtopology on in-plane dynamic crushing are analyzed with the adoption of finite element method. Most importantly, research on three dimensions can be carried out based on the concept of two dimensions.

2 Theoretical Models of Relative Density for Regular Re-entrant Squares and Staggered Re-entrant Squares

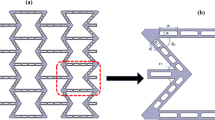
The term “re-entrant” indicates inward beams or negative angle for beams, as shown in Fig. 1. It can be seen that cell beams contribute significantly to the deformation of this cellular material, the mechanisms including deflection and axial deformation are in charge of the auxetic characteristics [16, 17].

Fig. 1
figure 1

Re-entrant square with three geometric parameters

Full size image

The present paper puts forward three geometrical parameters, namely the cell wall thickness t, re-entrant distance h and cell edge length L, as exhibited in Fig. 1.

Relative density \(\rho _{\mathrm {RD}}\) is the ratio of the equivalent density to the density of utilized material:

$$\begin{aligned} \rho _{\mathrm {RD}} =\frac{\rho _{\mathrm{c}} }{\rho _{\mathrm{s}} } \end{aligned}$$
(1)

where \(\rho _{\mathrm{c}} \) stands for equivalent density of this cellular structure and \(\rho _{\mathrm{s}} \) represents the density of utilized material constructing the cells.

The relative density \(\rho _{\mathrm {RD}} \) is presented in Figs. 2 and 3 for regular re-entrant squares (RRS) and staggered reentrant squares (SRS), respectively.

Fig. 2
figure 2

Relative density of two-dimensional RRS

Full size image
Fig. 3
figure 3

Relative density of two-dimensional SRS

Full size image

The relative density for the regular square \(\rho _{\mathrm {regular}} \) is therefore

$$\begin{aligned} \rho _{\mathrm {regular}} =\frac{S}{\left( {L/2} \right) ^{2}}=\frac{4S}{L^{2}}=\frac{4(S_1 +S_2 -S_3 )}{L^{2}} \end{aligned}$$
(2)

where \(S_{1} \) is total area of the two parallelograms in Fig. 2, \(S_{2} \) stands for the area of the square at the lower-right corner, and \(S_{3} \) is the total area of the two triangles in the lower small square.

According to the above-mentioned and corresponding geometrical relations, the relative density \(\rho _{\mathrm {regular}} \) of the RRS is expressed by

$$\begin{aligned} \rho _{\mathrm {regular}} =\frac{4t\sqrt{4h^{2}+L^{2}}}{L^{3}}\left( {L-\frac{t\sqrt{4h^{2}+L^{2}}}{L-2h}} \right) \end{aligned}$$
(3)

The relative density \(\rho _{\mathrm {staggered}} \) of the SRS is calculated similarly to that of the RRS:

$$\begin{aligned} \rho _{\mathrm {staggered}} =\frac{S_6 -S_5 -S_4 }{S_6 } \end{aligned}$$
(4)

where \(S_4 \) is the total area of the quadrilateral in Fig. 3, \(S_5 \) is the summed area of triangles, and \(S_6 \) is the total area of the rectangle.

Table 1 Design matrix of re-entrant squares for crushing analysis
Full size table
Fig. 4
figure 4

Finite element models of two arrangements of re-entrant squares. a Regular, b staggered

Full size image

The relative density \(\rho _{\mathrm {staggered}} \) is finally obtained as

$$\begin{aligned} \rho _{\mathrm {staggered}} =\frac{8t\sqrt{\left( {\frac{L}{2}} \right) ^{2}+h^{2}}\left[ {L^{2}-2hL-2t\sqrt{\left( {\frac{L}{2}} \right) ^{2}+h^{2}}} \right] }{L^{2}\left( {L-h} \right) \left( {L-2h} \right) }\nonumber \\ \end{aligned}$$
(5)

3 Effects of Micro-arrangements on Dynamic Crushing Behaviors

To explore the relationship between the microtopology and macrodynamic responses of re-entrant square cellular material, the design of experiments (DOE) method is employed to construct approximate models. This allows the selection of a limited number of sampling points from the overall design space with fewer tests, a shorter test period, and lower test costs [18]. Some design methods of selecting sample points in the design space more efficiently have been explored [19, 20]. The LHS method, for example, is a DOE method that has the advantages of an effective space filling capacity and better fitting nonlinear response. The LHS method is thus used herein to select sampling points with the result of obtaining models with higher quality and providing a basis for the following approximate models. What follows is the definition of ranges of the geometric configurations. Values of geometric parameters that are too large will lead to an overlap of cell walls, while values that are too small may eliminate concave characteristics. Hence, the ranges of thickness coefficient \(\alpha \) and re-entrant coefficient \(\beta \) are, respectively, selected as \(0.05\le \alpha \le 0.2\) and \(0.05\le \beta \le 0.2\) in the DOE design in this work under the condition that \(\alpha +\beta <0.5\), where \(\alpha =\frac{t}{L}\) and \(\beta =\frac{h}{L}\); both have three intervals. Moreover, \(v=\) 5, 10, 20, and 50 m/s. Sixteen groups of sampling points considered in this paper are enough for the sampling test with four factors and three levels. Table 1 presents the sampling points selected employing the LHS method.

Fig. 5
figure 5

Stress–strain curves of the two arrangements for four groups of variables. a Regular, b staggered

Full size image

3.1 Computational Models

To investigate the in-plane dynamic impact characteristics of the re-entrant material, Fig. 4 presents finite element models of the RRS and SRS. For the RRS, there are \(N_R =5 \times 5\) cells. For the SRS, there are five layers, with odd-numbered layers having six cells and even-numbered layers having five cells. The re-entrant cellular material is made of acrylonitrile butadiene styrene with density \(\rho =1.05 \hbox {g/cm}^{3}\), Young’s modulus \(E=1\) GPa, Poisson’s ratio \(\nu =0.39\), and yield strength \(\sigma _\mathrm{y} =26.75\) MPa. The nonlinear explicit finite element code Ls-dyna is employed in the calculation. A rigid plate moving at constant velocity is used to impact the material, and the re-entrant cellular material is clamped at its bottom surface and having both sides free. Adjacent nodes between cells are bonded using equivalence.

As shown in Fig. 4, the material has thickness of 1 mm and is meshed with tetrahedron elements. Single self-contact is set in the cellular material to guarantee in-plane deformation, neglecting out-plane deformation during impact process. Besides, the friction coefficient between the surfaces of rigid plate and the specimen are set as 0.

3.2 Numerical Simulation Analyses

From the results of the above simulation analysis, stress–strain curves of the impact plate for the RRS and SRS and four groups of variables are presented in Fig. 5. Among this, X axis stands for nominal strain, and Y axis demotes nominal stress.

Fig. 6
figure 6

Dynamic impact process for the selected four groups of variables with regular arrangement. a 3rd group, b 7th group, c 12th group, d 14th group

Full size image

The order of stress values \(\sigma _{12}>\sigma _{14}>\sigma _3 >\sigma _7 \) under the same strain is shown in Fig. 5 for both the RRS and SRS. This phenomenon is explained as follows. For the RRS, specific arrangements attributes to thickness coefficient \(\alpha \) and re-entrant coefficient \(\beta \). It is concluded that stress \(\sigma \) increases with the re-entrant coefficient \(\beta \) and thickness coefficient \(\alpha \).

Fig. 7
figure 7

Dynamic impact process for the four groups of variables with staggered arrangement. a 3rd group, b 7th group, c 12th group, d 14th group

Full size image
Fig. 8
figure 8

Stress–strain curves of the regular and staggered arrangements with four groups of variables. a 3rd group, b 7th group, c 12th group, d 14th group

Full size image

The local dynamic process is as follows. Fig. 6a presents the rotating phenomenon beyond the elastic stage for the third group of variables, which results in stress \(\sigma _3 \) not increasing with strain but reaching a plateau. In Fig. 6b, the thickness coefficient \(\alpha \) of the seventh group is smaller than that of the third group. There is thus a rotating phenomenon, the stress reaches a plateau, the rotation occurs earlier than that of the third group, and \(\sigma _7 <\sigma _3 \) eventually. Figure 6c shows that deformation characteristics of the 12th group are similar to those of the 14th group in that there is no obvious rotation. Stress \(\sigma _{12} \) is the highest because of the highest thickness coefficient \(\alpha \) and re-entrant coefficient \(\beta \) with the result that \(\sigma _{12} >\sigma _{14} \). The above therefore explains the relations between geometric parameters and stress \(\sigma \) for the RRS comprehensively; i.e., increases in the thickness coefficient \(\alpha \) and re-entrant coefficient \(\beta \) increase stress \(\sigma \).

For the SRS, it is clearly seen that the order of stress values is the same as that for the RRS, \(\sigma _{12}>\sigma _{14}>\sigma _3 >\sigma _7 \). The corresponding stress–strain curves and the local dynamic process shown in Fig. 7a–d reveal that the stress \(\sigma \) attributes to the starting time of rotation. As the rotation commences, the SRS starts to enter the plateau region, and it is concluded that the rotation starting time of the third group is later than that of the seventh group, which is earlier than that of the 14th group, and that of the 12th group is later than that of the 14th group. The four groups of variables have the same impact velocity and various geometric parameters, and varying the geometric parameters thus greatly affects the starting time of rotation. Changes in geometric parameters therefore affect stress \(\sigma \), and it is concluded that stress \(\sigma \) increases with re-entrant coefficient \(\beta \) and decreases with increasing thickness coefficient \(\alpha \).

Figure 8 shows the stress–strain curves obtained for the two cell arrangements. Table 2 shows the plateau stress and unit mass energy absorption of the RRS and SRS.

It is concluded that the staggered arrangement has higher plateau stress and unit mass energy absorption, which is dominated by the stress and the length of the plateau, than the regular arrangement. According to the evaluation criterion that the plateau region should have higher platform stress, the staggered arrangement has outstanding advantages over the regular arrangement. This is explained as follows. For both regular and staggered arrangements, there is a rotation phenomenon in the process of deformation, with the rotation center being exactly the center of the unit cell. The SRS comprises cells shifted a half-cellular beam length toward the center relative to the RRS. Owing to different contact patterns, point-to-point contact for the regular arrangement and edge-to-edge contact for the staggered arrangement, the arm of the force for the staggered arrangement is smaller than that for the regular arrangement. The SRS therefore needs a much larger external force than the RRS for the same deformation. The SRS is thus more stable than the RRS.

4 Effects of Impact Velocity on Dynamic Crushing Behaviors

The impact velocity is known to affect the dynamic crushing behaviors of a material. This paper only considers the commonly used impact velocities of automobiles of 5, 20, and 50 m/s. To fully determine the effects of the impact velocity on dynamic crushing behaviors, four groups of sampling points are selected for the two cell arrangement patterns as shown in Table 3.

Simulation analysis provides the corresponding stress–strain curves as shown in Fig. 9.

It is clearly seen that varying the impact velocity does not appreciably affect the stress–strain relation for each group with the same geometric parameters. This is explained in the following.

The impact velocity affects the dynamic response. Meanwhile, the dynamic responses of cellular materials are divided into three regions according to the impact velocity (with V indicating the initial impact velocity of the rigid plate). In the first region, \(V_{\mathrm{s}}>V_{\mathrm{w}} >V\) and the deformation is quasi-static. In the third region, \(V\ge V_{\mathrm{s}} \ge V_{\mathrm{w}} \) and the dynamic response area propagates the stable shock wave. In the second region, \(V_{\mathrm{s}}>V>V_{\mathrm{w}} \) and the dynamic response lies between quasi-static deformation and the static shock wave response [21, 22].

The “trapped wave” velocity was used by Honig et al to define the impact velocity [23]:

$$\begin{aligned} V_{\mathrm{w}} = \int _0^{\varepsilon _{\mathrm{w}}} c(\varepsilon )\hbox {d}\varepsilon \end{aligned}$$
(6)

where \(\varepsilon _{_{\mathrm{w}} } \) is the nominal stress representing the end of the elastic region,

$$\begin{aligned} c(\varepsilon )= & {} \sqrt{\frac{\sigma ^{{\prime }}(\varepsilon )}{\rho _0 }} \end{aligned}$$
(7)
$$\begin{aligned} \sigma ^{{\prime }}(\varepsilon )= & {} \frac{\hbox {d}\sigma }{\hbox {d}\varepsilon } \end{aligned}$$
(8)

The deformation tends to become localized with an increase in the impact velocity. The compression wave extends forward to control cell collapse in the form of a similar impact, and this kind of wave is called a “stable shock wave” [24]. The critical condition of stable shock wave propagation is expressed as

$$\begin{aligned} V\ge V_{\mathrm{s}} =\sqrt{\frac{2\sigma _0 \varepsilon _{\mathrm{d}} }{\rho _0 }} \end{aligned}$$
(9)

where \(V_{\mathrm{s}} \) is the speed of the shock wave under continuous medium transmission. Equation (9) shows that the critical shock wave speed depends on the quasi-static stress, lock strain, and initial density.

Table 2 Plateau stress and unit mass energy absorption of regular and staggered arrangements
Full size table

From the calculation, it is concluded that the selected impact velocities of 5, 20, and 50 m/s lie in the same first region; i.e., the deformation is quasi-static. For applications in the field of automotive collision, once the structure of the material is confirmed, energy absorption characteristics remain unchanged in the range of typical collision velocities; i.e., the optimal energy absorption property is achieved in all typical collision areas. This explains why the impact velocities selected slightly affect the stress for each group with the same geometric parameters.

Table 3 Four groups of sampling points selected for the two cell arrangements
Full size table
Fig. 9
figure 9

Corresponding stress–strain curves of four selected groups of variables with two cell arrangements. a 2nd and 11th groups with the regular arrangement, b 2nd and 11th groups with the staggered arrangement, c 10th and 14th groups with the regular arrangement, d 10th and 14th groups with the staggered arrangement

Full size image

5 Multi-objective Optimization

5.1 Approximate Models of the Re-entrant Squares

Approximate modeling is a method of approaching a set of design variables and response variables by establishing mathematical models based on sampling data selected in the design space. The response surface method (RSM) is a kind of approximate modeling method, which fits a response surface to simulate a real limit state surface through a series of deterministic “tests” [25]. The response surface model is usually of order 1–4. The higher the order is, the greater the fitting ability of the nonlinear model. The F test and \(R^{2}\) test are usually conducted to determine the construction precision of the response surface. The proximity of \(R^{2}\) to 1 is considered in the \(R^{2}\) test. The closer \(R^{2}\) is to 1, the more accurate the approximate model remains. Meanwhile, the approximate model approaches higher accuracy as the sum of squares for error (SSE) and root-mean-square error (RMSE) decrease. According to the selected sampling points in Table 1, the accuracy of the response surface models for the re-entrant structures with the two cell arrangements are presented in Table 4.

As is shown in Table 4, the highest power of fitting the approximate model of the regular arrangement is the same as that of the staggered arrangement, both being second order. The fitting formula of unit mass energy absorption W is obtained according to the response surface function.

Table 4 Accuracy of the response surface models for the re-entrant squares with the two cell arrangements
Full size table

For a given thickness coefficient \(\alpha \) and re-entrant coefficient \(\beta \), the unit mass energy absorption \(W_{\mathrm {regular}}\) of RRS is calculated according to

$$\begin{aligned} W_{\mathrm {regular}}= & {} -10460+209300\alpha +50640\beta \nonumber \\&+\,924800\alpha ^{2}-2513000\alpha \beta +847900\beta ^{2} \end{aligned}$$
(10)

Similarly, the unit mass energy absorption \(W_{\mathrm {staggered}} \) of the staggered arrangement is given by

$$\begin{aligned} W_{\mathrm {staggered}}= & {} (-0.1761-0.6646\alpha +5.262\beta \nonumber \\&+\,19.21\alpha ^{2}-3.313\alpha \beta -10.55\beta ^{2})\times 10^{11}\nonumber \\ \end{aligned}$$
(11)

5.2 Optimization of the SRS

As previously mentioned, the SRS has greater plateau stress and unit mass energy absorption than the RRS. Hence, in what follows, multi-objective optimization is performed for the SRS.

This work adopts a genetic algorithm, which is a kind of randomized search algorithm based on biological natural selection and a natural genetic mechanism. Genetic algorithm encodes the spaces of a problem; i.e., the problem space is mapped to the search space [26]. Selection, crossover, and mutation then occur with certain probability, producing individuals with high average fitness in each generation reserved. Finally, the individual with maximum fitness is obtained through gradual iterations and the purpose of optimization is achieved.

5.2.1 Optimization of Maximizing the Unit Mass Energy Absorption

As the re-entrant cellular material with a staggered arrangement acts as an energy absorber, it is important to maximize the unit mass energy. According to the above, unit mass energy absorption is closely related to the thickness coefficient \(\alpha \) and re-entrant coefficient \(\beta \). The corresponding optimization model is given as

$$\begin{aligned}&\hbox {Objective}:\max W_{\mathrm {staggered}} (\alpha ,\beta )\nonumber \\&\quad \hbox {s.t.}\left\{ {{\begin{array}{l} {\alpha \ge 0.05} \\ {\beta \ge 0.05} \\ {\alpha +\beta <0.5} \\ \end{array} }} \right. \end{aligned}$$
(12)

The optimization process is explained in Fig. 10. Optimal \(W_{\mathrm {staggered}} \) is obtained through 250 iterations.

Fig. 10
figure 10

Optimization of unit mass energy absorption \(W_{\mathrm {staggered}} \) for SRS

Full size image

5.2.2 Optimization of Minimizing the Relative Density

Structural lightness is important in design and manufacturing. As promising materials having a wide range of uses, re-entrant cellular materials with better performance and lower mass will be more competitive.

The optimization model for minimizing the relative density is expressed as

$$\begin{aligned}&\hbox {Objective}:\min \rho _{\mathrm {staggered}} (\alpha ,\beta ),\nonumber \\&\quad \hbox {s.t.}\left\{ {{\begin{array}{l} {\alpha \ge 0.05} \\ {\beta \ge 0.05} \\ {\alpha +\beta <0.5} \\ \end{array} }} \right. \end{aligned}$$
(13)

Figure 11 shows the specific optimization process of relative density \(\rho _{\mathrm {staggered}} \) for the SRS. It is seen that optimal \(\rho _{\mathrm {staggered}} \) is obtained through 300 iterations.

Fig. 11
figure 11

Optimization of relative density \(\rho _{\mathrm {staggered}} \) for SRS

Full size image
Table 5 Optimal results of single-objective optimization and multi-objective optimization
Full size table

5.2.3 Multi-objective Optimization Design of SRS

In general, several various design goals need to be considered in structural design at the same time. Different design goals have various requirements for design parameters. It is therefore necessary to seek a balance among various design goals. This work focuses on a multi-objective optimization design of SRS. The corresponding multi-objective optimization model is established as

$$\begin{aligned}&\hbox {Objective: }\left\{ {{\begin{array}{l} {\max W_{\mathrm {staggered}} (\alpha ,\beta )} \\ {\min \rho _{\mathrm {staggered}} (\alpha ,\beta )} \\ \end{array} }} \right. \nonumber \\&\hbox {s.t.}\left\{ {{\begin{array}{l} {\alpha \ge 0.05} \\ {\beta \ge 0.05} \\ {\alpha +\beta <0.5} \\ \end{array} }} \right. \end{aligned}$$
(14)

Here \(W_{\mathrm {staggered}} \) is the unit mass energy absorption of the SRS, \(\rho _{\mathrm {staggered}} \) is the relative density of the SRS, \(\alpha \) is the thickness coefficient, and \(\beta \) is the re-entrant coefficient.

Multiple Pareto non-inferior solutions are obtained through multi-objective genetic algorithm optimization. An evaluation function Q, also called the satisfaction function and given by the following equation, is put forward herein to seek an optimal solution. According to the definition of the satisfaction function, the solution improves as the satisfaction decreases:

$$\begin{aligned} Q=\omega _1 \frac{\left( {\rho (\alpha ,\beta )-\rho _{\min } } \right) }{(\rho _{\max } -\rho _{\min } )}+\omega _2 \frac{(W_{\max } -W(\alpha ,\beta ))}{(W_{\max } -W_{\min } )} \end{aligned}$$
(15)

where \(\rho _{\max } \) and \(\rho _{\min } \) are, respectively, the maximum and minimum relative densities in Pareto optimal solutions, \(W_{\max } \) and \(W_{\min } \) are, respectively, the maximum and minimum unit mass energy absorptions in Pareto optimal solutions, and \(\omega _1 \) and \(\omega _2 \) are, respectively, the weighting coefficients of the relative density and unit mass energy absorption.

Through the above optimization process, optimal results of single-objective optimization and multi-objective optimization are acquired, as shown in Table 5.

Table 5 shows that the unit mass energy absorption and relative density cannot achieve optimum values at the same time, whereas reasonable optimal results of both the unit mass energy absorption and relative density are expected through multi-objective optimization. Weighting coefficients \(\omega _1 \) and \(\omega _2 \) strongly affect the results of multi-objective optimization. Weighting coefficients are set according to the requirements of practical engineering. Higher \(\omega _2 \) is achieved when the re-entrant cellular structure is regarded as an energy absorber, while higher \(\omega _1 \) is obtained when the re-entrant cellular structure is considered for structural parts with higher requirements of lightness.

6 Conclusions

A new re-entrant square cellular material was proposed. In exploring the relationship between microtopology and macrodynamic responses, the finite element method was employed to investigate the effects of cell microtopology on the dynamic behavior of the material under in-plane impact loading. This paper initially developed theoretical models of relative density employing a two-dimensional unit cell in light of three geometric parameters: cell wall thickness t, cell edge length L, and re-entrant distance h. The effects of geometric features and configurations on dynamic properties were then explored. To improve the efficiency of simulation, the LHS method was used in selecting sampling points from the design space. Simulations indicate that variations in geometric parameters strongly affect properties. For both RRS and SRS, increases in the re-entrant coefficient \(\beta \) and thickness coefficient \(\alpha \) increase stress \(\sigma \). Another finding is that the SRS has higher plateau stress and unit mass energy absorption than the RRS. Subsequently, the effects of various impact velocities on dynamic crushing behaviors were illustrated. It was found that the commonly used impact velocities of automobiles lie in the quasi-static region and varying the impact velocity had only a slight effect on the dynamic crushing behaviors. On this basis, the RSM was used to obtain relations between the unit mass energy absorption and geometric features for both the RRS and SRS. Furthermore, with targets of maximum unit mass energy absorption and minimum relative density, the non-dominated sorting genetic algorithm was adopted to obtain optimal structural parameters. Meanwhile, a satisfaction function Q was proposed to select desired results from the Pareto solution set.

Analysis of the re-entrant square cellular material clarified the developed cellular material. Additionally, much of the analysis can contribute greatly to guiding design. Although the present study focused on two-dimensional cellular material, an extended analysis of three-dimensional re-entrant cellular material was carried out by identifying the dynamic processes. In future work, a systematic study of the overall performance of cellular material will be conducted by considering various boundary conditions, friction coefficients, cellular connections, and degrees of porosity. In addition, the study provides a detailed introduction to dynamic behaviors of cellular materials and guidance to design novel energy-absorbing structures with outstanding performances of energy absorption.