1 Introduction

Properties and synthesis of new isotopes have been prevalent issues in the field of nuclear physics and have attracted much attention in past years. In general, the new isotopes are produced via the fusion-evaporation reactions, fission of actinide nuclides, projectile fragmentation etc. However, the neutron-rich heavy nuclei beyond \(N = 100\) cannot be created [1, 2]. Recently, the multinucleon transfer (MNT) reactions for creating the heavy neutron-rich isotopes were proposed by Zagrebaev and Greiner [3,4,5,6]; in particular, for the neutron-rich isotopes in the reactions of \(^{136}\)Xe + \(^{208}\)Pb. It is necessary to further investigate the nuclear dynamics in the MNT reactions. Several models such as the GRAZING model [7, 8], dinuclear system (DNS) model [9,10,11], and dynamical model based on the Langevin equations [12], have been developed for describing the transfer reactions near barrier in nuclear collisions. On the experimental side, the damped collisions of two actinide nuclei were investigated at GSI for producing the superheavy nuclei (SHN) [13,14,15]. Recently, attempts to produce the neutron-rich nuclei around \(N = 126\) have been made in the reactions of \(^{136}\hbox {Xe }+^{208}\hbox {Pb}\) [16, 17] and \(^{136}\hbox {Xe }+ ^{198}\hbox {Pt}\) [18]. It was found that the shell closure plays an important role in the production of neutron-rich nuclei and MNT reactions show greater advantages than fusion or projectile fragmentation reactions in the region of heavy neutron-rich nuclei [1, 19]. Production of neutron-rich heavy and superheavy isotopes via the MNT reactions is also planned at the new facility of high-intense heavy-ion accelerator (HIAF) in Huizhou.

In this work, the dynamics of MNT reactions during the collision of two heavy nuclei is investigated with the DNS model. This article is organized as follows. In Sect. 2, we give a brief description of the DNS model. The nuclear dynamics is discussed in Sect. 3. Summary and perspective on mass-kinetic energy and dissipated kinetic energy distributions, yields distributions, and angular distributions are presented in Sect. 4.

2 The DNS model

In the DNS model, nucleon transfer is coupled to the relative motion on solving a set of microscopically derived master equations by distinguishing protons and neutrons [20,21,22]. The time evolution of the distribution probability \(P(Z_1,N_1,E_1,t)\) for a DNS fragment 1 with proton number \(Z_1\), neutron number \(N_1\), and with excitation energy \(E_1\) is governed by the master equations as follows:

$$\begin{aligned} \frac{{\mathrm {d}} P(Z_1,N_1,E_1,t)}{{\mathrm {d}} t} &= \sum _{Z'_1} W_{Z_1,N_1;Z'_1,N_1,}(t) \left[ d_{Z_1,N_1}P(Z'_1,N_1,E'_1,t) \right. \nonumber \\&\qquad \left. -\,d_{Z'_1,N_1}P(Z_1,N_1,E_1,t)\right] \nonumber \\&\quad + \sum _{N'_1} W_{Z_1,N_1;Z_1,N'_1,}(t) \left[ d_{Z_1,N_1}P(Z_1,N'_1,E'_1,t) \right. \nonumber \\&\qquad \left. -\,d_{Z_1,N'_1}P(Z_1,N_1,E_1,t)\right] . \end{aligned}$$
(1)

where \(W_{Z_1,N_1;Z'_1,N_1} (W_{Z_1,N_1;Z_1,N'_1})\) is the mean transition probability from the channel (\(Z_1,N_1,E_1\)) to (\(Z'_1, N_1, E'_1\)) ((\(Z_1,N_1,E_1\)) to (\(Z_1,N'_1,E'_1\))), and \(d_{Z_1,N_1}\) denotes the microscopic dimension corresponding to the macroscopic state (\(Z_1,N_1,E_1\)). Sequential nucleon transfer is considered in the model with there lation of \(Z'_1 = Z_1\pm 1\) and \(N'_1 = N_1\pm 1\). The transition probability is related to the local excitation energy and nucleon transfer, which is microscopically derived from the interaction potential in valence space as follows.

$$\begin{aligned} W_{Z_1,N_1;Z'_1,N_1,} &= \frac{\tau _{\text {mem}}(Z_1,N_1,E_1; Z'_1,N_1, E'_1)}{d_{Z_1, N_1}d_{Z'_1, N_1} \hbar ^2 } \nonumber \\&\quad \times \,\sum _{ii'} \left| \langle Z'_1, N_1, E'_1, i' |V| Z_1, N_1, E_1, i\rangle \right| ^2. \end{aligned}$$
(2)

The formula is similar for neutron transition coefficients. The relaxation time is evaluated by the deflection function method, typically having a value of several hundred \(\times \, 10 ^{-22}\,\hbox {s}\).

The local excitation energy \(E_1\) is determined from the dissipation energy originating from the relative motion and the potential energy surface of the DNS. The dissipation of the relative motion and angular momentum of the DNS is described by the Fokker–Planck equation [23, 24]. The energy dissipated into the DNS is expressed as follows.

$$\begin{aligned} E^{\text {diss}}(t) &= E_{\text {c.m.}} - B - \frac{\langle J(t)\rangle [\langle J(t)\rangle +1]\hbar ^2}{2\zeta } \nonumber \\&\quad -\,\langle E_{\text {rad}}(J,t)\rangle , \end{aligned}$$
(3)

where \(E_{\text {c.m.}}\) and B are the center of mass energy and Coulomb barrier, respectively. The radial energy is evaluated from

$$\begin{aligned} \langle E_{\text {rad}}(J,t)\rangle = E_{\text {rad}}(J,0) \exp {(-t/ \tau _{\text {r}})}. \end{aligned}$$
(4)

The relaxation time of the radial motion and the radial energy at the initial state are given by \(\tau _r= 5 \times 10^{-22}\hbox { s}\) and \(E_{\text {rad}}(J,0) = E_{\text {c.m.}} - B - J_i(J_i +1) \hbar ^2 / (2 \zeta _{\text {rel}})\), respectively. The dissipation of the relative angular momentum is described by the following expression.

$$\begin{aligned} \langle J(t)\rangle = J_{\text {st}} +(J_i - J_{\text {st}}) \exp (-t/ \tau _J). \end{aligned}$$
(5)

The angular momentum at the sticking limit is \(J_{\mathrm{st}} = J_i \zeta _{\text {rel}}/ \zeta _{\text {tot}}\) and the relaxation time is \(\tau _J = 15 \times 10^{-22}\) s. The \(\zeta _{\text {rel}}\) and \(\zeta _{\text {tot}}\) are the relative and total moments of inertia of the DNS, respectively. The initial angular momentum is set to be \(J_i = J\) in this work. In the relaxation process of relative motion, the DNS will be excited by the dissipation of the relative kinetic energy. The local excitation energy is determined from the excitation energy of the composite system and the potential energy surface of the DNS.

The cross sections of the primary fragments (\(Z_1\), \(N_1\)) after the DNS reaches the relaxation balance are calculated as follows.

$$\begin{aligned} \sigma _{\text {pr}} (Z_1, N_1, E_{\text {c.m.}}) &= \sum ^{J_{\text {max}}} _{J=0} \sigma _{\text {cap}}(E_{{\mathrm{c.m.}}, J}) \int f(B) \nonumber \\&\quad \times \,P(Z_1, N_1, E_1, B) {\mathrm {d}}B. \end{aligned}$$
(6)

The maximal angular momentum \(J_{\text {max}}\) is taken as that at the grazing collisions. The capture cross section is evaluated using the expression \(\sigma _{\text {cap}} = \pi \hbar ^2 (2J +1)/ (2\mu E_{\text {c.m.}})\,T(E_{\text {c.m.}}, J)\). \(T(E_{\text {c.m.}}, J)\) is the transmission probability of the two colliding nuclei overcoming the Coulomb barrier to form a DNS and is calculated using the method reported in Refs. [20,21,22]. For heavy systems, we directly use the Hill-Wheeler formula [25] with the barrier at the touching configuration. The barrier distribution function is taken as the Gaussian form of \(f (B) = \frac{1}{N} \exp {-[(B - B_{\text {m}})/ ]2}\) with the normalization constant satisfying the unity relation \(\int f(B) {\mathrm {d}}B = 1\). The quantities \(B_{\rm m}\) and \(\Delta\) are evaluated by \(B_{\text {m}} = (B_{\text {C}} + B_{\text {S}} )/2\) and \(\Delta = (B_{\text {C}} - B_{\text {S}} ) /2\), respectively. Here, \(B_{\rm C}\) and \(B_{\rm S}\) are the Coulomb barriers at waist to waist orientation and the minimum barrier on varying the quadrupole deformation parameters of colliding partners, respectively. The survived fragments are the decay products of the primary fragments after emitting the particles and \(\gamma\) rays in competition with fission [26]. The cross sections of the survived fragments are given by \(\sigma _{\text {sur}} = \sigma _{\text {pr}} \times W_{\text {sur}}(E_1, J_1, s)\).

The total kinetic energy (TKE) of the primary fragment is evaluated using the following expression.

$$\begin{aligned} \hbox {TKE} = E_{\text {c.m.}} + Q_{\text {gg}} - E^{\text {diss}}, \end{aligned}$$
(7)

where \(Q_{\text {gg}} = M_{\text {P}} + M_{\text {T}} - M_{\text {PLF}} -M_{\text {TLF}}\) and \(E_{\text {c.m.}}\) is the incident energy in the center of mass frame. The mass \(M_{\text {P}}\), \(M_{\text {T}}\), \(M_{\text {PLF}}\), and \(M_{\text {TLF}}\) correspond to projectile, target, projectile-like fragment, and target-like fragment, respectively. The total kinetic energy loss (TKEL) is given by \(\hbox {TKEL} = E_{\text {c.m.}} - \hbox {TKE}\). The TKE and TKEL manifest the dynamical and structure information in the MNT reactions.

The emission angle of the reaction products is helpful for arranging detectors in experiments. We use a deflection function method to evaluate the fragment angle, which is related to the mass of fragment, angular momentum, and incident energy. The deflection angle is composed of the Coulomb and nuclear interactions as given below.

$$\begin{aligned} \Theta (l_i) = \Theta (l_i)_{\text {C}}+\Theta (l_i)_{\text {N}} \end{aligned}$$
(8)

The Coulomb deflection function is given by the Rutherford function. The nuclear deflection function is given by the following expression.

$$\begin{aligned} \Theta (l_i)_{\text {N}} = \beta \Theta (l_i)_{\text {C}}^{\text {gr}} \frac{l_i}{l_{\text {gr}}} \left( \frac{\delta }{\beta }\right) ^{l_i / l_{\text {gr}}}, \end{aligned}$$
(9)

where \(\Theta _{\text {C}}^{\text {gr}}\) is the Coulomb scattering angle at the grazing angular momentum \(l_{\text {gr}}\). \(l_{\text {gr}} = 0.22R_{\text {int}}[A_{\text {red}}(E-V(R_{\text {red}}))]^{1/2}\). \(R_{\text {int}}\), \(A_{\text {red}}\), and \(V(R_{\text {int}})\) are radii of interaction, reduced mass of projectile and target, and interaction potential, respectively. The \(\delta\) and \(\beta\) are parameterized as follows.

$$\begin{aligned} \beta = \left\{ \begin{array}{ll} 75 f(\eta ) + 15, &{} \quad \eta <375 \\ 36 \exp (-2.17\times 10 ^{-3} \eta ), &{} \quad \eta \ge 375\\ \end{array}\right. \end{aligned}$$
(10)
$$\begin{aligned} \delta = \left\{ \begin{array}{ll} 0.07 f(\eta ) + 0.11, &{}\quad \eta <375 \\ 0.117 \exp (-1.34\times 10 ^{-4} \eta ), &{}\quad \eta \ge 375 \end{array}\right. \end{aligned}$$
(11)

and

$$\begin{aligned} f(\eta ) = \left[ 1 + \exp {\frac{\eta -235}{32}}\right] ^{-1}, \end{aligned}$$
(12)

where \(\eta = \frac{Z_1Z_2e^2}{\upsilon }\) and \(\upsilon = \sqrt{\frac{2}{A_{\text {red}}}(E_{\text {CM}})-V(R_{\text {int}})}\). Based on cross section of the primary fragment formula (6) and fluctuation equation (8), angular distribution is plotted in Fig. 4.

3 Results and discussion

Fig. 1
figure 1

(Color online) Total kinetic energy distributions of the primary binary fragments in the reaction of \(^{136}\hbox {Xe }+ ^{208}\hbox {Pb}\) at the center of mass energies of 423, 526, and 617 MeV, respectively

Full size image

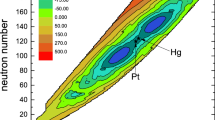
Within the DNS model, we have investigated the shell effect, isospin diffusion, and new isotope production in the MNT reactions [27,28,29]. In this work, nuclear dynamics in MNT reactions will be explored for the reaction \(^{136}\)Xe + \(^{208}\)Pb. Dissipated kinetic energy in a compound system is a crucial signal to explore the dynamical process. Hence, it is vital to calculate the kinetic energy spectra of primary fragment. The correlation of the fragment mass and TKE of primary binary fragments were calculated in the energy range around the Coulomb barrier (\(V_{\text {C}}\) = 435 MeV) to well above it and are shown in Fig. 1. Panels (a), (b), and (c) correspond to the energies of 617, 526, and 423 MeV, respectively. The structure of the calculated TKE is similar to the experimental data from Dubna [16]. More kinetic energy is dissipated with increasing beam energy and the distribution becomes broad. Moreover, the relaxation time influences the TKE structure, which is evaluated using the deflection function method for two colliding partners. It needs enough local excitation energy to overcome the PES for dissipating motion energy and transferring more nucleons. Figure 2 shows the distribution of TKEL. TKEL is related to the magnitude of energy dissipation due to the relative motion and excitation of the DNS. Higher TKEL is favorable for nucleon transfer away from the project or target nuclide.

Fig. 2
figure 2

The same as in Fig. 1, but the total kinetic energy loss

Full size image

The primary fragment yields were calculated and are shown in Fig. 3. These were compared with experimental data [16]. Two-humped shapes around the projectile and target-like fragments appear because of the quasi-elastic scattering. We calculated the primary fragments with tip–tip collisions and without deformation effects. The target-like fragment with a small peak around a mass number of 238 was obtained with a cross section of the 0.03 mb in the reaction for \(E = 526\) MeV, which implies that 30 nucleons are getting transferred from the projectile to target. Good agreement of the yields between calculations and experimental data in the symmetric region is observed from our previous calculation [29, 30]. Noticeably, the primary fragments are excited and will be decayed by evaporating particles and binary fission. The yields of the secondary fragments are reduced after the statistical decay process. The isospin relaxation dynamics dominates the isotope structure in the MNT reactions. The neutron shell closure is available for stabilizing the heavy neutron-rich nuclei. More degrees of freedom in the dissipation dynamics need to be implemented, i.e., the shape evolution, neck dynamics etc. These studies are in progress.

Fig. 3
figure 3

Primary fragment cross sections as a function of mass number in the reaction of \(^{136}\)Xe + \(^{208}\)Pb at the center of mass energies of 526 and 617 MeV, respectively. Circles with error bars are experimental data from Dubna [16]

Full size image
Fig. 4
figure 4

(Color online) Laboratory angular distributions of the Xe-like reaction products (top panel) and the Pb-like products (bottom panel)

Full size image

The emission angles provide the information of the kinematics of fragments in the MNT reactions. Accurate estimation of angular distributions is helpful for positioning detectors in experiments. Figure 4 shows the angular distributions of projector-like fragments (PLFs) and target-like fragments (TLFs) in the damped collisions. The PLFs tend to be created in the forward direction on increasing the beam energy. Opposite trends are found for the production of TLFs. A wider angular distribution for fragment formation in the MNT reactions is obtained as compared to that with the fusion reactions. The fragment angle is related to the incident energy and the emission source, i.e., the maximal cross section for TLFs located around \(48^ \circ\) at the beam energy of 870 MeV \((E_{\text {c.m.}} = 526\hbox { MeV})\). The trends are consistent with the experimental data from Dubna [16].

4 Conclusion

In summary, the MNT reaction mechanism in collisions of \(^{136}\hbox {Xe}\) on \(^{208}\hbox {Pb}\) near barrier energies has been investigated within the framework of the DNS model. The primary fragments are distributed in the broad energy range and the effect is more pronounced with increasing beam energy. Correlation of TKE and fragment mass manifests that the shell effect is of importance in producing the neutron-rich nuclei, especially for tip–tip collision. One expects cooling the excited heavy neutron-rich isotopes around the neutron shell closure. The MNT reactions are thus able to produce heavy neutron-rich nuclei, e.g., the cross section of 30 nucleons transferred from projectile to target being roughly 0.03 mb. The fragments tend to be formed in the forward range. The emission angle depends on the beam energy.