Elastic buckling loads of partially embedded piles in cohesive soil

Abstract

Buckling of piles may play an important role in the pile’s design especially for piles that are partially embedded in soil or when the upper layers of the fully embedded piles are loose or weak soils. In this paper, the elastic stability of partially embedded piles subjected to axial force is developed considering all the parameters that may be affecting the buckling load. These parameters are the ratio of the embedded length to the pile length, the elastic modulus of the soil, the pile overall length, and the flexural stiffness of pile that represents the cross section of the pile and its material. Both of the methods of finite element and the minimum potential energy are performed to obtain the buckling loads and then the effective length of the considered pile. The soil is considered as a continuous elastic medium that is replaced by many equally spaced elastic supports of equal rigidity in the finite element modelling. The numerical results are presented in charts to clarify the effect of each parameter on the effective length coefficient of the considered piles. The results of the coefficient of effective length that obtained by the energy technique and the finite element method are also compared in this paper.

Introduction

Piles are slender structural elements subjected to mainly axial forces that are used to transmit the structures loads to the strong deeper layers of soils. The buckling behaviour of piles may play the important role in the piles design especially piles subjected to heavy loads and partially embedded in soil or when the upper soil layers of the fully embedded piles are loose or weak soils. Most of the piles are fully embedded in soils as in buildings construction. In some practical cases, as in bridges and temporary bridges, the piles may be partially embedded in soils. Also, the fully embedded piles may be considered as partially embedded when the effect of the upper weak layers is neglected.

Many theoretical and experimental studies are performed to study the buckling behaviour of the fully and partially embedded piles. Some of these studies focus mainly on geotechnical aspects and other studies concern on structural part of considered piles as columns.

Terzaghi [1] recommended that the horizontal subgrade modulus can be assumed constant with depth for cohesive soils and linearly increased with depth for cohesionless soils.

The governing differential equation for buckling deflection is used by Davission and Robinson [3] to estimate the buckling loads of axially loaded piles. Partially embedded piles were treated in this case as free-standing columns with fixed bases.

Heelis et al. [4] proposed an analytical solution for predicting the buckling loads of fully and partially embedded piles and compared it with previous analyses of the problem and with tests on real structures. The proposed solution showed good agreement with compared data.

Buckling loads for the first three modes of both ends simply supported partially embedded piles are calculated by Seval and Hikmet [5]. They used the differential transform method (DTM) to solve the fourth order differential equations of both regions.

Khodair and Hassiotis [6] conducted a parametric study numerically to study the effect of the stiffness of the soil surrounding the pile, the pile length, and the pile end conditions. The result indicates that increasing the stiffness of the soil surrounding the pile is more effective in increasing the critical buckling loads of a single pile. Also, the results indicated that the critical buckling load of a single pile is more sensitive to the change in its length.

Kumar et al. [7] studied the buckling capacity of the partially embedded reinforced concrete piles under eccentricity considering the surrounding soil is sand.

Numerical analysis of buckling behaviour of concrete piles subjected to axial loads and partially embedded in sand is investigated by Jesmani et al. [8]. Also, finite element analysis is performed by Shatri et al. [9] to study the fully embedded piles in ground.

Lu and Zhao [10] developed an equation to calculate the length for buckling stability of steel partially embedded pipe pile. The equation is derived based on energy method and variation principles, where the form of the pile end condition was simplified as bottom fixing and top free.

A numerical study on the stability of piles end-bearing in soft soil subjected to axial loads is achieved by El Kamash and El Naggar [11]. The results indicated that the flexural stiffness of the pile should match with the stiffness of the soil to avoid large lateral displacement of the pile.

The major aim of the present paper is the determination of the effective buckling length (i.e. the critical load) of the partially embedded piles taking into consideration all the parameters that may affect the buckling behaviour of the considered piles. These parameters are the soil stiffness and the pile dimensions and properties (the embedded length, the pile overall length, and the flexural stiffness).

Model and assumptions

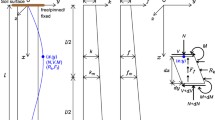
Consider a slender pile with specific length L subjected to axial load (P) at the top, and the pile considered pinned in the top and bottom. As shown in Fig. 1, the pile is assumed partially embedded where the unsupported length is L_un and the embedded length assumed as ratio to the unsupported length of the pile (α L_un). The soil is represented by continuous lateral elastic medium where the soil stiffness is K_s.

Fig. 1

Partially embedded pile: a actual partially embedded pile; b idealization of soil modulus considered constant within the depth

Methods of analysis

Energy approach

The deflection function of the buckled column under study can be taken in the form of the following trigonometric series (see [2]):

$$y = \sum\limits_{m = 1}^{\infty } {C_{m} \sin \frac{{m{\kern 1pt} \pi x}}{L}}$$

(1)

where C_m are the unknown constants to be determined.

The total strain energy, U, of the compressed piles is the summation of the strain energy of bending of the pile U₁ and the strain energy of the lateral reaction of the soil U₂.

Firstly, the strain energy of bending U₁ can be determined as follows

$$U_{1} = \frac{EI}{2}\int_{0}^{L} {\;\frac{{\,{\text{d}}^{2} {\kern 1pt} y\,}}{{{\text{d}}\,x^{2} }}\;} {\text{d}}x = \frac{{\,\pi^{4} EI\,}}{{4L^{3} }}\sum\limits_{m\; = 1}^{\infty } {\,m^{4} } \,C_{m}^{2}$$

(2)

Where E is the modulus of elasticity of the pile material and I is the moment of inertia of the pile cross section.

The lateral reaction on an element dx of the compressed element is (K_s·y·dx), and the corresponding energy is (K_s·y²/2dx). Then, the total energy of the elastic medium U₂ is

$$U_{2} = \frac{{\,K_{\text{s}} \,}}{2}\;\int_{0}^{{\alpha_{1} \;L}} {\;y^{2} \;} {\text{d}}x$$

(3)

Where α₁ is the ratio of the embedded length to the overall length of the pile = (α/α +1).

Substituting Eq. (1) in Eq. (3),

$$U_{2} = \frac{{K_{s\;} L}}{4}\left[ {\sum\limits_{m = 1}^{\infty } {\;C_{m}^{2} \,(} \alpha_{1} - S_{2m} ) + 2\sum\limits_{i = 1}^{m - 1} {\;\sum\limits_{j = i + 1}^{m} {\;C_{i} \;C_{j} } \,(S_{j - i} \, + S_{j + i} )} } \right]$$

(4)

Also, the work, T, done by the compressive force P is

$$T\,\, = \,\,\frac{\,P\,}{2}\,\,\int\limits_{0}^{l} {\,\left( {\frac{{{\text{d}}y}}{{{\text{d}}x}}} \right)^{2} \,} {\text{d}}{\kern 1pt} x = \frac{{P\pi^{2} }}{4L}\sum\limits_{m\; = 1}^{\infty } {m^{2} \,} C_{m}^{2}$$

(5)

Then the total energy (V) of the system is:

$$V\,\, = \,(\,U_{1} + U_{2} ) - T$$

(6)

Substituting Eqs. (2, 4, and 5) into Eq. (6),

$$V = \frac{{\pi^{4} EI}}{{4L^{3} }}\sum\limits_{m\; = 1}^{\infty } {m^{4} } C_{m}^{2} + \frac{{K_{s\,} L}}{4}\left[ {\sum\limits_{m = 1}^{\infty } {\;C_{m}^{2} \,(} \alpha_{1} - S_{2m} ) + 2\sum\limits_{i = 1}^{m - 1} {\;\sum\limits_{j = i + 1}^{m} {\;C_{i} \;C_{j} } \,(S_{j - i} \, + S_{j + i} )} } \right] \, - \frac{{P\pi^{2} }}{4L}\sum\limits_{m\; = 1}^{\infty } {m^{2} \,} C_{m}^{2}$$

(7)

This is a function of second degree with coefficients C₁, C₂, …..C_m. These coefficients must be chosen so as to make the total energy (V) a minimum, from which it follows that

$$\frac{\partial V}{{\partial C_{1} }} = 0\quad \frac{\partial V}{{\partial C_{2} }} = 0\quad \cdots \quad \frac{\partial V}{{\partial C_{m} }} = 0$$

(8)

This minimization procedure yields m homogeneous linear equations in C₁, C₂, …, Cm, which can be put in the following form

$$\left[ K \right]\;\;\left\{ {C} \right\}\; = \;\left\{ {0} \right\}$$

(9)

In which $\left\{ {C} \right\} = \left\{ {C_{1} , \, C_{2} , \, \ldots , \, C_{m} \, } \right\}^{T}$ and the (m × m) coefficient matrix [K] will be

$$\left[ K \right]\; = \;\left[ {k_{ij} } \right]_{mxm}$$

(10)

Where

$$k_{ii} = \frac{{\pi^{4} EI}}{{2L^{3} }}\;i^{4} + \frac{{K_{s\,} L\,}}{2}(\alpha - S_{2m} ) - \frac{{P\pi^{2} }}{2L}\;i^{2} \quad {\text{for }}i = j,$$

$$k_{ij} = \frac{{K_{s\;} L\,}}{2}(S_{j - i} - S_{j + i} )\quad {\text{for }}i \ne j,\quad i \prec j$$

$$k_{ij} = \frac{{K_{s\;} L\,}}{2}(S_{i - j} - S_{j + i} )\quad {\text{for }}i \ne j,\quad j \prec i$$

These equations will be satisfied by putting C₁, C₂,…, C_m equal to zero, which corresponds to the ideal compressive member. For a nontrivial solution, the buckling load of the compressive element can be obtained by equating to zero the determinate of [K]. By selecting the number of trigonometric series (m), the end compressive force P will be gradually increasing until arriving a value for which one of the coefficients C₁, C₂,…, C_m becomes infinity. The smallest of these values of P is called the end critical value corresponding to the assumed parameters. This method of calculating the critical buckling load brings us to a closer and closer approximation as the number (m) of the terms of the deflection function series given in Eq. (3) increases, and by taking (m) infinitely large, we obtain an exact solution.

Finite element method

Also, finite element method is applied to the considered piles modelling the soil as lateral elastic springs as shown in Fig. 1b.

Assuming different values for the main parameter considered in this study (the flexural rigidity EI, the unsupported length, ratio of the embedded length α, and the soil stiffness), the considered pile is modelled as a three-dimensional frame element as shown in Fig. 1b with very large number of elements (maximum length of segments in the column length direction is 0.01 m). The buckling load for each particular case is determined using SAP2000 software based on finite element method.

To describe the buckling behaviour of the considered piles, mode shapes for some cases of piles (α = 1.5) are shown in Fig. 2.

Fig. 2

Buckling shape of the partially embedded piles with different soil stiffness according to SAP2000 program based on finite element method

Generally, the critical buckling load P_cr for the axially compressed elements can be written in the following general form

$$P_{cr} \, = \;\frac{{\pi^{2} \;E\;I}}{{\left( {\beta \,L} \right)^{2} }} \,$$

(11)

Where β is the effective length coefficient that depends on the parameters discussed before.

Results and discussions

Figures 3, 4, 5 show the relations between the effective length coefficient and the ratio of embedded length to the unsupported length of pile for different practical values of flexural stiffness of pile, and soil stiffness considering the unsupported length L_un of the pile = 3.0, 4.0, and 5.0 ms respectively.

Fig. 3

Buckling load coefficient of partially embedded piles (L_un = 3.0 m); a soil stiffness K_s = 100 t/m², b soil stiffness K_s = 300 t/m², c soil stiffness K_s = 500 t/m², d soil stiffness K_s = 1000 t/m²

Fig. 4

Buckling load coefficient of partially embedded piles (L_un = 4.0 m); a soil stiffness K_s = 100 t/m², b soil stiffness K_s = 300 t/m², c soil stiffness K_s = 500 t/m², d soil stiffness K_s = 1000 t/m²

Fig. 5

Buckling load coefficient of partially embedded piles (L_un = 5.0 m); a soil stiffness K_s = 100 t/m², b Soil stiffness K_s = 300 t/m², c soil stiffness K_s = 500 t/m², d soil stiffness K_s = 1000 t/m²

Generally, from the previous figures, we can draw the following notes:

• As expected, the effective length coefficient decreases with the increasing of the embedded length ratio and the decreases are not pronounced if the embedded length ratio α is greater than two. Also, the effective length coefficient decreases with the increasing of the soil stiffness.

• The effective length coefficient increases with the increasing of the flexural stiffness of the pile, and this effect is reducing with the soil stiffness increasing.

From the theoretical analysis introduced in this paper, it is important to notice that the effective length coefficient depends on the unsupported length of the pile (in other words the overall length) where the effective length coefficient decreases with the increasing of the unsupported length.

The obtained charts cover the practical values of all the parameters may affect in the effective length coefficient (i.e. the buckling loads). From these charts, the effective length coefficient can be directly determined.

Where fully embedded piles can be considered particular cases of the partially embedded piles, the effective length coefficient of fully embedded piles can be determined by applying the same methods that are discussed before considering the unsupported length equal to zero (L_un = 0). Figure 6 shows the relations between the effective length coefficient and the length of the fully embedded piles for different practical values of flexural stiffness of piles and soil stiffness.

Fig. 6

Buckling load coefficient of fully embedded piles (L_un = 0.0 m); a Soil stiffness K_s = 100 t/m², b soil stiffness K_s = 300 t/m², c Soil stiffness K_s = 500 t/m², d soil stiffness K_s = 1000 t/m²

Validation of the proposed approach

To compare the results obtained by both the energy approach and the finite element method, Table 1 shows the percentage of difference between the effective length coefficient that obtained by these methods for the partially embedded piles considering as an example of the results the embedded length ratio α = 1.50 and the unsupported length = 4.0 ms. In the energy method, the values of the effective length coefficient β were obtained assuming the number of trigonometric series terms equals to eight (m = 8).

Table 1 Comparison of effective length coefficient of partially embedded piles β obtained by energy approach and finite element method subjected to axial load (α = 1.5, L_un = 4.0 ms)

It is obvious from this table that the results of the energy approach are very close to the finite element method results.

Table 2 shows the comparison of results obtained from this study with the numerical results solved by Seval and Hikmet [5]. The critical buckling loads of the considered piles in Seval and Hikmet [5] are determined by solving the fourth order differential equations of both regions using differential transform method (DTM) and analytical method.

Table 2 Comparison of the effective length coefficient of partially embedded piles β obtained by the present work (P. W.) with the numerical examples solved by Seval and Hikmet [5] using DTM

Based on the result tabulated in Table 2, the difference between the results of the present work and DTM method ranges is not exceed 3.30% while the used methods are introduced in simple manner compared with the numerical solution of the fourth order differential equations.

Conclusions

The stability problem of partially embedded piles subjected to end axial loads is presented in this paper using both of the finite element method and the energy approach. These methods of analysis are introduced in general and simple methodology for the predicting of the effective length of the partially or fully embedded piles that can be simply used by design engineers. The effective length for partially embedded piles can be simply determined by applying the resulted equations from the energy method using spread sheet programs or obtained by software modelling based on finite element method.

The results obtained from this study are introduced in many curves to describe the relation between the effective length coefficient and the different parameters that may affect in the buckling length, and these curves can be used directly by design engineers.

From these study and results, the effective length coefficient is inversely proportional with the ratio of embedded length to the overall length of pile, the unsupported length, and the soil stiffness but directly proportional to flexural stiffness of the piles.

Generally, the effective length coefficient can be obtained from the resulted charts or determined numerically for each particular case using one of the methods presented in this paper.