1 Introduction

Estimation of the bearing capacity of piles has been always a challenging issue for geotechnical engineers due to inherently complex behavior of soil, relatively long length extending into a variety of soil layers, deep embedment depth and soil–pile interaction. There are several different methods to estimate the bearing capacity of piles: (a) static analysis methods, (b) direct and indirect use of in situ test results, (c) static load test and (d) dynamic methods [1, 2].

Studies show that the bearing capacity may be far different from the reality if the deformations are neglected [3]. In addition, unless under ideal conditions, such as a rigid-perfectly plastic materials, there is no precise and unique definition of limit load for footings and piles. As a consequence, the bearing capacity and load–displacement analysis should be accomplished simultaneously, or, in other words, the first should be determined from the second. The load–displacement behavior of piles is often obtained by conducting a pile load test which is very costly and time consuming; or by complicated finite element modeling, which in turn requires a great deal of effort to properly define the soil properties to be considered in the analysis. There are also some simplified methods primarily based on statistical observations (\(t - \zeta\) and \(q - \zeta\) curves) which are only rough estimates to obtain satisfactory results.

In this study, a semi-analytical method with a theoretical basis based on a universally accepted and commonly used field test (cone penetration test, CPT) has been proposed. For this purpose, the CPT data, as a very useful tool due to its repeatability, accuracy and continuity of the records [4, 5] has been employed. The procedure comprises three different ingredients. First, a displacement field is constructed based on an adopted failure mechanism and fundamental requirements of the limit analysis. Then, the strain field is calculated which is nothing but the symmetric part of the gradient of the displacement field. Finally, the soil shear strength is assumed to be a function of the maximum shear strain and the residual shear resistance of the soil which is a legitimate assumption. This relationship can be found by direct and/or indirect use of CPT data based on which, the residual shear strength of the soil can be found. The strain field is then updated by further penetration of the pile into the soil and as a consequence, the stress field and the boundary load at the pile tip will be calculated. This procedure will provide a complete load–displacement curve of the pile. The results are verified with experimental data obtained from pile load test data available in the literature. In addition, further comparisons have been made with various methods based on the cone penetration test (CPT) data.

In what comes next, a brief review of the theory behind the procedure and a literature review is presented and afterwards, the procedure will be explained in detail with numerical results and comparisons.

2 Behind the Theory

2.1 Bearing Capacity of Driven Piles by CPT Records

In view of the wide range of methods and equipments now available in regard with the analysis, design and construction of deep foundations, a thorough geotechnical study is very reliable and nowadays, at hand, for most engineering projects. They also obviate any further need for laboratory tests which are often conducted on disturbed samples from discrete locations. In particular when a deep foundation is analyzed, in situ tests can be much efficiently used to perform a precise analysis. Among many in situ tests developed in the recent years, CPT resembles a pile under axial load which can be used as a model pile for both analysis and design [6, 7]. The CPT is basically developed for soft clays [8] and its application in very compacted sand and coarsely granular materials is limited. However, it can be used in loose to medium sands as well as most fine sands [9], which is the target soil in this paper.

The studies on the actual cases show that the toe and shaft resistance of piles are not the exact values of tip and sleeve resistances recorded by CPT, due to the scale differences between pile and CPT and also the stress level. The scale effects include the geometry, the rate of pile and CPT penetration in soil. The stress level is also a consequence of scale and the level of transmitted loads from the pile to the surrounding soil. Consequently, the deformation generated in soil in effect of CPT penetration is much higher than the one in effect of pile penetration. The soil fails during CPT penetration, however, it may not occur during the pile driving. As a result, the mobilized resistance along the CPT and the pile is different which is not considered in current CPT-based methods.

In this study, an analytical–numerical study has been conducted to estimate the bearing capacity and axial load–displacement behavior of driven piles in granular soils using CPT records. The ingredients of the computational procedure and assumptions behind it are presented in the next sections.

2.2 Stress Characteristics Method

The method of stress characteristics or the slip lines method is known as a standard method in solving some plasticity or stabilty problems in soils, which is often attributed to Sokolovski during 1960s [10]. This method was then developed and applied to many problems such as the complex bearing problem and extended to a variety of considerations. Among them, Martin and Houlsby [11] applied the slip line method for the bearing capacity estimation of the spudcan foundations under combined loading. Kumar [12] used the stress characteristics method to investigate the effect of footing roughness on the bearing capacity of foundations. Veiskarami et al. [13] implemented the slip line method to analyze the end-bearing capacity of driven piles in sands. Recently, Veiskarami et al. [14, 15] studied the effect of flow rule on the bearing capacity of strip foundations on sand by a new method composed of the stress characteristics together with the kinematic approach of the upper-bound limit analysis. These latter contributions are important as they are central to finding the displacement field of the current research.

The bearing capacity of foundations can be obtained by this method where both the equilibrium and yield equations are satisfied along the so-called slip line directions, simultaneously. Since these equations are transformed into ordinary differential equations along the slip lines, this method was also given the name of the “method of stress characteristics”.

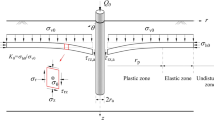
The Mohr stress circle is a useful graphical tool to visualize the characteristics directions. The finite difference method can be used to solve these equations simultaneously which has been well-described in the literature [16, 17]. The equilibrium equations, in absence of lateral body forces, in cylindrical coordinates system, with axial symmetry, in terms of coordinates, \(r\), \(\theta\) and \(z\), which are shown in Fig. 1, can be written as follows:

$$\left\{ {\begin{array}{*{20}{c}} {\frac{{\partial {\sigma _r}}}{{\partial r}}+\frac{{\partial {\tau _{rz}}}}{{\partial z}}+\frac{{{\sigma _r} - {\sigma _\theta }}}{r}=0} \\ {\frac{{\partial {\sigma _z}}}{{\partial z}}+\frac{{\partial {\tau _{rz}}}}{{\partial r}}+\frac{{{\tau _{rz}}}}{r}=\rho {\gamma _{\text{w}}}} \end{array}} \right.$$
(1)

where \({\sigma _r}\), \({\sigma _z}\), \({\sigma _\theta }\) and \({\tau _{rz}}\) are components of stress tensor, \(\rho {\gamma _{\text{w}}}\) is the body force along the \(z\) direction. According to Larkin [18] the direction of the major principal stress with \(z\) direction, is denoted by an angle \(\psi\) and the mean stress by \(\sigma\). Employing the Mohr–Coulomb yield criterion, i.e., \(\tau =\sigma \tan \phi +c\), with \(c\) and \(\phi\) as soil shear strength parameters, the stress state can be fully defined as follows [16]:

$${\sigma _r}=\sigma \left( {1 - \sin \phi \cos 2\psi } \right)$$
(2a)
$${\sigma _z}=\sigma \left( {1+\sin \phi \cos 2\psi } \right)$$
(2b)
$${\sigma _\theta }={\sigma _3}=\sigma \left( {1 - \sin \phi } \right)$$
(2c)
$${\tau _{rz}}=\sigma \sin \phi \sin 2\psi .$$
(2d)
Fig. 1
figure 1

a Mohr stress circle and the directions of slip lines; b the directions of slip lines with respect to principal stresses and c cylindrical coordinate system and stress components

Full size image

The equilibrium and yield equations can be combined together to find the stress characteristics equations. The system of equations found in this way can be then solved by the method of stress characteristics. The equations are as follows:

Along the positive (σ+) and the negative (σ−) stress characteristics:

$$\frac{{{\text{d}}r}}{{{\text{d}}z}}={\text{tan}}\left( {\psi \pm \mu } \right),$$
(3)
$${\text{d}}\sigma \cos \phi \pm 2\sigma \sin \phi {\text{d}}\psi +\frac{\sigma }{r}\left[ {\sin \phi \cos \phi ~{\text{d}}r \pm ({{\sin }^2}\phi - \sin \phi ){\text{d}}z} \right]= \mp \rho {\gamma _{\text{w}}}(\sin \phi {\text{d}}r - \cos \phi ~{\text{d}}z),$$
(4)

where \(\mu =\pi /4 - \phi /2\). Figure 1 shows the definition of parameters involved in these equations.

As it is known, the installation of a driven pile is different from the CPT sounding process. Hence, this discrepancy should be taken into account and addressed in predicting the load-settlement behavior of driven piles, since the CPT data just gives the in situ information of the stratum. For this purpose, the driving effect is considered on the model boundary conditions by definition of a passive lateral earth pressure along the pile shaft. In other words, the driven piles, often called displacement piles, can move the soil away and put it into the passive state during the driving process. Of course this is a limiting condition and the complete passive force may not be mobilized completely in ractive. However, such an assumption more or less complies better with the actual condition.

2.2.1 Non-Associated Flow Rule

The influence of flow rule is very important in estimation of the limit load based on plasticity theory. The angle of dilation reduces as the shear strains develop and it affects both the pattern of failure mechanism and the limit load. One should note that the limit load in the context of the limit analysis in perfectly plastic materials does not depend on the type of flow rule. However, the limit load obtained by a kinematically admissible failure mechanism depends on the geometry of the failure pattern which in turn depends on the flow rule. Non-associated materials exhibit a smaller failure pattern and a lower limit load. Therefore, the angle of dilation, as a measure of non-associativity, affects the failure pattern and the limit load.

An associated flow rule, as in many methods, is the basis of the stress characteristics method and most limit load theorems. It is conventional to find the solution based on an associated flow rule assumption but in fact, a non-associated flow rule governs the actual behavior of most geomaterials. Therefore, the non-associativity should be taken into account if an appropriate estimation of the bearing capacity is required. To include the influence of the flow rule, one significant step was taken by Drescher and Detournay [19] in computing equivalent values for soil cohesion and friction angle in case of a non-associated flow rule. Equivalent values can be computed by the following equations derived independently by Davis [20] and Rowe [21] based on equating the rate of plastic work for a non-associative and an equivalently associative material:

$$\tan {\phi ^*}=\eta \tan \phi ,$$
(5)
$${c^*}=\eta c,$$
(6)
$$\eta =\frac{{\cos \nu \cos \phi }}{{1 - \sin \nu \sin \phi }}.$$
(7)

In these equations, \(\nu\) is the soil angle of dilation, \(\phi\) is actual friction angle, \(c\) is cohesion, \({c^*}\) is the modified (or equivalent) cohesion due to non-associativeness and \({\phi ^*}\) is the modified (or equivalent) friction angle for spotting the non-associativity of soils.

Studies show that the equivalent shear strength terms do not change significantly when the dilation angle is around \(0.5\phi\) and smaller. In addition, for the bearing capacity problems, the shear strains are often high enough to reach a residual strength corresponding to very low volume change and very small dilation angles. Therefore, due mainly to rather very high shear deformations and very low dilation angles mobilized in the soil around a pile, the dilation angle is conservatively assumed to be \(\nu =0.1\phi\).

2.3 Soil Strength Parameter by Use of CPT Records

In this study, the shear strength parameter of soil (\(\phi\)), which is used as an input data for numerical modeling have been estimated first by the indirect use of CPT data. The results of equations presented by Robertson and Campanella [9], Bowles [22] and Kulhawy and Mayne [23] mentioned in Table 1 are investigated. The geometric cone resistance has been averaged over three different zones, i.e., \(2b\) below the cone tip (\(b\) is the pile diameter) and \(4b\) above (i.e., \(2b/4b\)), \(3b/6b\) and \(4b/8b\) are calculated to see which averaging method gives better estimations. From these zones, the zone \(4b/8b\) (i.e., averaging over a zone extended from \(4b\) below the cone tip to \(8b~\) above the tip) and the equation presented by Kulhawy and Mayne [23] are found to be more appropriate.

Table 1 Relations between \(\phi\) and \({q_{\text{c}}}\)
Full size table

3 Compiled Database

A database of case histories from the results of 98 full-scale pile load tests is recompiled with complete information on the soil type and the results of CPT soundings performed close to the pile locations. The cases were obtained from nine different sources. Forty case studies are used for calibration and fifty-eight cases for verification of the proposed approach. Tables 2 and 3 summarize these cases with reference to the soil and the pile characteristics.

Table 2 Case study records for calibration
Full size table
Table 3 Case study records for verification
Full size table

All piles are of “driven pile” type. Most of cases are in sand and some in silt and mixed soils. The shapes of piles are octagonal, square, round and pipe (opened and closed ended). The open-ended piles are assumed to be fully plugged. The pile width varies between 73 and 915 mm and the pile length between 3.44 and 67 m. Pile materials are concrete (with rather rough interface) or steel (with rather smooth interface).

4 Proposed Approach

Studies show that the response of a pile to an applied axial load can not be considered as the pile ultimate capacity, but it is a function of stress and strain conditions around the pile [3]. Therefore, it is necessary to simultaneously analyze the bearing capacity and the load–displacement response of pile.

Prediction of the load–displacement response of piles is often a difficult task. The pile load test is considered to be one of the most reliable methods for prediction of the load–displacement response. However, this test is both time consuming and expensive. Alternatively, it is more advantageous to develop simple analytical or numerical methods based on rather limited test results.

In this study, a new analytical–numerical method is proposed to estimate the bearing capacity and load–displacement behavior of axially loaded piles based on CPT records. The method of stress characteristics is used to obtain the stress field around the pile and the kinematics of the deformation (i.e., the failure pattern) has been also determined.

4.1 Stress Field from the Slip Lines Method

When the static analysis method is used, the failure mechanism around the pile tip or the shaft, should be either assumed, or, found naturally. For example, in methods based on the limit equilibrium or the upper bound limit analysis, the failure mechanism is assumed a priori. Whereas, in methods such as the lower bound limit analysis or the stress fields methods, it is obtained naturally.

Therefore, the actual stress field is first determined by the method of stress characteristics where the yield equation is satisfied, which is the initial failure pattern formed around the pile. Then, the failure mechanism is progressively extended by a hardening soil model and the plastic strains are developed in the soil around the pile. The concept is considered in this study by defining the progressive soil friction angle as an input data in numerical modeling and the stress characteristics network is updated in each step. In Fig. 2, the stress fields around the pile is illustrated for initial yield condition and the failure mechanism.

Fig. 2
figure 2

Stress field formed around the pile for a initial yield condition and b failure condition

Full size image

Studies show that the size of failure mechanism obtained by the stress characteristics method through initial yield to failure condition does not change perceptibly (as shown in Fig. 2). Therefore, it is assumed that the failure pattern found by a stress field at limiting equilibrium remains stationary along sliding discontinuities. This simplification can alternatively be used to reduce the computational effort.

The obtained failure pattern is then used to calculate the kinematics of progressing failure, i.e., the displacement field for a given displacement boundary. In the incremental load–displacement computation procedure, the incremental displacement field is constructed at each step and then the strain field will be obtained. The mobilized soil friction angle is a function of the shear strain and hence, at each step, the associated stress field is updated in accordance with the incremental displacement field. Thus, the stress characteristics network and the failure mechanism are updated in every step according to the displacement field and the mobilized friction angle. In the next section, the calculation of the displacement field is described.

4.2 Kinematics of Deformation and Displacement Field

In this section, the general outline of the procedure to find the displacement fields is presented. It is divided into two sections for the pile tip and the shaft, respectively. As stated in former section, the construction of the displacement field and the associated stress field is a progressive and incremental computation. In each step, the incremental displacement field is calculated, the shear strain increment is found and based on the shear strain, the mobilized friction angle and finally, the associated stress field at that particular step is calculated. In what comes next, the construction of the incremental displacement field is explained for the pile tip and the shaft.

4.2.1 Pile Tip

Once the stress state at every point around the pile has been computed using the slip lines equations, an admissible velocity field can be found corresponding to the failure mechanism already obtained by the stress characteristics. In other words, the stress characteristics network designates the extent of the failure mechanics and this failure mechanism can be then used to construct the displacement field. Construction of displacement field (in fact, the displacement increment or the velocity, in the terminology of the limit analysis) is done by making the velocity hodographs corresponding to the velocities of different rigid blocks enclosed by slip lines. One should note that the stress characteristics network defines the directions of slip and hence, the soil block enclosed by these lines, can be regarded as a rigid block. In fact, deformations are highly localized into the slip lines and in the exterior of the slip lines, deformations are elastic, or, even zero in case of a rigid-perfectly plastic material. This approach is recently presented and described in detail, by Veiskarami et al. [14] and applied to estimate the bearing capacity of strip foundations [15].

Figure 3 shows the failure pattern (obtained by the method of stress characteristics) and the velocity vectors acting on the slip lines. In associated flow rule condition, the stress characteristics lines coincide with the zero extension lines (i.e., lines of zero axial strains) and therefore, the slip lines can be considered as rigid links that can move or rotate without axial deformation. For non-associated flow rule, the procedure outlined in Sect. 2.3 can be utilized to arrive at an equivalent associated flow rule condition. Now, for a given deformation boundary condition, the generated displacements in the network can be computed by the following equation:

Fig. 3
figure 3

Velocity hodographs and rigid blocks

Full size image
$$\frac{{{\text{d}}u}}{{{\text{d}}v}}= - \frac{{{\text{d}}z}}{{{\text{d}}x}}.$$
(8)

In this equation, \(u\) and \(v\) are horizontal and vertical displacements. The finite difference forms of these equations can be used to find the displacement field for further computations which are presented in Eqs. 9 and 10:

$${\text{d}}u~{\text{d}}x+{\text{d}}v~{\text{d}}z=0,$$
(9)
$$\left\{ {\begin{array}{*{20}{c}} {\left( {{u_{B2}} - {u_{A2}}} \right)\left( {{x_{B2}} - {x_{A2}}} \right)+\left( {{v_{B2}} - {v_{A2}}} \right)\left( {{z_{B2}} - {z_{A2}}} \right)=0} \\ {\left( {{u_{B2}} - {u_{A3}}} \right)\left( {{x_{B2}} - {x_{A3}}} \right)+\left( {{v_{B2}} - {v_{A3}}} \right)\left( {{z_{B2}} - {z_{A3}}} \right)=0} \end{array}} \right..$$
(10)

When the velocity field has been found, the maximum shear strains can be determined, which is presented below:

$$\gamma =\frac{{\partial u}}{{\partial z}}+\frac{{\partial v}}{{\partial x}}.$$
(11)

The incremental displacement field can be obtained by incremental boundary displacement. In this case, the incremental boundary displacement is nothing but the vertical movement of the pile tip into the ground.

4.2.2 Pile Shaft

The same procedure should be taken for the pile shaft, i.e., the displacement field and the progressive failure pattern around the pile shaft in an incremental manner. As it is shown in Fig. 4, there is a sheared region (also called the smear zone) around the pile shaft in granular soils with a vertically aligned stretching [33]. The mobilization and ultimate value of the shaft friction is governed by the behavior of this narrow zone in the proximity of the pile surface [34]. Previous model tests have shown that the soil located far enough from the shaft remains largely undeformed [35]. A survey in the literature shows that the thickness of this shear zone, \({t_{\text{s}}}\), depends on the pile surface roughness and has a very wide range [36, 37]. A summary of these investigations on the thickness of the shear zone is shown in Table 4. According to this table, \({t_{\text{s}}}\), for this study, is assumed to be \(10{D_{50}}\) for sand as an average value of what has been suggested by researchers.

Fig. 4
figure 4

Shear pattern around pile in sand

Full size image
Table 4 The thickness of shear (or smear) zone around pile shaft
Full size table

In Fig. 5, the behavior of the shear zone during installation and static loading is shown. The shear displacement, \(\delta\), leads to mobilization of shaft capacity of pile. Therefore, the shear strain can be obtained by Eq. 12 as follows:

$$\gamma =\frac{\delta }{{{t_{\text{s}}}}}.$$
(12)
Fig. 5
figure 5

Behavior of the shear (or the smear) zone during installation and loading

Full size image

The pile unit shaft resistance, \({r_{\text{s}}}\), may be determined from the sleeve friction as expressed by:

$${r_{\text{s}}}=K{f_{\text{s}}}$$
(13)

where \(K\) is a dimensionless coefficient. The \(K\) coefficient depends on the pile shape and its material, cone type and embedment ratio. In sand, the coefficient, \(K\), ranges between 0.8 and 2 [38, 39].

5 CPT-Based Load–Displacement Curve for Piles

The numerical procedure has been developed as presented to obtain the stress and strain fields around the pile. Now, it is necessary to consider an appropriate constitutive model to study the load–displacement behavior of the piles. This is possible by studying the relationship between \(\sin {\phi _{{\text{mob.}}}}\)and \({\gamma _{{\text{max}}}}\) in each element of the soil obtained from the presented numerical modeling of the stress and strain field around the pile.

The mobilized soil friction angle and the maximum shear strain are functionally dependent. This functional relationship is highly important and very influential in stress analysis when the displacement field is prescribed. Unfortunately, an explicit and clear form of such equation has not been found by the authors in the literature. However, a very simple form of such a functional dependency can be found by assuming a hyperbolic relationship between \(\sin {\phi _{{\text{mob.}}}}\) and the maximum shear strain. This form can be visually supported by the form of conventional shear tests on frictional soils, e.g., [40, 41] and also, supported by the form of hardening laws presented by traditional soil models such as the hyperbolic soil model, e.g., [42, 43]. In addition, such an equation is not only capable of qualitative capturing of the soil behavior, but also requires the minimum number of parameters (only two) to be prescribed [44]. Therefore, the following equation has been chosen as a basis for the functional dependency of the mobilized friction angle and the maximum shear strain depicted graphically in Fig. 6a:

$$\sin {\phi _{{\text{mob.}}}}=\frac{\gamma }{{a+b\gamma }}.$$
(14)
Fig. 6
figure 6

a Hyperbolic relation between \(\sin {\phi _{{\text{mob.}}}}\) and maximum shear strain, b general form of predicted hyperbolic load transfer for each element of soil around the pile

Full size image

In this equation, two parameters of \(a\) and \(b\) can be considered as representatives of the geotechnical (or mechanical) parameters, i.e., the modulus of elasticity, \(E\) and the critical state (or the residual) friction angle, \(\phi_{\text{c.s.}}\) For instance, \(a\) is some measure of \(E\) and \(b=1/\sin {\phi _{{\text{c.s.}}}}\).

This hyperbolic relation is assumed to define the progressive soil friction angle and updated stress and strain field formed around the pile. This procedure continuous until the soil fails. Therefore, in each step, stress–strain response in every element of the soil obeys the same hyperbolic trend. The response of the soil for each increment of displacement as an output of numerical study is presented in Fig. 6b. Now, this local trend in soil elements could be generalized reasonably to load–displacement response of the pile under axial loading.

It is worth mentioning that, although Eq. 14 is not basically for layered soils as well as a soil with varying properties in depth, the non-homogeneity of the soil can be considered by use of CPT data in the proposed approach. As described in Sect. 2.4, the soil properties in different layers are obtained using CPT data, which reflect a continues (inch-by-inch) actual properties of the soil. Therefore, it can be said that, as the model parameters are linked to the corresponding CPT data at that particular depth, the non-homogeneity of the soil can be automatically considered.

This study shows that the input parameters required for load transfer (hyperbolic) curves have physical meaning and determined from analysis of proposed stress and strain fields formed around the pile. To calibrate the model parameters, 40 case studies (for which there was a complete database available), presented in Table 2, were used. The rest of case studies, presented in Table 3, were used to verify the calibrated parameters. Inspection of the results revealed that the input parameters for pile tip and shaft are functions of the ratio \({q_{\text{c}}}/{\sigma _0}\), \({\sigma _0}\) and \({f_{\text{s}}}\) where \({\sigma _0}\) is the initial soil pressure at the depth at which, these curves are required. This dependency seems to be logical as the stress level effect cannot be disregarded. However, the effect of pile geometry such an effect could not be well-recognized in this paper due to the rather tight range of pile dimensions in available collected database. The input parameters for the pile tip load transfer (hyperbolic) curve are shown in Fig. 7 with equations obtained below. In these equations, \(~q\) is the effective overburden pressure of soil at pile tip, \(t\) is shear stress at the pile shaft and \(\zeta\) is vertical movement of the pile:

$$q=\frac{\zeta }{{{a_{\text{t}}}+{b_{\text{t}}}\zeta }},$$
(15)
$${a_{\text{t}}}=0.03~\left( {\frac{{{q_{\text{c}}}}}{{{\sigma _0}}}} \right)+0.012,$$
(16)
$${b_{\text{t}}}=0.006~{\sigma _0}+1.39.$$
(17)
Fig. 7
figure 7

The input parameters of load–displacement curve for pile tip

Full size image

A similar analytical approach has been conducted for the parameters of the shaft load transfer curve with the results shown in Fig. 8 and parameters presented below:

$$t=\frac{\zeta }{{{a_{\text{s}}}+{b_{\text{s}}}\zeta }},$$
(18)
$${a_{\text{s}}}=0.55~\left( {{f_{\text{s}}}} \right)+0.01,$$
(19)
$${b_{\text{s}}}=21~{f_{\text{s}}}+0.21.$$
(20)
Fig. 8
figure 8

The input parameters of load–displacement curve for pile shaft

Full size image

Both the calibration and verification data points are shown in Figs. 7 and 8 separated by different notations (circles with solid fill or no fill, respectively). It is apparent that the linear predictions are suitable and show reasonable agreement.

The flowchart of the developed procedure is shown in Fig. 9 to clarify the proposed approach step-by-step.

Fig. 9
figure 9

Flowchart to summarize proposed approach

Full size image

6 Load–Displacement Results

The results of the numerical modeling of the load–displacement response of the proposed procedure for some arbitrary case studies from Table 3 are shown in Fig. 10. The responses to the toe and shaft resistances are separately presented and the overall response is compared with that, obtained by field tests. The accuracy of the predicted load–displacement responses is clear. It is worth mentioning that for cases no. 7, no. 11, no. 20 and no. 21, in Table 3, predictions showed less agreement with observed responses. This can be attributed to the inaccuracy of the empirical relationships between CPT results and soil shear strength parameters. Fortunately, the agreement between predictions and observations in the rest of case studies was quite reasonable and similar to those corresponding to cases shown in Fig. 10.

Fig. 10
figure 10

Predicted load–displacement responses of selected piles using proposed approach: a Case 24, b Case 27, c Case 32, d Case 36, e Case 37 and f Case 38 (from Table 3)

Full size image

7 Pile Bearing Capacity by Proposed Approach

To compare the results of the proposed method by other methods, the bearing capacity of 58 cases used for verification reported in Table 3 are estimated by the proposed approach and also other CPT-based methods. For this purpose, seven methods were used comprising: UniCone [31], TCD-03 [45], ICP-05 [46], NGI-05 [47], Fugro-05 [48], UWA-05 [49], German [50]. The results are presented in Fig. 11. It is worth mentioning that in this study, the plunging failure is taken as the ultimate bearing capacity of the piles, since the bearing capacity of pile is estimated based on CPT, which is a large strain test. Furthermore, the Brinch Hansen 80%-criterion [51] is used for the cases that the failure load is not clearly defined. Since the 80%-criterion normally agrees well with the intuitively perceived plunging of the pile [52], it can be observed that the proposed approach provides fairly better predictions rather than the other ones.

Fig. 11
figure 11

Estimated versus measured bearing capacity of piles by different CPT-based methods

Full size image

8 Conclusions

Based on the principles of the plasticity theory, the stress field is not independent of the displacement and/or deformation fields. Therefore, a more reliable analysis will be achieved if the bearing capacity and load–displacement behavior of piles are analyzed simultaneously.

The main objective of this paper is to propose a method to predict the load–displacement behavior and the bearing capacity of driven piles in sand. A new analytical–numerical method has been proposed to estimate the bearing capacity and axial load–displacement behavior of driven piles using CPT records.

For this purpose, the method of stress characteristics is employed to analyze the stress field below and around the pile. Furthermore, the load–displacement behavior of piles is studied by the implementation of a displacement field on the current actual stress field obtained by the stress characteristics method. The geotechnical parameters required for numerical analyses are obtained from in situ tests. To do this, the CPT data has been both directly and indirectly incorporated into the analyses to estimate the soil shear strength parameters and the bearing capacity of piles. A simple hyperbolic relationship has been introduced to relate the shear strain and the mobilized shear resistance of soil in terms of the mobilized friction angle. The procedure comprises some steps through which, the load–displacement and bearing capacity of driven piles can be obtained.

To calibrate the load–displacement hyperbolic relationship, a rather large pile load test database, including 98 driven piles in sand, has been recompiled with CPT data available. Pile materials are concrete or steel and the shapes of piles are octagonal, square, round and pipe (opened and closed ended). The pile width and length vary between 73–915 mm and 3.44–67 m, respectively. Calibration of the parameters has been made first for 40 case histories and then, it is verified for the remaining of the pile load test data.

Finally, the axial pile bearing capacity estimated by the proposed method is compared by the results obtained by seven direct CPT-based methods. Comparisons showed that this proposed approach is capable of promoting accuracy and the predictions are in acceptable agreement with full-scale pile load tests results. The reason may lie behind the fact that the proposed approach integrates several ingredients of the plasticity theory and limit analysis, direct and indirect use of the CPT results, i.e., a theoretical approach on the basis of a rather accurate and continuous record of the soil properties. Of course, the accuracy of the proposed approach mainly depends on the type of the conducted in situ test. In addition, in this study, the bearing capacity is estimated considering the displacements occurred in the soil, which has not been concerned in the other common CPT-based methods. As far as the CPT data are available and representing the actual subsoil condition, the proposed approach can be a good alternative among other methods for the load–displacement as well as the bearing capacity analysis of driven piles.