1 Introduction

Conventionally, the structure is designed for the fixed-base condition or soil–structure interaction (SSI) with a nonlinear soil behaviour. The same thing is followed for the nuclear structure, in which it is assumed that the foundation movement is in a conservative seismic design. However, foundation movement takes place due to the interface of soil and foundation and leads to a change in the dynamic behaviour of the structure. Moreover, the structural nonlinearity may change the dynamic response of soil and foundation due to the change in stiffness and damping characteristics of the system. The delicacy of the structural response to layered soil strata plays an essential role as there are always some uncertainties in the soil properties.

Additionally, the nonlinear behaviour of the foundation could be associated with the inexpensive permanent settlement, rocking, and sliding. Therefore, avoiding the soil–structure interaction (SSI) could mislead to inappropriate and inconsistent seismic demands, which is crucial for the facilities related to the nuclear power plant (NPP). It is incredibly vital to evaluate the soil–structure interaction modelling to understand the complex and complicated behaviour and accomplish a more appropriate seismic evaluation of the NPP structures.

The safety of NPP structures is a primary interest to the general public and regulating agencies because of the adverse socio-economic effects that could arise from structural failure and damage. However, a small probability of seismically induce failure to nuclear energy-related structures established a particular safety concern. It makes the inner portion and cooling radiated water from the containment cell vulnerable, which is a high health hazard to the general public in the neighbourhood of the NPP and a threat of biological risk over the broader region for several centuries (Newmark and Hall 1969). Therefore, a comprehensive estimation of the seismic response of NPP-related structures is crucial to perform an accurate seismic evaluation of NPPs.

Newmark and Hall (1969) observed that vibration transfer to the soil from the structure and energy dissipation at the superstructure and substructure interaction noticeably diminishes the reactions transferred to structures. However, for nonlinear structures, in some particular conditions of structures and ground motions, SSI effects may result in significantly high ductility demands due to rocking (Mylonakis and Gazetas 2000). Foundation uplifting and rocking could produce a critical level of base shear in structures with a considerably short period on relatively soft soil (Yim and Chopra 1984). In the recent past, seismic evaluation of foundations in rocking has been broadly investigated with experiments as well as using numerical methods. Seismic SSI mechanisms related to shallow foundations have been studied using a shake table (Knappett et al. 2004, Qin and Chouw Qin et al. 2010). Gajan (2006) and Ugalde et al. (2010) has conducted centrifuge tests on a shallow foundation to study the rocking mechanism.

Various researchers (Raychowdhury and Hutchinson 2009, 2010; Gajan et al. 2010; Tang and Zhang 2011; Figini et al. 2012; Gazetas et al. 2013; Kamgar et al. 2020; Tavakoli et al. 2020) have investigated the nature of soil–structure–foundation interaction under the influence of earthquake load. Kamgar et al. (2020), Tavakoli et al. (2020) and Kamgar and Rahgozar (2020) have studied the effect of SSI on high-rise steel building and outrigger belt system for the evaluation of seismic performance of the building. In the case of nonlinear soil, it is found that with an increase in the relative density and decrease in foundation aspect ratio, rocking stiffness increases (Ghersi et al. 2000). Nevertheless, declination of the same is observed for increasing foundation rotations, low relative densities, and high soil deformation. Wen et al. (2002) have found a higher probability of damage for softer sites in the case of far-field earthquakes. It has been observed that SSI effects depend on various parameters viz. structure–foundation stiffness ratio, structure–earthquake frequency ratio, damping coefficient impedance, advancement of plasticity in structures, and rocking in the foundations (Zhang and Tang (2009). In another SSI study performed by Tang and Zhang (2011) has noticed that maximum inter-story drift is more sensitive to the friction angle of soil. The inter storey drift and ductility demand in a shear wall decrease when foundation yielding is considered in a static nonlinear study of shear wall with the effect of SSI effect (Marzban et al. 2011). The settlement, rocking, and translation induce in the foundation during seismic load may change the whole dynamic features of the structure, including period, stiffness, spectral, and ductility demand due to change in damping of the overall system and flexibility (Raychowdhury and Hutchinson (2011).

Inclusively, the general design is reticent to integrate the influence of SSI in the standard designing practices of the structures. However, various provisions such as FEMA 368 and ASCE/SEI 7–05 have considered SSI by basically increasing the damping and fundamental period of the system. Mylonakis and Gazatas (2000) have suggested that without proper normalizing periods and ductility demand in a fixed-base case as a decreasing function of the structural period may lead to errors. Nevertheless, in a force-based design approach, an appropriate increment in the fundamental period is essential.

Evans and Keogh (1987) have evaluated the effect of nonlinearity and foundation behaviour of the NPP containment using the FEM and found that shear strength of containment can be improved by providing shear links that upgrade the general functioning of the NPP containment cell. Venancio et al. (1997) performed an analytical study on NPP containment to investigate the effect of SSI using the frequency-domain method. Zentner (2010) used artificially generated ground motion time history to perform the dynamic nonlinear response analysis and prepared fragility curves for NPP units and related structures. Saxena and Paul (2012) have concluded that the embedment foundation depth plays a vital role in the case of slip and, subsequently, other various response parameters.

In view of the above literature, there is no study in which the nonlinear behaviour of structure and soil is considered simultaneously. Furthermore, most of the NPPs are considered homogeneous soil mass. Therefore, in this paper, the emphasis is made to develop the finite element model of NPP structure founded on the layered soft soil considering the nonlinearity of soil as well as structure.

2 Numerical Modelling of NPP and Soil

2.1 Dynamic Implicit Method

The implicit method uses an automatic increment scheme based on the success rate of a full Newton–Raphson iteration solution (Rostami and Kamgar 2021).

$$\Delta x^{{\left( {i + 1} \right)}} = \Delta x^{\left( i \right)} + K_{\left( j \right)}^{ - 1} .\left( {F^{\left( i \right)} - I^{\left( i \right)} } \right)$$
(1)

where \(K_{j}\) is the current tangent stiffness matrix, F is the load vector, I is the internal force vector, and \(\Delta x\) is the increment of displacement.

Hilber et al. (1978) have defined a dynamic implicit procedure algorithm as follows:

$$F^{{\left( {i + 1} \right)}} = M\ddot{x}^{{\left( {i + 1} \right)}} + \left( {1 + \alpha } \right)Kx^{{\left( {i + 1} \right)}} - \alpha Kx^{\left( i \right)}$$
(2)

where F is the force vector, x the displacement vector, M the mass matrix, and K the stiffness matrix, which can be defined as:

$$x^{{\left( {i + 1} \right)}} = x^{\left( i \right)} + \Delta t\dot{x}^{\left( i \right)} + \Delta t^{2} \left( {\frac{1}{2} - \beta } \right)\ddot{x}^{\left( i \right)} + \beta \ddot{x}^{{\left( {i + 1} \right)}}$$
(3)

and

$$\dot{x}^{{\left( {i + 1} \right)}} = \dot{x}^{\left( i \right)} + \Delta t\left( {\left( {1 - \delta } \right)\ddot{x}^{\left( i \right)} + \delta \ddot{x}^{{\left( {i + 1} \right)}} } \right)$$
(4)

where \(\beta = \frac{1}{4}(1 - \alpha^{2}\)), \(\delta = \left( {\frac{1}{2} - \alpha } \right), \frac{1}{3} \le \alpha \le 0,\) \(\alpha = - 0.05\) is ABAQUS by default value as a low damping term to remove the high-frequency noise without having a significant effect on necessary, flatter frequency response.

Sun et al. (2000) have concluded that the numerical damping induced in the implicit method depicts its relation to decompose the noise and provides more accurate results since it has a much larger stable time period than that of the other available algorithms. It takes less time increment for the procedure with long time history.

2.2 Boundary Condition

The primary difficulty in dynamic analysis of the SSI modelling is to maintain a balance between appropriate and feasible modelling of the far-field medium. However, the equivalent characteristics are lumped at nodes near to truncated boundaries instead of the semi-infinite soil medium (Ladhane & Sawant 2016). The deduction in the calculation domain makes the analysis feasible and less time-consuming; however, the performance of these boundary conditions could affect the accuracy of the results (Kontoe et al. 2007). These boundaries can be classified as elementary, consistent, and local. Elementary boundaries are usually applicable in static analysis in which stresses and displacement are considered zero at the boundaries of the calculation domain. Nevertheless, elementary boundaries are not consistent with the geometrical spreading of energy towards infinity. Therefore, consistent local boundaries are introduced to prevent the back-propagation of waves into a calculating domain; however, the radiation condition is achieved at the boundaries of a domain in the case of local boundaries. The local absorbing boundary is generally used in engineering problems as these are computationally more feasible than other available boundary conditions (e.g. Tavakoli et al. 2019; Kamgar et al. 2020). However, consistent boundaries are frequency dependent and capture the radiation condition at the truncated boundaries (Novak and Mitwally 1988).

In the present study, the Kelvin element boundary (spring and dashpot connected in parallel) is used at the truncated boundary of the calculation domain to reduce the effect of the reflected wave at the boundaries. Novak (1974) equation is used to calculate the dashpot and spring constant for the Kelvin element in the horizontal and vertical direction.

$$K^{c} = \frac{G}{{2\pi R_{o} }}\left[ {x_{1} + ix_{2} } \right]$$
(5)

where \(K^{c}\) is the complex stiffness; G is the shear modulus of the soil; \(R_{o}\) is the radial distance of the Kelvin element node from the source of vibration; and \(x_{1}\) and \(x_{2}\) are frequency-dependent dimensionless parameters given by Novak and Mitwally (1988)); however, the real and imaginary parts in Eq. (5) characterize the stiffness and damping coefficient, respectively. \(x_{1}\) and \(x_{2}\) are calculated with respect to the frequency of the NPP system.

2.3 CDP Model for Structural Component

In this study, for the concrete nonlinearity, a constitutive material model CDP (concrete damage plasticity) is used to assess the failure and damage phenomena in NPP structures. The CDP is extensively used for the concrete structure under dynamic and cyclic loading. In the ABAQUS FEM package, the CDP is based on the methodology proposed by Lubiner et al. (1989), Lee and Fenves (1998) and Hillerborg et al. (1976). CDP model uses the isotropic damaged elasticity with isotropic tensile and compressive plasticity to characterize the inelastic behaviour of the concrete material.

In CDP, there are two primary failure mechanisms, viz. concrete tensile cracking and compressive crushing. However, the material’s damage is characterized by the degradation in the initial elastic stiffness of the material. The strain rate is disintegrated into elastic (\(\varepsilon^{{{\text{elastic}}}}\)) and plastic strain (\(\varepsilon^{plastic}\)), and the elastic stiffness degradation is isotropic and represented by a scalar degrading damage variable D, as follows:

$$\sigma = \frac{{\left( {1 - D} \right) E_{0} }}{{\varepsilon^{{{\text{plastic}}}} - \varepsilon^{{{\text{elastic}}}} }}$$
(6)

where \({\upsigma }\) is the stress and \({\text{E}}_{0}\) is the initial elastic modulus. The damage (D) varies from 0 to 1, which represents undamaged and fully damaged material, respectively. Equation (6) can be further modified to calculate the stress–strain curve under the uniaxial compression and tension load as follows (Fig. 1):

$$\sigma_{c} = \frac{{\left( {1 - D_{c} } \right) E_{0} }}{{\varepsilon_{{{\text{comp}}}}^{{{\text{plastic}}}} - \varepsilon_{{{\text{comp}}}}^{{{\text{elastic}}}} }}$$
(6.1)
$$\sigma_{t} = \frac{{\left( {1 - D_{t} } \right) E_{0} }}{{\varepsilon_{{{\text{comp}}}}^{{{\text{plastic}}}} - \varepsilon_{{{\text{comp}}}}^{{{\text{elastic}}}} }}$$
(6.2)

where \({\upsigma }_{c} and {\upsigma }_{t}\) are compressive and tension stresses, respectively, and \(\varepsilon_{{{\text{comp}}}}^{{{\text{plastic}}}}\) and \(\varepsilon_{{{\text{comp}}}}^{{{\text{elastic}}}}\) the corresponding strains. The plasticity parameters of the CDP model are given in Table 1.

Fig. 1
figure 1

a Showing compressive stress–strain curve of concrete of strength 50 MPa. b Tensile stress–strain curve for M50

Full size image
Table 1 Plasticity parameter of CDP model
Full size table

2.4 Drucker–Prager Model for Soil

The Drucker–Prager (D–P) constitutive material model is 3D pressure dependent that is used in soil mechanics to evaluate the stress level at the ultimate strength. The D.P. failure criterion is derived from the Mohr–Coulomb (M–C) criterion for soils (Drucker and Prager 1952) and can be expressed as:

$$\sqrt {H_{2} } = \gamma I_{1}^{^{\prime}} + K$$
(7)

where \(\gamma\) and K are the material constants, H2 is the second invariant of the stress deviator tensor, and \(I_{1}^{^{\prime}}\) is the first invariant of the stress tensor, which are expressed as follows:

$$I_{1}^{^{\prime}} = \sigma_{1}^{^{\prime}} + \sigma_{2}^{^{\prime}} + \sigma_{3}^{^{\prime}}$$
(8)
$$H_{2} = \frac{1}{6}\{ (\sigma_{1}^{^{\prime}} - \sigma_{2}^{^{\prime}} )^{2} + (\sigma_{1}^{^{\prime}} - \sigma_{3}^{^{\prime}} )^{2} + (\sigma_{3}^{^{\prime}} - \sigma_{1}^{^{\prime}} )^{2} \}$$
(9)
$$\gamma = \frac{2 \sin \emptyset }{{\sqrt 3 \left( {3 \pm \sin \emptyset } \right)}}, K = \frac{6C \cos \emptyset }{{\sqrt 3 \left( {3 \pm \sin \emptyset } \right)}}.$$
(10)

\(\sigma_{1}^{^{\prime}}\), \(\sigma_{2}^{^{\prime}}\), and \(\sigma_{3}^{^{\prime}}\) are the principal effective stresses, \(\emptyset\) is the soil internal friction angle, and c is the soil cohesion value. Here, the positive and negative signs in Eq. (10) indicate the tensile and compression behaviour, respectively. It is also called an extension of the von Mises failure criterion. Trochanis et al. (1991) have found a satisfactory comparison between FEM model prediction of D–P model and experimental results in their three-dimensional study on piles.

3 Verification of Model

In order to validate the proposed model, a simply supported beam is analysed using the ABAQUS, i.e. finite element program. The material and beam section properties are taken from Qingfu et al. (2020). The cross section and detailing of the reinforcement are shown in Fig. 2. The compressive strength of the concrete is 27.3 MPa. This compressive strength is used in the calculation of CDP parameters. The constitutive behaviour of concrete is modelled using the CDP model, while the reinforcement is modelled in the linear elastic range only. The concrete element is modelled using the eight-noded solid linear brick elements (C3D8R), while the reinforcement is modelled using the two-noded beam element. The embedded constraint is used for the modelling of reinforcement inside the concrete.

Fig. 2
figure 2

Cross section and detailing of reinforcement in R.C. beam (after, Qingfu et al. 2020)

Full size image

Figure 3(a) and (b) shows the load–displacement curve at the top and bottom fibre of the R.C. beam, respectively. It can be seen that the load–displacement curve obtained from the finite element modelling of the R.C. beam is in good agreement with those provided by the experimental method. The results of experimental data are extracted directly from Qingfu et al. (2020) and may contain a small error. Therefore, the present method of analysis can be further used in the seismic performance of the NPP structure.

Fig. 3
figure 3

Load deflection curve at a top fibre and b bottom fibre of beam

Full size image

4 Material Properties and Model Description

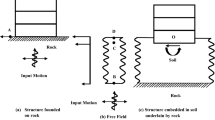
To study the seismic performance of the NPP structure, three models have been prepared. Model-1 consists of NPP superstructure geometry, similar to Saxena and Paul (2012), which includes a cylindrical arrangement of 45 m diameter, with the dome at the top of the cylinder structure, constructed on the circular raft foundation (Fig. 4a). The total height and thickness of the structure are considered 72.5 m and 1.59 m, respectively. The reinforcement bars are provided at @ 80 mm of 40-mm-diameter bars with an effective cover of 100 mm. In the raft foundation, 6 m thickness is provided, and an eight-layered soil is considered; the material characteristics of the soil and concrete structures are presented in Tables 2 and 3, respectively. In Model-2, the raft is embedded into the soil by 3 m to capture the effect of the embedment of the foundation (Fig. 4b). Finally, in Model-3, the soil is removed, and the NPP structure is considered as a fixed base (Fig. 4c); however, the 1D soil effect is considered in the fixed-base condition.

Fig. 4
figure 4

Three models considered in the present study: a effect of embedment of foundation; b NPP structure on soil strata (without embedment), and c fixed base

Full size image
Table 2 Material properties of the soil in different depths used in the model (after, Boominathan, 2004)
Full size table
Table 3 Material properties of the NPP structure
Full size table

5 FEM Modelling of NPP

A 3D finite element model of a nuclear power plant (NPP) with a soil–structure interaction system is developed using the ABAQUS software package (Fig. 5). It includes three components, viz. structure, raft foundation, and layered soil. Three models are considered in this study. The first model includes soil, raft foundation, and structure, and the raft is embedded 3 m in the soil (Fig. 5a). The second model also includes soil, raft, and structure; the only difference is that the raft is placed at the top of the soil (Fig. 5b). The third model includes only the raft and structure shown in Fig. 5c, and the raft is kept fixed. The soil domain is considered as 200 × 200x30 m after the domain size sensitivity analysis (Maheshwari and Firoj 2020); the proportion of the soil domain in the horizontal direction is two times the diameter of the foundation to counteract the boundary effects.

Fig. 5
figure 5

FEM model of NPP a with embedment; b without embedment, and c fixed base with 1D soil

Full size image

Moreover, the effect of soil in the fixed-base condition is incorporated using the 1D ground response analysis. The motion applied at the fixed base is taken after the ground response analysis. The soil domain is modelled using eight-noded solid linear brick elements (C3D8R). A 20-noded quadratic brick element (C3D20R) is used for the raft foundation. The superstructure (containment structure) of NPP is modelled as eight-noded shell element (S8R). The size of the mesh for soil is considered 5 × 5 × 1 m and 5 × 5 m for concrete structure. The mesh is adopted based on sensitivity analysis. The length of the element based on fundamental frequency is calculated using the following equation (Kramer 1996):

$$L_{e} \le \frac{{\lambda_{\min } }}{a} = \frac{{V_{s} }}{{af_{\max } }}$$
(11)

where \(\lambda_{\min }\) is the minimum wavelength of the shear wave, \(V_{s}\) is the shear wave velocity of soil, and \(a\) is the factor varying from 5 to 8. In the present study, \(a\) equal to 8 is considered so as to capture the shortest wavelength.

All the outer nodes of the soil are attached to the spring dashpot to absorb the incoming waves. In the model, the SSI effect is incorporated using the master and slave surface concepts. Master surface acts as a rigid body (superstructure and substructure), while slave surface acts as a flexible body (soil).

6 Results and Discussion

6.1 Model Analysis

Free vibration analysis is carried out for the NPP structure considering embedment, without embedment, and a fixed-base model to assess the influence of SSI on the fundamental period of the structure. It is noticed that the fundamental period of the NPP structure is shifted from 0.223 s to 0.314 s and 0.371 s for the fixed-base model to the embedded model and without the embedded model, respectively. It can be observed that as the flexibility is instigated, the fundamental period of the NPP model is increased by 40.8% and 66.4% for the embedded model and without embedment model, respectively. The observed period ratio is within the permissible limit, i.e. 1.66 and 1.40, for the embedded and without embedded NPP structure. This period ratio can range between 1 and 2.25 on consideration of SSI (Marzban et al. 2011); the period for two different modes is shown in Table 4.

Table 4 Period of models
Full size table

6.2 Pushover Analysis

Static pushover analysis is carried out for the NPP as per the FEMA-356 (2000) procedure for the fixed-base and nonlinear problems. The incremental force is applied at the dome of the NPP structure. The adopted push over analysis method and determining the yield displacement and yield force are presented in Fig. 6a. Figure 6b represents the pushover curve obtained for the NPP showing the variation of roof displacement with base shear. From Fig. 6c, it is observed that the yield force of fixed base, with an embedment and without embedment problems, is 46 kN, 44 kN, and 31 kN, respectively, implying a 4.35% and 32.61% reduction in force demand in with and without embedment nonlinear SSI case, respectively. It is observed that incorporating the nonlinearity SSI effect provides more flexibility to the structure, therefore reducing the system’s force demand. However, in the case of with and without embedment, a 29.55% reduction has been observed. This shows that without embedment of foundation provides more flexibility than embedment, which can lead to underestimating the fixity of structure. Furthermore, the yielding displacements are found to be 3.0 cm, 7.5 cm, and 9.5 cm, respectively, for fixed, with an embedment, and without embedment problem, depicting a 150% and 216.67% increase in the yield displacement. Nevertheless, there is a 26% increase in the yielding displacement in without embedment than embedment nonlinear SSI case.

Fig. 6
figure 6

a Typical representation of nonlinear pushover analysis; b representation of estimating procedure of yielding displacement from pushover curve; c estimated pushover curve for different models

Full size image

6.3 Cyclic Loading

At the soil–foundation interface of the structure, the energy dissipation plays an essential and critical aspect in the variation of the displacement and force demand of the structure. In this study, a cyclic loading analysis is performed on the NPP with a fixed base and two nonlinear (with an embedment and without embedment) cases. A sine wave having stepped amplitude of Dy, 2Dy, and 3Dy is applied as an input motion to perform cyclic loading analysis (Fig. 7); this method of cyclic loading analysis is adopted as per the FEMA (2000). Figure 6a and b shows that as the nonlinearity is introduced in the structure, a sufficient broadening occurred in the hysteresis loop (Fig. 8). Figure 8a, b, and c depicts the behaviour of the NPP structure by means of cyclic load–deformation response for with embedment, without embedment, and fixed-base case, respectively. Figure 8a, b, and c shows a significantly lower initial and post-yielding stiffness in the nonlinear cases in contrast to the fixed base, implying extra flexibility of the system due to soil–foundation interaction. The peak force of demand in a fixed-base case can be observed as near to 478,000 MN, but 438,000 MN and 467,000 MN embedment and without embedment case (nonlinear cases), respectively, indicating a reduction of 8.37% and 2.3% in peak force demand on considering embedment and without embedment nonlinear case, respectively. However, a higher displacement demand of approximately 7.9 cm and 8.7 cm has been observed in with embedment and without embedment nonlinear cases, respectively, in contrast to fixed base 3.9 cm. Furthermore, the slope of the loop in the nonlinear case is flatter in comparison with the fixed base, indicating higher energy dissipation, which may be caused by excess energy dissipation at the soil–structure interface due to nonlinear soil response. However, from Fig. 8a–c, it is also observed that without embedment nonlinear case flatter loop depicts higher energy dissipation than that of the with embedment case.

Fig. 7
figure 7

Prescribed displacement for cyclic loading

Full size image
Fig. 8
figure 8

Hysteresis response of NPP structure a with embedment; b without embedment; and c fixed base

Full size image

6.4 Ground Motion Data

A nonlinear time history dynamic analysis is performed using an ensemble of ten Indian and ten international earthquake events to investigate seismic performance and demand of the NPP soil–structure system. These 20 ground motions are selected from the COSMOS ground motion database (Tables 5 and 6). Figure 9a, b provides the matched response spectrum with the design response spectrum for the Indian and international earthquake, respectively. These response spectra are matched up to a period of 3 s as the maximum fundamental period of all models is 0.371 s, i.e. less than the fundamental period.

Table 5 Indian earthquake event selected for IDA
Full size table
Table 6 International earthquake event selected for IDA
Full size table
Fig. 9
figure 9

Matched response spectrum with design spectrum: a Indian earthquake, b international earthquake

Full size image

6.5 Dynamic Analysis

A dynamic study of the NPP structure is performed using the incremental dynamic analysis (IDA) method in the present study. In the IDA method, the intensity measure of an earthquake is equivalent to spectral acceleration (Sa) at the fundamental period (T) of the fixed base. This intensity measure is chosen because it involves both ground motion characteristics and structural properties (Kurama and Farrow 2003) as the response spectrum is matched for all periods of each mode. In IDA, selected ground motions are scaled and applied as input motions. The input earthquake motions for the IDA are generated using the software Seismo-Match. For that, initially, actual earthquake records from the COSMOS website, whose characteristics are closely matching with the design response spectrum at the engineering bedrock (Fig. 9), were collected. The scaling of ground motions is done such that for each ground motion, the value of spectral acceleration is matched for the design response spectrum. With an increment of 0.1 g, six simulations are performed for each of the 20 ground motions for the fixed, embedment, and without-embedment nonlinear cases, making a total of 360 simulations.

The engineering demand parameter (EDP) considered in this study is presented in Table 7. Here, W is the weight of NPP structure, Fmax is the peak absolute base shear, \(\Delta_{{{\text{roof}}}}\) is the peak displacement at the top, \(\Delta_{y}\) is the yielding displacement estimated from pushover analysis, H is the height of the NPP, Zf,max is the peak absolute foundation settlement, Df,max is the absolute peak foundation sliding, and Mmax represents the peak base absolute moment. An EDP can be estimated from the IDA and can be denoted as EDP(Vi, Ij, Gk), where Vi represents the base conditions (fixed or nonlinear), Ij represent the earthquake intensity level of (0.1 g to 0.6 g), and Gk represents the ground motion (selected from 10 earthquakes). The seismic response of the structure can be denoted as the average of EDP(Vi, Ij, Gk) for all earthquake events at a particular PGA level Ij and for all base fixity conditions (fixed or nonlinear) Vi.

$$\overline{EDP} \left( {V_{i} ,I_{j} } \right) = \frac{1}{n}\mathop \sum \limits_{k = 1}^{n} EDP\left( {V_{i} , I_{j} , G_{k} } \right)$$
(12)

where n is the number of the strong motions applied; using the above equation, the average demand is estimated for each intensity of earthquake ground motion and base conditions and presented as a function of spectral acceleration (Sa) in a two-dimensional plot.

Table 7 EDPs selected for the dynamic analysis
Full size table

Figure 10 depicts the distribution of base shear (Fmax), i.e. EDP1 with PGA level; it is noticed that EDP1 deflates on incorporating the foundation flexibility. This reduction is more in without embedment nonlinear case and maximum in with nonlinear embedment case. Base shear (EDP1) shows increasing trends with an increase in ground motion intensity. However, it can be seen that reduction is more for higher PGA level, which may be because at higher intensity capacity of surrounding soil mobilized, such as at 0.3 g, a 37.8% increase in EDP1 occurs in with embedment case and a reduction of 10.16% in without embedment case as compared to fixed-base condition. Figure 11 shows the variation of absolute peak moment (EDP2). It shows a reduction of 30.61% at 0.3 g in with embedment case and a reduction of 54.42% in without embedment case as compared to the fixed base.

Fig. 10
figure 10

Normalized base shear (EDP1) variation with PGA

Full size image
Fig. 11
figure 11

Normalized peak moment (EDP2) variation with PGA

Full size image

Figures 12 and 13 show the top drift ratio of NPP (EDP3) and peak displacement ductility demand (EDP4) distribution against ground motion intensity. Displacement ductility demand can be defined as the ratio of maximum displacement at the top of the structure and the yielding displacement estimated from the pushover curve (Bhaumik and Raychowdhaury 2013). It is observed that the drift demand of NPP is increased with the incorporation of SSI; for instance, at 0.4 g, it increased by 38.73% and 16.67% in the case of without embedment and with embedment, respectively. It could be due to foundation movement providing flexibility to the system and increasing displacement demands in the case of without embedment. It implies that considering SSI without embedment may lead to the improper determination of roof displacement demands. Nevertheless, the displacement ductility curve (Fig. 13) represents a decreasing trend with a reduction of 44.08% and 50.26% at 0.4 g in with and without embedment case on the inclusion of SSI; furthermore, it is also observed that this reduction is increasing with the increase in ground motion intensity.

Fig. 12
figure 12

Normalized drift ratio (EDP3) variation with PGA

Full size image
Fig. 13
figure 13

Normalized displacement ductility (EDP4) variation with PGA

Full size image

To understand the SSI effect more comprehensively on NPP structure, the max settlement (EDP5) and max sliding demand (EDP6) of the raft base are studied for each PGA level (Figs. 14–15). It is noticed that with embedment settlement increases linearly up to 0.5 g; however, without embedment settlement increases linearly up to 0.3 g and increases sharply for intensity > 0.3 g, which indicates that without embedment underestimates the settlement of the foundation of NPP–foundation–soil system. In the case of EDP6, i.e. peak sliding demand, a steep rise is observed in the without embedment case with an increase in ground motion intensity, whereas in the case of with embedment, a low and steady amount of sliding is noted. For example, at 0.5 g ground motion intensity without embedment foundation, peak sliding demand is two times peak sliding demand of with embedment foundation. It indicates that neglecting foundation embedment can overestimate the sliding demand, leading to the high structural design requirement.

Fig. 14
figure 14

Normalized settlement (EDP5) variation with PGA

Full size image
Fig. 15
figure 15

Normalized sliding (EDP6) variation with PGA

Full size image

6.6 Effect of Superstructure Nonlinearity

In most SSI problems, the nonlinearity of soil is considered by the constitutive soil model, while the structural material nonlinear behaviour is ignored. However, the material nonlinearity of the superstructure significantly affects the seismic response of the NPP structure. In the present analysis, the effect of superstructure nonlinearity is investigated by including the CDP model in the structural component and results are compared with the linear elastic behaviour of structural component with SSI effect. Figure 16 shows the displacement time history at the top of the NPP structure. The peak displacement observed in the linear and nonlinear behaviour of the structure is 0.138 m and 0.160 m, respectively. Due to the structural nonlinearity, the maximum response of the NPP structure is increased by 13.7%. It can also be noticed that at the end of time history, there is a permanent displacement at the top of the structure in linear and nonlinear behaviour of superstructure. In the linear structure behaviour, this permanent deformation of the structure is due to the nonlinear behaviour of soil. Therefore, it can be said that superstructure nonlinear behaviour increases the peak displacement demand and permanent displacement of the structure by a significant amount.

Fig. 16
figure 16

Displacement time history at the top of NPP structure

Full size image

7 Conclusions

Most of the structures are designed with fixed-base conditions; the basis of this idea is that the SSI will provide a traditional design solution and so can be ignored; however, in some deign, nonlinearity is considered without embedment of foundation, which may also lead to the higher structure design requirement. The present study allowed us to address this problem through performing static, cyclic, and dynamic analysis using the IDA method on an NPP of FEM model resting on layered soil. The seismic performance of NPP facilities is checked out in terms of base shear, displacement demand of the superstructure, settlement and sliding demand of foundation, represented by EDPs. The following key points are observed in this study:

  1. 1.

    From pushover analysis, it is found that yielding force may reduce up to 8.37% and 2.37% in the case of with and without embedment, respectively, as compared to a fixed base.

  2. 2.

    IDA uncovers that moment demand may reduce up to 25.89% and 51.31% in the case of with and without embedment, respectively, as compared to a fixed base. Similarly, in base shear, demands may increase up to 21.85% in the case of with embedment and may reduce up to 29.08% in the case of without embedment of foundation as compared to a fixed base, indicating that without embedment can lead to improper seismic design.

  3. 3.

    Drift demand of NPP structure is increased up to 14.47% and 38.16% in the case of with and without embedment of foundation, respectively, compared to a fixed base. In contrast, displacement ductility demand reduced up to 47.95% and 57.52% in the case of with and without embedment of foundation.

  4. 4.

    Settlement demand increased linearly in the case of with embedment with respect to ground motion intensity; however, it increases sharply for ground motion intensity > 0.3 g in the case of without embedment.

  5. 5.

    The sliding demand of foundation increase with a low and fixed quantity of sliding is estimated in the case of with embedment case; however, it rises steeply in the case of without embedment case, indicating that without considering the embedment effect may increase the design requirement and therefore lead to uneconomical designing.

  6. 6.

    Structural nonlinearity increased the seismic response of the NPP structure by 13.7%. There is a permanent displacement at the top of the structure in the linear and nonlinear behaviour of the superstructure. Therefore, nonlinear superstructure behaviour increases the peak displacement demand and permanent displacement of the structure by a significant amount.

From the above points, it can be concluded that neglecting SSI and ignoring the embedment effect of the raft can lead to an erroneous estimation of the seismic response of NPP and uneconomical design. Furthermore, in the present study, consideration of nonlinearity of superstructure using CDP and soil nonlinearity using Drucker–Prager model increases the response of NPP structure by significant amount. Therefore, these issues should be reviewed for critical and vital facilities like NPP structures, as improper and inaccurate evaluation of the seismic response of these facilities can cause severe structural damage and health consequences.