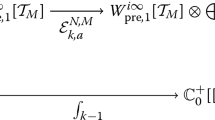Formulas for non-holomorphic Eisenstein series and for the Riemann zeta function at odd integers

Abstract

New expressions are given for the Fourier expansions of non-holomorphic Eisenstein series with weight k. Among other applications, this leads to non-holomorphic analogs of formulas of Ramanujan, Grosswald and Berndt containing Eichler integrals of holomorphic Eisenstein series.

1 Introduction

1.1 Eisenstein series

Let ${\Gamma }={\mathrm {SL}}_2({\mathbb {Z}})$ act on the upper half plane ${\mathbb {H}}$ in the usual way, with ${\Gamma }_{\infty }=\left\{ \pm (\begin{matrix}1 &{} n \\ 0 &{} 1 \end{matrix}) : n\in {\mathbb {Z}}\right\}$ the subgroup of translations fixing ${\infty }$. Throughout it is assumed that $z=x+iy \in {\mathbb {H}}$. The holomorphic Eisenstein series are basic modular forms with definition

$$\begin{aligned} E_k(z):= \sum _{{\gamma }\in {\Gamma }_{\infty }\backslash {\Gamma }} \frac{1}{j({\gamma }, z)^k} = \frac{1}{2} \sum _{\begin{array}{c} c,d \in {\mathbb {Z}}\\ \gcd (c,d)=1 \end{array}} \frac{1}{(cz+d)^k} \end{aligned}$$

(1.1)

for even $k \geqslant 4$ as in for example [40, (9) p. 13], where $j((\begin{matrix}a &{} b \\ c &{} d \end{matrix}),z):=cz+d$. They have weight k, meaning that

$$\begin{aligned} E_k({\gamma }z) = j({\gamma }, z)^{k} E_k(z) \end{aligned}$$

(1.2)

for all ${\gamma }\in {\Gamma }$. Their Fourier expansions are given by

$$\begin{aligned} E_k(z)=1+\frac{2}{\zeta (1-k)} \sum _{m=1}^\infty \sigma _{k-1}(m) e^{2\pi i m z} \end{aligned}$$

(1.3)

with $\zeta (s)$ the Riemann zeta function and $\sigma _s(m):=\sum _{d|m} d^s$ the divisor power function. The Fourier coefficients of $E_k(z)$ are rational by the relation $2/\zeta (1-k)=-2k/B_k$, with $B_k$ indicating the kth Bernoulli number. Since it is always convergent, (1.3) may be used to extend the definition of $E_k(z)$ to all $k \in 2{\mathbb {Z}}$ (and indeed to all $k\in {\mathbb {C}}$). However we cannot expect (1.2) will continue to hold.

Maass introduced and developed a similar kind of Eisenstein series that is not holomorphic but is instead an eigenfunction of the hyperbolic Laplacian and hence real analytic on ${\mathbb {H}}$. To introduce its most symmetric form, for each $k \in 2{\mathbb {Z}}$ we set

$$\begin{aligned} E_k(z,s):= \sum _{{\gamma }\in {\Gamma }_{\infty }\backslash {\Gamma }} \left( \frac{j({\gamma }, z)}{|j({\gamma }, z)|}\right) ^{-k} {\mathrm {Im}}({\gamma }z)^s \qquad ({\mathrm {Re}}(s)>1). \end{aligned}$$

(1.4)

These series satisfy

$$\begin{aligned} E_k({\gamma }z,s) = \left( \frac{j({\gamma }, z)}{|j({\gamma }, z)|}\right) ^{k} E_k(z,s) \end{aligned}$$

(1.5)

for all ${\gamma }\in {\Gamma }$, and this property may be described as transforming with non-holomorphic weight k to distinguish it from the holomorphic weight in (1.2). With the identity ${\mathrm {Im}}({\gamma }z)=y/|j({\gamma },z)|^2$ we clearly have

$$\begin{aligned} y^{-k/2} E_k(z,s)= \sum _{{\gamma }\in {\Gamma }_{\infty }\backslash {\Gamma }} \frac{{\mathrm {Im}}({\gamma }z)^{s-k/2}}{j({\gamma }, z)^k} \end{aligned}$$

(1.6)

and the holomorphic Eisenstein series is recovered from (1.6) when $s=k/2$ for even $k \geqslant 4$:

$$\begin{aligned} E_k(z)=y^{-k/2} E_k(z,k/2). \end{aligned}$$

(1.7)

In general, a function transforming with non-holomorphic weight k may be converted into one with holomorphic weight k by multiplying it by $y^{-k/2}$; for the other direction multiply by $y^{k/2}$.

The reason we restrict to k even in (1.1) and (1.4) is that the sign of $j({\gamma },z)^k$ is not well-defined for ${\gamma }\in {\Gamma }_{\infty }\backslash {\Gamma }$ when k is odd. To make (1.1) and (1.4) well-defined we could quotient by $B:=\left\{ (\begin{matrix}1 &{} n \\ 0 &{} 1 \end{matrix}) : n\in {\mathbb {Z}}\right\}$ instead of ${\Gamma }_{\infty }$ (as in the series on the right of (1.1)) but then everything cancels when k is odd since $(\begin{matrix}-1 &{} 0 \\ 0 &{} -1 \end{matrix}) \in {\Gamma }$. Taking k odd, quotienting by B and restricting to matrix elements with positive bottom left entry gives a non-zero result in the holomorphic case, with a Fourier expansion similar to (1.3), but it does not transform with weight k. See (10.6) for a similar construction that does transform correctly.

As in [23, Sect. 3.4] set

$$\begin{aligned} \theta (s) := \pi ^{-s} {\Gamma }(s) \zeta (2s). \end{aligned}$$

With this notation, the functional equation for the Riemann zeta function becomes

$$\begin{aligned} \theta ((1-s)/2) = \theta (s/2) \end{aligned}$$

(1.8)

and if we let $\mathcal {Z}$ be the set of non-trivial zeros of $\zeta (s)$, then $\theta (s)$ has its zeros exactly in $\mathcal {Z}/2$. Also $\theta (s)$ has only two poles; they are simple and at $s=0,1/2$ with residues $-1/2$ and 1 / 2 respectively. Next, for $k \in 2{\mathbb {Z}}$, put

$$\begin{aligned} \theta _k(s)&:= \theta (s) \cdot s(s+1) \cdots (s+|k|/2 -1) \nonumber \\&= \pi ^{-s} {\Gamma }(s+|k|/2) \zeta (2s) \end{aligned}$$

(1.9)

and define the completed non-holomorphic Eisenstein series of weight k as

$$\begin{aligned} E^*_k(z,s):= \theta _k(s) E_k(z,s). \end{aligned}$$

(1.10)

This is our main object of study. Non-holomorphic Eisenstein series are fundamental modular forms with many connections in the literature and we mention a small sample here. In weight 0, $E^*_{0}(z,s)$ is associated with the Epstein zeta function and evaluation of the second term in the Laurent expansion of $E^*_{0}(z,s)$ at $s=0$ or 1 gives the Kronecker limit formula [16] with important number theoretic applications. Higher terms in the Laurent expansion of $E^*_{k}(z,s)$ at $s=k/2$ are used in [28] to give a basis for polyharmonic Maass forms. The Rankin–Selberg method [10, Sect. 1.6] gives the convolution L-function for two cusp forms and requires $E^*_{0}(z,s)$ if the cusp forms have the same weight and $E^*_{k}(z,s)$ if the difference of their weights is k. The continuous spectrum for the weight k hyperbolic Laplacian is constructed with Eisenstein series; see [23] for weight 0 and [15, Sect. 4] for general weights. Recent interest in the series $E^*_{k}(z,s)$ comes with their connection to modular graph functions [8, 14]. In this paper we focus on applications to evaluating the Riemann zeta function and automorphic L-functions at integers.

1.2 Main results

For the Fourier expansion of $E^*_0(z,s)$ we need the next definitions. Let

$$\begin{aligned} K_w(y):=\frac{1}{2}\int _0^\infty e^{-y(t+1/t)/2} t^{w-1}\, dt \qquad (w\in {\mathbb {C}}, \ y>0) \end{aligned}$$

(1.11)

be the modified Bessel function. It is entire in the parameter w and, following (1.26), (1.27) in [23], a convenient Whittaker function variant may be defined as

$$\begin{aligned} W_s(z) := 2|y|^{1/2} K_{s-1/2}(2\pi |y|)\cdot e^{2\pi i x} \end{aligned}$$

(1.12)

for $s \in {\mathbb {C}}$ and $z \in {\mathbb {C}}-{\mathbb {R}}$. This gives $W_s(z) = W_s(\overline{z})$ and

$$\begin{aligned} W_s(z) \sim e^{2\pi i z} \quad \text {as} \quad y\rightarrow \infty . \end{aligned}$$

As seen in [10, Sect. 1.6] or [23, Sect. 3.4] for example, the Fourier expansion of the weight 0 Eisenstein series for the modular group is given by

$$\begin{aligned} E^*_{0}(z,s) = \theta (s) y^s+ \theta (1-s) y^{1-s} + \sum _{m \in {\mathbb {Z}}_{\ne 0}} \frac{ \sigma _{2s-1}(|m|)}{|m|^s} W_s(m z). \end{aligned}$$

(1.13)

Since all the terms on the right are defined for $s\in {\mathbb {C}}$, and the function $W_s(z)$ has exponential decay, (1.13) furnishes us with the meromorphic continuation of $E^*_{0}(z,s)$ to all $s\in {\mathbb {C}}$. The only poles are contributed by the constant (with respect to x) term $\theta (s) y^s+ \theta (1-s) y^{1-s}$. They are at $s=0,$ 1 and simple with

$$\begin{aligned} \mathop {\mathrm{Res}}\limits _{s=0} E^*_{0}(z,s) = -1/2, \qquad \mathop {\mathrm{Res}}\limits _{s=1} E^*_{0}(z,s) = 1/2. \end{aligned}$$

(1.14)

We will develop the theory of non-holomorphic, weight k Eisenstein series using (1.13) as the starting point and our first result is essentially obtained by differentiating (1.13). For n,  $r\in {\mathbb {Z}}$ define the polynomial $P^n_r(x) \in {\mathbb {Z}}[x]$ as follows. When $n\geqslant 0$ set

$$\begin{aligned} P^n_r(x) := \sum _{\ell =|r|}^n \frac{(2n)! }{(n-\ell )! (\ell +r)! (\ell -r)!} (-x)^\ell , \end{aligned}$$

(1.15)

giving a variant of the generalized Laguerre polynomial. When $n<0$ define $P_r^{n}(x)$ to be $(-1)^r P_r^{-n}(-x)$.

Theorem 1.1

For all $k \in 2{\mathbb {Z}}$ and all $s\in {\mathbb {C}}$ with ${\mathrm {Re}}(s)>1$,

$$\begin{aligned} E^*_k(z,s)= & {} \theta _k(s) y^s+\theta _k(1-s) y^{1-s} \nonumber \\&+\, 2^{-|k|} \sum _{m \in {\mathbb {Z}}_{\ne 0}} \frac{ \sigma _{2s-1}(|m|)}{|m|^s} \sum _{r=-|k|/2}^{|k|/2} \left( \frac{m}{|m|}\right) ^r P^{k/2}_r(4\pi my) \cdot W_{s+r}(mz). \end{aligned}$$

(1.16)

The right hand side of (1.16) converges absolutely and uniformly on compacta for all $s\in {\mathbb {C}}$, giving the meromorphic continuation of $E^*_k(z,s)$ to the whole s plane. When k is nonzero, $E^*_k(z,s)$ is an entire function of s.

The expansion (1.16) for $E^*_k(z,s)$ appears to be new and is more suited to our needs in this paper than the expansions in the literature in terms of Whittaker functions $W_{\kappa ,\mu }$ or other confluent hypergeometric functions; see the comparisons at the end of Sect. 3.

The well-known functional equation for this Eisenstein series takes the form

$$\begin{aligned} E^*_k(z,1-s) = E^*_k(z,s) \end{aligned}$$

(1.17)

and is evident from (1.16) and the identities

$$\begin{aligned} \sigma _w(m)=m^w \sigma _{-w}(m), \qquad K_w(y)=K_{-w}(y). \end{aligned}$$

The relation

$$\begin{aligned} E^*_{-k}(z,s) = \overline{E^*_k(z,\overline{s})} \end{aligned}$$

(1.18)

may also be verified using (1.16), or more simply with (1.4) and analytic continuation to all $s\in {\mathbb {C}}$.

For $k \in 2{\mathbb {Z}}$, $h \in {\mathbb {Z}}$ and $u \in {\mathbb {Z}}_{\geqslant 0}$, define the integers

$$\begin{aligned} h^*:=|h-1/2| -1/2 = {\left\{ \begin{array}{ll} h-1 &{}\quad \text { if }\, h \geqslant 1; \\ -h &{}\quad \text { if }\, h \leqslant 0, \end{array}\right. } \end{aligned}$$

(1.19)

and

$$\begin{aligned} \mathcal {A}^k_h(u) := {\left\{ \begin{array}{ll} \displaystyle (-1)^{u+k/2} u! \left( {\begin{array}{c}k/2+h-1\\ u\end{array}}\right) \left( {\begin{array}{c}k/2-h\\ u\end{array}}\right) &{} \quad \text { if }\, k\geqslant 0;\\ \displaystyle (-1)^u \frac{[(u-k/2)!]^2}{u!} \left( {\begin{array}{c}h-1\\ u-k/2\end{array}}\right) \left( {\begin{array}{c}-h\\ u-k/2\end{array}}\right)&\quad \text { if }\, k \leqslant 0. \end{array}\right. } \end{aligned}$$

(1.20)

Note that throughout this paper we use the usual generalized binomial coefficients as given in (4.1). With this notation we may describe the Fourier development of $E^*_k(z,s)$ very explicitly when s is an integer:

Theorem 1.2

For all $h \in {\mathbb {Z}}$ and $k \in 2{\mathbb {Z}}$, except $(h,k)=(0,0)$ or (1, 0),

$$\begin{aligned} E^*_k(z,h)= & {} \theta _k(h) y^h+\theta _k(1-h) y^{1-h} + \sum _{m =1}^\infty \frac{ \sigma _{2h-1}(m)}{m^h} \ e^{2\pi i m z} \sum _{u=0}^{h^* +k/2} \mathcal {A}^k_h(u) \cdot (4\pi m y)^{-u+k/2}\nonumber \\&+\,\sum _{m =1}^\infty \frac{ \sigma _{2h-1}(m)}{m^h} \ e^{-2\pi i m \overline{z}} \sum _{u=0}^{h^*-k/2} \mathcal {A}^{-k}_h(u) \cdot (4\pi m y)^{-u-k/2}. \end{aligned}$$

(1.21)

Since some of the $\mathcal {A}$ coefficients are zero, the upper bounds for the indices of the inner sums in (1.21) may be reduced exactly in the following cases. If $h^*<k/2$ then the upper bound of $h^*+k/2$ for the first inner sum may be reduced to $k/2-1-h^*$. If $h^*<-k/2$ then the upper bound of $h^*-k/2$ for the second inner sum may be reduced to $-k/2-1-h^*$.

Fig. 1

The lattice of Eisenstein series in the hk plane

All the terms in (1.21) are simple to calculate. For the constant term coefficients we have the following useful formula which derives from the basic properties of $\zeta (s)$ and ${\Gamma }(s)$. For all $k,m \in {\mathbb {Z}}$ with k even and $(k,m) \ne (0,0)$,

$$\begin{aligned} \theta _{k}(m)={\left\{ \begin{array}{ll} \pi ^{-m} (m+|k|/2-1)! \zeta (2m) &{} \quad \text {if} \quad 0 \leqslant m; \\ 0 &{} \quad \text {if} \quad -|k|/2< m < 0; \\ \displaystyle (-1)^{k/2}(4\pi )^m \frac{(2|m|)!}{(|m|-|k|/2)!} \zeta (1-2m) &{} \quad \text {if} \quad m \leqslant -|k|/2. \end{array}\right. } \end{aligned}$$

(1.22)

Figure 1 illustrates the lattice of Eisenstein series described in Theorem 1.2. Each dot in position (h, k) represents the one dimensional ${\mathbb {C}}$-vector space generated by $E^*_k(z,h)$. The lattice naturally breaks into four triangular regions. In the upper triangle we have $h^*<k/2$, and by (1.21) the Eisenstein series here are exactly those with no negative terms in their Fourier expansions (i.e. no terms containing $e^{2\pi i m \overline{z}}$ with m negative). In the lower triangle we have $h^*<-k/2$, and these series have no positive terms (i.e. no terms containing $e^{2\pi i m z}$ with m positive). These upper and lower triangles are interchanged by conjugation. This reflective symmetry $k \leftrightarrow -k$ is indicated with arrows in the figure and comes from (1.18). The left-right symmetry $h \leftrightarrow 1-h$ from (1.17) is also indicated. The main diagonal line $h=k/2$ is shown along with its three images under these symmetries. The Eisenstein series corresponding to points on these lines are studied in Sect. 8.

Theorem 1.2 was first stated in [17, Thm. 3.1] and the proof, which we give here in full, briefly sketched. Theorem 1.2 was used there in providing new proofs of Manin’s Periods Theorem and results of Kohnen and Zagier. We summarize some of these ideas in Sects. 9 and 10. Almost all of the methods and results of [17] are contained in Chapter 12 of [12], as acknowledged in that book’s online errata. Theorem 1.2 appears there in Section 12.2. We note that Theorem 1.2 must also be equivalent to the many cases in Corollaries 2.4, 2.5 and 2.7 of [25]. Recent computations of Brown in [8, 9] are equivalent to Theorem 1.2 when $|k/2|<h$ (the right triangular region in Fig. 1) as described in Sect. 6.

In Sect. 5 we show that Theorem 1.2 may be used to prove and generalize a result in [11] related to spectral zeta functions associated to a torus. A formula of Terras and Grosswald on values of the Riemann zeta function at odd integers is also proven and generalized using Theorem 1.2 in Sect. 7. Terras [36] and Grosswald [21] both mention the inspiring earlier formula of Ramanujan concerning $\zeta (2h-1)$. This is entry 21(i) of Chapter 14 in the second notebook; see [4, p. 276]. We refer the reader to [3, 5] for a detailed account of this formula, its history and the related work of many authors. It has been greatly generalized by Grosswald, see for example [19, Sect. 4], and in a different direction by Berndt in [3, Thm. 2.1], giving the transformation formula of a very general type of Eisenstein series. A special case of Berndt’s formula is [3, Thm. 2.2] and we state a slightly rearranged version of this as follows. For all $z\in {\mathbb {H}}$ and $k\in {\mathbb {Z}}$,

$$\begin{aligned}&z^k \left( 1+(-1)^k\right) \sum _{\ell =1}^\infty \sigma _{k-1}(\ell ) e^{2\pi i \ell z} - \left( 1+(-1)^k\right) \sum _{\ell =1}^\infty \sigma _{k-1}(\ell ) e^{2\pi i \ell (-1/z)} \nonumber \\&\quad = (2\pi i)^{1-k} \sum _{\begin{array}{c} u,v \in {\mathbb {Z}}_{\geqslant 0} \\ u+v=2-k \end{array}} \frac{B_{u}}{u!}\frac{B_{v}}{v!} z^{1-v} -{\left\{ \begin{array}{ll} \pi i -\log z &{}\quad \text {if }\, k=0; \\ \left( z^k-(-1)^k\right) \zeta (1-k) &{}\quad \text {if }\, k\ne 0. \end{array}\right. } \end{aligned}$$

(1.23)

Note that the sum containing Bernoulli numbers on the right is empty and vanishes when $k>2$. If k is odd then the left side of (1.23) disappears and, letting $k=1-m$, a short calculation results in

$$\begin{aligned} \zeta (m)= {\left\{ \begin{array}{ll} -(2\pi i)^{m}B_{m}/(2 \cdot m!) &{}\quad \text {if }\, m\in 2{\mathbb {Z}}_{\geqslant 0}; \\ 0 &{}\quad \text {if }\, m\in 2{\mathbb {Z}}_{< 0}, \end{array}\right. } \end{aligned}$$

(1.24)

incorporating Euler’s famous formula. Set

$$\begin{aligned} U_k(z):= \sum _{m=1}^\infty \sigma _{k-1}(m) e^{2\pi i m z}=\sum _{m=1}^\infty \frac{m^{k-1}}{e^{-2\pi i m z}-1}. \end{aligned}$$

For $k\in 2{\mathbb {Z}}$, (1.23) then becomes what we may call the master formula:

$$\begin{aligned}&2\left( z^k U_k(z) - U_k(-1/z) \right) = (2\pi i)^{1-k} \sum _{\begin{array}{c} u,v \in {\mathbb {Z}}_{\geqslant 0} \\ u+v=1-k/2 \end{array}} \frac{B_{2u}}{(2u)!}\frac{B_{2v}}{(2v)!} z^{1-2v}\nonumber \\&\quad +{\left\{ \begin{array}{ll} -\pi i/2 +\log z &{}\quad \text {if }\, k=0; \\ \left( 1-z^k\right) \zeta (1-k) &{}\quad \text {if }\, k\ne 0. \end{array}\right. } \end{aligned}$$

(1.25)

This is equivalent to Ramanujan’s formula for $k \ne 0$ and z purely imaginary. The negative even k cases of (1.25) first appeared in [20, p. 11]. The reader may follow in the footsteps of Ramanujan, Grosswald [20, 21] and Berndt [3] by employing this master formula to produce elegant identities. For example, substituting $z=i$ and $k=-2$ gives

$$\begin{aligned} \zeta (3)=\frac{7\pi ^3}{180}-2\sum _{m=1}^\infty \sigma _{-3}(m) e^{-2\pi m}. \end{aligned}$$

(1.26)

Letting $z=i$ and $k=2-2h$ gives the general form, for all $h \in 2{\mathbb {Z}}$,

$$\begin{aligned} \zeta (2h-1) = -\frac{(2\pi )^{2h-1}}{2} \sum _{\begin{array}{c} u,v \in {\mathbb {Z}}_{\geqslant 0} \\ u+v=h \end{array}} (-1)^u \frac{B_{2u}}{(2u)!}\frac{B_{2v}}{(2v)!} -2\sum _{m=1}^\infty \sigma _{1-2h}(m) e^{-2\pi m} \end{aligned}$$

(1.27)

which is originally due to Lerch [4, p. 276] for positive even h. Moreover, (1.25) may be used to study the algebraic nature of the odd zeta values, as shown in [19].

We next describe a natural non-holomorphic counterpart to the master formula (1.25). Set

$$\begin{aligned} V_k(z):= \sum _{m=1}^\infty \sigma _{k-1}(m) e^{-2\pi i m \overline{z}}\sum _{u=0}^{-k} \frac{(4\pi m y)^{u}}{u!}. \end{aligned}$$

(1.28)

Theorem 1.3

For all $k\in 2{\mathbb {Z}}$ and $z\in {\mathbb {H}}$ we have

$$\begin{aligned}&2\left( z^k V_k(z) - V_k(-1/z) \right) = \frac{2\zeta (2-k)}{(2\pi i)^k} \left( \frac{y}{\pi }\right) ^{1-k}\left( |z|^{2k-2}-z^k \right) \nonumber \\&\quad -(2\pi i)^{1-k} \sum _{\begin{array}{c} u,v \in {\mathbb {Z}}_{\geqslant 0} \\ u+v=1-k/2 \end{array}} \frac{B_{2u}}{(2u)!}\frac{B_{2v}}{(2v)!} z^{1-2v} + {\left\{ \begin{array}{ll} 0 &{}\quad \text {if }\, k>0; \\ \pi i/2 +\overline{\log z} &{}\quad \text {if }\, k=0; \\ \left( 1- z^k\right) \zeta (1-k) &{}\quad \text {if }\, k< 0. \end{array}\right. } \end{aligned}$$

(1.29)

Theorem 1.3 is proved, and some of its consequences explored, in Sect. 8. For example (1.27) has a companion identity and adding (1.27) to its companion shows, for even $h\geqslant 2$,

$$\begin{aligned} \zeta (2h-1) = \frac{4^{h-1}}{\pi }\zeta (2h) -\sum _{m=1}^\infty \sigma _{1-2h}(m) e^{-2\pi m}\left( 1+\sum _{u=0}^{2h-2} \frac{(4\pi m)^u}{u!}\right) , \end{aligned}$$

(1.30)

or equivalently, employing (1.24) and the incomplete ${\Gamma }$ function,

$$\begin{aligned} \zeta (2h-1) = \frac{(4\pi )^{2h-1}|B_{2h}|}{2(2h)!} -\sum _{m=1}^\infty \sigma _{1-2h}(m) \Big (e^{-2\pi m}+ {\Gamma }(2h-1,4\pi m) \cdot e^{2\pi m} \Big ). \end{aligned}$$

(1.31)

As we see in Sect. 8, $V_k(z)$ arises along with $U_k(z)$ in a naturally occurring harmonic Maass form of holomorphic weight k that seems to have been first studied by Pribitkin in [13]. Define $\varepsilon (k)$ to be 2 if $k\geqslant 0$ and 1 if $k< 0$. Then for all $k \in 2{\mathbb {Z}}$, the Maass form in question, by an application of Theorem 1.2, is

$$\begin{aligned} {\mathbb {E}}_k(z) = 1 + \frac{\varepsilon (k)}{\zeta (1-k)} \left[ \frac{\zeta (2-k)}{(2\pi i)^k} \left( \frac{y}{\pi }\right) ^{1-k} + U_k(z) + V_k(z)\right] . \end{aligned}$$

2 Applying the raising and lowering operators

Define the raising and lowering operators of Maass as

$$\begin{aligned} R_k := 2iy \frac{\partial }{\partial z} + \frac{k}{2} \qquad \text {and} \qquad L_k := -2iy \frac{\partial }{\partial \overline{z}} - \frac{k}{2} \end{aligned}$$

respectively. Here $\frac{\partial }{\partial z} := \frac{1}{2}(\frac{\partial }{\partial x}-i\frac{\partial }{\partial y})$, $\frac{\partial }{\partial \overline{z}} := \frac{1}{2}(\frac{\partial }{\partial x}+i\frac{\partial }{\partial y})$ and it is easy to check that $L_k f = \overline{R_{-k} \overline{f}}$. If a function has non-holomorphic weight k, in the sense of (1.5), then applying $R_k$ raises its weight to $k+2$ and applying $L_k$ lowers its weight to $k-2$; see for example [10, Lemma 2.1.1]. The weight k Laplacian is

$$\begin{aligned} \Delta _k :=-4y^2\frac{\partial ^2}{\partial z \partial \overline{z}}+ik y \left( \frac{\partial }{\partial z} + \frac{\partial }{\partial \overline{z}}\right) = -y^2 \left( \frac{\partial ^2}{\partial x^2} + \frac{\partial ^2}{\partial y^2}\right) +ik y \frac{\partial }{\partial x} \end{aligned}$$

and, as in [10, Sect. 2.1], satisfies

$$\begin{aligned} \Delta _k = -L_{k+2} \circ R_k -\frac{k}{2}\left( 1+\frac{k}{2} \right) = -R_{k-2} \circ L_k +\frac{k}{2}\left( 1-\frac{k}{2} \right) . \end{aligned}$$

(2.1)

Our definitions of $R_k,$ $L_k$ and $\Delta _k$ follow those of Bump in [10] and have a symmetrical effect on the Eisenstein series as we see next. Maass’s original operators were $K_k=R_k$, $\Lambda _k=-L_k$ and he used the Laplacian with the opposite sign. These conventions of Maass are followed in [24] and [15, Sect. 4], for example. To act on spaces of functions transforming with holomorphic weight k, such as harmonic Maass forms, the operators must be adjusted; see for example (8.2) at the start of Sect. 8.

Assuming $k \in 2{\mathbb {Z}}$ and ${\mathrm {Re}}(s)>1$, a calculation with (1.4) shows

$$\begin{aligned}&R_k E_k(z,s) = (s+k/2)E_{k+2}(z,s), \end{aligned}$$

(2.2)

$$\begin{aligned}&L_k E_k(z,s) = (s-k/2)E_{k-2}(z,s). \end{aligned}$$

(2.3)

Hence

$$\begin{aligned} R_k E^*_k(z,s)&= {\left\{ \begin{array}{ll} E^*_{k+2}(z,s) &{}\quad k\, \geqslant 0; \\ (s+|k|/2-1)(s-|k|/2) E^*_{k+2}(z,s) &{}\quad k\, < 0, \end{array}\right. } \end{aligned}$$

(2.4)

$$\begin{aligned} L_k E^*_k(z,s)&= {\left\{ \begin{array}{ll} E^*_{k-2}(z,s) &{}\quad k\, \leqslant 0; \\ (s+|k|/2-1)(s-|k|/2) E^*_{k-2}(z,s) &{}\quad k\, > 0. \end{array}\right. } \end{aligned}$$

(2.5)

As a consequence of (2.1)–(2.5), for $k \in 2{\mathbb {Z}}$ and ${\mathrm {Re}}(s)>1$,

$$\begin{aligned} \Delta _k E_k(z,s) = s(1-s) E_k(z,s), \qquad \Delta _k E^*_k(z,s) = s(1-s) E^*_k(z,s). \end{aligned}$$

(2.6)

A convenient notation for n applications of the raising operator, going from weight 0 to weight 2n, is

$$\begin{aligned} R^n_0 := R_{2n-2} \circ R_{2n-4} \circ \cdots \circ R_{2} \circ R_{0}. \end{aligned}$$

Therefore, with $k/2 \in {\mathbb {Z}}_{\geqslant 0}$ and ${\mathrm {Re}}(s)>1$,

$$\begin{aligned} R_0^{k/2}E^*_0(z,s) = E^*_k(z,s) \end{aligned}$$

(2.7)

and to prove Theorem 1.1 we apply $R_0^{k/2}$ to (1.13). The next lemma is required for this and was first derived in [34, Sect. 5] by simplifying recurrences. We give a new proof based on the properties of the polynomials $P_r^n(x)$ defined in (1.15). For $n \geqslant 0$ these polynomials may also be expressed as

$$\begin{aligned} P_r^n(x) = \left( {\begin{array}{c}2n\\ n+r\end{array}}\right) \sum _{\ell =|r|}^n (n-\ell )! \left( {\begin{array}{c}n+r\\ \ell +r\end{array}}\right) \left( {\begin{array}{c}n-r\\ \ell -r\end{array}}\right) (-x)^\ell \end{aligned}$$

or, in terms of the generalized Laguerre polynomials $L_m^{(\alpha )}(x)$, as

$$\begin{aligned} P_r^n(x) = \frac{(2n)!}{(n+r)!}(-x)^r L_{n-r}^{(2r)}(x) \qquad \text {with} \qquad L_m^{(\alpha )}(x):=\sum _{j=0}^m \left( {\begin{array}{c}m+\alpha \\ m-j\end{array}}\right) \frac{(-x)^j}{j!}. \end{aligned}$$

(2.8)

Lemma 2.1

For all $k/2 \in {\mathbb {Z}}_{\geqslant 0}$, $m\in {\mathbb {R}}_{\ne 0}$ and $z\in {\mathbb {H}}$ we have

$$\begin{aligned} R^{k/2}_0 W_s(mz) = 2^{-k}\sum _{r=-k/2}^{k/2} \left( \frac{m}{|m|}\right) ^r P^{k/2}_r(4\pi my) \cdot W_{s+r}(mz). \end{aligned}$$

(2.9)

Proof

Verify that

$$\begin{aligned} 4\frac{d}{dx}P_r^n(x) = \frac{1}{x} P_r^{n+1}(x)+\left( 2-\frac{4n+2}{x} \right) P_r^n(x) + P_{r+1}^n(x) + P_{r-1}^n(x) \end{aligned}$$

and hence

$$\begin{aligned} y \frac{d}{dy} P_r^{k/2}(4\pi my)= & {} \frac{1}{4} P_r^{k/2+1}(4\pi my) +\left( 2\pi m y-\frac{k+1}{2}\right) P_r^{k/2}(4\pi my)\nonumber \\&+\,\pi m y \left( P_{r+1}^{k/2}(4\pi my) +P_{r-1}^{k/2}(4\pi my)\right) . \end{aligned}$$

(2.10)

We also require the identity

$$\begin{aligned} 2iy \frac{d}{dz} W_{s+r}(m z) = -\pi |m|y \bigl ( W_{s+r-1}(m z) + W_{s+r+1}(m z) \bigr ) +\left( \frac{1}{2}-2\pi m y\right) W_{s+r}(m z) \end{aligned}$$

(2.11)

which follows from $2\frac{d}{dy} K_w(y) = -K_{w+1}(y)- K_{w-1}(y)$. The proof now proceeds by induction on k / 2. The equality (2.9) is true when $k=0$ and if it holds for k then

$$\begin{aligned} R^{(k+2)/2}_0 W_s(mz)&= R_k \circ R^{k/2}_0 W_s(mz) \\&= 2iy \frac{d}{dz}\left( R^{k/2}_0 W_s(mz)\right) +\frac{k}{2} \left( R^{k/2}_0 W_s(mz)\right) , \end{aligned}$$

giving

$$\begin{aligned} R^{(k+2)/2}_0 W_s(mz)= & {} 2^{-k}\sum _{r=-k/2}^{k/2} \left( \frac{m}{|m|}\right) ^r \bigg \{ y \frac{d}{dy} P_r^{k/2}(4\pi my) \cdot W_{s+r}(mz) \\&+\,P_r^{k/2}(4\pi my) \cdot 2iy \frac{d}{dz} W_{s+r}(mz) + \frac{k}{2} P_r^{k/2}(4\pi my) \cdot W_{s+r}(mz) \bigg \}. \end{aligned}$$

Simplifying this with (2.10) and (2.11) shows the induction step and completes the proof. $\square$

For all $s\in {\mathbb {C}}$ an induction shows

$$\begin{aligned} R^{k/2}_0 \big (\theta (s) y^s \big ) = \theta _k(s) y^s \end{aligned}$$

(2.12)

and it is easy to check that $\theta _k(s)y^s + \theta _k(1-s)y^{1-s}$ for $k \ne 0$ is an entire function of s. Lemma 2.1 and (2.12) show that formally applying the raising operator to each term in the weight 0 expansion (1.13) produces the weight $k\geqslant 0$ expansion (1.16). The relation (1.18) allows us to access negative weights and is equivalent to applying the lowering operator. For this, conjugate the right side of (2.9) and replace s with $\overline{s}$. With (1.12) it may be verified that $\overline{W_{\overline{s}+r}(m z)} = W_{s+r}((-m)z)$ and hence, with our definition of $P^n_r(x)$ for negative n after (1.15), we formally obtain (1.16) for negative k also. In the next section we make the necessary estimates to prove these expansions are valid.

3 Bounds for $E^*_k(z,s)$

3.1 Initial estimates

Note that (1.11) implies $|K_w(y)|\leqslant K_r(y)$ for all $w\in {\mathbb {C}}$ with real part r. Also $K_r(y)$ is always positive and equals $K_{-r}(y)$.

Lemma 3.1

For $r\in {\mathbb {R}}$ and $y>0$,

$$\begin{aligned} K_r(y) <2^{2|r|+1}\left( 1+\frac{{\Gamma }(|r|+1)}{y^{|r|+1}} \right) e^{-y}. \end{aligned}$$

(3.1)

Proof

Assume that $r \geqslant 0$. We have

$$\begin{aligned} 2K_r(y) = K_r(y)+K_{-r}(y) \,\,&= \frac{1}{2} \int _0^\infty e^{-y(t+1/t)/2} (t^{r}+ t^{-r})\, \frac{dt}{t} \\&= \int _1^\infty e^{-y(t+1/t)/2} (t^{r}+ t^{-r})\, \frac{dt}{t}. \end{aligned}$$

For $T\geqslant 1$ the lower part of this last integral is

$$\begin{aligned} \int _{1}^T e^{-y(t+1/t)/2} (t^{r}+ t^{-r})\, \frac{dt}{t} < \int _{1}^T e^{-y} (2 T^{r})\, \frac{dt}{t} = 2e^{-y} T^r \log T. \end{aligned}$$

(3.2)

The upper part is

$$\begin{aligned} \int _{T}^\infty e^{-y(t+1/t)/2} (t^{r}+ t^{-r})\, \frac{dt}{t}&< \int _{T}^\infty e^{-y t/2} (2 t^{r-1})\, dt \nonumber \\&= 2 \int _{0}^\infty e^{-y (T+u)/2} (T+u)^{r}\, \frac{du}{T+u} \nonumber \\&< \frac{2}{T} e^{-y T/2} \int _{0}^\infty e^{-y u/2} (T+u)^{r}\, du. \end{aligned}$$

(3.3)

Using the bound $(T+u)^{r} \leqslant (2T)^r+(2u)^r$ for $T,u,r\geqslant 0$, computing the resulting integrals and adding to (3.2) shows

$$\begin{aligned} K_r(y) < e^{-y} T^r \log T + \frac{2}{T} e^{-y T/2} \left( \frac{(2T)^{r}}{y}+ \frac{4^r {\Gamma }(r+1)}{y^{r+1}} \right) . \end{aligned}$$

Choosing $T=2$ and simplifying completes the proof. $\square$

If in (3.3) we instead use

$$\begin{aligned} \frac{(T+u)^r}{T+u} \leqslant \frac{(2T)^r+ (2u)^r}{T+u} \leqslant 2^r\left( T^{r-1}+u^{r-1}\right) , \end{aligned}$$

then the same arguments lead to

$$\begin{aligned} K_r(y) <4^{|r|}\left( 1+\frac{1}{y}+\frac{{\Gamma }(|r|)}{y^{|r|}} \right) e^{-y} \qquad \text {for} \qquad y>0,r\in {\mathbb {R}}_{\ne 0}. \end{aligned}$$

(3.4)

This improves (3.1) for small y but is not valid at $r=0$ as the ${\Gamma }$ function has a pole there.

Proposition 3.2

Let $S_k(z,s)$ be the series over m on the right of (1.16). For all $z\in {\mathbb {H}}$ and $s\in {\mathbb {C}}$ this series is absolutely convergent and satisfies $S_k(z,s)=S_k(z,1-s)$. Bounding the absolute value of its terms for $\sigma :={\mathrm {Re}}(s) \geqslant 1/2$ yields

$$\begin{aligned} S_k(z,s) \ll \left( y^{|k|/2+1/2}+y^{-\sigma -|k|/2-1}\right) e^{-2\pi y} \end{aligned}$$

(3.5)

for an implied constant depending only on k and s.

Proof

As we saw in (1.17), the terms of $S_k(z,s)$ are invariant as $s \rightarrow 1-s$, so we may assume $\sigma \geqslant 1/2$. Simple bounds show

$$\begin{aligned} \left| |m|^{-s} \sigma _{2s-1}(|m|)\right| \leqslant |m|^\sigma , \qquad \left| P_r^{k/2}(4\pi my) \right| \leqslant (4\pi )^{|k|/2}(|k|+1)!\left( 1+(my)^{|k|/2} \right) \end{aligned}$$

and so we may also assume for simplicity that $k\geqslant 0$. Hence

$$\begin{aligned} S_k(z,s) \ll y^{1/2}\sum _{m=1}^\infty m^{\sigma +1/2}\left( 1+(my)^{k/2}\right) \sum _{r=-k/2}^{k/2} K_{\sigma +r-1/2}(2\pi m y) \end{aligned}$$

(3.6)

and Lemma 3.1 implies

$$\begin{aligned} S_k(z,s) \ll y^{1/2}\sum _t \sum _{m=1}^\infty m^{\sigma +1/2}\left( 1+(my)^{k/2}\right) \left( 1+\frac{1}{(m y)^{t}}\right) e^{-2\pi m y} \end{aligned}$$

(3.7)

where $t\geqslant 1$ takes the values $|\sigma +r-1/2|+1$ for integers r with $-k/2\leqslant r\leqslant k/2$.

For $y>0$, $r\in {\mathbb {R}}$ and $r':=\max (0,r)$, the inequality

$$\begin{aligned} \sum _{m=1}^\infty m^r e^{-m y} \leqslant e^{-y} \left( 1+2^{r'} e^{-y} + 3^{r'} \frac{{\Gamma }(r'+1)}{y^{r'+1}} \right) \end{aligned}$$

(3.8)

follows by comparing the series on the left to the ${\Gamma }$ function integral. Expanding (3.7) and employing (3.8) proves (3.5). The $y^{-\sigma -|k|/2-1}$ term in (3.5) comes from estimating

$$\begin{aligned} y^{1/2} \sum _{m=1}^\infty m^{\sigma +1/2}\frac{1}{(m y)^{t}} e^{-2\pi m y} \qquad \text {when} \qquad t=\sigma +k+1/2. \end{aligned}$$

$\square$

3.2 The analytic continuation of $E_k^*(z,s)$

Proof of Theorem 1.1

Let

$$\begin{aligned} S_k^*(z,s) := \theta _k(s) y^s+\theta _k(1-s) y^{1-s} +S_k(z,s) \end{aligned}$$

be the right side of (1.16). For ${\mathrm {Re}}(s)>1$ and $k=0$ we have seen in (1.13) that $E_0^*(z,s) = S_0^*(z,s)$. Applying $R_0$ to $E_0^*(z,s)$ gives $E_2^*(z,s)$ and, continuing this procedure as in (2.7), $R_0^{k/2}E^*_0(z,s)$ equals $E_{k}^*(z,s)$. The terms of $S_k^*(z,s)$ are differentiable in x and y with continuous derivatives. We saw in Sect. 2 that $S_k^*(z,s)$ is obtained by repeatedly raising the terms of $S_0^*(z,s)$ and is absolutely convergent by Proposition 3.2. Suppose we have established that $E_k^*(z,s) = S_k^*(z,s)$. To show that $E_{k+2}^*(z,s) = S_{k+2}^*(z,s)$, we require the uniform convergence of the raising operator’s derivatives. Let $S_k(z,s)_x$ be the series $S_k(z,s)$ but with each term replaced by its partial derivative with respect to x and define similarly $S_k(z,s)_y$ with the partial derivatives with respect to y. Then $S_k(z,s)_x$ may be bounded as in (3.6) but with an extra m factor. The proof of Proposition 3.2 goes through and shows that $S_k(z,s)_x$ converges uniformly for z in compact subsets of ${\mathbb {H}}$. The terms of $S_k(z,s)_y$ may be computed with (2.10) and (2.11). We find they are bounded by the estimates for $S_{k+2}(z,s)$ in Proposition 3.2 and hence also converge uniformly.

These results prove that (1.16) is true for ${\mathrm {Re}}(s)>1$ and even $k\geqslant 0$. The relation (1.18) extends this to $k<0$. The estimates in Proposition 3.2 are valid for all $s \in {\mathbb {C}}$. Since the bounds from Lemma 3.1 and (3.8) are uniform for s in compact subsets of ${\mathbb {C}}$, Proposition 3.2 also shows that, for each $z \in {\mathbb {H}}$, $S_k(z,s)$ is an entire function of s. In this way the Fourier expansion $S_k^*(z,s)$ gives the analytic continuation of $E_k^*(z,s)$ to all $s \in {\mathbb {C}}$. The only poles come from the constant term when $k=0$. $\square$

The next corollary now follows from Theorem 1.1 and Proposition 3.2; see [23, Cor. 3.5] for a similar estimate when $k=0$. We will need this result, and in particular its bound on $E^*_k(z,s)$ as $y \rightarrow 0$, in the proof of Proposition 9.1.

Corollary 3.3

For all $s\in {\mathbb {C}}$ with real part $\sigma$, we have

$$\begin{aligned} E^*_k(z,s)= \theta _k(s) y^s+\theta _k(1-s) y^{1-s} +O\left( \left( y^{|k|/2+1/2}+y^{-|\sigma -1/2|-|k|/2-3/2}\right) e^{-2\pi y}\right) \end{aligned}$$

where the implied constant depends only on $k \in 2{\mathbb {Z}}$ and $\sigma$.

By analytic continuation, the fundamental non-holomorphic weight k transformation property (1.5) remains valid for $E^*_{k}(z,s)$ for all $s\in {\mathbb {C}}$. We next prove that the eigenvalue identity (2.6) also extends to all s (avoiding the poles $s=0,1$ when $k=0$). With Theorem 1.1 we have shown that for even $k \geqslant 0$

$$\begin{aligned} E^*_{k}(z,s) = R_0^{k/2}\left( \theta (s) y^s + \theta (1-s) y^{1-s}\right) + \sum _{m \in {\mathbb {Z}}_{\ne 0}} \frac{ \sigma _{2s-1}(|m|)}{|m|^s} R_0^{k/2}\left( W_s(m z)\right) . \end{aligned}$$

(3.9)

The relations in (2.1) imply $\Delta _k \circ R_{k-2}=R_{k-2} \circ \Delta _{k-2}$ so that, for all $s\in {\mathbb {C}}$,

$$\begin{aligned} \Delta _k E^*_{k}(z,s)&= \Delta _k \circ R_0^{k/2}\left( \theta (s) y^s+ \theta (1-s) y^{1-s}\right) + \sum _{m \in {\mathbb {Z}}_{\ne 0}} \frac{ \sigma _{2s-1}(|m|)}{|m|^s} \Delta _k \circ R_0^{k/2}\left( W_s(m z)\right) \\&= R_0^{k/2} \circ \Delta _0\left( \theta (s) y^s+ \theta (1-s) y^{1-s}\right) + \sum _{m \in {\mathbb {Z}}_{\ne 0}} \frac{ \sigma _{2s-1}(|m|)}{|m|^s} R_0^{k/2} \circ \Delta _0\left( W_s(m z)\right) . \end{aligned}$$

Applying the identities

$$\begin{aligned} \Delta _0 y^s = s(1-s) y^s, \qquad \Delta _0 W_s(m z) = s(1-s) W_s(m z) \end{aligned}$$

(3.10)

now gives

$$\begin{aligned} \Delta _k E^*_{k}(z,s) = s(1-s) E^*_{k}(z,s) \qquad \text {for all} \qquad s\in {\mathbb {C}}\end{aligned}$$

(3.11)

where, as usual, the relation for $k<0$ follows from (1.18). Similar methods extend the identities (2.2)–(2.5) to all $s \in {\mathbb {C}}$.

3.3 Whittaker functions

Following the original derivation of Maass, the Fourier development of $E^*_k(z,s)$ is often given in terms of the Whittaker functions $W_{\kappa ,\mu }$. In our normalization, Maass’s result [29, p. 210] is

$$\begin{aligned}&E^*_k(z,s)= \theta _k(s) y^s+\theta _k(1-s) y^{1-s} + \frac{(-1)^{k/2}}{{\Gamma }(s-|k|/2)}\sum _{m=1}^\infty \frac{\sigma _{2s-1}(m)}{m^{s}}\nonumber \\&\qquad \times \, \Bigl \{{\Gamma }(s-k/2) \cdot W_{k/2,s-1/2}(4\pi m y) \cdot e^{2\pi i m x}\nonumber \\&\qquad +\, {\Gamma }(s+k/2) \cdot W_{-k/2,s-1/2}(4\pi m y) \cdot e^{-2\pi i m x} \Bigr \}. \end{aligned}$$

(3.12)

For this see [2, Sect. 2] where the results of Maass are translated into the $E_k(z,s)$ form. The development (3.12) is equivalent to Eqs. (1.6), (1.7) in [24] when $s=1/2+it$.

The Whittaker functions satisfy

$$\begin{aligned} \frac{d^2}{dy^2} W_{\kappa ,\mu }(y)+\left[ -\frac{1}{4}+\frac{\kappa }{y}+\frac{1/4-\mu ^2}{y^2} \right] W_{\kappa ,\mu }(y) =0, \end{aligned}$$

(3.13)

have exponential decay as $y\rightarrow \infty$ and possess various integral representations as in [37, Chap. 16] and [32, Sect. 13.16]. They are entire in the $\kappa$ and $\mu$ parameters with $W_{\kappa ,\mu }(y) = W_{\kappa ,-\mu }(y)$. The Eisenstein series are eigenfunctions of $\Delta _k$ as we saw in (3.11) and of period 1 in x. Writing their Fourier expansion and separating variables gives a differential equation for the coefficients that may be transformed into (3.13). This shows that the terms in (3.12) must take the form they do, and for $n \in {\mathbb {Z}}_{\ne 0}$

$$\begin{aligned} \left( \Delta _k -s(1-s)\right) \left( W_{k\cdot n/|n|,s-1/2}(4\pi |n| y) e^{2\pi i nx}\right) = 0. \end{aligned}$$

(3.14)

The relationship of $W_s(z)$ from (1.12) with $W_{\kappa ,\mu }(y)$ is

$$\begin{aligned} W_s(z)=W_{0,s-1/2}(4\pi |y|)\cdot e^{2\pi i x} \end{aligned}$$

and the right equation in (3.10) is the $k=0$ case of (3.14).

The Fourier expansion of weight k Eisenstein series for the group ${\Gamma }_0(N)$ is described in [1, Sect. 3]. Similar developments to (3.12) but employing other confluent hypergeometric variants are [13, Eq. (1)], [25, Cor. 2.2] and [30, Thm. 7.2.9] where characters are included.

Comparing (3.12) with Theorem 1.1 provides the Whittaker function relation:

Corollary 3.4

For all $k\in 2{\mathbb {Z}}$, $s\in {\mathbb {C}}$ and $y>0$,

$$\begin{aligned} W_{k/2,s-1/2}(y)=\frac{(-1)^{k/2}}{2^{|k|}}\frac{{\Gamma }(s-|k|/2)}{{\Gamma }(s-k/2)}\sum _{r=-|k|/2}^{|k|/2}P^{k/2}_r(y)\cdot W_{0,s+r-1/2}(y). \end{aligned}$$

(3.15)

4 The Eisenstein series $E^*_k(z,s)$ at integer values of s

In this section we prove Theorem 1.2. The Bessel function $K_w(y)$ may be expressed as a rational function times the exponential function when $w \in {\mathbb {Z}}+1/2$ and the simple idea of the proof is to put this expression into Theorem 1.1.

4.1 Raising $W_h(mz)$

For the falling factorial, write $z^{\underline{n}} := z(z-1) \cdots (z-n+1)$ with $z \in {\mathbb {C}}$ and $n \in {\mathbb {Z}}_{\geqslant 0}$ (and $z^{\underline{0}}=1$). The generalized binomial coefficients are given by

$$\begin{aligned} \left( {\begin{array}{c}z\\ n\end{array}}\right) :={\left\{ \begin{array}{ll} z^{\underline{n}}/n! &{} \, \text { if }\, n\in {\mathbb {Z}}_{\geqslant 0},\\ 0 &{} \, \text { if }\, n\in {\mathbb {Z}}_{< 0}.\end{array}\right. } \end{aligned}$$

(4.1)

Recalling (1.19), we see that for $n,j \in {\mathbb {Z}}$

$$\begin{aligned} \left( {\begin{array}{c}n-1+j\\ 2j\end{array}}\right) \ne 0 \quad \text {if and only if} \quad 0 \leqslant j \leqslant n^*. \end{aligned}$$

(4.2)

Lemma 4.1

For all $n \in {\mathbb {Z}}$ and $y>0$,

$$\begin{aligned} K_{n-1/2}(y)=\left( \frac{\pi }{2y}\right) ^{1/2} e^{-y} \sum _{j= 0}^{n^*} \left( {\begin{array}{c}n-1+j\\ 2j\end{array}}\right) \frac{(2j)!}{j! (2y)^j} . \end{aligned}$$

(4.3)

Proof

The formula (4.3) is well-known for $n=1$. Use $K_{w+1}(y)=\frac{w}{y} K_w(y)-\frac{d}{dy} K_w(y)$ and induction to verify (4.3) for all larger integer values of n. The identity $K_w(y)=K_{-w}(y)$ shows that the left side of (4.3) does not change as $n \rightarrow 1-n$. It is elementary to check that the right side is also unchanged as $n \rightarrow 1-n$ and so (4.3) is true for all $n \in {\mathbb {Z}}_{\leqslant 0}$ as well. $\square$

Recall the definition of $\mathcal {A}^k_h(u)$ in (1.20).

Proposition 4.2

For $k/2 \in {\mathbb {Z}}_{\geqslant 0}$, $h \in {\mathbb {Z}}$ and $m\in {\mathbb {R}}_{\ne 0}$ we have

$$\begin{aligned} R^{k/2}_0 W_h(m z) = {\left\{ \begin{array}{ll} \displaystyle e^{2\pi i m z} \sum _{u=0}^{h^* +k/2} \mathcal {A}^k_h(u) \cdot (4\pi |m|y)^{-u+k/2} &{}\, \text { if }\, m> 0,\\ \displaystyle e^{2\pi i m \overline{z}} \sum _{u=0}^{h^*-k/2^{}} \mathcal {A}^{-k}_h(u) \cdot (4\pi |m|y)^{-u-k/2} &{} \, \text { if }\, m < 0. \end{array}\right. } \end{aligned}$$

Proof

Put $\delta := m/|m|$. By Lemmas 2.1 and 4.1 we have

$$\begin{aligned} R^{k/2}_0 W_h(m z)= & {} 2^{-k} \sum _{|r| \leqslant k/2} \delta ^r P^{k/2}_r(4 \pi m y) W_{h+r}(mz) \\= & {} \frac{e^{2\pi i m x- 2\pi |m|y}}{2^k} \sum _{|r| \leqslant k/2} \delta ^r \sum _{\ell =|r|}^{k/2}\frac{k! (-4 \pi my)^\ell }{(k/2-\ell )! (\ell +r)! (\ell -r)!}\\&\quad \times \sum _{j=0}^{(h+r)^*} \left( {\begin{array}{c}h+r-1+j\\ 2j\end{array}}\right) \frac{(2j)!}{j! (4\pi |m| y)^j}. \end{aligned}$$

Interchanging the order of summation and writing $v=j-\ell$ gives

$$\begin{aligned} R^{k/2}_0 W_h(m z)= \frac{k!}{2^k} \ e^{2\pi i m x- 2\pi |m|y} \sum _{v=-k/2}^{h^*} (-\delta )^{v} \frac{\alpha _k(h,v;\delta )}{(4 \pi |m|y)^v} \end{aligned}$$

(4.4)

for

$$\begin{aligned} \alpha _k(h,v;\delta )&:= \sum _{j=\max (0,v)}^{k/2+v} (-\delta )^{j} \frac{(2j)!}{j! (k/2+v-j)!} \beta (h,v,j;\delta ), \end{aligned}$$

(4.5)

$$\begin{aligned} \beta (h,v,j;\delta )&:= \sum _{|r| \leqslant j-v} \left( {\begin{array}{c}h+r-1+j\\ 2j\end{array}}\right) \frac{\delta ^r}{(j-v+r)!(j-v-r)!}. \end{aligned}$$

(4.6)

The sum in (4.6) is initially over all r such that $|r| \leqslant j-v$ and $j \leqslant (h+r)^*$. With (4.2) the condition $j \leqslant (h+r)^*$ may be removed.

To simplify these formulas we first assemble the combinatorial results we shall need.

Lemma 4.3

For all $a,b,c \in {\mathbb {Z}}$ with $a \geqslant 0$, we have

$$\begin{aligned} \sum _{\ell =0}^a \left( {\begin{array}{c}a\\ \ell \end{array}}\right) \left( {\begin{array}{c}b+\ell \\ c\end{array}}\right)&= \sum _{i=0}^a \left( {\begin{array}{c}a\\ i\end{array}}\right) \left( {\begin{array}{c}b\\ c-i\end{array}}\right) 2^{a-i}, \end{aligned}$$

(4.7)

$$\begin{aligned} \sum _{\ell =0}^a \left( {\begin{array}{c}a\\ \ell \end{array}}\right) \left( {\begin{array}{c}b\\ c-\ell \end{array}}\right)&= \left( {\begin{array}{c}a+b\\ c\end{array}}\right) , \end{aligned}$$

(4.8)

$$\begin{aligned} \sum _{\ell =0}^a (-1)^\ell \left( {\begin{array}{c}a\\ \ell \end{array}}\right) \left( {\begin{array}{c}b+\ell \\ c\end{array}}\right)&= (-1)^a \left( {\begin{array}{c}b\\ c-a\end{array}}\right) , \end{aligned}$$

(4.9)

$$\begin{aligned} \sum _{\ell =0}^a (-1)^\ell \left( {\begin{array}{c}a\\ \ell \end{array}}\right) \left( {\begin{array}{c}2\ell \\ c\end{array}}\right)&= (-1)^a \left( {\begin{array}{c}a\\ c-a\end{array}}\right) 2^{2a-c}. \end{aligned}$$

(4.10)

Proof

Recall that the general binomial theorem implies

$$\begin{aligned} (1+x)^n=\sum _{\ell =0}^\infty \left( {\begin{array}{c}n\\ \ell \end{array}}\right) x^\ell \end{aligned}$$

for all x when $n\in {\mathbb {Z}}_{\geqslant 0}$ and for all x with $|x|<1$ when $n \in {\mathbb {Z}}_{<0}$. To prove (4.7) we evaluate in two ways $(1+1+x)^a(1+x)^b$. For $|x|<1$,

$$\begin{aligned} (1+(1+x))^a(1+x)^b = \sum _{\ell =0}^a \left( {\begin{array}{c}a\\ \ell \end{array}}\right) (1+x)^{b+\ell } = \sum _{\ell =0}^a\sum _{c=0}^\infty \left( {\begin{array}{c}a\\ \ell \end{array}}\right) \left( {\begin{array}{c}b+\ell \\ c\end{array}}\right) x^c \end{aligned}$$

(4.11)

and also

$$\begin{aligned} (2+x)^a(1+x)^b&= 2^a (1+x/2)^a(1+x)^b \nonumber \\&= 2^a \sum _{i=0}^a \sum _{j=0}^\infty \left( {\begin{array}{c}a\\ i\end{array}}\right) \left( {\begin{array}{c}b\\ j\end{array}}\right) (x/2)^i x^j = \sum _{i=0}^a \sum _{c=0}^\infty \left( {\begin{array}{c}a\\ i\end{array}}\right) \left( {\begin{array}{c}b\\ c-i\end{array}}\right) 2^{a-i} x^c. \end{aligned}$$

(4.12)

Comparing coefficients of $x^c$ in (4.11), (4.12) yields (4.7). Similar proofs using the elementary identities

$$\begin{aligned} (1+x)^a(1+x)^b&= (1+x)^{a+b}, \\ (1-(1+x))^a(1+x)^b&= (-x)^a (1+x)^b, \\ (1-(1+x)^2)^a&= (-x)^a(2+x)^a \end{aligned}$$

give (4.8), (4.9) and (4.10) respectively. $\square$

In the following two lemmas the integers k,  h,  v and j are restricted to the ranges required in (4.4) and (4.5). Explicitly: $k/2 \in {\mathbb {Z}}_{\geqslant 0}$, $-k/2 \leqslant v \leqslant h^*$ and $\max (0,v) \leqslant j \leqslant k/2+v$.

Lemma 4.4

We have

$$\begin{aligned}&\beta (h,v,j;-1) = \frac{(-1)^{j+v} }{(2j-2v)!} \left( {\begin{array}{c}h+v-1\\ 2v\end{array}}\right) , \end{aligned}$$

(4.13)

$$\begin{aligned}&\beta (h,v,j;1) = \sum _{\ell =0}^{2j-2v} \frac{2^\ell }{\ell ! (2j-2v-\ell )!} \left( {\begin{array}{c}h+v-1\\ 2v+\ell \end{array}}\right) . \end{aligned}$$

(4.14)

Proof

Put $t=r+j-v$ to get

$$\begin{aligned} \beta (h,v,j;\delta )= \frac{\delta ^{j+v} }{(2j-2v)!} \sum _{t=0}^{2j-2v} \delta ^t \left( {\begin{array}{c}2j-2v\\ t\end{array}}\right) \left( {\begin{array}{c}h+v-1+t\\ 2j\end{array}}\right) . \end{aligned}$$

Apply (4.7) and (4.9) to complete the proof. $\square$

Lemma 4.5

We have $\alpha _k(h,v;-1)=0$ unless $k/2\leqslant v \leqslant h^*$. Also

$$\begin{aligned}&\alpha _k(h,v;-1) = (-1)^{k/2} \frac{2^k}{k!} \frac{(h+v-1)^{\underline{2v}}}{(v-k/2)!} \qquad \text {for} \qquad k/2\leqslant v \leqslant h^*, \end{aligned}$$

(4.15)

$$\begin{aligned}&\alpha _k(h,v;1) = (-1)^{k/2+v} \frac{2^k}{k!} (h+v-1)^{\underline{v+k/2}} \left( {\begin{array}{c}h+k/2-1\\ v+k/2\end{array}}\right) . \end{aligned}$$

(4.16)

Proof

Put (4.13) into (4.5) and use (4.2), (4.10) to simplify and obtain the stated formulas for $\alpha _k(h,v;-1)$. Put (4.14) into (4.5) to get

$$\begin{aligned} \alpha _k(h,v;1)&= \frac{1}{(k/2+v)!} \sum _{j=0}^{k/2+v} (-1)^j \left( {\begin{array}{c}k/2+v\\ j\end{array}}\right) \sum _{\ell =0}^{2j-2v} \frac{2^\ell (2j)!}{\ell ! (2j-2v-\ell )!} \left( {\begin{array}{c}h+v-1\\ 2v+\ell \end{array}}\right) \\&= \frac{1}{(k/2+v)!} \sum _{\ell =0}^{k} \frac{2^{\ell }}{\ell !} \left( {\begin{array}{c}h+v-1\\ 2v+\ell \end{array}}\right) (2v+\ell )! \sum _{j=v+\lceil \ell /2 \rceil }^{v+k/2} (-1)^j \left( {\begin{array}{c}k/2+v\\ j\end{array}}\right) \left( {\begin{array}{c}2j\\ 2v+\ell \end{array}}\right) . \end{aligned}$$

Using (4.10) to find the inner sum produces

$$\begin{aligned} \alpha _k(h,v;1) = (-1)^{k/2+v} 2^k \sum _{\ell =0}^{k} \frac{(h+v-1)^{\underline{2v+\ell }}}{(v-k/2+\ell )! \ (k-\ell )! \ \ell !}. \end{aligned}$$

(4.17)

Breaking up the numerator as

$$\begin{aligned} (h+v-1)^{\underline{2v+\ell }} = (h+v-1)^{\underline{v+k/2}} \times (h-k/2-1)^{\underline{v-k/2+\ell }}, \end{aligned}$$

shows that (4.17) may be rewritten as

$$\begin{aligned} \alpha _k(h,v;1) = (-1)^{k/2+v} \frac{2^k}{k!}(h+v-1)^{\underline{v+k/2}} \sum _{\ell } \left( {\begin{array}{c}h-k/2-1\\ v+k/2-\ell \end{array}}\right) \left( {\begin{array}{c}k\\ \ell \end{array}}\right) \end{aligned}$$

and an application of (4.8) is the last step. $\square$

We may now complete the proof of Proposition 4.2 by using Lemma 4.5 in (4.4). For $m>0$ we obtain

$$\begin{aligned} R^{k/2}_0 W_h(m z)= e^{2\pi i m z} \sum _{v=-k/2}^{h^*} (-1)^{k/2} (h+v-1)^{\underline{v+k/2}} \left( {\begin{array}{c}h+k/2-1\\ v+k/2\end{array}}\right) (4 \pi |m|y)^{-v}. \end{aligned}$$

Letting $u=v-k/2$ this becomes

$$\begin{aligned} R^{k/2}_0 W_h(m z)= e^{2\pi i m z} \sum _{u=0}^{h^*+k/2} (-1)^{k/2} u! \left( {\begin{array}{c}h-k/2-1+u\\ u\end{array}}\right) \left( {\begin{array}{c}h+k/2-1\\ u\end{array}}\right) (4 \pi |m|y)^{-u+k/2}. \end{aligned}$$

Applying the identity

$$\begin{aligned} \left( {\begin{array}{c}-z\\ u\end{array}}\right) = (-1)^u \left( {\begin{array}{c}z+u-1\\ u\end{array}}\right) \end{aligned}$$

(4.18)

to the first binomial coefficient produces the desired formula.

The case when $m<0$ is similar. By Lemma 4.5, the summands in (4.4) can only be non-zero for $k/2 \leqslant v \leqslant h^*$ and so we use the new index $u=v+k/2$. $\square$

4.2 The $\mathcal {A}$ coefficients

Proposition 4.6

For all $k/2, h \in {\mathbb {Z}}$ and $u \in {\mathbb {Z}}_{\geqslant 0}$ the following are true.

• (i) $\mathcal {A}^k_h(u) \in {\mathbb {Z}}.$

• (ii) $\mathcal {A}^k_{1-h}(u)=\mathcal {A}^k_h(u)$.

• (iii) We have the representation

  $$\begin{aligned} \mathcal {A}^k_h(u) = \frac{(-1)^{k/2}}{u!} \prod ^{\max (0,k/2)}_{\ell =k/2+1-u} \left[ (h-1/2)^2-(\ell -1/2)^2 \right] . \end{aligned}$$

  (4.19)

  The product in (4.19) is empty when $u=0$ and $k\geqslant 0$. In that case the product should be interpreted as 1 and so $\mathcal {A}^k_h(0) = (-1)^{k/2}$ for $k\geqslant 0$.

• (iv) For $h^* < k/2$ we have $\mathcal {A}^k_h(u) \ne 0$ if and only if $0 \leqslant u \leqslant k/2-1- h^*$.

• (v) For $h^* \geqslant k/2$ we have $\mathcal {A}^k_h(u) \ne 0$ if and only if $0 \leqslant u \leqslant k/2+ h^*$.

Proof

Parts (i) and (ii) follow directly from the definition (1.20). Also from the definition, for $k \geqslant 0$,

$$\begin{aligned} \mathcal {A}^k_h(u)= & {} \frac{(-1)^{k/2}}{u!} \prod ^{u-1}_{r=0} (k/2+h-1-r)(h-k/2+r) \\= & {} \frac{(-1)^{k/2}}{u!} \prod ^{u-1}_{r=0} \left[ (h-1/2)-(k/2-r-1/2) \right] \left[ (h-1/2)+(k/2-r-1/2) \right] \\= & {} \frac{(-1)^{k/2}}{u!} \prod ^{k/2}_{\ell =k/2+1-u} \left[ (h-1/2)^2-(\ell -1/2)^2 \right] . \end{aligned}$$

Similarly for $k<0$ and part (iii) is verified. To prove parts (iv) and (v), note that (iii) implies that $\mathcal {A}^k_h(u) =0$ if and only if there exists an $\ell$ in the range $k/2+1-u \leqslant \ell \leqslant \max (0,k/2)$ with $h^* = \ell ^*$.

Suppose $h^* < k/2$. This implies that $k>0$. If $k/2+1-u \leqslant h^*+1$ then there exists an $\ell$ with $h^* = \ell ^*$, namely $\ell =h^*+1$, and so $\mathcal {A}^k_h(u) =0$. But if $k/2+1-u > h^*+1$ then $h^* = \ell ^*$ is not possible and so $\mathcal {A}^k_h(u) \ne 0$. This proves part (iv).

Suppose $h^* \geqslant k/2$. In this case it is impossible to have $h^* = \ell ^*$ for $\ell \geqslant 0$. Thus $\mathcal {A}^k_h(u) =0$ is only possible if we have an $\ell$ equalling $-h^*$. This happens when $k/2+1-u \leqslant -h^*$. Hence $\mathcal {A}^k_h(u) \ne 0$ if and only if $k/2+1-u > -h^*$, proving part (v). $\square$

As well as (1.20) and (4.19), a compact representation of $\mathcal {A}^k_h(u)$ is given in [17, (3.1)]:

$$\begin{aligned} \mathcal {A}^k_h(u) = \frac{(-1)^{k/2}}{u!} \frac{{\Gamma }(h-k/2+u)}{{\Gamma }(h-k/2)} \frac{{\Gamma }(h+|k|/2)}{{\Gamma }(h+k/2-u)}. \end{aligned}$$

(4.20)

Note that if any of the ${\Gamma }$ function arguments above are in ${\mathbb {Z}}_{\leqslant 0}$ then the limiting values of the quotients are meant.

Proof of Theorem 1.2

Using Proposition 4.2 in (3.9) gives (1.21) for even $k \geqslant 0$. Conjugate both sides and use (1.18) to obtain (1.21) for k negative. With parts (iv) and (v) of Proposition 4.6 we see when the range of the indices may be reduced. $\square$

In (3.15) we have already seen a connection between Whittaker functions and the Laguerre polynomials that we defined in (2.8). A second relation is the identity

$$\begin{aligned} W_{(\alpha +1)/2+n,\alpha /2}(y)=(-1)^n n! \, e^{-y/2}y^{(\alpha +1)/2} L^{(\alpha )}_n(y) \qquad \qquad (n \in {\mathbb {Z}}_{\geqslant 0}) \end{aligned}$$

(4.21)

from [32, (13.18.17)]. Substituting (4.21) into Maass’s formula (3.12) provides another route to some cases of Theorem 1.2. If (4.21) is valid for all $\alpha \in {\mathbb {Z}}$ then it may be verified that we obtain Theorem 1.2 in this way when $h^* \geqslant |k|/2$, corresponding to Eisenstein series in the left and right triangles in Fig. 1. A referee kindly provided the following proof of (4.21), valid for all $\alpha \in {\mathbb {R}}$ and $y>0$. From the definition in [37, Sect. 16.1],

$$\begin{aligned} W_{(\alpha +1)/2+n,\alpha /2}(y)= - n! \, e^{-y/2} y^{(\alpha +1)/2+n} \frac{1}{2\pi i} \int _{\infty }^{(0+)} (-t)^{-n-1}(1+t/y)^{n+\alpha } e^{-t}\,dt \end{aligned}$$

(4.22)

provided $-y$ is outside the contour of integration. Under the change of variables $t=uy/(1-u)$, the right side of (4.22) becomes

$$\begin{aligned} (-1)^n n! \, e^{-y/2} y^{(\alpha +1)/2} \frac{1}{2\pi i} \oint _{|u|=\rho <1} u^{-n-1}(1-u)^{-\alpha -1} e^{-uy/(1-u)}\,du. \end{aligned}$$

(4.23)

The well-known generating function for the Laguerre polynomials is

$$\begin{aligned} \sum _{n=0}^\infty L^{(\alpha )}_n(y) \cdot u^n = (1-u)^{-\alpha -1} e^{-uy/(1-u)} \end{aligned}$$

so that (4.23) equals the right side of (4.21) by Cauchy’s Theorem.

5 Values of the spectral zeta function of a torus

In the following sections we give some applications of Theorems 1.1 and 1.2. This section provides a direct proof of an identity in [11] and we give some of its context here next.

For a d-tuple of positive integers $N=(n_1,\dots ,n_d)$, the Cayley graph of the product of cyclic groups ${\mathbb {Z}}/n_1{\mathbb {Z}}\times \cdots \times {\mathbb {Z}}/n_d{\mathbb {Z}}$ may be thought of as a d-dimensional discrete torus. The set of eigenvalues of the combinatorial Laplacian acting on this torus is

$$\begin{aligned} \Lambda _N=\Big \{2d-2\cos (2\pi k_1/n_1)- \cdots - 2\cos (2\pi k_d/n_d) \ \Big | \ 0\leqslant k_j < n_j, \ 1\leqslant j \leqslant d \Big \} \end{aligned}$$

and the associated spectral zeta function is

$$\begin{aligned} \zeta _N(s):= \sum _{0 \ne \lambda \in \Lambda _N} \frac{1}{\lambda ^s}. \end{aligned}$$

As the components of N go to infinity at comparable rates, it is shown by Chinta et al. [11] that $\zeta _N(s)$ approaches the spectral zeta function of the corresponding real torus; see [11, Theorem, p. 125]. Combining their asymptotic results with work of Duplantier and David, they obtain in [11, Eq. (11)] for the case $d=2$ and $s=2$ the following formula

$$\begin{aligned} \sum _{\begin{array}{c} m,n \in {\mathbb {Z}}\\ (m,n)\ne (0,0) \end{array}} \frac{1}{((my)^2 +n^2)^2}&= \left( \frac{2\pi }{y}\right) ^2 \left( \frac{(2\pi y)^2}{2^4\cdot 45} + \frac{\zeta (3)}{4\pi y}\right. \nonumber \\&\quad \qquad \qquad \left. + \frac{1}{2\pi y}\sum _{n=1}^\infty \frac{1}{n^3}\frac{e^{-2\pi n y}}{1-e^{-2\pi n y}} + \sum _{n=1}^\infty \frac{1}{n^2}\frac{e^{-2\pi n y}}{(1-e^{-2\pi n y})^2}\right) ,\nonumber \\ \end{aligned}$$

(5.1)

with $y>0$. See [11, Sections 1.3, 7.3, 7.4] for the details.

We may use Theorem 1.2 to give a direct proof of (5.1) and also extend it to higher integer values of s. The left side of (5.1) may be expressed in general, for ${\mathrm {Re}}(s)>1$, as

$$\begin{aligned} \sum _{\begin{array}{c} m,n \in {\mathbb {Z}}\\ (m,n)\ne (0,0) \end{array}} \frac{1}{((my)^2 +n^2)^s}&= \sum _{\ell =1}^\infty \sum _{\begin{array}{c} c,d \in {\mathbb {Z}}\\ \gcd (c,d)=1 \end{array}} \frac{1}{(\ell ^2 (cy)^2+\ell ^2 d^2)^s} \nonumber \\&= \zeta (2s) \sum _{\begin{array}{c} c,d \in {\mathbb {Z}}\\ \gcd (c,d)=1 \end{array}} \frac{1}{|c i y +d|^{2s}} \nonumber \\&= \frac{2 \zeta (2s)}{y^s} \sum _{{\gamma }\in {\Gamma }_{\infty }\backslash {\Gamma }} {\mathrm {Im}}({\gamma }(iy))^s = \frac{2}{{\Gamma }(s)} \left( \frac{\pi }{y}\right) ^s E_0^*(iy,s). \end{aligned}$$

(5.2)

With $k=0$ and $h\in {\mathbb {Z}}-\{0,1\}$, Theorem 1.2 gives

$$\begin{aligned} E_0^*(z,h)= & {} \theta _0(h) y^h+\theta _0(1-h) y^{1-h}\nonumber \\&+ \sum _{m =1}^\infty \frac{ \sigma _{2h-1}(m)}{m^{h}} \left( e^{2\pi i m z}+ e^{-2\pi i m \overline{z}}\right) \sum _{u=0}^{h^*} \mathcal {A}^0_h(u) \cdot (4\pi m y)^{-u} \end{aligned}$$

(5.3)

for

$$\begin{aligned} \mathcal {A}^0_h(u) = (-1)^u u! \left( {\begin{array}{c}h-1\\ u\end{array}}\right) \left( {\begin{array}{c}-h\\ u\end{array}}\right) = u!\left( {\begin{array}{c}h-1\\ u\end{array}}\right) \left( {\begin{array}{c}h-1+u\\ u\end{array}}\right) . \end{aligned}$$

Also $\theta _0(h)$, $\theta _0(1-h)$ may be found with (1.22) and so we obtain the weight $k=0$ case of Theorem 1.2 when $h\in {\mathbb {Z}}_{\geqslant 2}$:

$$\begin{aligned} E_0^*(z,h)= & {} (h-1)!\zeta (2h)\frac{y^h}{\pi ^h} +\frac{(2h-2)!}{(h-1)!}\zeta (2h-1) (4\pi y)^{1-h} \nonumber \\&+\,\sum _{m =1}^\infty \frac{ \sigma _{2h-1}(m)}{m^{h}} \left( e^{2\pi i m z}+ e^{-2\pi i m \overline{z}}\right) \sum _{u=0}^{h-1} \frac{(h-1+u)!}{(h-1-u)!u!} (4\pi m y)^{-u}. \end{aligned}$$

(5.4)

Note that (5.4) agrees with [14, Eq. (1.13)].

To get (5.3) or (5.4) to match (5.1), let $z=iy$ and substitute $\sigma _{1-2h}(m)/m^{1-h}$ for $\sigma _{2h-1}(m)/m^{h}$ to find

$$\begin{aligned} E_0^*(iy,h) = \theta _0(h) y^h+\theta _0(1-h) y^{1-h} + 2\sum _{m =1}^\infty \frac{ \sigma _{1-2h}(m)}{m^{1-h}} \ e^{-2\pi m y} \sum _{u=0}^{h-1} \mathcal {A}^0_h(u) \cdot (4\pi m y)^{-u} \end{aligned}$$

(5.5)

for $h\in {\mathbb {Z}}_{\geqslant 2}$. Reorder the right of (5.5) as

$$\begin{aligned} 2\sum _{u=0}^{h-1} \mathcal {A}^0_h(u) \cdot (4\pi y)^{-u} \sum _{m =1}^\infty \Bigl ( \sum _{d | m} d^{1-2h}\Bigr ) m^{h-1-u} \ e^{-2\pi m y} \end{aligned}$$

(5.6)

and letting $m=d \ell$ shows that (5.6) becomes

$$\begin{aligned} 2\sum _{u=0}^{h-1} \mathcal {A}^0_h(u) \cdot (4\pi y)^{-u} \sum _{d =1}^\infty d^{-h-u} \sum _{\ell =1}^\infty \ell ^{h-1-u} \ e^{-2\pi d\ell y}. \end{aligned}$$

(5.7)

The last series in (5.7) may be expressed in terms of the polylogarithm ${\text {Li}}_{s}(z):=\sum _{n=1}^\infty z^n/n^s$. For indices $-m \in {\mathbb {Z}}_{\leqslant 0}$, Euler showed that the polylogarithm is in fact a rational function of the form

$$\begin{aligned} {\text {Li}}_{-m}(z) = \frac{z \cdot A_m(z)}{(1-z)^{m+1}}. \end{aligned}$$

(5.8)

The first two Eulerian polynomials are constant: $A_0(z)=1$, $A_1(z)=1$. The next three are

$$\begin{aligned} A_2(z)=1+z, \quad A_3(z)=1+4z+z^2, \quad A_4(z)=1+11z+11z^2+z^3. \end{aligned}$$

Frobenius showed that

$$\begin{aligned} A_m(z) = \sum _{k=0}^m k! {\genfrac\rbrace \lbrace {0.0pt}{}{m}{k}} (z-1)^{m-k} \qquad \quad (m \in {\mathbb {Z}}_{\geqslant 0}) \end{aligned}$$

with the Stirling number ${\genfrac\rbrace \lbrace {0.0pt}{}{m}{k}}$ indicating the number of partitions of m elements into k non-empty subsets. See for example [35, Sect. 8.2] for more information on these topics.

Assembling our calculations proves the next result, of which (5.1) is a special case.

Proposition 5.1

For all $h \in {\mathbb {Z}}_{\geqslant 2}$ and $y>0$,

$$\begin{aligned}&\sum _{\begin{array}{c} m,n \in {\mathbb {Z}}\\ (m,n)\ne (0,0) \end{array}} \frac{1}{((my)^2 +n^2)^h} \\&\quad = 2\zeta (2h)+2\pi \zeta (2h-1) \left( {\begin{array}{c}2h-2\\ h-1\end{array}}\right) (4y)^{1-h}\\&\qquad + \sum _{u=0}^{h-1} \left( {\begin{array}{c}h-1+u\\ u\end{array}}\right) \frac{4^{1-u}\pi ^{h-u}}{(h-1-u)!} \sum _{n=0}^\infty \frac{1}{(ny)^{h+u}} \frac{e^{-2\pi n y}A_{h-1-u}(e^{-2\pi n y})}{(1-e^{-2\pi n y})^{h-u}}. \end{aligned}$$

As an aside we note that (5.3) may be proved by using Lemma 4.1 in (1.13). Then another means of proving Theorem 1.2 is to apply $R_0^{k/2}$ to (5.3). The computations are similar to those of Sect. 4 and this was the proof sketched for [17, Thm. 3.1]. The advantage of first proving Theorem 1.1 is that it is a more general result.

6 The formulations of Maass and Brown

Maass defined his Eisenstein series as

$$\begin{aligned} G(z, \overline{z};\alpha ,\beta ):= \sum _{\begin{array}{c} m,n \in {\mathbb {Z}}\\ (m,n)\ne (0,0) \end{array}}(mz+n)^{-\alpha }(m\overline{z}+n)^{-\beta } \end{aligned}$$

(6.1)

for $z\in {\mathbb {H}}$, $\alpha -\beta \in 2{\mathbb {Z}}$, ${\mathrm {Re}}(\alpha +\beta )>2$ and proved fundamental properties such as their Fourier expansion in terms of Whittaker functions, meromorphic continuation in $\alpha ,$ $\beta$, functional equation and eigenvalue properties. This work is described in [29, Chap. 4]. A detailed presentation of these results is also given in [2, Sect. 2.2].

For $a,b \in {\mathbb {Z}}_{\geqslant 0}$ with $a+b=w$ positive and even, Brown in [8, Sect. 4] has similarly defined

$$\begin{aligned} \mathcal {E}_{a,b}(z):=\frac{w!}{(2\pi i)^{w+2}}\frac{1}{2} \sum _{\begin{array}{c} m,n \in {\mathbb {Z}}\\ (m,n)\ne (0,0) \end{array}} \frac{-2\pi y}{(mz+n)^{a+1}(m\overline{z}+n)^{b+1}}. \end{aligned}$$

(6.2)

With a short calculation similar to (5.2), the series (6.1) and (6.2) may be related to (1.4). This shows

$$\begin{aligned} G(z, \overline{z};\alpha ,\beta )&= \frac{2}{{\Gamma }((\alpha +\beta )/2+|\alpha -\beta |/2)} \left( \frac{y}{\pi }\right) ^{(\alpha +\beta )/2}E^*_{\alpha -\beta }(z,(\alpha +\beta )/2), \nonumber \\ \mathcal {E}_{a,b}(z)&= (-4\pi y)^{-w/2} \frac{{\Gamma }(w+1)}{2 {\Gamma }(w/2+1+|a-b|/2)} E^*_{a-b}(z,w/2+1). \end{aligned}$$

(6.3)

We see that Brown’s series $\mathcal {E}_{a,b}(z)$ corresponds to $E^*_k(z,h)$ with the restriction $|k/2|<h$, and these are the series appearing in the right triangle of Fig. 1. The Fourier expansion of $\mathcal {E}_{a,b}(z)$ follows as an exercise from Theorem 1.2. With the formulation in Section 4 of [8] it may be written neatly as

$$\begin{aligned} \mathcal {E}_{a,b}(z) = \mathcal {E}^0_{a,b}(z) + R_{a,b}(z) + \overline{R_{b,a}(z)} \end{aligned}$$

where

$$\begin{aligned} \mathcal {E}^0_{a,b}(z)&= \frac{\pi y B_{w+2}}{(w+1)(w+2)} + (-1)^a \frac{w!}{2} \left( {\begin{array}{c}w\\ a\end{array}}\right) (4\pi y)^{-w} \zeta (w+1), \\ R_{a,b}(z)&= \frac{(-1)^a}{2} \sum _{u=0}^a \frac{(a+b)!}{(a-u)!} \left( {\begin{array}{c}b+u\\ b\end{array}}\right) (4\pi y)^{-u-b} \sum _{m=1}^\infty \frac{\sigma _{w+1}(m)}{m^{b+1+u}}e^{2\pi i m z}. \end{aligned}$$

This is proved in Sections 5.3 and 5.4 of [9] as part of a larger framework.

7 A formula of Terras and Grosswald for $\zeta (2h-1)$

The Chowla–Selberg formula gives a series expansion for the Epstein zeta function $\zeta _Q(s)$ and may be recognized as special case of the expansion (1.13) of $E_0^*(z,s)$ where z depends on the binary quadratic form Q. See Sections 2 and 3 of [16], for example, for a discussion of these ideas. Terras generalized the Chowla–Selberg formula to n-ary quadratic forms and used this theory in [36] to discover a new formula for $\zeta (2h-1)$, similar to that of Lerch and Ramanujan in (1.26) and (1.27). The first cases are

$$\begin{aligned} \zeta (3)&=\frac{2\pi ^3}{45}-2\sum _{m=1}^\infty \sigma _{-3}(m) e^{-2\pi m}\left( 1+2\pi m +4\pi ^2 m^2\right) , \end{aligned}$$

(7.1)

$$\begin{aligned} \zeta (5)&=\frac{4\pi ^5}{945}-2\sum _{m=1}^\infty \sigma _{-5}(m) e^{-2\pi m}\left( 1+2\pi m +2\pi ^2 m^2 + \frac{4}{3} \pi ^3m^3\right) , \end{aligned}$$

(7.2)

and in general, for $h \in {\mathbb {Z}}_{\geqslant 2}$,

$$\begin{aligned} \zeta (2h-1)&= \frac{(h-2)!}{(2h-2)!}\left\{ \frac{(4\pi )^{2h-1} h! |B_{2h}|}{2(2h)!}\right. \nonumber \\&\quad \left. -\sum _{m=1}^\infty \sigma _{1-2h}(m) e^{-2\pi m}\left( \sum _{\ell =0}^h \frac{(h+\ell -2)! \big [h(h-1)+\ell (\ell -1)\big ]}{\ell !(h-\ell )!} (4\pi m)^{h-\ell } \right) \right\} .\nonumber \\ \end{aligned}$$

(7.3)

Grosswald provided the explicit form of (7.3) in [22].

We may use Theorem 1.2 to prove (7.3), and indeed generalize it, as follows. For $S := \left( \begin{matrix}0 &{} -1 \\ 1 &{} 0 \end{matrix}\right)$ we have $S i = i$ and $j(S,i)=i$. Hence by (1.5), $E_k(i,s)=i^k E_k(i,s)$ and so

$$\begin{aligned} E^*_k(i,s) \equiv 0 \qquad \text {for} \qquad k \equiv 2 \bmod 4. \end{aligned}$$

(7.4)

Taking (7.4) with $s=1-h$ for $h \in {\mathbb {Z}}_{\geqslant 1}$ and expanding with Theorem 1.2 gives the identity

$$\begin{aligned}&\theta _k(h)+\theta _k(1-h)\nonumber \\&\quad = -\sum _{m=1}^\infty \frac{\sigma _{1-2h}(m)}{m^{1-h}} e^{-2\pi m}\left( \sum _{u=0}^{h-1+k/2} \mathcal {A}^k_h(u) \cdot (4\pi m)^{-u+k/2}+\sum _{u=0}^{h-1-k/2} \mathcal {A}^{-k}_h(u) \cdot (4\pi m)^{-u-k/2} \right) \nonumber \\ \end{aligned}$$

(7.5)

for all $k \equiv 2 \bmod 4$. We may assume that k and h are positive in (7.5) since it is invariant as $k \rightarrow -k$ and $h \rightarrow 1-h$ (except for replacing $\sigma _{1-2h}(m)/m^{1-h}$ by $\sigma _{2h-1}(m)/m^{h}$). Also $\theta _k(1-h) = 0$ for $2\leqslant h \leqslant |k|/2$ by (1.22), so it is natural to consider (7.5) in the three cases: (i) $h=1$, (ii) $2\leqslant h\leqslant k/2$ and (iii) $k/2<h$. The first case easily gives

$$\begin{aligned} \frac{\zeta (2) k}{2\pi } + \zeta (0) = -\sum _{m=1}^\infty \sigma _{-1}(m) e^{-2\pi m} \sum _{r=1}^{k/2} (-1)^r \left( {\begin{array}{c}k/2\\ r\end{array}}\right) \frac{(4\pi m)^{r}}{(r-1)!} \end{aligned}$$

(7.6)

where the left side of (7.6) is just $(\pi k-6)/12$.

Proposition 7.1

Let h and k be positive integers with $k \equiv 2 \bmod 4$ and $2\leqslant h\leqslant k/2$. Then

$$\begin{aligned} \zeta (2h) = -\pi ^h \sum _{m=1}^\infty \frac{\sigma _{1-2h}(m)}{m^{1-h}} e^{-2\pi m} \sum _{r=1-h}^{k/2} (-1)^r \left( {\begin{array}{c}k/2-h\\ k/2-r\end{array}}\right) \frac{(4\pi m)^{r}}{(h-1+r)!}. \end{aligned}$$

Proof

For these values of h equation (7.5) implies

$$\begin{aligned} \theta _k(h) = -\sum _{m=1}^\infty \frac{\sigma _{1-2h}(m)}{m^{1-h}} e^{-2\pi m} \sum _{u=0}^{h-1+k/2} \mathcal {A}^k_h(u) \cdot (4\pi m)^{-u+k/2}. \end{aligned}$$

Simplifying and letting $r=k/2-u$ gives the result. $\square$

Examples of Proposition 7.1 with $(h,k)=(2,6)$, (3, 6) and (3, 10) are

$$\begin{aligned} \zeta (4)&= \frac{8\pi }{3}\sum _{m=1}^\infty \sigma _{-3}(m)e^{-2\pi m}\left( -\pi ^3 m^3 + \pi ^4 m^4\right) , \\ \zeta (6)&= \frac{8\pi }{15}\sum _{m=1}^\infty \sigma _{-5}(m)e^{-2\pi m}\left( \pi ^5 m^5 \right) , \\ \zeta (6)&= \frac{8\pi }{15}\sum _{m=1}^\infty \sigma _{-5}(m)e^{-2\pi m}\left( \pi ^5 m^5 -\frac{4}{3} \pi ^6 m^6 + \frac{8}{21} \pi ^7 m^7 \right) . \end{aligned}$$

These may be compared with (1.24).

Proposition 7.2

Let h and k be positive integers with $k \equiv 2 \bmod 4$ and $h > k/2$. Then

$$\begin{aligned}&\zeta (2h-1) = \frac{(h-k/2-1)!}{(2h-2)!}\Bigg \{ \frac{(4\pi )^{2h-1} (h+k/2-1)! |B_{2h}|}{2(2h)!}-\sum _{m=1}^\infty \sigma _{1-2h}(m) e^{-2\pi m} \nonumber \\&\qquad \qquad \qquad \times \sum _{\ell =1-k/2}^{h} \frac{k!(h+\ell -2)!}{(\ell +k/2-1)!(h-\ell )!} \left[ \left( {\begin{array}{c}k/2+h-1\\ k\end{array}}\right) +\left( {\begin{array}{c}k/2+\ell -1\\ k\end{array}}\right) \right] (4\pi m)^{h-\ell } \Bigg \}.\nonumber \\ \end{aligned}$$

(7.7)

Proof

We use (7.5) and write the sums in parentheses as

$$\begin{aligned} \sum _{u=0}^{h-1+k/2} (4\pi m)^{-u+k/2} \left( \mathcal {A}^k_h(u) + \mathcal {A}^{-k}_h(u-k) \right) \end{aligned}$$

with the understanding that $\mathcal {A}^{-k}_h(u-k)=0$ for $u<k$. Using the identity (4.18) to make all the entries positive we obtain

$$\begin{aligned} \mathcal {A}^k_h(u)&= (-1)^{k/2} u! \left( {\begin{array}{c}k/2+h-1\\ u\end{array}}\right) \left( {\begin{array}{c}h-1-k/2+u\\ u\end{array}}\right) \\&= -\frac{1}{u!} \cdot \frac{(h-1-k/2+u)!}{(h-1+k/2-u)!} \cdot \frac{(h-1+k/2)!}{(h-1-k/2)!}. \end{aligned}$$

Similarly,

$$\begin{aligned} \mathcal {A}^{-k}_h(u-k)&= (-1)^{k/2} \frac{[(u-k/2)!]^2}{(u-k)!} \left( {\begin{array}{c}h-1\\ u-k/2\end{array}}\right) \left( {\begin{array}{c}h-1+u-k/2\\ u-k/2\end{array}}\right) \\&= -\frac{1}{(u-k)!} \cdot \frac{(h-1-k/2+u)!}{(h-1+k/2-u)!} \end{aligned}$$

for $k\leqslant u \leqslant h-1+k/2$. Rewrite the term $1/(u-k)!$ above as $\frac{k!}{u!} \left( {\begin{array}{c}u\\ k\end{array}}\right)$ to get the formula we want for $0\leqslant u \leqslant h-1+k/2$. Simplifying and setting $\ell = u-k/2+1$ finishes the proof. $\square$

Clearly, the Terras–Grosswald formula (7.3) is the first case of Proposition 7.2 when $k=2$. The following examples show the results of Lerch–Ramanujan and Terras–Grosswald, respectively, for $\zeta (7)$:

$$\begin{aligned} \zeta (7)&= \frac{19 \pi ^7}{56700} - 2\sum _{m=1}^\infty \sigma _{-7}(m) e^{-2\pi m}, \\ \zeta (7)&= \frac{32 \pi ^7}{70875} - 2\sum _{m=1}^\infty \sigma _{-7}(m) e^{-2\pi m}\left( 1+2\pi m+\frac{28\pi ^2 m^2}{15}+\frac{16\pi ^3 m^3}{15}+\frac{16\pi ^4 m^4}{45}\right) . \end{aligned}$$

By comparison, Proposition 7.2 with $h=4$ and $k=6$ gives

$$\begin{aligned} \zeta (7)= & {} \frac{32 \pi ^7}{4725} - 2\sum _{m=1}^\infty \sigma _{-7}(m) e^{-2\pi m}\\&\times \left( 1+2\pi m+ 4\pi ^2 m^2+\frac{16\pi ^3 m^3}{3}+\frac{16\pi ^4 m^4}{3}+\frac{64\pi ^5 m^5}{15}+\frac{128\pi ^6 m^6}{45}\right) . \end{aligned}$$

8 Harmonic Eisenstein series

For each $k \in 2{\mathbb {Z}}$ set

$$\begin{aligned} {\mathbb {E}}_k(z) := y^{-k/2}\frac{E^*_k(z,k/2)}{\theta _k(k/2)}. \end{aligned}$$

(8.1)

This definition has poles when $k=0$ and so we interpret ${\mathbb {E}}_0(z)$ as $\lim _{s\rightarrow 0} E^*_0(z,s)/\theta _0(s)$. These series are studied by Pribitkin in [13] and have also appeared recently in [6, Sect. 6.1.4]. Clearly ${\mathbb {E}}_k(z)$ has holomorphic weight k. For even $k \geqslant 4$ we have from (1.7), (1.10) that ${\mathbb {E}}_k(z) = E_k(z)$ and so we just recover the usual holomorphic Eisenstein series for these k. We may regard ${\mathbb {E}}_k(z)$ for even $k \leqslant 2$ as natural extensions of these holomorphic Eisenstein series.

It follows from (3.11) that

$$\begin{aligned} \left( y^{-k/2} \circ \Delta _k \circ y^{k/2} - k/2(1-k/2)\right) {\mathbb {E}}_k(z) = 0. \end{aligned}$$

(8.2)

Therefore

$$\begin{aligned} \left( -y^2 \left( \frac{\partial ^2}{\partial x^2} + \frac{\partial ^2}{\partial y^2}\right) +ik y \left( \frac{\partial }{\partial x}+i\frac{\partial }{\partial y} \right) \right) {\mathbb {E}}_k(z) = 0 \end{aligned}$$

which implies that ${\mathbb {E}}_k(z)$ is a harmonic Maass form. See for example [7, 33] for more on harmonic Maass forms and surveys of their important applications. We next obtain the Fourier expansion of ${\mathbb {E}}_k(z)$ and see that the result can be formulated in a way that is valid for all even k. It will also be apparent that for nonzero even $k \leqslant 2$, ${\mathbb {E}}_k(z)$ differs from $E_k(z)$ in its extended Fourier expansion definition (1.3) and is not holomorphic.

Theorem 8.1

Define $\varepsilon (k)$ to be 2 if $k\geqslant 0$ and 1 if $k< 0$. Then for all $k \in 2{\mathbb {Z}}$ we have

$$\begin{aligned} {\mathbb {E}}_k(z)= & {} 1 + \frac{\varepsilon (k)}{\zeta (1-k)} \Bigg [\frac{\zeta (2-k)}{(2\pi i)^k} \left( \frac{y}{\pi }\right) ^{1-k} \nonumber \\&+\, \sum _{m =1}^\infty \sigma _{k-1}(m) \ e^{2\pi i m z} + \sum _{m =1}^\infty \sigma _{k-1}(m) \ e^{-2\pi i m \overline{z}} \sum _{u=0}^{-k} \frac{(4\pi m y)^{u}}{u!}\Bigg ]. \end{aligned}$$

(8.3)

Proof

This is a straightforward application of Theorem 1.2 and we review the different cases. For $k\geqslant 2$ and $h=k/2$ then $h^*=k/2-1<k/2$ and

$$\begin{aligned} E^*_k(z,k/2)= \theta _k(k/2) y^{k/2}+\theta _k(1-k/2) y^{1-k/2} + \sum _{m =1}^\infty \frac{ \sigma _{k-1}(m)}{m^{k/2}} \ e^{2\pi i m z} \mathcal {A}^k_{k/2}(0) \cdot (4\pi m y)^{k/2}. \end{aligned}$$

We have $\mathcal {A}^k_{k/2}(0) = (-1)^{k/2}$ and hence

$$\begin{aligned} {\mathbb {E}}_k(z) = 1+ \frac{\theta _k(1-k/2)}{\theta _k(k/2)} y^{1-k}+ \frac{(-4\pi )^{k/2}}{\theta _k(k/2)} \sum _{m =1}^\infty \sigma _{k-1}(m) \ e^{2\pi i m z} \qquad (k\geqslant 2). \end{aligned}$$

With (1.22) we have $\theta _k(k/2) = \pi ^{-k/2}(k-1)!\zeta (k)$. Also $\theta _k(1-k/2)$ is $\zeta (0)=-1/2$ if $k=2$ and 0 if $k>2$. Therefore

$$\begin{aligned} {\mathbb {E}}_2(z) = 1 - \frac{3}{\pi y} -24 \sum _{m=1}^\infty \sigma _1(m) e^{2\pi i mz} \end{aligned}$$

(8.4)

and, using $(2\pi i)^{k} \zeta (1-k)=2 (k-1)!\zeta (k)$ for $k\geqslant 2$,

$$\begin{aligned} {\mathbb {E}}_k(z) = 1 +\frac{2}{\zeta (1-k)} \sum _{m=1}^\infty \sigma _{k-1}(m) e^{2\pi i mz} \qquad (k\geqslant 4) \end{aligned}$$

(8.5)

as expected. Equations (8.4) and (8.5) match (8.3) because $\zeta (2-k)$ is zero for even $k\geqslant 4$ and the last sum, over u in an empty range, vanishes for positive k. The important weight 2 non-holomorphic form ${\mathbb {E}}_2(z)$ was found by Hecke; see for example [40, Sect. 2.3] where it is denoted $E^*_2(z)$. Hence $-3/(\pi y)$ must be added to $E_2$ in (1.3) so that it transforms with weight 2.

For $k=0$ we have

$$\begin{aligned} {\mathbb {E}}_0(z) = \lim _{s\rightarrow 0} \frac{E^*_0(z,s)}{\theta _0(s)} = \lim _{s\rightarrow 0} \frac{\theta _0(s) +O(1)}{\theta _0(s)} = \lim _{s\rightarrow 0} \frac{-1/(2s) +O(1)}{-1/(2s) +O(1)} =1. \end{aligned}$$

Since $\zeta (s)$ has a pole at $s=1$ we take $\varepsilon (k)/\zeta (1-k)$ to be 0 when $k=0$ and so (8.3) confirms that ${\mathbb {E}}_0(z)=1$.

Lastly we assume $k\leqslant -2$ and $h=k/2$ so that $h^*=-k/2$. Theorem 1.2 implies that

$$\begin{aligned} {\mathbb {E}}_k(z)= & {} 1+ \frac{\theta _k(1-k/2)}{\theta _k(k/2)} y^{1-k}+ \frac{(4\pi )^{k/2}}{\theta _k(k/2)} \sum _{m =1}^\infty \sigma _{k-1}(m) \ e^{2\pi i m z} \mathcal {A}^k_{k/2}(0) \nonumber \\&+\, \frac{1}{\theta _k(k/2)} \sum _{m =1}^\infty \frac{\sigma _{k-1}(m)}{(my)^{k/2}} \ e^{-2\pi i m \overline{z}} \sum _{u=0}^{-k} \mathcal {A}^{-k}_{k/2}(u) \cdot (4\pi m y)^{-u-k/2} \qquad (k\leqslant -2).\nonumber \\ \end{aligned}$$

(8.6)

With (1.20), (4.18) and writing $-k$ as |k| for clarity

$$\begin{aligned} \mathcal {A}^k_{k/2}(0)&= [(|k|/2)!]^2 \left( {\begin{array}{c}-|k|/2-1\\ |k|/2\end{array}}\right) \left( {\begin{array}{c}|k|/2\\ |k|/2\end{array}}\right) = (-1)^{k/2} [(|k|/2)!]^2 \left( {\begin{array}{c}|k|\\ |k|/2\end{array}}\right) = (-1)^{k/2} |k|!,\\ \mathcal {A}^{-k}_{k/2}(u)&= (-1)^{u+k/2} u! \left( {\begin{array}{c}-1\\ u\end{array}}\right) \left( {\begin{array}{c}|k|\\ u\end{array}}\right) = (-1)^{k/2} u! \left( {\begin{array}{c}|k|\\ u\end{array}}\right) = (-1)^{k/2} \frac{|k|!}{(|k|-u)!}. \end{aligned}$$

With (1.22) we see

$$\begin{aligned} \theta _k(k/2) =(-4\pi )^{k/2} |k|! \zeta (1-k), \qquad \theta _k(1-k/2) =\pi ^{k/2-1} |k|! \zeta (2-k). \end{aligned}$$

The proof is finished by substituting these calculations into (8.6) and simplifying. $\square$

Fig. 2

Eisenstein series on the main diagonal

As seen in Fig. 2, the harmonic Eisenstein series ${\mathbb {E}}_k(z)$ times $y^{k/2}$ may be used as representatives for the spaces generated by $E^*_k(z,h)$ on the main diagonal $h=k/2$. We indicated on the left of Fig. 1 that, with (2.4), (2.5), the raising operators naturally move up the lattice and the lowering operators move down. Thus we see that $y^{k/2}{\mathbb {E}}_k(z)$ for $k/2 \in {\mathbb {Z}}_{\geqslant 1}$ generates the upper triangle of Fig. 2 by applying the raising operators – recall that the left and right sides of this triangle are equal by (1.17). We may not leave the upper triangle by means of the lowering operator since $L_k E^*_k(z,k/2)=0$ for $k/2\in {\mathbb {Z}}_{\geqslant 2}$ (though $L_2 E^*_2(z,1)=1/2$). The left and right triangles of Fig. 2 are generated by $y^{k/2}{\mathbb {E}}_k(z)$ for $k/2 \in {\mathbb {Z}}_{\leqslant -1}$ and the raising operators (or alternatively $y^{k/2}\overline{{\mathbb {E}}}_k(z)$ for $k/2 \in {\mathbb {Z}}_{\leqslant -1}$ and the lowering operators).

8.1 The holomorphic part of ${\mathbb {E}}_k(z)$

In this subsection we assume that k is even and negative. The holomorphic series in (8.3) may be rewritten as

$$\begin{aligned} U_k(z):=\sum _{m =1}^\infty \sigma _{k-1}(m) \ e^{2\pi i m z} = (2\pi i)^{1-k}\sum _{m =1}^\infty \frac{\sigma _{1-k}(m)}{(2\pi i m)^{1-k}} \ e^{2\pi i m z}. \end{aligned}$$

(8.7)

Hence it is a constant times a $(1-k)$ fold integral of $E_{2-k}(z)-1$, as noted by Pribitkin in [13]:

$$\begin{aligned} U_k(z)=\frac{(1-k)!\zeta (2-k)}{2\pi i} \int _{i\infty }^z \cdots \int _{i\infty }^{z_2} \int _{i\infty }^{z_1} (E_{2-k}(z_0)-1)\, dz_0 \, dz_1 \, \cdots \, dz_{|k|}. \end{aligned}$$

Integrating by parts shows the alternate expression

$$\begin{aligned} U_k(z) = \frac{(1-k)\zeta (2-k)}{2\pi i} \int _{i\infty }^z (E_{2-k}(w)-1)(w-z)^{-k} \, dw. \end{aligned}$$

(8.8)

The integral $U_k(z)$ is a type of Eichler integral and transforms with weight k except for an additional rational function of z. Following [13, (7)] we have:

Lemma 8.2

Let ${\gamma }=\left( \begin{matrix}* &{} * \\ c &{} * \end{matrix}\right) \in {\Gamma }$ with $c\ne 0$. Then

$$\begin{aligned} j({\gamma },z)^{-k} U_k({\gamma }z) - U_k(z)= & {} \frac{(1-k)\zeta (2-k)}{2\pi i}\Bigg \{\frac{1}{c^{1-k}(1-k)}\left( j({\gamma },z)^{1-k}+\frac{1}{j({\gamma },z)} \right) \nonumber \\&+\,\int ^{i \infty }_{{\gamma }^{-1}(i \infty )}\left( E_{2-k}(w)-1-\frac{1}{j({\gamma },w)^{2-k}} \right) (w-z)^{-k}\, dw\Bigg \}.\nonumber \\ \end{aligned}$$

(8.9)

Proof

Recall the identity

$$\begin{aligned} j({\gamma },z)(w-{\gamma }z) = j({\gamma }^{-1},w)({\gamma }^{-1}w-z) \end{aligned}$$

for all $z,w\in {\mathbb {H}}$ and any invertible ${\gamma }$. Then

$$\begin{aligned}&\frac{2\pi i}{(1-k)\zeta (2-k)} j({\gamma },z)^{-k} U_k({\gamma }z)\\&\quad = \int _{i\infty }^{{\gamma }z} (E_{2-k}(w)-1)\left[ j({\gamma },z)(w-{\gamma }z)\right] ^{-k} \, dw \\&\quad = \int _{i\infty }^{{\gamma }z} (E_{2-k}(w)-1)\left[ j({\gamma }^{-1},w)({\gamma }^{-1}w-z) \right] ^{-k} \, dw \\&\quad = \int _{{\gamma }^{-1}(i\infty )}^{z} (E_{2-k}({\gamma }u)-1)\left[ j({\gamma }^{-1},{\gamma }u)(u-z) \right] ^{-k} j({\gamma }^{-1},{\gamma }u)^2 \, du \\&\quad = \int _{{\gamma }^{-1}(i\infty )}^{z} \left( E_{2-k}(u)-\frac{1}{j({\gamma },u)^{2-k}} \right) (u-z)^{-k} \, du. \end{aligned}$$

Rewrite this last integral as

$$\begin{aligned}&\frac{2\pi i}{(1-k)\zeta (2-k)}U_k(z) +\int ^{i \infty }_{{\gamma }^{-1}(i \infty )}\left( E_{2-k}(w)-1-\frac{1}{j({\gamma },w)^{2-k}} \right) (w-z)^{-k}\, dw\\&\quad -\int _{i\infty }^{z} \frac{(w-z)^{-k}}{j({\gamma },w)^{2-k}}\, dw + \int _{{\gamma }^{-1}(i\infty )}^{z} (w-z)^{-k}\, dw \end{aligned}$$

and we obtain the result. Note that the Fourier expansion (1.3) implies $E_{2-k}(z)=1+O(e^{-2\pi y})$ as $y={\mathrm {Im}}(z) \rightarrow \infty$. Also if $u\rightarrow {\gamma }^{-1}(i\infty )$ then we may write $u={\gamma }z$ with ${\mathrm {Im}}(z) \rightarrow \infty$. As a consequence of the automorphy of $E_{2-k}$,

$$\begin{aligned} E_{2-k}(u) = j({\gamma },u)^{k-2}(1+O(e^{-2\pi y})) \quad \text {as} \quad u \rightarrow {\gamma }^{-1}(i\infty ). \end{aligned}$$

It follows that all the integrals in the proof are absolutely convergent. $\square$

Letting ${\gamma }= S$ in (8.9) produces

$$\begin{aligned}&z^{-k} U_k\left( \frac{-1}{z}\right) - U_k(z) = \frac{(1-k)\zeta (2-k)}{2\pi i}\Bigg \{\frac{1}{1-k}\left( z^{1-k}+\frac{1}{z} \right) \nonumber \\&\quad +\int ^{i \infty }_{0}\left( E_{2-k}(w)-1-\frac{1}{w^{2-k}} \right) (w-z)^{-k}\, dw\Bigg \}. \end{aligned}$$

(8.10)

Except for a term 1 / z, the right side of (8.10) is a polynomial in z and as in [39, Sect. 2] we may compute it explicitly.

Proposition 8.3

For $z\in {\mathbb {H}}$ and even $k\leqslant -2$,

$$\begin{aligned} 2\left( z^k U_k(z) - U_k(-1/z) \right) = (2\pi i)^{1-k} \sum _{\begin{array}{c} u,v \in {\mathbb {Z}}_{\geqslant 0} \\ u+v=1-k/2 \end{array}} \frac{B_{2u}}{(2u)!}\frac{B_{2v}}{(2v)!} z^{1-2v} + \left( 1-z^k\right) \zeta (1-k). \end{aligned}$$

Proof

With $n=2-k \geqslant 4$, the integral on the right of (8.10) is

$$\begin{aligned} \sum _{r=0}^{n-2} \left( {\begin{array}{c}n-2\\ r\end{array}}\right) (-z)^{n-2-r} i^{r+1} \int _0^\infty \left( E_n(iy)-1-\frac{1}{i^n y^n}\right) y^r\, dy. \end{aligned}$$

(8.11)

Let $c_n:=(2\pi i)^n/({\Gamma }(n)\zeta (n))$. For ${\mathrm {Re}}(s)$ large enough, the completed L-function associated to $E_n$ is

$$\begin{aligned} L^*(E_n,s):=\int _0^\infty \left( E_n(it)-1\right) t^{s-1}\, dt = \frac{c_n {\Gamma }(s)}{(2\pi )^s} \sum _{m = 1}^\infty \frac{\sigma _{n-1}(m)}{m^s}. \end{aligned}$$

Rewriting as

$$\begin{aligned} L^*(E_n,s) = \int _1^\infty \left( E_n(it)-1\right) t^{s-1}\, dt + \int _0^1 \left( E_n(it)-\frac{1}{i^n t^n}\right) t^{s-1}\, dt -\frac{1}{s}-\frac{1}{i^n(n-s)} \end{aligned}$$

(8.12)

shows that $L^*(E_n,s)$ has a meromorphic continuation to all $s\in {\mathbb {C}}$ with poles only at $s=0,n$. Combining $E_n(i/y)=i^ny^n E_n(iy)$ with (8.12) also gives the functional equation

$$\begin{aligned} L^*(E_n,n-s) = (-1)^{n/2} L^*(E_n,s). \end{aligned}$$

(8.13)

For $0<{\mathrm {Re}}(s)<n$ we see that

$$\begin{aligned} \int _0^\infty \left( E_n(iy)-1-\frac{1}{i^n y^n}\right) y^{s-1}\, dy = L^*(E_n,s) \end{aligned}$$

(8.14)

since both sides agree with the right side of (8.12). Therefore (8.11) equals

$$\begin{aligned} \sum _{r=0}^{n-2} \left( {\begin{array}{c}n-2\\ r\end{array}}\right) (-z)^{n-2-r} i^{r+1} L^*(E_n,r+1). \end{aligned}$$

(8.15)

For ${\mathrm {Re}}(s)$ large,

$$\begin{aligned} \sum _{m = 1}^\infty \frac{\sigma _{n-1}(m)}{m^s} = \sum _{d=1}^\infty \sum _{r=1}^\infty \frac{d^{n-1}}{(rd)^s} = \zeta (s)\zeta (s+1-n). \end{aligned}$$

Recall that $\zeta (1-n)=(-1)^{n+1}B_n/n$ for $n\in {\mathbb {Z}}_{\geqslant 1}$. This means $\zeta (0)=-1/2$ and $\zeta (n)=0$ for all negative even n. We have

$$\begin{aligned} L^*(E_n,n-1)=c_n (n-2)! (2\pi )^{1-n}\zeta (n-1)\zeta (0) \end{aligned}$$

and by (8.13), $L^*(E_n,1)$ is $(-1)^{n/2}$ times this value. For integers r with $2\leqslant r\leqslant n-2$,

$$\begin{aligned} L^*(E_n,r)=c_n (r-1)! (2\pi )^{-r} \zeta (r)\zeta (r+1-n) \end{aligned}$$

and this vanishes for odd r. For even r in this range

$$\begin{aligned} L^*(E_n,r)= (-1)^{n+r}c_n \frac{(r-1)!}{(2\pi )^{r}} \frac{(2\pi )^r |B_r|}{2\cdot r!}\frac{B_{n-r}}{(n-r)!}. \end{aligned}$$

Assembling these calculations and simplifying completes the proof. $\square$

Proposition 8.3 confirms (1.25) for even $k\leqslant -2$. For even $k\geqslant 2$, the identity (1.25) follows from the fact that ${\mathbb {E}}_k(z)$ has holomorphic weight k. The weight $k=0$ case may be shown with the Kronecker limit formula as in [16, Sect. 3], for example.

As discussed in [13, pp. 466-467] and [5, Remark 5.2], (and returning to k being even and negative), adding a $(1-k)$ fold integral of the constant term of $E_{2-k}(z)$ to $U_k(z)$ gives it a neater transformation property. Under the action of $S=\left( \begin{matrix}0 &{} -1 \\ 1 &{} 0 \end{matrix}\right)$ it will now transform with weight k up to a polynomial instead of a rational function—this is the period polynomial of $E_{2-k}(z)$ with respect to S.

These ideas generalize and the period polynomial with respect to S of any modular form f has coefficients that may be expressed in terms of $L^*(f,r)$ with integer r satisfying $1\leqslant r \leqslant k-1$. This is due to work of Grosswald, Razar, Weil and others; see Sections 4 and 5 of [19] or Section 5 of [5] and the contained references. There is also a nice detailed treatment in Sections 11.5-11.7 of [12], though without references.

8.2 The non-holomorphic part of ${\mathbb {E}}_k(z)$

As in (1.28), write the non-holomorphic series in (8.3) as

$$\begin{aligned} V_k(z):= \sum _{m=1}^\infty \sigma _{k-1}(m) e^{-2\pi i m \overline{z}}\sum _{u=0}^{-k} \frac{(4\pi m y)^{u}}{u!}. \end{aligned}$$

(8.16)

It is identically zero for k positive. The finite sum in (8.16) may be expressed, for $x>0$ and $m\in {\mathbb {Z}}_{\geqslant 0}$, as

$$\begin{aligned} \sum _{u=0}^m \frac{x^u}{u!}&= \frac{x^{m+1}}{m!} \int _0^\infty (t+1)^m e^{-xt}\, dt, \end{aligned}$$

(8.17)

$$\begin{aligned}&= \frac{e^x}{m!} \int _x^\infty t^{m} e^{-t}\, dt = \frac{e^x}{m!} {\Gamma }(m+1,x). \end{aligned}$$

(8.18)

Using (8.17) or (8.18) we obtain a similar identity to (8.8),

$$\begin{aligned} V_k(z) = \frac{(1-k)\zeta (2-k)}{2\pi i}\int _{i\infty }^{-\overline{z}} (E_{2-k}(w)-1)(w+z)^{-k} \, dw \end{aligned}$$

for even $k \leqslant 0$. This is equivalent to the expression in [13, p. 466]. With (8.18) we may also write

$$\begin{aligned} V_k(z) = \sum _{m=1}^\infty \frac{\sigma _{k-1}(m)}{|k|!} e^{-2\pi i m z} \cdot {\Gamma }(1-k,4\pi my). \end{aligned}$$

In this formulation using the incomplete ${\Gamma }$ function, Theorem 8.1 matches the general Fourier development expected for a harmonic Maass form with polynomial growth at the cusps, as given in [28, Lemma 4.4] for example.

Proof of Theorem 1.3

We have $z^k {\mathbb {E}}_k(z) - {\mathbb {E}}_k(-1/z) = 0$ since ${\mathbb {E}}_k(z)$ has holomorphic weight k. Expressing this relation with the Fourier expansion from Theorem 8.1 shows

$$\begin{aligned} 2\left( z^k V_k(z) - V_k(-1/z) \right)= & {} \frac{2\zeta (2-k)}{(2\pi i)^k} \left( \frac{y}{\pi }\right) ^{1-k}\left( |z|^{2k-2}-z^k \right) \nonumber \\&+\,2\frac{\zeta (1-k)}{\varepsilon (k)}\left( 1- z^k\right) - 2\left( z^k U_k(z) - U_k(-1/z) \right) \nonumber \\ \end{aligned}$$

(8.19)

for all nonzero $k\in 2{\mathbb {Z}}$. Then substituting (1.25) into (8.19) and simplifying gives the result when $k\ne 0$. For $k=0$ we have

$$\begin{aligned} 2\left( U_0(z) - U_0(-1/z) \right) = \pi i(z+1/z)/6-\pi i/2+\log z \end{aligned}$$

(8.20)

by (1.25). Clearly $V_0(z)=\overline{U_0(z)}$ and so, by conjugating (8.20),

$$\begin{aligned} 2\left( V_0(z) - V_0(-1/z) \right) = -\pi i(\overline{z}+1/\overline{z})/6+\pi i/2+\overline{\log z}. \end{aligned}$$

(8.21)

Verify that the theorem gives (8.21) for $k=0$. $\square$

Letting $z=i$ and $k=2-2h$ in Theorem 1.3 gives the following companion identity to (1.27)

$$\begin{aligned} \zeta (2h-1)= & {} \frac{(4\pi )^{2h-1}|B_{2h}|}{(2h)!}+\frac{(2\pi )^{2h-1}}{2} \sum _{\begin{array}{c} u,v \in {\mathbb {Z}}_{\geqslant 0} \\ u+v=h \end{array}} (-1)^u \frac{B_{2u}}{(2u)!}\frac{B_{2v}}{(2v)!}\nonumber \\&-2\sum _{m=1}^\infty \sigma _{1-2h}(m) e^{-2\pi m}\sum _{u=0}^{2h-2} \frac{(4\pi m)^u}{u!}, \end{aligned}$$

(8.22)

for even $h \geqslant 2$. The Bernoulli numbers sum appears with opposite signs in (1.27) and (8.22) so that adding them gives the simpler identities (1.30) and (1.31) we saw in the introduction. It may easily be checked that Proposition 7.2 for $k=2h-2$ also gives (1.30) and (1.31).

8.3 Ramanujan polynomials

Alternatively, we may obtain the Bernoulli numbers sum without the $\zeta (2h-1)$ term by taking the difference of (1.27) and (8.22). More generally we may consider the polynomials

$$\begin{aligned} \mathcal {R}_k(z) := \sum _{\begin{array}{c} u,v \in {\mathbb {Z}}_{\geqslant 0}\\ u+v=1-k/2 \end{array}} \frac{B_{2u}}{(2u)!}\frac{B_{2v}}{(2v)!} z^{2u} \end{aligned}$$

appearing in (1.25) and named the Ramanujan polynomials in [19, 31]. We continue our practice of using the weight k as the index; $\mathcal {R}_k(z)$ corresponds to $R_{1-k}(z)$ in the cited papers. The simplest nonzero polynomials are $\mathcal {R}_2(z)=1$, $\mathcal {R}_0(z)=(1+z^2)/12$ and $\mathcal {R}_{-2}(z)=(-1+5z^2-z^4)/720$. Detailed properties of the zeros of $\mathcal {R}_k(z)$ are proved in [31] including: for even $k \leqslant 0$ all nonreal zeros lie on the unit circle and, for even $k \leqslant -2$, there are exactly four real zeros and they lie in the interval $[-2.2,2.2]$.

A consequence of (1.25) is that for negative even k

$$\begin{aligned} (2\pi i)^{1-k} \frac{\mathcal {R}_k(z)}{z(z^{-k}-1)} + \zeta (1-k) = \frac{2\left( U_k(z)-z^{-k}U_k(-1/z) \right) }{z^{-k}-1}. \end{aligned}$$

(8.23)

They further show in [31] that for each even $k\leqslant -8$, there is a zero $\alpha$ of $\mathcal {R}_k(z)$ with $\alpha \in {\mathbb {H}}$, $|\alpha |=1$ and $\alpha ^{-k}\ne 1$. Hence $\zeta (1-k)$ equals the right hand side of (8.23) evaluated at the algebraic number $\alpha$. This gives circumstantial evidence that $\zeta (1-k)$ is transcendental because [19, Thm. 2.1] says that as $\beta \in {\mathbb {H}}$ runs over all algebraic numbers, with $\beta ^{-k}\ne 1$, the right of (8.23) evaluated at $\beta$ has an algebraic value at most once. This unique algebraic value would have to be $\zeta (1-k)$ for $\zeta (1-k)$ to be algebraic.

Theorem 1.3 gives a new expression for the Ramanujan polynomials in terms of the non-holomorphic components $V_k(z)$. Similarly to (8.23) we may write, for even $k<0$,

$$\begin{aligned}&-(2\pi i)^{1-k} \frac{\mathcal {R}_k(z)}{z(z^{-k}-1)} + \zeta (1-k) = \frac{2\left( V_k(z)-z^{-k}V_k(-1/z) \right) }{z^{-k}-1}\nonumber \\&\quad +\frac{B_{2-k}}{2(2-k)!}(4\pi y)^{1-k}\frac{z^{-k}|z|^{2k-2}-1}{z^{-k}-1}. \end{aligned}$$

(8.24)

Further results and conjectures related to the Ramanujan polynomials are discussed in [5, Sect. 7].

9 An inner product formula

For two functions f and g on ${\mathbb {H}}$ with holomorphic weight k, their Petersson inner product is

$$\begin{aligned} \langle \,f , g \,\rangle :=\int _{{{\Gamma }\backslash {\mathbb {H}}}} y^{k} f(z) \overline{g(z)} \, \frac{dx dy}{y^2}. \end{aligned}$$

(9.1)

This converges, for example, if one of the functions has exponential decay at infinity and one has at most polynomial growth. The following proposition links a convolution L-series with the inner product of a cusp form f and a product of Eisenstein series. This is an important step in the method of Diamantis and the author in [17] and we give a new direct proof here based on Theorem 1.1.

Proposition 9.1

Let $f(z)=\sum _{n=1}^\infty a_f(n) e^{2\pi i nz}$ be a weight k cusp form and suppose $k_1, k_2 \in 2 \mathbb {Z}$ satisfy $k_1+k_2=k$ and $k_2 \geqslant 0$. Then for all $u, v \in \mathbb {C}$ satisfying

$$\begin{aligned} -{\mathrm {Re}}(u)-k/2+1/2<|{\mathrm {Re}}(v)-1/2|<{\mathrm {Re}}(u)-k_2/2-7/2 \end{aligned}$$

(9.2)

we have

$$\begin{aligned}&\Bigl \langle f, y^{-k/2}E^*_{k_1}(\cdot , \overline{u}) E^*_{k_2}(\cdot , \overline{v}) \Bigr \rangle \nonumber \\&\quad = \left[ (-1)^{k_2/2} 2 \pi ^{k/2} \zeta (2u) \frac{{\Gamma }(|k_1|/2+u)}{{\Gamma }(k_1/2+u)} \frac{ {\Gamma }(s) {\Gamma }(w)}{(2 \pi )^{s+w}} \right] \sum _{n=1}^{\infty }\frac{a_f(n) \sigma _{2v-1}(n)}{n^{w}} \end{aligned}$$

(9.3)

where

$$\begin{aligned} s=u-v+k/2, \quad w=u+v+k/2-1. \end{aligned}$$

(9.4)

Proof

Note that the right inequality in (9.2) implies ${\mathrm {Re}}(u)>7/2$ and the left inequality implies ${\mathrm {Re}}(s)>0$ and ${\mathrm {Re}}(w)>0$. With (1.18), the left side of (9.3) is

$$\begin{aligned} \int _{{{\Gamma }\backslash {\mathbb {H}}}} y^{k/2} f(z) E^*_{-k_1}(z, u) E^*_{-k_2}(z, v) \, \frac{dx dy}{y^2}. \end{aligned}$$

(9.5)

For ${\mathrm {Re}}(u)>1$ we may unfold $E_{-k_1}(\cdot , u)$ in (9.5) using its series expansion (1.4) to produce

$$\begin{aligned} \theta _{k_1}(u)\int _0^\infty \int _0^1 y^{k/2+u-2} f(z) E^*_{-k_2}(z, v) \, dxdy. \end{aligned}$$

(9.6)

We need conditions on u and v for (9.6) to converge. In fact we require the convergence of (9.6) when f(z) and $E^*_{-k_2}(z, v)$ are replaced by their Fourier expansions, bounded termwise in absolute value. Employing Hecke’s bound $a_f(n) \ll n^{k/2}$ we have, with (3.8),

$$\begin{aligned} f(z) \ll \sum _{n=1}^\infty n^{k/2} e^{-2\pi n y} \ll (1+y^{-k/2-1})e^{-2\pi y}. \end{aligned}$$

Corollary 3.3 gives the bounds we need for $E^*_{-k_2}(z, v)$ and we see that the integrand in (9.6) is bounded by

$$\begin{aligned} y^{k/2+{\mathrm {Re}}(u)-2} \cdot y^{-k/2-1} \cdot y^{-|{\mathrm {Re}}(v)-1/2|-k_2/2-3/2} \quad \text {as} \quad y\rightarrow 0. \end{aligned}$$

Hence the desired convergence of (9.6) is ensured by the right inequality of (9.2).

Writing the Fourier expansion of $E^*_{-k_2}(z, v)$ as $\sum _{m \in {\mathbb {Z}}} e_{-k_2}(m;y,v) e^{2\pi i m x}$, the expression (9.6) becomes

$$\begin{aligned} \theta _{k_1}(u)\sum _{n=1}^\infty a_f(n) \int _0^\infty e^{-2\pi ny} e_{-k_2}(-n;y,v) y^{k/2+u-2} \, dy \end{aligned}$$

after integrating with respect to x. Theorem 1.1 tells us that

$$\begin{aligned} e_{-k_2}(-n;y,v) = \frac{1}{2^{k_2-1}} \frac{ \sigma _{2v-1}(n)}{n^v} \sum _{r=-k_2/2}^{k_2/2} P^{k_2/2}_r\bigl (4\pi n y \bigr ) (n y)^{1/2} K_{v+r-1/2}(2 \pi n y) \end{aligned}$$

and so we need the integral

$$\begin{aligned}&\int _0^\infty e^{-2\pi ny} P^{k_2/2}_r (4\pi n y ) (ny)^{1/2} K_{v+r-1/2}(2 \pi ny) y^{k/2+u-2} \, dy\\&\quad =\sum _{\ell =|r|}^{k_2/2} \psi ^{k_2/2}_r(\ell )\int _0^\infty e^{-2\pi ny} (-4\pi n y )^\ell (ny)^{1/2} K_{v+r-1/2}(2 \pi ny) y^{k/2+u-1} \, \frac{dy}{y}\\&\quad =\sum _{\ell =|r|}^{k_2/2} \frac{(-2)^\ell \psi ^{k_2/2}_r(\ell ) }{(2\pi )^{1/2} (2\pi n)^{k/2+u-1}} \int _0^\infty e^{-2\pi ny} (2\pi n y)^{k/2+u-1/2+\ell } K_{v+r-1/2}(2 \pi ny) \, \frac{dy}{y} \end{aligned}$$

with $\psi ^{k_2/2}_r(\ell )$ the coefficient of $(-x)^\ell$ in $P^{k_2/2}_r(x)$. This last integral equals

$$\begin{aligned} \int _0^\infty e^{-t} t^{k/2+u-1/2+\ell } K_{v+r-1/2}(t) \, \frac{dt}{t} =\frac{2^{-k/2+1/2-u-\ell } \pi ^{1/2} {\Gamma }(s+\ell -r){\Gamma }(w+\ell +r)}{{\Gamma }(k/2+u+\ell )} \end{aligned}$$

provided ${\mathrm {Re}}(s)+\ell -r>0$ and ${\mathrm {Re}}(w)+\ell +r>0$; see for example [23, p. 205]. These conditions hold since ${\mathrm {Re}}(s),$ ${\mathrm {Re}}(w)>0$.

Putting our results together, simplifying and reordering the summation shows that the left side of (9.3) equals

$$\begin{aligned}&\frac{k_2! \theta _{k_1}(u)}{2^{k_2} (4\pi )^{k/2+u-1}}\sum _{n=1}^\infty \frac{a_f(n) \sigma _{2v-1}(n) }{n^{w}}\sum _{\ell =0}^{k_2/2} \frac{( -1)^\ell }{{\Gamma }(k/2+u+\ell ) (k_2/2 -\ell )!} \nonumber \\&\quad \times \sum _{r=-\ell }^\ell \frac{ {\Gamma }(s+\ell -r){\Gamma }(w+\ell +r)}{(\ell -r)!(\ell +r)!}. \end{aligned}$$

(9.7)

The general binomial theorem implies that

$$\begin{aligned} \sum _{j=0}^\infty \frac{{\Gamma }(a+j)}{{\Gamma }(a) j!} x^j =\frac{1}{(1-x)^a} \end{aligned}$$

for all $|x|<1$ and $a>0$. Hence, expanding both sides of $(1-x)^{-a} (1-x)^{-b} = (1-x)^{-a-b}$ proves

$$\begin{aligned} \sum _{m+n=\ell } \frac{{\Gamma }(a+m){\Gamma }(b+n)}{{\Gamma }(a){\Gamma }(b)\ m! n!} = \frac{{\Gamma }(a+b+\ell )}{{\Gamma }(a+b)\ \ell !} \end{aligned}$$

(9.8)

and (9.8) is valid for all $a,b \in {\mathbb {C}}$ by meromorphic continuation. Thus the innermost sum in (9.7) evaluates to ${\Gamma }(s) {\Gamma }(w) {\Gamma }(s+w+2\ell )/({\Gamma }(s+w) (2\ell )!)$ and (9.7) becomes

$$\begin{aligned} \frac{k_2! \theta _{k_1}(u)}{2^{k_2} (4\pi )^{k/2+u-1}}\frac{{\Gamma }(s) {\Gamma }(w)}{{\Gamma }(s+w)}\sum _{n=1}^\infty \frac{a_f(n) \sigma _{2v-1}(n) }{n^{w}} \sum _{\ell =0}^{k_2/2} ( -1)^\ell \frac{ {\Gamma }(s+w+2\ell ) }{{\Gamma }(k/2+u+\ell ) (k_2/2 -\ell )! (2\ell )!}. \end{aligned}$$

The next lemma computes the above sum over $\ell$ (writing $s+w$ as $k-1+2u$).

Lemma 9.2

For even $k,k_2 \geqslant 0$ and all $u \in {\mathbb {C}}$

$$\begin{aligned} \sum _{\ell =0}^{k_2/2} ( -1)^\ell \frac{{\Gamma }(k-1+2u+2\ell ) }{{\Gamma }(k/2+u+\ell ) \ (k_2/2 -\ell )! \ (2\ell )!}=\frac{(2i)^{k_2}}{k_2!} \frac{{\Gamma }(k-1+2u)}{{\Gamma }(k/2-k_2/2 +u)}. \end{aligned}$$

(9.9)

Proof

Assume first that u is a positive integer and let $d=k/2+u-1$. The left side of (9.9) is

$$\begin{aligned} \sum _{\ell =0}^{k_2/2} ( -1)^\ell \frac{(2d+2\ell )!}{(2\ell )! (k_2/2-\ell )!(d+\ell )!} = \frac{(2d)!}{(k_2/2+d)!} \sum _{\ell } (-1)^\ell \left( {\begin{array}{c}2d+2\ell \\ 2d\end{array}}\right) \left( {\begin{array}{c}d+k_2/2\\ d+\ell \end{array}}\right) . \end{aligned}$$

Replace $\ell$ by $\ell -d$ in this sum to get

$$\begin{aligned} \frac{(-1)^d (2d)!}{(k_2/2+d)!} \sum _{\ell } (-1)^\ell \left( {\begin{array}{c}2\ell \\ 2d\end{array}}\right) \left( {\begin{array}{c}d+k_2/2\\ \ell \end{array}}\right) =\frac{(2i)^{k_2} (2d)!}{(d-k_2/2)! k_2!}=\frac{(2i)^{k_2} {\Gamma }(k-1+2u)}{{\Gamma }(k/2-k_2/2+u) \ k_2!}, \end{aligned}$$

employing (4.10). Let A(u) denote the left side of (9.9) and B(u) the right side. Now $A(u) {\Gamma }(u)/{\Gamma }(2u)$ must be a rational function of u and similarly for B(u). Therefore

$$\begin{aligned} \frac{{\Gamma }(u)}{{\Gamma }(2u)} A(u)=\frac{A_1(u)}{A_2(u)}, \qquad \frac{{\Gamma }(u)}{{\Gamma }(2u)} B(u)=\frac{B_1(u)}{B_2(u)} \end{aligned}$$

for polynomials $A_1,A_2,B_1,B_2$. We have demonstrated that

$$\begin{aligned} A_1(u)B_2(u) = A_2(u) B_1(u) \end{aligned}$$

(9.10)

for infinitely many integers u. Hence the left and right sides of (9.10) are identical and $A(u)=B(u)$ for all $u \in {\mathbb {C}}$, as required. $\square$

This completes the proof of Proposition 9.1. $\square$

A similar inner product to $\langle f, y^{-k/2}E^*_{k_1}(\cdot , \overline{u}) E^*_{k_2}(\cdot , \overline{v}) \rangle$ for the group ${\Gamma }(N)$ is computed in a different way in [26, Prop. 2.5]. This result is used there to prove relations among products of Eisenstein series that mirror the Manin relations.

The L-function of f is $L(f,s) := \sum _{n=1}^\infty a_f(n) n^{-s},$ defined for ${\mathrm {Re}}(s)$ large. The completed L-function,

$$\begin{aligned} L^*(f,s):=(2\pi )^{-s}{\Gamma }(s) L(f,s) = \int _0^\infty f(iy) y^{s-1} \, dy, \end{aligned}$$

(9.11)

is now an analytic function for all $s \in {\mathbb {C}}$. Suppose f is a Hecke eigenform that is normalized to have $a_f(1)=1$. Then the convolution L-series from (9.3) satisfies

$$\begin{aligned} \sum _{n=1}^\infty \frac{a_f(n) \sigma _{2v-1}(n)}{n^w} = L(f,s) L(f,w)/\zeta (2u), \end{aligned}$$

for ${\mathrm {Re}}(w)$ large enough, by comparing Euler products as in [17, Eq. (2.11)]. Therefore Proposition 9.1 and analytic continuation give the next corollary which is [17, Prop. 2.1].

Corollary 9.3

Let $k_1$, $k_2 \geqslant 0$ be even with $k=k_1+k_2$ and f a normalized Hecke eigenform of weight k. Then for all $u,v \in {\mathbb {C}}$ we have the following relation, with s and w given by (9.4),

$$\begin{aligned} (-1)^{k_2/2} \Bigl \langle f, y^{-k/2}E^*_{k_1}(\cdot , \overline{u})E^*_{k_2}(\cdot , \overline{v})\Bigr \rangle = 2 \cdot \pi ^{k/2} L^*(f,s) L^*(f,w). \end{aligned}$$

(9.12)

10 The kernel for products of L-functions

Let $S_k$ be the ${\mathbb {C}}$-vector space of holomorphic cusp forms of weight k. We may choose a basis $\mathcal {B}_k$ of normalized Hecke eigenforms. For every $s,w \in {\mathbb {C}}$, the condition

$$\begin{aligned} \langle \,f , H_{\overline{s}, \overline{w}} \,\rangle = L^*(f,s) L^*(f,w) \qquad \text {for all} \qquad f \in \mathcal {B}_k, \end{aligned}$$

uniquely defines the kernel $H_{s,w}$ as a cusp form in $S_k$.

Suppose we have $n \in {\mathbb {Z}}_{\geqslant 0}$ and even $k_1,k_2 \geqslant 4$ so that $k=k_1+k_2+2n$. Zagier in [38, Sect. 5] gave an explicit description of $H_{n+1,n+k_2}$ in terms of the Rankin–Cohen bracket $[E_{k_1}, E_{k_2}]_n$ of two Eisenstein series:

$$\begin{aligned} (-1)^{k_1/2} 2^{3-k} \frac{k_1 k_2}{B_{k_1} B_{k_2}}\left( {\begin{array}{c}k-2\\ n\end{array}}\right) H_{n+1,n+k_2}=\frac{[E_{k_1}, E_{k_2}]_n}{(2\pi i)^n} \end{aligned}$$

(10.1)

where

$$\begin{aligned}{}[E_{k_1}, E_{k_2}]_n := \sum _{r=0}^n (-1)^r \left( {\begin{array}{c}k_1+n-1\\ n-r\end{array}}\right) \left( {\begin{array}{c}k_2+n-1\\ r\end{array}}\right) E_{k_1}^{(r)}E_{k_2}^{(n-r)}. \end{aligned}$$

(10.2)

(The $n=0$ case of (10.1) is due to Rankin.) The Fourier coefficients of $E_{k_1}, E_{k_2}$ are rational and so it follows from (10.1) that the Fourier coefficients of $H_{n+1,n+k_2}$ are rational also. This is the key step used in [38, Sect. 5] and [27, p. 202] to prove

Theorem 10.1

(Manin’s Periods Theorem) For each $f \in \mathcal {B}_k$ there exist real numbers $\omega _+(f), \ \omega _-(f)$ with $\omega _+(f) \omega _-(f) = \bigl \langle f, f \bigr \rangle$ and

$$\begin{aligned} L^*(f,s)/\omega _+(f), \quad L^*(f,w)/\omega _-(f) \in K_f \end{aligned}$$

for all s, w with $1 \leqslant s, w \leqslant k-1$ and s even, w odd. Here $K_f$ is the finite extension of ${\mathbb {Q}}$ obtained by adjoining all the Fourier coefficients of f.

For this see also the discussion in [17, Sect. 4.3]. In [17] we showed another way to demonstrate the rationality of the Fourier coefficients of $H_{s,w}$ as summarized next. Suppose that $F:{\mathbb {H}}\rightarrow {\mathbb {C}}$ is smooth, transforms with holomorphic weight k and has at most polynomial growth at ${\infty }$. Then there exists a unique cusp form in $S_k$, which we label $\pi _{hol}(F)$ so that

$$\begin{aligned} \langle \,g , F \,\rangle = \langle \,g , \pi _{hol}(F) \,\rangle \qquad \text {for all} \qquad g \in S_k. \end{aligned}$$

(10.3)

The cusp form $\pi _{hol}(F)$ is called the holomorphic projection of F. If $F(z) =O(y^{-\epsilon })$ as $y\rightarrow \infty$ for some $\epsilon >0$ and has Fourier expansion $F(z)=\sum _{\ell \in {\mathbb {Z}}} F_\ell (y) e^{2\pi i \ell x}$, then letting g in (10.3) be the $\ell$th Poincaré series and unfolding gives the formula

$$\begin{aligned} \frac{(4\pi \ell )^{k-1}}{(k-2)!} \int _0^\infty F_\ell (y) e^{-2 \pi \ell y} y^{k-2} \, dy \end{aligned}$$

(10.4)

for the $\ell$th Fourier coefficient of $\pi _{hol}(F)$.

It follows from Corollary 9.3 that

$$\begin{aligned} H_{s,w}= \frac{1}{2 \cdot \pi ^{k/2}} \pi _{hol}\left( (-1)^{k_2/2} y^{-k/2}E^*_{k_1}(\cdot , \overline{u})E^*_{k_2}(\cdot , \overline{v})\right) \end{aligned}$$

for all $s,w \in {\mathbb {C}}$ where, by (9.4), $2u=s+w-k+1$ and $2v=-s+w+1$. Therefore, we may find the Fourier coefficients of $H_{s,w}$ from those of $E^*_{k_1}(\cdot , \overline{u})E^*_{k_2}(\cdot , \overline{v})$ by the formula (10.4). The case when s and w are integers of opposite parity in the range $1\leqslant s,w\leqslant k-1$ corresponds exactly, by [17, Lemma 3.2], to u and v being integers for which there exist positive even $k_1,k_2$ where $k_1+k_2=k$,

$$\begin{aligned} 1-k_1/2 \leqslant u \leqslant k_1/2 \quad \text {and} \quad 1-k_2/2 \leqslant v \leqslant k_2/2. \end{aligned}$$

(10.5)

Hence $u^*<k_1/2$ and $E^*_{k_1}(z,u)$ is in the upper triangle of Fig. 1, having only positive Fourier coefficients. The same is true of $E^*_{k_2}(z,v)$ and so the Fourier coefficients of the product $E^*_{k_1}(z,u)E^*_{k_2}(z,v)$ are finite sums with terms given by Theorem 1.2. In section 3 of [17] this calculation is carried out and (10.4) applied to find the $\ell$th Fourier coefficient of $H_{s,w}$. Precisely, this $\ell$th coefficient is given by the finite formula on the right of [17, Eq. (1.12)] divided by $2^{2-k}(k-2)!$. In particular it is rational as required for the proof of Theorem 10.1.

A further interesting expression for $H_{s,w}(z)$ is found in [18] in terms of the ‘double Eisenstein series’

$$\begin{aligned} {\varvec{E}}_{s, k-s}(z,w):= \sum _{\begin{array}{c} {\gamma }, \, \delta \in B \backslash {\Gamma }\\ c_{{\gamma }\delta ^{-1}} >0 \end{array}} \left( c_{{\gamma }\delta ^{-1}} \right) ^{w-1} \left( \frac{j({\gamma },z)}{j(\delta ,z)} \right) ^{-s}j(\delta ,z)^{-k} \end{aligned}$$

(10.6)

where $B:=\left\{ (\begin{matrix}1 &{} n \\ 0 &{} 1 \end{matrix}) : n\in {\mathbb {Z}}\right\}$ and $c_{{\gamma }\delta ^{-1}}$ indicates the bottom left entry of the matrix ${\gamma }\delta ^{-1}$. This series converges for $2<{\mathrm {Re}}(s)<k-2$ and ${\mathrm {Re}}(w)<{\mathrm {Re}}(s)-1, k-1-{\mathrm {Re}}(s)$ to a holomorphic cusp form of weight k; see Section 4 of [18]. By [18, Thm. 2.3],

$$\begin{aligned} H_{s,w}(z) =\left[ \frac{ e^{s i \pi /2} {\Gamma }(s) {\Gamma }(k-s) {\Gamma }(k-w)\zeta (1-w+s)\zeta (1-w+k-s)}{2^{3-w}\pi ^{k+1-w} {\Gamma }(k-1) }\right] {\varvec{E}}_{s, k-s}(z,w). \end{aligned}$$

We close with one more example of the holomorphic projection of a product. For $q=e^{2\pi i z}$, let $\Delta (z):=q\prod _{n=1}^\infty (1-q^n)^{24}$ be the discriminant function in $S_{12}$. Its Fourier coefficients are given by Ramanujan’s tau function $\tau (n)$. Recall the harmonic Eisenstein series ${\mathbb {E}}_{-2}(z)$ of weight $-2$ with Fourier coefficients given in Theorem 8.1. The weight 10 cusp form $\pi _{hol}(\Delta \cdot {\mathbb {E}}_{-2})$ must be identically zero. Hence its nth Fourier coefficient is zero and we obtain by (10.4), for all $n\in {\mathbb {Z}}_{\geqslant 1}$,

$$\begin{aligned}&\tau (n)\left( \zeta (3)-\frac{11}{16 n^3}\right) = -\sum _{m=1}^{n-1} \tau (n-m) \sigma _{-3}(m)\nonumber \\&\quad - \sum _{m=1}^{\infty } \tau (m+n) \sigma _{-3}(m) \sum _{u=0}^2 \left( {\begin{array}{c}u+8\\ 8\end{array}}\right) \frac{m^u n^9}{(m+n)^{u+9}}. \end{aligned}$$

(10.7)

This formula (10.7) may be compared with the more rapidly converging series for $\zeta (3)$ in (1.26), (1.30), (7.1) and (8.22).