1 Introduction

Nowadays, the demand for alternative energy sources is of utmost importance. Among the possible means of generating energy in an environment-friendly way, the exploitation of crops for the production of biofuels is becoming widely popular. The Jatropha plants originated in the tropical zone, initially from Mexico and the central part of the USA. The plants spread then in Latin America, Africa and SouthEast Asia and in India. This plant can easily be grown in arid and infertility conditions, even in sandy and salty soils, with minimal costs for cultivation.

Jatropha curcas seeds contain between 27 and 40 % triglycerides that can be used to produce a better quality substitute eco-fuel (Sahoo et al. 2009; Achten et al. 2007). The Jatropha plants have been chosen for massive production of renewable biodiesel because they have no competitor among the other commercial food or cash crops. But in addition to these qualities, Jatropha plants play a crucial role also in the environment, for instance as degraded land developers, soil erosion controllers and carbon sequesters (Pandey et al. 2012).

However, a major drawback on the widespread use of the Jatropha plant is the fact that it is easily affected by the mosaic virus Begomovirus. It heavily affects the Jatropha plants, causing. e.g., leaf damage, namely yellowing leaves, and sap drainage, and in particular attacking its fruits, considerably reducing the production of seeds. This plant virus is carried by infected whiteflies Bemisia tabaci (Gennadius). Its spread is normally determined by the whitefly vectors as well as density of host plant. Interestingly, however, the low density of Jatropha curcas plants allows a fast disease transmission compared with other host plants with higher density (Fauquet and Fargette 1990). Environmental conditions such as temperature and rainfall also influence the disease spread. It has been observed that heavy rains may constitute an obstacle to the spread of the whiteflies (Fargette et al. 1994).

The whiteflies are tiny flying insects, maturing from eggs through a sequence of instars. To protect themselves in harsh situations, the adult insects cover the outer part of their body with a layer of dry wax (Whitefly 2006).

A possible way to protect the Jatropha curcas plants from the mosaic virus is the use of insecticides spraying to control the vector whiteflies (Roy et al. 2015b). In particular, insecticidal soap is an organic insecticide, so harmless and safe that one can eat the vegetables or fruits on which the soap has been sprayed. It helps by reducing the amounts of eggs that are deposited by the whitefly population and prevents the adult flies to migrate from one plant to another (http://bugspray.com/article/whiteflies.html; Thurston 1998).

In this investigation we consider large Jatropha plantations. The corresponding model differs sensibly from a parallel investigation in which a major emphasis is given to the individual behavior of the producers of small “backyard” Jatropha crops (Roy et al. 2015a).

The paper is organized as follows. In the next section we formulate the model. In Sect. 3 we analyze its equilibria; Sect. 4 contains the sensitivity analysis; in Sect. 5, we reformulate the problem as a control problem. Simulations are carried out throughout the paper, to substantiate the analytical findings. A final discussion concludes the paper.

2 Formulation of the mathematical model

We consider the plant and vector population into the model without explicitly including the mosaic virus. However, mosaic virus affects both these populations, it is implicitly present in the model via the infected Jatropha and infected vector. Here, y(t) and v(t) denote the infected Jatropha plant and infected whitefly population respectively. Their corresponding healthy counterparts are denoted by x(t) and u(t).

As for every vector-carried disease, the mosaic virus passes from an infected whitefly to a susceptible plant and vice-versa from an infected Jatropha to a susceptible insect. Further, the Begomovirus itself can not be passed to offsprings of whitefly Bemisia tabaci (Gennadius) (Bosco et al. 2004). Bosco et al. (2004) remarked that the infection itself cannot be vertically transmitted. Therefore, based on this field evidence and experimental results, in the model formulation we assume that the newborn whiteflies are all susceptible.

We assume the logistic growth for healthy Jatropha plants due to the finite area of the plantation with net replanting rate r and carrying capacity k. Let λ be the contact rate from an infected vector to a susceptible plant, while β is the rate of disease transmission from an infected plant to a healthy whitefly. Thus a successful contact between infected vectors with a healthy plant makes it infected. Similarly, healthy whitefly feeding on an infected plant makes it infected. Further, the infection cannot be vertically transmitted.

For the mosaic virus vector, we assume logistic growth, with net birth rate b. The effect of temperature on life-history traits of Bemisia tabaci population is significant (Bonato et al. 2006). So the growth of whiteflies is highly dependent on the variation of temperature (T). The birth rate b of whitefly is defined as follows:

$$\begin{aligned} b\,=\, & {} \alpha \mathrm{e}^{-\delta T} T^c. \end{aligned}$$
(1)

The term b is defined as above because of the growth curve of whitefly. Here \(\alpha \), \(\delta , ~c\) are constants and are so chosen that value of b lies between its ranges.

In view of the fact that the cultivation in large areas is accounted as their environment, the carrying capacity of the cultivation is taken as the amount of Jatropha total leaf biomass, both healthy and infected, available within the entire plantation. This is indeed the case, because Bemisia tabaci generally attacks the leaves but not stem flowers and fruits. In turn, total leaf biomass is related to the plant abundance in the plantations as proportional (Sequeira and Naranjo 2008; Naranjo and Flint 1995). Denoting by a the maximum number of vectors that can survive on a plant, \(a(x+y)\) represents then the environmental carrying capacity of the vectors. Letting also m and \(\mu \) be the sum of the natural and the virus-related mortalities of the infected plants and vectors, respectively, the model can be written as follows, for \(x+y>0\):

$$\begin{aligned} \frac{\mathrm{d}x}{\mathrm{d}t}=\, & {} r x\left[ 1-\frac{x+y}{k}\right] -\lambda x v,\\ \nonumber \frac{\mathrm{d}y}{\mathrm{d}t}=\, & {} \lambda x v-m y,\\ \nonumber \frac{\mathrm{d}u}{\mathrm{d}t}=\, & {} b(u+v)\left[ 1-\frac{u+v}{a(x+y)}\right] -\beta u y,\\ \nonumber \frac{\mathrm{d}v}{\mathrm{d}t}=\, & {} \beta u y - \mu v. \end{aligned}$$
(2)

Clearly for \(x+y=0\) the plantation would be nonexistent, and there would be no need of the model, so that we can exclude this case from further consideration. With \(J_{11}=r[1 - (2 x + y )k^{-1}]-\lambda v\), the Jacobian is:

$$\begin{aligned} J=\left[ J_{ij} \right] = \left[ \begin{array}{cccc} J_{11} &{} ~~-\frac{r x}{k} &{} 0 &{} -\lambda x\\ \lambda v &{} ~~-m &{} 0 &{} \lambda x\\ \ \\ \frac{b(u+v)^2}{a(x+y)^2} &{} ~~-\beta u + \frac{b(u+v)^2}{a(x+y)^2} &{} ~~~b-\beta y - \frac{2 b (u+v)}{a(x+y)} &{} ~~~ b-\frac{2 b (u+v)}{a(x+y)}\\ \ \\ 0 &{} \beta u &{} \beta y &{} -\mu \\ \end{array} \right] . \end{aligned}$$

3 Equilibria and stability

Fig. 1
figure 1

Growth rate of whitefly is plotted as a function of temperature, taking \(\alpha =0.1896\), \(\delta =0.02\), and \(c=0.6\)

Full size image

3.1 Equilibria assessment

There are only three possible equilibria for system (2): the insect-and-disease-free equilibrium \(E_1=(k,0,0,0)\), the disease-free equilibrium \(E_2=(k,0,ak,0)\) and the endemic equilibrium \(E^*=(x^*,y^*,u^*,v^*)\), whose population values cannot be completely given. Summing the first and second equations in (2) as well as the second and the fourth one, we obtain y and u in terms of x and using these into the fourth equation we obtain also v as a function of x, as follows:

$$\begin{aligned} y^* = rx^* \frac{k-x^*}{rx^* +km}, \quad u^* = \frac{m\mu }{\beta \lambda x^*}, \quad v^* = \frac{mr}{\lambda } \frac{k-x^*}{rx^* +km}. \end{aligned}$$

Clearly from the above values, the endemic equilibrium is feasible if

$$\begin{aligned} k\ge x^*. \end{aligned}$$
(3)

Substituting these population values into the third equation of (2), we can find an equation of degree five for the unknown x population, \(\Psi (x)= \sum _{i=0} ^5 h_ix^i =0\). The coefficients can all explicitly be calculated, but they are rather complicated, and we provide only the two most relevant ones: \(h_0=- b k^2 m^2 \mu ^2 \beta ^{-1} <0\), \(h_5=a r^2 (\beta +\mu )>0\). From these, it is easily seen that at least one positive root \(x^*\) for equation \(\Psi (x)=0\) must exists. The remaining coefficients do not appear to have easily determined signs, so that the application of Descartes’ rule of sign is not necessary. Although sufficient conditions could be given for one, three or five positive roots, we do not investigate further for the uniqueness of this equilibrium.

Table 1 Values of the parameters used in the numerical simulations, obtained in part from the literature
Full size table
Fig. 2
figure 2

Population densities are plotted as a function of time for \(\lambda =0.005, ~T=\,30\,^{\circ }\mathrm{C}\) and other parameters as given in Table 1

Full size image

3.2 Stability

The equilibrium \(E_1\) is unstable, as its eigenvalues are r, \(-m\), b, \(-\mu \). \(E_2\) consists two eigenvalues easily are obtained as \(-b\) and \(-r\), and the remaining characteristic equation is a quadratic, for which the Routh–Hurwitz conditions are

$$\begin{aligned} m+\mu>0, \quad m\mu -ak^2 \beta \lambda >0. \end{aligned}$$
(4)

The first one holds, the second one gives the stability condition

$$\begin{aligned} \lambda \beta \,<\,\frac{m \mu }{ak^2}. \end{aligned}$$
(5)

At \(E^*\) the characteristic equation is given by:

$$\begin{aligned} \rho ^4 + \sigma _1 \rho ^3 + \sigma _2 \rho ^2 + \sigma _3 \rho + \sigma _4 = 0, \end{aligned}$$
(6)

where,

$$\begin{aligned} \sigma _1&=\,-[J_{11} + J_{22} + J_{33} +J_{44}],\nonumber \\ \sigma _2&=\,J_{33} J_{44} + J_{22} J_{44} + J_{11} J_{44} - J_{34} J_{43} - J_{24} J_{42} \nonumber \\&\quad+ J_{22} J_{33} + J_{11} J_{33} + J_{11} J_{22} - J_{12} J_{21},\nonumber \\ \sigma _3&=\,- J_{22} J_{33} J_{44} - J_{11} J_{33} J_{44} - J_{11} J_{22} J_{44} + J_{12} J_{21} J_{44} + J_{22} J_{34} J_{43} \nonumber \\&\quad+ J_{11} J_{34} J_{43} - J_{24} J_{32} J_{43} - J_{14} J_{31} J_{43} + J_{24} J_{33} J_{42} \nonumber \\&\quad+ J_{11} J_{24} J_{42} - J_{14} J_{21} J_{42} - J_{11} J_{22} J_{33} + J_{12} J_{21} J_{33},\nonumber \\ \sigma _4&=\,J_{11} J_{22} J_{33} J_{44} - J_{12} J_{21} J_{33} J_{44} - J_{11} J_{22} J_{34} J_{43} + J_{12} J_{21} J_{34} J_{43} \nonumber \\&\quad+ J_{11} J_{24} J_{32} J_{43} - J_{14} J_{21} J_{32} J_{43} - J_{12} J_{24} J_{31} J_{43} \nonumber \\&\quad+ J_{14} J_{22} J_{31} J_{43} - J_{11} J_{24} J_{33} J_{42} + J_{14} J_{21} J_{33} J_{42}. \end{aligned}$$
(7)

In this case some of the entries of the Jacobian matrix simplify as:

$$\begin{aligned} J_{11}&=\,-\frac{r x^*}{k}, \quad J_{12} \,=\,-\frac{r x^*}{k} , \quad J_{14}\,=\,-\lambda x^*, \quad J_{21}\,=\, \lambda v^*, \quad J_{22}\,=\,-m, \\ J_{24}&\,=\,\lambda x^*, \quad J_{31}\,=\,\frac{b(u^*+v^*)^2}{a(x^*+y^*)^2}, \quad J_{32}\,=\,-\beta u^* + \frac{b(u^*+v^*)^2}{a(x^*+y^*)^2}, \\ J_{33}&\,=\, b-\beta y^*-\frac{2 b (u^*+v^*)}{a(x^*+y^*)}, \quad J_{34} \,=\,b-\frac{2 b (u^*+v^*)}{a(x^*+y^*)}, \\ J_{42}&\,=\beta u^*, \quad J_{43}\,=\,\beta y^*, J_{44}\,=\,-\mu . \end{aligned}$$

The Routh–Hurwitz criterion provides the stability requirements as:

$$\begin{aligned}& \sigma _1> 0,\quad \sigma _4> 0,\quad \sigma _1 \sigma _2 - \sigma _3> 0, \\ &\quad (\sigma _1 \sigma _2 - \sigma _3) \sigma _3 - \sigma _1^2 \sigma _4 >0. \end{aligned}$$
(8)

Numerical evidence shows that these conditions are nonempty (see Fig. 2).

Fig. 3
figure 3

Persistent populations oscillations are plotted as a function of time for \(\lambda =0.015\) and other parameters as given in Table 1

Full size image
Fig. 4
figure 4

Bifurcation diagram in terms of the bifurcation parameter \(\lambda \); the other parameters are kept fixed at the values given in Table 1

Full size image

3.3 Bifurcation analysis

Now, we study possible existence of Hopf bifurcations in the system (2). At \(E_2\), in view of the strict inequality in the first Routh–Hurwitz condition (4), the quadratic will not have purely imaginary eigenvalues, thus preventing the possible occurrence of Hopf bifurcations around this equilibrium point.

For the endemic equilibrium \(E^*\) we consider the Hopf bifurcation as a function of the parameter \(\lambda \in \mathbf{R}\).

Let \(\Psi \) : \((0,\infty )\rightarrow \mathbf{R}\) be the following continuously differentiable function of \(\lambda \):

$$\begin{aligned} \Psi (\lambda ):=\sigma _1(\lambda )\sigma _2(\lambda )\sigma _3(\lambda )-\sigma _3^2(\lambda ) -\sigma _4(\lambda )\sigma _1^2(\lambda ). \end{aligned}$$

Then for occurring the Hopf bifurcation, it is to be required that the spectrum \(\sigma (\lambda )=\{\rho :D(\rho )=0\}\) of the characteristic equation is such that there exists \(\lambda ^*\in (0, \infty )\), at which a pair of complex eigenvalues \(\rho (\lambda ^*), \bar{\rho }(\lambda ^*)\in \sigma (\lambda )\) satisfy

$$\begin{aligned} {\text {Re}} \rho (\lambda ^*)=0, \quad {\text {Im}} \rho (\lambda ^*)=\omega _0>0, \end{aligned}$$

along with the transversality condition

$$\left. \frac{{\rm d}{\rm Re} \rho (\lambda )}{{\rm d}\lambda }\right| _{\lambda ^*}\,\ne\,0$$

Furthermore, all other elements of \(\sigma (\lambda )\) must have negative real parts.

Theorem 1

The system (2) around the endemic equilibrium \(E^*\) enters into Hopf bifurcation at \(\lambda =\lambda ^*\in (0,\infty )\) if and only if \(\Psi (\lambda ^*)=0\) and

$$\begin{aligned} \sigma _1^3\sigma _2'\sigma _3(\sigma _1-3\sigma _3) >2(\sigma _2\sigma _1^2-2\sigma _3^2)(\sigma _3'\sigma _1^2-\sigma _1'\sigma _3^2) \end{aligned}$$
(9)

and all other eigenvalues are of negative real parts, where \(\rho (\lambda )\) is purely imaginary at \(\lambda =\lambda ^*\).

Proof

By the condition \(\Psi (\lambda ^*)=0\), the characteristic equation can be written as

$$\begin{aligned} \left( \rho ^2+\frac{\sigma _3}{\sigma _1}\right) \left( \rho ^2+\sigma _1\rho +\frac{\sigma _1\sigma _4}{\sigma _3}\right) =0. \end{aligned}$$

If it has four roots, say \(\rho _i\), (i = 1, 2, 3, 4) with the pair of purely imaginary roots at \(\lambda =\lambda ^*\) as \(\rho _1=\bar{\rho }_2\), then we have

$$\begin{aligned} \rho _3+\rho _4 = -\sigma _1, \quad \omega _0^2+\rho _3\rho _4 = \sigma _2, \quad \omega _0^2(\rho _3+\rho _4) = -\sigma _3, \quad \omega _0^2\rho _3\rho _4 = \sigma _4. \end{aligned}$$
(10)

where \(\omega _0={\text {Im}} \rho _1(\lambda ^*)\). By dividing the third and the first equations in (10), we find \(\omega _0=\sqrt{\sigma _3 \sigma _1^{-1}}\). Now, if \(\rho _3\) and \(\rho _4\) are complex conjugate, from (10), it follows that \(2{\text {Re}} \rho _3=-\sigma _1\); if they are real roots, then by (6) and (10) \(\rho _3<0\) and \(\rho _4<0\). To complete the discussion, it remains to verify the transversality condition.

As \(\Psi (\lambda ^*)\) is a continuous function of all its roots, there exists an open interval \(\lambda \in (\lambda ^*-\epsilon ,\lambda ^*+\epsilon )\) where \(\rho _1\) and \(\rho _2\) are complex conjugate for \(\lambda \). Suppose that their general forms in this neighborhood are

$$\begin{aligned} \rho _{1,2} (\lambda )= & {} \chi (\lambda ) \pm i\nu (\lambda ). \end{aligned}$$

Now, we shall verify the transversality condition

$$\begin{aligned} \frac{\mathrm{d} \mathrm{Re}(\rho _j (\lambda ))}{\mathrm{d}\lambda }|_{\lambda = \lambda ^*}\ne 0 ,\quad j=1,\ 2. \end{aligned}$$

Substituting \(\rho _j (\lambda ) =\chi (\lambda )\pm i\nu (\lambda )\), into (6) and differentiating, we have

$$\begin{aligned} K(\lambda )\chi '(\lambda ) -L(\lambda )\nu '(\lambda )+M(\lambda ) =0,\\ \nonumber L(\lambda )\chi '(\lambda )+K(\lambda )\nu '(\lambda ) +N(\lambda ) =0, \end{aligned}$$
(11)

where

$$\begin{aligned} K(\lambda )&\,=\,4\chi ^3-12\chi \nu ^2+3\sigma _1(\chi ^2-\nu ^2)+2\sigma _2\chi +\sigma _3, \\ L(\lambda )&\,=\,12\chi ^2\nu +6\sigma _1\chi \nu -4\chi ^3+2\sigma _2\chi , \\ M(\lambda )&\,=\,\sigma _1\chi ^3-3\sigma _1'\chi \nu ^2+\sigma _2'(\chi ^2-\nu ^2)+\sigma _3'\chi , \\ N(\lambda )&\,=\,3\sigma _1'\chi ^2\nu -\sigma _1'\nu ^3+2\sigma _2'\chi \nu +\sigma _3'\chi . \end{aligned}$$

Solving (11) for \(\chi '(\lambda ^*)\) we have

$$\begin{aligned} \left[ \frac{\mathrm{d} \mathrm{Re}(\rho _j(\lambda ))}{\mathrm{d}\lambda }\right] _{\lambda =\lambda ^*}=\chi '(\lambda )_{\lambda =\lambda ^*} =-\frac{L(\lambda ^*)N(\lambda ^*)+K(\lambda ^*)M(\lambda ^*)}{K^2(\lambda ^*)+L^2(\lambda ^*)} \\ = \frac{\sigma _1^3\sigma _2'\sigma _3(\sigma _1-3\sigma _3) -2(\sigma _2\sigma _1^2-2\sigma _3^2) (\sigma _3'\sigma _1^2-\sigma _1'\sigma _3^2)}{\sigma _1^4(\sigma _1-3\sigma _3)^2+4(\sigma _2\sigma _1^2-2\sigma _3^2)^2}>0 \end{aligned}$$

which holds in view of (9).

Thus the transversality conditions hold, and consequently, a Hopf bifurcation occurs at \(\lambda =\lambda ^*\).

4 Sensitivity analysis

Table 2 Parameters effects on the system’s populations
Full size table

We now provide a local sensitivity analysis of the solutions of (2) (Saltelli and Scott 1997; Saltelli et al. 1999). In this way we evaluate which parameters most affect the system dynamics. Consistency of the model with respect to small uncertainties in parameter values allows reliable predictions.

To study the forward, or direct sensitivity, of a population P with respect to the parameter \(\eta \), one must plot the values of \(\frac{\partial P}{\partial \eta }\) as function of time. For this task, we use MATLAB software that calculates the sensitivities by combining the original model system with the auxiliary differential equations for the sensitivities. These additional equations are obtained by differentiating the original equations with respect to parameters.

5 The optimal control problem

In this section, we formulate the problem as an optimal control problem, to minimize the costs involved in insecticide spraying.

Here, we do not consider the migration of infected vectors population. We assume that all the infected vectors of a particular region fall possibly under the control of spraying of insecticide. We reformulate the model (2) introducing the control \(0\le \gamma (t) \le 1\), as follows:

$$\begin{aligned} \frac{\mathrm{d}x}{\mathrm{d}t}&\,=\,r x\left[ 1-\frac{x+y}{k}\right] -(1-\gamma (t))\lambda x v,\\ \nonumber \frac{\mathrm{d}y}{\mathrm{d}t}&\,=\,(1-\gamma (t))\lambda x v-m y,\\ \nonumber \frac{\mathrm{d}u}{\mathrm{d}t}&\,=\,b(u+v)\left[ 1-\frac{u+v}{a(x+y)}\right] -\beta u y(1-\gamma (t)),\\ \nonumber \frac{\mathrm{d}v}{\mathrm{d}t}&=\,\beta y u(1-\gamma (t))-\mu v. \end{aligned}$$
(12)

Note that for \(\gamma =0\), there is no reduction in the contact rate between infected vectors and healthy plants, while for \(\gamma =1\), we have no such contact rate whatsoever. The role of \(\gamma \) is to express the reduction of the transmission from carrier to the susceptible plant by use of insecticide.

The cost function (i.e., objective functional) is taken in quadratic to ensure the existence of minimum spraying, as follows:

$$\begin{aligned} J(\gamma (t))=\int _{t_{0}}^{t_{f}}[P \gamma (t)^2 + Q y^2 - R x^2]\mathrm{d}t. \end{aligned}$$
(13)

The objective functional is taken in such a way that we can account the costs of spraying, insecticide and labor expressed by the first term, the damage of the crop due to infected plants, whose presence needs to be minimized, second term, and for the extra revenues obtained by a larger population of healthy Jatropha plants, expressed by last term. Here, the objective is to minimize the cost by finding a suitable \(\gamma (t)\).

To solve the problem we construct the Hamiltonian as follows:

$$\begin{aligned} H= & \, P \gamma (t)^2 + Q y^2 - R x^2+\xi _1\left[r x\left[1-\frac{x+y}{k}\right] -\lambda x v(1-\gamma (t))\right]\nonumber \\&+\xi _2\left[\lambda x v(1-\gamma (t))-m y\right]+\xi _3\left[b(u+v)\left[1-\frac{u+v}{a(x+y)}\right]\right.\\ \nonumber&\left.-\beta u y(1-\gamma (t))\right]+\xi _4\left[\beta y u(1-\gamma (t))-\mu v\right], \end{aligned}$$
(14)

where the \(\xi _i\), \(i=1, \ldots 4\) are the adjoint variables.

Applying “Pontryagin Minimum Principle” for the existence of the optimal control, we obtain the following result:

Theorem 2

If the objective function \(J(\gamma )\) is minimum for the optimal control \(\gamma ^*(t)\), then there exists adjoint variables \(\xi _i\), \(i=1, \ldots 4\), which satisfy the equations below:

$$\begin{aligned} \frac{\partial \xi _1}{\partial x}&\,=\, -\xi _1 r \left( 1-\frac{2 x+y}{k}\right) +\xi _1 \lambda v(1-\gamma (t))-\xi _2 \lambda v(1-\gamma (t)) \\ \nonumber&-\xi _3 \frac{b(u+v)^2}{a(x+y)^2},\\ \nonumber \frac{\partial \xi _2}{\partial y}&\,=\,-2Qy\frac{\xi _1 r x}{k}+\xi _2m -\xi _3 \frac{b(u+v)^2}{a(x+y)^2} -\xi _4 \beta u(1-\gamma (t)), \\ \nonumber \frac{\partial \xi _3}{\partial u}&\,=\,\xi _3 b \left( 1-\frac{2(u+v)}{a(x+y)}\right) -\xi _3 \beta y(1-\gamma (t))-\xi _3 c+ \xi _4(\beta y(1-\gamma (t))), \\ \nonumber \frac{\partial \xi _4}{\partial v}&\,=\,\xi _1 \lambda x(1-\gamma (t))-\xi _2 x (1-\gamma (t)) -\xi _3 b \left( 1-\frac{2(u+v)}{a(x+y)}\right) +\xi _4 \mu , \end{aligned}$$
(15)

with the transversality condition satisfying \(\xi _i(t_f)=0\), \(i=1, \ldots 4\).

The optimal control policy is given by:

$$\begin{aligned} \gamma ^*(t)=\max \left\{ 0, \min \left\{ 1, \frac{\lambda x v(\xi _2-\xi _1) +\beta y u(\xi _4-\xi _3)}{2P} \right\} \right\} . \end{aligned}$$
(16)

Proof

Applying the “Pontryagin Minimum Principle” (Fleming and Rishel 1975), the optimal control variable \(\gamma ^*(t)\) satisfies:

$$\begin{aligned} \frac{\partial H}{\partial \gamma ^*(t)}=0. \end{aligned}$$
(17)

From (14) and (17), we can get the following expression for \(\gamma ^*\):

$$\begin{aligned} \gamma ^*(t)=\frac{\lambda x v(\xi _2-\xi _1)+\beta y u(\xi _4-\xi _3)}{2P}. \end{aligned}$$

For the boundedness of the optimal control, we have

$$\begin{aligned} \gamma ^*(t)= \left\{ \begin{array}{ll} 0,\qquad\qquad\qquad\quad\,\, \frac{\lambda x v(\xi _2-\xi _1)+\beta y u(\xi _4-\xi _3)}{2P} \le 0,\\ \frac{\lambda x v(\xi _2-\xi _1)+\beta y u(\xi _4-\xi _3)}{2P},\quad 0<\frac{\lambda x v(\xi _2-\xi _1)+\beta y u(\xi _4-\xi _3)}{2P}<1, &{} \hbox {} \\ 1,\qquad\qquad\qquad\quad\,\,\frac{\lambda x v(\xi _2-\xi _1)+\beta y u(\xi _4-\xi _3)}{2P} \ge 1. &{} \hbox {} \end{array} \right. \end{aligned}$$

Hence the compact form of \(\gamma ^*(t)\) is given by (16).

The above equations are the necessary conditions satisfying the optimal control \(\gamma (t)\) and also the state variables of the system. According to “Pontryagin Minimum Principle” (Fleming and Rishel 1975), the existence conditions are established by the corresponding adjoint equations:

$$\begin{aligned} \frac{\mathrm{d} \xi _1}{\mathrm{d}t}=-\frac{\partial H}{\partial x},~~~\frac{\mathrm{d} \xi _2}{\mathrm{d}t}=-\frac{\partial H}{\partial y},\nonumber \\ \frac{\mathrm{d} \xi _3}{\mathrm{d}t}=-\frac{\partial H}{\partial u},~~~\frac{\mathrm{d} \xi _4}{\mathrm{d}t}=-\frac{\partial H}{\partial v}. \end{aligned}$$
(18)

From set of equations (18), we immediately find (15).

Fig. 5
figure 5

The control function \(\gamma (t)\) is plotted as a function of time with parameter values given in Table 1

Full size image
Fig. 6
figure 6

The dynamics of all four species of the system with control effect with parameter values given in Table 1

Full size image

6 Numerical simulations

In theoretical study, we have illustrated the analytical method using optimal control theoretic approach for the qualitative analysis of the dynamical system to control the whitefly population. We carry out the numerical simulation of the model system on the outlook of the analytical behaviors. We take \(x(0)=10,~ y(0)=8, ~u(0)=5,~ v(0)=2\) as initial conditions.

It is observed by Kashina et al. (2013) and Ramkat et al. (2011) that the Indian Cassava mosaic virus can cause the mosaic disease in Jatropha curcas plant. Furthermore, the phylogenetic nature of Cassava plants and the Jatropha plants are not same; thus, their growth and death rates differ but the plantation methods are very similar. For this reason, we have estimated the parameter values from the literature (Holt et al. 1997) for numerical simulations.

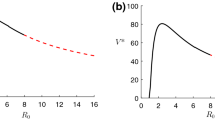
The effect of temperature on growth rate is shown in Fig. 1. Maximum growth is seen around a temperature of \(30\,^{\circ }\mathrm{C}\). Here, \(\alpha =0.1896\), \(\delta =0.0200\) and \(c=0.6\). Their values are so chosen that b lies between its ranges. We plot the growth rate b as a function of temperature (T) and see that at \(30\,^{\circ }\mathrm{C}\) whitefly growth rate is the maximum which is agreeable with Bonato et al. (2006). That means disease transmission is also higher particularly within this temperature. So, we think it is reasonable to analyze and control the system when the transmission rate gets maximized. Thus we take \(b=0.8\) for our numerical simulations.

We observe the behavioral changes of the system for different values of parameters. In Fig. 2, we portray the time series characteristic of all the four population taking the parameter values as given in Table 1. We notice that all the population oscillates up to 1200 days (approximately). But initially the magnitudes of this oscillation are very high, but slowly it becomes stable with the following time after 1400 days, all the populations go to stable in nature. In Fig. 3, we display the same population up to 2500 days. But here we assume the value of parameter \(\lambda \) i.e., the infection rate that is equal to 0.015 and other parameters are taken as same as in Fig. 2. In this case, oscillations are periodic. It is observed that as the value of \(\lambda \) increases, oscillation become periodic.

Figure 4 represents the bifurcation diagram of four populations with respect to the parameter \(\lambda \). Form this figure, it is clear that for a particular value of the infection rate (\(\lambda =0.0147\)), the system starts to bifurcate or diverge, that means it moves from stable to unstable situation. Thus, it is again established that the system dynamics depends significantly on this parameter. Here we find that for the value close to 0.0147 of the parameter \(\lambda \), the complete system starts to split.

Figure 5 describes the control effect that is plotted as a function of time. We operate the control through insecticide spraying up to 100 days. In Fig. 6, we portray the dynamical behavior of all four populations with the influence of optimal control. In this figure, we notice that due to effort of control, healthy plant population slowly increases from its initial position and becomes stable near about 150 days. It maintains its stable position throughout the remaining time. In case of infected plant population, it goes to extinction within first 35 days (approximately). Noninfected vector population also enhances up to first 120 days and then becomes stable throughout the following time period. Infected plant population reduces within very short days and finally moves to extinction. We observe that effect of optimal control by means of insecticide spraying has a great contribution to make the system stable and maintain the stable nature in the remaining portion of time span.

Fig. 7
figure 7

Sensitivity index as a function of time for different parameters of system (2). The vertical axes contain the partial derivatives of each population with respect to the indicated parameter

Full size image

In Fig. 7, we display the sensitivity characteristic of all parameters introduced into our proposed ecological system. Here we observe that all eight parameters are sensitive (some are positively sensitive and some are negatively sensitive). This actually validates our formulated mathematical model. The summary of sensitivity analysis of the model with respect to parameter is shown in Table 2. We notice that all the parameters used in our model are sensitive. Here ‘+ve’ means positively sensitive and ‘−ve’ means negatively sensitive.

7 Conclusion

Here, a mathematical model is formulated to study the dynamics of Jatropha mosaic disease and its possible control by using insecticide spraying. From the study, we observe that the parameter \(\lambda \) i.e., the disease transmission rate is very crucial. All the populations of the model system are going to oscillate for the cause of variation in the value of the parameter \(\lambda \). Also for discrepancy of the value of \(\lambda \), the system starts to diverge or bifurcate. Thus in a nut shell, it has the capacity to stabilize or destabilize the system. The application of insecticides minimizes the effect of oscillation in the system and makes the system stable. So, the control policy with minimum use of insecticidal soap is very significant. Numerical simulation also shows that optimal spraying is needed to control mosaic virus and to minimize the cost of cultivation. There is no requirement of control application of spraying during first 10 days. After that optimal spraying policy required for three months to eradicate the disease. Control measure has the ability to condense the oscillating nature of the population. Therefore spraying has a better effect on the population. Hence we can apply the insecticide on the host plants systematically. In this way, we would be liberally developed ourselves for advanced socioeconomical insight in the days to come.