Dynamic Strength of AZ31B-4E and AMX602 Magnesium Alloys Under Shock Loading

Abstract

Free surface velocity histories for two magnesium (Mg) alloys are obtained from planar shock compression experiments. Symmetric plate impacts at velocities of approximately 400, 600, 800, and 1000 m/s are reported, where axisymmetric cylindrical specimens (flat-faced discs) are launched in single stage light gas guns. The studied specimens have been produced from an equal channel angular extrusion process for Mg AZ31B-4E and from a hot extrusion of consolidated powder prepared via a spinning water atomization process for Mg AMX602. The present studies focus on the region of the velocity profiles spanning the Hugoniot elastic limit through the plastic rise up to the Hugoniot state, as opposed to wave reflection, release and spall studied previously in these materials. A semi-analytical method is invoked to extract inelastic constitutive response information from particle velocity histories. The only parameters entering the procedure are fundamental thermoelastic properties—notably including elastic constants up to order three—and the ratio of plastic work to energy storage of defects generated in the crystal lattice. Plastic shock velocities are not available from the present data; these are estimated from the initial bulk modulus, its pressure derivative, and known shock velocities in conventional Mg AZ31B. Shear stress, plastic strain, plastic strain rate, temperature, and dislocation density are computed outcomes. Results demonstrate similar trends in extracted behaviors for the two alloys, whereby maximum strength in the plastic shock front increases with increasing impact velocity in each material. Strain rate sensitivity appears to be greater in AZ31B-4E than AMX602. Flow stress on the Hugoniot is calculated as 295 to 336 MPa for AZ31B-4E and 163 to 293 MPa for AMX602. Maximum flow stress in the plastic rise, as extracted from tests with maximum impact velocity, is on the order of 700 MPa for each alloy.

Introduction

Due to their high strength-to-weight ratios and potential for further improvements in strength and ductility, magnesium (Mg) and its alloys have gained much attention for potential use in the defense industry [1, 2]. The shock responses of Mg in various forms, including pure single crystals, pure polycrystals, and alloys of different compositions, have been studied over the past five decades by numerous researchers [3,4,5,6,7,8,9,10]. Many of these studies have focused on the spall behavior of magnesium under extreme dynamic loading [6,7,8,9,10]. Deformation mechanisms activated in regimes spanning from the Hugoniot elastic limit (HEL), through the plastic wave front, then up to the fully shock-compressed state, are not completely understood, and integration with post-test microstructure observations, e.g., microscopy on recovered samples, is lacking. Combined experimentation and modeling of the shock response of Mg alloys are in order to advance understanding of their dynamic high-pressure response and to help identify processing parameters that influence microstructure–property relationships. The present work seeks an improved understanding of mechanics and thermodynamics of dynamic deformation of two Mg alloys [8, 9] in these very high strain-rate, high-pressure regimes through coupled plate impact experiments and modeling, whereby the latter is used to infer shear strength, plastic strain, and other response functions incurred during the former weak shock experiments.

The high rate mechanical behavior of magnesium alloys can be understood by a combined modeling and experimental approach. This method has been well documented for crystal plasticity models fit to quasi-static mechanical data [11,12,13,14,15]. These models have the benefit that they can be used to interpret strength and activity of individual deformation mechanisms. The quasi-static and dynamic mechanical response of fine-grained Mg alloys AMX602 and ECAE-AZ31B have been documented for strain rates up to $10^{4}\,{\text {s}}^{-1}$ [16,17,18,19,20]. For strain rates in excess of $10^{4}\,{\text {s}}^{-1},$ the only combined modeling-experimental work concerns the shock response of pure Mg single crystals loaded along different orientations [21, 22]. Validation experiments were performed by combining back surface velocity measurements with in situ X-ray diffraction to confirm the volume fraction and orientation of dynamic deformation twinning was consistent with model predictions [23]. Forward modeling of polycrystalline shock experiments is a useful tool for inferring additional information from experimental results, but requires considerable expertise, time for development, and computational resources [24].

In this work, a method developed in [25, 26] is used to obtain shear stress, plastic strain, and other quantities from particle velocity histories in the weak shock regime. Experimentally measured particle velocity histories (i.e., shock profiles) are input to the analysis, along with thermoelastic material properties. The shock is partitioned into a steady elastic precursor, an unsteady portion linking the precursor with the slower-moving plastic wave, a steady plastic wave, and finally the fully compressed state. This fully compressed state, also referred to as the Hugoniot state, corresponds to a local plateau in particle velocity history profile, whereby stress and other thermodynamic variables do not vary appreciably with time, prior to any significant stress relaxation and release.

Local continuum laws of mass conservation and linear momentum conservation enable calculation of the total uniaxial deformation and axial, i.e., longitudinal or shock, stress. Constitutive equations derived from nonlinear isotropic Eulerian thermoelasticity [27,28,29] are invoked. An assumption of a fixed portion of inelastic work contributing to entropy production is used, along with plastic incompressibility and plastic isotropy. These propositions enable calculation of plastic strain, plastic strain rate, temperature, and entropy throughout the shock profile. Geometrically necessary dislocations can be obtained from gradients of plastic deformation [30,31,32] which in turn are related to local plastic strain rates in the steady portion of the plastic wave [25, 26].

Results obtained from this method can be used to motivate, calibrate, and/or validate inelastic constitutive models for dynamic inelasticity [29, 33,34,35,36,37]. The present work follows an approach similar to that originally conceived by D. C. Wallace in the early 1980s [38,39,40]. The method used here and first derived in [25, 26] is obtained under a potentially more accurate treatment of thermoelasticity and a more general treatment of dislocation kinematics and stored energy, and it is supplemented by new information on dislocation densities. Other distinctions, advantages, and limitations are described in [25, 26]. Two potential limitations imposed here for textured Mg alloys are an assumed isotropic response and omission of effects of twinning on elastic coefficients due to lattice reorientation across the habit plane. These limitations did not apply to polycrystalline Al and Cu studied previously [26]. Inelastic deformation from twinning is not omitted in the present case; rather, it is combined into a measure of total isochoric plastic strain that does not distinguish between individual contributions from slip and twinning. Dissipation from twinning is likewise not omitted, but rather is included with that from slip in the total inelastic rate of working.

This paper is organized as follows. Experiments and materials are described in “Experimental Design and Protocols” section. The general method of calculation of shear, i.e., flow, stress and inelastic response from wave profile data is reviewed in “Shock Wave Profile Data Analysis” section. Response histories for the two Mg alloys of study are reported in “Weak Shock Behavior of Mg Alloys” section. Comparisons of the responses of the two alloys, along with comparisons with published data on other Mg alloys, are given in “Discussion” section. Concluding remarks follow subsequently.

Experimental Design and Protocols

Two magnesium alloys fabricated by severely plastic deformation processes were interrogated via gas gun-driven plate impact experiments. The AZ31B-4E Mg was processed using equal-channel angular extrusion (ECAE), and the AMX602 was processed using spinning water atomization process (SWAP). Both processes resulted in materials with fine-grained microstructures (1–5 $\upmu$m). Processing methods and plate impact experiments used for both Mg alloys are summarized in what follows next.

Materials

Magnesium crystals occupy a hexagonal structure under ambient conditions. Inelastic deformation mechanisms most operative at low to moderate temperatures include basal slip, prismatic slip, pyramidal slip, extension twinning, and contraction twinning. In conventional alloys such as Mg AZ31B, basal slip demonstrates by far the lowest resistance (i.e., lowest strength), followed by extension twinning. See, e.g., [12, 41] for schematics and quantitative values of yield strength for each mechanism.

Mg AZ31B-4E

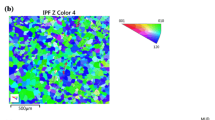
Equal-channel angular extrusion (ECAE) plate impact samples were fabricated from a rectangular AZ31B-H24 Mg alloy plate with in-plane dimensions of 152.4 mm $\times$ 152.4 mm and a thickness of 12.7 mm. The plate was extruded by ECAE through a die using a hybrid 4E route. The 4E route implies that the plate was rotated about the plate normal 180$^{\circ }$ after the first pass, 90$^{\circ }$ after the second pass, and 180$^{\circ }$ after the third pass, then extruded through the die for a total of four passes. The processing temperature of the plate was 498 K during the first two passes, then 473 K on the subsequent two passes. Plate extrusions were performed with a back pressure ranging from 4.14 to 6.89 kPa, and the extrusion speed was 4.6 mm/min. The nominal grain size resulting from this severe plastic deformation process was approximately 3 $\upmu$m. Plate impact samples were fabricated from the through-thickness direction of the ECAE plate, which is also the shock direction, using wire electro-discharge machining. A strong $\langle 0001 \rangle$ fiber texture, 6–7 times random, was observed from electron backscatter diffraction. Detailed microstructure characterization is of this AZ31B-4E Mg alloy is documented in [8]. Properties are listed in Table 1, to be discussed more later.

Table 1 Linear elastic wave speeds, mass densities, and elastic constants (averaged over five measurements [8, 9])

Mg AMX602

Spinning water atomization process (SWAP) the plate from which the plate impact samples were fabricated was fine-grained non-flammable AMX602 (Mg–6% Al–0.5% Mn–2% Ca, in wt%) alloy, provided by the Joining and Welding Research Institute, Osaka University, Japan. The material was consolidated from alloyed powder obtained via SWAP. This process uses a combined gas and water-atomized powder deposition to produce ultrafine-grained microstructures and super-saturation of alloying elements. From the manufacturer and other pertinent microstructure characterization, the SWAP process results in powder aggregates having irregular shapes, with a size in the range of 1–5 mm, and a submicrometer-sized grain structure (1 $\upmu$m or smaller). The as-received powder was subsequently consolidated at room temperature into billets by cold compaction and then hot-extruded between 573 and 673 K into rectangular bars. The resulting bars had final dimensions of 25.4 mm (thickness) $\times$ 101.6 mm (width)  $\times$ 1000 mm (length). Microstructures of this this AMX602 Mg alloy, which tend to demonstrate a strong basal texture, are characterized further in [9, 18, 42,43,44]. No evidence of residual porosity was observed [18]. The resulting plate impact samples were fabricated using wire electro-discharge machining from the through-thickness direction of the plate, which is consistent with the shock direction. Properties are listed in Table 1.

Methods

Light Gas Gun Plate Impact Experiments

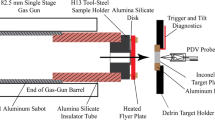
All shock experiments on AZ31B-4E and AMX602 Mg alloys were conducted using single stage 51 mm (smooth bore) and 102 mm (slotted bore) diameter light gas guns at the U.S. Army Research Laboratory (ARL, Aberdeen Proving Ground, Maryland, USA). The 51 mm diameter gun was employed for impact velocities equal to or less than 700 m/s, and the 102 mm diameter gun for velocities greater than 700 m/s. The standard shock loading configuration employed here was previously described in [45, 46]. All plate impact experiments were symmetric, meaning that the impactor and sample (target) materials were identical. The nominal diameter of the AZ31B-4E Mg alloy samples was approximately 42 mm, and the nominal thickness was approximately 6 mm. The nominal diameter and thickness of the impactor were 42 mm and 3 mm, respectively. The nominal diameter of the AMX602 Mg alloy samples was also approximately 42 mm, and the nominal thickness was also approximately 6 mm. However, the nominal diameter and thickness of the impactor were 42 mm and 2 mm, respectively, for AMX602. The impactor velocity was determined by a series of charged pins, and uncertainty associated with the pin positions was determined to be less than $10^{-4}$ mm, corresponding to an error in the final impactor velocity of less than 2%. Measured impact velocities are listed in Table 2; in subsequent text and figures, these are approximated as 400, 600, 800, and 1000 m/s for ease of reference and comparison. The tilt at impact was determined using laser alignment to be normal to within 0.5 mrad. Free surface velocity–time histories were acquired using photonic Doppler velocimetry (PDV).

Table 2 Impact velocities (m/s) measured from charged pins in planar impact tests [8, 9]

Wave Profile Data

Shock wave profile data reported in Fig. 1 on both the AZ31B-4E and AMX602 Mg alloys is acquired using generally accepted methods [47, 48]. In the present analysis, emphasized are features of the deformation histories spanning from the HEL to the stable Hugoniot state. Latter portions of each profile encompassing release and pull-back associated with spallation have been studied in detail previously [8,9,10] and are not discussed further herein.

Fig. 1

Complete free surface velocity profiles at impact velocities ranging from approximately 400 m/s to 1000 m/s: a Mg AZ31B-4E [8] and b Mg AMX602 [9]. Arrival of precursor waves at rear surface corresponds to $t=0$

Mg AZ31B-4E

Shown in Fig. 1a are the velocity–time profiles of the free surface motion of the AZ31B-4E Mg samples shock-compressed to different stable Hugoniot states. The origin of the time axis corresponds to the arrival times of elastic–plastic (precursor) waves at the rear surface of the samples. The average peak free surface velocities were determined by PDV to be $391.0 \pm 1.6$ m/s, $571.8 \pm 2.6$ m/s, $848.1 \pm 0.9$ m/s, and $995.0 \pm 2.5$ m/s, respectively. These free surface velocities correspond to peak shock stresses ranging from around 1 to 5 GPa depending on the estimated plastic shock velocity (not measured) in the material for each test. The measured free surface velocity profiles in Fig. 1a exhibit an elastic precursor wave followed by a brief transition region to a relatively steep plastic shock wave. The total velocity profiles are characteristic of elastic–plastic materials undergoing shock compression, release, and then spallation [10, 47, 48]. The nominal HEL determined from the free surface velocity–time profiles is approximately $181 \pm 3$ MPa. Longitudinal and shear wave velocities for low-amplitude elastic loading, denoted by $c_{L}$ and $c_{S},$ respectively, were measured, with averages over five such measurements recorded in Table 1 along with ambient mass density $\rho _{0}.$ Linear isentropic elastic constants were computed from these wave speeds by inverting the following standard relations [10, 25, 49], valid under the assumption of isotropy:

$$\begin{aligned}&c_{L} = \sqrt{ \frac{B_{0} + \textstyle {\frac{4}{3}} G_{0}}{\rho _{0}}} = \sqrt{ \frac{{E}_{0}}{\rho _{0}} \left[ \frac{1-\nu }{(1+\nu )(1-2\nu )} \right] }, \\&c_{S} = \sqrt{\frac{G_{0}}{\rho _{0}}} = \sqrt{ \frac{{E}_{0}}{\rho _{0}} \left[ \frac{1}{2(1+\nu )} \right] }, \\&c_{B} = \sqrt{\frac{B_{0}}{\rho _{0}}} = \sqrt{ \frac{{E}_{0}}{\rho _{0}} \left[ \frac{1}{3(1-2\nu )} \right] }. \end{aligned}$$

(1)

The ambient bulk and shear modulus are $B_{0}$ and $G_{0},$ respectively. Ambient Young’s modulus is $E_{0},$ and ambient Poisson’s ratio is $\nu .$ Bulk sound speed is $c_{B}.$ Note that $c_{L}$ corresponds to the velocity of an elastic plane wave (uniaxial strain) and differs from the uniaxial stress wave speed (e.g., as in a rod) $\sqrt{E_{0} / \rho _{0}}$ [49]. Since $\nu$ is on the order of 0.3, singularities that arise in the incompressible limit ($\nu \rightarrow 0.5$) are not an issue.

Mg AMX602

Similarly, the free surface velocity–time histories of the rear surface motion of the AMX602 Mg alloy are shown in Fig. 1b. Again, the origin of the time axis corresponds to the arrival time of the precursor wave at the rear surface of the sample. Average peak free surface velocities were determined by PDV to be approximately $375.2 \pm 0.7$ m/s, $594.1 \pm 0.2$ m/s, $782.5 \pm 3.2$ m/s, and $980.4 \pm 5.7$ m/s, respectively. The corresponding peak shock stresses were estimated as just slightly lower than those for Mg AZ31B-4E—given the lower value of $B_{0}$ for AMX602 corresponding to a slower plastic wave—again ranging between 1.5 and 5 GPa depending on estimated plastic shock speed. The HEL from these experiments was estimated as $187 \pm 11$ MPa. Table 1 shows the linear elastic wave velocities averaged over five measurements, and the isotropic linear elastic constants obtained from substitution of these into (1).

Shock Wave Profile Data Analysis

The method of profile analysis used here follows primarily from [25] (Chapter 8) and [26]. Only essential features are summarized here, in conjunction with new discussion on issues pertinent to the Mg alloys of present study.

General Theory

A continuum theory is invoked for the response of each material particle or material element. Such an element centered at Lagrangian coordinates $\{X_{K}\}$ is assumed to contain a sufficient number of locally anisotropic crystals. Each crystal is large enough to encompass a continuum density of dislocations, as well as deformation twins, stacking faults, and other likely defects. Total dislocation density is represented by an internal state variable.

Kinematics

A multiplicative decomposition of the deformation gradient into terms associated with thermoelasticity and residual inelasticity is invoked, similar to that of [32, 50, 51] for single crystal plasticity. A two-term decomposition into generic recoverable and residual parts is

$${{{\varvec{F}}}}= \nabla _{0} {{{\varvec{x}}}} = {{{\varvec{F}}}}^{E} {\bar{{{\varvec{F}}}}} \leftrightarrow F_{iJ} = \frac{\partial x_{i}}{\partial X_{J} } = F^{E}_{i \alpha } {\bar{F}}_{\alpha J}.$$

(2)

Spatial coordinates are related to reference coordinates by ${{{\varvec{x}}}} = {{{\varvec{x}}}}({{{\varvec{X}}}},t),$ and $\nabla _{0}(\cdot )$ is the gradient with respect to ${{{\varvec{X}}}}.$ The recoverable thermoelastic deformation is denoted by ${{{\varvec{F}}}}^E,$ and all residual inelastic deformation is included in ${\bar{{{\varvec{F}}}}}.$ The Jacobian determinant measuring density change is $J = \det {{{\varvec{F}}}} > 0.$

Residual deformation is attributed to dislocations and deformation twins. Deformation ${{{\varvec{F}}}}^{P}$ reflects isochoric contributions from conventional dislocation glide and slip or shuffle of twinning partial dislocations. More refined approaches whereby slip and twinning are delineated by separate terms in a multiplicative decomposition are possible [32, 51, 52], but the present combining of both mechanisms into a single ${{{\varvec{F}}}}^{P}$ term is used in the present work. The wave profile data analyzed subsequently, alone, do not provide sufficient information to enable determination of distinct kinematic variables for slip and twinning. Residual dislocations, stacking faults, and twin boundaries remaining in the element affect the lattice structure and contribute to stored energy. Changes in volume and/or shape of the element due to these residual defects are quantified by ${{{\varvec{F}}}}^{I}$ [32, 53,54,55]. Local reorientation or reflection of the lattice due to deformation twinning [32, 51, 56] is omitted, but inelastic deformation due to twinning is included in ${{{\varvec{F}}}}^{P}.$

A three-term decomposition like those advocated in [32, 55, 57,58,59] is used:

$${{{\varvec{F}}}} = {{{\varvec{F}}}}^{E} {{{\varvec{F}}}}^{I} {{{\varvec{F}}}}^{P}\leftrightarrow F_{iJ} = F^{E}_{i \alpha } F^{I}_{\alpha \beta } F^{P}_{\beta J}.$$

(3)

The total residual deformation, both lattice-affecting (residual defects, ${{{\varvec{F}}}}^{I}$) and lattice-preserving (glide of slip and twinning dislocations, ${{{\varvec{F}}}}^{P}$), obeys a two-term decomposition:

$${\bar{{{\varvec{F}}}}}= {{{\varvec{F}}}}^{I} {{{\varvec{F}}}}^{P} \leftrightarrow {\bar{F}}_{\beta J} = F^{I}_{\beta \alpha } F^{P}_{\alpha J}.$$

(4)

The total lattice deformation, including thermoelastically recoverable (${{{\varvec{F}}}}^{E}$) and locally residual elastic (${{{\varvec{F}}}}^{I}$) parts, is

$${{{\varvec{F}}}}^{L} = {{{\varvec{F}}}}^{E} {{{\varvec{F}}}}^{I} \leftrightarrow F^{L}_{i \beta } = F^{E}_{i \alpha } F^{I}_{\alpha \beta }.$$

(5)

Lattice deformation ${{{\varvec{F}}}}^{L}$ does not quantify dislocation slip or deformation twinning; rather, both processes are quantified by ${{{\varvec{F}}}}^{P}.$ Combining (2), (5), and (4) produces (3).

It is emphasized that the present analysis fully accounts for effects of twinning on irreversible inelastic deformation, stresses, and dissipation. The only aspect of twinning omitted in subsequent applications—for monotonically increasing inelastic deformation during the shock compression process—is its effect on (anisotropic) elastic constants due to rotation of the lattice vectors across habit planes [12, 32]. Stored energy from twin boundary planes [51, 60] is implicitly included in total energy of cold working, but it is not explicitly delineated from that attributed to residual elastic fields of dislocations.

The deformation gradient obeys the polar decompositions ${{{\varvec{F}}}} = {{{\varvec{R}}}} {{{\varvec{U}}}} = {{{\varvec{V}}}} {{{\varvec{R}}}},$ where ${{{\varvec{R}}}}$ is proper orthogonal and ${{{\varvec{U}}}}$ and ${{{\varvec{V}}}}$ are symmetric and positive definite right and left stretch tensors. Similarly, ${{{\varvec{F}}}}^{E},$ ${{{\varvec{F}}}}^{P},$ and ${{{\varvec{F}}}}^{I}$ are presumed invertible with positive determinants, so each individually can be decomposed into the product of a rotation and symmetric positive definite stretch tensor, via either a right or left polar decomposition.

Internal Energy

The Eulerian thermoelastic strain tensor, labeled ${{{\varvec{D}}}}^{E},$ is used following prior analysis on different strain measures for crystals under shock compression [27, 28, 61]:

$${{{\varvec{D}}}}^{E} = {\textstyle {\frac{1}{2}}} [ \mathbf{1 } - ({{{\varvec{F}}}}^{E})^{-1}({{{\varvec{F}}}}^{E})^{- {\text {T}}}] \leftrightarrow D^{E}_{\alpha \beta } = {\textstyle {\frac{1}{2}}}[\delta _{\alpha \beta } - (F^{E})^{-1}_{\alpha i}(F^{E})^{-1}_{\beta i}].$$

(6)

The constitutive theory invokes this strain measure in the internal energy potential, measured on a per unit volume basis in intermediate configuration achieved from the current state via unloading through the inverse thermoelastic deformation $({{{\varvec{F}}}}^{E})^{-1}.$ This strain tensor, though constructed from “Eulerian” field variable ${{{\varvec{F}}}}^{E-1}({{{\varvec{x}}}},t),$ is referred to intermediate configuration coordinates, so it is naturally invariant under changes of spatial observer and thus suitable for use as a state variable for both isotropic and anisotropic materials [25, 27].

Cauchy stress is $\pmb {\sigma }$ and velocity gradient is ${{{\varvec{l}}}} = \nabla \pmb {\upsilon } = \dot{{{\varvec{F}}}} {{{\varvec{F}}}}^{-1}.$ The symmetric part of ${{{\varvec{l}}}},$ i.e., the total Eulerian strain rate, is denoted by ${{{\varvec{d}}}} = {{{\varvec{l}}}}_{\text {S}} =\frac{1}{2}({{{\varvec{l}}}} + {{{\varvec{l}}}}^{\text {T}}).$ Stress power per unit reference volume is

$$\begin{aligned} J \pmb {\sigma }:{{{\varvec{l}}}}= & {} J \pmb {\sigma }:{{{\varvec{d}}}} = J \pmb {\sigma }: \left[ {{{\varvec{d}}}}^{E} + ({{{\varvec{F}}}}^{E} \dot{{{\varvec{F}}}}^{I} {{{\varvec{F}}}}^{I-1} {{{\varvec{F}}}}^{E-1})_{\text {S}}\right. \\&\quad \left. + ({{{\varvec{F}}}}^{L} \dot{{{\varvec{F}}}}^{P} {{{\varvec{F}}}}^{P-1} {{{\varvec{F}}}}^{L-1})_{\text {S}} \right] , \end{aligned}$$

(7)

with ${{{\varvec{d}}}}^{E} = (\dot{{{\varvec{F}}}}^{E} {{{\varvec{F}}}}^{E \,-1})_{\text {S}} = {\varvec{F}}^{E} \dot{{{\varvec{D}}}}^{E} ({{{\varvec{F}}}}^{E})^{\text {T}}$ the Eulerian thermoelastic strain rate [25,26,27]. For symmetric plane wave loading, this relation ultimately affects entropy production via the first of (26), as derived in [25, 26]. The general three-dimensional nonlinear theory invokes no assumptions of additive elastic and inelastic strains nor of purely elastic and inelastic Eulerian strain rates. Thermodynamic admissibility of the theory is proven in [25, 26].

The internal energy function is [25, 26], with Greek indices denoting Voigt notation,

$$\begin{aligned} {\bar{U}} ({{{\varvec{D}}}}^{E}, {\bar{\eta }}, {\bar{N}}_{T})&= {\textstyle {\frac{1}{2}}} {\mathsf {C}}_{\alpha \beta } D^{E}_{\alpha } D^{E}_{\beta } + {\textstyle {\frac{1}{6}}} {\mathsf {C}}_{\alpha \beta \gamma } D^{E}_{\alpha } D^{E}_{\beta } D^{E}_{\gamma }\\&\quad - {T}_{0} [ {\gamma }_{0} (D^{E}_{1} + D^{E}_{2} + D^{E}_{3}) \varDelta {\bar{\eta }}\\&\quad + {\textstyle {\frac{1}{2}}} {\gamma }_{0 \alpha \beta } D^{E}_{\alpha } D^{E}_{\beta } \varDelta {\bar{\eta }} - \varDelta {\bar{\eta }} - {\textstyle {\frac{1}{2}}} (\varDelta \bar{\eta })^{2} / \mathsf {c}_{0} ]\\&\quad + {\textstyle {\frac{1}{2}}} G_{0} b^{2} {\bar{N}}_{\text {T}}. \end{aligned}$$

(8)

Second- and third-order isentropic elastic constants are ${\mathsf {C}}_{\alpha \beta }$ and ${\mathsf {C}}_{\alpha \beta \gamma },$ respectively. For isotropic thermoelastic coupling, the nominal Grüneisen parameter is $\gamma _{0},$ and the standard assumption $\rho \gamma = \rho _{0} \gamma _{0}$ [3, 38] leads to ${\gamma }_{0 \alpha \beta } = 5 \gamma _{0} \delta _{\alpha } \delta _{\beta }$ [25, 27]. Entropy change from the reference state at temperature $T_{0}$ is $\varDelta {\bar{\eta }},$ and $\mathsf {c}_{0}$ is the specific heat at constant thermoelastic strain. A characteristic shear modulus and Burgers vector magnitude are denoted by $G_{0}$ and b in the rightmost term that accounts for stored energy of dislocations of total length per unit intermediate volume ${\bar{\eta }}_{T}.$ Contributions to stored energy from stacking faults and internal or twin boundaries are not resolved explicitly, unlike more refined models in [25, 51], for example. Derivatives of (8) furnish the symmetric thermodynamic stress tensor and the absolute temperature:

$${\hat{{{\varvec{S}}}}} = \frac{ \partial {\bar{U}} }{ \partial {{{\varvec{D}}}}^{E}} = J^{E} ({{{\varvec{F}}}}^{E})^{\text {T}} \pmb {\sigma } {{{\varvec{F}}}}^{E}, \quad T = \frac{\partial {\bar{U}}}{ \partial {\bar{\eta }}}.$$

(9)

Thermoelastic volume change is measured by $J^{E} = \det {{{\varvec{F}}}}^{E}.$

For isotropic thermoelastic response, elasticity tensors reduce to simpler forms [25, 62]. Two independent second- and three independent third-order constants are

$${\mathsf {C}}_{11},{\mathsf {C}}_{12}; \quad {\mathsf {C}}_{111},{\mathsf {C}}_{112},{\mathsf {C}}_{123}.$$

(10)

Second-order constants (${\mathsf {C}}_{11},{\mathsf {C}}_{12}$) are related to the familiar shear and bulk moduli and Poisson’s ratio via

$$\begin{aligned}&G_{0} = {\textstyle {\frac{1}{2}}}( {\mathsf {C}}_{11} - {\mathsf {C}}_{12}), \quad B_{0} = {\textstyle {\frac{1}{3}}}( {\mathsf {C}}_{11} + 2 {\mathsf {C}}_{12}), \\&\nu = {\mathsf {C}}_{12}/({\mathsf {C}}_{11} + {\mathsf {C}}_{12}). \end{aligned}$$

(11)

As verified in [27, 28], second-order thermoelastic constants are equivalent among Eulerian and Lagrangian [32, 63, 64] representations. Third-order Eulerian thermoelastic constants are related to Lagrangian counterparts typically reported from experimental data [64, 65] via equations [25, 27, 28]. Pressure derivatives of the bulk and shear modulus at the ambient state obey [27]

$$\begin{aligned} {B}'_{0}= & {} -\frac{1}{3 {B}_{0} } \left( \frac{1}{3} {\mathsf {C}}_{111} + 2 {\mathsf {C}}_{112} + \frac{2}{3} {\mathsf {C}}_{123} \right) + 4, \\ {G}'_{0}= & {} -\frac{1}{6 {B}_{0} } ( {\mathsf {C}}_{111} - {\mathsf {C}}_{123} - 11 {\mathsf {C}}_{11} - {\mathsf {C}}_{12} ) - 1. \end{aligned}$$

(12)

Residual Lattice Deformation and Stored Energy

Slip and twinning deformations comprise ${{{\varvec{F}}}}^{P},$ which, in agreement with the physics of these mechanisms, obeys $J^{P} = \det {{{\varvec{F}}}}^{P} = 1.$ Volumetric contributions from local nonlinear elastic fields and core effects of defects contained within a local volume element are included in the description, however, whereby the isotropic or spherical assumption for ${{{\varvec{F}}}}^{I}$ is used in (3). Then, with $\delta$ the residual volume change per unit intermediate crystal volume,

$${{{\varvec{F}}}}^{I}= (J^{I})^{1/3} \mathbf{1 }, \quad {J}^{I} = 1/(1-\delta ), \quad \dot{J^{I}} / {J^{I}} = {\dot{\delta }}/(1-\delta ).$$

(13)

Following the usual approach that omits the unknown core dilatation contribution [58, 66, 67], and letting $\alpha$ denote the fraction of edge versus screw dislocation content,

$$\begin{aligned} \delta (\alpha , {\bar{N}}_{\text {T}})&= \frac{1}{2} G_{0} b^{2} {\bar{N}}_{\text {T}} \biggr [ \frac{\alpha }{3 B_{0}} \frac{1 - \nu -2 \nu ^{2}}{(1-\nu )^{2} } \left( B_{0}' - 1\right) \\&\quad + \frac{\alpha }{3 G_{0} } \frac{2 - 2 \nu + 2 \nu ^{2}}{(1-\nu )^{2} } \left( G_{0}' - \frac{G_{0}}{B_{0}} \right) + \frac{1- \alpha }{G_{0}} \left( G_{0}' - \frac{G_{0}}{B_{0}} \right) \biggr ]. \end{aligned}$$

(14)

This expression has been deemed accurate within a factor of two from comparison with experimental data on a number of metallic polycrystals [58, 66, 67], though validation data for Mg alloys do not exist. Stored energy is related to total dislocation line density as

$$(1-\beta ){\bar{W}} = {\textstyle {\frac{1}{2}}} G_{0} b^{2} {\bar{N}}_{\text {T}},$$

(15)

where ${\bar{W}}$ is cumulative inelastic work and $\beta$ is the cumulative Taylor–Quinney parameter [68,69,70]. Possible contributions to dilatation from stacking faults and twin boundaries [60, 66] are not calculated explicitly; rather, their energies are implicitly included in total stored energy of cold working that gives rise to the right side of (14).

Inelasticity and Defect Kinetics

A generic treatment of polycrystalline inelasticity, limited primarily to basic kinematics, is sufficient for the application that follows. Explicit kinetic models of plastic flow, including slip and deformation twinning, and dislocation density evolution equations are not required. Rather, the extracted shear stress and inelastic responses obtained from the wave profile analysis described later can be used to develop predictive inelastic constitutive models for other loading scenarios.

The total residual inelastic deformation gradient is dominated by irreversible or dissipative deviatoric contributions from dislocation glide and deformation twinning. Entropy production and associated temperature rise are included in the analysis through application of the local balance of energy and thermodynamic relations derived and presented in full in [25, 26]. Under the isotropic material assumption, any effects of lattice reorientation are, by construction, deemed inconsequential. Detwinning and reverse slip are also not addressed subsequently, wherein only monotonic loading from the HEL through the plastic waveform to the fully compressed Hugoniot state is analyzed.

The instantaneous Taylor–Quinney parameter $\beta '$ is assumed constant over the complete history of the deformation process, leading to equivalence of cumulative Taylor–Quinney factor $\beta = \beta '.$ In a real materials $\beta '$ will vary with time over an arbitrary deformation history [69,70,71,72,73,74]. The range $0 \le \beta ' \le 1$ is consistent with positive net dissipation. Use of (15) in the time derivative of (14) gives the following differential equation for residual dilatation:

$$\begin{aligned} {\dot{\delta }}&= (1-\beta )\dot{\bar{W}} \biggr [ \frac{\alpha }{3 B_{0}} \frac{1 - \nu -2 \nu ^{2}}{(1-\nu )^{2} } \left( B_{0}' - 1\right) \\&\quad + \frac{\alpha }{3 G_{0} } \frac{2 - 2 \nu + 2 \nu ^{2}}{(1-\nu )^{2} } \left( G_{0}' - \frac{G_{0}}{B_{0}} \right) + \frac{1- \alpha }{G_{0}} \left( G_{0}' - \frac{G_{0}}{B_{0}} \right) \biggr ]. \end{aligned}$$

(16)

The rate of plastic working ${\dot{\bar{W}}}$ is the only transient variable entering (16). No constitutive equations for yielding, plastic flow (including slip and twinning), or evolution of dislocation density are needed or used herein. Rather, inelastic deformation and dislocation density are extracted from wave profile data using conservation laws of momentum and energy in conjunction with thermoelasticity and (15).

Plane Wave Loading

The net response of the polycrystal is assumed isotropic, both elastically and plastically. This is a noted limitation for the present alloys that have a strong basal texture (“Materials” section and [8, 9]). Magnesium can also demonstrate plastic anisotropy induced by deformation twinning and other sources of lattice realignment. The isotropy assumption is necessary, however, to enable use of the symmetry restrictions on stress state and plastic deformation that render the analysis tractable. Anisotropy cannot be addressed by the present techniques, nor by those in [38,39,40], without imposing further assumptions on the symmetries (or lack thereof) of thermoelastic constants and the magnitudes of plastic deformation in different directions. For isotropic material response, any direction is a pure mode direction, and no transverse motion occurs for ideal planar impact.

Kinematics

Uniaxial total deformation occurs along the Cartesian $X = X_{1}$ axis. Field variables depend on (X, t). The lone nonzero component of particle velocity is $\upsilon (X,t) = \upsilon _{1} (X_{1},t).$ The total deformation gradient representing the change of state from the initial configuration (Lagrangian coordinate X) to any state within the waveform (Eulerian coordinate x) is

$$\begin{aligned} &{{{\varvec{F}}}}(X,t) = \begin{bmatrix} F_{11}(X,t)&0&0 \\ 0&1&0 \\ 0&0&1 \\ \end{bmatrix} = \begin{bmatrix} J(X,t)&0&0 \\ 0&1&0 \\ 0&0&1 \\ \end{bmatrix}; \\&F_{11}(X,t) = J(X,t) = \frac{\partial x (X,t)}{\partial {X}}.\end{aligned}$$

(17)

The deformation gradient ${{{\varvec{F}}}}$ is decomposed into diagonal lattice (${{{\varvec{F}}}}^{L} = {{{\varvec{F}}}}^{E} {{{\varvec{F}}}}^{I}$) and plastic (${{{\varvec{F}}}}^{P}$) parts according to (3). Pure mode loading and material symmetry considerations lead to the following reduced forms:

$$\begin{aligned} {{{\varvec{F}}}}^{L} = {{{\varvec{F}}}}^{E} {{{\varvec{F}}}}^{I} = \begin{bmatrix} F^{L}_{11}&0&0 \\ 0&F^{L}_{22}&0 \\ 0&0&F^{L}_{22} \\ \end{bmatrix} =(J^{I})^{1/3} \begin{bmatrix} F^{E}_{11}&0&0 \\ 0&F^{E}_{22}&0 \\ 0&0&F^{E}_{22} \\ \end{bmatrix}, \end{aligned}$$

(18)

$$\begin{aligned} {{{\varvec{F}}}}^{P} = \begin{bmatrix} F^{P}_{11}&0&0 \\ 0&F^{P}_{22}&0 \\ 0&0&F^{P}_{22} \\ \end{bmatrix} = \begin{bmatrix} F^{P}_{11}&0&0 \\ 0&(F^{P}_{11})^{-1/2}&0 \\ 0&0&(F^{P}_{11})^{-1/2} \\ \end{bmatrix}. \end{aligned}$$

(19)

A scalar logarithmic measure of axial plastic strain $\varepsilon ^{P},$ positive in compression, is [39]

$$\varepsilon ^{P} = - \ln F^{P}_{11} \Leftrightarrow F^{P}_{11} = \exp ( - \varepsilon ^{P}).$$

(20)

From the symmetric and diagonal forms of (17)–(19), ${{{\varvec{F}}}} = {{{\varvec{U}}}} = {{{\varvec{V}}}},$ and logarithmic stretch components are simply additive, e.g., $\ln F_{11} = \ln F^{L}_{11} + \ln F^{P}_{11} = \ln F^{L}_{11} - \varepsilon ^{P}.$ Such simplicity is absent in arbitrary 3D motions, for which a more general definition of equivalent plastic strain than (20) is required. In such cases, ${{{\varvec{F}}}}^{P}$ cannot be expressed in terms of a single scalar function as in (19).

Stresses

Let $P = - P_{11} = -\sigma _{11}$ denote the longitudinal shock stress, positive in compression. Symmetry constrains the Cauchy stress tensor to be of the following form for pure mode loading in an isotropic solid:

$$\begin{aligned} \pmb {\sigma } = \begin{bmatrix} \sigma _{11}&0&0 \\ 0&\sigma _{22}&0 \\ 0&0&\sigma _{22} \\ \end{bmatrix} =\begin{bmatrix} -P&0&0 \\ 0&2 \tau - P&0 \\ 0&0&2 \tau - P \\ \end{bmatrix}. \end{aligned}$$

(21)

The Cauchy stress tensor is decomposed into spherical (p) and deviatoric ($\pmb {\sigma }'$) parts:

$$\pmb {\sigma } = \pmb {\sigma }' - p \mathbf{1 } \leftrightarrow \sigma _{ij} = \sigma '_{ij} - p \delta _{ij}.$$

(22)

Cauchy pressure is $p = -\frac{1}{3} \sigma _{kk}.$ The maximum Cauchy shear stress is defined as follows [39, 75], where applying $\sigma _{22} = \sigma _{33}$ from (21) gives

$${\tau } = - {\textstyle {\frac{1}{2}}} (\sigma _{11} - \sigma _{22}) = {\textstyle {\frac{1}{2}}} (P + \sigma _{22}).$$

(23)

Normally $|P| \ge |\sigma _{22}|,$ with equality holding in the hydrodynamic limit. It follows from (21)–(23) that

$$p = P - {\textstyle {\frac{4}{3}}} \tau , \quad \sigma '_{11} = - {\textstyle {\frac{4}{3}}} \tau , \quad \sigma '_{22} = \sigma '_{33} = {\textstyle {\frac{2}{3}}} \tau .$$

(24)

Balance Laws

Conservation laws of linear momentum, mass, and energy reduce to the following for one-dimensional adiabatic flow:

$$\begin{aligned}&\frac{\partial P(X,t)}{\partial {X}} = - \rho _{0} \frac{\partial \upsilon (X,t)}{\partial {t}}, \quad \frac{\partial \upsilon (X,t)}{\partial {X}} = \frac{\partial J(X,t)}{\partial {t}}, \\&\frac{\partial U(X,t)}{\partial {t}} = -P(X,t) \frac{\partial \upsilon (X,t)}{\partial {X}}. \end{aligned}$$

(25)

Reference and spatial mass densities are related as usual by $\rho _{0} = \rho J.$ Internal energy per unit initial volume is $U = {\bar{U}}/(1-\delta ).$ Local entropy production is

$$T [\dot{\bar{\eta }} + {\bar{\eta }} {\dot{\delta }} / (1-\delta )] = \beta ' J^{E} [2 \tau {\dot{\varepsilon }}^{P} - J^{I} (p + \rho \psi ) {\dot{\delta }}] \ge 0 ,$$

(26)

with $\psi$ the Helmholtz free energy per unit mass and $\beta ' = \beta .$

Reduced Constitutive Equations

The thermoelastic constitutive model with an internal state variable (${\bar{N}}_{T}$) is invoked to obtain explicit equations for axial shock stress P,  shear stress $\tau ,$ and temperature T,  where the history of residual deformation is extracted from experimental shock profile data. The thermodynamic stress variable, ${\hat{{{\varvec{S}}}}},$ conjugate to the Eulerian thermoelastic strain is defined in (9). For isotropic material response and symmetric plane wave loading [25, 26],

$$\begin{aligned}&P = -(J^{E})^{-1} (F^{E}_{11})^{-2} {\hat{S}}_{1} = - \frac{ \exp (-2 \varepsilon ^{P}) }{J^{3} (1-\delta )^{5/3}} {\hat{S}}_{1}, \\&\tau = - \frac{ \exp (-2 \varepsilon ^{P}) }{ 2 J^{3} (1-\delta )^{5/3}} \left[ {\hat{S}}_{1} - J^{2} {\hat{S}}_{2} \exp (3 \varepsilon ^{P}) \right] \end{aligned}$$

(27)

with ${\hat{S}}_{\alpha }$ in Voigt notation. The only non-vanishing components of the Eulerian thermoelastic strain tensor are

$$\begin{aligned}&D^{E}_{1} = {\textstyle {\frac{1}{2}}} [ 1 - {J}^{-2}(1-\delta )^{-2/3} \exp (-2 \varepsilon ^{P})] , \\&D^{E}_{2} = D^{E}_{3} = {\textstyle {\frac{1}{2}}}[1 - (1-\delta )^{-2/3} \exp ( \varepsilon ^{P})]. \end{aligned}$$

(28)

Discretization and Calculations

Certain portions of an elastic–plastic waveform emerging from planar impact are idealized as steady waves. Here, as in [38, 40], a planar waveform is deconstructed into a fast steady elastic precursor followed by an unsteady region and then a trailing steady plastic wave.

Characteristic Waveforms

As shown in Fig. 2 [25], a typical waveform monitored as a velocity history $\upsilon (X,t)$ at a material particle X consists of an elastic precursor moving at steady Lagrangian speed ${\mathsf {U}}^{E}_{0},$ ahead of which the material is quiescent at state $(\cdot )_{\text {a}}.$ Immediately behind, the material is deformed to the HEL state $(\cdot )_{\text {b}};$ stress at state $(\cdot )_{\text {b}}$ is $P_{\text {HEL}}.$ An unsteady region connects states $(\cdot )_{\text {b}}$ and $(\cdot )_{\text {c}},$ where the latter corresponds to conditions immediately ahead of the plastic wave. State $(\cdot )_{\text {c}}$ transitions to state $(\cdot )_{\text {d}}$ upon traversal of the plastic wave moving at steady Lagrangian speed ${\mathsf {U}}_{0}^{P}.$ The end Hugoniot state behind the plastic wavefront at equilibrium is $(\cdot )_{\text {d}}.$ Here, the material has been maximally deformed, corresponding to the (first) main plateau in the particle velocity history profile. Longitudinal stress and plastic strain attain local maxima, and the strain rate is effectively zero. Unloading from state $(\cdot )_{\text {d}}$ that would occur eventually in any experiment is not addressed. For weak shocks, $\upsilon _{\text {b}} \ll \upsilon _{\text {d}}.$ If the impacted target has a free back surface at which velocity history is measured, the limiting material particle velocity as this surface is approached internally is very close, for weak shocks, to half of the measured free surface velocity [75]. This free surface approximation, which is used herein for Mg alloys, is accurate to within 0.8% and 0.6% of the true measured particle velocity behind the plastic shock front in aluminum 2024 and copper, respectively for $J_{\text {d}} \ge 0.9$ [75].

Fig. 2

Characteristic particle velocity profile for planar impact inducing a weak shock in a ductile metal. Elastic precursor and plastic shock velocities are ${\mathsf {U}}_{0}^{E}$ and ${\mathsf {U}}_{0}^{P},$ respectively, in Lagrangian coordinates

The elastic precursor linking states $(\cdot )_{\text {a}}$ and $(\cdot )_{\text {b}}$ is a steady wave moving at speed ${\mathsf {U}}^{E}_{0}.$ The shock velocity of the elastic precursor is found analytically using Eulerian thermoelasticity theory [27, 28, 76]. Herein, $t_{\text {b}} \approx t_{\text {a}}$ with the rise time of the elastic precursor nearly negligible relative to time scales involved in the plastic wave structure. The precursor shock speed and thermoelastic state variables immediately behind the precursor are then given by relations in [25, 27, 28, 76]. States $(\cdot )_{\text {b}}$ and $(\cdot )_{\text {c}}$ are characterized by constant particle velocities immediately trailing the steady precursor and immediately preceding the steady plastic wave, respectively. Following [38], particle velocity is linearly interpolated in the unsteady region between these two steady states. Equations invoked are given in [25, 26, 38, 40], omitted here. Separation of the elastic and plastic waves increases with time since ${\mathsf {U}^{E}_{0}} > {\mathsf {U}^{P}_{0}}$ in the weak shock regime. The wave profile is steady between states $(\cdot )_{\text {c}}$ and $(\cdot )_{\text {d}}.$ Expressions for volume ratio and axial stress at any paired location and time (X, t) within the plastic wave characterized by particle velocity $\upsilon (X,t)$ are also available in [25, 26, 38, 40].

Numerical Methods

The steady plastic wave velocity can be often obtained directly from experimental measurements. When such direct measurements are unavailable, as is the case in the current work, the empirical linear shock velocity versus particle velocity relationship described in [3, 25, 75, 77] is often appropriate in the absence of phase changes:

$${\mathsf {U}}^{P}_{0} = C_{0} + s \upsilon _{\text {d}}.$$

(29)

Denoted by $C_{0}$ and s are empirical constants for a given material, and $\upsilon _{\text {d}}$ is particle velocity in the Hugoniot state.

Calculations are undertaken for the history of plastic deformation and the thermodynamic state of the material throughout the process of passage of an elastic–plastic waveform of the sort described in Fig. 2. The experimental particle velocity history $\upsilon (X,t)$ at a material point X is known a priori, along with precursor and plastic wave speeds, where these are determined from the analytical solution [25, 27] and (29) in the present work. Typically the experimental data is obtained by monitoring surface velocity through a window, followed by a transformation from surface to particle velocity to account for impedance differences between the metallic specimen and the window material. In the context of Fig. 2, the following discrete pieces of data are input to the analysis: ${\mathsf {U}}^{E}_{0},$ ${\mathsf {U}}^{P}_{0},$ $\upsilon _{\text {a}},$ $\upsilon _{\text {b}},$ $\upsilon _{\text {c}},$ and $\upsilon _{\text {d}}.$ Velocity history $\upsilon (X,t)$ is also known, in continuous or approximately continuous form by interpolation of discrete experimental data, throughout the steady plastic wave profile, between states $(\cdot )_{\text {c}}$ and $(\cdot )_{\text {d}}.$ Ambient mass density $\rho _{0}$ as well as thermoelastic properties entering the internal energy function (8) are also assumed known a priori. A constant value of $\beta \in [0,1]$ is assigned, approximating experimental evidence.

Deformation and longitudinal stress histories are first generated for the entire shock process using equations derived from (25). These enable calculation of J(X, t) and P(X, t) given the experimental information outlined above and the ambient mass density. At state $(\cdot )_{\text {a}},$ the material is at rest, undeformed, and unstressed. At state $(\cdot )_{\text {b}},$ the material has been deformed thermoelastically to the HEL, whereby $J = J^{E}$ and $P = P_{\text {HEL}}.$ At the HEL, plastic deformation is pending but has not yet accumulated, and additional dislocations beyond those present initially have not yet been generated: $\varepsilon ^{P} = 0$ and ${\bar{N}}_{\text {T}} = 0.$ Entropy and temperature rise due to passage of the thermoelastic precursor shock are computed from the Eulerian thermoelastic solution [25, 27, 28, 76].

Acquisition of the plastic strain history and thermodynamic state variables in the unsteady regime connecting elastic and plastic waves between states $(\cdot )_{\text {b}}$ and $(\cdot )_{\text {c}},$ as well as acquisition of these quantities within the structured steady plastic wave from state $(\cdot )_{\text {c}}$ through and including state $(\cdot )_{\text {d}},$ requires use of the thermodynamic model framework of “General Theory” section along with suitable geometric reductions of the governing equations for symmetric plane wave loading described in “Plane Wave Loading” section. An incremental and iterative numerical procedure is invoked, where explicit details are given in [26]. The end result is the time history, at point X where $\upsilon (X,t)$ is recorded, of the set of response functions ($\tau ,\varepsilon ^{P},{\bar{\eta }},T,{\bar{N}}_{\text {T}},\delta$). Plastic strain rate is computed from numerical differentiation of $\varepsilon ^{P}.$

Weak Shock Behavior of Mg Alloys

The analysis procedure of “Shock Wave Profile Data Analysis” section are applied to analyze weak shock profiles in polycrystalline Mg alloys AZ31B-4E and AMX602. Material properties entering the subsequent calculations are described in “Material Properties” section. Results and their interpretation follow in “Results and Interpretation: Mg AZ31B-4E” and “Results and Interpretation: Mg AMX602” sections for Mg AZ31B-4E and Mg AMX602, respectively.

Material Properties

Physical properties of both alloys are listed in Table 3. Values are obtained from references quoted in the table, where if no reference is listed on a particular row, the reference from the row above it applies. Second-order elastic constants are consistent with those obtained from linear elastic wave velocities in Table 1. Since third-order elastic constants are subject to significant uncertainty, the only known polycrystalline values for an Mg alloy [78] are compared with pertinent single crystal values [79] corresponding to plane wave loading parallel to [0001], given the strong basal texture of the two alloys of present consideration. Since slip resistance is lowest in the basal plane for Mg [12, 80], the Burgers vector corresponds to full basal slip, giving $b= a$ with a the lattice parameter. The Taylor–Quinney factor $\beta$ is held constant; experimentally measured ranges of the cumulative value $\beta$ range from 0.2 to 1.0 in conventional Mg AZ31B depending on orientation, loading rate, and strain level [70]. These values are obtained from dynamic compression-shear Kolsky bar tests, which produce strain rates orders of magnitude lower than those typical of weak shocks. In the absence of plastic dilatation data for Mg, the value of $\alpha = 0.285$ is chosen following reasoning given in [25, 26] for an Al alloy.

Table 3 Properties of Mg AZ31B-4E and Mg AMX602 ($T_{0} = 295$ K, $\rho _{0}$ in kg/m$^{3},$ ${\mathsf {C}}_{\alpha \beta \ldots }$ in GPa, ${\mathsf {c}}_{0}$ in MPa/K)

Since data of “Experimental Design and Protocols” section do not enable sufficiently accurate calculation of plastic wave speeds, values of $C_{0}$ and s relating particle velocity and plastic shock velocity in (29) are input to the analyses as follows. The intercept is taken as slightly exceeding the bulk linear elastic wave speed computed from longitudinal and shear wave measurements of “Experimental Design and Protocols” section under the isotropic elastic assumption, i.e., $C_{0} = 1.06 c_{B} = 1.06 \sqrt{B_{0}/\rho _{0}}.$ The ratio of 1.06, neither available from experiments [8, 9] or other references on these particular alloys, is thought to be a reasonable approximation, slightly larger than that for conventional Mg AZ31B but lower than that of Ti [3, 26]. The slope $s =1.3$ is comparable to that for standard Mg AZ31B (1.26 [5]), where a slightly higher value is consistent with the nonlinear elastic constants used here. For example, $B'_0 \approx 4s - 1$ [25, 77] is larger for polycrystalline, single crystalline, and null Eulerian third-order elastic constants considered subsequently (ranging from 4.0 to 6.5 [81]) than 3.9 for conventional Mg [82]. In summary, $C_{0}$ and s are chosen as a compromise between measured values for conventional Mg alloys and limited nonlinear elastic properties from the literature used in the thermoelastic formulation that provide a stiffer response. Shock waves do not become overdriven until impact velocities (twice particle velocities) on the order of 1.5 to 2 km/s are imposed. Maximum impact velocities imposed in experiments of the present analysis are $\approx 1$ km/s, well within the weak shock regime.

Results and Interpretation: Mg AZ31B-4E

Shock compression data for Mg AZ31B-4E presented in “Mg AZ31B-4E” section and Fig. 1a, reported originally in [8] in the context of spall, are now addressed via the framework outlined in “Shock Wave Profile Data Analysis” section. Shots are labeled according to approximate impact velocities of Table 2: 400 m/s, 600 m/s, 800 m/s, and 1000 m/s. Particle velocities achieved at the Hugoniot state for each symmetric test are then approximately 200 m/s, 300 m/s, 400 m/s, and 500 m/s. Longitudinal Hugoniot stresses range from approximately 2 to 5 GPa. In each case, $P_{\text {d}} > P_{\text {HEL}}$ and $P_{\text {d}}$ is lower than the overdriven threshold, so a two-wave structure emerges characteristic of weak elastic–plastic shocks.

Wave profile data are reproduced for all four shots in Fig. 3. Data in these and subsequent figures are not smoothed. The time window for wave profile analysis is discretized into several thousand or more steps, and linear interpolation is applied to experimental free surface velocity history data for steps sizes finer than the resolution afforded by the experimental diagnostics. Maximum step sizes were checked to ensure that further refinement did not affect outcomes of the analysis. Post-peak response data at late times in Fig. 1a where particle velocity drops (e.g., spall) are omitted since such late time data do not enter the analysis that terminates at the stable Hugoniot state $(\cdot )_{\text {d}}$. Particle velocity profiles are shown in Fig. 3a. In analysis of all four shots, $\upsilon _{\text {b}} = 30$ m/s is used for the transition point between the unsteady region and the steady plastic wave, a value chosen following observed shapes of the profiles. The rightmost data point in each figure is the velocity at the Hugoniot state $(\cdot )_{\text {d}}.$ Profiles are staggered in time by 0.2 $\upmu$s such that they do not overlap within each figure. Shock stress and deformation histories are generated using methods outlined in “Discretization and Calculations” section, with the full set of equations given in [26]. These are shown, respectively, in Fig. 3b and c. The corresponding equations invoke universal kinematics and the linear momentum balance but not any constitutive assumptions on thermoelasticity or plasticity. However, the plastic shock velocity of (29) is invoked. The stronger the shock stress, the shorter the rise time and narrower the width of each plastic wavefront. Uniaxial compressive strains at the Hugoniot state range from 3.7 to 9.0%.

Fig. 3

Reconstructed shock profiles for Mg AZ31B-4E: a particle velocity versus time, b longitudinal shock stress versus time and c total volume change (axial strain) versus time

Shown in Fig. 4 are extracted logarithmic plastic strain, plastic strain rate, and shear stress, where the latter is normalized by the initial shear modulus $G_{0}.$ Plastic strains in Fig. 4a increase monotonically in time, reaching values at the Hugoniot state of 2 to 6% depending on impact velocity. Plastic strain rates in Fig. 4b demonstrate sharp peaks within the rapidly rising portion of each waveform. Maximum rates, which tend to increase with increasing impact velocity, are on the order of $5 \times 10^{5}$/s for the three weaker shocks, but reach $4 \times 10^{6}$/s for the strongest shock with impact velocity of 1000  m/s. Peak shear stresses increase with increasing impact velocity, ranging from 1 to 2% of the shear modulus. Maximum shear stresses tend to correlate with peaks in plastic strain rate, suggesting rate dependent strength. Shear stresses in the terminal Hugoniot state are similar among tests at different impact velocities, all on the order of 1% of $G_{0}.$

Fig. 4

Extracted wave profile characteristics for Mg AZ31B-4E: a plastic strain versus time, b plastic strain rate versus time and c shear stress versus time

Temperature normalized by initial temperature, total dislocation density normalized by the square of the Burgers vector, and inelastic dilatation from lattice defects are presented in Fig. 5. Temperature and dislocation density increase monotonically with plastic strain for all shots, where slight nonlinearity is observed in each of Fig. 5a, b. For the 1000 m/s shot, maximum absolute temperature on the Hugoniot is predicted as approximately 350 K. If stored energy of lattice defects is omitted and all plastic work is converted to heat energy, then the maximum predicted temperature increases to 360 K.

Fig. 5

Extracted wave profile characteristics for Mg AZ31B-4E: a temperature versus plastic strain, b total dislocation density versus plastic strain and c residual volume change versus time

Maximum absolute dislocation densities, obtained via rearrangement of (15), are large but not inconceivable, $\approx 10^{15}$ to $10^{16}$ m$^{-2}.$ Unreasonably high values would suggest that the prescribed value of $\beta = 0.7$ is too small, estimated energy per unit defect line length is too low, or that other energy storage mechanisms are active. For example, surface energies of twin boundaries and stacking faults should account for some of the stored energy assigned totally to dislocations in the present calculations; their inclusion should reduce the predicted dislocation density. Geometrically necessary dislocations were calculated using methods derived in [25, 26]. As was the case in these prior works on Al and Cu, total dislocation density was found to be dominated by statistically stored dislocations for weak shock compression of Mg. However, the model idealizes each material element as a homogeneous polycrystal, so local defects in the vicinity of grain and twin boundaries are not resolved. Importantly, dislocation density predictions do not significantly affect extracted shear stress, plastic strain, or plastic strain rate, so accuracy of such predictions is not essential with regard to other information obtained from the wave profile analysis.

Volume changes from defects are small and positive in sign, corresponding to dilatation. Maximum values of $\delta$ increase with increasing impact velocity, reaching 0.09% for the 1000 m/s shot. These volume changes do not significantly influence the axial stress P but can have non-negligible effects on shear stress $\tau$ when the latter is very low, as in pure Cu [26]. For the present material, inclusion or omission of $\delta$ does not significantly alter the extracted material strength.

As noted in [25, 26, 40, 65], third-order elastic constants are prone to measurement error, and values are especially scarce for polycrystals. All foregoing results were obtained using the only known set of isotropic polycrystal constants for Mg [78], corresponding to a tool plate of different chemical composition than the alloys tested in the present shock experiments. As indicated by parentheses in Table 3, single crystal third-order constants [79] were invoked in additional analysis for comparison. Only the dominant constants were used corresponding to c-axis compression; the full set of anisotropic constants for hexagonal symmetry was not invoked, consistent with the isotropic assumption used for second-order elastic constants and the governing equations of “Shock Wave Profile Data Analysis” section. A third set of calculations was undertaken with null Eulerian third-order constants. Von Mises flow stresses $\sigma = 2 \tau$ are reported versus plastic strain $\varepsilon ^{P}$ for the shots of impact velocity 600 m/s, 800 m/s, and 1000 m/s in Fig. 6. Flow stresses are smaller, and larger maximum plastic strains are achieved, when the polycrystalline ${\mathsf {C}}_{\alpha \beta \gamma }$ are used. Comparably higher values of $\sigma$ are extracted from velocity history data when single crystal values or null values (${\mathsf {C}}_{\alpha \beta \gamma } = 0$) are invoked. Results obtained with polycrystalline third-order constants are deemed most valid, since maximum and final flow stresses appear unreasonably large for this alloy when the alternative constants are used.

Fig. 6

Extracted Von Mises-equivalent flow stress $\sigma = 2 \tau$ for Mg AZ31B-4E for different choices of third-order elastic constants: a 600 m/s, b 800 m/s and c 1000 m/s

Results and Interpretation: Mg AMX602

Shock compression data for Mg AMX602 presented in Fig. 1b of “Mg AMX602” section and reported originally in [9] in a study of spall failure are now addressed via the framework of “Shock Wave Profile Data Analysis section. As was the case for Mg AZ31B-4E, shots are labeled according to approximate impact velocities: 400 m/s, 600 m/s, 800 m/s, and 1000 m/s. Longitudinal stresses at the Hugoniot state range from just under 2 to just under 5 GPa, again within the weak shock regime.

Extracted and truncated early-time wave profile data for all four shots are given in Fig. 7. Particle velocity profiles are shown in Fig. 7a. As was the case for Mg AZ31B-4E, $\upsilon _{\text {b}} = 30$ m/s is used for the transition point between the unsteady region and the steady plastic wave. Profiles are again staggered in time by 0.2 $\upmu$s in each figure. Axial stress and strain are shown, respectively, in Fig. 7b and c. The stronger the shock stress, the shorter the rise time and smaller the plastic shock width. Uniaxial compressive strains $1-J$ at the Hugoniot state range from 3.8 to 9.4%.

Fig. 7

Reconstructed shock profiles for Mg AMX602: a particle velocity versus time, b longitudinal shock stress versus time and c total volume change (axial strain) versus time

Shown in Fig. 8 are extracted logarithmic plastic strain, plastic strain rate, and shear stress normalized by the initial shear modulus. Plastic strains in Fig. 8a increase monotonically in time, reaching values in the Hugoniot state of 2.2 to almost 6.5% depending on impact velocity. Plastic strain rates in Fig. 8b show sharp peaks within the rapidly rising portion of each waveform. Maximum rates increase with increasing impact velocity and reach $1.2 \times 10^{7}$/s for the strongest shock. Peak shear stresses increase with increasing impact velocity, ranging from 0.8 to 1.8% of the shear modulus. Maximum shear stresses appear to correlate with peaks in plastic strain rate, suggesting rate dependent strength. Shear stresses in the final Hugoniot state are similar among the three tests with lower impact velocities. Notably however, the Hugoniot state shear stress for the 1000 m/s shot is significantly lower, with prominent oscillations that result from fluctuations in the late-time particle velocity history of Fig. 7a, also evident in Fig 1b. The lower shear stress at higher impact velocity could be affected by thermal softening, or it could be an artifact of inaccurate higher-order thermoelastic constants [38]. Some results for FCC metals at compressions and plastic strains reaching similar magnitudes in [26] demonstrate a similar trend.

Fig. 8

Extracted wave profile characteristics for Mg AMX602: a plastic strain versus time, b plastic strain rate versus time and c shear stress versus time

Temperature, total dislocation density, and inelastic dilatation are reported for all four shots in Fig. 9. Trends in results are very similar to those for Mg AZ31B-4E discussed in the context of Fig. 5. Temperature and dislocation density increase monotonically with plastic strain, maximum T is approximately 350 K for the 1000 m/s shot. and maximum dislocation densities are large, though smaller than those shown in Fig. 5b. Volume changes from defects are small and positive, reaching 0.09% for the 1000 m/s test.

Fig. 9

Extracted wave profile characteristics for Mg AZ31B-4E: a temperature versus plastic strain, b total dislocation density versus plastic strain and c residual volume change versus time

The foregoing results were obtained using isotropic polycrystal constants [78]. Single crystal constants [79] and null Eulerian third-order constants were invoked in additional analysis for comparison. Flow stresses $\sigma = 2 \tau$ are shown versus plastic strain $\varepsilon ^{P}$ for shots of impact velocity 600 m/s, 800 m/s, and 1000 m/s in Fig. 10. Transient late-time oscillations in the particle velocity history of the 1000 m/s shot lead to vertical drops in flow stress at fixed $\varepsilon ^{P}$ in Fig. 10c. Since $\varepsilon ^{P}$ is forbidden to decrease in the extraction algorithm, a sharp decrement in $\upsilon$ at fixed plastic strain induces a drop in elastic shear strain and conjugate shear stress. Similar to results obtained on the other Mg alloy, flow stresses are smaller, and larger maximum plastic strains are achieved, when the polycrystalline ${\mathsf {C}}_{\alpha \beta \gamma }$ are used. However, for Mg AMX602, differences between flow stresses obtained using single crystal values versus null values (${\mathsf {C}}_{\alpha \beta \gamma } = 0$) are more substantial. Results obtained with polycrystalline third-order constants are again deemed most valid, since flow stresses appear unreasonably high for the other prescriptions.

Fig. 10

Extracted Von Mises-equivalent flow stress $\sigma = 2 \tau$ for Mg AMX602 for different choices of third-order elastic constants: a 600 m/s, b 800 m/s and c 1000 m/s.

Figures 6 and 10 show an apparent “softening” behavior, whereby, after attaining a local maximum, shear strength $\sigma = 2 \tau$ decreases as logarithmic plastic strain $\varepsilon ^{P}$ increases beyond at least 2%. However, importantly, strain rate is not constant during the shock compression process. Maximum values of $\sigma$ tend to correlate with maximum plastic strain rates, with ${\dot{\varepsilon }}^{P} \rightarrow 0$ at maximum $\varepsilon ^{P},$ corresponding to a steady Hugoniot state. The apparent softening is most likely attributed to rate sensitivity, noting the extreme decrease in strain rate from its maximum that occurs within the plastic rise. Thermal softening is also possible, though static data on several Mg alloys [83] suggest that, for temperature rises observed here not exceeding 60 K, the reduction in flow stress due to thermal softening should not exceed 100 MPa. Dynamic recrystallization would lead to softening, but no evidence of recrystallization was observed in recovered samples [8, 9]. Profuse twinning was also not reported [8, 9], and twinning tendency has been suggested to decrease with decreasing grain size [84]. Reorientation of basal slip planes upon twinning could lower strength, but twin boundaries may act as barriers to slip and thereby increase strength. Similar apparent softening is observed in extracted flow stresses of copper and aluminum [25, 26, 40], neither of which undergoes dynamic recrystallization or deformation twinning in the weak shock regime.

Discussion

Strength behaviors inferred for the two Mg alloys, AZ31B-4E and AMX602, in the present study are compared in “Dynamic Strengths of Mg AZ31B-4E and Mg AMX602” section. More general comparisons with other available static and dynamic data on other Mg materials, along with discussion on various experimental techniques, follow in “Comparison with Lower Strain Rate Data” section. Finally, several other methods for acquisition of dynamic strength from shock experiments are discussed in “Other Methods for Measuring Strength in a Shock” section.

Dynamic Strengths of Mg AZ31B-4E and Mg AMX602

Peak flow stresses extracted from the plastic rise of each wave profile are reported versus maximum strain rates extracted from the same dataset in Fig. 11. Results for all eight shots (four for each alloy) are shown as discrete points. For each material, positive correlation is evident between maximum stress and maximum strain rate, suggesting a rate-sensitive plastic response, i.e., strain-rate hardening. Results for the two lowest impact velocities, 400 and 600 m/s, are very similar between the two materials, with slightly lower maximum $\sigma$ observed for Mg AMX602. Shots leading to higher inelastic strain rates suggest a stronger strain-rate dependence of strength in Mg AZ31B-4E than AMX602, though this inference would benefit from additional test data.

Fig. 11

Maximum Von Mises-equivalent stress $\sigma$ versus maximum logarithmic plastic strain rate extracted from all wave profiles on both Mg alloys

Values of logarithmic plastic strain $\varepsilon ^{P}$ and flow stress $\sigma$ are compared for the end Hugoniot state $(\cdot )_{\text {d}}$ for all eight shots in Table 4. Plastic strains at the Hugoniot state are larger for AMX602 by a relative margin of 1.5 to 15%. Plastic strains all increase with increasing impact velocity. Shear stresses at the Hugoniot state are smaller for AMX602 by a relative margin of around 10% for impact velocities of 400, 600, and 800 m/s. However, at 1000 m/s, shear stress in AMX602 is much lower and just slightly exceeds half that of AZ31B-4E. Reasons for this discrepancy are not fully understood. Applying the kinematic description in “Kinematics” section, when total compression $J \approx 0.9,$ on the order of that attained in the 1000 m/s experiments, $-D^{E}_{22} \gtrsim -D^{E}_{11}$ for $\varepsilon ^{P} \gtrsim 7\%.$ This calculation indicates that if plastic strain accumulates very rapidly relative to total compressive strain, longitudinal and transverse elastic compressive strains will become nearly equal, collapsing the Hugoniot to a spherical stress state. Values of $\varepsilon ^{P}$ and J for the 1000 m/s shot in AMX602 reflect this phenomenon. Values for Hugoniot strength of AZ31B-4E are comparable to those inferred by lateral gauges in a different Mg AZ61 alloy for impact stresses up to 3 GPa [85], but are lower than those reported for AZ61 at impact stress on the order of 5 GPa.

Table 4 Hugoniot state values of plastic strain and flow stress for shocked Mg AZ31B-4E and Mg AMX602

Comparison with Lower Strain Rate Data

Quasistatic and dynamic compression experiments have been performed on ECAE AZ31B and AMX602 Mg alloys by other researchers [16,17,18,19,20]. During these experiments, a state of uniaxial stress is imposed on the material and it is loaded to finite plastic strains. As indicated from Figs. 6 and 10, the logarithmic plastic strain $\varepsilon ^{P}$ at peak flow stress achieved during shock experiments does not exceed 2.5% (for the realistic case with polycrystalline ${\mathsf {C}}_{\alpha \beta \gamma }$). To compare the strength inferred from quasistatic and dynamic compression experiments with shock data, only the initial yield point is of interest. For dynamic compression experiments subjected to strain rates from $10^{3}\,{\text {to}}\,10^{4}\,{\text {s}}^{-1},$ this corresponds to the approximate strain level for which the sample has reached a constant strain rate. Due to the low plastic strains at peak stress in the shock experiments, we approximate that this peak stress is approximately equal to the yield strength of the material, $\sigma _{y},$ at a prescribed strain rate. The combination of existing yield strength data and the strengths inferred in this work are plotted in Fig. 12.

Fig. 12

Von Mises equivalent flow strength at yield $\sigma _{y}$ for ECAE-AZ31B [16, 19, 20] and AMX602 [17, 18] as a function of strain rate compared with the peak flow stress inferred in the present analysis from shock experiments. Vertical bars denote variations in strength response when the strengths for multiple orientations were reported, not experimental error

Because of the pronounced plastic anisotropy of Mg alloys, several experiments conducted tests on two or three orthogonal sample directions. This is reflected in the plots by including error bars, which span the range of reported strengths of each individual orientation. Additionally, sample preparation deviated in most cases from the exact processing route utilized in the present work. For the ECAE AZ31B, the quasistatic and dynamic experiments studied the $4{{\text {B}}_{\text {c}}}$ route as opposed to the 4E route in this work. This implies the sample was rotated $90^{\circ }$ after each ECAE pass as opposed to 4E route discussed in  “Mg AZ31B-4E” section. Both routes give approximately the same texture, and the resultant grain size depends more on the extrusion temperature than the route. For SWAP AMX602, the powder between different experiments should be similar, although the extrusion temperature, ratio, and sample dimensions influence strength.

Increased rate sensitivity in ductile metals is most often attributed to a transition in mechanism. At low to moderate rates, resistance to slip is controlled by local obstacles, with dislocation motion thermally activated. At higher rates pertinent to shock compression, slip resistance becomes more strongly dependent on viscous and phonon drag, where relativistic effects limit maximum dislocation glide velocities. Homogeneous nucleation of dislocations becomes more important at higher impact stresses. Constitutive models for polycrystals intended to address both thermally activated and drag regimes are discussed in [35, 86,87,88, 88]. In particular, modeling efforts to address the transition between regimes are summarized in [86]. Under shock loading conditions, pressures become large relative to shear stress in ductile metals, and effects of pressure on yield stress may also affect observed strength [89]. Such pressure dependence is of much lower importance for experiments performed at low to moderate rates, i.e., static and Kolsky bar tests.

Despite differences in processing histories, both ECAE AZ31B and AMX602 Mg alloys show a low sensitivity of strength on strain rate for strain rates ranging from $10^{-4}\,{\text {to}}\,10^{4}\,{\text {s}}^{-1}.$ For the peak strength in the shock regime inferred in this work, e.g., strain rates spanning $10^{5}$–$10^{7}\,{\text {s}}^{-1},$ a large increase in $\sigma$ is observed as strain rates approach $10^{7}\,{\text {s}}^{-1}.$ This observation is consistent with previously reported increases in flow stress at strain rates in excess of $10^{5}\,{\text {s}}^{-1}.$ Although this increase in rate-sensitivity is most often attributed, in arbitrary ductile metals, to a transition in rate-limiting dislocation kinetics (as noted in the previous paragraph and  [35, 86,87,88]), there is not enough information from the present analysis to isolate a particular attribute of defect kinetics [90]. Interpretation is further complicated by the fact that both twinning and dislocation slip occur simultaneously in these Mg materials.

Care is taken to differentiate Fig. 12 from similar plots made using the Swegle–Grady scaling relationship [91], e.g., $\dot{\varepsilon }\propto \sigma _{d}^{m},$ where $m\approx 4.$ Although the plots for most metals have a similar shape to the curve in Fig. 12, the Swegle–Grady relationship specifically refers to the flow stress at the end Hugoniot state behind the shock front, $\sigma _{d},$ and not the peak flow stress experienced in the experiment that occurs within the plastic rise where strain rates are immense.

Other Methods for Measuring Strength in a Shock

Several other methods can provide information on the strength of the material at the Hugoniot state. Unlike the present method, these are not capable of accurately resolving strength within the plastic rise. Time-resolved measurements of lateral stress [85, 92,93,94] can be used to determine strength at the Hugoniot state. Given lateral stress $\sigma _{22}$ and longitudinal stress $\sigma _{11} = -P,$ shear stress can be obtained from (23): $\tau = -\frac{1}{2}(\sigma _{11}-\sigma _{22}).$ If the flow stress is low (e.g., ranging from tens to hundreds of MPa) relative to pressure, small measurement errors in either of $\sigma _{11}$ or $\sigma _{22},$ here on the order of GPa, will lead to substantial errors in $\tau .$ Typical precision of experimental methods is 1% for longitudinal stress and 5% for lateral stress [94]. Another popular method for estimating strength from shock compression experiments is use of (24): $\tau = \frac{3}{4}(P-p),$ where P is known from the plate impact test and p is obtained from a hydrostatic compression curve. Errors are magnified by the subtraction process just as for the previous method, and corrections are needed to account for the difference between static isothermal compression and dynamic adiabatic compression in plate impact. A third possibility is reshock and release [95]. This method likewise involves the difference of two very similar numbers to obtain strength in materials with low flow stress, and it requires further assumptions on the elastic–plastic response.

Conclusions

A method for inferring internal state variables and thermodynamic quantities of interest from planar shock experiments has been applied to Mg alloys ECAE AZ31B-4E and SWAP AMX602. Peak strength inferred from shock experiments has extended the known strength response of these alloys from 7 to 11 decades in strain rate, e.g., $10^{-4}$–$10^{7}\,{\text {s}}^{-1},$ without introduction of additional constitutive models or associated numerical methods for resolving steady shock waves. These findings indicate that Mg alloys experience an increase in strain rate sensitivity for strain rates in excess of $10^{5}\,{\text {s}}^{-1}.$ Additionally, for the range of impact velocities investigated, these results indicate that the strength of these fine-grained Mg alloys (1–5 $\upmu {\text {m}}$) may approach 700 MPa. Additional investigation is required to determine if similar strength levels can be achieved in more conventional coarse-grained Mg alloys with grain sizes on the order of 10–30 $\upmu {\text {m}}.$