Introduction

Titanium and its alloys have among the highest strength-to-weight ratios of the structural metals. They possess good ductility and formability, and, due to the formation of an oxide coating, have good resistance to corrosion. These properties make them useful for a variety of aerospace, marine, automotive, and biomedical applications. Among the alloys developed, Ti–6Al–4V is the most commonly used. It is a two-phase (α and β) alloy that is heat-treatable and easily machined. Unfortunately production costs for aerospace grades of Ti–6Al–4V are comparatively high, and this limits more widespread use. In response to this, recent efforts have led to the development of reduced-cost production techniques. These are discussed by Wood [1], and include the use of Electron Beam Cold-Hearth Melting (EBCHM). During ECBHM, the raw material is melted under vacuum with electron beam guns into a water-cooled hearth. It then travels through a refining hearth and into a water cooled ingot. Raw material includes titanium sponge and Ti–V master alloy and also a variety of Ti–6Al–4V scrap. Because it is a single melt process, there are substantial cost savings over the usual energy-intensive double or triple Vacuum-Arc Remelting (VAR). In addition, it can be used to make large ingots that can be directly rolled into plate. The thermo-mechanical characterization of this material over a range of strain-rates and temperatures is the subject of this paper.

As an important engineering material, much prior work has been done with Ti–6Al–4V. The constitutive response has been studied by, for example, [2,3,4,5,6]. In addition, much work has been done on alloys fabricated using the ECBHM process. Basic mechanical response and modeling, along with the influence of impurities (e.g., oxygen) are discussed in [7,8,9]. More sophisticated experiments and modeling, to account for the effects of anisotropy and asymmetric tension/compression behavior, are described in [10, 11]. Other recent work includes investigations into fatigue [12,13,14,15].

One failure mechanism of Ti–6Al–4V is thermoplastic shear localization, i.e., the formation of Adiabatic Shear Bands (ASBs). This is well known, for example [16,17,18,19,20]. ASB formation is also important in titanium machining operations [21, 22]. It is generally accepted that the development of an ASB is governed by the competing effects of the ASB-promoting mechanism of thermal softening and the ASB-opposing mechanisms of strain and strain-rate hardening as the material deforms plastically under high-rate, nearly adiabatic conditions. This phenomenon has been studied extensively, see the comprehensive works by Bai and Dodd [23], and Wright [24]. Typically, initial plastic deformation of the material is stable and therefore homogeneous because the opposing effects dominate. As a result, plastic strain accumulates uniformly and is accompanied by a uniform temperature rise. At some point, however, the thermal softening is large enough that the deformation becomes unstable and localizes. This process then escalates: as localization occurs, conditions within the localization become favorable for further localization due to extensive plastic work within the shear band heating the localized area. As a result, fully formed bands typically have widths on the order of tens of microns and contain very high local strains, strain-rates, and temperatures. This was observed specifically for a Ti–6Al–4V alloy by Liao and Duffy [25], who found localized strains as high as 350%, rates of 80 k/s, and temperatures approximately 500 °C.

In theory, any constitutive model that includes the effects of rate, strain, and temperature can be used to describe this process. Unfortunately, the conditions within a shear band exceed that which are easily measurable with macro-scale laboratory experiments, and the reality is that predictive capabilities for shear bands are lacking. Because of their complexity, shear band problems are most often studied numerically and there are additional complications which arise due to the application of numerical techniques to problems with the sharp gradients and large deformations that exist within shear bands.

The present paper documents an effort to overcome some of these obstacles. The mechanical behavior of the low-cost alloy described above is studied in uniaxial stress compression over a range of strain-rates and temperatures. Experiments to understand temperature dependence are performed in a servo-hydraulic load frame at low-rates (0.01/s) over a range of 81 to 673 K. The Split Hopkinson pressure bar, or Kolsky bar, is used to study the high-rate behavior, with specialized small diameter bars (1.59 mm and 794 μm) to obtain rates as high as 80,000/s, relevant to conditions expected within a shear band. Kolsky bar recovery techniques were used to generate larger strain, quasi-isothermal data at high rates to help establish the saturation of strain-hardening. Finally, a parameter set for the Zerilli-Armstrong recovery strain model [26] is given, along with a Johnson–Cook model in a modified form that includes the recovery strain feature.

Material

The material was provided by the Titanium Metals Corporation (TIMET) in the form of a 1 m × 1 m by 127 mm thick plate. It was manufactured primarily from a mixture of titanium sponge and Ti–6Al–4V turnings (32 and 62% by weight) by an EBCHM process and meets requirements specified in MIL-DTL-46077. Its overall chemical composition, as supplied by the manufacturer, is shown in Table 1. In addition, the material contains 29 ppm H2 and less than 10 ppm Yttrium. At room temperature it contains both an alpha phase (bright regions) and a transformed beta phase (dark regions). Figure 1 shows the grain-structure. The grains are elongated. Typical lengths are ~ 35 µm, typical widths ~ 6 µm (aspect ratio 5.6). The density was found to be 4412 kg/m3 using a buoyancy method based on Archimedes principle. Elastic properties were found using ultrasound and a pulse echo overlap technique. The elastic modulus, shear modulus, and Poisson’s ratio are 119, 45.3, and 0.315 GPa, respectively.

Table 1 Chemical composition of the subject alloy (wt%, balance titanium)
Full size table
Fig. 1
figure 1

Microstructure of the Ti–6Al–4V alloy

Full size image

Experiments

Low-Rate Experiments over a Range of Temperatures

Room-temperature (~ 295 K), low-rate compression tests were performed with an Instron model 1332 servo-hydraulic load frame. An Instron model 3156 116 load cell was used to measure force. Deformation was measured with an LVDT measurement of machine deflection, using a correction for machine compliance. The majority of the specimens were cylindrical, nominally 6.35 mm in length and diameter (L/D = 1). They were prepared by first removing oversized cores from the plate in the thickness direction by electrical discharge machining (EDM). The cores were next finished to their final diameters by centerless grinding and EDM cut to length. Finally, the top and bottom surfaces were ground lightly using special fixtures to maintain the parallel surfaces. During the experiments, contact surfaces were lubricated with a MoS2 grease. Tests were conducted at true strain rates of 0.001, 0.01, 0.1/s. A subset of the results is shown in Fig. 2. Deformation at these rates is typically assumed isothermal, although it is reasonable to assume non-negligible heating at the higher rates, especially 0.1/s. This is evident in the figure, where the hardening rates decrease slightly as rate increases from 0.001 to 0.01/s, and then to 0.1/s; this may be due to heating of the sample as plastic deformation accumulates and is estimated to be as high as 30 °C.

Fig. 2
figure 2

a Example stress–strain curves over a range of strain-rates (initially at room temperature), along with model fits. The model fits assume adiabatic conditions with β = 0.7. b Additional repeated stress strain curves at 10 k/s and 22 k/s, along with corresponding ZA model fits, to show scatter in the data. (Color figure online)

Full size image

Low rate (0.1/s) experiments were also conducted at temperatures of 81, 294, 473, and 673 K to establish a thermal softening trend. Elevated temperatures were achieved using a clam-shell oven (Applied Test Systems, Inc., 3210 series), and were monitored with thermocouples adhered to each specimen. The low temperature was achieved by immersion in liquid nitrogen. The data are reported in Fig. 3 which shows true stress at 10% true strain as a function of temperature. Also shown in the figure are data from Khan et al. [7], from their experiments with a similar material. The agreement is excellent, although note the Khan data, stress at yield, was performed at a lower strain-rate of 0.001/s. Also shown is the β-transition at 1280 K [7], and the melt temperature of 1933 K [5].

Fig. 3
figure 3

Temperature data and model fits. Although there is no data at high rates and elevated temperatures, model fits at 1000/s are shown to demonstrate that the predicted behavior is reasonable

Full size image

Additional low-rate experiments were conducted with some of the smaller samples used for the high rate experiments to check for specimen geometry effects, i.e., to confirm consistency in the measured mechanical behavior between the larger samples and the smaller samples that were necessary for obtaining high strain-rates. This will be discussed in a later section.

High-Rate Experiments

High rate experiments (all compression) were performed with five different diameter Kolsky bars: 9.5, 6.35, 3.18, 1.59, and 0.794 mm. The basic operation of the Kolsky bar can be found in [27,28,29,30]. Bars are made from a variety of high strength steels. All high rate experiments were conducted at room temperature (~ 294 K) and are assumed adiabatic. Each sample was lubricated with the same MoS2 grease used in the low-rate experiments.

In general, the smaller bars and samples were used to achieve higher strain-rates. The exceptions are the experiments conducted with the 9.5 mm bar. These were all conducted at a strain-rate of 3 k/s and incorporated a high speed camera (DRS Hadland Imacon 200) to take images of the deforming sample. Note some experiments used tapered strikers to pulse shape and achieve constant strain-rates [31], although this has minimal effect on the results presented here.

The smaller bar diameters are somewhat unusual and are used to increase the rise-time of the measurements during high rate experiments. This produces data with higher resolution at the higher-rates [32,33,34,35]. The smaller bars are also more compatible with small specimen sizes. This leads to better states of quasistatic equilibrium which is a key assumption in the Kolsky bar tests. Because of the small sizes, the 1.59 and 0.794 mm bars are instrumented optically with Normal Displacement Interferometers (NDI) and Transverse Displacement Interferometers (TDI) instead of strain gages [36,37,38] because the latter become impractical at these sizes. Figure 4 shows data from an experiment with the smallest bar (0.794 mm diameter). Figure 4a shows the particle velocity as measured by the interferometers, i.e., the TDI on the input bar and the NDI on the output bar. Figure 4b shows the resulting stress–strain curve for the specimen along with the strain-rate. Note that in terms of particle velocity, the sense of the reflection is positive, whereas in terms of strain it is negative. Otherwise the miniature bars are the same in operation as conventional bars. For the 3.18 mm bar, the output bar only was instrumented with an NDI, while the input bar used conventional strain gage instrumentation. This was done out of convenience rather than necessity.

Fig. 4
figure 4

Example a velocity signals and b stress–strain curve for an experiment with the 794 µm diameter steel bar. (Color figure online)

Full size image

Table 2 summarizes the sample geometry used for each bar. All of the cylindrical samples were made using the centerless grinding technique described above. It was found that our process could not produce adequate cylindrical samples at sizes smaller than 1.59 mm, so the samples for the smaller two bars were rectangular prisms that approximated cubes (sizes are given in the table). Note the longer dimension is the gage length. The cube geometry was used for the sole reason that this geometry was easier to finish to the desired precision with available machining techniques than were cylinders at a comparable size. Cube specimens were manufactured by first removing oversized cubes from the plate by EDM. All six faces of each cube were finished to a 1 µm finish with an Allied HighTech, Inc. TechPrep polisher, a machine designed for precise parallel polishing. A minimum of 100 µm was removed from each face to completely remove the EDM affected zone.

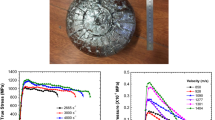
Table 2 Specimen geometry used with each Kolsky bar
Full size table

In all, 46 high-rate experiments were performed. Representative stress–strain curves are plotted in Fig. 2. Figure 5 plots the strain-rate hardening effect from the low and high rate experiments, grouped according to specimen size (true stress at 0.06 true strain, or ~ 0.05 plastic strain, plotted against rate of true strain). Note the vertical axis does not start at zero stress. In this plot, “large samples” refer to the 3.18 and 6.35 mm cylinders. The other two groups are for the two different size cubes. Unsurprisingly, more scatter results from experiments with the smaller samples. This is true both at low (Instron machine) and high (mini Kolsky bar) strain rates. We attribute this mainly due to heterogeneity within the samples. With the microstructure shown in Fig. 1, the largest samples contain on the order of a million grains, while the smallest on the order of perhaps a thousand. The smaller specimens are also more likely to capture local heterogeneities from within the plate. This fact makes it difficult to achieve higher strain-rates with this fairly large-grained material using the Kolsky bar and the specimen equilibrium assumption. To obtain higher rates, smaller samples would have to be used, but this would lead to increased scatter that would eventually exceed an acceptable threshold. For this reason, higher rate experiments were not attempted with this material. Similar scatter has been observed with bars and samples at higher rates and a much smaller scale, see [39].

Fig. 5
figure 5

Flow stress as a function of strain-rate, including model fits. The model fits account for thermal softening due to adiabatic heating at the higher strain-rates which accounts for the discontinuity at ~ 0.1/s. All specimens are initially at room temperature

Full size image

Also shown in Fig. 5 are two additional sets of data. The first are from Khan et al. [7], for a similar low-cost alloy. The trends of strain-rate-hardening are in good agreement, although Khan did not report data beyond 5 k/s. The next set of data (true stress at 10% true strain) is from Wulf [2], who used a direct impact technique to characterize a higher grade Ti–6Al–4V alloy (SAE AMS 4911B, extra-low interstitial, annealed). Although the materials are processed differently, this data is relevant because it spans a high-rate range. Represented by open squares in the figure, this data shows less scatter then the present set and shows a much larger strain-rate hardening than measured here. Considering the scatter in the present experiments, we do not see convincing evidence of such an enhanced strain rate hardening with the low-cost material.

Spletzer and Dandekar [40] conducted plane shock wave experiments (uniaxial strain) on specimens made from the same plate of material studied here. They reported Hugoniot Elastic Limits (HEL) ranging from 2.02 to 2.95 GPa. From these values, a yield stress range can be estimated from 1080 to 1580 MPa according to:

$${\sigma _y}={\sigma _{HEL}}\left( {\frac{{1 - 2\upnu }}{{1 - \upnu }}} \right)$$
(1)

It is difficult to associate precise strain-rates with these values; they are estimated to range from 100 k/s to 1 M/s.

In most cases, the high-rate experiments resulted in fracture of the specimen. The fracture surfaces occurred along planes oriented approximately 45° from the loading axis, corresponding to planes of maximum shear stress. It is presumed that the fractures were preceded by adiabatic shear localization. Figure 6 shows a series of images taken during an experiment at 3000/s. The fracture is clear starting at frame 7.

Fig. 6
figure 6

Deformation and failure of a specimen at a strain-rate of about 3000/s. The incident bar is to the right and the frames are 12 μs apart. Note the fracture along a 45° shear plane starting at frame 7. Splattering of the black MoS2 grease is also seen and should not be misinterpreted as failed specimen material

Full size image

The data from the high-rate experiments can be used to identify the onset of instability preceding thermoplastic localization because these experiments are adiabatic. This can be done by locating the peak-stress on the true-stress/true-strain curves, i.e., the strain at which dσ/dε = 0. Further deformation beyond this strain is unstable and unreliable for determining material properties. In reality, even the peak stress data is unreliable because it cannot be assured that the prior deformation was entirely homogenous. Unfortunately, it is critical to consider this point when developing constitutive models for adiabatic shear because it has a profound effect on predictions of band formation. In most of the adiabatic experiments, peak stress occurred between 0.2 and 0.3 true strain. Figure 7 shows three adiabatic stress–strain curves (~ 3000/s) where peak stresses can be defined (in this case, ranging from 0.22 to 0.32 strain).

Fig. 7
figure 7

Stress–strain curves at ~ 3000/s. Note the variation in the location of peak stress (i.e., the onset of instability). (Color figure online)

Full size image

High-Rate Quasi-Isothermal Experiments

Because the high-rate experiments are largely adiabatic, the measured material response is complicated by the presence of a changing temperature. Furthermore, since a material like Ti–6Al–4V localizes under adiabatic conditions, specimens tend to fail prior to achieving large homogeneous strains. This makes it difficult to study large strain behavior at high rates.

In an attempt to determine the high-rate response at large strains, quasi-isothermal stress–strain curves were obtained at average rates of 1000/s and 2000/s. This procedure involves incrementally loading and recovering plastically deformed specimens, allowing them to cool to room temperature, and then reloading to generate quasi-isothermal stress–strain curves, as described by [41]. With each consecutive reloading, a flow stress can be measured at a negligible plastic strain, generating a point on an “isothermal” stress–strain curve.

In general, recovery with a Kolsky bar is difficult because reverberating stress waves in the bars re-load the specimen after the desired loading is complete. There are several techniques to avoid this, for example [41], has developed momentum traps on the incident bar to eliminate re-loading reverberations. Others have used “stop-rings” around the specimen to limit deformation to a desired amount. Here we use the method described by [42]. If the specimen is not too soft, simple momentum considerations in the bars can be adequate to ensure the specimen is not reloaded. The idea is to select appropriate bar and specimen dimensions, along with an appropriate projectile and impact speed, to ensure that during successive reverberations, the transmitter bar moves “down range” from the specimen at a greater rate than the incident bar. If this is the case, the gap between the bars (i.e., that contains the specimen) only increases and the specimen can fall into a recovery tank.

An example loading sequence for one such specimen is shown in Fig. 8. The rate is approximately 2000/s (3.18 mm bar, L = D = 1.59 mm sample) and is shown in Fig. 9. Points along the “isothermal” stress–strain curve are marked in Fig. 8. These are selected by picking a point soon after yield in each loading cycle where equilibrium is presumed adequate but before significant heating has occurred, essentially 1 or 2% plastic strain beyond yield. Note the deviation from the isothermal trend in each adiabatic loading cycle, which can also be seen in the jumps in the stress–strain curves; because the samples have cooled to room temperature, they increase in strength due to the lack of thermal softening. The strain-rate history, aside from the elastic loading and unloading, is reasonably constant at ~ 2000/s.

Fig. 8
figure 8

Loading history with recovery at 2000/s. From the four tests, four points along the quasi-isothermal stress–strain curve are obtained

Full size image
Fig. 9
figure 9

The strain-rate history for a quasi-isothermal test at a nominal rate of 2000/s. Note the plastic deformation occurs at roughly 2000/s

Full size image

In all, 37 experiments (12 different specimens) were performed to generate quasi-isothermal data. After each loading, specimens were examined under low power magnification. Testing was discontinued with any specimen that exhibited visible signs of localization (aside from the unavoidable “barreling” due to friction) or damage. The deformed specimen dimensions (i.e., final lengths) were also checked after each loading cycle with a micrometer to ensure they agreed with that measured by the Kolsky bar analysis, confirming that the specimen was not reloaded.Footnote 1

Additional points along the quasi-isothermal stress–strain curves for the remaining experiments are given in Fig. 10; note the vertical axis does not start at zero stress. Two things are notable. The first is that indeed more total strain is obtained before failure than when the specimens are compressed adiabatically in a single loading (35% rather than ~ 20%). Again this is attributed to the suppression of localization by allowing specimens to reach uniform temperatures between compression cycles. The second is that there is some evidence of strain-hardening saturation at strains above 30%; in fact, in some cases the stress seems to decrease slightly. Unfortunately, larger strains could not be obtained using this method, as specimens failed (in shear) almost immediately after. This observation in itself may suggest that the strain hardening is approaching a saturation point; without appreciable strain-hardening, rapid localization is expected after even minimal additional plastic strain.

Fig. 10
figure 10

Isothermal low-rate data along with quasi-isothermal high-rate data. Model fits are also given. The rates of 960/s and 2200/s for the experimental data are average values; in reality loading histories are similar to that shown in Fig. 9. (Color figure online)

Full size image

Constitutive Modeling

The Johnson–Cook [43] and Zerilli-Armstrong [44] equations are widely used constitutive models that capture the effects of strain hardening, strain-rate hardening, and thermal softening. The JC model is written as:

$$\sigma =\left( {{\sigma _0}+B{\varepsilon ^n}} \right)\left( {1+C\ln \frac{{\dot {\varepsilon }}}{{{{\dot {\varepsilon }}_0}}}} \right)\left[ {1 - {{\left( {T^{*}} \right)}^m}} \right]$$
(2)

where σ0, B, n, C, and m are material constants and \({\dot {\varepsilon }_0}\) is a reference strain-rate. T* is the homologous temperature defined as:

$${T^*}=\frac{{T - {T_r}}}{{{T_m} - {T_r}}}$$
(3)

where Tr and Tm are a reference temperature and the melting temperature, respectively. σ is the Von-Mises stress, ε is the effective plastic strain, and T is the absolute temperature. It is an empirical model, and has been used in many modified forms to suit particular applications.

The ZA model for bcc metals is written as:

$$\sigma ={\sigma _a}+B{e^{ - \beta T}}+K{\varepsilon ^n}$$
(4)
$$\beta ={\beta _0} - {\beta _1}\ln \dot {\varepsilon }$$
(5)

where σ a , B, K, n, β0, β1 are material constants. In the original form, n = ½, but it is routinely taken as a free parameter to improve model fits.

Because both of these models have a power law form for strain hardening, the flow stress rises without limit as plastic strain increases. The strain-hardening in many materials, however, tends to saturate at large strains, and this type of behavior can be critical to the formation of shear bands. Zerilli and Armstrong recognized this with their original model and introduced a modified version [26] (MZA) that replaces the strain hardening term with an exponential form that allows the strain-hardening to saturate at large levels of plastic strain. This is written as:

$$\sigma ={\sigma _a}+B{e^{ - \beta T}}+{B_0}{\left[ {{\varepsilon _r}\left( {1 - {e^{{\raise0.7ex\hbox{${ - \varepsilon }$} \!\mathord{\left/ {\vphantom {{ - \varepsilon } {{\varepsilon _r}}}}\right.\kern-0pt}\!\lower0.7ex\hbox{${{\varepsilon _r}}$}}}}} \right)} \right]^n}{e^{ - \alpha T}}$$
(6)

where

$$\alpha ={\alpha _0} - {\alpha _1}\ln \dot {\varepsilon }$$
(7)

and ε r is a recovery strain which governs when strain saturation occurs. Again, they use the assumption of Taylor strain hardening, n = 1/2, but it can be generalized to allow more flexibility in matching experimental data. The exponential term involving α permits possible effects of temperature and rate on work hardening to be included. For small strains, the strain hardening term reduces to the power law hardening of the original form \(B{\varepsilon ^n}\). For large strains, it approaches a maximum finite value, effectively limiting the strain-hardening.

Some implementations of the Johnson–Cook equation use a maximum stress value to effectively cap the stress (see for example the form used in Johnson et al., [45]), although in a discontinuous fashion. However the original form can also be modified to incorporate the strain hardening term extracted from the ZA equation:

$${B_0}{\left[ {{\varepsilon _r}\left( {1 - {e^{{\raise0.7ex\hbox{${ - \varepsilon }$} \!\mathord{\left/ {\vphantom {{ - \varepsilon } {{\varepsilon _r}}}}\right.\kern-0pt}\!\lower0.7ex\hbox{${{\varepsilon _r}}$}}}}} \right)} \right]^n}$$
(8)

This term can then be used to replace the strain hardening term in a JC form (MJC).

$$\sigma =\left[ {{\sigma _0}+{B_0}{{\left[ {{\varepsilon _r}\left( {1 - {e^{\frac{{ - \varepsilon }}{{{\varepsilon _r}}}}}} \right)} \right]}^n}} \right]\left( {1+C\ln \frac{{\dot {\varepsilon }}}{{{{\dot {\varepsilon }}_0}}}} \right)\left[ {1 - {{\left( {{T^*}} \right)}^m}} \right]$$
(9)

This modification permits an additional degree of freedom in describing the strain-hardening behavior which again can be critical when describing shear localization. Note for small strains, or a very large εr, this equation reduces to Eq. 2. For large strains, however, the strain hardening term asymptotes to (σ0 + Bεr), a limiting value that is scaled by the rate and temperature terms.

Parameters for these four models were determined from the experimental data using various least squares/absolute value optimization schemes along with additional ad hoc modifications in an attempt to best represent the experimental data in Figs. 2, 3, 5, 7, and 10. During this process, experiments below a strain rate of 0.01/s are assumed isothermal. Higher rates are assumed adiabatic, using a specific heat value of 586 J/kg-K and a 70% conversion of plastic work to heat based on [7].

Because of our emphasis on populating models that can be used to simulate shear bands, emphasis was placed on the ability of the models to capture the peak stresses (occurring at strains of ~ 0.2 to 0.3, Fig. 7) on the adiabatic curves. It was found that this additional requirement of the models could not be met with either of the original JC or ZA models, i.e., the modified versions, MZA and MJC, had to be used. Final parameter sets for these models are given in Tables 3 and 4, and the material behavior predicted by these parameter sets are given along with the experimental data in relevant figures.Footnote 2 Peak stresses in the adiabatic curves predicted by these fits typically range between 0.32 and 0.36 true strain, which exceeds that measured in the experiments. This is justified because any real experiment will always have some amount of non-uniform deformation (most significantly due to friction at the loading surfaces) so that at best a measured strain at peak stress will represent a minimum bound for that which would be measured in an ideal experiment.

Table 3 MJC parameters for the Ti–6Al–4V alloy
Full size table
Table 4 MZA parameters for the Ti–6Al–4V alloy
Full size table

Conclusion

The goal of this research was to develop constitutive models for low-cost Ti–6Al–4V alloy that would (1) represent the overall mechanical response over a range of dynamic conditions, and (2) provide a predictive capability for adiabatic shear. The basic assumption behind the latter is that the simplest description of adiabatic shear localization is adequate: the formation of shear bands is governed by the competing effects of strain/strain-rate hardening and thermal softening. A simple constitutive model which contains these effects is then adequate to describe shear localization provided it is calibrated over the temperature, strain, and strain-rate ranges that are observed in actual ASBs. It is difficult to create these conditions with basic mechanical experiments in such a way that useful measurements of the material behavior can be made. In particular, very high strain-rate data is difficult to obtain due to a lack of easily available techniques; in this case we have used miniature Kolsky bars to measure the response at strain-rates as high as 80 k/s. In addition, because of this material’s propensity to localize and fail, it is difficult to maintain uniform deformation during a mechanical test. It is therefore difficult to measure the large strain behavior, especially at high-rate, adiabatic conditions. For this reason, we have used Kolsky bar recovery methods to obtain quasi-isothermal stress–strain curves.

It was found that the recovery strain parameter provided an extra degree of freedom in both models to represent the experimental data and give reasonable approximations of the peak stress instability. These models provide a good representation of the material behavior over the conditions studied: strain-rates from 0.001/s to 80 k/s, temperatures from 295 to ~ 550 K, and strains as high as 35%. Behavior beyond these ranges is extrapolated.

Strong evidence of enhanced strain-rate hardening, due to dislocation relativistic effects or phonon drag for example, was not observed. This is in contrast to the data reported by Wulf [2]. This is an important behavior to understand because a strong rate hardening, of the type observed by Wulf, would have a strong opposing effect on shear band formation, in addition to strain hardening. The models selected here assume monotonically increasing flow stress with the logarithm of strain-rate; a more complicated model would be required to represent the more complex behavior. However, especially in consideration of the scatter at the higher strain-rates, the models selected here seem adequate.

Dynamic recovery leading to strain saturation is somewhat speculative based on the isothermal and quasi-isothermal experiments and the adiabatic stress–strain curves; it was not possible to investigate larger stain behavior using uniaxial stress techniques. Again, this is due to the difficulties encountered in sustaining unstable but homogeneous deformation during an experiment. As shown in Fig. 8, specimens typically fractured along a 45° plane. This suggests shear is the predominant failure mode. In future work, Pressure Shear Plate Impact (PSPI) experiments [49, 50] may be useful because the shear fracture would be suppressed. This would permit larger strains to develop in the material. The PSPI technique could also provide additional high-rate data. Additional information may also be obtained, although indirectly, from other experimental methods. In the past, researchers have used various experiments to infer material behavior outside those conditions obtained with straightforward mechanical tests, e.g., to fine-tune constitutive model parameters. For this purpose, the cylinder impact test is commonly employed [51]. Shear-punch experiments, or the very similar “top-hat” specimen developed by [52], are also useful, with specific applications to titanium alloys by [53,54,55].