1 Introduction

Over the last few years, control of unmanned surface vessels (USV) has been widely addressed in the control area and the trajectory tracking problem of USVs took a part of a lot of studies and experiments [1], due to its large domain of application: in civil and military fields, such as reconnaissance and surveillance. Considerable studies and researches have been devoted to the trajectory tracking problem of the USVs, adaptive trajectory tracking control for a fully actuated unmanned surface vehicle (USV) is proposed in [2]. A combination of back-stepping with adaptive feedback approximation techniques in order to investigate the control problem of tracking a desired trajectory for a fully actuated USV is studied in [3], a nonlinear H-infinity (optimal) control approach for the problem of the control of the depth and heading angle of an autonomous submarine [4], and a new model-free approach based on intelligent proportional-derivative (iPD) control is investigated in [5]. However, some of works mentioned above are based on systematic control methods that are depending on the model of the system; and they poorly reject significant disturbances or uncertainties. This pushes toward an alternative methodology to control such a challenging type of vehicles. The most important challenge in the control design for USVs is to cope with uncertainties and disturbances effects. For this reason, observer-based controllers took a deep attention in this area; model predictive controller with disturbance observer is presented for path following with environment disturbance in [6], the problem of trajectory tracking control of a surface vessel subjected to parametric uncertainties, external disturbances, and thruster faults addressed in [7], adaptive estimator-based control in [8], novel robust back-stepping controller based on disturbances observer is introduced for trajectory tracking control of marine surface vessels in [9], and an adaptive finite-time tracking control (ARFTTC) scheme for trajectory tracking of a fully actuated USV with unknown disturbances in [10]. Despite of the performances ensured by the previous approaches, they are still heavy and complex in term of design and implementation; in addition to the neglect of one practical problem which is the measurements noise especially after been amplified by the observer’s gains. One of the most promising approaches in disturbances and uncertainties rejection is the active disturbances rejecter control (ADRC) presented by Han in the 1990s [11]. This control strategy has shown very encouraging results in the robotic field, e.g., unmanned aerial vehicles (UAV) control [12] and wheeled mobile robots [13, 14]. ADRC controllers have been considered in the control marine vehicles under uncertainties and disturbances, such as the control of USV course based on ADRC in [15], ADRC controller with sliding mode control (SMC) has been introduced for the path-following problem of surface ships with uncertainties of internal dynamics and external disturbances in [16], a novel trajectory following controller based on ADRC technique is proposed for path-following control of USV in [17], and a nonlinear ADRC for USV course control in [18]. In spite of the remarkable robustness of the ADRC in the previous works, traditional ESO-based controllers are mostly focusing on coping with constant or slow-varying type disturbances and offer insufficient estimation quality in presence of fast time-varying type disturbances, as illustrated in [19, 20]. However, the disturbances caused by waves, sea current, and wind are seldom constant in practice, but rather opposing; fast-varying sinusoidal is usually the model used to govern the external disturbances in ships control [6, 9, 10, 21,22,23,24,25]. Therefore, some attempts to increase the efficiency of ADRC-based USV control has been made; a modified ADRC based on a reduced-order ESO for trajectory tracking control of USV in [26] and an improved ADRC based on higher-order ESO addressed also as generalized proportional integral (GPI) observer in [27]. In [28], it is shown that higher-order ESO can improve the estimation accuracy of fast time-varying sinusoidal disturbances, in condition that the ESO bandwidth is set to be larger than the frequency of the disturbance, this improved ADRC was addressed and analyzed in [29, 30] and for Attitude Control of Quadrotor Vehicles in [31]. Higher-order ESO was combined with SMC in [32] in order to reduce disturbances and chattering effects. In this paper higher-order ESO (HOESO) or Generalized ESO (GESO) is considered to cope with time-varying disturbances, such as sinusoidal type. The proposed GESO is n+m-th order (with n is the system’s order and m depends on the disturbances considered dynamics), and this approach is considered to achieve the convergence of the dynamic error of the ESO for the class of disturbances that are time varying but can be expressed in time polynomial function form, such as \(d(t) = d_0 + d_1t + d_2t^{2} +d_3t^{3} + o(t^{3}).\) The obtained results have shown that the proposed 5th-order GESO has clearly improved the estimation accuracy of sinusoidal external disturbances. However, there still exists a periodic estimation error that might decrease the control accuracy of the closed-loop system. Thus, we propose to embed the disturbance dynamics (sinusoidal dynamics) into the GESO, to form a harmonic or periodic GESO which has obviously increased the sinusoidal disturbance estimation.

The use of disturbances observer is mostly effective. However, the biggest drawback about it is the measurements noise that will be amplified by the observer’s gains which is unavoidable practical problem and it risks to affect the convergence of the closed loop especially in case of high-gain observers, because the observers use the output signal of the system as input and the amplification of the noise by the observer’s gains will deliver a noisy state estimation in input, and if the noise is sufficiently large it could destabilize the closed-loop system. One solution to this problem has been proposed in [33], by combining an integral state with the observer. Our main contribution can be resumed in two main points:

  • Embedding the disturbances dynamic into the usual ESO and applying this observer for the trajectory tracking problem of USV in presence of fast time-varying sinusoidal-like disturbances.

  • Then, an integral extension is proposed in the ESO in order to attenuate the perturbations caused by the noisy measurement.

In this context, numerical simulations are performed and obtained results are discussed. Then, we compare the effectiveness of both the improved ADRCs (HESO and GESO) and the conventional ADRC in rejecting complex and fast-varying disturbances, since the comparison between ADRC and PID has been widely addressed in the literature.

The paper is structured as follows. Section 2 presents the USV modeling. The design of linear ADRC-based control law for the USV to track the desired trajectory is developed in Sect. 3. Numerical simulation results and discussion are provided in Sect. 4. Finally, conclusions are drawn in Sect. 5.

2 System modeling

2.1 Kinematics

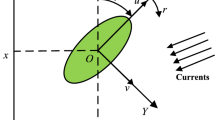
In order to reduce the kinematic and dynamic modeling complexity, the following assumptions have been considered to simplify the modeling and the control design task (Fig. 1):

  • The USV operates at low speed.

  • The USV is symmetric via the XZ and YZ planes.

  • The USV is supposed to be equipped with sufficient propellers to generate forces and torques in all directions. In other words, equations in the next sections are written in function of generalized forces not allocated forces.

Fig. 1
figure 1

USV coordinate system

Full size image
Table 1 Degrees of freedom of USV
Full size table

The different possible movements by the USV are listed in Table 1

$$\eta = \left[ {x,y,\psi } \right]$$
(1)
$$\xi = \left[ {x_{b} ,y_{b} ,\psi _{b} } \right]$$
(2)
$$v = \left[ {u,v,r} \right]$$
(3)

The motion of the USV can be described by

$$\dot{\eta } = J\left( \eta \right)v$$
(4)

where \(\eta\) is the velocity vector expressed in the earth frame, {E} and {B} are the position and velocity vectors expressed in the body frame, and J is the transformation matrix between {B} and {E} determined by

$$\left( {\begin{array}{*{20}c} {\dot{x}} \\ {\dot{y}} \\ {\dot{\psi }} \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\cos (\psi )} & { - \sin (\psi )} & 0 \\ {\sin (\psi )} & {\cos (\psi )} & 0 \\ 0 & 0 & 1 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} u \\ v \\ r \\ \end{array} } \right){\text{ }}$$
(5)

3 Dynamics

In the dynamic modeling, forces acting on the plant and its physical characteristics are taken into consideration while studying the motion of the vehicle. The full USV dynamic model for 3 DOF is

$$M {\dot{\nu }} +C(\nu )\nu +D(\nu )\nu +g(\eta )\,=\,\tau$$
(6)

where M is the mass and inertia matrix, C the Coriolis and centripetal matrix, D the hydrodynamic dumping matrix, and g gravitational and Buoyancy matrix.

Equation (6) can be rewritten as

$$\begin{aligned} {\left\{ \begin{array}{ll} m_{11}{\dot{u}} +X_{u}u+X_{u|u|}u|u|-m_{22}vr=\tau _x \\ m_{22}{\dot{v}} +Y_{v}v+Y_{v|v|}v|v|-m_{11}ur=\tau _y\\ m_{33}{\dot{r}} +N_{r}r+N_{r|r|}r|r|+(m_{22}-m_{11})uv=\tau _r \end{array}\right. } \end{aligned}$$
(7)

with

$$\begin{aligned} {\left\{ \begin{array}{ll} m_{11}=m-X_u\\ m_{22}=m-Y_v\\ m_{33}=m-N_r \end{array}\right. } \end{aligned}$$
(8)

4 Control system

4.1 Disturbances

In marine vessels control design, it is common to assume the superposition principle for wave and wind disturbances according to [21] and to add the generalized wind-wave-induced force to the right side of Eq. (9).

$$\begin{aligned} M {\dot{\nu }} +C(\nu )\nu +D(\nu )\nu +g(\eta )=\tau +\tau _\omega \end{aligned}$$
(9)

An effective approximation of wind and wave disturbances simulation model is presented in [21] as

$$\begin{aligned} {\left\{ \begin{array}{ll} C_x(\gamma _\omega )\approx -c_x \cos (\gamma _\omega )\\ C_y(\gamma _\omega )\approx c_y \sin (\gamma _\omega )\\ C_N(\gamma _\omega )\approx c_n \sin (2\gamma _\omega ) \end{array}\right. } \end{aligned}$$
(10)

with \(C_{x}\), \(C_{y}\), and \(C_{n}\) as constants and is the wind angle of attack. Similar models have been considered for computer simulations of USV control in [6, 9, 10, 22, 23] and for autonomous underwater vehicles (AUVs) control [24,25,26], where the unknown external disturbances including ocean winds, waves, and currents is assumed to be governed by fast-varying sinusoidal-type signals.

4.2 Control design

Considering the dynamic model of the vessel, an ADRC-based controller has been designed for each DOF. The control design for one channel is presented in Eq. (11) and detailed in this section. Similar controllers are designed for each other DOF of the USV.

The surge dynamic equation with added disturbances and unknown dynamics is

$$\begin{aligned} m_{11}{\dot{u}} +X_{u}u+X_{u|u|}u|u|-m_{22}vr=\tau _x+\tau _\omega \end{aligned}$$
(11)

where \(\tau _\omega\) is the full disturbance term.

By assuming small variation of the yaw angle \(\psi\):

$$\begin{aligned} {\dot{x}}=u \end{aligned}$$
(12)

So Eq. (11) can be expressed in the inertial frame {B} by

$$\begin{aligned} m_{11}\ddot{x} -X_{{\dot{x}}} {\dot{x}}- X_{{\dot{x}}|{\dot{x}}|}{\dot{x}}|{\dot{x}}|-m_{22}{\dot{y}}{\dot{\psi }}=\tau _x +\tau _\omega \end{aligned}$$
(13)

4.2.1 Generalized ESO design

The state space form of the system (13) can be written as

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{x}}_1=x_2\\ {\dot{x}}_2=f({\dot{x}},{\dot{y}},{\dot{\psi }},\tau _\omega )+\frac{1}{b_x}\tau _x\\ y=x_1 \end{array}\right. } \end{aligned}$$
(14)

The conventional \(3^{d}\) order ESO can be expressed as

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{z}}_1=z_2-l_1e_1\\ {\dot{z}}_2=z_3-l_2e_1+b_1U_1 , e_1=y-z_1\\ z_3=-l_3e_1 \end{array}\right. } \end{aligned}$$
(15)

This ESO can ensure a sufficient estimation quality of the disturbances in the case where the dynamics of the function f is negligible, which is not the case if the disturbances are time varying and assumed to be r-derivable expressed in time as a combination of polynomial component and a harmonic component as

$$\begin{aligned} d(t)=d_p(t)+d_h(t) \end{aligned}$$
(16)

with

$$\begin{aligned} {\left\{ \begin{array}{ll} d_p(t)=d_0+d_1t+d_2t^2+\epsilon (t)\\ d_h(t)=A_h \sin (\omega _ht+\xi ) \end{array}\right. } \end{aligned}$$
(17)

In this paper we consider \(r=3\), and we propose to consider extra state variables \((x_3, x_4, x_5)\) for disturbances, estimation in place of the conventional one state variable.

$$\begin{aligned} {\left\{ \begin{array}{ll} x_3=f_x({\dot{x}},{\dot{y}},{\dot{\psi }},\tau _\omega )\\ x_4={\dot{f}}_x({\dot{x}},{\dot{y}},{\dot{\psi }},\tau _\omega )\\ x_5=\ddot{f}_x({\dot{x}},{\dot{y}},{\dot{\psi }},\tau _\omega ) \end{array}\right. } \end{aligned}$$
(18)

presents a generalized disturbances state system, and the generalized system state is presented below

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{x}}_1=x_2\\ {\dot{x}}_2=x_3+b_xU_x \\ {\dot{x}}_3={\dot{f}}_x\\ {\dot{x}}_4=\ddot{f}_x \\ {\dot{x}}_5=f^{(3)}_x \end{array}\right. } \end{aligned}$$
(19)

Since, the proposed strategy to deal with the disturbances d is employed to design the following generalized ESO as

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{z}}_1=z_2-l_1e_1\\ {\dot{z}}_2=z_3-l_2e_1+b_1U_1 \\ {\dot{z}}_3=z_4-l_3e_1\\ {\dot{z}}_4=-\omega _d^2z_3+z_5-l_4e_1\\ {\dot{z}}_5=-l_5e_1 \end{array}\right. } \end{aligned}$$
(20)

In an attempt to simplify the tuning of the parameters of the Linear ESO and the controller, they were expressed in function of \(\omega _0\) and \(\omega _c\) so as the tuning is reduced from 7 to 2 parameters as

$$\begin{aligned} {\left\{ \begin{array}{ll} l_1=5 \omega _0\\ l_2=10\omega _0^2\\ l_3=10\omega _0^3\\ l_4=5\omega _0^4\\ l_5=\omega _0^5\\ K_p=\omega _c^2\\ K_d=2\omega _c \end{array}\right. } \end{aligned}$$
(21)

where \(\omega _0\) is the observer bandwidth and \(\omega _c\) is the closed-loop bandwidth. And the ESO and controller gains are set as Eq. (21) to ensure the Hurwitz stability [34, 35].

4.2.2 Noise cancellation ESO

In practice, sensors noise is inevitable. Since the estimated noisy state will be used in the feedback and compensation loop, it risks to be amplified by the GESO’s gains and may even affect the closed-loop stability in case of large noisy signals. By considering the measurement as noisy the system (14) becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{x}}_1=x_2\\ {\dot{x}}_2=f({\dot{x}},{\dot{y}},{\dot{\psi }},\tau _\omega )+\frac{1}{b_x}\tau _x\\ y=x_1+N \end{array}\right. } \end{aligned}$$
(22)

The dynamics of the estimation error are expressed as

$$\begin{aligned} e^{(5)}+l_1 e^{(4)}+l_2 e^{(3)}+l_3 e^{(3)}+l_4\ddot{e}+l_4 {\dot{e}}+l_5e=f(.)^{(3)} \end{aligned}$$
(23)

with

$$\begin{aligned} e=y-z_1=y-{\hat{x}}_1 \end{aligned}$$
(24)

Since \(y=x_1+N\) so

$$\begin{aligned} e=x_1+N-{\hat{x}}_1=\epsilon +N \end{aligned}$$
(25)

Then, the new dynamics of the estimation error can be expressed as

$$\begin{aligned}&\epsilon ^{(5)}+l_1 \epsilon ^{(4)}+l_2 \epsilon ^{(3)}+l_3 \epsilon ^{(3)}+l_4\ddot{\epsilon }+l_4{\dot{\epsilon }}+l_5\epsilon =f(.)^{(3)}-(N^{(5)}+l_1 N^{(4)}+l_2 N^{(3)}\nonumber \\&\quad +l_3 N^{(3)}+l_4\ddot{N}+l_4 {\dot{N}}+l_5N) \end{aligned}$$
(26)

Equation (26) demonstrates the proportional affectation of the noise with gains of the GESO, which will amplify them. In order to overcome this problem an integral extended state \(x_N\) is added to the state space as follows:

$$\begin{aligned} x_N=\int _{0}^{t} y(\tau )d\tau =\int _{0}^{t}x(\tau )+N(\tau )d\tau \end{aligned}$$
(27)

So the final space of the state representation can be expressed as

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{x}}_N=x_1+N\\ {\dot{x}}_1=x_2\\ {\dot{x}}_2=x_3+b_xU_x\\ {\dot{x}}_3=x_4\\ {\dot{x}}_4=x_5 \end{array}\right. } \end{aligned}$$
(28)

The new GESO (NGESO) is now expressed as

$$\begin{aligned}&{\left\{ \begin{array}{ll} {\dot{z}}_N=z_1-l_0\xi \\ {\dot{z}}_1=z_2-l_1\xi \\ {\dot{z}}_2=z_3-l_2\xi +b_xU_x\\ {\dot{z}}_3=z_4-l_3\xi \\ {\dot{z}}_4=-\omega _d^2+z_5-l_4\xi \\ {\dot{z}}_5=-l_5\xi \end{array}\right. } \end{aligned}$$
(29)
$$\begin{aligned}&\xi ^{(5)}+l_1 \xi ^{(4)}+l_2 \xi ^{(3)}+l_3 \xi ^{(3)}+l_4\ddot{\xi }+l_4 {\dot{\xi }}+l_5\xi =f(.)^{(3)}-N^{(5)} \end{aligned}$$
(30)

Equation (29) shows that noise dynamics are no longer amplified by the gains of the GESO \(l_1-l_5\) as was the case in Eq. (26).

4.2.3 Control design

The primary control law is given by a simple PD as follows:

$$\begin{aligned} U_0=k_p e+k_d {\dot{e}} \end{aligned}$$
(31)

Then, after canceling the estimated total disturbances, the final control law illustrated in Fig. 2 can be described by the following equation.

$$\begin{aligned} U_{x}=\dfrac{u_{0}-{\hat{f}}}{b_{1}} \end{aligned}$$
(32)

By replacing Eq. (32) in (14), we obtain

$$\begin{aligned} \ddot{x}=f+b_{1}\dfrac{u_{0}-{\hat{f}}}{b_{1}}=u_{0} \end{aligned}$$
(33)

Finally, the system can be expressed as the following disturbance-free system.

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{x}}_1=x_2\\ {\dot{x}}_2=u_0\\ y=x_1 \end{array}\right. } \end{aligned}$$
(34)
Fig. 2
figure 2

Improved ADRC control scheme

Full size image

5 Simulations results

5.1 Effectiveness of the proposed generalized ESO

In order to verify the effectiveness and robustness of the proposed approaches in the USV trajectory tracking control problem, numerical simulations are carried out on USV 3 DOF (surge, sway, and yaw) to analyze the disturbance rejection performance of LESO-based ADRC (indexed as \(ADRC_1\)), the proposed polynomial or higher-order ESO-based ADRC (indexed as \(ADRC_2\)), and the proposed generalized (polynomial + harmonic) ESO-based ADRC (indexed as \(ADRC_3\)). The vehicle is set to track a desired narrow channel curve [36], as illustrated in Fig. 3. The USV parameters are listed in Table 2.

Table 2 USV parameters [37]
Full size table

The initial conditions values are set all to zero, and the desired sinusoidal trajectory is defined as

$$\begin{aligned} {\left\{ \begin{array}{ll} {x}_d=0.5t\\ {y}_d=10\cos (0.01t)\\ {\psi }_d=10\sin (0.01) \end{array}\right. } \end{aligned}$$
(35)

The simulations are performed with the following conditions:

  • Uncertain parameters: we introduced parameter changes as \(m=m+\delta m = m+ 0.2m\)

  • The external disturbances d(t) takes the fast time-varying type specified as d.

$$\begin{aligned} d=\begin{pmatrix} d_x\\ d_y\\ d_\psi \\ \end{pmatrix}=\begin{pmatrix} 3sin(t)\\ 3sin(t-\frac{\pi }{3})\\ sin(t)+3 \end{pmatrix} \end{aligned}$$
(36)

The proposed \(ADRC_2\) and \(ADRC_3\) based on GESO and HESO, respectively, are compared with a standard \(ADRC_1\) based on the usual LESO method under the same conditions and with the same parameters. The obtained results are presented in the figures below.

The numerical simulation demonstrates the effectiveness of the proposed control scheme for USV trajectory tracking. As shown in Fig. 3, the vessel can track the desired trajectory with high accuracy. Higher precision has been noticed for \(ADRC_2\) approach comparing to the conventional \(ADRC_1\). However, \(ADRC_3\) has shown the best performances. Figures 4, 5, 6, and 7 illustrate the tracking performances and errors of the proposed controllers compared to the conventional ADRC.

Figure 4 shows the vessel positions with respect to time, the desired (blue-dashed line), and tracked positions as \(ADRC_1\) (blue line), \(ADRC_2\) (green line), and \(ADRC_3\) (red line). From this figure, the superiority of \(ADRC_3\) and \(ADRC_2\) over \(ADRC_1\) in tracking the desired trajectory is noticed. Then, the tracking errors are shown in the figures below.

Figures 5, 6, and 7 and Table 3 present the tracking errors in 3 directions, comparing to the classical ADRC, and the GESO-based control (\(ADRC_2\)) has shown better ability of disturbance rejection than the conventional one (\(ADRC_1\)). However, the HESO-based \(ADRC_3\) has offered better disturbances rejection over the previous two ADRCs, due to the better sinusoidal disturbances estimation ensured by the HESO. Figure 8 shows control inputs or the torques with respect to time, and it can be seen that for the almost same control inputs, the proposed improved ADRCs have obviously offered better tracking performance than that of the conventional \(ADRC_1\).

Fig. 3
figure 3

Trajectory tracking

Full size image
Fig. 4
figure 4

Position tracking

Full size image
Fig. 5
figure 5

Surge tracking errors

Full size image
Fig. 6
figure 6

Sway tracking errors

Full size image
Fig. 7
figure 7

Yaw tracking errors

Full size image
Fig. 8
figure 8

Control input \(\tau _x\), \(\tau _y\), and \(\tau _\omega \psi\)

Full size image
Table 3 Comparison of periodic tracking error between conventional and proposed ADRC
Full size table

The increasing of the number of states to 5 in the generalized ESO in \(ADRC_2\) has provided better estimation of the total disturbances compared to the conventional ESO in \(ADRC_1\), by estimating more dynamics of the function f which allowed better reconstruction of the disturbance values and then canceling them in real time from the primary control signal. In addition to that the improved ESO of \(ADRC_3\) has provided more improvement by including a partial information about the disturbance form (periodic). As a result to the high quality of disturbance estimation, better tracking performances are noted for \(ADRC_3\) and \(ADRC_2\) over \(ADRC_1\) where the periodic tracking errors caused by the fast-sinusoidal disturbance has been significantly decreased as illustrated in Figs. 5, 6, and 7.

5.2 Effectiveness of noise reducer ESO

In order to verify the effectiveness of the proposed noise reducing approach a comparison between \(ADRC_3\) from the previous section and \(ADRC_{3N}\) has been established after including the noise reducer state. Numerical simulations are carried out on USV one DOF.

Fig. 9
figure 9

Position estimation (state \(x_1\)) with \(ADRC_3\) and \(ADRC_3N\)

Full size image
Fig. 10
figure 10

Velocity estimation (state \(x_{2}\)) with \(ADRC_3\) and \(ADRC_{3N}\)

Full size image
Fig. 11
figure 11

Control inputs

Full size image

The presented results showed in Figs. 9 and 10 show the effects of noisy measurements on the state variables \(x_1\) and \(x_2\) estimation. Those effects have been obviously reduced by \(ADRC_{3N}\) where an added noise cancellation technique has been employed in the design of the ESO. The control signal in Fig. 11 profile follows the same form as the state variables estimations.

6 Conclusion

In this work, a new improved ADRC is proposed in order to cope with some particular problems that can possibly reduce the robustness and efficiency of conventional ADRC controllers, such as the presence of time-varying disturbances, like polynomial type or harmonic disturbances, and sensor noise.

The proposed solution employs a noise reduction approach; consequently, it limits the risk of destabilizing the ESO by amplifying the measurement noise with the observer's gains. The considered method offers as well a real-time compensation of the total disturbance and reduces the problem of controlling a nonlinear, uncertain, and disturbed time-varying system into a simpler control of a linear system. Moreover, two improved ESOs have been proposed in order to cope with complex time varying and periodic disturbances; which offered very satisfactory results in the tracking precision and disturbances rejection.

Numerical simulations have been carried out and the obtained results confirm the effectiveness of the proposed approach in handling complex disturbances and reducing the noise measurements effects, which has improved the disturbance estimation quality and accurate noise-free state estimation.

In spite of the satisfactory results showed in simulations results, the proposed methods meet a limitation linked to the hypothetical assumption that in order to encounter the best performances of the proposed GESO and HESO, the considered disturbance function has to be approximated by a polynomial form (periodic in case of HESO), which might not be always the case in reality, since there exist signals that does not follow this condition.

As a future perspective of this research, experimental validation of the proposed approach is intended to be done as well as

  • Implementing our improved ADRC in a real USV and comparing the experimental results to some related works.

  • Exploiting optimization algorithms in order to have the best possible tuning of ADRC parameters.

  • Considering more amelioration to the Extended State Observer since it is the vital part of the ADRC.

  • Formation control or cooperative control of multi-USV based on ADRC