Introduction

Electrolyte solutions are present in many natural and industrial processes. Water treatment, desalinization of water, extraction of petroleum from under the sea bed, precipitation, and crystallization of minerals in geothermal fluids are only a few examples of processes in which the knowledge of the thermodynamic properties of electrolyte solutions is essential. In view of this, it is fundamental that chemists and chemical engineers become familiar not only with the basic concepts of the thermodynamics of electrolyte solutions, but also with the limitations and achievements of the most common ion activity models.

A quick check in the literature [1,2,3,4] shows an increasing number of theoretical and experimental works about the physicochemical properties of electrolyte solutions from the 1950s. By-mid 1970 and 1980, one observes the development of more sophisticated treatments (e.g., Pitzer equations [5, 6], ELECNRTL model [7,8,9], and Meissner model [10,11,12]) of the ion-ion and ion-solvent interactions, which allowed estimating mean activity coefficients in multicomponent solutions of high ionic strength. Later, other relevant activity models for electrolyte solutions were also proposed, such as the mixed solvent electrolyte model (MSE) [13,14,15] and the extended UNIQUAC model [16,17,18].

However, despite the observed conceptual evolution, the topic of thermodynamics of electrolyte solutions in undergraduate and graduate textbooks is still superficial and sometimes misleading. One of the reasons for this scenario is the lack of mathematical formalism in the description of the ion–ion and ion-solvent interactions. Moreover, very little has been said about how P.J.W. Debye (1884–1966) and E.A.A.J. Hückel (1896–1980) developed the ionic cloud theory [19,20,21] and how the famous Debye-Hückel equation influenced the development of other well-known ion activity models [22].

Hence, this work aims to examine some aspects of the ionic cloud theory that are usually not discussed in graduate and undergraduate courses of physical chemistry. In particular, the strategy adopted by Debye and Hückel to calculate the time-averaged spatial distribution of the charge density around a reference ion is presented by underlining the main conceptual assumptions and mathematical steps involved. Also, the success and deficiencies of the Debye-Hückel equation in the estimation of the mean activity coefficients are discussed, as well as the most known extensions of the Debye-Hückel equation. Although the content of this work is tailored to the teaching of thermodynamics of electrolytes in undergraduate and graduate courses, it may also be a helpful guide to choosing the most appropriate ion activity model in speciation software.

Non-ideality of electrolyte solutions

From the microscopic point of view, the structure of electrolyte solutions is quite different from that observed for molecular solutions. In contrast with the latter, where dipole–dipole and dispersion forces are the predominant intermolecular interactions, in an electrolyte solution, the most noticeable intermolecular interactions are the ion–ion and ion-dipole forces. Thanks to the ion–ion and ion-dipole forces, electrolyte solutions show deviations from the ideal behavior, even if they are very dilute. In other terms, electrolyte solutions are not ideal and, therefore, the relation

$$\begin{aligned} \mu _{\text{i}}\left( \hbox {ideal}\right) =\mu _{\text{i}}^{*}\left( \hbox {ideal}\right) +RT\ln \left( x_{\text{i}}\right)\quad {\text{i}}=1,\ldots ,{\text{j}}\,, \end{aligned}$$
(1)

does not hold, where \(\mu _{\text{i}}\) and \(\mu _{\text{i}}^{*}\) are respectively the chemical potential and the standardFootnote 1 chemical potential of the species i, R is the gas constant, T is the thermodynamic temperature, and \(x_{\text{i}}\) is the mole fraction of the species i.

To deal with the non-ideality of electrolyte solutions, one may follow the approach suggested by G.N. Lewis (1875–1946) in his seminal article “Outlines of a new system of thermodynamic chemistry” [23]. One introduces a correction factor \(f_{\text{i}}\) for the concentration and expresses the chemical potential \(\mu _{\text{i}}\) as

$$\begin{aligned} \mu _{\text{i}}\left( \hbox {real}\right) =\mu _{\text{i}}^{*}\left( \hbox {real}\right) +RT\ln \left( f_{\text{i}}x_{\text{i}}\right)\quad {\text{i}}=1,\ldots ,{\text{j}}\,, \end{aligned}$$
(2)

where \(f_{\text{i}}\) is the rational activity coefficient of the species i at the temperature and pressure of the solution. Moreover, by defining \(a_{\text{i}}=f_{\text{i}}x_{\text{i}}\), one has

$$\begin{aligned} \mu _{\text{i}}\left( \hbox {real}\right) =\mu _{\text{i}}^{*}\left( \hbox {real}\right) +RT\ln \left( a_{\text{i}}\right) \,, \end{aligned}$$
(3)

where \(a_{\text{i}}\) is the activity of the species i. Then, it is not difficult to see that \(a_{\text{i}}=x_{\text{i}}\), if and only if \(f_{\text{i}}=1\). In this case, the species i behaves ideally, and Eq. (2) reduces to Eq. (1).

For electrolyte solutions, the notion of ideality does not exist rigorously. However, one may consider a hypothetical electrolyte solution, where ions behave ideally and only dipole-dipole forces are in play. In this case, the ion valence \(z_{\text{i}}\) reduces to zero and \(f_{\text{i}}=1\) for all values of \(x_{\text{i}}\). Now, consider an imaginary process [24], where the ions of this hypothetical ideal solution are gradually charged through small increments of charge, so that at the final state each ion assumes a charge different from zero. Thus, the change of chemical potential for each ion i in this imaginary process is

$$\begin{aligned} \mu _{\text{i}}\left( \hbox {real}\right) -\mu _{\text{i}}\left( \hbox {ideal}\right) =RT\ln \left( f_{\text{i}}\right) \,, \end{aligned}$$
(4)

where one assumed that ions have the same standard states in ideal and real electrolyte solutions.

The quantity \(\mu _{\text{i}}\left( \hbox {real}\right) -\mu _{\text{i}}\left( \hbox {ideal}\right)\) is nothing else than the electrostatic energy \(W_{\text{i}}\) necessary to assemble a conductor i into a group of charges from a reference potential conveniently set as equal to zero [25]. By recalling that \(W_{\text{i}}=Q_{\text{i}}\varphi _{\Sigma }/2\), where \(Q_{\text{i}}\) is the charge on the conductor i and \(\varphi _{\Sigma }\) is the electric potential due to the other conductors of the group of charges, the difference \(\mu _{\text{i}}\left( \hbox {real}\right) -\mu _{\text{i}}\left( \hbox {ideal}\right)\) equals to

$$\begin{aligned} \mu _{\text{i}}\left( \hbox {real}\right) -\mu _{\text{i}}\left( \hbox {ideal}\right) =\dfrac{N_{\text{A}}z_{\text{i}}e_{\text{o}}}{2}\varphi _{\Sigma }\,, \end{aligned}$$
(5)

where \(N_{\text{A}}\) is the Avogadro constant and \(e_{\text{o}}\) is the elementary charge. Therefore, by combining Eqs. (4) and (5), one has

$$\begin{aligned} \ln \left( f_{\text{i}}\right) =\dfrac{N_{\text{A}}z_{\text{i}}e_{\text{o}}}{2RT}\varphi _{\Sigma }\,, \end{aligned}$$
(6)

which shows that the activity coefficient \(f_{\text{i}}\) is closely related to the electric potential acting on the ion i due to the other ions in solution.

Although Eq. (6) provides a link between the electric potential \(\varphi _{\Sigma }\) and the activity coefficient \(f_{\text{i}}\), it is still not practical. First, since the principle of electroneutrality prevents varying any property of a cation \(\mathrm {M}^{z+}\) while the properties of an anion \(\mathrm {X}^{z-}\) are held fixed, neither \(f_{\mathrm {M}^{z+}}\) nor \(f_{\mathrm {X}^{z-}}\) are measurable. Second, it remains to calculate \(\varphi _{\Sigma }\) and how it depends on the ions distribution in solution.

Concentration scale and activity coefficient

In the previous section, the chemical potential was given in terms of the mole fraction \(x_{\text{i}}\) and the rational activity coefficient \(f_{\text{i}}\). Similarly, one could also write the chemical potential of the species i in terms of the molality \(m_{\text{i}}\). In this case, one has

$$\begin{aligned} \mu _{\text{i}}\left( \hbox {real}\right) =\mu _{\text{i}}^{*}\left( \hbox {real}\right) +RT\ln \left( \gamma _{\text{i}}\dfrac{m_{\text{i}}}{m^{\text{o}}}\right) \quad {\text{i}}=1,\ldots ,{\text{j}}\,, \end{aligned}$$
(7)

where \(\gamma _{\text{i}}\) is the molal activity coefficient, \(m^{\text{o}}=1.0\,\mathrm {mol}\,\mathrm{kg}^{-1}\), and \(\mu _{\text{i}}^{*}\) refers to the chemical potential of a hypothetical ideal solution at \(m_{\text{i}}=1.0\,\mathrm{mol}\,\mathrm{kg}^{-1}\) and at the system temperature and pressure. In turn, if one writes the chemical potential in terms of the molarity \(c_{\text{i}}\), it follows that

$$\begin{aligned} \mu _{\text{i}}\left( \hbox {real}\right) =\mu _{\text{i}}^{*}\left( \hbox {real}\right) +RT\ln \left( y_{\text{i}}\dfrac{c_{\text{i}}}{c^{\text{o}}}\right) \quad {\text{i}}=1,\ldots ,{\text{j}}\,, \end{aligned}$$
(8)

where \(y_{\text{i}}\) is the molar activity coefficient, \(c^{\text{o}}=1.0\,\mathrm {mol}\,\mathrm{L}^{-1}\), and \(\mu _{\text{i}}^{*}\) refers to the chemical potential of a hypothetical ideal solution at \(c_{\text{i}}=1.0\,\mathrm {mol}\,\mathrm{L}^{-1}\) and at the system temperature and pressure.

Apparently, the above definitions seem innocuous and without any physical motivation. However, one should remember that the standard chemical potential of ions and the experimental activity data for electrolytes are frequently reported on the molal scale. On the other hand, ion activity models usually give quantities on the mole fraction scale. Therefore, for the sake of comparison of experimental and theoretical data, it is frequently necessary to convert activity coefficients from one concentration scale to another. This aspect will be exploited later.

Electroneutrality and mean activity coefficient

Electroneutrality is required in all chemical systems. More than stating that a chemical system must neither possess an excess of cation nor an excess of anions, electroneutrality imposes restrictions on the physicochemical properties of electrolyte solutions: for example, cations and anions do not exist independently of each other and, consequently, experimental values of physicochemical properties refer to the electrolytes as a whole rather than individual ions [1].

To address this issue, consider the complete dissociation of an electrolyte in water that leads to the formation of \(\nu _{+}\) moles of cations \(\mathrm {M}^{z+}\) and \(\nu _{-}\) moles of anions \(\mathrm {X}^{z-}\). The aim is to calculate the change of Gibbs energy G of the electrolyte solution from the individual contributions of the ions at pressure p and temperature T. By using the definition \(\mu _{\text{i}}=\left( \partial G/\partial n_{\text{i}}\right) _{p,T,n_{{\text{i}}\ne {\text{j}}}}\) and Eq. (2), where \(n_{\text{i}}\) is the amount of substance of the species i, one obtains

$$\begin{aligned} \nu _{+}\mu _{+}= & {} \nu _{+}\mu ^{*}_{+}+\nu _{+}RT\ln \left( f_{+}x_{+}\right) ,\end{aligned}$$
(9)
$$\begin{aligned} \nu _{-}\mu _{-}= & {} \nu _{-}\mu ^{*}_{-}+\nu _{-}RT\ln \left( f_{-}x_{-}\right) , \end{aligned}$$
(10)

where the indexes \(+\) and − represent the cation and anion, respectively. Then, by adding Eqs. (9) and (10) and dividing the resulting equation by \(\nu =\nu _{+}+\nu _{-}\), one has

$$\begin{aligned} \mu _{\pm }=\mu ^{*}_{\pm }+RT\ln \left( f_{\pm }x_{\pm }\right) , \end{aligned}$$
(11)

where

$$\begin{aligned} \mu _{\pm }=\dfrac{\left( \nu _{+}\mu _{+}+\nu _{-}\mu _{-}\right) }{\nu }&\quad \mu _{\pm }^{*}=\dfrac{\left( \nu _{+}\mu _{+}^{*}+\nu _{-}\mu _{-}^{*}\right) }{\nu }\,,\\ x_{\pm }=\left( x_{+}^{\nu _{+}}x_{-}^{\nu _{-}}\right) ^{1/\nu }&\quad f_{\pm }=\left( f_{+}^{\nu _{+}}f_{-}^{\nu _{-}}\right) ^{1/\nu }\,,\nonumber \end{aligned}$$
(12)

and \(f_{\pm }\) is the rational mean activity coefficient.

Note that \(\mu _{\pm }\), \(x_{\pm }\), and \(f_{\pm }\) represent average quantities. Particularly, \(\mu _{\pm }\) is an arithmetic average since the partial molar Gibbs energy is an additive property. On the other hand, \(f_{\pm }\) and \(x_{\pm }\) are geometric averages as the partial molar Gibbs energy has a multiplicative dependence on the activity coefficient and the mole fraction.

Foundations of the ionic cloud theory

Consider an aqueous solution of a single true symmetrical electrolyte (formerly known as strong electrolyte), so that only ions with the same valence \(z_{\text{i}}\) and water molecules are present. Also, assume that the electrolyte solution is stationary, no external forces act on the solution, and the ions are point charges immersed in the solvent. If one takes one of these ions as a reference species, the electrolyte solution may be represented as a reference ion j spherically surrounded by a charge density \(\rho\) due to the other ions. To complete the problem formulation, consider that the solvent is a linear dielectric material of relative permittivity \(\epsilon _{\text{W}}\) and the electric field \({\mathbf {E}}\) is irrotational. In this case, time variations of the electric current are negligible, and the electric field is given by the gradient of the electric potential,

$$\begin{aligned} {\mathbf {E}}=-\nabla \varphi _{\text{total}}\,, \end{aligned}$$
(13)

where \(\varphi _{\text{total}}\) is the electric potential due to the reference ion j and all remaining ions in solution. Then, according to the Gauss’ law, the charge density \(\rho\) within an arbitrary volume element is related to the net electric flux by

$$\begin{aligned} \mathrm {div}\left( {\mathbf {E}}\right) =\dfrac{4\pi \rho }{\epsilon _{\text{o}}\epsilon _{\text{W}}}\,. \end{aligned}$$
(14)
Fig. 1
figure 1

From the microscopic point of view, an electrolyte solution consists of ions and water molecules, where only ion–ion and ion-dipole forces are in play. Alternatively, an electrolyte solution may be represented as a dielectric continuum of relative permittivity \(\epsilon _{\text{W}}\), where ions regarded as point charges are immersed. The gray shading shows how the charge density is spread on the solution. The stronger the gray shading is, the larger the charge density

Full size image

In Fig. 1, the arrangement of ions around the reference species is known as the ionic cloud and includes both positive and negative ions. In fact, the ionic cloud formed around the reference ion is not a long-term arrangement, but rather a structure that is constantly formed and disrupted because of the thermal and electrostatic forces acting on the ions.

Another characteristic of the ionic cloud is that the ions are not concentrated in a specific region, but rather they spread out in the solution. For a positive reference ion, as considered in Fig. 1, the largest concentration of anions is on average adjacent to the reference ion, where the attractive electrostatic forces are most capable of overcoming the thermal forces. On the other hand, as the radial distance from the reference species increases, the attractive electrostatic forces become weaker, and the thermal forces prevail. As a consequence, the concentration of anions in the outskirts of the reference ion is on average low.

Alternatively, Eq. (14) may be rewritten as

$$\begin{aligned} \nabla ^{2}\varphi _{\text{total}}=-\dfrac{4\pi \rho }{\epsilon _{\text{o}}\epsilon _{\text{W}}}\,, \end{aligned}$$
(15)

that in spherical coordinates becomes

$$\begin{aligned} \dfrac{1}{r^{2}}\dfrac{\text{d}}{\text{d}r}\left( r^{2}\dfrac{{\text{d}}\varphi _{\text{total}}}{\text{d}r}\right) =&-\dfrac{4\pi }{\epsilon _{\text{o}}\epsilon _{\text{W}}}\rho \,,\\ =&-\dfrac{4\pi }{\epsilon _{\text{o}}\epsilon _{\text{W}}}{\displaystyle \sum _{{\rm i}=1}^{\rm j}}\varrho _{\text{i}}z_{\text{i}}e_{\text{o}}\,,\nonumber \end{aligned}$$
(16)

where \(\varrho _{\text{i}}\) is the number density of the ion i. Note that \(\varphi _{\text{total}}\) and \(\varrho _{\text{i}}\) only depend on the radial distance r because of the spherical symmetry of the charges distribution around the reference ion. Therefore, the ionic cloud reduces to an infinite set of concentric spherical Gaussian surfaces (Fig. 2), such that each Gaussian surface has a well-defined number density, electric potential, and potential energy. Because of this, if one assumes that at the temperature T all Gaussian surfaces are in thermal equilibrium with each other, then the ratio between the number density \(\varrho _{\text{i}}\) at the distance r and the number density \(\varrho _{\text{i}}^{\infty }\) at the bulk solution (\(r\rightarrow\infty\)) is constant and given by the Boltzmann factor [26, 27],

$$\begin{aligned} \dfrac{\varrho _{\text{i}}}{\varrho _{\text{i}}^{\infty }}=\exp \left( \dfrac{-z_{\text{i}}e_{\text{o}}\varphi _{\text{total}}}{k_{\text{B}}T}\right) \,, \end{aligned}$$
(17)

where \(k_{\text{B}}\) is the Boltzmann constant. If the electrostatic forces between the ions i at the distance r and the reference ion are predominantly attractive, then \(\varphi _{\text{total}}<0\) and \(\varrho _{\text{i}}>\varrho _{\text{i}}^{\infty }\). Conversely, if the electrostatic forces between the ions i at the distance r and the reference ion are predominantly repulsive, then \(\varphi _{\text{total}}>0\) and \(\varrho _{\text{i}}<\varrho _{\text{i}}^{\infty }\).

Fig. 2
figure 2

Representation of the ionic cloud in terms of spherical Gaussian surfaces of thickness dr. Each Gaussian surface is characterized by a well-defined number density, electric potential, and potential energy

Full size image

By replacing Eq. (17) into Eq. (16), one obtains

$$\begin{aligned} \dfrac{1}{r^{2}}\dfrac{\text{d}}{\text{d}r}\left( r^{2}\dfrac{{\text d}\varphi _{\text{total}}}{\text{d}r}\right) ={\displaystyle -\dfrac{4\pi }{\epsilon _{\text{o}}\epsilon _{\text{W}}}\sum _{\text{i}=1}^{\text{j}}}\varrho _{\text{i}}^{\infty }z_{\text{i}}e_{\text{o}}\exp \left( \dfrac{-z_{\text{i}}e_{\text{o}}\varphi _{\text{total}}}{k_{\text{B}}T}\right) \,. \end{aligned}$$
(18)

To make Eq. (18) simpler, one expands the exponential term in a Taylor series,

$$\begin{aligned}&\exp \left( \dfrac{-z_{\text{i}}e_{\text{o}}\varphi _{\text{total}}}{k_{\text{B}}T}\right) \nonumber \\&\quad =1-\dfrac{z_{\text{i}}e_{\text{o}}\varphi _{\text{total}}}{k_{\text{B}}T}+\dfrac{1}{2!}\left( \dfrac{-z_{\text{i}}e_{\text{o}}\varphi _{\text{total}}}{k_{\text{B}}T}\right) ^{2}+\ldots \,, \end{aligned}$$
(19)

and restricts the analysis to those electrolyte solutions in which the electric potential energy \(z_{\text{i}}e_{\text{o}}\varphi _{\text{total}}\) is much smaller than the thermal energy \(k_{\text{B}}T\). This is only true for very dilute electrolyte solutions, where ions move randomly and independently of each other. In this case, the power series (19) may be truncated at the second term and Eq. (18) becomes:

$$\begin{aligned} \dfrac{1}{r^{2}}\dfrac{\text{d}}{\text{d}r}\left( r^{2}\dfrac{\text{d}\varphi _{\text{total}}}{\text{d}r}\right) =-\dfrac{4\pi }{\epsilon _{\text{o}}\epsilon _{\text{W}}}\left( {\displaystyle \sum _{{\rm i}=1}^{\rm j}}\varrho _{\text{i}}^{\infty }z_{\text{i}}e_{\text{o}}-\dfrac{\varphi _{\text{total}}}{k_{\text{B}}T}{\displaystyle \sum _{{\rm i}=1}^{\rm j}}\varrho _{\text{i}}^{\infty }z_{\text{i}}^{2}e_{\text{o}}^{2}\right) \,. \end{aligned}$$
(20)

The first term on the right-hand side is just the charge density \(\rho _{\infty }\) at the bulk solution and is equal to zero because of the solution electroneutrality. Therefore, one finally has

$$\begin{aligned} \dfrac{1}{r^{2}}\dfrac{\text{d}}{\text{d}r}\left( r^{2}\dfrac{\text{d} \varphi _{\text{total}}}{\text{d}r}\right) =\dfrac{4\pi \varphi _{\text{total}}}{\epsilon _{\text{o}}\epsilon _{\text{W}} k_{\text{B}}T}{\displaystyle \sum _{{\rm i}=1}^{\rm j}}\varrho _{\text{i}}^{\infty }z_{\text{i}}^{2}e_{\text{o}}^{2}\,, \end{aligned}$$
(21)

which is the linearized Poisson-Boltzmann equation.

To solve Eq. (21), Debye and Hückel [19, 20] imposed the following boundary conditions onto the total electric potential,

$$\begin{aligned} \lim _{r\rightarrow \infty }\varphi _{\text{total}}\left( r\right) =0\quad \varphi _{\text{total}}\left( 0\right) =\dfrac{z_{\text{j}}e_{\text{o}}}{\epsilon _{\text{o}}\epsilon _{\text{W}} r}\,. \end{aligned}$$
(22)

The first boundary condition states that the electric potential disappears at the bulk solution, whereas the second boundary condition ensures that the reference ion located at \(r=0\) behaves as an isolated point charge. In this case, \(\varphi _{\text{total}}\left( 0\right) =\varphi _{\text{j}}\), where \(\varphi _{\text{j}}\) gives the electric potential at a distance r from the reference ion. Hence, the solutionFootnote 2 of Eq. (21) is

$$\begin{aligned} \varphi _{\text{total}}(r)=\dfrac{z_{\text{i}}e_{\text{o}}}{\epsilon _{\text{o}}\epsilon _{\text{W}} r}\exp \left( -\kappa r\right) \quad \kappa =\sqrt{\dfrac{4\pi }{\epsilon _{\text{o}}\epsilon _{\text{W}} k_{\text{B}}T}{\displaystyle \sum _{{\rm i}=1}^{\rm j}}\varrho _{\text{i}}^{\infty }z_{\text{i}}^{2}e_{\text{o}}^{2}}\,, \end{aligned}$$
(23)

which indicates that \(\varphi _{\text{total}}\) exponentially decays as the radial distance r increases.

In fact, the potential \(\varphi _{\text{total}}\left( r\right)\) found in Eq. (23) is the sum of the electric potential due to the reference ion at \(r=0\) and the electric potential due to those ions surrounding the reference species j (Fig. 3). Then, from the principle of superposition of electric potentials, one has

$$\begin{aligned} \varphi _{\Sigma }\left( r\right)&=\varphi _{\text{total}}\left( r\right) -\varphi _{\text{j}}\,,\\&=\dfrac{z_{\text{i}}e_{\text{o}}}{\epsilon _{\text{o}}\epsilon _{\text{W}} r}\exp \left( -\kappa r\right) -\dfrac{z_{\text{i}}e_{\text{o}}}{\epsilon _{\text{o}}\epsilon _{\text{W}} r}\,,\nonumber \\&=\dfrac{z_{\text{i}}e_{\text{o}}}{\epsilon _{\text{o}}\epsilon _{\text{W}} r}\left[ \exp \left( -\kappa r\right) -1\right] \,.\nonumber \end{aligned}$$
(24)

Equation (24) may be simplified, if one expands the exponential term in a Taylor series,

$$\begin{aligned} \exp \left( -\kappa r\right) =1-\kappa r+\dfrac{\left( \kappa r\right) ^{2}}{2!}+\ldots \,, \end{aligned}$$
(25)

and truncates the series at the second term as in Eq. (19). In view of this, one obtains

$$\begin{aligned} \varphi _{\Sigma }=-\dfrac{z_{\text{i}}e_{\text{o}}\kappa }{\epsilon _{\text{o}}\epsilon _{\text{W}}}\,, \end{aligned}$$
(26)

and, consequently, Eq. (6) becomes

$$\begin{aligned} \ln \left( f_{\text{i}}\right) =-\dfrac{N_{\text{A}}e_{\text{o}}^{2}z_{\text{i}}^{2}\kappa }{2RT\epsilon _{\text{o}}\epsilon _{\text{W}}}\,. \end{aligned}$$
(27)
Fig. 3
figure 3

Sketch of the principle of superposition of electric potentials. The total electric potential \(\varphi _{\text{total}}\) at a distance r from the reference ion is the sum of the electric potential \(\varphi _{\text{j}}\) due to the reference ion located at \(r=0\) and the electric potential \(\varphi _{\Sigma }\) due to those ions surrounding the species j

Full size image

Before proceeding with the analysis of Eq. (27), it is convenient to resume Eqs. (16) and (21) to better investigate the dimensions of the ionic cloud. By equalizing Eqs. (16) and (21) and making use of Eq. (23), one obtains

$$\begin{aligned} \rho =-\dfrac{z_{\text{i}}e_{\text{o}}\kappa ^{2}}{4\pi r}\exp \left( -\kappa r\right) \,, \end{aligned}$$
(28)

which may be integrated over the whole surface area of the ionic cloud to give the net charge \(Q_{\text{c}}\) enclosing the reference ion j,

$$\begin{aligned} Q_{\text{c}}=&\int _{0}^{\infty }4\pi \rho r^{2}\text{d}r\,,\nonumber \\ =&-\int _{0}^{\infty }z_{\text{i}}e_{\text{o}}\kappa ^{2}\exp \left( -\kappa r\right) r\text{d}r\,,\nonumber \\ =&-z_{\text{i}}e_{\text{o}}\,. \end{aligned}$$
(29)

Therefore, from Eq. (29), it follows that the net charge \(Q_{\text{c}}\) of the ionic cloud is equal, but of opposite sign to that of the reference ion. Moreover, if one analyzes the gradient \(\nabla {(4\pi \rho r^{2})}\), one may determine whether the charge is distributed on the ionic cloud. Precisely, one is interested in establishing a radial distance r, where the charge reaches a maximum. Mathematically, one has:

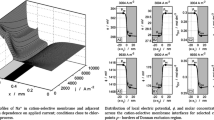
$$\begin{aligned}&\nabla (4\pi \rho r^{2})= 0\,,\nonumber\\& \nabla \left[ z_{\text{i}}e_{\text{o}}\kappa ^{2}r\exp \left( -\kappa r\right) \right] = 0\,,\nonumber \\& r= \dfrac{1}{\kappa }\,. \end{aligned}$$
(30)

The quantity \(\kappa ^{-1}\) is known as the Debye length and describes the effective radius of the ionic cloud. In other terms, \(\kappa ^{-1}\) gives the screening length over which the reference ion is neutralized by the net charge of the ionic cloud. Then, it is not surprising that the charge reaches a maximum at \(r=\kappa ^{-1}\), as shown in Fig. 4.

Fig. 4
figure 4

Gradient of charge versus the radial distance r. The calculations were performed for an electrolyte solution of ionic strength \(0.1\,\mathrm {mol}\,\mathrm {L}^{-1}\) and temperature equal to \(298.15\,\mathrm {K}\). The maximum of the gradient of charge is reached at \(r=1/\kappa\). Note that the Debye length (\(0.95\,\mathrm {nm}\)) does not depend on the ion valence

Full size image

So far, only solutions containing a single true symmetrical electrolyte have been considered in the calculations. Now, consider solutions containing more than one true electrolyte that may be symmetrical or unsymmetrical (for example, a mixture of \(\mathrm {KCl(aq)}\) and \(\mathrm {CaCl}_{2}\mathrm{(aq)}\)). To make the calculations of the mean activity coefficient valid for solutions containing either a single true symmetrical electrolyte or a mixture of true electrolytes, one follows the strategy adopted by G.N. Lewis and M. Randall [28] and introduces the ionic strength I of an electrolyte solution as

$$\begin{aligned} I={\displaystyle \sum _{{\rm i}=1}^{\rm j}}\dfrac{c_{\text{i}}z_{\text{i}}^{2}}{2}\,, \end{aligned}$$
(31)

where the product \(c_{\text{i}}z_{\text{i}}^{2}\) is divided by two because both cations and anions have been included in the calculation of I. By rewritting the number density at the bulk solution as \(\varrho _{\text{i}}^{\infty }=0.001N_{\text{A}}c_{\text{i}}\) and replacing this expression into the right-hand side of Eq. (23), it follows that

$$\begin{aligned} \kappa =B\sqrt{I}\quad B=\sqrt{\dfrac{8\pi N_{\text{A}}e_{\text{o}}^{2}}{1000\epsilon _{\text{o}}\epsilon _{\text{W}} k_{\text{B}}T}}\,. \end{aligned}$$
(32)

Precisely, Eqs. (23) and (32) indicate that at high ionic strengths the electric potential drops to its bulk value within a short radial distance, that is, the ionic cloud becomes more compact (Figs. 5, 6). The reason for this behavior is that the larger the ionic strength, the larger the charge density around the reference ion and, consequently, more ions are able to screen the charge of the reference species j.

Fig. 5
figure 5

Dependence of the total electric potential \(\varphi _{\text{total}}\) with the radial distance for solutions of different ionic strengths. Calculations performed for a monovalent cation and temperature equal to \(298.15\,\mathrm {K}\)

Full size image
Fig. 6
figure 6

Dependence of the radius of the ionic cloud with the ionic strength at \(298.15\,\mathrm {K}\). Note that the radius of the ionic cloud exponentially decreases as the ionic strength increases. The rough typical values of the ionic strength of some samples are also indicated in the figure

Full size image

Common ion activity models

Once the relation between the electric potential \(\varphi _{\Sigma }\) and the ion distribution has been established, one may exploit Eq. (12) to estimate the mean activity coefficient of an electrolyte. By applying the natural logarithm on both sides of \(f_{\pm }=\left( f_{+}^{\nu _{+}}f_{-}^{\nu _{-}}\right) ^{1/\nu }\) and using Eq. (27), one obtains

$$\begin{aligned} \ln \left( f_{\pm }\right) =\left( \dfrac{-N_{\text{A}}e_{\text{o}}^{2}\kappa }{2RT\epsilon _{\text{o}}\epsilon _{\text{W}}}\right) \left( \dfrac{\nu _{+}z_{+}^{2}+\nu _{-}z_{-}^{2}}{\nu }\right) \,. \end{aligned}$$
(33)

The Debye-Hückel equation

If the electroneutrality condition \(\nu _{+}\left| z_{+}\right| =\nu _{-}\left| z_{-}\right|\) of an electrolyte solution is exploited, Eq. (33) reduces to

$$\begin{aligned} \ln \left( f_{\pm }\right) =\left( \dfrac{-N_{\text{A}}e_{\text{o}}^{2}\kappa }{2RT\epsilon _{\text{o}}\epsilon _{\text{W}}}\right) \left| z_{+}z_{-}\right| \,. \end{aligned}$$
(34)

Then, since \(\kappa =B\sqrt{I}\), Eq. (34) assumes the final form of the Debye-Hückel equation:

$$\begin{aligned} \log \left( f_{\pm }\right) =-A\left| z_{+}z_{-}\right| \sqrt{I}\quad A=\dfrac{1}{2.303}\dfrac{N_{\text{A}}e_{\text{o}}^{2}B}{2RT\epsilon _{\text{o}}\epsilon _{\text{W}}}\,. \end{aligned}$$
(35)

Unfortunately, the theoretical results from Eq. (35) may not be directly compared with the experimental ones because the Debye-Hückel equation gives results on the mole fraction scale, while the experimental results are given on the molal scale. Hence, to make possible the comparison of results, one should convert the rational mean activity coefficient \(f_{\pm }\) into the mean activity coefficient \(\gamma _{\pm }\) via the following definition \(\gamma _{\pm }=x_{\text{W}}f_{\pm }\) [18, 29]. In this case, it follows that

$$\begin{aligned} \log \left( \gamma _{\pm }\right) =\log (x_{\text{W}})-A\left| z_{+}z_{-}\right| \sqrt{I}\,, \end{aligned}$$
(36)

where \(x_{\text{W}}\) is the mole fraction of water.

Figure 7 shows the comparison between the experimental and theoretical mean activity coefficients of three different electrolytes. According to Fig. 7, a better agreement between experimental and theoretical data is observed in the region of lower ionic strength, where the thermodynamic behavior of the electrolyte solutions approaches to the ideality, and the mean activity coefficients tend to the unity for all ions. In fact, as the electrolyte solution becomes more concentrated, one sees that Eq. (36) underpredicts the values of the mean activity coefficients and the deviations between the experimental and theoretical data increase substantially.

Fig. 7
figure 7

Comparison between the experimental mean activity coefficients and those predicted by the Debye-Hückel equation for 1:1, 1:2, and 1:3 electrolytes. Calculations performed at \(298.15\,\mathrm {K}\) and experimental data obtained from [3]

Full size image

Moreover, according to the Debye-Hückel equation, the mean activity coefficient decreases with the ionic strength, and this trend only depends on the ion valence. However, if one analyzes Fig. 8, one sees that the curves \(\gamma _{\pm }\) versus I depend on the particular electrolyte, and not only on \(z_{+}\) and \(z_{-}\). In other terms, different 1:1 electrolytes (this reasoning may be extended to 1:2, 2:1, 1:3, etc., electrolytes) have different thermodynamic behaviors in solution, which contradicts the predictions made from Eq. (36). Therefore, in view of these limitations, the Debye-Hückel equation must be revised and its range of applicability extended to more concentrated solutions.

Fig. 8
figure 8

Comparison between the experimental and theoretical mean activity coefficients for three different 1:1 electrolytes. The theoretical curve was predicted by the Debye-Hückel equation. Calculations performed at \(298.15\,\mathrm {K}\) and experimental data obtained from [3]

Full size image

The extended Debye-Hückel equation

One of the main assumptions of the ionic cloud theory is that ions are point charges. If this hypothesis is valid, then the mean radius of the ionic cloud remains negligible in dilute and concentrated solutions. Nevertheless, it was previously shown that the dimensions of the ionic cloud decrease as the solution becomes more concentrated. In addition, a quick calculation [26] shows that, for a \(1.0\,\mathrm {mol}\,\mathrm {L}^{-1}\) solution of a 1:1 electrolyte at \(298.15\, \mathrm {K}\), the ratio between the dimensions of the ionic cloud and the reference ion is about 3:1. Likewise, for a \(0.1\,\mathrm {mol}\,\mathrm {L}^{-1}\) solution of a 1:1 electrolyte at \(298.15\, \mathrm {K}\), the ratio between the dimensions of the ionic cloud and the reference ion is about 10:1. On the other hand, for a \(0.001\,\mathrm {mol}\,\mathrm {L}^{-1}\) solution of the same electrolyte, the ratio between the dimensions of the ionic cloud and the reference ion is about 100:1. These numbers reveal that the point charges assumption is reasonable only in dilute solutions, and the finite size of ions must be taken into account in calculating mean activity coefficients in non-dilute solutions.

By recalling Eq. (22), one sees that one of the boundary conditions used to solve the linearized Poisson-Boltzmann equation is the assumption that at \(r=0\) the reference ion behaves as an isolated point charge. Now, in view of the finite-size ion assumption, this boundary condition should be replaced by

$$\begin{aligned} {\left\{ \begin{array}{ll} r\le a &{} \varphi _{\text{total}}=\dfrac{z_{\text{j}}e_{\text{o}}}{\epsilon _{\text{o}}\epsilon _{\text{W}} a}\,,\\ \\ r> a &{} \varphi _{\text{total}}=\dfrac{z_{\text{j}}e_{\text{o}}}{\epsilon _{\text{o}}\epsilon _{\text{W}} r}\,, \end{array}\right. } \end{aligned}$$
(37)

where a is the mean distance of closest approach of the ions. Then, Eq. (37) merely states that, for \(r\le a\), \(\varphi _{\text{total}}\) is equal to the potential calculated at the mean distance of closest approach. In turn, for distances larger than a, the total electric potential reduces to the potential φj of the reference ion at a distance r.

Here, it is convenient to emphasize that a is not the radius of the reference ion, but rather the maximum distance from the center of the reference ion within which the center of no other ion can penetrate [24, 27]. As a fair estimation, the parameter a may be taken as the summation of the hydrated ionic radiiFootnote 3. However, ions are in constant motion, and sometimes they might collide with each other, so that their hydration shells are deformed (Fig. 9). As a consequence, the mean distance of closest approach is constantly changing, and the best way of dealing with this issue is to regard a as an empirical parameter. For example, for 1:1 and 1:3 electrolytes, a varies from \(4.0\,{{\AA }}\) to \(4.8\,{{\AA }}\), and from \(6.0\,{{\AA }}\) to \(7.0\,{{\AA }}\), respectively. In turn, for 1:2 electrolytes, a is about \(5.0\,{{\AA }}\).

Fig. 9
figure 9

a Summation of the hydrated ionic radius and b ions with deformed hydration shells. Usually, the mean distance of closest approach is larger than the summation of the crystallographic ionic radii, but less than the summation of the hydrated ionic radii

Full size image

The procedure to obtain an expression for the rational mean activity coefficient \(f_{\pm }\) as a function of the ionic strength and the mean distance of closest approach is similar to that used in Sect. “Foundations of the ionic cloud theory.” Initially, Eq. (21) is solved for the potential \(\varphi _{\text{total}}\) by considering that at the bulk of the electrolyte solution the electric potential is null. Next, the boundary conditions given by Eq. (37) are imposed onto the solution of the differencial equation. At the end, the solution of the linearized Poisson-Boltzmann equation is

$$\begin{aligned} \varphi _{\text{total}}=\dfrac{z_{\text{i}}e_{\text{o}}}{\epsilon _{\text{o}}\epsilon _{\text{W}} r}\dfrac{\exp \left( \kappa a\right) }{1+\kappa a}\exp \left( -\kappa r\right) \,. \end{aligned}$$
(38)

To complete the problem formulation, one should determine the electric potential \(\varphi _{\Sigma }\) through the expression \(\varphi _{\text{total}}=\varphi _{\text{j}}+\varphi _{\Sigma }\) and replace the result into Eq. (6). Then, by using the definition of \(f_{\pm }\), one obtains the extended Debye-Hückel equation,

$$\begin{aligned} \log \left( \gamma _{\pm }\right) =\log (x_{\text{W}})-\dfrac{A\left| z_{+}z_{-}\right| \sqrt{I}}{1+\kappa a}\,, \end{aligned}$$
(39)

which reduces to Eq. (36) when \(\kappa a\ll 1\), that is, when the radius of the ionic cloud becomes much larger than a. In short, both Eqs. (39) and (36) only account for the interionic forces, but in the extended Debye-Hückel equation the denominator shows how these forces are affected by the finite size of ions.

Fig. 10
figure 10

Comparison between the experimental mean activity coefficients and those predicted by the extended Debye-Hückel equation for four different electrolytes. Calculations performed at \(298.15\,\mathrm {K}\) and experimental data obtained from [3]

Full size image

Figure 10 shows the performance of the extended Debye-Hückel equation for four different electrolytes. From Fig. 10, one sees that Eq. (39) performs very well up to \(I=0.1\,\mathrm {mol}\,\mathrm {L}^{-1}\). However, despite the improvement, the extended form of the Debye-Hückel equation still cannot correctly predict the mean activity coefficients in more concentrated solutions, where solvation effects and ion pairing become relevant.

According to the Debye-Hückel equation and the extended Debye-Hückel equation, \(\gamma _{\pm }\) continually decreases as I increases. Nevertheless, experimentally one observes that \(\gamma _{\pm }\) decreases and then increases again with the ionic strength (Fig. 11). This change in trend is due to the variations in the number of solvent molecules present in the hydration shell of an ion as the solution becomes more concentrated [27, 30]. In an electrolyte solution, some of the solvent molecules are tightly bonded to the ions in the hydration shell, and others are still free and available to solvate ions that may eventually be added to the solution. As the concentration increases and more ions are added to the solution, the number of free solvent molecules decreases since part of them is used to solvate these ions. Therefore, the number of free solvent molecules drops and the activity of the electrolyte increases.

Fig. 11
figure 11

Experimental mean activity coefficients versus the ionic strength. Experimental data obtained from [27]

Full size image

Moreover, in concentrated solutions of unsymmetrical electrolytes, the probability that ions with opposite charges form ion pairs, e.g., \({\mathrm {CaHCO}_{3}}^{+}\left( \mathrm {aq}\right)\), \({\mathrm {FeSO}_{4}}^{+}\left( \mathrm {aq}\right)\), \(\mathrm {CoHPO4}^{+}\left( \mathrm {aq}\right)\), etc., is relatively high. According to Bjerrum’s ion association theory [31], ion pairs are formed whenever oppositely charged ions are within a critical distance of one another, and the electrical attraction energy of the two ions overcomes the thermal energies of the individual ions. Under such conditions, the ion pairs are sufficiently stable even after colliding with solvent molecules. Then, as the concentration increases, the probability that oppositely charged ions are close enough to each other to form ion pairs also rises.

In view of the above, if one wishes to deal with natural waters and other high-saline solutions, it is essential to look for extensions of the Debye-Hückel equation that encompass ion-solvent interactions as well as the formation of ion pairs. A comprehensive discussion of these extensions is found in Refs. [3, 6].

The Robinson-Stokes equation

Under high ionic strength conditions, the Debye-Hückel equation and the extended Debye-Hückel equation predict mean activity coefficients smaller than those experimentally observed. As previously discussed, these poor results are a consequence of the theoretical treatment used in Sects. “Foundations of the ionic cloud theory” and “The extended Debye-Hückel equation,” where only ion-ion interactions are taken into account.

To overcome these limitations and extend the applicability of Eqs. (36) and (39) to more concentrated solutions, one should include ion-solvent interactions or, more precisely, the effect of ionic solvation in the thermodynamic treatment of electrolyte solutions [24, 27, 30]. To this end, consider a solution composed of \(n_{\text{W}}\) moles of water and \(\nu\) moles of an electrolyte fully dissociated into \(\nu _{+}\) moles of cations \(\mathrm {M}^{z+}\) and \(\nu _{-}\) moles of anions \(\mathrm {X}^{z-}\). Then, the Gibbs energy of the electrolyte solution is given by,

$$\begin{aligned} G'=\left( n_{\text{W}}-n_{\text{H}}\right) \mu '_{\text{W}}+\nu _{+}\mu '_{+}+\nu _{-}\mu '_{-}\,, \end{aligned}$$
(40)

where \(\mu _{\text{W}}\) is the chemical potential of the solvent, \(n_{\text{H}}\) is the moles of water present in the hydration shell, \(n_{\text{W}}-n_{\text{H}}\) is the moles of free solvent, and the prime index stands for quantities calculated on the basis of solvated species.

In fact, the Gibbs energy G of the electrolyte solution remains the same whether ions are treated as solvated or unsolvated species. Likewise, the chemical potential of the solvent does not depend on whether the solute is a solvated species or an unsolvated one. This means that the Gibbs energy of the solution on the basis of unsolvated species,

$$\begin{aligned} G=n_{\text{W}}\mu _{\text{W}}+\nu _{+}\mu _{+}+\nu _{-}\mu _{-}\,, \end{aligned}$$
(41)

is equal to \(G'\) and \(\mu '_{\text{W}}=\mu _{\text{W}}\). Therefore, by introducing the respective expressions for the chemical potential and rearranging the expression in terms of the mean activity coefficient, one obtains

$$\begin{aligned}&\nu _{+}\left( \mu _{+}-\mu '^{*}_{+}\right) +\nu _{-}\left( \mu _{-}-\mu '^{*}_{-}\right) +n_{\text{H}}\mu _{\text{W}}\nonumber \\&\quad =-n_{\text{H}}RT\ln \left( a_{\text{W}}\right) +\nu RT\ln \left( f'_{\pm }\right) -\nu RT\ln \left( f_{\pm }\right) +\nonumber \\&\quad +\nu RT\ln \left( \dfrac{\nu +n_{\text{W}}}{\nu +n_{\text{W}}-n_{\text{H}}}\right) \,, \end{aligned}$$
(42)

where \(a_{\text{W}}\) is the activity of water and the following expressions were used:

$$\begin{aligned} x_{\text{i}}=\dfrac{\nu _{\text{i}}}{n_{\text{W}}+\nu }\quad x'_{\text{i}}=\dfrac{\nu _{\text{i}}}{n_{\text{W}}-n_{\text{H}}+\nu }\,. \end{aligned}$$
(43)

Equation (42) must be valid for both infinitely dilute and high-saline solutions. If the solution is infinitely dilute, then \(n_{\text{W}}\gg \nu\) and \(a_{\text{W}}\rightarrow 1\). Similarly, \(f_{\pm }\) and \(f'_{\pm }\) tend to unity and the left-hand side of Eq. (42) is equal to zero. Hence, it follows that:

$$\begin{aligned} \log \left( f_{\pm }\right) =\log \left( f'_{\pm }\right) +\dfrac{n_{\text{H}}}{\nu }\log \left( a_{\text{W}}\right) +\log \left( \dfrac{\nu +n_{\text{W}}}{\nu +n_{\text{W}}-n_{\text{H}}}\right) \,, \end{aligned}$$
(44)

where the first term on the right-hand side represents the interionic forces, whereas the second and third terms on the right-hand side account for the changes in the free energy due to the variation in the number of the free solvent molecules in solution and the formation of the hydration shell around the ions, respectively.

R.A. Robinson (1904–1979) and R.H. Stokes (1918–2016) [27] claimed that since a is the mean distance of closest approach of the ions in solution and its value is larger than the summation of the ionic crystallographic radius, it seems reasonable to believe that the extended Debye-Hückel equation applies to solvated species rather than unsolvated ions. As a consequence, the term \(\log \left( f'_{\pm }\right)\) is given by Eq. (39), so that Eq. (44) becomes

$$\begin{aligned}&\log \left( f_{\pm }\right) =-\dfrac{A\left| z_{+}z_{-}\right| \sqrt{I}}{1+\kappa a}+\dfrac{n_{\text{H}}}{\nu }\log \left( a_{\text{S}}\right) \nonumber \\&\quad +\log \left( \dfrac{\nu +n_{\text{S}}}{\nu +n_{\text{S}}-n_{\text{H}}}\right) \,, \end{aligned}$$
(45)

which is the Robinson-Stokes equation. At low concentrations, ion-ion interactions predominate, and \(f_{\pm }\) decreases with the increase of the ionic strength until reaching a minimum. However, at high concentrations, the terms due to the ion-solvent interactions are larger than the contribution from the interionic forces, and \(f_{\pm }\) starts increasing with I.

Notwithstanding the success of Eq. (45), Robinson and Stokes [30] observed that it is not practical. Equation (45) is a two-parameter equation that requires the knowledge of the activity of water and the number of solvent molecules in the hydration shell. In fact, the activity of water may be estimated from osmotic coefficients, but values for \(n_{\text{H}}\) are not so easy to be obtained. In view of this, they abandoned Eq. (45) in favor of a one-parameter equation that is as successful as the latter, although mathematically more complex. For further information about the work developed by Robinson and Stokes, please see Refs. [27, 30].

The Davies equation

The Davies equation [32] was originally proposed in 1938 as

$$\begin{aligned} \log \left( f_{\pm }\right) =-A\left| z_{+}z_{-}\right| \left( \dfrac{\sqrt{I}}{1+\sqrt{I}}-0.2I\right) \,, \end{aligned}$$
(46)

where 0.2I is an empirical parameter common for all ionic species that later was modified to 0.3I to give better results. Other values for this empirical parameter are also possible, but 0.3I is frequently recognized as the final value.

Note that the Davies equation does not require ion-specific parameters. In fact, the Davies equation shares the same idea as the Debye-Hückel equation, that is, only the ion valences are considered in the calculation of the mean activity coefficient. Consequently, all ions of the same valence behave identically. Also, the Davies equation ignores possible ion pairing in solution, which makes it unsuitable for unsymmetrical electrolytes (see Fig. 12). In general, the Davies equation performs very well for solutions of 1:1 electrolytes whose ionic strengths vary up to \(0.7\,\mathrm {mol}\,\mathrm {L}^{-1}\).

The Truesdell-Jones equation

Unlike Eq. (46), the Truesdell-Jones equation [33], also referred to as the WATEQ equation, is suitable for solutions of symmetrical and unsymmetrical electrolytes whose ionic strengths vary up to \(1.0\,\mathrm {mol}\,\mathrm {L}^{-1}\). Besides, the Truesdell-Jones equation accounts for ion-specific parameters \(\alpha _{\text{i}}\) and \(\beta _{\text{i}}\) whose values may be found in [33] as well as in the database of the speciation software PHREEQC [34].

Although the Truesdell-Jones equation makes reference to quantities of individual ions,

$$\begin{aligned} \log \left( f_{\text{i}}\right) =\dfrac{-Az_{\text{i}}^{2}\sqrt{I}}{1+\alpha _{\text{i}}\kappa }+\beta _{\text{i}}I\,, \end{aligned}$$
(47)

its final aim is to estimate the mean activity coefficient. In other terms, one estimates the activity coefficients of the cation and anion via Eq. (47) and later uses Eq. (12) to estimate \(f_{\pm }\).

If \(\beta _{\text{i}}=0\), Eq. (47) reduces to the extended Debye-Hückel equation. This suggests that the ion-specific parameter \(\alpha _{\text{i}}\) is somehow related to the hydrated ionic radius. On the other hand, if the first term on the right-hand side of Eq. (47) is neglected, one obtains the Setschenow equation, which is valid for uncharged species,

$$\begin{aligned} \log \left( f_{\text{i}}\right) =\beta _{\text{i}}I\,, \end{aligned}$$
(48)

where \(\beta _{\text{i}}=0.1\) unless otherwise specified.

Estimation of individual activity coefficients: the mean salt method

Speciation software commonly reports the activity coefficient of individual ions as well as the mean activity coefficient of electrolytes. While the steps to obtain \(\gamma _{\pm }\) follow the premises presented in the previous sections, the procedure used to estimate activity coefficients of single ions may at a first glance be considered less obvious.

According to Wilczek-Vera and Vera [35], experimental attempts to measure the activity coefficient of single ions have been performed since the 1920s. Nowadays, thanks to the last advances in the technology of ion-selective electrodes and a better understanding of the non-equilibrium behavior of electrolyte solutions, the measurement of individual activity coefficients became a reality, but not without skepticism and heated debates among researchers [36, 37].

On the other hand, a more established approach to estimate individual activity coefficients is the mean salt method [38]. This approach relies on the MacInnes convention [39] according to which the activity coefficients of \(\mathrm {K}^{+}(\mathrm {aq})\) and \(\mathrm {Cl}^{-}(\mathrm {aq})\) are equal to each other and to the mean activity coefficient of \(\mathrm {KCl}(\mathrm {aq})\) at any concentration, \(\gamma _{\mathrm {K}^{+}}=\gamma _{\mathrm {Cl}^{-}}=\gamma _{\pm \left( \mathrm {KCl}\right) }\). Note that the choice of potassium chloride is arbitrary since any other electrolyte could be chosen as a reference. Anyway, regardless of the choice of the reference electrolyte, one may easily estimate the activity coefficient of any individual ion by exploiting the MacInnes convention, as illustrated below.

Example 1

Calculation of the activity coefficient of \(\mathrm {Ca}^{2+}(\mathrm {aq})\) from \(\mathrm {CaCl}_{2}(\mathrm {aq})\) and \(\mathrm {KCl}(\mathrm {aq})\).

By definition, one has:

$$\begin{aligned} \gamma _{\pm \left( \mathrm {CaCl}_{2}\right) }&=\left[ \gamma _{\mathrm {Ca}^{2+}}\left( \gamma _{\mathrm {Cl}^{-}}\right) ^{2}\right] ^{{1}/{3}}\,,\nonumber \\ \gamma _{\pm \left( \mathrm {CaCl}_{2}\right) }&=\left[ \gamma _{\mathrm {Ca}^{2+}}\left( \gamma _{\pm \left( \mathrm {KCl}\right) }\right) ^{2}\right] ^{{1}/{3}}\,. \end{aligned}$$
(49)

Then, by rearranging the above expression, it follows that

$$\begin{aligned} \gamma _{\mathrm {Ca}^{2+}}=\dfrac{\gamma _{\pm \left( \mathrm {CaCl}_{2}\right) }^{3}}{\gamma _{\pm \left( \mathrm {KCl}\right) }^{2}}\,, \end{aligned}$$
(50)

where both \(\gamma _{\pm \left( \mathrm {CaCl}_{2}\right) }\) and \(\gamma _{\pm \left( \mathrm {KCl}\right) }\) are experimentally known.

Example 2

Calculation of the activity coefficient of \(\mathrm {SO}_{4}^{2-}(\mathrm {aq})\) from \(\mathrm {K}_{2}\mathrm{SO}_{4}(\mathrm {aq})\) and \(\mathrm {KCl}(\mathrm {aq})\).

By definition, one has:

$$\begin{aligned} \gamma _{\pm \left( \mathrm {K}_{2}\mathrm{SO}_{4}\right) }&=\left[ \left( \gamma _{\mathrm {K}^{+}}\right) ^{2}\gamma _{\mathrm {SO}_{4}^{2-}}\right] ^{{1}/{3}}\,,\\ \gamma _{\pm \left( \mathrm {K}_{2}\mathrm{SO}_{4}\right) }&=\left[ \left( \gamma _{\pm \left( \mathrm {KCl}\right) }\right) ^{2}\gamma _{\mathrm {SO}_{4}^{2-}}\right] ^{{1}/{3}}\,.\nonumber \end{aligned}$$
(51)

Then, by rearranging the above expression, it follows that:

$$\begin{aligned} \gamma _{\mathrm {SO}_{4}^{2-}}=\dfrac{\gamma _{\pm \left( \mathrm {K}_{2}\mathrm{SO}_{4}\right) }^{3}}{\gamma _{\pm \left( \mathrm {KCl}\right) }^{2}}\,, \end{aligned}$$
(52)

where both \(\gamma _{\pm \left( \mathrm {K}_{2}\mathrm{SO}_{4}\right) }\) and \(\gamma _{\pm \left( \mathrm {KCl}\right) }\) are experimentally known.

If the procedure described above is repeated for several electrolytes at different ionic strengths, one may obtain a table similar to Table 1. In this case, the validation of the individual activity coefficients follows from Eq. (12) since the values of \(\gamma _{+}\) and \(\gamma _{+}\) must a priori reproduce the values of \(\gamma _{\pm }\) of an electrolyte.

Table 1 Values of some individual activity coefficients at \(298.15\,\mathrm {K}\) as a function of the ionic strength [28]. Values for other ions may be found in [40]
Full size table

Also, in using the mean salt method to estimate the individual activity coefficients, one should be aware that both \(\gamma _{\pm \left( \mathrm {KCl}\right) }\) and \(\gamma _{\pm \left( \mathrm{{M}}_{m}X_{n}\right) }\) must be related to solutions of equal concentration. One should also carefully choose the electrolyte \(\mathrm {M}_{m}X_{n}\left( \mathrm {aq}\right)\) to avoid the formation of ion pairs. Here, some general rules [41] may be used to select the proper electrolyte \(\mathrm {M}_{m}X_{n}\left( \mathrm {aq}\right)\):

  • 1:1 electrolytes do not form ion pairs. The higher the ion valence is, the greater the probability of formation of ion pairs;

  • In general, the concentration of ion pairs involving monovalent cations is not significant;

  • Chloride and nitrate salts when dissolved in water hardly form ion pairs;

  • Sulfate and bisulfate salts usually form ion pairs with multivalent cations;

  • Formation of ion pairs between \(\mathrm {H}_{2}\mathrm{PO}_{4}^{-}\left( \mathrm {aq}\right)\), \(\mathrm {HPO}_{4}^{2-}\left( \mathrm {aq}\right)\), and \(\mathrm {PO}_{4}^{3-}\left( \mathrm {aq}\right)\) and multivalent cations is substantial;

  • Formation of ion pairs between \(\mathrm {HCO}_{3}^{-}\left( \mathrm {aq}\right)\) and multivalent cations is significant, especially in very alkaline solutions.

Overview of the ion activity models

Throughout this manuscript, some of the most common ion activity models found in the literature were presented. Despite its obvious limitations, the Debye-Hückel equation played an important role in the description of the ion–ion interactions and the study of the thermodynamics of electrolyte solutions. In fact, one can say that some ion activity models are extensions of the Debye-Hückel equation, as briefly shown in this work. Later, from the 1970s more sophisticated ion activity models (e.g., Meissner model, Pitzer equations, ELECNRTL model, MSE model, extended UNIQUAC model) were developed, and normally their ranges of applicability are much broader. Nowadays, together with the Pitzer equations and ELECNRTL model, the MSE approach and extended UNIQUAC method are among the most relevant thermodynamic models available in commercial process simulators. However, notwithstanding this, the extended Debye-Hückel equation, Davies equation, and Truesdell-Jones equation are still very useful and commonly found in speciation software because of their mathematical simplicity.

Table 2 summarizes some characteristics of the ion activity models presented in this work. First, note that by origin none of the ion activity models shown in Table 2 apply to solutions containing potential electrolytes (formerly known as weak electrolytes). Therefore, the use of the Debye-Hückel equation and its extensions to estimate mean activity coefficients of potential electrolytes must be followed by chemical equilibrium calculations and other premises. This topic, however, was not covered in this manuscript.

Second, Table 2 is only a guide that suggests which equation is more appropriate for a range of ionic strength. Nevertheless, unfortunately, it is not uncommon that the most appropriate equation sometimes provides poor results for some electrolytes, as shown in Fig. 12. In the end, the performance of the equations given in Table 2 depends on quantities that must be obtained by regressing experimental mean activity coefficients. Hence, the ion activity models are as good as their theoretical limitations and the quality of the model parameters.

Fig. 12
figure 12

Comparison between the experimental mean activity coefficients and those predicted by the ion activity models presented in this manuscript. Experimental data obtained from [3, 27]

Full size image
Table 2 Summary of the ion activity models described in this work
Full size table