Introduction

Meningitis is one of the deadly infectious diseases that has caused an increase in the mortality rate of the populace. It is the inflammation of the meninges which are the protective membrane that covers the spinal cord and the brain [1, 2]. Meningitis can be caused by a variety of microorganisms, as well as non-infectious causes like cancer, injury in the head, and through the use of certain medications [3]. Bacterial meningitis has been identified to be the highest global burden among others, because of its widespread morbidity and mortality [2, 4]. Haemophilus influenzae, Streptococcus pneumoniae, Listeria monocytogenes, Group B Streptococcus, and Neisseria meningitidis are some of the bacteria that can cause it. In this study, we focus on Neisseria meningitidis which is responsible for causing meningococcal diseases [5, 6].

Although, meningococcal diseases are found globally; however, the highest-burden is in the sub-Saharan African meningitis belt. This region has the countries between Senegal and Ethiopia which include but is not limited to countries like Guinea, Gambia, Burkina Faso, Central African Republic, Togo, Ghana, Kenya, Mali, Niger, Uganda, and Nigeria which is the focus country in this study [6, 7]. In this region, an increase in meningitis incidence has been associated with the beginning of the dry season known as the harmattan season (from November to March). The season is characterized by a dry wind blowing south from the Sahara desert to the Gulf of Guinea [2, 5, 6].

Neisseria meningitidis is a human infection that can be passed from person to person via throat secretion or droplets of respiratory from a carrier of an infected individual. In addition, a close or prolonged personal contact with such individuals through kissing, sneezing, or sharing eating or drinking utensils with a susceptible person can facilitate the transmission of the disease. The incubation period of this disease varies between 2 and 10 days, thus, following contact with an infected individual, the symptoms characterized with meningitis are expected to start showing [2, 6]. These symptoms include high fever, severe headaches, the appearance of rashes, and some other flu-like symptoms. Complications from this disease can cause permanent disabilities such as deafness, brain damage, epilepsy, hearing loss, and individual can die in the absence of early diagnosis or proper treatment [1].

Treatment of infected individuals and the use of preventive measures for susceptible people are the primary ways to reduce the incidence of meningitis in the population. In areas with inadequate health infrastructure and resources, an infected individual can be treated with antibiotic medications after effective contact with the deadly disease [1]. Antibiotics and fluids can be given directly into a patient’s veins to prevent dehydration, and oxygen can be given through a face mask if there are complications or breathing difficulties. Another treatment option for meningitis is to use steroid medication to help reduce any swelling around the brain in any patient who has a brain complication [8]. Treatment care is mainly administered for meningitis-infected people, however, this disease can be mainly prevented by vaccination. Mass vaccination of the susceptible population and early detection of infected individuals have contributed to the mitigation of the meningitis epidemic [9]. Just like many other diseases, vaccination has been shown to reduce the outbreak of meningitis in many regions [10, 11]. Particularly, the administration of vaccines has been shown to prevent the disease in both children and adults. Conjugate and polysaccharide vaccines are the two types of vaccines that are currently used in Sub-Saharan Africa during routine immunization schedules, preventive campaigns, and response to the epidemic. These types of vaccines include monovalent A, C, and tetravalent A, C, Y, W. Conjugate vaccines provide long-time immunity and confer herd immunity. Polysaccharide vaccines can be bivalent (protecting against serogroups A and C), trivalent (protecting against serogroups A, C, and W), or tetravalent (protecting against serogroups A, C, Y, and W) [1, 12]. They have been available and in use, since the 1970s [13] with limited efficacy [9, 14], and they do not yield herd immunity [9, 15].

Mathematical models have become an effective useful tool that has been used by many researchers to understand the epidemiology of diseases in each population. Many models have been developed and analyzed using different methods to provide a better understanding of the transmission dynamics and control of the disease. Examples of these studies include [16,17,18,19,20,21,22,23,24,25]. More specifically, some studies have been carried out to provide a better understanding of the transmission of meningitis (see [1, 26,27,28]), and few of these studies focus on the effect of vaccination in controlling meningitis outbreaks in Nigeria [2, 6].

In this study, we employ the use of a fractional-order mathematical model to investigate the effect of vaccination and treatment on the control of meningitis in Nigeria. Numerous researchers have used fractional-order models to study the dynamics of different diseases (see [29,30,31,32,33,34,35] and references therein). Studies have shown that fractional-order models are more advantageous in characterizing memory of biological and epidemiological systems than the classical integral-order models [36, 37]. Other related studies via different modelling approach can be found in [38,39,40,41,42,43,44,45,46,47]. In addition, fractional-order models have been used in research to answer arising problems in different fields of study. Particularly, Atagana-Baleanu fractional operator has been used by many researchers to answer different questions. For examples of these studies, see [48,49,50,51] and the references therein. The memory properties of this operator allow the integration of more information from the past, to increase the accuracy of the model predictions. In the light of this advantage, we employ the use of a fractional-order model to study the effect of vaccination and treatment on the burden of meningitis in Nigeria. To the best of our knowledge, this is the first study to use a fractional-order model in investigating the dynamics of meningitis in the population. Another novelty of this study is the use of the explicit Euler fractional method to numerically simulate the effect of treatment and vaccination parameters on the dynamical behavior of a meningitis model. We first discuss the proposed model in detail in the integer case, then use the ABC derivative to extend the model into fractional-order and obtain the required findings. The rest of the article is organized as follows: Section two deals with the formulation of the model, section three deals with the analysis of the model in the integer-order and we extend it to the fractional-order model in section four. Section 5 discusses numerical simulations and a description of the fractional-order model. Finally, we concluded by summarizing our work in section six.

Formulation of Mathematical Model

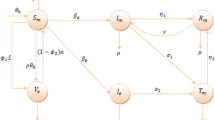
To understand the transmission dynamics of meningitis, we formulate a deterministic model with six compartments based on the epidemiological status of individuals. The compartments are susceptible S(t), Vaccinated V(t), Exposed E(t), Infected I(t) hospitalized Q(t) and Recovered R(t). We assume that the population of the susceptible class is increased either by immigration or by birth at a constant rate \(\theta \), the vaccinated population loses immunity at a rate \(\tau \). Movement from susceptible class to vaccinated class is at a rate \(\alpha \). Movement rate between exposed to infected class is at a rate \(\epsilon \). We assume a natural recovery rate for infected individuals at a rate \(\gamma \) or after receiving treatment from the hospital at a rate \(\phi \). Recovered individuals lose immunity and become susceptible upon recovery at a rate \(\sigma \), natural death occurs in all the classes at a rate \(\mu \) while meningitis induced death is at a rate \(\delta \). The population of the susceptible individuals is reduced through interaction with an individual in the infected class at a rate \(\lambda (t)\). Where \(\lambda (t) = \dfrac{\psi \{\rho E(t) + I(t)\}}{N(t)}\).

The effective transmission probability per contact with the infected individuals is denoted by \(\psi \) and the parameters \(\rho \le 1\) is a modification parameter that indicates the infectivity of individuals in the exposed class. The effectiveness of the vaccine is about 86-90% but not completely effective, therefore, we assume that vaccinated class decreases due to infection at the rates \((1 - \omega )\lambda (t)\) where \(0 \le \omega \le 1\). \(\omega \) determines the effectiveness of the vaccine. For instance, if \(\omega = 1\) in this case, the vaccine is assumed to be 100% effective. Thus, the above descriptions can be represented by a set of differential equations in (2.1), the compartmental diagram in Fig. 1 also illustrates the above descriptions.

$$\begin{aligned} \begin{aligned} \dfrac{dS}{dt}=&\theta - (\mu + \lambda (t))S + \sigma R + \tau V - \alpha S \\ \dfrac{dV}{dt}=&\alpha S - (1 - \omega )\lambda (t) V - (\tau + \mu )V \\ \dfrac{dE}{dt}=&\lambda (t) S - (\varepsilon + \mu )E + (1 - \omega )\lambda (t) V \\ \dfrac{dI}{dt}=&\varepsilon E - (\delta + \beta + \gamma + \mu )I \\ \dfrac{dQ}{dt}=&\beta I - (\phi + \delta + \mu )Q \\ \dfrac{dR}{dt}=&\gamma I + \phi Q - (\sigma + \mu )R \end{aligned} \end{aligned}$$
(2.1)
Fig. 1
figure 1

Schematic Diagram of the Meningitis Model

Full size image
Table 1 Details Definition of Variables and Parameters
Full size table

Analysis of the Model

This section comprises the study of positivity and boundedness of the solutions, invariant region, condition of existence of equilibrium points, and basic reproduction number \((\mathcal {R}_0)\) of the meningitis model.

Positivity of the Solution

Considering the positivity solution of the meningitis in equation (2.1) with all positive initial conditions.

Theorem 1

If S(0), V(0), E(0), I(0), Q(0), R(0), be positive, then we can say that the solutions \(\left( S(t), V(t), E(t), I(t), Q(t), R(t), \right) \) in equation (2.1) are positive \(\forall \) \(t > 0\).

Proof

Let \(t^{*}= sup \{t> 0 : S(t)>0,V(t)> 0, E(t)>0, I(t)> 0, Q(t)> 0, R(t)> 0 \}\), so that \(t^{*} > 0\). From the equation (2.1), considering the first equation that is

$$\begin{aligned} \dfrac{dS}{dt}= \theta - \mu S - \lambda (t) S + \sigma R + \tau V - \alpha S \ge \theta - \lambda (t) S - (\mu + \alpha )S \end{aligned}$$
(3.1)

Using integrating factor and multiplying it with equation (3.1) to obtain

$$\begin{aligned} \left( e^{\int _{0}^{t^{*}}{\lambda (\eta )}d\eta + (\mu + \alpha )t}\right) \dfrac{d S}{dt} + (\mu + \lambda (t) + \alpha ) \left( e^{\int _{0}^{t^{*}}{\lambda (\eta )}d\eta + (\mu + \alpha )t}\right) S \ge \theta \left( e^{\int _{0}^{t^{*}}{\lambda (\eta )}d\eta + (\mu + \alpha )t}\right) \end{aligned}$$

Integrating both sides from \(t = 0\) to \(t = t^{*}\) and making \(S(t^{*})\) subject of the formula, we obtain

$$\begin{aligned} \begin{aligned} S(t^{*}) \ge S(0)\left( e^{-\int _{0}^{t^{*}}{\lambda (\eta )}d\eta + (\mu + \alpha )t}\right) + \left( e^{-\int _{0}^{t^{*}}{\lambda (\eta )}d\eta + (\mu + \alpha )t}\right) \int _{0}^{t^{*}}{\theta \left( e^{\int _{0}^{x}{\lambda (\eta )}d\eta + (\mu + \alpha )x}\right) } > 0 \end{aligned} \end{aligned}$$

From the above result, it is clearly showed that \(S(t^{*})\) is \(\ge \) to the sum of positive terms which is positive. Similarly, following the same argument, we can show that \(E(t) \ge 0, I(t) \ge 0, Q(t) \ge 0, R(t) \ge 0, V(t) \ge 0\), \(\forall ~t^{*} > 0\). \(\square \)

Boundedness of the Solution

Theorem 2

All solutions S(0), V(0), E(0), I(0), Q(0), R(0) of the meningitis model(2.1) are bounded. This means that, if

$$\begin{aligned} \begin{aligned} \lim _{t \rightarrow \infty } \sup ~ N_h(t) \le \dfrac{\theta }{\mu } \end{aligned} \end{aligned}$$

then \(N(t) = S(t) + V(t)+E(t) + I(t) + Q(t) + R(t) \).

Proof

It is important to know that \(0 < I(t) \le N(t)\). Adding all the six equations of the meningitis model (2.1), we can say that

$$\begin{aligned} \begin{aligned} \dfrac{dN}{dt} =&\theta - \mu N - \delta (I + Q) \end{aligned} \end{aligned}$$
(3.2)

This can be seen that all solutions of meningitis model (2.1) are bounded. Therefore, equation (3.2) can be written as

\(\theta - \left( \mu + \delta \right) N(t) \le \dfrac{dN(t)}{dt} \le \theta - \mu N(t)\)

and we have

$$\begin{aligned} \begin{aligned} \dfrac{\theta }{(\mu + \delta )} \le \lim _{t \rightarrow \infty } \inf ~ N(t) \le \lim _{t \rightarrow \infty } \sup ~ N(t) \le \dfrac{\theta }{\mu } \end{aligned} \end{aligned}$$
(3.3)

\(\square \)

Invariant Region of Meningitis Model

Theorem 3

The region \(\Theta \subset \mathbb {R}^6_+ \) is non-negatively invariant of the meningitis model (2.1) with positive initial conditions \(\mathbb {R}^6_+\).

Proof

To proof, Let \({\Theta }\) stand for feasible region of the meningitis model (2.1), this can now be written as

$$\begin{aligned} \Theta \subset \mathbb {R}^6_+ \end{aligned}$$

with

$$\begin{aligned} \begin{aligned} \Theta = \left\{ (S, V, E, I, Q, R) \in \mathbb {R}^6_+ : S + V + E + I + Q + R \le \dfrac{\theta }{\mu } \right\} \end{aligned}. \end{aligned}$$

The conditions that are required to show the positive invariance of \(\Theta \) i.e. the solution in \(\Theta \) still remains in \(\Theta ~ \forall ~ t > 0\). This is obtained by adding equations of the meningitis model (2.1)

$$\begin{aligned} \begin{aligned} \dfrac{dN(t)}{dt}&\le \theta - \mu N(t)\quad \end{aligned} \end{aligned}$$

Using the standard comparison theorem [52], we can say that

$$\begin{aligned} \begin{aligned} N(t) \le N(0)e^{-\mu t}+ \dfrac{\theta }{\mu } \left( 1 - e^{-\mu t} \right) \end{aligned} \end{aligned}$$
(3.4)

Particularly, \(N(t) \le \dfrac{\theta }{\mu }\) if \(N(0) \le \dfrac{\theta }{\mu }\). Therefore, the region \(\Theta \) is non-negative invariant. \(\square \)

Existence of Equilibrium Point of Meningitis Model

In this section, it is necessary to discuss the existence of equilibrium points of the meningitis model. This can be divided into Meningitis free equilibrium (MFE) and Endemic equilibrium (EE) points. Considering the existence of meningitis free equilibrium point (MFEP), by equating the right-hand side of all the equations in (2.1) as well as setting E, I, Q and R to be zero, to obtain

$$\begin{aligned} \begin{aligned} E_{0}=\left( S_{0}, V_{0}, E_{0}, I_{0}, Q_{0}, R_{0}\right) \quad \quad \quad \quad \quad \quad \quad \quad \\ E_{0}=\left( \dfrac{\theta (\tau + \mu )}{\mu (\alpha + \tau + \mu )},\dfrac{\theta \alpha }{\mu (\alpha + \tau + \mu )},0,0,0,0\right) \end{aligned} \end{aligned}$$
(3.5)

Also, considering the existence of endemic equilibrium point (EEP) if I is non-zero and all the equations on the right hand side of model (2.1) are equating to be zero then by substituting \(S=S^{*}\), \(V=V^{*}\), \(E=E^{*}\), \(I=I^{*}\), \(Q=Q^{*}\) and \(R=R^{*}\) into model (2.1), we have

$$\begin{aligned} \begin{aligned}&S^{*}= \dfrac{\theta + \sigma R^{*} + \tau V^{*}}{\alpha + \lambda ^{*} (t) + \mu } \\&V^{*}=\dfrac{\alpha S^{*}}{(1 - \omega )\lambda ^{*} (t) + (\tau + \mu )} \\&E^{*}=\dfrac{\lambda ^{*} (t) S^{*} + (1 - \omega ) \lambda ^{*} (t) V^{*}}{\varepsilon + \mu } \\&I^{*}=\dfrac{\varepsilon E^{*}}{\delta + \beta + \gamma + \mu } \\&Q^{*}=\dfrac{\beta I^{*}}{\phi + \delta + \mu } \\&R^{*}=\dfrac{\gamma I^{*} + \phi Q^{*}}{\sigma + \mu } \end{aligned} \end{aligned}$$
(3.6)

Simplifying further gives

$$\begin{aligned} \begin{aligned} S^{*}=&{\dfrac{a_{3}\,a_{4}\,a_{5}\,a_{6}\,\theta \left( \left( 1+\omega \right) \lambda \left( t \right) +a_{2} \right) }{b_{1}\, \left( \lambda \left( t \right) \right) ^{2}+b_{2}\,\lambda \left( t \right) +a_{3}}} \\ V^{*}=&{\dfrac{a_{3}\,a_{4}\,a_{5}\,a_{6}\,\theta \,\alpha }{b_{1}\, \left( \lambda \left( t \right) \right) ^{2}+b_{2}\,\lambda \left( t \right) +a_{3}}} \\ E^{*}=&{\dfrac{a_{4}\,a_{5}\,a_{6}\,\theta \, \left( \left( 1-\omega \right) \left( \alpha +\lambda \left( t \right) \right) +a_{2} \right) \lambda \left( t \right) }{b_{1}\, \left( \lambda \left( t \right) \right) ^{2}+b_{2}\,\lambda \left( t \right) +a_{3}}} \\ I^{*}=&{\dfrac{a_{5}\,a_{6}\,\theta \varepsilon \, \left( \left( 1+\omega \right) \left( \alpha +\lambda \left( t \right) \right) +a_{2} \right) \lambda \left( t \right) }{b_{1}\, \left( \lambda \left( t \right) \right) ^{2}+b_{2}\,\lambda \left( t \right) +a_{3}}} \\ Q^{*}=&{\frac{\varepsilon \,\beta \,a_{6}\,\theta \left( \left( 1-\omega \right) \left( \alpha +\lambda \left( t \right) \right) +a_{2} \right) \lambda \left( t \right) }{b_{1}\, \left( \lambda \left( t \right) \right) ^{2}+b_{2}\,\lambda \left( t \right) +a_{3}}} \\ R^{*}=&{\dfrac{\varepsilon \theta \, \left( a_{5}\,\gamma +\beta \,\phi \right) \left( \left( 1-\omega \right) \left( \alpha +\lambda \left( t \right) \right) +a_{2} \right) \lambda \left( t \right) }{b _{1}\, \left( \lambda \left( t \right) \right) ^{2}+b_{2}\,\lambda \left( t \right) +a_{3}}} \end{aligned} \end{aligned}$$
(3.7)

where \(\lambda ^{*} (t) = \dfrac{\psi \{\rho E^{*} + I^{*}\}}{N^{*}}\), \(a_{1}=\alpha +\mu \), \(a_{2}=\tau +\mu \), \(a_{3}=\varepsilon +\mu \), \(a_{4}=(\delta +\beta +\gamma +\mu )\), \(a_{5}=(\phi +\delta +\mu )\), \(a_{6}=\sigma +\mu \), \(b_{1}= \left( 1-\omega \right) \left( a_{3}\,a_{4}\,a_{5}\,a_{6}-a_{5}\,\gamma \,\sigma \,\varepsilon -\beta \,\phi \,\sigma \,\varepsilon \right) \), \(b_{2}= \left( 1-\omega \right) \left( a_{1}\,a_{3}\,a_{4}\,a_{5}\,a_{6}-a_{5}\,\alpha \,\gamma \,\sigma \,\varepsilon -\alpha \,\beta \,\phi \,\sigma \,\varepsilon \right) \) and \(b_{3}=a_{3}\,a_{4}\,a_{5}\,a_{6} \left( a_{1}\,a_{2}-\alpha \,\tau \right) \)

From Eqs. (3.5) and (3.7), it has showed clearly that model (2.1) exists and has two equilibriums in the non-negative of \(\mathbb {R}_+^6\).

Basic Reproduction Number \((\mathcal {R}_0)\) of Meningitis Model

In this section, we shall consider basic reproduction number (\(\mathcal {R}_0\)) in order to determine the nature of the meningitis disease. To this end, we will use next generation matrix method to find basic reproduction number (\(\mathcal {R}_0\)). Therefore, meningitis model (2.1) can be written as

$$\begin{aligned} \mathcal {F}(X) = \left( \begin{array}{c} 0 \\ 0 \\ \lambda (t) S + (1-\omega )\lambda (t) V \\ 0 \\ 0 \\ 0 \end{array} \right) \end{aligned}$$
(3.8)

and

$$\begin{aligned} \mathcal {V}(X) = \left( \begin{array}{c} \mu S + \alpha S - \theta - \sigma R - \tau V \\ (\tau + \mu ) V - \alpha S \\ (\varepsilon +\mu )E \\ (\delta +\beta + \gamma +\mu ) I - \varepsilon E \\ (\phi + \delta + \mu ) Q - \beta I \\ (\sigma + \mu ) R - \gamma I - \phi Q \end{array} \right) \end{aligned}$$
(3.9)

Using Jacobian Matrix to solve equations (3.8) and (3.9), we respectively obtain equations (3.10) and (3.11).

$$\begin{aligned} \mathbf {F} = \left( \begin{array}{ccc} \dfrac{\psi \rho S_{0} + (1 -\omega )\psi \rho V_{0}}{S_{0} + V_{0}} &{} \dfrac{\psi S_{0} + (1 - \omega )\psi V_{0}}{S_{0} + V_{0}} &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \end{array} \right) \end{aligned}$$
(3.10)

and

$$\begin{aligned} \mathbf {V} = \left( \begin{array}{cccc} (\varepsilon + \mu ) &{} 0 &{} 0 \\ -\varepsilon &{} (\delta +\beta + \gamma +\mu ) &{} 0 \\ 0 &{} -\beta &{} (\phi + \delta + \mu ) \end{array} \right) \end{aligned}$$
(3.11)

According to [53] basic reproduction number is the obtained as the spectral radius of \(\mathbf {F} \mathbf {V}^{-1}\). Therefore,

$$\begin{aligned} \begin{aligned} \mathcal {R}_0= {\dfrac{\psi \left( \left( \delta +\beta +\gamma +\mu \right) \rho +\varepsilon \right) \left( S_{0}+ \left( 1-\omega \right) V_{0} \right) }{\left( S_{0}+V_{0} \right) \left( \varepsilon +\mu \right) \left( \delta +\beta +\gamma +\mu \right) }}\\[0.2cm] \mathcal {R}_0= {\dfrac{\psi \left( \left( \delta +\beta +\gamma +\mu \right) \rho +\varepsilon \right) \left( \tau +\mu + \left( 1-\omega \right) \alpha \right) }{ \left( \delta +\beta +\gamma +\mu \right) \left( \varepsilon +\mu \right) \left( \alpha +\tau +\mu \right) }} \end{aligned} \end{aligned}$$
(3.12)

Local stability of Disease-Free Equilibrium (DFE)

The following theorem establishes the local stability of disease-free equilibrium.

Theorem 4

When \(R_0 < 1,\) the disease-free equilibrium \(E_0\) is locally asymptotically stable, otherwise it is unstable.

Proof

The Jacobian matrix of the system 2.1 at disease-free equilibrium point \(E_0\) is obtained as follows:

Now, four of the six eigenvalues of the Jacobian matrix \(J_0\) can be easily obtained as \(-\mu , -(\mu +\sigma ), -(\alpha +\mu +\tau )\) and \( -(\delta +\phi +\mu )\). The other two eigenvalues can be given as:

$$\begin{aligned} \frac{\zeta - \sqrt{\zeta ^2 - 4 \varkappa }}{2 (\alpha +\mu +\tau )} \end{aligned}$$
(3.13)

and

$$\begin{aligned} \frac{\zeta + \sqrt{\zeta ^2 - 4 \varkappa }}{2 (\alpha +\mu +\tau )} \end{aligned}$$
(3.14)

where

$$\begin{aligned} \begin{array}{l} \zeta = -\alpha \beta -\alpha \gamma -\alpha \delta -\alpha \varepsilon -2 \alpha \mu -\beta \mu -\gamma \mu -\delta \mu -\varepsilon \mu -2 \mu ^2-\beta \tau -\gamma \tau -\delta \tau - \\ \quad \varepsilon \tau -2 \mu \tau +\psi \rho +\mu \psi \rho +\tau \psi \rho +\psi \rho \omega \\ \varkappa = \alpha (\beta +\gamma +\delta + \mu ) \big ( \alpha (\epsilon +\mu )+2 \mu \tau \big ) + \mu ^2 \big ( 2\alpha (\beta +\gamma + \delta +\epsilon )+\epsilon (\beta +\gamma +\delta ) \big ) \\ \quad + \mu ^3 ( 2\alpha +\beta +\gamma + \delta +\epsilon ) + \mu ^4 + (\beta +\gamma + \delta ) \big ( (2\alpha +2 \mu + \tau ) \epsilon \tau + 2 \alpha \mu \epsilon \big ) + 2 \mu ^2 \tau ( \\ \quad \alpha + \beta +\gamma + \delta +\epsilon +\mu )+ \mu \tau ^2 (\beta +\gamma +\delta +\epsilon +\mu ) - \epsilon \psi \Big ( \alpha \big ( \alpha + \alpha \omega + (\mu +\tau ) (2+\omega ) \big ) \\ \quad +\mu ^2 + \mu (2\mu +\tau ) \Big ) - \psi \rho \Big (\alpha (\beta + \mu + \gamma + \delta ) + \beta \mu (1+\alpha )+\mu \big ( (1+\alpha )(\gamma +\delta )\big ) - \\ \quad \mu ^2 (1+\alpha +\beta + \gamma +\delta +\mu )- (\beta +\gamma +\delta +\mu ) \big (\tau (1+\alpha +2\mu ) + (\tau ^2 + (\alpha +\mu +\tau )\omega )\big ) \Big ) \end{array} \end{aligned}$$

Now Consider \(R_0<1 \), which implies

$$\begin{aligned} \psi \left( \left( \delta +\beta +\gamma +\mu \right) \rho +\varepsilon \right) \left( \tau +\mu + \left( 1-\omega \right) \alpha \right) < \left( \delta +\beta +\gamma +\mu \right) \left( \varepsilon +\mu \right) \left( \alpha +\tau +\mu \right) \end{aligned}$$
(3.15)

which further implies:

$$\begin{aligned} \begin{array}{l} \psi \rho \big (\tau + \mu + (1-\omega )\alpha \big )< (\epsilon + \mu ) (\alpha + \tau +\mu ) \\ \implies \dfrac{\psi \rho }{\alpha } \left( \dfrac{\tau }{\alpha }+ \dfrac{\mu }{\alpha }+ (1-\omega ) \right)< (\epsilon + \mu ) (\alpha + \tau +\mu ) \\ \implies \psi \rho \big (\tau + \mu + 1-\omega \big )< (\epsilon + \mu ) (\alpha + \tau +\mu ) \big ( \because \alpha \in (0,1) \big ) \\ \implies \psi \rho \tau + \psi \rho \mu + \psi \rho + \psi \rho \omega< \epsilon \alpha + \epsilon \tau + \epsilon \mu + \mu \alpha + \mu \tau + \mu ^2 \\ i.e. \psi \rho \tau + \psi \rho \mu + \psi \rho + \psi \rho \omega < \alpha \beta +\alpha \gamma +\alpha \delta +\alpha \varepsilon +2 \alpha \mu +\beta \mu +\gamma \mu +\delta \mu + \\ \varepsilon \mu +2 \mu ^2+\beta \tau +\gamma \tau +\delta \tau \varepsilon \tau +2 \mu \tau \end{array} \end{aligned}$$
(3.16)

which implies \(\zeta < 0\). Now it can be easily verified that all the eigenvalues of \(J_0\) have a negative real part. Hence Meningitis free equilibrium Point (MFEP) is locally asymptotically stable provided \(R_0<1\), and unstable when \(R_0 > 1\). \(\square \)

Global Stability of Disease-Free Equilibrium (DFE)

In order to derive the conditions for the global stability of \(E_0\), we will use the method provided in [54]. Here is the brief overview of the technique. If we have a model system in the below form.

$$\begin{aligned} \frac{dU}{dt}=F(U,V)\\ \frac{dV}{dt}=G\left( U,V\right) , G\left( U,0\right) =0\\ \end{aligned}$$

where \(U\in {\varvec{R}}^{\varvec{m}}\) represents the uninfected individuals whereas \(V\in {\varvec{R}}^{\varvec{n}}\) is the infected population. Now, if \(R_0 <1\) then the two criteria given below establish the global stability of the disease-free equilibria. (N1) For \(\frac{dU}{dt}=F(U,0)\), \(U_0\) is globally asymptotically stable. (N2) \(G\left( U,V\right) =BV-\hat{G}\left( U,V\right) \), where \(\hat{G}\left( U,V\right) \ge 0\) for \((U,V)\in \Theta \).

Here, \(B=D_VG\left( U_0,0\right) \) represents an M-matrix (M-matrix is a matrix whose non-diagonal elements are non-negative) and \(\Theta \) is the region where the model makes biological sense. Now, using this result, we can provide the following theorem:

Theorem 5

If \(R_0<1\), the disease-free equilibrium is globally asymptotically stable and unstable for \(R_0>1\).

Proof

With respect to the notations of the method described above, the meningitis free equilibrium (MFE) can be given by \(Q_0=(U_0,0)\). In order to prove this theorem we need to prove conditions (N1) and (N2). We begin by showing (N1). Consider

$$\begin{aligned} \frac{dU}{dt}= F(U,0) \end{aligned}$$

Here,

$$\begin{aligned} F(U,0) = \begin{bmatrix} \theta -(\mu +\alpha )S+\tau V+\sigma R \\ \alpha S -(\tau +\mu ) V \\ -(\sigma +\mu ) R\\ \end{bmatrix} \end{aligned}$$

and the corresponding Jacobian matrix can be given as:

$$\begin{aligned} J_{F(U,0)}= \begin{bmatrix} -(\mu +\alpha ) &{} \tau &{} \sigma \\ \alpha &{} -(\tau +\mu ) &{} 0 \\ 0 &{} 0 &{} -(\sigma +\mu ) \\ \end{bmatrix} \end{aligned}$$

The characteristics polynomial of the above system is

$$\begin{aligned} (\lambda +\mu +\sigma )(\lambda ^2 + \lambda (2\mu +\alpha +\tau ) +\mu (\mu +\alpha +\tau )) \end{aligned}$$

We can clearly see that, one eigenvalue is \(-(\mu +\sigma )\) and other two eigenvalues are either -ve or have -ve real part. Hence \(U_0\) is globally asymptotically stable. Hence (N1) is satisfied. Now we will show (N2) as follows: We have,

$$\begin{aligned} \begin{array}{c} G\left( U,V\right) =BV-\hat{G}\left( U,V\right) \\ = \begin{bmatrix} \frac{\psi \rho }{N(t)}S_0-(\epsilon +\mu )+\frac{(1-\omega )\psi \rho }{N(t)}V_0 &{} \frac{\psi }{N(t)}S_0+\frac{(1-\omega )\psi }{N(t)}V_0 &{} 0 \\ \epsilon &{} -(\delta +\beta +\gamma +\mu ) &{} 0 \\ 0 &{} 0 &{} -(\phi +\delta +\mu ) \\ \end{bmatrix} \begin{bmatrix} E \\ I \\ Q\\ \end{bmatrix} \\ -\begin{bmatrix} \frac{\psi \rho }{N(t)}\left( (s_0-S)+(1-\omega )(V_0-V)\right) E+ \frac{\psi }{N(t)} \left( (s_0-S)+(1-\omega )(V_0-V)\right) I \\ 0\\ 0\\ \end{bmatrix} \end{array} \end{aligned}$$

Clearly, B is M-Matrix and \(\hat{G}\left( U,V\right) \ge 0\) which implies (N2) holds for the system. Hence, we have shown that both (N1) and (N2) holds for the system, which also completes the proof of the theorem. \(\square \)

Stability of Endemic Equilibrium

We will use the Routh-Hurwitz stability criterion to derive the conditions under which the endemic equilibrium point (EEP) is locally stable. The Jacobian matrix of the model system 2.1 at endemic equilibrium point (3.7) can be given as:

In order to avoid further complication, we will write the matrix \(J_0\) equivalent to

$$\begin{aligned} J^*_0 = \begin{bmatrix} a_{11} &{} \tau &{} a_{13} &{} a_{14} &{} 0 &{} \sigma \\ \alpha &{} a_{22} &{} a_{23} &{} a_{24} &{} 0 &{} 0 \\ \lambda ^* &{} a_{32} &{} a_{33} &{} a_{34} &{} 0 &{} 0 \\ 0 &{} 0 &{} \epsilon &{} a_{44} &{} 0 &{}0\\ 0&{} 0 &{} 0 &{} \beta &{} a_{55} &{} 0\\ 0 &{} 0 &{} 0 &{} \gamma &{} \phi &{} a_{66}\\ \end{bmatrix} \end{aligned}$$

Here, \(a_{i,J}\) where \( i = 1,2...6 \) and \( j = 1,2...6\) are the corresponding entries. Now, the characteristic equation of the matrix \(J^*_0\) can be given as:

$$\begin{aligned} \begin{array}{l} -\epsilon \sigma \left( x \gamma +\beta \phi -\gamma a_{55}\right) \left( \alpha a_{32}+\left( x-a_{22}\right) \lambda ^*\right) +\left( -x+a_{55}\right) \left( -x+a_{66}\right) (\left( -x+a_{44}\right) \\ \left( \left( \alpha a_{13}+\left( x-a_{11}\right) a_{23}\right) a_{32}+(x^2-\alpha \tau -x a_{22}+a_{11} \left( -x+a_{22}\right) \right) \left( -x+a_{33}\right) \\ +\left( a_{13} \left( x-a_{22}\right) +\tau a_{23}\right) \lambda ^*)-\epsilon (\left( x^2-\alpha \tau -x a_{22}+a_{11} \left( -x+a_{22}\right) \right) a_{34}+a_{24} ((x \\ -a_{11}) a_{32}+\tau \lambda ^*)+a_{14} \left( \alpha a_{32}+\left( x-a_{22}\right) \lambda ^*)\right) ) = 0 \end{array} \end{aligned}$$
(3.17)

Now, the above equation [3.17] is further written in form of a polynomial equation as

$$\begin{aligned} x^6 + A_1 x^5 + A^2 x^4+ A_3 x^3 + A_4 x^2 + A_5 x +A_6 = 0 \end{aligned}$$

The values of \(A_{i^s}: i= 1,2...6\) are provided in Appendix (See: Section 7).

Now, the endemic equilibrium point (8) will be locally stable provided the following four conditions hold:

  1. (i)

    \( A_i > 0 \forall i = 1,2,...6.\)

  2. (ii)

    \(A_1A_2> A_3, A_1 A_2 A_3 +A_1A_5 >A^2_1 A_4 + A^2_3\).

  3. (iii)

    \( A_1A_4(A_2A_3+2A_5)+A_2(A^2_1 A_6+A_3A_6)> A_1(A_1A^2_4+A^2_2A_5+A_3A_6)+A^2_3A_4+A^2_5\).

  4. (iv)

    \( A_2A_3A^2_5+A^3_3A_6>A^2_3A_4A_5+A^3_5+A^3_1A^2_6+A^2_1(A^2_4A_5-A_3A_4A_6-2A_2A_5A_6)+ A_1(A^2_2A^2_5+A_2A_3(-A_4A_5+A_3A_6)+A_5(-2A_4A_5+3A_3A_6))\).

Bifurcation Analysis

The presence of endemic equilibrium suggests that backward bifurcation is exist. We will use the “Center Manifold based theorem" present in [55], to validate the existence of backward bifurcation.

The estimate expression for \(R_0\) in 3.12 is

$$\begin{aligned} R_0 = \frac{\psi \left( \left( \delta +\beta +\gamma +\mu \right) \rho +\varepsilon \right) \left( \tau +\mu + \left( 1-\omega \right) \alpha \right) }{ \left( \delta +\beta +\gamma +\mu \right) \left( \varepsilon +\mu \right) \left( \alpha +\tau +\mu \right) } \end{aligned}$$

which gives \(\psi :\) effective transmission probability as the bifurcation parameter and \(\psi ^*\) as the critical point of bifurcation. Setting \(R_0 = 1\), we obtain

$$\begin{aligned} \psi ^* = \frac{ \left( \delta +\beta +\gamma +\mu \right) \left( \varepsilon +\mu \right) \left( \alpha +\tau +\mu \right) }{\left( \left( \delta +\beta +\gamma +\mu \right) \rho +\varepsilon \right) \left( \tau +\mu + \left( 1-\omega \right) \alpha \right) } \end{aligned}$$
(3.18)

At \(\psi = \psi ^*\), the jacobian of the model system at Meningitis free equilibrium point (MFEP) is

It can be easily verified that zero is one eigenvalue of \(J_0\). Now the associated right eigenvector \(\mathbb {W} = (w_1,w_2,w_3,w_4,w_5,w_6)\) corresponding to eigenvalue zero and matrix \(J_0\) can be obtained by solving the following system of equations:

$$\begin{aligned} \begin{array}{c} -(\mu +\alpha ) w_1 + \tau w_2 -P (\tau +\mu ) w_3 -P\dfrac{(\tau +\mu )}{\rho } w_4 + \sigma w_6 = 0 \\ \alpha w_1 -(\tau +\mu ) w_2 -P(1-\omega ) \alpha w_3 -P \dfrac{(1-\omega )\alpha }{\rho } w_4 = 0 \\ \left( -(\epsilon +\mu )+(\alpha (1-\omega )+\tau +\mu )P \right) w_3 + \dfrac{(\alpha (1-\omega )+\tau +\mu )P}{\rho } w_4 = 0 \\ \epsilon w_3 - (\delta +\beta =\gamma =\mu ) w_4 = 0 \\ \beta w_4 -(\phi +\delta +\mu ) w_5 = 0 \\ \gamma w_4 + \phi w_5 -(\sigma +\mu ) w_6 = 0 \end{array} \end{aligned}$$
(3.19)

Here \( P = \dfrac{\psi \rho }{\alpha +\tau +\mu }\).

On solving system of equations 3.19, we get

$$\begin{aligned} (w_1,w_2,w_3,w_4,w_5,w_6)^T = \begin{pmatrix} -\frac{P\left( \alpha \tau (1-\omega )+(\tau +\mu )^2\right) }{\mu (\alpha +\tau +\mu )}\left( 1+\frac{\epsilon }{\rho (\delta +\beta +\gamma +\mu )}\right) \\ \frac{P\alpha }{\mu +\tau } \left( 1+\frac{\epsilon }{\rho (\delta +\beta +\gamma +\mu )}\right) \left( (1-\omega ) - \frac{\alpha \tau (1-\omega )+(\tau +\mu )^2}{\mu (\alpha +\tau +\mu )}\right) \\ 1 \\ \frac{\epsilon }{\delta +\beta +\gamma +\mu } \\ \frac{\beta \epsilon }{(\phi +\delta +\mu )(\delta +\beta +\gamma +\mu )} \\ \frac{\gamma \epsilon (\phi +\delta +\mu )+\phi \beta \epsilon }{(\sigma +\mu )(\phi +\delta +\mu )(\delta +\beta +\gamma +\mu )} \end{pmatrix} \end{aligned}$$
(3.20)

Also the left eigenvector \(\mathbb {V} = (v_1,v_2,v_3,v_4,v_5,v_6)\) and satisfying \( \mathbb {W}.\mathbb {V} = 1\) can be obtained by solving:

$$\begin{aligned} \begin{array}{c} -(\mu +\alpha ) v_1 + \alpha v_2 = 0 \\ \tau v_1 -(\tau +\mu ) v_2 = 0 \\ -P(\tau +\mu ) v_1 -P(1+\omega )\alpha v_2 + \left( -(\epsilon +\mu )+ \left( \alpha (1+\omega )+\tau +\mu \right) P\right) v_3 + \epsilon v_4 = 0 \\ -P \dfrac{(\tau +\mu )}{\rho } v_1 -P \dfrac{(1-\omega )\alpha }{\rho } v_2 + \dfrac{\left( \alpha (1-\omega )+\tau +\mu \right) P}{\rho } v_3 -(\delta +\beta +\gamma +\mu ) v_4 + \beta v_5 + \gamma v_6 = 0 \\ -(\phi +\delta +\mu )v_5 + \phi v_6 = 0 \\ \sigma v_1 -(\sigma +\mu )v_6 = 0 \end{array} \end{aligned}$$
(3.21)

Further calculations leads us to

$$\begin{aligned} \mathbb {V} = \left( 0,0, \frac{\delta +\beta +\gamma +\mu }{\delta +\beta +\gamma +\mu -1}, \frac{(\delta +\beta +\gamma +\mu )\left( (\epsilon +\mu )-[\alpha (1-\omega +\tau +mu]\right) }{\mu (\delta +\beta +\gamma +\mu -1)},0,0 \right) ^T \end{aligned}$$
(3.22)

Using Theorem 2 of article [55] the coefficients a and b can be computed as:

$$\begin{aligned} a = \sum _{k,i,j=1}^{6} v_kw_i w_j \frac{\partial ^2f_k(E_0,\psi ^*)}{\partial x_i \partial x_j} and b = \sum _{k,i=1}^{6} v_k w_i \frac{\partial ^2f_k(E_0,\psi ^*)}{ \partial x_i \partial \psi } \end{aligned}$$
(3.23)

Further calculations lead to:

$$\begin{aligned}&\frac{\partial ^2 f_3}{\partial x_3 \partial x_1} = \frac{\psi \rho \mu }{\theta } = \frac{\partial ^2 f_3}{\partial x_1 \partial x_3} \frac{\partial ^2 f_3}{\partial x_4 \partial x_1} = \frac{\psi \mu }{\theta } = \frac{\partial ^2 f_3}{\partial x_1 \partial x_4}\\&\frac{\partial ^2 f_3}{\partial x_3 \partial x_2} = \frac{(1+\omega )\psi \rho \mu }{\theta } = \frac{\partial ^2 f_3}{\partial x_2 \partial x_3} \frac{\partial ^2 f_3}{\partial x_4 \partial x_2} = \frac{(1+\omega )\psi \mu }{\theta } = \frac{\partial ^2 f_3}{\partial x_2 \partial x_4}\\&\frac{\partial ^2 f_3}{\partial x_3 \partial \psi } = \frac{\mu \rho (\tau +\mu +(1-\omega )\alpha ) }{\alpha +\tau +\mu }\\&\frac{\partial ^2 f_3}{\partial x_4 \partial \psi } = \frac{\mu (\tau +\mu +(1+\omega )\alpha ) }{\alpha +\tau +\mu } \end{aligned}$$

Substituting these values in expressions of a and b i.e. expression 3.23, we obtain:

$$\begin{aligned} a= & {} \frac{2 \mu }{\theta } \frac{(\delta +\beta +\gamma +\mu )}{(\delta +\beta +\gamma +\mu -1)} \psi ^* \Bigg [ P \left( 1+ \frac{\epsilon }{\rho (\delta +\beta +\gamma +\mu )}\right) \Bigg ( \frac{-\left( \alpha \tau (1+\omega )+(\tau +\mu )^2 \right) }{\mu (\alpha +\tau +\mu )} \nonumber \\&\left( 1 + \frac{(1+\omega )\alpha }{\mu +\tau } \right) + \frac{(1-\omega )^2 \alpha }{\mu +\tau } \Bigg ) \Bigg ] \times \left( \rho +\frac{\epsilon }{\delta +\beta +\gamma +\mu } \right) \end{aligned}$$
(3.24)
$$\begin{aligned} b= & {} \frac{\mu (\delta +\beta +\gamma +\mu ) (\tau +\mu +(1-\omega )\alpha )}{\theta (\delta +\beta +\gamma +\mu -1)(\alpha +\tau +\mu )} \left( \rho + \frac{\epsilon }{(\delta +\beta +\gamma +\mu )}\right) \end{aligned}$$
(3.25)

Now from the derived expressions of a and b i.e. equations 3.24 and 3.25 it is clear that our proposed model will exhibit backward bifurcation only if

$$\begin{aligned} \left( \alpha \tau (1-\omega )+(\tau +\mu )^2 \right) (\mu +\tau +(1+\omega )\alpha ) > (1-\omega )^2 \alpha (\alpha +\tau +\mu ). \end{aligned}$$

Analysis of Fractional Order Meningitis Model

In this section, we present some properties of Atangana-Baleanu Operator. [29, 56,57,58,59] which will be used in the analysis of the fractional order meningitis model 4.7.

Definition 1

Let a function \(\phi _1\in F^1(a,b)\) such that \(a<b\) and \(p\in [0,1]\) represent the fractional order, then the Atangana-Baleanu (AB) operator can be expressed as

$$\begin{aligned} ^{ABC}_{a}D^p_t \phi _1 (t)=\frac{M(p)}{1-p}\int _{a}^{t}\phi _1^{'} (X) G_p \left[ \frac{-p(t-X)^p}{1-p}\right] dX \end{aligned}$$
(4.1)

Definition 2

If \(\phi _1\in F^1(a,b)\) such that \(b>a\) and \(p\in [0,1]\), then we have the form ABC in the Riemann- Liouville sense (ABR) expressed as

$$\begin{aligned} ^{ABR}_{a}D^p_t \phi _1 (t)=\frac{1-p}{M(p)}\phi _1(t)+\frac{p}{M(p)\varGamma (p)}\int _{a}^{t}\phi _1(X)(t-X)^{p-1}dX. \end{aligned}$$
(4.2)

Definition 3

The AB fractional integral operator can be expressed as

$$\begin{aligned} ^{ABC}_{a}I^p_t (\phi _1 (t))=\frac{1-p}{M(p)}\phi _1(t)+\frac{p}{M(p)\varGamma (p)}\int _{a}^{t}\phi _1(X)(t-X)^{p-1}dX, \end{aligned}$$
(4.3)

where M(p) represent normalized function.

Theorem 6

If \(\phi _1\) is continuous on [a, b], the inequality holds.

$$\begin{aligned} \parallel ^{ABR}_{a}D^p_t \phi _1 (t)\parallel <\frac{M(p)}{1-p}\parallel \phi _1(X)\parallel ,where \parallel \phi _1(X)\parallel =max_{a\le x\le b} \mid \phi _1(X)\mid . \end{aligned}$$
(4.4)

Theorem 7

The ABR and ABC derivatives satisfy the Lipschitz criteria below

$$\begin{aligned}&\parallel ^{ABR}_{a}D^p_t \phi _1 (t)-^{ABR}_{a}D^p_t \phi _2 (t)\parallel <p\parallel \phi _1(t)-\phi _2(t)\parallel \end{aligned}$$
(4.5)
$$\begin{aligned}&\parallel ^{ABC}_{a}D^p_t \phi _1 (t)-^{ABC}_{a}D^p_t \phi _2 (t)\parallel <p\parallel \phi _1(t)-\phi _2(t)\parallel . \end{aligned}$$
(4.6)

Fractional Order Meningitis Model

The fractional order version of the meningitis model 2.1 in AB derivative can be written as

$$\begin{aligned} \begin{aligned} ^{ABC}D^p_t S=&\theta - (\mu + \lambda (t))S + \sigma R + \tau V - \alpha S, \\ ^{ABC}D^p_t V=&\alpha S - (1 - \omega )\lambda (t) V - (\tau + \mu )V, \\ ^{ABC}D^p_t E=&\lambda (t) S - (\varepsilon + \mu )E + (1 - \omega )\lambda (t) V, \\ ^{ABC}D^p_t I=&\varepsilon E - (\delta + \beta + \gamma + \mu )I, \\ ^{ABC}D^p_t Q=&\beta I - (\phi + \delta + \mu )Q, \\ ^{ABC}D^p_t R=&\gamma I + \phi Q - (\sigma + \mu )R,\\ \end{aligned} \end{aligned}$$
(4.7)

with the initials for each of the variables given as \(S(0)=n_1, V(0)=n_2, E(0)=n_3, I(0)=n_4, Q(0)=n_5, R(0)=n_6\).

Existence and Uniqueness of the Fractional Order Solution

In this section, we show that the existence and uniqueness of the fractional ABC model in 4.7 using fixed point theory. We express 4.7 in equivalent form as

$$\begin{aligned} \begin{aligned} ^{ABC}D^p_t[S(t)] =&G_1(t,S),\\ ^{ABC}D^p_t[V(t)] =&G_2(t,V),\\ ^{ABC}D^p_t[E(t)] =&G_3(t,E),\\ ^{ABC}D^p_t[I(t)] =&G_4(t,I),\\ ^{ABC}D^p_t[Q(t)] =&G_5(t,Q),\\ ^{ABC}D^p_t[R(t)] =&G_6(t,R).\\ \end{aligned} \end{aligned}$$
(4.8)

The fractional integral derivative of ABC on 4.7 is given as

$$\begin{aligned} \begin{aligned} S(t)=&S(0)+ ^{ABC}{} \mathbf{I} ^p_t(\theta - (\mu + \lambda (t))S + \sigma R + \tau V - \alpha S),\\ V(t)=&V(0)+ ^{ABC}{} \mathbf{I} ^p_t(\alpha S - (1 - \omega )\lambda (t) V - (\tau + \mu )V),\\ E(t)=&E(0)+ ^{ABC}{} \mathbf{I} ^p_t(\lambda (t) S - (\varepsilon + \mu )E + (1 - \omega )\lambda (t) V),\\ I(t)=&I(0)+ ^{ABC}{} \mathbf{I} ^p_t(\varepsilon E - (\delta + \beta + \gamma + \mu )I),\\ Q(t)=&Q(0)+ ^{ABC}{} \mathbf{I} ^p_t(\beta I - (\phi + \delta + \mu )Q),\\ R(t)=&R(0)+ ^{ABC}{} \mathbf{I} ^p_t(\gamma I + \phi Q - (\sigma + \mu )R ).\\ \end{aligned} \end{aligned}$$
(4.9)

Using the definition of integral fractional derivative in AB sense, we have that

$$\begin{aligned} \begin{aligned} S(t)=&S(0)+\frac{(1-p)}{M(p)}G_1(t,S(t))+\frac{p}{M(p)\Gamma (p)}\int _{0}^{t}(t-\varLambda )^{p-1}G_1(\varLambda ,S(\varLambda ))d\varLambda ,\\ V(t)=&V(0)+\frac{(1-p)}{M(p)}G_2(t,V(t))+\frac{p}{M(p)\Gamma (p)}\int _{0}^{t}(t-\varLambda )^{p-1}G_2(\varLambda ,V(\varLambda ))d\varLambda ,\\ E(t)=&E(0)+\frac{(1-p)}{M(p)}G_3(t,E(t))+\frac{p}{M(p)\Gamma (p)}\int _{0}^{t}(t-\varLambda )^{p-1}G_3(\varLambda ,E(\varLambda ))d\varLambda ,\\ I(t)=&I(0)+\frac{(1-p)}{M(p)}G_4(t,I(t))+\frac{p}{M(p)\Gamma (p)}\int _{0}^{t}(t-\varLambda )^{p-1}G_4(\varLambda ,I(\varLambda ))d\varLambda ,\\ Q(t)=&Q(0)+\frac{(1-p)}{M(p)}G_5(t,Q(t))+\frac{p}{M(p)\Gamma (p)}\int _{0}^{t}(t-\varLambda )^{p-1}G_5(\varLambda ,Q(\varLambda ))d\varLambda ,\\ R(t)=&R(0)+\frac{(1-p)}{M(p)}G_6(t,R(t))+\frac{p}{M(p)\Gamma (p)}\int _{0}^{t}(t-\varLambda )^{p-1}G_6(\varLambda ,R(\varLambda ))d\varLambda .\\ \end{aligned} \end{aligned}$$
(4.10)

Theorem 8

The kernel \(G_1\) satisfy the Lipschitz condition and contaction if the inequality in holds

$$\begin{aligned} 0\le (\psi \beta _1+\beta _2)<1 \end{aligned}$$
(4.11)

Proof

To establish the Lipschitz condition, we consider two functions, S and \(S_1\)

$$\begin{aligned} \begin{aligned} \parallel G_1(t,S(t))-G_1(t,S_1(t))\parallel =&\parallel \frac{-\psi (\rho E+ I)}{N}S(t)-S_1(t)-\alpha (S(t)-S_1(t))-\mu (S(t)-S_1(t))\parallel \\ \le&\psi \parallel \rho E+ I\parallel \parallel S(t)-S_1(t)\parallel +(\alpha +\mu )\parallel S(t)-S_1(t)\parallel \\ \le&{\psi \beta _1+\beta _2}\parallel S(t)-S_1(t)\parallel \\ \le&\sigma _1 \parallel S(t)-S_1(t)\parallel . \end{aligned} \end{aligned}$$
(4.12)

                              \(\square \)

Where

$$\begin{aligned} \sigma _1= {\psi \beta _1+\beta _2}, and \beta _2=\alpha +\mu \end{aligned}$$
(4.13)

This implies that

$$\begin{aligned} \parallel G_1(t,S(t))-G_1(t,S_1(t))\parallel \le \sigma _1 \parallel S(t)-S_1(t)\parallel . \end{aligned}$$
(4.14)

The rest of the equations followed the same procedure

$$\begin{aligned} \begin{aligned} \parallel \parallel G_2(t,V(t))-G_2(t,V_1(t))\parallel \le&\sigma _2 \parallel V(t)-V_1(t)\parallel ,\\ \parallel G_3(t,E(t))-G_3(t,E_1(t))\parallel \le&\sigma _3 \parallel E(t)-E_1(t)\parallel ,\\ \parallel G_4(t,I(t))-G_4(t,I_1(t))\parallel \le&\sigma _4 \parallel I(t)-I_1(t)\parallel ,\\ \parallel G_5(t,Q(t))-G_5(t,Q_1(t))\parallel \le&\sigma _5 \parallel Q(t)-Q_1(t)\parallel ,\\ \parallel G_6(t,R(t))-G_6(t,R_1(t))\parallel \le&\sigma _6 \parallel R(t)-R_1(t)\parallel .\\ \end{aligned} \end{aligned}$$
(4.15)

Where \(\sigma _1\),,,,\(\sigma _6\) represent the corresponding Lipschitz constants. As a result, the Lipschitz conditions are met. The model in 4.7 can be written in a recursive terms as

$$\begin{aligned} \begin{aligned} S_n(t)=&S(0)+\frac{(1-p)}{M(p)}G_1(t,S_{n-1}(t))+\frac{p}{M(p)\Gamma (p)}\int _{0}^{t}(t-x)^{p-1}G_1(\varLambda ,S_{n-1}(\varLambda ))d\varLambda ,\\ V_n(t)=&V(0)+\frac{(1-p)}{M(p)}G_2(t,V_{n-1}(t))+\frac{p}{M(p)\Gamma (p)}\int _{0}^{t}(t-x)^{p-1}G_2(\varLambda ,V_{n-1}(\varLambda ))d\varLambda ,\\ E_n(t)=&E(0)+\frac{(1-p)}{M(p)}G_3(t,E_{n-1}(t))+\frac{p}{M(p)\Gamma (p)}\int _{0}^{t}(t-x)^{p-1}G_3(\varLambda ,E_{n-1}(\varLambda ))d\varLambda ,\\ I_n(t)=&I(0)+\frac{(1-p)}{M(p)}G_4(t,I_{n-1}(t))+\frac{p}{M(p)\Gamma (p)}\int _{0}^{t}(t-x)^{p-1}G_4(\varLambda ,I_{n-1}(\varLambda ))d\varLambda ,\\ Q_n(t)=&Q(0)+\frac{(1-p)}{M(p)}G_5(t,Q_{n-1}(t))+\frac{p}{M(p)\Gamma (p)}\int _{0}^{t}(t-x)^{p-1}G_5(\varLambda ,Q_{n-1}(\varLambda ))d\varLambda ,\\ R_n(t)=&R(0)+\frac{(1-p)}{M(p)}G_6(t,R_{n-1}(t))+\frac{p}{M(p)\Gamma (p)}\int _{0}^{t}(t-x)^{p-1}G_6(\varLambda ,R_{n-1}(\varLambda ))d\varLambda .\\ \end{aligned} \end{aligned}$$
(4.16)

Furthermore, the difference of successive terms is expressed as

$$\begin{aligned} \begin{aligned} \varphi _{1,n}(t)=&S_n(t)-S_{n-1}(t)=\frac{(1-p)}{M(p)}(G_1(t,S_{n-1}(t))-G_{1}(t,S_{n-2}(t))\\&+\frac{p}{M(p)\Gamma (p)}\int _{0}^{t}(t-\varLambda )^{p-1}(G_1(\varLambda ,S_{n-1}(\varLambda ))-G_{1}(\varLambda ,S_{n-2}(\varLambda )))d\varLambda ,\\ \varphi _{2,n}(t)=&V_n(t)-V_{n-1}(t)=\frac{(1-p)}{M(p)}(G_2(t,V_{n-1}(t))-G_{2}(t,V_{n-2}(t))\\&+\frac{p}{M(p)\Gamma (p)}\int _{0}^{t}(t-\varLambda )^{p-1}(G_2(\varLambda ,V_{n-1}(\varLambda ))-G_{2}(\varLambda ,V_{n-2}(\varLambda )))d\varLambda ,\\ \varphi _{3,n}(t)=&E_n(t)-E_{n-1}(t)=\frac{(1-p)}{M(p)}(G_3(t,E_{n-1}(t))-G_{3}(t,E_{n-2}(t))\\&+\frac{p}{M(p)\Gamma (p)}\int _{0}^{t}(t-\varLambda )^{p-1}(G_3(\varLambda ,E_{n-1}(\varLambda ))-G_{3}(\varLambda ,E_{n-2}(\varLambda )))d\varLambda ,\\ \varphi _{4,n}(t)=&I_n(t)-I_{n-1}(t)=\frac{(1-p)}{M(p)}(G_4(t,I_{n-1}(t))-G_{4}(t,I_{n-2}(t))\\&+\frac{p}{M(p)\Gamma (p)}\int _{0}^{t}(t-\varLambda )^{p-1}(G_4(\varLambda ,I_{n-1}(\varLambda ))-G_{4}(\varLambda ,I_{n-2}(\varLambda )))d\varLambda ,\\ \varphi _{5,n}(t)=&Q_n(t)-Q_{n-1}(t)=\frac{(1-p)}{M(p)}(G_5(t,Q_{n-1}(t))-G_{5}(t,Q_{n-2}(t))\\&+\frac{p}{M(p)\Gamma (p)}\int _{0}^{t}(t-\varLambda )^{p-1}(G_5(\varLambda ,Q_{n-1}(\varLambda ))-G_{5}(\varLambda ,Q_{n-2}(\varLambda )))d\varLambda ,\\ \varphi _{6,n}(t)=&R_n(t)-R_{n-1}(t)=\frac{(1-p)}{M(p)}(G_1(t,R_{n-1}(t))-G_{6}(t,R_{n-2}(t))\\&+\frac{p}{M(p)\Gamma (p)}\int _{0}^{t}(t-\varLambda )^{p-1}(G_6(\varLambda ,R_{n-1}(\varLambda ))-G_{6}(\varLambda ,R_{n-2}(\varLambda )))d\varLambda .\\ \end{aligned} \end{aligned}$$
(4.17)

Consider that,

$$\begin{aligned} \left\{ \ \begin{array}{l} S_n(t) = \sum _{i=0}^{n}\varphi _{1i}(t),\\ V_n(t) = \sum _{i=0}^{n}\varphi _{2i}(t),\\ E_n(t) = \sum _{i=0}^{n}\varphi _{3i}(t),\\ I_n(t) = \sum _{i=0}^{n}\varphi _{4i}(t),\\ Q_n(t) = \sum _{i=0}^{n}\varphi _{5i}(t),\\ R_n(t) = \sum _{i=0}^{n}\varphi _{6i}(t).\\ \end{array} \right. \end{aligned}$$
(4.18)

Hence, we have

$$\begin{aligned} \left\{ \ \begin{array}{l} \varphi _{1,n-1} = S_{n-1}(t)-S_{n-2}(t),\\ \varphi _{2,n-1} = V_{n-1}(t)-V_{n-2}(t),\\ \varphi _{3,n-1} = E_{n-1}(t)-E_{n-2}(t),\\ \varphi _{4,n-1} = I_{n-1}(t)-I_{n-2}(t),\\ \varphi _{5,n-1} = Q_{n-1}(t)-Q_{n-2}(t),\\ \varphi _{6,n-1} = R_{n-1}(t)-R_{n-2}(t).\\ \end{array} \right. \end{aligned}$$
(4.19)

Furthermore, we derive the relation

$$\begin{aligned} \begin{aligned} \parallel \varphi _{1,n}(t)\parallel \le \frac{(1-p)}{M(p)}\sigma _{1}\parallel \varphi _{1,n-1}(t)\parallel +\frac{p}{M(p)\varGamma (p)}\sigma _{1}\int _{0}^{t}(t-\varLambda )^{p-1}\parallel \varphi _{1,n-1}(\varLambda )\parallel d\varLambda ,\\ \parallel \varphi _{2,n}(t)\parallel \le \frac{(1-p)}{M(p)}\sigma _{2}\parallel \varphi _{2,n-1}(t)\parallel +\frac{p}{M(p)\varGamma (p)}\sigma _{2}\int _{0}^{t}(t-\varLambda )^{p-1}\parallel \varphi _{2,n-1}(\varLambda )\parallel d\varLambda ,\\ \parallel \varphi _{3,n}(t)\parallel \le \frac{(1-p)}{M(p)}\sigma _{3}\parallel \varphi _{3,n-1}(t)\parallel +\frac{p}{M(p)\varGamma (p)}\sigma _{3}\int _{0}^{t}(t-\varLambda )^{p-1}\parallel \varphi _{3,n-1}(\varLambda )\parallel d\varLambda ,\\ \parallel \varphi _{4,n}(t)\parallel \le \frac{(1-p)}{M(p)}\sigma _{4}\parallel \varphi _{4,n-1}(t)\parallel +\frac{p}{M(p)\varGamma (p)}\sigma _{4}\int _{0}^{t}(t-\varLambda )^{p-1}\parallel \varphi _{4,n-1}(\varLambda )\parallel d\varLambda ,\\ \parallel \varphi _{5,n}(t)\parallel \le \frac{(1-p)}{M(p)}\sigma _{5}\parallel \varphi _{5,n-1}(t)\parallel +\frac{p}{M(p)\varGamma (p)}\sigma _{5}\int _{0}^{t}(t-\varLambda )^{p-1}\parallel \varphi _{5,n-1}(\varLambda )\parallel d\varLambda ,\\ \parallel \varphi _{6,n}(t)\parallel \le \frac{(1-p)}{M(p)}\sigma _{1}\parallel \varphi _{6,n-1}(t)\parallel +\frac{p}{M(p)\varGamma (p)}\sigma _{6}\int _{0}^{t}(t-\varLambda )^{p-1}\parallel \varphi _{6,n-1}(\varLambda )\parallel d\varLambda .\\ \end{aligned} \end{aligned}$$
(4.20)

Hence, S(t), V(t), E(t), I(t), Q(t), R(t) are bounded functions.

Theorem 9

The solution of the meningitis fractional order model 4.7 exist and is unique if there exist \(t_0\) such that;

$$\begin{aligned} \frac{1-p}{M(p)}\sigma _{i}+\frac{p}{M(p)\varGamma (p)}\sigma _{i};t_{0}<1,i=1,,,,6 \end{aligned}$$
(4.21)

Proof

It is established that S(t), V(t), E(t), I(t), Q(t), R(t) are bounded functions and satisfy Lipschitz conditions. From 4.20, we obtain the succeeding expression below

$$\begin{aligned} \begin{aligned} \parallel \varphi _{1,n}(t)\parallel \le \parallel S_{0}(t)\parallel \left[ \frac{(1-p)}{M(p)}\sigma _{1}+\frac{t_{0}}{M(p)\varGamma (p)}\sigma _{1}\right] ^n,\\ \parallel \varphi _{2,n}(t)\parallel \le \parallel V_{0}(t)\parallel \left[ \frac{(1-p)}{M(p)}\sigma _{2}+\frac{t_{0}}{M(p)\varGamma (p)}\sigma _{2}\right] ^n,\\ \parallel \varphi _{3,n}(t)\parallel \le \parallel E_{0}(t)\parallel \left[ \frac{(1-p)}{M(p)}\sigma _{3}+\frac{t_{0}}{M(p)\varGamma (p)}\sigma _{3}\right] ^n,\\ \parallel \varphi _{4,n}(t)\parallel \le \parallel I_{0}(t)\parallel \left[ \frac{(1-p)}{M(p)}\sigma _{4}+\frac{t_{0}}{M(p)\varGamma (p)}\sigma _{4}\right] ^n,\\ \parallel \varphi _{5,n}(t)\parallel \le \parallel Q_{0}(t)\parallel \left[ \frac{(1-p)}{M(p)}\sigma _{5}+\frac{t_{0}}{M(p)\varGamma (p)}\sigma _{5}\right] ^n,\\ \parallel \varphi _{6,n}(t)\parallel \le \parallel R_{0}(t)\parallel \left[ \frac{(1-p)}{M(p)}\sigma _{6}+\frac{t_{0}}{M(p)\varGamma (p)}\sigma _{6}\right] ^n.\\ \end{aligned} \end{aligned}$$
(4.22)

\(\square \)

The existence of the solutions are proved. We define the following functions in order to show that 4.22 represent the solution of the fraction order model 4.7

$$\begin{aligned} \left\{ \ \begin{array}{l} S(t)-S(0)=S_{n}(t)-C_{1}(t),\\ V(t)-V(0)=V_{n}(t)-C_{2}(t),\\ E(t)-E(0)=E_{n}(t)-C_{3}(t),\\ I(t)-I(0)=I_{n}(t)-C_{4}(t),\\ Q(t)-Q(0)=Q_{n}(t)-C_{5}(t),\\ R(t)-R(0)=R_{n}(t)-C_{6}(t).\\ \end{array} \right. \end{aligned}$$
(4.23)

Further, we get

$$\begin{aligned} \begin{aligned} \parallel&C_{1n}(t)\parallel =\parallel \frac{1-p}{M(p)}(G_{1}(t,S(t))-G_{1}(t,S_{n-1}(t)))\\ {}&+\frac{p}{M(p)\varGamma (p)}\int _{0}^{t}(t-\varLambda )^{p-1}(G_{1}(\varLambda ,S(\varLambda ))-G_{1}(\varLambda ,S_{n-1}(\varLambda )))d\varLambda \parallel \\,&\le \frac{1-p}{M(p)}\parallel G_{1}(t,S(t))-G_{1}(t,S_{n-1}(t))\parallel \\&\quad +\frac{p}{M(p)\varGamma (p)}\int _{0}^{t}\parallel G_{1}(\varLambda ,S(\varLambda ))-G_{1}(\varLambda ,S_{n-1}(\varLambda ))\parallel d\varLambda ,\\&\le \frac{1-p}{M(p)}\sigma _{1}\parallel S-S_{n-1}\parallel + \frac{p}{M(p)\varGamma (p)}\sigma _{1}\parallel S-S_{n-1}\parallel t. \end{aligned} \end{aligned}$$
(4.24)

By repeating the same procedure at \(t_0\) we have

$$\begin{aligned} \parallel C_{1n}(t)\parallel \le \left[ \frac{(1-p)}{M(p)}+\frac{pt_{0}}{M(p)\varGamma (p)}\sigma _{1}\right] \sigma _{1}^{n+1} \end{aligned}$$
(4.25)

Taking the limit of 4.25 as \(n \longrightarrow \infty \) clearly, \(\parallel C_{1n}(t)\parallel \longrightarrow \)0. By the same procedure, \(\parallel C_{2n}(t)\parallel \), \(\parallel C_{3n}(t)\parallel \), \(\parallel C_{4n}(t)\parallel \), \(\parallel C_{5n}(t)\parallel \) and \(\parallel C_{6n}(t)\parallel \) \(\longrightarrow \)0.

Theorem 10

The solution of the fractional order model 4.7 is unique if the assumption below holds

$$\begin{aligned} \left( 1-\frac{(1-p)}{M(p)}\sigma _{1}+\frac{p}{M(p)\varGamma (p)}\sigma _{1}t\right) \geqslant 0 \end{aligned}$$
(4.26)

Proof

In other to proof the uniqueness of the solution of 4.7, we consider another solution such as, \(S_{1}(t),V_{1}(t),E_{1}(t),I_{1}(t),Q_{1}(t),R_{1}(t)\) then,

$$\begin{aligned} S(t)-S_{1}(t)= & {} \frac{1-p}{M(p)}(G_{1}(t,S(t))-G_{1}(t,S_{1}(t))) \nonumber \\&+ \frac{p}{M(p)\varGamma (p)}\int _{0}^{t}( G_{1}(\varLambda ,S(\varLambda ))-G_{1}(\varLambda ,S_{1}(\varLambda ))) d\varLambda , \end{aligned}$$
(4.27)
$$\begin{aligned} \parallel S(t)-S_{1}(t)= & {} \parallel \frac{1-p}{M(p)}( G_{1}(t,S(t))-G_{1}(t,S_{1}(t)))\nonumber \\&\quad +\frac{p}{M(p)\varGamma (p)}\int _{0}^{t}( G_{1}(\varLambda ,S(\varLambda ))-G_{1}(\varLambda ,S_{n-1}(\varLambda ))) d\varLambda ,\nonumber \\&\le \frac{1-p}{M(p)}\sigma _{1}\parallel S(t)-S_{1}(t)\parallel + \frac{p}{M(p)\varGamma (p)}\sigma _{1}\parallel S(t)-S_{1}(t)\parallel t.\nonumber \\&\parallel S(t)-S_{1}(t)\parallel \left( 1-\frac{(1-p)}{M(p)}\sigma _{1}+\frac{p}{M(p)\varGamma (p)}\sigma _{1}t\right) \leqslant 0. \end{aligned}$$
(4.28)

\(\square \)

Hence, \(S(t)=S_{1}(t)\), if the condition 4.26 holds. Similarly, \( V(t)=V_{1}(t), E(t)=E_{1}(t), I(t)=I_{1}(t), Q(t)=Q_{1}(t)\) and \(R(t)=R_{1}(t)\). Hence, the solution is unique.

Numerical Simulation

Some of the parameter values were obtained from the literature, as shown in Table 2, and the demographic parameter values were estimated. The natural death rate is estimated to be \(\mu =\frac{1}{60.87 \times 365}\), with Nigerians having an average life expectancy of 60.87 years [60]. Furthermore, the recruitment rate is estimated by \(\mu \times N\), where the total population N is reported as 219,463,862 [60].

Table 2 Parameter and value descriptions
Full size table
Fig. 2
figure 2

Profile of S(t), V(t), E(t) in classical and fractional sense describe in (A), (B), (C), respectively

Full size image
Fig. 3
figure 3

Profile of I(t), Q(t), R(t) in classical and fractional sense describe in (A), (B), (C), respectively

Full size image
Fig. 4
figure 4

Variation of fractional order p for S(t), V(t), E(t) in (A), (B), (C), respectively

Full size image
Fig. 5
figure 5

Variation of fractional order p for I(t), Q(t), R(t) in (A), (B), (C), respectively

Full size image
Fig. 6
figure 6

vaccine rate \(\alpha \) on S with increasing and decreasing values. (A) classical sense (B) fractional sense

Full size image
Fig. 7
figure 7

treatment rate on I and \(\beta \) with increasing and decreasing values. (A) classical sense (B) fractional sense

Full size image

The numerical dynamics of the meningitis outbreak as modeled with the ABC operator are examined in this section, while the remaining parameters are taken from Table 2. In this paper, an explicit Euler fractional type numerical approach is used to simulate fractional ABC type ordinary differential equations. The approach itself, as well as its complete analysis based on convergence and error boundaries, may be found in [61,62,63]. Because of its simplicity and versatility, the numerical approach devised for this purpose has garnered a lot of praise in the current literature. The use of such readily available routines on MathWorks made simulations far more useful for the current research study for the ABC meningitis model. It should be noted that we utilize the MATLAB program version (R2019a).

We ran simulations for each state variable using the ABC operator model. This simulation consists of two charts for each class, one comparing the classical and fractional order derivatives Figs. 2, 3 and the other varying the fractional-order Figs. (4), (5) values to study the dynamics of the compartments. Susceptible people appear to diminish with fractional value variation, however, the vaccinated and exposed groups exhibit symmetrical behavior with the bell-shaped curve representing, once again, the true behavior of the disease. Concerning the infectious and quarantine classes, they fall dramatically at first but thereafter follow the bell-shaped structure. Last but not least, the recovered class’s behavior is depicted in Fig. (5(C)). There aren’t many deaths in this class since the infectious population declines after a while, and as a result, people begin to recover, as seen. We also test the effect of the vaccine by varying the values of the vaccine rate on the susceptible population as can be seen in Fig. (6). The treatment rate shows sensitive behavior as the infectious class got decreased with increasing values of the treatment rate (7). Based on this information, it is possible to conclude that the meningitis outbreak is manageable if it can be prevented from spreading by increasing the rate of vaccination. Vaccinating against meningitis is the most effective strategy to lessen the disease’s incidence and effects by providing long-term protection. Treatments are also given to people who are at a high risk of contracting meningococcal illness. Controlling meningitis epidemics, on the other hand, necessitates both vaccine and therapy.

Conclusion

A new mathematical model for the transmission dynamics of meningitis in fractional ABC derivatives has been investigated. The meningitis outbreak is particularly fast-acting and has shockingly dangerous implications. It is vital to investigate the dynamics of this epidemic in greater depth. The fractional operator utilized in this study has been shown in the literature to be effective for analyzing the transmission dynamics of various epidemic models. p is the fractionalized order. As a result, the model formulation, existence, and uniqueness of the solution via the fixed point theorem, bifurcation analysis, global and local stability analysis, and, most importantly, the basic number of reproductions for the suggested fractional version of the model have all been demonstrated. Furthermore, the model’s parameters are derived from actual cases of the infection. Data from the 2017 Nigerian meningitis outbreak was used to parameterize the model [6]. It is worth mentioning that the fractional type illness model under consideration understands disease behavior better than the integer-order variation. The treatment and vaccine’s effect has been demonstrated by altering the vaccine rate values. Furthermore, several numerical simulations were run using an efficient numerical scheme to provide more light on the model’s behavior. Moreover, in order to predict meningitis eradication, we investigated the effects of multiple control techniques in reducing the disease’s prevalence in the population. The findings of the study are expected to provide a necessary framework for assessing meningitis management in any part of the world. Because the prevalence of meningitis varies by region, our analytical results can show the genuine picture of meningitis dynamics in a given region.

Appendix

The values of \(A_{i^s}: i= 1,2...6\) used in Section 3.8 are given as:

  • \( A_1 = (- a_{11} - a_{22} - a_{33} - a_{44} - a_{55} - a_{66}) \).

  • \( A_2 = -\alpha \tau - \lambda a_{13} - a_{23}a_{32} - \epsilon a_{34} + a_{11} (a_{22}+a_{33}+a_{44}+a_{55}+a_{66}) + a_{22}(a_{33} +a_{44}+a_{55}+a_{66})\ +\) \(a_{33}(a_{44}+a_{55}+a_{66}) + a_{44}(a_{55}+a_{66})+a_{55}a_{66} \)

  • \( A_3 = -\epsilon a_{24} a_{32}+\alpha \tau (a_{33}+a_{44})+\epsilon a_{22} a_{34}+a_{23} a_{32} a_{44}-a_{22} a_{33}( a_{44}-a_{55} - a_{66}) + \big ( \alpha \tau +a_{23} a_{32} +\epsilon a_{34} -(a_{22} -a_{33}) a_{44} \big ) a_{55}\ +\) \(\big (\alpha \tau +a_{23} a_{32} + \epsilon a_{34} -(a_{22} -a_{33}) a_{44} -a_{55}(a_{22} -a_{33} -a_{44}) \big ) a_{66} +a_{11} \big (a_{23} a_{32}+\epsilon a_{34}-a_{33} a_{44}-a_{33} a_{55}-a_{44} a_{55}-(a_{33} -a_{44} -a_{55}) a_{66}\ -\) \(a_{22} \big (a_{33} +a_{44}+a_{55}+a_{66}\big )\big )-\epsilon a_{14} \lambda ^*-\tau a_{23} \lambda ^*+a_{13} (-\alpha a_{32}+(a_{22}+a_{44}+a_{55}+a_{66}) \lambda ^*) \)

  • \( A_4 = \alpha \epsilon \tau a_{34}+\alpha a_{13} a_{32} (a_{44}+a_{55}+a_{66})-\alpha \tau a_{33}( a_{44}+a_{55} +a_{66})+\epsilon a_{24} a_{32} a_{55}- \epsilon a_{22} a_{34} a_{55}\ -\) \((\alpha \tau -a_{23} a_{32} +a_{22} a_{33}) a_{44} a_{55}+\epsilon a_{24} a_{32} a_{66} -\epsilon a_{22} a_{34} a_{66}- \big ( \alpha \tau -a_{23} a_{32} +a_{22} a_{33}\big )a_{44} a_{66}\ +\) \((-\alpha \tau - a_{23} a_{32} +a_{22} a_{33} -\epsilon a_{34} +a_{22} a_{44} +a_{33} a_{44})a_{55} a_{66} +a_{11} ( (\epsilon a_{24} -a_{23} a_{44}-a_{23} a_{55} ) a_{32}-\epsilon a_{34} a_{55}+a_{33} a_{44} a_{55}- \big (a_{23} a_{32} -\epsilon a_{34} + a_{33} a_{44} +a_{33} a_{55} +a_{44} a_{55}\big ) a_{66} +a_{22} (-\epsilon a_{34}+a_{44} a_{55}+a_{44} a_{66}+a_{55} a_{66}\ +\) \(a_{33} (a_{44}+a_{55}+a_{66})))- \lambda ^* \Big (\gamma \epsilon \sigma -\epsilon \tau a_{24} -a_{13} a_{22} a_{44} +\tau a_{23} a_{44} - (a_{13} a_{22} +\tau a_{23} a_{13} a_{44} )a_{55} - a_{66}(a_{13} a_{22} +\tau a_{23} -a_{13} a_{44} -a_{13} a_{55}) +\epsilon a_{14} \left( -\alpha a_{32}+\left( a_{22}+a_{55}+a_{66}\right) \right) \Big )\).

  • \( A_5 = ((\alpha \tau -a_{11} a_{22} ) a_{55}+(\alpha \tau a_{11} a_{22}) a_{66}) a_{33} a_{44} +(\alpha \tau a_{33} - a_{11} a_{22} a_{33} +\alpha \tau a_{44} - a_{11} a_{22} a_{44} - (a_{11} -a_{22} )a_{33} a_{44} ) a_{55} a_{66} \ +\) \(\epsilon a_{34} ((-\alpha \tau +a_{11} a_{22}) a_{66}+a_{55} (-\alpha \tau +a_{22} a_{66}+a_{11} (a_{22}+a_{66})))-a_{32} (\alpha \gamma \epsilon \sigma +\alpha a_{13} a_{44} a_{55}+\alpha a_{13} a_{44} a_{66}+(\alpha a_{13} +\epsilon a_{24} -a_{23} a_{44}) a_{55} a_{66}-\alpha \epsilon a_{14} (a_{55}+a_{66})+a_{11} (\epsilon a_{24} (a_{55}+a_{66})-a_{23} (a_{55} a_{66}+a_{44} (a_{55}+a_{66}))))\ -\) \(\lambda ^* \big (\beta \epsilon \sigma \phi +\gamma \epsilon \sigma a_{22} +(\gamma \epsilon \sigma - \epsilon a_{14} a_{22} +\epsilon \tau a_{24} +a_{13} a_{22} a_{44} -\tau a_{23} a_{44}) a_{55} -(\epsilon a_{14} a_{22} +\epsilon \tau a_{24} +a_{13} a_{22} a_{44} -\tau a_{23} a_{44} )a_{66} -(\epsilon a_{14} +a_{13} a_{22} -\tau a_{23} +a_{13} a_{44} )a_{55}a_{66} \big ) \).

  • \(A_6 = \big (\epsilon \left( \alpha \tau -a_{11} a_{22}\right) a_{34} -(\alpha \tau +a_{11} a_{22} )a_{33} a_{44} \big ) a_{55} a_{66}+a_{32} (-\alpha \beta \epsilon \sigma \phi +a_{55} (-\alpha \epsilon a_{14} a_{66}+a_{11} (\epsilon a_{24}-a_{23} a_{44}) a_{66}+\alpha (\gamma \epsilon \sigma +a_{13} a_{44} a_{66})))\ +\) \(\lambda ^*\Big [\beta \epsilon \sigma \phi a_{22} -\gamma \epsilon \sigma a_{22} a_{55} + a_{55} a_{66}\big (\epsilon a_{14} a_{22} -\epsilon \tau a_{24} -a_{13} a_{22} a_{44} + \tau a_{23} a_{44} \big ) \Big ] \)