On Dynamics of Current-Induced Static Wall Profiles in Ferromagnetic Nanowires Governed by the Rashba Field

Abstract

This article deals with the analytical study of propagation of static wall profiles in ferromagnetic nanowires under the effect of spin–orbit Rashba field. We consider the governing dynamics for the evolution of magnetization inside the ferromagnetic material as an extended version of Landau–Lifshitz–Gilbert–Slonczewski equation of micromagnetism. It comprises the nonlinear dissipation factors like dry-friction and viscous. We establish the threshold and Walker-type breakdown estimates of the external sources in the steady-regime and also illustrate the obtained results numerically.

Introduction

Over the recent years, the study of ferromagnetic materials has gained a great attention due to its enormous application in magnetic storage devices such as hard-disks, magnetic random access memory (MRAM), ferroelectric random access memory (FeRAM) etc. In particular, ferromagnetic nanowires have been extensively used in these storage devices which not only reduce the size but also provide the low energy consumption. In storage devices, reading and writing processes of the data are closely associated with the formation and evolution of magnetic domain walls (DWs), a thin transition layer which separates the uniformly magnetized regions (domains) oriented in different directions [1]. More precisely, in case of MRAMs (FeRAMs) the data bit is achieved by passing the magnetic field (electric current pulses) through the material (see [2, 3]). Therefore, for the development of these devices, it becomes essential to understand the DW motions under the action of magnetic fields and spin-polarized electric currents.

Experimentally, it has been observed that in presence of external source (magnetic fields or electric currents) DW motion experiences two different dynamical regimes. For small value of fields (currents), the equilibrium wall profile moves rigidly with constant velocity along the wire axis which leads to a steady-regime of high DW mobility. The minimum value of the field (current) for which the wall motions are observed in steady-regime is known as threshold value. The maximum value of external sources for which DW motion remains steady is referred as Walker breakdown. As the field (current) exceeds the breakdown value, DW structure gets altered due to the internal deformation which leads to the oscillatory motion of magnetization configuration between Bloch and Néel structures. Such a dynamic regime is called precessional [4, 5].

Landau and Lifschitz introduced an equation which governs the evolution of magnetization inside the ferromagnetic medium in their pioneer work [6]. Later, Brown [7] laid the foundation of micromagnetic theory which rely on the fact that the static wall configurations (equilibrium states) also referred as relevant wall configurations of magnetization minimize a given energy functional consisting of several components. Gilbert [8], modified the Landau–Lifschitz equation by replacing the dissipation term with an equivalent torque term arising from a viscous force. This modified equation describes the motion in metallic ferromagnets with no crystallographic defects. Such materials are termed as ideal ferromagnets. In order to understand the dynamics in the materials with structural disorder (non-ideal ferromagnets), the Gilbert linear dissipation term is generalized through the two additional dissipation torque terms which account for nonlinear viscous and dry-friction dissipation [9–13] and this equation is known as extended Landau–Lifschitz–Gilbert (ELLG) equation. Slonczewski [14] further modified the LLG equation and included the effect of spin-polarized electric current into the dynamics.

In the current induced DW motion, spin-polarized electric current that enters into a ferromagnet exerts a torque on the magnetization due to the transfer of spin angular momentum. This torque term is called spin transfer torque (STT). The dynamics which includes the effect of STT is known as Landau–Lifschitz–Gilbert–Slonczewski equation. In our study, we consider the metallic ferromagnet with a strong structural inversion asymmetry. In such materials a strong spin–orbit coupling leads to the additional spin–orbit torque which contributes in total effective field and termed as Rashba field. The spin–orbit Rashba field can induce the DW motion along the current direction and delays the Walker breakdown (for instance see [13, 15–18]).

In this work, we mainly focus on the dynamics of magnetic DWs in steady-state regime under the influence of spin-polarized currents and Rashba field in ferromagnetic nanowire. We also examine the wall motions under the action of magnetic fields to distinguish between the features of current driven and field driven DW motion. In doing so, we consider a one dimensional model of extended Landau–Lifschitz–Gilbert–Slonczewski equation (ELLGS) comprise of nonlinear dissipations viscous and dry-friction along with the standard Gilbert dissipation term. To be precise, using standard traveling wave ansatz we describe a Bloch DW structure and study the wall motions in steady-regime under the separate action of external sources. We organize this article as follows:

In “Considered Model and Governing Dynamics” section, we present the schematic of the considered model and describe the governing dynamics. In “Description of Wall Motions” section, we establish the threshold and Walker-type breakdown condition of the external sources in different scenarios. To elucidate the DW motion, analytical results obtained in previous section are illustrated numerically in “Illustration of Wall Motions Under Different Scenarios” section. In the last section, we conclude this article and introduce some possible extensions in the same research lines.

Considered Model and Governing Dynamics

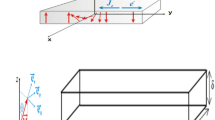
We consider an infinite ferromagnetic nanowire of circular cross section. It is arranged along the $\vec {e}_{1}$-direction and characterized by a time varying spontaneous magnetization vector field m:

$$\begin{aligned} m: \mathbb R^{+} \times \mathbb R \rightarrow \mathbb R^{3}, \end{aligned}$$

where $(\vec {e}_{1}, \vec {e}_{2}, \vec {e}_{3})$ is the canonical basis of $\mathbb R^{3}$. The magnetic moment m connects the magnetic induction B and the magnetic field H by the relation $B={m}+H$. We assume that material is saturated to a constant magnetization $M_{s}$. After renormalization, it yields:

$$\begin{aligned} |m(t,x)|=1 ~~ \text {for} ~~(t,x) \in \mathbb R^{+} \times \mathbb R ~~a.e. \end{aligned}$$

(1)

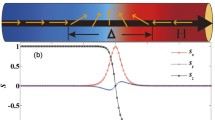
where the abbreviation a.e. stands for almost everywhere. We consider metallic ferromagnets with high perpendicular magnetocrystalline anisotropy and assume the energetically preferred direction of spontaneous magnetization also referred as easy axis along the $\vec {e}_{2}$-direction. We, then subject this nanowire to an external sources viz. magnetic field and electric current field which are both constant in time and uniform in space. Let us consider the applied magnetic field $\mathscr {H}_{a}$ is directed along the easy axis whereas the electric current density $\mathbf J$ is acting along the wire axis i.e $\mathscr {H}_{a}=h\vec {e}_2$ and $\mathbf J =J\vec {e}_{1}.$ The constants h and J denote the magnitude of applied magnetic field and current density respectively. We assume the relevant configuration of magnetization is in the direction of easy axis. More precisely, it modelizes a $180^{\circ }$ domain wall of thickness $\lambda$ separating the domain in which $m \sim \vec {e}_{2}$ as $x \rightarrow - \infty$ with the domain in which $m \sim -\vec {e}_{2}$ as $x \rightarrow + \infty$ as exhibited in Fig. 1.

Fig. 1

Schematics of a straight magnetic nanowire of circular cross section depicting $180^{\circ }$ Bloch-type domain wall

The governing dynamics for the evolution of magnetization inside the ferromagnetic medium driven by a spin-polarized electric current is described by the Landau–Lifschitz–Gilbert–Slonczewski (LLGS) equation [19, 20]

$$\begin{aligned} \dfrac{\partial m}{\partial t }= \gamma (\mathscr {H}_{eff} \times m)+\mathscr {T}_{d}+\mathscr {T}_{stt}. \end{aligned}$$

(2)

In the sequel, we use the notation $\frac{\partial }{\partial x}=\partial _{x}, \frac{\partial ^{2}}{\partial x^{2}}=\partial _{xx}$ for the partial derivatives and overdot for the ordinary derivatives. The constant $\gamma =M_{s}\mu _{0}\gamma _{e}$ is defined in terms of the magnetic permeability of the vacuum $\mu _{0}$ and the gyromagnetic ratio $\gamma _{e}=\frac{ge}{m_e}$, where g, e and $m_{e}$ represent the Landè factor, electron charge and the electron mass respectively.

The first term on the right hand side of (2) delineates the precession of magnetization m around the effective field $\mathscr {H}_{eff}$ and termed as the Larmor precession. The total effective field $\mathscr {H}_{eff}$ is derived from the micromagnetism energy $\mathscr {E}(m)$ by the relation $\mathscr {H}_{eff}=-\partial _{m}\mathscr {E}(m)$. It consists several components namely exchange $\mathscr {H}_{ex}$, anisotropy $\mathscr {H}_{an}$, demagnetizing $\mathscr {H}_{d}$, applied magnetic field $\mathscr {H}_{a}$ and the spin–orbit Rashba field $\mathscr {H}_{R}$.

$$\begin{aligned} \mathscr {H}_{eff}(m)=\mathscr {H}_{ex}(m)+\mathscr {H}_{an}(m)+\mathscr {H}_{d}(m) +\mathscr {H}_{a}+\mathscr {H}_{R}(J). \end{aligned}$$

(3)

The exchange field is defined as [21, 22]

$$\begin{aligned} \mathscr {H}_{ex}(m)=A\partial _{xx}m, \end{aligned}$$

where the constant A is expressed in terms of the exchange constant $A_{ex}$ as:

$$\begin{aligned} A=\dfrac{2A_{ex}}{\mu _{0}M_{s}^{2}}. \end{aligned}$$

Magnetic field due to the high perpendicular magnetocrystalline anisotropy is:

$$\begin{aligned} \mathscr {H}_{an}(m)=\beta (m \cdot \mathbf e )\mathbf e , \end{aligned}$$

where the unit vector $\mathbf e$ denotes the direction of the easy axis and the constant $\beta =\dfrac{2K}{\mu _{0}M_{s}^{2}}, K$ being the anisotropy constant depends on the material property [23].

The demagnetizing or stray field is due to the magnetic field induced by the medium itself and characterized by the Maxwell equations:

$$\begin{aligned} {\left\{ \begin{array}{ll} \text {curl} \mathscr {H}_{d}(m)=0 ~~\text {in}~\mathbb R^{3},\\ \text {div}(\mathscr {H}_{d}(m)+{m})=0~~ \text {in}~ \mathbb R^{3}. \end{array}\right. } \end{aligned}$$

In this work, we are in the framework of a straight nanowire of infinite length with circular cross section and it is assumed that the radius of the wire is very small in comparison to the length of the wire. In this set up, an expression for demagnetizing field is derived using the $\Gamma$-convergence arguments (for details see [24, 25] and [21]) and given as:

$$\begin{aligned} \mathscr {H}_{d}(m)=-m_{2}\vec {e}_{2}-m_{3}\vec {e}_{3}, \end{aligned}$$

where $(m_{1}, m_{2},m_{3})$ are the coordinates of m in $\mathbb R^{3}.$

Finally, the Rashba field is expressed as [13]:

$$\begin{aligned} \mathscr {H}_{R}(J)=\dfrac{\alpha _{R}P}{\mu _{0}\mu _{B}M_{s}^{2}}(\mathbf e \times \mathbf J ), \end{aligned}$$

in which $\alpha _{R}, P$ and $\mu _{B}$ stand for the Rashba parameter, the polarization factor of the current and the Bohr magneton respectively. We express the Rashba field in terms of the spin-torque velocity $v_{s}(J):$

$$\begin{aligned} \mathscr {H}_{R}(J)=-\varepsilon v_{s}\vec {e}_{3}, \end{aligned}$$

where $\varepsilon =(2e/g\mu _{0}\mu _{B}^{2}M_{s})\alpha _{R}$ and the spin-torque velocity $\mathbf {v_{s}}$ is a vector directed along the direction of electric current motion (i.e in $\vec {e}_{1}$-direction) with the amplitude $v_{s}=\dfrac{g\mu _{B}P}{2eM_{s}}J$.

Next, we move on to the second term $\mathscr {T}_{d}$ in (2). It is the dissipative torque which describes the dissipation of energy in the system. We consider the general phenomenological form of the dissipative torque and write it as:

$$\begin{aligned} \mathscr {T}_{d}=\mathscr {T}_{d_{1}}+\mathscr {T}_{d_{2}}= m \times \mathscr {F}_{1}(\partial _{t}m)+ \gamma \xi _{d} \left( m \times \mathscr {F}_{2}(\partial _{t}m)\right) , \end{aligned}$$

with

$$\begin{aligned} \mathscr {F}_{1}(\partial _{t}m)= \xi _{G} \displaystyle \sum \limits _{\mathrm {k} \ge 0}\xi _{\mathrm {k}}\left( \frac{\partial _{t}m}{\gamma }\right) ^{2\mathrm {k}}\partial _{t}m, \end{aligned}$$

(4)

where $\xi _{\mathrm {k}}$’s are dimensionless coefficients with $\xi _{0}=1$. Taking the first order approximation of Taylor series expansion of R.H.S. term appears in (4), we obtain

$$\begin{aligned} \mathscr {T}_{d_{1}}=\left[ \xi _{G}\left( 1+\dfrac{\xi _{v}}{\gamma ^{2}}(\partial _{t}m)^{2} \right) \right] \left( m \times \partial _{t}m \right) . \end{aligned}$$

(5)

In (5), the first term represents the linear viscous-type Gilbert dissipative torque which describes the dissipation phenomenon in the case of magnetic materials without any intrinsic defects i.e. ideal materials. Second term describes a rate dependent nonlinear viscous dissipation. Here the positive dimensionless constants $\xi _{G}$ and $\xi _{v}$ represent the classical Gilbert damping and nonlinear viscous dissipation coefficients respectively [12, 26] (for the sake of notation, we use $\xi _{v}$ in place of $\xi _{1}$).

Dissipation torque $\mathscr {T}_{d_{2}}$ accounts for the presence of magnetic inclusions such as dislocations, impurities and other metallic defects in the ferromagnetic materials. Due to such inclusions an internal friction also known as dry-friction, takes place in the material which in turn opposes the DW propagation. This mechanism is rate-independent and responsible for the hysteresis and Barkhausen effect. This additional term is described by the maximal monotone operator $\mathscr {F}_{2}$ defined as (see [9, 10, 27–29]):

$$\begin{aligned} {\mathscr {F}}_{2} (\partial _{t} m) = \left\{ \!\!{\begin{array}{ll} {\frac{{\partial _{t} m}}{{|\partial _{t} m|}}} &{} \quad {{\text {if}}\quad \partial _{t} m \ne 0,} \\ {B(0,1)} &{} \quad {{\text {if}}\quad \partial _{t} m = 0.} \end{array} } \right. \end{aligned}$$

where B(0, 1) denotes the unit ball centered at origin in $\mathbb R^{3}$. $\xi _{d}$ is a positive dry-friction parameter which accounts for the average distributions of defects in the material.

Thus, $\mathscr {T}_{d}$ takes the following form:

$$\begin{aligned} \mathscr {T}_{d}=\left[ \xi _{G}\left( 1+\dfrac{\xi _{v}}{\gamma ^{2}}(\partial _{t}m)^{2} \right) + \dfrac{\gamma \xi _{d}}{|\partial _{t}m|} \right] \left( m \times \partial _{t}m \right) . \end{aligned}$$

(6)

Equation (6) is valid for $\partial _{t}m \ne 0$. For $\partial _{t}m = 0$, we choose the arbitrary constant vector which belongs to B(0, 1) in such a way that the dry-friction dissipation torque vanishes. For simplicity, we choose such an arbitrary vector to be as m.

The last term $\mathscr {T}_{stt}$ in (2) represents the spin transfer torque (STT) defined as:

$$\begin{aligned} \mathscr {T}_{stt}=v_{s}\left( -1+\zeta m \times \right) \partial _{x}m, \end{aligned}$$

(7)

where the spin-torque velocity $v_{s}$ is directly proportional to the current density J. The first term in (7) depicts the adiabatic contribution and describes a reactive STT whereas the second term is non-adiabatic and represents the dissipative torque. The constant $\zeta$ accounts for the phenomenological non-adiabatic spin-torque parameter [10, 14, 17, 19].

We rewrite the LLGS equation (2) as:

$$\begin{aligned} \begin{aligned} \partial _{t}m\!-\!\left[ \xi _{G}\left( 1\!+\!\dfrac{\xi _{v}}{\gamma ^{2}}(\partial _{t}m)^{2} \right) \!+\! \dfrac{\gamma \xi _{d}}{|\partial _{t}m|} \right] \left( m \times \partial _{t}m \right) \!=\!\left( \gamma \mathscr {H}_{eff}\!-\!v_{s}m \times \partial _{x}m -\zeta v_{s}\partial _{x}m \right) \times m. \end{aligned} \end{aligned}$$

(8)

with

$$\begin{aligned} \mathscr {H}_{eff}=A\partial _{xx}m+\beta (m \cdot \mathbf e )\mathbf e -m_{2}\vec {e}_{2}-m_{3}\vec {e}_{3}+h\vec {e}_2-\varepsilon v_{s}\vec {e}_{3}. \end{aligned}$$

In the subsequent section, we derive the equation of motion in steady-state regime and characterize the DW motion in different scenarios.

Description of Wall Motions

To understand the DW dynamics, we consider the unit magnetization vector in a nanowire in polar coordinate system as:

$$\begin{aligned} m=\left( \sin \theta \cos \phi , \cos \theta , \sin \theta \sin \phi \right) . \end{aligned}$$

(9)

where $\theta$ denotes the angle with the easy axis termed as polar angle and $\phi$ denotes the azimuthal angle. Both the angles $\theta$ and $\phi$ vary with space variable x and time variable t.

By substituting (9) in (8), we transform the LLGS equation in the spherical polar coordinates framework as:

$$\begin{aligned}&\sin \theta \partial _{t}\phi + \left[ \xi _{G}\left( 1\!+\!\dfrac{\xi _{v}}{\gamma ^{2}}\left( (\partial _{t}\theta )^{2} + \sin ^{2}\theta (\partial _{t}\phi )^{2}\right) \right) \!+\!\gamma \xi _{d}\left( (\partial _{t}\theta )^{2}\!+\!\sin ^{2}\theta (\partial _{t}\phi )^{2}\right) ^{-1/2} \right] \partial _{t}\theta \nonumber \\&\quad = A \gamma \partial _{xx}\theta \!-\! A\gamma \sin \theta \cos \theta (\partial _{x}\phi )^{2} - h \gamma \sin \theta \!-\! \gamma \varepsilon v_{s} \cos \theta \sin \phi \!-\!v_{s}\sin \theta \partial _{x}\phi \nonumber \\&\qquad - \zeta v_{s}\partial _{x}\theta - \left( \beta -\cos ^{2}\phi \right) \gamma \sin \theta \cos \theta . \end{aligned}$$

(10)

$$\begin{aligned}&\qquad - \!\partial _{t}\theta \!+\! \left[ \xi _{G} \left( 1\!+\!\dfrac{\xi _{v}}{\gamma ^{2}}\left( (\partial _{t}\theta )^{2}\!+\!\sin ^{2}\theta (\partial _{t}\phi )^{2}\right) \right) \!+\!\gamma \xi _{d}\left( (\partial _{t}\theta )^{2}\!+\!\sin ^{2}\theta (\partial _{t}\phi )^{2}\right) ^{-1/2} \right] \sin \theta \partial _{t}\phi \nonumber \\&\quad = A \gamma \sin \theta \partial _{xx}\phi + 2A \gamma \cos \theta \partial _{x}\theta \partial _{x}\phi +v_{s}\partial _{x}\theta -\zeta v_{s} \sin \theta \partial _{x}\phi -\gamma \sin \theta \sin \phi \cos \phi \nonumber \\&\qquad - \gamma \varepsilon v_{s} \cos \phi . \end{aligned}$$

(11)

In the steady propagating regime, DW shifts rigidly at a constant speed with a constant azimuthal angle. We denote the DW velocity in the steady-regime by the constant $v_{d} > 0.$ We consider the standard traveling wave ansatz to describe the DW motion in the form [5, 10, 12, 13, 23]

$$\begin{aligned} {\left\{ \begin{array}{ll} \theta =\theta (\sigma );~~ \sigma :=x-v_{d}t,\\ \phi =\phi _{0}=\text {constant}. \end{array}\right. } \end{aligned}$$

(12)

With the assumption (12), Eqs. (10) and (11) reduce to couple of ordinary differential equations:

$$\begin{aligned}&\displaystyle \left[ \xi _{G}\left( 1+ \dfrac{\xi _{v}}{\gamma ^{2}}v_{d}^{2}({\dot{\theta }})^{2} \right) v_{d}-\zeta v_{s} \right] {\dot{\theta }} +\rho = -A \gamma {\ddot{\theta }}+h\gamma \sin \theta +\gamma \varepsilon v_{s}\cos \theta \sin \phi _{0}\nonumber \\&\displaystyle +(\beta -\cos ^{2}\phi _{0})\gamma \sin \theta \cos \theta , \end{aligned}$$

(13)

$$\begin{aligned}&\displaystyle \left( v_{s}-v_{d} \right) {\dot{\theta }}=\gamma \sin \theta \sin \phi _{0} \cos \phi _{0}+\gamma \varepsilon v_{s}\cos \phi _{0}, \end{aligned}$$

(14)

where $\rho =\gamma \xi _{d}\text {sign}(v_{d}{\dot{\theta }})$ and overdot represents the ordinary derivative with respect to the traveling wave variable $\sigma$. We rewrite Eq. (14) as:

$$\begin{aligned} {\dot{\theta }}(\sigma )=\dfrac{1}{\lambda }\left( \sin \theta (\sigma ) + \mu \right) , \end{aligned}$$

(15)

with

$$\begin{aligned} \lambda ^{-1}=\dfrac{\gamma \sin (2 \phi _{0})}{2(v_{s}-v_{d})} ~~\text {and}~~ \mu =\dfrac{\lambda \gamma \varepsilon v_{s}cos\phi _{0}}{(v_{s}-v_{d})}. \end{aligned}$$

(16)

The material parameter $\lambda$ describes the DW thickness. To derive an expression for the analytical solution of traveling wave profile m(x, t), we solve (15) together with the boundary conditions $\theta (-\infty )=0$ and $\theta (+\infty )=\pi$ ($m \sim \pm \vec {e}_{2}$ as $x \rightarrow \mp \infty$) for different values of $\mu$. To do so, we consider the cases when $\mu =0, |\mu | <1$ and $|\mu |>1$. In the absence of Rashba field, i.e. for $\alpha _{R}=0$ which implies $\mu =0$, the solution takes the following form [10, 13, 23]:

$$\begin{aligned} \theta (\sigma )=\arccos \left( \dfrac{1-\exp (2\sigma /\lambda )}{1+\exp (2\sigma /\lambda )} \right) . \end{aligned}$$

(17)

By inserting (17) in (9), we obtain

$$\begin{aligned} m(x,t)=\text {sech}(\sigma / \lambda )\left( \cos \phi _{0}\vec {e}_{1}+\sin \phi _{0}\vec {e}_{3} \right) -\text {tanh}(\sigma / \lambda )\vec {e}_{2}. \end{aligned}$$

(18)

For $|\mu | < 1$, (15) admits the solution of the form [13, 23]

$$\begin{aligned} \theta (\sigma )=\arccos \left( \dfrac{1-\psi ^{2}(\sigma )}{1+\psi ^{2}(\sigma )} \right) , \end{aligned}$$

(19)

where

$$\begin{aligned}&\displaystyle \psi (\sigma )=-\frac{\tau (1+\sqrt{1-\mu ^{2}})\exp (\sigma \sqrt{1-\mu ^{2}}/\lambda )+(-1+\sqrt{1-\mu ^{2}})}{\mu (\tau \exp (x\sqrt{1-\mu ^{2}}/ \lambda )-1)},\\&\displaystyle \tau =\dfrac{1-|\mu |-\sqrt{1-\mu ^{2}}}{1-|\mu |+\sqrt{1-\mu ^{2}}}. \end{aligned}$$

In the case of $|\mu | >1$, solution is obtained using the condition that the variable $\theta$ takes the value zero at the center of the DW [13].

$$\begin{aligned} \theta (\sigma )=2\arctan \left( \dfrac{\sqrt{\mu ^{2}-1}\tan (\sigma \sqrt{\mu ^{2}-1}/\lambda +\tau _{1})-1}{\mu } \right) , \end{aligned}$$

(20)

with

$$\begin{aligned} \tau _{1}=\dfrac{1}{\sqrt{\mu ^{2}-1}}\arctan \left( \dfrac{\mu +1}{\sqrt{\mu ^{2}-1}} \right) . \end{aligned}$$

Our prime goal is to understand the variation of DW velocity $v_{d}$ in the steady-regime under the action of applied magnetic field h and spin-torque velocity $v_{s}$. In doing so, we establish the relation of the steady DW velocity $v_{d}$ with magnetic field h, spin-torque velocity $v_{s}$ and the Rashba parameter $\alpha _{R}$. Substituting (15) into (13), we have:

$$\begin{aligned} {P}\sin \theta + {Q}\sin ^{2}\theta + {R}\sin ^{3}\theta + {S}\sin \theta \cos \theta +{T}\cos \theta +{U}=0. \end{aligned}$$

(21)

where

$$\begin{aligned}&\displaystyle P =\dfrac{3\mu ^{2}\xi _{v} \xi _{G} v_{d}^{3}}{\gamma ^{2}\lambda ^{3}} +\dfrac{\left( \xi _{G}v_{d}-\zeta v_{s} \right) }{\lambda }-\gamma h \nonumber \\&\displaystyle Q =\dfrac{3\mu \xi _{v} \xi _{G} v_{d}^{3}}{\gamma ^{2}\lambda ^{3}} \nonumber \\&\displaystyle R =\dfrac{\xi _{v} \xi _{G} v_{d}^{3} }{\gamma ^{2}\lambda ^{3}}\\&\displaystyle S = \dfrac{A \gamma }{\lambda ^{2}}-\left( \beta - \cos ^{2}\phi _{0} \right) \gamma \nonumber \\&\displaystyle T =\dfrac{A \gamma \mu }{\lambda ^{2}}-\gamma \varepsilon v_{s}\sin \phi _{0}\nonumber \\&\displaystyle U =\dfrac{\mu ^{3}\xi _{v} \xi _{G} v_{d}^{3}}{\gamma ^{2}\lambda ^{3}} +\dfrac{\left( \xi _{G}v_{d}-\zeta v_{s} \right) \mu }{\lambda } + \rho . \nonumber \end{aligned}$$

(22)

We obtain the classical expression of the DW thickness $\lambda$ from (21) :

$$\begin{aligned} \lambda =\sqrt{\dfrac{A}{(\beta -\cos ^{2}\phi _{0})}}, \end{aligned}$$

(23)

which is independent of the considered dissipation factors. We take the average of (21) over the wall thickness $\left( \text {i.e.}~\text {for}~ 0 \leqslant \theta \leqslant \pi \right)$ which in turn yields a cubic equation of the DW velocity in the steady-regime with a DW of Bloch type $(\phi _{0}=\pi /2)$ (cf. [10, 23] and [13])

$$\begin{aligned} \begin{aligned} \xi _{v}v_{d}^{3}&+\dfrac{12(1+\frac{\pi }{2}\varepsilon v_{s})}{(6\pi \varepsilon ^{3}v_{s}^{3}+36\varepsilon ^{2}v_{s}^{2}+9\pi \varepsilon v_{s}+8)}\gamma ^{2}\lambda ^{2}v_{d}\\&- \dfrac{12}{(6\pi \varepsilon ^{3}v_{s}^{3}+36\varepsilon ^{2}v_{s}^{2}+9\pi \varepsilon v_{s}+8)}\dfrac{\gamma ^{2}\lambda ^{2}}{\xi _{G}}\left[ \zeta v_{s}(1+\frac{\pi }{2}\varepsilon v_{s})+\gamma \lambda h-\frac{\pi }{2}\gamma \lambda \xi _{d} \right] =0. \end{aligned} \end{aligned}$$

(24)

Under the impression of the physical constraint $v_{d} \ge 0$ and using (24), we derive the threshold condition:

$$\begin{aligned} \left[ \zeta v_{s}\left( 1+\frac{\pi }{2}\varepsilon v_{s}\right) +\gamma \lambda h-\frac{\pi }{2}\gamma \lambda \xi _{d} \right] \ge 0. \end{aligned}$$

(25)

Let us represent the threshold value for the applied magnetic field and spin-torque velocity, when the external sources act separately, by $h^{\sharp }$ and $v_{s}^{\sharp }$ respectively. Then from (25),

$$\begin{aligned}&v_{s}=0 \Rightarrow h^{\sharp }=\dfrac{\pi }{2}\xi _{d}. \end{aligned}$$

(26)

$$\begin{aligned}&h=0 \Rightarrow v_{s}^{\sharp }= {\left\{ \begin{array}{ll} \dfrac{\pi \gamma \lambda \xi _{d}}{2 \zeta }, ~~ \text {when} ~ \varepsilon =0\\ \dfrac{1}{\pi \varepsilon }\left( -1 +\sqrt{1+(\pi ^{2}\varepsilon \gamma \lambda \xi _{d}/\zeta )} \right) , ~~ \text {when} ~ \varepsilon \ne 0. \end{array}\right. } \end{aligned}$$

(27)

It is evident that $\varepsilon =0$ corresponds to the situation of absence of Rashba field. Next, we notice that (16) yields

$$\begin{aligned} \sin (2 \phi _{0})=\dfrac{2(v_{s}-v_{d})}{\gamma \lambda }, \end{aligned}$$

(28)

which immediately returns the following condition on the steady DW velocity $v_{d}$

$$\begin{aligned} v_{s}-\dfrac{\gamma \lambda }{2} \le v_{d} \le v_{s}+\dfrac{\gamma \lambda }{2}. \end{aligned}$$

(29)

Equation (29) describes the range in which the DW propagates with a constant velocity $v_{d}$. The left and right side of inequalities are referred as the lower and upper Walker-like breakdown velocities respectively. When the domain wall velocity exceeds the upper breakdown value, the magnetization oscillates between the Bloch $\big (\phi _{0}=\frac{\pi }{2}\big )$ and Néel $(\phi _{0}=0)$ wall. In this dynamic regime, magnetization precesses about the easy axis with a constant angular speed.

To get the clear understanding about the DW motions and Walker-like breakdown conditions of the external sources in presence of considered dissipation factors in the steady-regime, we take the following three different cases. In the first case, we investigate the wall motions in sole presence of Gilbert (linear) dissipation whereas in second case we deal with the linear and nonlinear dry friction dissipations. In the last case, we address the situation in which all the three dissipation factors viz. linear, nonlinear dry friction and viscous dissipations are present.

Wall Motions in Presence of Gilbert (Linear) Dissipation

In the sole presence of Gilbert (linear) dissipation $\left( \xi _{G} \ne 0; \xi _{d}=0; \xi _{v}=0 \right)$, Eq. (24) gives a following expression of DW velocity $v_{d}$ in terms of the parameters involved in the model:

$$\begin{aligned} v_{d}=\dfrac{\zeta v_{s}}{\xi _{G}}+\dfrac{\gamma \lambda h}{\xi _{G}(1+\frac{\pi }{2}\varepsilon v_{s})}. \end{aligned}$$

(30)

We insert (30) in (28) to obtain:

$$\begin{aligned} \left| \dfrac{h}{(1+\frac{\pi }{2}\varepsilon v_{s})}+\dfrac{v_{s}}{\gamma \lambda }(\zeta -\xi _{G})\right| \le \dfrac{\xi _{G}}{2}. \end{aligned}$$

(31)

Equation (31) depicts the breakdown condition of the applied sources for which the motion remains steady. We represent the Walker-like breakdown value of the applied magnetic field and spin-torque velocity, when applied separately, as $h^{*}$ and $v_{s}^{*}$ respectively.

It is apparent from (31):

$$\begin{aligned} \begin{aligned}&v_{s}=0 \Rightarrow h^{*}=\dfrac{\xi _{G}}{2}, \\&h= 0 \Rightarrow v_{s}^{*}=\dfrac{\xi _{G}\gamma \lambda }{2|\zeta -\xi _{G}|}. \end{aligned} \end{aligned}$$

(32)

Equation (32) gives the maximum value of the external sources for which motion occurs in steady-state regime. It is worth to notice that the steady DW motion originates for any non null values of applied sources. To be precise, there are no threshold condition for the external sources. Therefore, the wall motions are occurred for $0 \le h \le h^{*}$ and $0 \le v_{s} \le v_{s}^{*}$.

Wall Motions in Presence of Linear and Dry-Friction Dissipations

In the present case, we have the framework in which $\xi _{G} \ne 0; \xi _{d} \ne 0; \xi _{v}=0$. With the help of (24), we express the DW velocity as:

$$\begin{aligned} v_{d}=\dfrac{\zeta v_{s}}{\xi _{G}}+\dfrac{\gamma \lambda h}{\xi _{G}(1+\frac{\pi }{2}\varepsilon v_{s})}-\dfrac{\pi \gamma \lambda \xi _{d}}{\xi _{G}(1+\frac{\pi }{2}\varepsilon v_{s})}. \end{aligned}$$

(33)

In order to determine the threshold and Walker-type breakdown condition of the external sources, we put the value of $v_{d}$ in (28) and get

$$\begin{aligned} \left| \dfrac{v_{s}(\zeta -\xi _{G})}{\gamma \lambda }+ \dfrac{h}{(1+\frac{\pi }{2}\varepsilon v_{s})}-\dfrac{\pi \xi _{d}}{2(1+\frac{\pi }{2}\varepsilon v_{s})}\right| \le \dfrac{\xi _{G}}{2}. \end{aligned}$$

(34)

Under the separate action of external sources, using (34) we derive an expression for Walker-like breakdown condition of the applied magnetic field and spin-torque velocity in a similar way as described in the first case. Thus,

$$\begin{aligned} \begin{aligned}&v_{s}=0 \Rightarrow h^{*}=\dfrac{(\xi _{G}+\pi \xi _{d})}{2} \end{aligned} \end{aligned}$$

(35)

Now for the Walker-like breakdown condition of the spin-torque velocity, we have the following possibilities:

(i) In the absence of Rashba field i.e. when $\alpha _{R}=0$, we have

$$\begin{aligned} h=0 \Rightarrow v_{s}^{*}=\dfrac{\gamma \lambda }{2|\zeta - \xi _{G}|}\left[ \xi _{G}+\pi \xi _{d} \right] . \end{aligned}$$

(36)

(ii) In the presence of the Rashba field i.e. when $\alpha _{R} \ne 0, v_{s}^{*}$ is the lowest positive solution of the following quadratic equation.

$$\begin{aligned} \begin{aligned} h=0 \Rightarrow ~ K_{1}v_{s}^{2}+\left( \dfrac{4K_{1}-\pi \varepsilon \xi _{G}}{2 \pi \varepsilon } \right) v_{s}-\dfrac{1}{\pi \varepsilon }(\xi _{G}+\pi \xi _{d})=0, \end{aligned} \end{aligned}$$

(37)

where

$$\begin{aligned} K_{1}=\dfrac{(\zeta - \xi _{G})}{\gamma \lambda }. \end{aligned}$$

The threshold values of the external sources $h^{\sharp }$ and $v_{s}^{\sharp }$ are given by (26) and (27). Thus, DW motion is observed for the range $h^{\sharp } \le h \le h^{*}$ and $v_{s}^{\sharp } \le v_{s} \le v_{s}^{*}$.

Wall Motions in Presence of Linear, Dry-Friction and Viscous Dissipations

In presence of all the considered dissipative factors $( \xi _{G} \ne 0; \xi _{d} \ne 0; \xi _{v} \ne 0)$, the DW velocity is given by (24). First, we establish the threshold and Walker-like breakdown condition for the applied magnetic field in the absence of spin-torque velocity.

Equation (29) renders:

$$\begin{aligned} v_{s}=0 \Rightarrow v_{d}^{*}=\dfrac{\gamma \lambda }{2}. \end{aligned}$$

where $v_{d}^{*}$ denotes the upper Walker-like breakdown DW velocity in the absence of $v_{s}$. We insert $v_{d}=v_{d}^{*}$ and $v_{s}=0$ in (24) to get the upper breakdown condition of magnetic field i.e $h^{*}$, above which the motion is no longer steady.

$$\begin{aligned} h^{*}= \dfrac{\xi _{G}}{2}\left( 1+\dfrac{\xi _{v}}{6}\right) +\dfrac{\pi \xi _{d}}{2}. \end{aligned}$$

(38)

Whereas, the threshold value of the applied magnetic field $h^{\sharp }$, below which no DW motion take place, is given by (26).

Now, we carry out an exposition to derive the range of spin-torque velocity for which the motion happens in steady-state regime with $h=0$. In order to extract the threshold condition of spin-torque velocity $v_{s}$ in presence of Rashba field, we substitute the value of lower breakdown DW velocity from (29) into (24) which returns:

$$\begin{aligned} 2\pi \xi _{v}\varepsilon ^{3}({v_{s}})^{6}+ & {} 3\left( -\pi \xi _{v}\varepsilon ^{3}\gamma \lambda + 4\xi _{v}\varepsilon ^{2} \right) ({v_{s}})^{5}+3\left( \frac{\pi }{2}\xi _{v}\varepsilon ^{3}\gamma ^{2}\lambda ^{2} -6\xi _{v}\varepsilon ^{2}\gamma \lambda + \pi \xi _{v}\varepsilon \right) ({v_{s}})^{4}\nonumber \\+ & {} \left( -\frac{\pi }{4}\xi _{v}\varepsilon ^{3}\gamma ^{3}\lambda ^{3}+9\xi _{v}\varepsilon ^{2}\gamma ^{2}\lambda ^{2}-\frac{9\pi }{2}\xi _{v}\varepsilon \gamma \lambda +\frac{8}{3}\xi _{v} \right) ({v_{s}})^{3}\nonumber \\+ & {} \left[ -\frac{3}{2}\xi _{v}\varepsilon ^{2}\gamma ^{3}\lambda ^{3}+\left( 2+\frac{9}{4}\xi _{v}-\frac{2\zeta }{\xi _{G}} \right) \pi \varepsilon \gamma ^{2}\lambda ^{2}-4\xi _{v}\gamma \lambda \right] ({v_{s}})^{2} \nonumber \\+ & {} \left[ -\left( 1+\frac{3}{8}\xi _{v} \right) \pi \varepsilon \gamma ^{3}\lambda ^{3}+2\left( 2+\xi _{v}-\frac{2\zeta }{\xi _{G}} \right) \gamma ^{2}\lambda ^{2} \right] ({v_{s}})\nonumber \\+ & {} \left( -2-\frac{1}{3}\xi _{v}+\frac{2\pi }{\xi _{G}}\xi _{d} \right) \gamma ^{3}\lambda ^{3}=0. \end{aligned}$$

(39)

We denote the effective threshold value of spin-torque velocity by $(\bar{v}_{s})^{\sharp }$ at which DW motion initiates and it is given as:

$$\begin{aligned} \left( \bar{v}_{s}\right) ^{\sharp }=\max \left\{ v_{s}^{\sharp }, (\bar{v}_{s})_{1} \right\} , \end{aligned}$$

(40)

where $v_{s}^{\sharp }$ is given by (27) and $(\bar{v}_{s})_{1}$ is the lowest positive solution of (39). We draw the Walker-like breakdown condition of spin-torque velocity $v_{s}$ by inserting the value of upper breakdown DW velocity from (29) into (24) which renders:

$$\begin{aligned} 2\pi \xi _{v}\varepsilon ^{3}({v_{s}})^{6}+ & {} 3\left( \pi \xi _{v}\varepsilon ^{3}\gamma \lambda + 4\xi _{v}\varepsilon ^{2} \right) ({v_{s}})^{5}+3\left( \frac{\pi }{2}\xi _{v}\varepsilon ^{3}\gamma ^{2}\lambda ^{2} +6\xi _{v}\varepsilon ^{2}\gamma \lambda + \pi \xi _{v}\varepsilon \right) ({v_{s}})^{4}\nonumber \\+ & {} \left( \frac{\pi }{4}\xi _{v}\varepsilon ^{3}\gamma ^{3}\lambda ^{3}+9\xi _{v}\varepsilon ^{2}\gamma ^{2}\lambda ^{2}+\frac{9\pi }{2}\xi _{v}\varepsilon \gamma \lambda +\frac{8}{3}\xi _{v} \right) ({v_{s}})^{3}\nonumber \\+ & {} \left[ \frac{3}{2}\xi _{v}\varepsilon ^{2}\gamma ^{3}\lambda ^{3}+\left( 2+\frac{9}{4}\xi _{v}-\frac{2\zeta }{\xi _{G}} \right) \pi \varepsilon \gamma ^{2}\lambda ^{2}+4\xi _{v}\gamma \lambda \right] ({v_{s}})^{2} \nonumber \\+ & {} \left[ \left( 1+\frac{3}{8}\xi _{v} \right) \pi \varepsilon \gamma ^{3}\lambda ^{3}+2\left( 2+\xi _{v}-\frac{2\zeta }{\xi _{G}} \right) \gamma ^{2}\lambda ^{2} \right] ({v_{s}})\nonumber \\+ & {} \left( 2+\frac{1}{3}\xi _{v}+\frac{2\pi }{\xi _{G}}\xi _{d} \right) \gamma ^{3}\lambda ^{3}=0. \end{aligned}$$

(41)

We represent the effective Walker-like breakdown value by $(\tilde{v}_{s})^{*}$ above which the wall motion is oscillatory and express it as:

$$\begin{aligned} \left( \tilde{v}_{s}\right) ^{*}=\min \left\{ (\bar{v}_{s})_{2}, (\tilde{v}_{s})_{1} \right\} , \end{aligned}$$

(42)

where $(\bar{v}_{s})_{2}$ is the next positive solution of (39), whereas $(\tilde{v}_{s})_{1}$ represents the lowest positive solution of (41). Therefore, the range of the external sources for which the motion happens in steady-state regime are $h^{\sharp } \le h \le h^{*}$ and $\left( \bar{v}_{s}\right) ^{\sharp } \le v_{s} \le \left( \tilde{v}_{s}\right) ^{*}$.

In the absence of Rashba field i.e $\alpha _{R}=0$ which in turn implies $\varepsilon =0$, the threshold and breakdown condition of the external sources can be drawn with the similar arguments as discussed above. More precisely, the desired conditions are obtained by substituting $\varepsilon =0$ in (39) and (41).

In the next section, we illustrate the analytical results established in different scenario under the separate action of external sources numerically.

Illustration of Wall Motions Under Different Scenarios

To perform the numerical analysis, we consider the value of the parameters involved in the model as proposed in [13, 15, 16]. We deal with the metallic ferromagnet having saturation magnetization $M_{s}=3 \times 10^{5} \text {A/m}$, anisotropy constant $K=2 \times 10^{5} \text {J}/\text {m}^{3}$, exchange constant $A_{ex}=10^{-11} \text {J/m}$, Landè factor $g=2$, Gilbert damping constant $\xi _{G}=0.2$, polarization factor $P=0.5$ with Rashba parameter $\alpha _{R}=10^{-11} \text {eVm}$. It is worth to mention that nature of the solutions of (39) and (41) changes in the scenarios when $\zeta < \xi _{G}$ and $\zeta > \xi _{G}$. This, in turn affects the value of threshold and breakdown conditions. Therefore, we consider the two values for the non-adiabatic parameter as $\zeta =0.1$ and $\zeta =0.4$ which correspond to the cases $\zeta <\xi _{G}$ and $\zeta > \xi _{G}$ respectively.

We investigate the steady DW motions driven by an applied magnetic field and electric current separately. We discuss the DW motion for the several values of dry-friction and viscous coefficients and analyze the dynamics for ideal (absence of nonlinear dissipation factors) and non-ideal ferromagents.

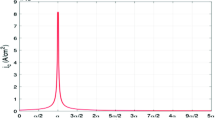
Field driven wall motions are exhibited in Fig. 2 under different scenarios. The steady wall motion starts at the threshold value $h^{\sharp }$ as mentioned in (26) which increases with an increase of dry-friction dissipation coefficient. As we gradually increase the magnetic field h, the Walker-type breakdown velocity $v_{d}^{*}=\frac{\gamma \lambda }{2}$ is achieved at the breakdown value of magnetic field $h^{*}$ as given in (38). It is apparent from the figure that the presence of dry-friction parameter pushes the DW velocity $v_{d}$ to deviate towards higher values of magnetic field h in a linear way while the presence of viscous dissipation reflects the nonlinear shift of $v_{d}$ towards h. We notice that the steady DW velocity $v_{d}$ for a given value of applied field is larger in the case of ideal $(\xi _{v}=0, \xi _{d}=0)$ ferromagnets as compared to the non-ideal.

Fig. 2

Illustration of Walker-type breakdown condition of DW velocity, threshold and breakdown values of applied magnetic field in the steady-state regime

We provide an insight of current driven DW motion in steady-state regime in Figs. 3 and 4 which correspond to the scenarios $\zeta > \xi _{G}$ and $\zeta < \xi _{G}$. To elucidate the sole effect of Rashba field on the DW dynamics, we further consider the two cases corresponding to the absence and presence of Rashba field.

In particular, Fig. 3a reflects the variation of DW velocity $v_{d}$ with the current induced spin-torque velocity $v_{s}$ under the situation when $\zeta >\xi _{G}$ in the absence of Rashba field. Similar to the field driven motion, the progressive increase of dry-friction dissipation is responsible for the linear shift of $v_{d}$ towards higher values of $v_{s}$ whereas with an increase of viscous dissipation, $v_{d}$ deviates towards $v_{s}$ in a nonlinear fashion. The DW motion originates at the effective threshold value $(\bar{v}_{s})^{\sharp }$ as obtained in (40). The motion starts at $(\bar{v}_{s})^{\sharp }=v_{s}^{\sharp }$ for the values of dry-friction dissipation parameter $\xi _{d}=0$ and $\xi _{d}=0.075$ whilst the threshold value for $\xi _{d}=0.15$ is $(\bar{v}_{s})^{\sharp }=(\bar{v}_{s})_{1}$.

Fig. 3

Variation of steady DW velocity with the current induced spin-torque velocity under the scenario when $\zeta > \xi _{G}$. a In the absence of Rashba field $(\varepsilon = 0)$. b In the presence of Rashba field $(\varepsilon \ne 0)$

Fig. 4

Variation of steady DW velocity with the current induced spin-torque velocity under the scenario when $\zeta < \xi _{G}$. a In the absence of Rashba field $(\varepsilon = 0)$. b In the presence of Rashba field $(\varepsilon \ne 0)$

The steady DW motion breakdowns at the effective breakdown value of spin-torque velocity $\left( \tilde{v}_{s}\right) ^{*}$ as given in (42). In the sole presence of dry-friction dissipation the breakdown condition of the spin-torque velocity is achieved at $\left( \tilde{v}_{s}\right) ^{*}=(\tilde{v}_{s})_{1}$. As we moderately increase the viscous dissipation, for smaller values $(\xi _{v}=0.22)$ the breakdown occurs at upper-breakdown value of spin-torque velocity $(\tilde{v}_{s})_{1}$. With the progressive increase in viscous dissipation the DW velocity shifts from the linear behavior and as a consequence breakdown is attained at the lower breakdown $(\bar{v}_{s})_{2}$.

In the presence of Rashba field, features of current driven wall motions are portrayed in Fig. 3b. It can be perceived from the figure that steady DW motion starts for the smaller values of spin-torque velocity in presence of nonlinear dissipations as compared to the scenario of absence of Rashba field. In the only presence of dry-friction dissipation, the breakdown value is reached at upper breakdown value of spin-torque velocity $(\tilde{v}_{s})_{1}$. However, the presence of dry-friction dissipation causes the nonlinear dependence of DW velocity with spin-torque velocity [see (33)]. Also, for large values of $v_{s}$, the domain wall velocity approximates with the DW velocity obtained when $\xi _{d}=0$. As a contrast to the case of absence of Rashba field, in the presence of viscous dissipation, the breakdown value is accomplished at the lower breakdown $(\bar{v}_{s})_{2}$ even for the smaller values of viscous dissipation $(\xi _{v}=0.22)$.

The variation of DW velocity with the current induced spin-torque velocity in the situation when $\zeta < \xi _{G}$ is depicted in Fig. 4. We have pointed out earlier that nature of the solutions of (39) and (41) varies in the cases when $\zeta > \xi _{G}$ and $\zeta < \xi _{G}$. In the present scenario $\zeta < \xi _{G}$, (39) admits a real positive solution whereas (41) does not render a positive solution. As a consequence, the solutions $(\bar{v}_{s})_{2}$ and $(\tilde{v}_{s})_{1}$ do not exist. Therefore, the steady DW motion always originates at $(\bar{v}_{s})^{\sharp }=v_{s}^{\sharp }$ and breaks at $(\tilde{v}_{s})^{*}=(\bar{v}_{s})_{1}$ as displayed in Fig. 4. We observe the similar behavior of Rashba field on wall dynamics as was observed in the scenario when $\zeta > \xi _{G}$. Identical to the field driven motion, the DW velocity for a given value of spin-torque velocity is higher in the metallic ferromagnets with no impurities.

Conclusion

In this article, we investigate the DW motion in the steady-state regime triggered by the magnetic field and spin-polarized electric current in ferromagnetic nanowires. To derive the equation of motion, we adopt the standard traveling wave ansatz which describes a Bloch wall structure in the steady-state regime. We observe that the motion in the case of ideal ferromagnets is much faster irrespective to the nature of external sources which is also pointed out theoretically in [12, 13] and numerically in [10, 11]. In field driven motion, Walker-type breakdown condition of DW velocity is independent of the dissipation coefficients and remain same in all the scenarios. However, in case of current driven motion it depends on the dissipation coefficients and varies under the different situations. We also notice that in current driven motion, the Walker-type breakdown of DW velocity is higher as compared to the field driven motion and therefore broadens the steady-state regime. On the other hand, the presence of Rashba field characterizes the nonlinear dependence of DW velocity with spin-torque velocity in presence of nonlinear dissipations.

This work branches out some problems such as the analysis of DW motions in the precessional regime, the study of wall motions with the inclusion of thermal effects.