TODIM Method Based on Cumulative Prospect Theory for Multiple Attributes Group Decision Making Under Probabilistic Hesitant Fuzzy Setting

Abstract

In the era of uncertain information everywhere, the Probabilistic Hesitant Fuzzy sets (PHFs), utilizing the possible numbers and its possible membership degrees to descript decision-makers’ behavior, has been brought about widespread attention. Scholars from all over the world applied numerous approaches in this environment since Probabilistic Hesitant Fuzzy sets (PHFs) has been come up with, and there are still untapped territories. The TODIM (TOmada deDecisão Iterativa Multicrite´rio) method is a common decision-making method which is based on the prospect theory (PT). Unlike the other multiple criteria decision making (MCDM) methods, the TODIM method think over the bounded rationality of decision makers to choose the optimal alternative according to the decision maker’s psychological reality. In this essay, we introduce the Extended TODIM Based on Cumulative Prospect Theory (CPT) for probabilistic hesitant fuzzy multiple attributes group decision-making (MAGDM). In addition, the entropy is applied to calculate the weights between attributes. Finally, the developed method is used to solve the decision-making case study. To test the reasonability of this new method, we utilize a numerical case to compare the extended TODIM method with other methods.

1 Introduction

When we make decisions, the sufficiency and accuracy of data is necessary. However, we always can’t obtain the definite value in most conditions[1,2,3,4]. For example, we can’t use a definite value to depict how comfortable the chair is or how is the weather today[5,6,7,8,9]. In these conditions, the comfort of the chair and the feel about the weather is a fuzzy expression, which often appears in our everyday lives. Therefore, to make decisions with the fuzzy description, Zadeh [10]first introduced the idea of fuzzy sets, and this theory has been applied in many fields such as the cornerstone for the research and decision-making and control. Then, the extension of fuzzy set for instance, intuitionistic fuzzy sets (IFSs) was proposed by Atanassov [11] containing membership function, non-membership function and hesitation function was then introduced. With the development of this theory, the conception of the hesitant fuzzy set (HFS) was then proposed by Torra [12] to extend the fuzzy set which is to denote the uncertainty caused by hesitation solving the common phenomenon in decision-making. In the environment of hesitant fuzzy, the membership degree could be indicated by some possible number. The definition brings about the rapid development of hesitant fuzzy set which has a great breakthrough in decision-making. Then, the hesitant fuzzy element(HFE) proposed by Xia and Xu [13] is to solve the problem of determining the element’s membership to a set on account of the uncertainty between different numbers and then prove the between intuitionistic fuzzy set and hesitant fuzzy set. With the proposition of the HFE, the idea of correspondent operators to aggerate hesitant fuzzy information was obtained. Not long after this, the score function and Xu and Xia [14] raised the idea of the score function,deviation function and the comparison rule and set the basis on the calculation. Xu and Cai [15] provided the aggregating operators to integrate the hesitant fuzzy information. Nevertheless, HFE can be regarded as a particular equivalent form whose occurring probabilities of the possible value is equal. The probabilistic hesitant fuzzy set and the corresponding score function, deviation function and its comparison law were proposed by Xu and Zhou [16]. Moreover, the probabilistic hesitant fuzzy weighted averaging geometric operators (PHFWA) were introduced by Xu and Zhou [16] to process PHFE information. Then the improved PHFS was introduced by Zhang, Xu and He [17] to give more space of hesitation and the integrations of the improved PHES can be calculated by the improved operators.

A large amount of methods to solve the MADM problem are proposed, like VIKOR method [18], MABAC method [19,20,21], TODIM method [22], EDAS method [23, 24], MOORA method [25]. Among them, the TODIM method is specific in its piecewise function to denote the distance between two elements. Besides TODIM take the negative and positive attributes into consideration by introducing the parameter in the calculation process. Qin, Liang, Li, Chen and Yu [26] used the TODIM method and the triangular intuitionistic fuzzy numbers to solve MAGDM problems. Krohling, Pacheco and Siviero [27] utilized the TODIM in intuitionistic fuzzy environment. Zhang and Xu [28] expound the novel measured functions-based TODIM approach under hesitant fuzzy environment. Hanine, Boutkhoum, Tikniouine and Agouti [29] compared the fuzzy AHP and fuzzy TODIM methods to select landfill location. Passos, Teixeira, Garcia, Cardoso and Gomes [30] used the TODIM-FSE method solve the oil spill response problems. Tseng, Lin, Tan, Chen and Chen [31] used TODIM method to assess green supply chain under uncertainty environment. Li, Shan and Liu [32] used the developed TODIM method for MAGDM with interval intuitionistic fuzzy information. Wei, Ren and Rodriguez [33]used the hesitant fuzzy linguistic TODIM method based on a score function to solve MAGDM problems. Liu and Teng [34] used the TODIM method based on two-dimension uncertain linguistic variable to solve MAGDM problems. Ren, Xu and Gou [35] used Pythagorean fuzzy TODIM approach to solve MAGDM problems. Zhang, Liu and Shi [36] used the extended TODIM based on neutrosophic numbers. Zhang, Du and Tian [37]utilized the TODIM under probabilistic hesitant fuzzy circumstance to promise venture capital project. Zhang, Wang and Wang [38] applied the TODIM method to deal with the MAGDM problems under probabilistic interval-valued hesitant fuzzy environment. With the failure to determine the attribute weight, this method was then improved. Tian, Xu and Gu [39] improved the classical TODIM method by using Cumulative Prospect Theory (CPT). Even though the CPT has been proposed for years, several scholars combine CPT with TODIM [40,41,42,43,44]. This improved method integrates the advantages of TODIM and CPT and solves the problem which cannot be solved by traditional methods. Even so, this method still has several problems, for example, it can’t distinguish positive and negative attributes. In practice, the decisions are always made by three or more people, so it is more rewarding to research MAGDM under PHFSs. Thus, this paper improves TODIM which bases on CPT and investigates its use for MAGDM under probabilistic hesitant fuzzy environment.

The main scientific values of this paper are as follows: (i) a developed TODIM method based on CPT with PHF information is introduced to better represent the decision-making circumstance and the psychological state of the decision maker (ii) This novel TODIM method with uncertainty information is also applied in the PHF environment which contains more information than other circumstance. (iii) In this newly proposed method, the integration of CPT and classical TODIM method improves the shortcomings of the original method.

The main thread of this article are as follows: Sect. 2 introduces the basics of this article briefly. In Sect. 3, this improved TODIM method is then applied to solve the problem under probabilistic hesitant fuzzy MAGDM. Section 4 demonstrates the adhibition of the new method and measure with the classical method to testify its availability. In the end, the Sect. 5 shows we draw a conclusion based on the research in this article.

2 Preliminary Knowledge

In this section, we review the basic knowledges of PHFS, including the definition of PHFS, the classical computational algorithms, newly process of normalization and its correspondent calculation formula. In addition, we construct a structure of the developed TODIM method which is based on cumulative prospect theory (CPT).

2.1 Probabilistic Hesitant Fuzzy Sets

Definition 1

[16]. Assume $G$ be a fixed set, and a probabilistic hesitant fuzzy set (PHFS) on $G$ is denoted as the following mathematical equation:

$$L = \{ < g,\gamma _{g} (b_{g} ) > |g \in G\}$$

(1)

where the function $\gamma _{g} (b_{g} )$ is the combination of different statistics which is in [0,1], denoting the possible membership degree of element $g$ in $G$ to set $L$, and the $b_{g}$ is the probability of occurrence of the membership degree.$k_{{(g)}} b_{{(g)}}$ is the probabilistic hesitant fuzzy element (PHFE) and it can be abbreviated as $k(b)$. PHFE can be denoted by $\gamma (b) = \{ k_{g}^{\lambda } (b_{g}^{\lambda } )|g = 1,2,...,\# k,\lambda = 1,2, \cdot \cdot \cdot j\}$, where the probability of the membership degree $b_{g}^{\lambda }$ satisfies $\sum\nolimits_{{\lambda = 1}}^{{\# k}} {b_{g}^{\lambda } = 1}$,$\# k$ denotes the quantity of the possible values.

Definition 2

[16]. Let $\gamma _{g} (b_{g} ) = \{ k_{g}^{\lambda } (b_{g}^{\lambda } )\}$,$\gamma _{1} (b_{1} ) = \{ k_{m}^{{\lambda _{{_{m} }} }} (b_{m}^{{\lambda _{m} }} )\}$ and $\gamma _{2} (b_{2} ) = \{ k_{n}^{{\lambda _{n} }} (b_{n}^{{\lambda _{n} }} )\}$ represent three PHFEs, then we can obtain the following algorithms:

• 1. $\gamma _{1} (b_{1} ) \oplus \gamma _{2} (b_{2} ) = \cup _{{\lambda _{m} = 1, \cdot \cdot \cdot ,\# k_{1} ,\lambda _{n} = 1, \cdot \cdot \cdot ,\# k_{2} }} \{ (k_{m}^{{\lambda _{m} }} + k_{n}^{{\lambda _{n} }} - k_{m}^{{\lambda _{m} }} k_{n}^{{\lambda _{n} }} )(b_{m}^{{\lambda _{m} }} b_{n}^{{\lambda _{n} }} )\}$;

• 2. $\gamma _{1} (b_{1} ) \otimes \gamma _{2} (b_{2} ) = \cup _{{\lambda _{m} = 1, \cdot \cdot \cdot ,\# k_{1} ,\lambda _{n} = 1, \cdot \cdot \cdot ,\# k_{2} }} \{ k_{m}^{{\lambda _{m} }} k_{n}^{{\lambda _{n} }} (b_{m}^{{\lambda _{m} }} b_{n}^{{\lambda _{n} }} )\}$;

• 3. $\varpi \gamma (b) = \cup _{{\lambda = 1, \cdot \cdot \cdot ,\# k}} \{ 1 - (1 - k_{g}^{\lambda } )^{\varpi } )(b_{{_{g} }}^{\lambda } )\}$;

• 4. $(\gamma (b))^{\varpi } = \cup _{{\gamma = 1, \cdot \cdot \cdot \# k}} \{ (k_{g}^{\lambda } )^{\varpi } (b_{g}^{\lambda } )\}$

Definition 3

[16]. For a PHFE, the score function of $\gamma (b)$ can be obtained by Eq. (2)

$$s(\gamma (b)) = \sum\limits_{{\lambda = 1}}^{{\# k}} {k_{g}^{\lambda } } b_{g}^{\lambda }$$

(2)

where $\# k$ represents the value of the diverse membership degrees, $b_{g}^{\lambda }$ represents the probability of the membership degree which satisfies $\sum\nolimits_{{\lambda = 1}}^{{\# k}} {b_{g}^{\lambda } = 1}$.

Definition 4

[16]. For a PHFE, the deviation degree of $\gamma (b)$ can be obtained by expression:

$$d(\gamma (b)) = \sum\limits_{{\lambda = 1}}^{{\# k}} {b_{g}^{\lambda } } [k_{g}^{\lambda } - s(\gamma (b))]^{2}$$

(3)

By analogy the score and deviation functions with the expectation and variance of the random variance, we can compare two different PHFEs $\gamma _{1} (b_{1} ) = \{ k_{m}^{{\lambda _{{_{m} }} }} (b_{m}^{{\lambda _{m} }} )\}$ and $\gamma _{2} (b_{2} ) = \{ k_{n}^{{\lambda _{n} }} (b_{n}^{{\lambda _{n} }} )\}$ by the following laws:

• 1. (1) $\gamma _{1} (b_{1} ) > \gamma _{2} (b_{2} )$, if $s(\gamma _{1} (b_{1} )) > s(\gamma _{2} (b_{2} ))$

• 2. (2) $\gamma _{1} (b_{1} ) > \gamma _{2} (b_{2} )$, if $s(\gamma _{1} (b_{1} )) = s(\gamma _{2} (b_{2} ))$ and $d(\gamma _{1} (b_{1} )) < d(\gamma _{2} (b_{2} ))$

• 3. (3) $\gamma _{1} (b_{1} ) = \gamma _{2} (b_{2} )$, if $s(\gamma _{1} (b_{1} )) = s(\gamma _{2} (b_{2} ))$ and $d(\gamma _{1} (b_{1} )) = d(\gamma _{2} (b_{2} ))$

• 4. (4) $\gamma _{1} (b_{1} ) < \gamma _{2} (b_{2} )$, if $s(\gamma _{1} (b_{1} )) = s(\gamma _{2} (b_{2} ))$ and $d(\gamma _{1} (b_{1} )) > d(\gamma _{2} (b_{2} ))$

Definition 5

[16]. Let $\gamma _{1} (b_{1} )$ and $\gamma _{2} (b_{2} )$ be two PHFEs with the same number of the different membership values. The Hamming distance $d(\gamma _{1} (b_{1} ),\gamma _{2} (b_{2} ))$ which is between $\gamma _{1} (b_{1} ) = \{ k_{m}^{{\lambda _{{_{m} }} }} (b_{m}^{{\lambda _{m} }} )\}$ and $\gamma _{2} (b_{2} ) = \{ k_{n}^{{\lambda _{n} }} (b_{n}^{{\lambda _{n} }} )\}$ is calculated by Eq. (4)

$$d(\gamma _{1} (b_{1} ),\gamma _{2} (b_{2} )) = \frac{1}{{\# k_{1} }}\sum\nolimits_{{\lambda = 1}}^{{\# k_{1} }} {|b_{m}^{{\lambda _{m} }} } k_{m}^{{\lambda _{m} }} - b_{n}^{{\lambda _{n} }} k_{n}^{{\lambda _{n} }} |,\;\# k_{1} = \# k_{2}$$

(4)

where $\# k_{1}$ denotes the value of the membership degree, $k_{m}^{{\lambda _{m} }}$ and $k_{n}^{{\lambda _{n} }}$ is the $\lambda - th$ largest number in $\gamma _{1} (b_{1} )$ and $\gamma _{2} (b_{2} )$ separately, $b_{m}^{{\lambda _{m} }}$ and $b_{n}^{{\lambda _{n} }}$ shows the possibility of the different membership degrees.

For two PHFEs, the value of $\# k_{1}$ and $\# k_{2}$ may be different from each other. It is of necessity to normalize the PHFEs. Zhang, Xu and He [17] introduced the normalization process.

Definition 6 [17]

Assume $\# k_{1} > \# k_{2}$, $\rho ^{ + }$ and $\rho ^{ - }$ be the maximum and minimum memberships in $\gamma _{1} (b_{1} )$, and $\kappa$ ($0 < \kappa < 1$) be the parameter which denotes the decision-makers’ attitudes of risk. And the added membership can be calculated as Eq. (5)

$$\rho = \kappa \rho ^{ + } + (1 - \kappa )\rho ^{ - }$$

(5)

then we can add the number of $\rho$ to $\gamma _{2} (b_{2} )$,with the value of possibility of it is 0. Then the decision matrix can be normalized like that:

When $\kappa$ = 0, which denotes the decision maker is a risk-averter, the added membership is determined by Eq. (6)

$$\rho = \rho ^{ - }$$

(6)

When $\kappa$ = 1, which denotes the decision maker is a risk-seeker, the added membership is determined as Eq. (7)

$$\rho = \rho ^{{\text{ + }}}$$

(7)

When $\kappa$ = 0.5, which denotes the decision maker is a risk-neuter, the added membership is determined as Eq. (8)

$$\rho = \frac{{\rho ^{{\text{ + }}} {\text{ + }}\rho ^{ - } }}{2}$$

(8)

2.2 Some HPFE-Weighted Operators

One of the most important things to pay attention to when processing information is how to integrate the information of group decision-making. With the deepening of related research, the weighted aggregation operators may be the suitable means. The PHFWA operator and the PHFWG operator is introduced[16].

Definition 7

[16]. Let $N_{g} (g = 1,2, \cdot \cdot \cdot ,x)$ be the aggregation of PHFNs, and the equation of PHFWA operator is shown as Eq. (9)

$$\begin{gathered} PHFWA(N_{1} ,N_{2} , \cdot \cdot \cdot ,N_{x} ) = \mathop \oplus \limits_{{g = 1}}^{x} (N_{g} v_{g} ) \hfill \\ = \mathop \cup \limits_{{k_{1} \in N_{1} ,k_{2} \in N_{2} , \cdot \cdot \cdot ,k_{x} \in N_{x} }} \{ 1 - \mathop \Pi \limits_{{g = 1}}^{x} (1 - k_{g} )^{{v_{g} }} (b_{1} b_{2} \cdot \cdot \cdot b_{x} )\} \hfill \\ \end{gathered}$$

(9)

where $v_{g} = (v_{1} ,v_{2} , \cdot \cdot \cdot ,v_{x} )$ is the weight vector of the $N_{x}$, and $\sum\nolimits_{{g = 1}}^{x} {v_{g} } = 1$, $v_{g} \in [0,1]$, and $b_{g}$ represents the probability.

Definition 8

[16]. Let $N_{x} (g = 1,2, \cdot \cdot \cdot ,x)$ be a set of PHFNs, and the equation of probabilistic hesitant fuzzy weighted geometric (PHFWG) operator is shown as Eq. (10):

$$\begin{gathered} PHFWG = (N_{1} ,N_{2} , \cdot \cdot \cdot ,N_{g} ) = \mathop \oplus \limits_{{g = 1}}^{x} (N_{g} )^{{v_{g} }} \hfill \\ = \mathop \cup \limits_{{k_{1} \in N_{1} ,k_{2} \in N_{2} , \cdot \cdot \cdot ,k_{x} \in N_{x} }} \{ \mathop \Pi \limits_{{g = 1}}^{x} (k_{g} )^{{v_{g} }} (b_{1} b_{2} \cdot \cdot \cdot b_{x} )\} \hfill \\ \end{gathered}$$

(10)

where $v_{g} = (v_{1} ,v_{2} , \cdot \cdot \cdot ,v_{x} )$ is the weight vector of the $N_{x}$, and $\sum\nolimits_{{g = 1}}^{x} {v_{g} } = 1$.

2.3 Extended Normalized PHFEs, Distance and Other Operations

With the development of the relevant areas, the normalized process in Definition 6 has some limitations. The normalized algorithms are influenced by the different risk-preferences of different decision-makers. which may result in different distance between PHFEs. Therefore, a new process to obtain the normalized PHEFs is introduced by Li, Chen, Niu and Wang [45]. With this new method of normalizing, the set of probability is the same which avoid the calculation of probabilities.

Definition 9

[45]. Set $\gamma _{g} (b_{g} )$ = $\{ k_{g} (b_{g} )\}$,$\gamma _{1} (b_{1} ) = \{ k_{m} (b_{m} )\}$ and $\gamma _{2} (b_{2} ) = \{ k_{n} (b_{n} )\}$ be three PHFEs separately. The specific steps of normalizing are as follows:

Step 1. Determine the first element of normalized PHFEs, where $\gamma _{g}^{ * } (b_{g}^{ * } )$ denotes the normalized PHFEs. If $b_{1}^{1} < b_{2}^{1}$, then $k_{1}^{1} (b_{1}^{1} ) = k_{1}^{1} (b_{1}^{1} )$ and $k_{2}^{1} (b_{2}^{1} ) = k_{2}^{1} (b_{1}^{1} )$, otherwise, $k_{1}^{1} (b_{1}^{1} ) = k_{1}^{1} (b_{2}^{1} )$ and $k_{2}^{1} (b_{2}^{1} ) = k_{2}^{1} (b_{2}^{1} )$.

Step 2. Determine the second element of normalized PHFEs. If $b_{1}^{1} < b_{2}^{1}$ and $b_{2}^{1} - b_{1}^{1} \le b_{1}^{2}$, then $k_{1}^{2} (b_{1}^{2} ) = k_{1}^{2} (b_{2}^{1} - b_{1}^{1} )$ and $k_{2}^{2} (b_{2}^{2} ) = k_{2}^{1} (b_{2}^{1} - b_{1}^{1} )$. If $b_{1}^{1} < b_{2}^{1}$ and $b_{2}^{1} - b_{1}^{1} > b_{1}^{2}$, then $k_{1}^{2} (b_{1}^{2} ) = k_{1}^{2} (b_{1}^{2} )$ and $k_{2}^{2} (b_{2}^{2} ) = k_{2}^{1} (b_{1}^{2} )$. If $b_{1}^{1} \ge b_{2}^{1}$ and $b_{1}^{1} - b_{2}^{1} \le b_{2}^{2}$, then $k_{1}^{2} (b_{1}^{2} ) = k_{1}^{1} (b_{1}^{1} - b_{2}^{1} )$ and $k_{2}^{2} (b_{2}^{2} ) = k_{2}^{2} (b_{1}^{1} - b_{2}^{1} )$. If $b_{1}^{1} \ge b_{2}^{1}$ and $b_{1}^{1} - b_{2}^{1} > b_{2}^{2}$, then $k_{1}^{2} (b_{1}^{2} ) = k_{1}^{1} (b_{2}^{2} )$ and $k_{2}^{2} (b_{2}^{2} ) = k_{2}^{2} (b_{2}^{2} )$.

Step 3. Determine the second element of normalized PHFEs. If $b_{1}^{1} \ge b_{2}^{1}$, $b_{1}^{1} - b_{2}^{1} \le b_{2}^{2}$ and $b_{2}^{1} \le b_{2}^{2} - b_{1}^{1} + b_{2}^{1}$, then $k_{1}^{3} (b_{1}^{3} ) = k_{1}^{2} (b_{1}^{2} )$ and $k_{2}^{3} (b_{2}^{3} ) = k_{2}^{2} (b_{1}^{2} )$. If $b_{1}^{1} \ge b_{2}^{1}$, $b_{1}^{1} - b_{2}^{1} \le b_{2}^{2}$ and $b_{2}^{1} > b_{2}^{2} - b_{1}^{1} + b_{2}^{1}$, then $k_{1}^{3} (b_{1}^{3} ) = k_{1}^{2} (b_{2}^{2} + b_{2}^{1} - b_{1}^{1} )$ and $k_{2}^{3} (b_{2}^{3} ) = k_{2}^{2} (b_{2}^{2} + b_{2}^{1} - b_{1}^{1} )$. If $b_{1}^{1} \ge b_{2}^{1}$, $b_{1}^{1} - b_{2}^{1} > b_{2}^{2}$ and $b_{1}^{2} \ge b_{2}^{2} + b_{2}^{3}$, then $k_{1}^{3} (b_{1}^{3} ) = k_{1}^{2} (b_{2}^{3} )$ and $k_{2}^{3} (b_{2}^{3} ) = k_{2}^{3} (b_{2}^{3} )$. If $b_{1}^{1} \ge b_{2}^{1}$, $b_{1}^{1} - b_{2}^{1} > b_{2}^{2}$ and $b_{1}^{2} < b_{2}^{2} + b_{2}^{3}$, then $k_{1}^{3} (b_{1}^{3} ) = k_{1}^{2} (b_{1}^{2} - b_{2}^{2} )$ and $k_{2}^{3} (b_{2}^{3} ) = k_{2}^{3} (b_{1}^{2} - b_{2}^{2} )$. If $b_{1}^{1} < b_{2}^{1}$, $b_{2}^{1} - b_{1}^{1} \le b_{1}^{2}$ and $b_{1}^{2} + b_{1}^{1} \le b_{2}^{2} + b_{2}^{1}$, then $k_{1}^{3} (b_{1}^{3} ) = k_{1}^{2} (b_{1}^{2} - b_{2}^{1} + b_{1}^{1} )$ and $k_{2}^{3} (b_{2}^{3} ) = k_{2}^{2} (b_{1}^{2} - b_{2}^{1} + b_{1}^{1} )$. If $b_{1}^{1} < b_{2}^{1}$, $b_{2}^{1} - b_{1}^{1} > b_{1}^{2}$ and $b_{2}^{1} + b_{1}^{2} \le b_{1}^{3} + b_{1}^{1}$, then $k_{1}^{3} (b_{1}^{3} ) = k_{1}^{3} (b_{2}^{1} - b_{1}^{1} - b_{1}^{2} )$ and $k_{2}^{3} (b_{2}^{3} ) = k_{2}^{1} (b_{2}^{1} - b_{1}^{1} - b_{1}^{2} )$. If $b_{1}^{1} < b_{2}^{1}$, $b_{2}^{1} - b_{1}^{1} > b_{1}^{2}$ and $b_{2}^{1} + b_{1}^{2} > b_{1}^{3} + b_{1}^{1}$, then $k_{1}^{3} (b_{1}^{3} ) = k_{1}^{3} (b_{1}^{3} )$ and $k_{2}^{3} (b_{2}^{3} ) = k_{2}^{1} (b_{1}^{3} )$ where $b_{1}^{1} + b_{1}^{2} + \cdot \cdot \cdot b_{1}^{{\# k_{1} }} = 1$ and $b_{2}^{1} + b_{2}^{2} + \cdot \cdot \cdot b_{2}^{{\# k_{2} }} = 1$, $\# k_{1} = \# k_{2}$.

With this new normalized process introduced, the new algorithm of distance and the algorithms of PHFEs are also developed.

Definition 10

[37]. Set $\gamma _{1} (b_{1} )$ and $\gamma _{2} (b_{2} )$ be two PHFEs. And their normalized forms are $\gamma _{1}^{ * } (b_{1}^{ * } ) = \{ k_{m}^{{\lambda _{m} }} (b_{m}^{{\lambda _{m} }} )|\lambda _{m} = 1,2 \cdot \cdot \cdot ,\# k_{1} \}$ and $\gamma _{2}^{ * } (b_{2}^{ * } ) = \{ k_{n}^{{\lambda _{n} }} (b_{n}^{{\lambda _{n} }} )|\lambda _{n} = 1,2 \cdot \cdot \cdot ,\# k_{2} \}$, where $\# k_{1} = \# k_{2} = \# k$ and $b_{m}^{{\lambda _{m} }} = b_{n}^{{\lambda _{n} }} = b^{\lambda }$. The distance calculation is developed as Eq. (11)

$$d(\gamma _{1} (b_{1} ),\gamma _{2} (b_{2} )) = \frac{1}{{\# k}}\sum\limits_{{\lambda = 1}}^{k} {|k_{m}^{{\lambda _{m} }} b^{\lambda } - k_{n}^{{\lambda _{n} }} b^{\lambda } |}$$

(11)

where $\# k$ denotes the value of the membership degree, $b^{\lambda }$ represents the probability of the memberships, $k_{m}^{{\lambda _{m} }}$ and $k_{n}^{{\lambda _{n} }}$ is the $\lambda - th$ largest value in $\gamma _{1} (b_{1} )$ and $\gamma _{2} (b_{2} )$ separately.

Definition 11

[45]. Let $\gamma _{1} (b_{1} )$ and $\gamma _{2} (b_{2} )$ be two PHFEs. And their normalized forms are $\bar{\gamma }_{1} (\bar{b}_{1} ) = \{ \bar{k}_{m}^{{\lambda _{m} }} (\bar{b}_{m}^{{\lambda _{m} }} )|\bar{\lambda }_{m} = 1,2 \cdot \cdot \cdot ,\# \bar{k}_{1} \}$ and $\bar{\gamma }_{2} (\bar{b}_{2} ) = \{ \bar{k}_{n}^{{\lambda _{n} }} (\bar{b}_{n}^{{\lambda _{n} }} )|\bar{\lambda }_{n} = 1,2 \cdot \cdot \cdot ,\# \bar{k}_{2} \}$, where $\# \bar{k}_{1} = \# \bar{k}_{2} = \# k$ and $\bar{b}_{m}^{{\lambda _{m} }} = \bar{b}_{n}^{{\lambda _{n} }} = b^{\lambda }$. The algorithms between them are developed as follows:

$$\bar{\gamma }_{1} (\bar{b}_{1} ) \oplus \bar{\gamma }_{2} (\bar{b}_{2} ) = \cup _{{\bar{\lambda }_{m} = 1, \cdot \cdot \cdot ,\# \bar{k}_{1} ,\bar{\lambda }_{n} = 1, \cdot \cdot \cdot ,\# \bar{k}_{2} }} \{ (\bar{k}_{m}^{{\bar{\lambda }_{m} }} + \bar{k}_{n}^{{\bar{\lambda }_{n} }} - \bar{k}_{m}^{{\bar{\lambda }_{m} }} \bar{k}_{n}^{{\bar{\lambda }_{{_{n} }} }} )(b^{\lambda } )\};$$

(12)

$$\bar{k}_{1} (\bar{b}_{1} ) \otimes \bar{k}_{2} (\bar{b}_{2} ) = \cup _{{\bar{\lambda }_{m} = 1, \cdot \cdot \cdot ,\# \bar{k}_{1} ,\bar{\lambda }_{n} = 1, \cdot \cdot \cdot ,\# \bar{k}_{2} }} \{ \bar{k}_{m}^{{\bar{\lambda }_{m} }} \bar{k}_{n}^{{\bar{\lambda }_{n} }} (b^{\lambda } )\};$$

(13)

Definition 12

[16]. Let $N_{g} (g = 1,2, \cdot \cdot \cdot ,x)$ be an aggregation of PHFNs, and the algorithm of PHFWA operator is shown as Eq. (14):

$$PHFWA(N_{1} ,N_{2} , \cdot \cdot \cdot ,N_{x} ) = \mathop \oplus \limits_{{g = 1}}^{x} (N_{g} v_{g} )$$

$$\begin{gathered} PHFWA(N_{1} ,N_{2} , \cdot \cdot \cdot ,N_{x} ) = \mathop \oplus \limits_{{g = 1}}^{x} (N_{g} v_{g} ) \hfill \\ = \mathop \cup \limits_{{k_{1} \in N_{1} ,k_{2} \in N_{2} , \cdot \cdot \cdot ,k_{x} \in N_{x} }} \{ 1 - \mathop \Pi \limits_{{g = 1}}^{x} (1 - k_{g} )^{{v_{g} }} (b^{\lambda } )\} \hfill \\ \end{gathered}$$

(14)

where $v_{g} = (v_{1} ,v_{2} , \cdot \cdot \cdot ,v_{x} )$ is the weight vector of the $N_{x}$, and $\sum\nolimits_{{g = 1}}^{x} {v_{g} } = 1$, $v_{g} \in [0,1]$,

Definition 13

[16]. Let $N_{g} (g = 1,2, \cdot \cdot \cdot ,x)$ be a set of PHFNs, and the algorithm of PHFWG operator is shown as Eq. (15):

$$\begin{gathered} PHFWG = (N_{1} ,N_{2} , \cdot \cdot \cdot ,N_{x} ) = \mathop \oplus \limits_{{g = 1}}^{x} (N_{g} )^{{v_{g} }} \hfill \\ = \mathop \cup \limits_{{k_{1} \in N_{1} ,k_{2} \in N_{2} , \cdot \cdot \cdot ,k_{x} \in N_{x} }} \{ \mathop \Pi \limits_{{g = 1}}^{x} (k_{g} )^{{v_{g} }} (b^{\lambda } )\} \hfill \\ \end{gathered}$$

(15)

where $v_{g} = (v_{1} ,v_{2} , \cdot \cdot \cdot ,v_{x} )$ is the weight vector of the $N_{x}$, and $\sum\nolimits_{{g = 1}}^{x} {v_{g} } = 1$, $v_{g} \in [0,1]$.

2.4 TODIM Method Based on Cumulative Prospect Theory

In this section, we recommend the classical TODIM method based on the cumulative prospect theory (CPT-TODIM) which is applied in the MADM and other area, firstly. Nevertheless, the limit of the classical TODIM method has been revealed that this method is not enough to gain the inter-attribute weight. Then the extended TODIM method which is based on CPT is proposed to improve the limit.

The MADM matrix is as follows:

$$R = \left[ {\begin{array}{*{20}c} {\gamma _{{11}} } & \ldots & {\gamma _{{1q}} } & \cdots & {\gamma _{{1d}} } \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ {\gamma _{{p1}} } & \cdots & {\gamma _{{pq}} } & \cdots & {\gamma _{{pd}} } \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ {\gamma _{{c1}} } & \ldots & {\gamma _{{cq}} } & \cdots & {\gamma _{{cd}} } \\ \end{array} } \right]_{{c \times d}} ;\;p = 1,...,c,q = 1...,d$$

The matrix $\left[ {\begin{array}{*{20}c} {e_{1} ,} & {e_{2} ,} & { \cdots ,} & {e_{d} } \\ \end{array} } \right]$ denotes the weighting vector of attributes meeting the condition that $\sum\nolimits_{{q = 1}}^{d} {e_{q} } = 1$, and the alternatives are expressed as $S = \{ S_{{1,}} S_{{2...,}} S_{c} \}$ and the attributes is expressed as $U = \{ U_{{1,}} U_{{2...,}} U_{d} \}$,and the weight of the attribute is unclear.

The calculating process of CPT-TODIM method is designed as follows:

Step 1. Calculate the prospect value refers to the gains and losses of decision values which is relative to reference points.

Suppose that $\Delta \gamma _{1} \ge \cdot \cdot \cdot \Delta \gamma _{k} \ge 0 \ge \Delta \gamma _{{k + 1}} \ge \Delta \gamma _{c}$,

$$V_{{pkq}} = \sum\limits_{{p = 1}}^{k} {w_{{pkq}}^{ + } (\Delta \gamma _{{pkq}} ) \cdot \psi _{{pkq}}^{ + } (\Delta \gamma _{{pkq}} )} + \sum\limits_{{p = k + 1}}^{c} {w_{{pkq}}^{ - } (\Delta \gamma _{{pkq}} )} \cdot \psi _{{pkq}}^{ - } (\Delta \gamma _{{pkq}} )$$

(16)

where $\psi _{{pkq}}^{{ + ( - )}} (\Delta \gamma _{{pkq}} )$ and $w_{{pkq}}^{{ + ( - )}}$ denoting the value function whose algorithms and the weight for the gains and losses respectively are denoted as the Eq. (17) and Eq. (18)

$$\left\{ {\begin{array}{ll} {\psi _{{pkq}}^{ + } (\Delta \gamma _{{pkq}} ) = d(\gamma _{{pq}} ,\gamma _{{kq}} )^{\alpha } } & {{\text{if }}\gamma _{{pq}} \ge \gamma _{{kq}} } \\ {\psi _{{pkq}}^{ - } (\Delta \gamma _{{pkq}} ) = - \varepsilon (d(\gamma _{{pq}} ,\gamma _{{kq}} ))^{\beta } } & {{\text{if }}\gamma _{{pq}} < \gamma _{{kq}} } \\ \end{array} } \right.$$

(17)

where $\alpha$ and $\beta$ are the exponent parameters, and $\varepsilon$ reflects the degree of risk aversion of decision makers. The experiment of Tversky and Kahneman [46] gave the value of these parameters: $\varepsilon {\text{ = 2}}{\text{.25}}$$\alpha$ = 0.88,$\beta$ = 0.88.

$$\left\{ {\begin{array}{ll} {w_{{pkq}}^{ + } = H_{{pkq}}^{ + } (\sum\limits_{{t = 1}}^{d} {e_{t} } ) - H_{{pkq}}^{ + } (\sum\limits_{{t = q + 1}}^{d} {e_{t} } )} & {{\text{if }}\gamma _{{pq}} \ge \gamma _{{kq}} } \\ {w_{{pkq}}^{ - } = H_{{pkq}}^{ - } (\sum\limits_{{t = 1}}^{q} {e_{t} } ) - H_{{pkq}}^{ - } (\sum\limits_{{t = 1}}^{{q - 1}} {e_{t} } )} & {{\text{if }}\gamma _{{pq}} < \gamma _{{kq}} } \\ \end{array} } \right.\;\;\;\;t = 1, \cdot \cdot \cdot ,d$$

(18)

where the nonlinear function of gain $H_{{pkq}}^{ + } (e_{t} )$ and loss $H_{{pkq}}^{ - } (e_{t} )$ can be calculated as follows:

$$\left\{ {\begin{array}{ll} {H_{{pkq}}^{ + } (e_{t} ) = \frac{{e_{q} ^{\eta } }}{{(e_{q} ^{\eta } + (1 - e_{q} )^{\eta } )^{{\frac{1}{\eta }}} }}} & {{\text{if }}\gamma _{{pq}} \ge \gamma _{{kq}} } \\ {H_{{pkq}}^{ - } (e_{t} ) = \frac{{e_{q} ^{\mu } }}{{(e_{q} ^{\mu } + (1 - e_{q} )^{\mu } )^{{\frac{1}{\mu }}} }}} & {{\text{if }}\gamma _{{pq}} < \gamma _{{kq}} } \\ \end{array} } \right.$$

(19)

where $\eta$ and $\mu$ are the parameter which represents the decision-maker’s attitudes towards gains and losses separately. According to the experiment did by Tversky and Kahneman [46] the value of these two parameter is 0.61 and 0.69, respectively.

Step 2. Calculate the relative weight $w_{{pkq}}^{ * }$ by using Eq. (20)

$$w_{{pkq}}^{ * } = \frac{{w_{{pkq}} }}{{w_{{pkl}} }}$$

(20)

where $w_{{pkq}}$ and $w_{{pkl}}$ are all determined from Eq. (18) for the alternative $S_{p}$ to $S_{k}$ which are determined by the value of $s(\gamma _{{pq}} ) - s(\gamma _{{kq}} )$, while $w_{{pkq}}$ represents the transformed weight of the alternative $S_{p}$ underneath the attribute ${\text{q - th}}$, $w_{{pkl}}$ means the transformed weight of the alternative $S_{k}$ which satisfies $w_{{pkl}} = \max (w_{{pkq}} |q = 1,2,\ldots,d)$.

Step 3. Count the relative dominance of alternative $S_{p}$ to $S_{k}$ underneath the attribute $q$ according to Eq. (21)

$$\tau (S_{p} ) = \tau (S_{p} ,S_{k} ) = \sum\limits_{{p = 1}}^{c} {\sum\limits_{{q = 1}}^{d} {\xi _{{pkq}} } (S_{p} ,S_{k} )}$$

(21)

where the preference index value $\xi _{{pkq}} (S_{p} ,S_{k} )$ is figured out as Eq. (22):

$$\xi _{{pkq}} (S_{p} ,S_{k} ) = \left\{ {\begin{array}{ll} {\frac{{w_{{pkq}}^{ * } \times V_{{pkq}} }}{{\sum\nolimits_{{q = 1}}^{d} {w_{{pkq}}^{ * } } }}} & {{\text{if }}\gamma _{{pq}} \ge \gamma _{{kq}} } \\ {\frac{{(\sum\nolimits_{{q = 1}}^{d} {w_{{pkq}}^{ * } } ) \times V_{{pkq}} }}{{w_{{pkq}}^{ * } }}} & {{\text{if }}\gamma _{{pq}} < \gamma _{{kq}} } \\ \end{array} } \right.$$

(22)

Step 4. Compute out the overall dominance degree of the alternative $S_{{p,}}$ by Eq. (23)

$$\vartheta (S_{p} ) = \frac{{\tau (S_{p} ) - \mathop {\min }\limits_{p} (\tau (S_{p} ))}}{{\mathop {\max }\limits_{p} (\tau (S_{p} )) - \mathop {\min }\limits_{p} (\tau (S_{p} ))}}\;\;\;\;p = 1,2,...,c$$

(23)

Step 5. Ranking the overall dominance degree $\vartheta (S_{p} )$. The greater the number of the overall dominance degree $\vartheta (S_{p} )$ is, the more appropriate the alternative is.

3 Extended TODIM Based on CPT for Probability Hesitant fuzzy MAGDM

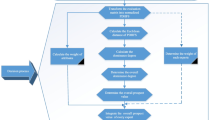
The MAGDM matrix $R^{g} = [\gamma ^{g} _{{pq}} (b_{{pq}} )]_{{c \times d}}$ and the set of the decision-maker is $N_{g} = \{ N_{{1,}} N_{2} ,...,N_{x} \}$, whose weight vector is $a_{g} = (a_{{1,}} a_{2} ,...,a_{x} )$,($g = 1,2,...,x$), $\sum\limits_{{g = 1}}^{x} {a_{g} } = 1$.Next, we introduce probability hesitant fuzzy MAGDM using extended CPT-TODIM. The framework is shown in the Fig. 1. The computational procedure of CPT-TODIM method for probability hesitant fuzzy MAGDM is designed as follows:

Fig. 1

The Framework of the probability hesitant fuzzy MAGDM using CPT-TODIM

Step 1. Normalize the decision matrices.

When $U_{q}$ is the positive attribute, the normalized probabilistic hesitant fuzzy element is determined by Eq. (24)

$$\gamma _{{pq}}^{ * } = \{ k_{{pq}} (b_{{pq}} )\} ;\;q = 1...,d$$

(24)

When $U_{q}$ is the negative attribute, the normalized probabilistic hesitant fuzzy element is determined by Eq. (25)

$$\gamma _{{pq}}^{ * } = \{ (1 - k_{{pq}} )(b_{{pq}} )\} ;\;q = 1...,d$$

(25)

$\gamma _{{pq}} ^{*}$ represents the value of normalized decision matrix.

Then normalize the decision matrices using the steps in Definition 9.

Step 2. Aggregate the information to synthesize PHFE decision matrices into the integrated PHFE decision matrix $\bar{R} = [\bar{\gamma }_{{pq}} (\bar{b}_{{pq}} )]_{{c \times d}}$ by PHFWA which calculated by Eq. (26)

$$\begin{gathered} PHFWA(N_{1} ,N_{2} , \cdot \cdot \cdot ,N_{x} ) = \mathop \oplus \limits_{{g = 1}}^{x} (N_{g} v_{g} ) \hfill \\ = \mathop \cup \limits_{{k_{1} \in N_{1} ,k_{2} \in N_{2} , \cdot \cdot \cdot ,k_{x} \in N_{x} }} \{ 1 - \mathop \Pi \limits_{{g = 1}}^{x} (1 - k_{g} )^{{v_{g} }} (b^{\lambda } )\} \hfill \\ \end{gathered}$$

(26)

Step 3. Figure out the distance between $\bar{\gamma }_{{pq}}$ and $\tilde{\gamma }_{q}$ using Eq. (27)

$$d(\bar{\gamma }_{{pq}} ,\tilde{\gamma }_{q} ) = \frac{1}{{\# k}}\sum\nolimits_{{\lambda = 1}}^{{\# k}} {|\bar{k}_{q}^{\lambda } } \bar{b}_{q}^{\lambda } - \tilde{k}_{q}^{\lambda } \tilde{b}_{q}^{\lambda } |$$

(27)

Step 4. Obtain weights among attributes using the Entropy weighting method whose calculate equation is Eq. (28)

$$e_{q} = \frac{{1 - y_{q} }}{{\sum\nolimits_{{q = 1}}^{d} {(1 - y_{q} )} }}\;\;\;\;q = 1,2, \cdot \cdot \cdot ,d$$

(28)

where $y_{q}$ represents the entropy of the ${\text{q - th}}$ attributes and calculate it by Eq. (29)

$$y_{q} = - \frac{1}{{\ln c}}\sum\nolimits_{{p = 1}}^{c} {\left[ {\frac{{d(\bar{\gamma }_{{pq}} ,\tilde{\gamma }_{q} )}}{{\sum\nolimits_{{p = 1}}^{c} {d(\bar{\gamma }_{{pq}} ,\tilde{\gamma }_{q} )} }}\ln (\frac{{d(\bar{\gamma }_{{pq}} ,\tilde{\gamma }_{q} )}}{{\sum\nolimits_{{p = 1}}^{c} {d(\bar{\gamma }_{{pq}} ,\tilde{\gamma }_{q} )} }})} \right]}$$

(29)

where $\tilde{\gamma }_{q}$ means the ${\text{q - th}}$ negative ideal point, $d(\bar{\gamma }_{{pq}} - \tilde{\gamma }_{q} )$ denotes the distance of $\bar{\gamma }_{{pq}}$ and $\tilde{\gamma }_{q}$.

Step 5. Obtain the prospect value according to the gains and losses of decision values by Eq. (30) to (33).

Calculate the prospect value refers to the gains and losses of decision values which is relative to reference points.

Suppose that $s(\Delta \bar{\gamma }_{1} ) \ge \cdot \cdot \cdot s(\Delta \bar{\gamma }_{k} ) \ge 0 \ge s(\Delta \bar{\gamma }_{{k + 1}} ) \ge s(\Delta \bar{\gamma }_{c} )$,

$$\bar{V}_{{pkq}} = \sum\limits_{{p = 1}}^{k} {\bar{w}_{{pkq}}^{ + } (\Delta \bar{\gamma }_{{pkq}} ) \cdot \bar{\psi }_{{pkq}}^{ + } (\Delta \bar{\gamma }_{{pkq}} )} + \sum\limits_{{p = k + 1}}^{c} {\bar{w}_{{pkq}}^{ - } (\Delta \bar{\gamma }_{{pkq}} )} \cdot \bar{\psi }_{{pkq}}^{ - } (\Delta \bar{\gamma }_{{pkq}} )$$

(30)

where $\bar{\psi }_{{pkq}}^{{ + ( - )}} (\Delta \bar{\gamma }_{{pkq}} )$ and $\bar{w}_{{pkq}}^{{ + ( - )}} (\Delta \bar{\gamma }_{{pkq}} )$ denoting the value function whose algorithms and the weight for the gains and losses respectively are denoted as the Eq. (31) and Eq. (32)

$$\left\{ {\begin{array}{ll} {\bar{\psi }_{{pkq}}^{ + } (\Delta \bar{\gamma }_{{pkq}} ) = d(\bar{\gamma }_{{pq}} ,\bar{\gamma }_{{kq}} )^{\alpha } } & {{\text{if s(}}\bar{\gamma }_{{pq}} ) \ge s(\bar{\gamma }_{{kq}} )} \\ {\bar{\psi }_{{pkq}}^{ - } (\Delta \bar{\gamma }_{{pkq}} ) = - \varepsilon (d(\bar{\gamma }_{{pq}} ,\bar{\gamma }_{{kq}} ))^{\beta } } & {{\text{if s( }}\gamma _{{pq}} ) < s(\gamma _{{kq}} )} \\ \end{array} } \right.$$

(31)

where $\alpha$ and $\beta$ are the exponent parameters, and $\varepsilon$ reflects the degree of risk aversion of decision makers. The experiment of Tversky and Kahneman [46] gave the value of these parameters: $\varepsilon {\text{ = 2}}{\text{.25}}$$\alpha$ = 0.88,$\beta$ = 0.88.

$$\left\{ {\begin{array}{ll} {\bar{w}_{{pkq}}^{ + } = \bar{H}_{{pkq}}^{ + } (\sum\limits_{{t = 1}}^{d} {e_{t} } ) - \bar{H}_{{pkq}}^{ + } (\sum\limits_{{t = q + 1}}^{d} {e_{t} } )} & {if{\text{ }}s(\bar{\gamma }_{{pq}} ) \ge s(\bar{\gamma }_{{kq}} )} \\ {\bar{w}_{{pkq}}^{ - } = \bar{H}_{{pkq}}^{ - } (\sum\limits_{{t = 1}}^{q} {e_{t} } ) - \bar{H}_{{pkq}}^{ - } (\sum\limits_{{t = 1}}^{{q - 1}} {e_{t} } )} & {if{\text{ }}s(\bar{\gamma }_{{pq}} ) < s(\bar{\gamma }_{{kq}} )} \\ \end{array} } \right.\;\;\;\;t = 1, \cdot \cdot \cdot ,d,$$

(32)

where $\bar{H}_{{pkq}}^{ + } (e_{t} )$ and $\bar{H}_{{pkq}}^{ - } (e_{t} )$ denotes the nonlinear function of gain and loss separately and its specific calculation process is as follows:

$$\left\{ {\begin{array}{ll} {\bar{H}_{{pkq}}^{ + } (e_{t} ) = \frac{{e_{q} ^{\eta } }}{{(e_{q} ^{\eta } + (1 - e_{q} )^{\eta } )^{{\frac{1}{\eta }}} }}} & {{\text{if s(}}\bar{\gamma }_{{pq}} ) \ge s(\bar{\gamma }_{{kq}} )} \\ {\bar{H}_{{pkq}}^{ - } (e_{t} ) = \frac{{e_{q} ^{\mu } }}{{((e_{q} ^{\mu } + (1 - e_{q} )^{\mu } )^{{\frac{1}{\mu }}} )}}} & {{\text{if s(}}\bar{\gamma }_{{pq}} ) < s(\bar{\gamma }_{{kq}} )} \\ \end{array} } \right.$$

(33)

where $\eta$ and $\mu$ are the parameter which represents the decision-maker’s attitudes towards gains and losses separately. According to the experiment did by Tversky and Kahneman [46] the value of these two parameter is 0.61 and 0.69 respectively.

Step 6. Compute the relative weight $\bar{w}_{{pkq}}^{ * }$ by using Eq. (34).

$$\bar{w}_{{pkq}}^{ * } = \frac{{\bar{w}_{{pkq}} }}{{\bar{w}_{{pkl}} }}$$

(34)

where $\bar{w}_{{pkq}}$ and $\bar{w}_{{pkl}}$ are all determined from Eq. (33) for the alternative $S_{p}$ to $S_{k}$ which are determined by the value of $s(\bar{\gamma }_{{pq}} ) - s(\bar{\gamma }_{{kq}} )$, while $\bar{w}_{{pkq}}$ represents the transformed weight of the alternative $S_{p}$ underneath the attribute ${\text{q - th}}$, $\bar{w}_{{pkl}}$ means the transformed weight of the alternative $S_{k}$ which satisfies $\bar{w}_{{pkl}} = \max (\bar{w}_{{pkq}} |q = 1,2, \cdot \cdot \cdot ,d)$.

Step 7. count down the relative dominance of alternative using Eq. (35) and (36)

The equation of relative dominance of alternative which is underneath the attribute $q$ in probabilistic hesitant fuzzy condition is shown as Eq. (35).

$$\bar{\tau }(S_{p} ) = \bar{\tau }(S_{p} ,S_{k} ) = \sum\limits_{{p = 1}}^{c} {\sum\limits_{{q = 1}}^{d} {\bar{\xi }_{{pkq}} } (S_{p} ,S_{k} )}$$

(35)

where the preference index value $\bar{\xi }_{{pkq}} (S_{p} ,S_{k} )$ is figured out as Eq. (36):

$$\bar{\xi }_{{pkq}} (S_{p} ,S_{k} ) = \left\{ {\begin{array}{ll} {\frac{{\bar{w}_{{pkq}}^{ * } \times \bar{V}_{{pkq}} }}{{\sum\nolimits_{{q = 1}}^{d} {\bar{w}_{{pkq}}^{ * } } }}} & {{\text{if s(}}\bar{\gamma }_{{pq}} ) \ge s(\bar{\gamma }_{{kq}} )} \\ {\frac{{(\sum\nolimits_{{q = 1}}^{d} {\bar{w}_{{pkq}}^{ * } } ) \times \bar{V}_{{pkq}} }}{{\bar{w}_{{pkq}}^{ * } }}} & {{\text{if s(}}\bar{\gamma }_{{pq}} ) < s(\bar{\gamma }_{{kq}} )} \\ \end{array} } \right.$$

(36)

Step 8. Calculate the overall dominance degree of the alternative by Eq. (37).

$$\bar{\vartheta }(S_{p} ) = \frac{{\bar{\tau }(S_{p} ) - \mathop {\min }\limits_{p} (\bar{\tau }(S_{p} ))}}{{\mathop {\max }\limits_{p} (\bar{\tau }(S_{p} )) - \mathop {\min }\limits_{p} (\bar{\tau }(S_{p} ))}}\;p = 1,2,...,c$$

(37)

Step 9. Obtain the final rank of overall dominance degree $\bar{\vartheta }(S_{p} )$, then rank in descending order.

4 Numerical Examples

In the operation and management of an enterprise, how to make use of idle funds for indirect investment is an important matter that needs to be carefully considered. How to make investment decisions is related to the company’s economic interests and long-run development. Since the purpose of buying stocks is to obtain partial ownership of listed companies and dividends on earnings, investors need to make a choice between long-run investment and short-run speculation in the securities investment market.

Long-term investors must always pay attention to all kinds of market information dynamics, but also must put up with a long wait for the opportunity to make a great profit. Additionally, long-term investment also needs to be sold after all, the fundamental purpose of long-term investment is profit, thus investors must seek appropriate investment time. In the ever-changing stock market, the choice of stock investment is affected by many factors. At the same time, the investment department of the company will allocate multiple investment advisers to participate in the decision making. The stock investment selection problem is a kind of multi-attribute group decision making issue.

Based on the above analysis, we have selected six factors that may affect the decisions of investment advisers in this paper: (1) $U_{1}$ is the development prospect of the industry, (2) $U_{2}$ is the influence of economic circumstance,(3) $U_{3}$ is the sustainable development of the enterprise,(4) $U_{4}$ is extent to which the stock market price is below its intrinsic value, (5) $U_{5}$ is the cash flow of the enterprise (6) $U_{6}$ is the capital cost. Except (6) is the negative attribute, the other attributes are positive. We use $S = \{ S_{1} ,S_{2} , \cdot \cdot \cdot S_{5} \}$ to denote the five selections of the investment portfolio. The alternative was chosen by the company’s three experts whose weighting vector is $e = (a_{1} ,a_{2} ,a_{3} )^{T}$ $= (0.3,0.4,0.3)^{T}$. Then the probabilistic decision matrices which are given by the three experts are shown below (Tables 1, 2, and 3):

Table 1 Decision matrix $N_{1}$ given by the first expert

Table 2 Decision matrix $N_{2}$ given by the second expert

Table 3 Decision matrix $N_{3}$ given by the third expert

We use the following model for calculation, and the specific steps are as follows.

Step 1. Use Eq. (24) and Eq. (25) to transform the negative into positive and then normalize. The result is shown in Tables 4, 5, and 6.

Table 4 Normalize decision matrix $N_{1}$ given by the first expert

Table 5 Normalize decision matrix $N_{2}$ given by the second expert

Table 6 Normalize decision matrix $N_{3}$ given by the third expert

Step 2. Calculate the PHFWA to synthesize the decision matrices into group decision matrix using Eq. (26), and it is shown in Table 7.

Table 7 Group decision matrix

Step 3. Calculate the distance between negative ideal point using Eq. (27), and the result is shown in Table 8

Table 8 The distance between $\bar{\gamma }_{{pq}}$ and $\tilde{\gamma }_{q}$

Step 4. Calculate the weights among attributes using Eq. (28) and (29).

$e_{q} = (0.138,0.171,0.177,0.119,0.265,0.130)$.

Step 5. Obtain the prospect value by Eq. (30) to (33). The results are shown in Table 9.

Table 9 The prospect value

Step 6. Calculate the relative weight $\bar{w}_{{pkq}}^{ * }$ and then shown in Table 10.

Table 10 The relative weight

Step 7. Obtain the preference index and then calculate the relative dominance $\bar{\tau }(S_{p} )$ of alternative $S_{p}$ to $S_{k}$ underneath the attribute $q$ by Eq. (35) to (36) the result is shown in Table 11.

Table 11 The preference index value

$\bar{\tau }(S_{1} ) = - 1.826$, $\bar{\tau }(S_{2} ) = - 1.704$,$\bar{\tau }(S_{3} ) = 0.223$,

$\bar{\tau }(S_{4} ) = - 2.645$,$\bar{\tau }(S_{5} ) = - 2.808$.

Step 8. Obtain the overall dominance degree of the alternative by Eq. (37)

$\bar{\vartheta }(S_{1} ) = 0.324$,$\bar{\vartheta }(S_{2} ) = 0.364$,$\bar{\vartheta }(S_{3} ) = 1.000$,$\bar{\vartheta }(S_{4} ) = 0.054$,$\bar{\vartheta }(S_{5} ) = 0.000$.

Step 9. Rank the overall dominance degree $\bar{\vartheta }(S_{p} )$,$p = 1,2,3,4,5$

$$\bar{\vartheta }(S_{3} ) > \bar{\vartheta }(S_{2} ) > \bar{\vartheta }(S_{1} ) > \bar{\vartheta }(S_{4} ) > \bar{\vartheta }(S_{5} )$$

Thus, the alternative $S_{3}$ is the optimal one.

5 Comparative Analysis

In this section, we will take the advantage of classical TODIM (PHF-TODIM) method[37], PHFWA operator[16], PHFWG operator[16], probabilistic hesitant fuzzy TOPSIS (PHF-TOPSIS) method[47] and the novel TODIM method proposed by Tian, Niu, Ma and Xu [48] to compare with the improved TODIM based on prospect theory. To make a better comparison, we use the same data from the Table 1, 2, and 3 and the attributes weight vector obtained from Step 4 is as follows:

$$e_{q} = (0.138,0.171,0.177,0.119,0.265,0.130)$$

5.1 Comparison with PHF-TODIM Method

The classical TODIM method under probabilistic hesitant fuzzy condition proposed by Zhang, Du and Tian [37] is a common method to solve the selection issues. Therefore, we utilize it to prove the effectiveness of the newly TODIM method. And the concrete procedures are listed as follows:

Firstly, the value of ***Table 700 is used as the standardized value of decision matrix and the weighting vector of attributes is $e_{q} = (0.138,0.171,0.177,0.119,0.265,0.130)$, and the relative weight can be calculated by Eq. (38)

$$e_{q}^{ * } = \frac{{e_{q} }}{{\hat{e}}}$$

(38)

where $\hat{e}$ denotes the maximum value of the attributes’ weight.

And then calculate the dominance degree of the alternative $S_{k}$ over the other alternative, and the dominance degree of each alternative is figured out as Eq. (39)

$$\tau (S_{p} ) = \tau (S_{p} ,S_{k} ) = \sum\limits_{{p = 1}}^{c} {\sum\limits_{{q = 1}}^{d} {\xi _{{pkq}} (S_{p} ,S_{k} )} }$$

(39)

In Eq. (40), the preference index number is computed by Eq. (40)

$$\xi _{{pkq}} (S_{p} ,S_{k} )\left\{ {\begin{array}{ll} {\sqrt {\frac{{e_{q}^{ * } \times d(\gamma _{{pq}} ,\gamma _{{kq}} )}}{{\sum\nolimits_{{q = 1}}^{d} {e_{q}^{ * } } }}} } & {{\text{if s(}}\gamma _{{pq}} ) \ge s(\gamma _{{kq}} } \\ { - \theta \sqrt {\frac{{\sum\nolimits_{{q = 1}}^{d} {e_{q}^{ * } } \times d(\gamma _{{pq}} ,\gamma _{{kq}} )}}{{e_{q}^{ * } }}} } & {{\text{if s(}}\gamma _{{pq}} ) < s(\gamma _{{kq}} )} \\ \end{array} } \right.$$

(40)

Finally, calculate the overall dominance degree of the alternative by Eq. (41) (Table 12).

$$\vartheta (S_{p} ) = \frac{{\tau (S_{p} ) - \mathop {\min }\limits_{p} (\tau (S_{p} ))}}{{\mathop {\max }\limits_{p} (\tau (S_{p} )) - \mathop {\min }\limits_{p} (\tau (S_{p} ))}}\;p = 1,2,...,c$$

(41)

Table 12 The results about PHF-TODIM method

5.2 Comparison with PHFWA and PHFEG

Aggregation operator is used as a fundamental method to figure out MAGDM problems. The result of probabilistic hesitant fuzzy aggregation operators is shown in Tables 13 and 14.

Table 13 The outcome about PHFWA operator

Table 14 The outcome about PHFWG operator

5.3 Comparison with PHF-TOPSIS Method

The TOPSIS method introduced by Wu, Liu, Wang and Zhang [47] under the condition of the probabilistic hesitant fuzzy can be used to testify the validity of the extended method. Here are the steps.

At first, use the value of Table 700*** as the normalized value of decision matrix and the weighting vector of attributes obtained by entropy is $e_{q} = (0.138,0.171,0.177,0.119,0.265,0.130)$, and based on the score function, compute the negative and positive ideal point. Meanwhile, calculate the distance between the negative and positive ideal point $d^{ - }$ and $d^{{\text{ + }}}$ respectively. Then obtain the relative closeness coefficients by the following equations (Table 15).

$$J_{p} = \frac{{D_{p}^{ - } }}{{D_{p}^{ - } + D_{p}^{ + } }}$$

(42)

where $D_{k}^{ + }$ and $D_{k}^{ - }$ can be computed by Eq. (43) and (44)

$$D_{p}^{ + } = \sum\limits_{{q = 1}}^{d} {e_{q} } d^{ + }$$

(43)

$$D_{p}^{ - } = \sum\limits_{{q = 1}}^{d} {e_{q} } d^{ - }$$

(44)

Table 15 The outcomes about PHF-TOPSIS method

5.4 Comparison with Novel TODIM Method Based on Prospect Theory (PT)

The newly proposed TODIM method with PHF circumstance introduced by Tian, Niu, Ma and Xu [48] is based on prospect theory. To better compare the two methods, we use the same data in Table 700*** and the weighting vector of the attributes $e_{q} = (0.138,0.171,0.177,0.119,0.265,0.130)$. The following is a simple model of its approach.

First, with the original weight of the attributes, calculate the transformed probability weight $\bar{H}_{{pkq}}^{{ + ( - )}}$ according to Eq. (33), then we can acquire the relative weight $\bar{H}_{{pkq}}^{ * }$ which can be worked out by the Eq. (45)

$$\bar{H}_{{pkq}}^{ * } = \frac{{\bar{H}_{{pkq}} }}{{\bar{H}_{{pkl}} }},\;\;\;\;l,q \in D,\forall (p,k)$$

(45)

where $\bar{H}_{{pkl}} = \max (\bar{H}_{{pkq}} |q \in D)$ is regarded as the reference weight of the attribute.

Then, calculate the relative prospect dominance degrees according to Eq. (46)

$$\bar{\varphi }_{{pkq}} (S_{p} ,S_{k} ) = \left\{ {\begin{array}{ll} {\frac{{H_{{pkq}}^{ * } (d(\bar{\gamma }_{{pq}} ,\bar{\gamma }_{{kq}} ))^{\alpha } }}{{\sum\nolimits_{{q = 1}}^{d} {H_{{pkq}}^{ * } } }}} & {s(\bar{\gamma }_{{pq}} ) \ge s(\bar{\gamma }_{{kq}} )} \\ {\frac{{ - \varepsilon (\sum\nolimits_{{q = 1}}^{d} {H_{{pkq}}^{ * } } )(d(\bar{\gamma }_{{pq}} ,\bar{\gamma }_{{kq}} ))^{\beta } }}{{H_{{pkq}}^{ * } }}} & {s(\bar{\gamma }_{{pq}} ) < s(\bar{\gamma }_{{kq}} )} \\ \end{array} } \right.$$

(46)

where $\alpha$ and $\beta$ are the exponent parameters, and $\varepsilon$ reflects the degree of risk aversion of decision makers. The experiment of Tversky and Kahneman [46] gave the value of these parameters: $\varepsilon {\text{ = 2}}{\text{.25}}$$\alpha$ = 0.88,$\beta$ = 0.88, $d(\bar{\gamma }_{{pq}} ,\bar{\gamma }_{{kq}} )$ denotes the corresponding distance obtained by Eq. (11).

Count the relative dominance of alternative $S_{p}$ to $S_{k}$ underneath the attribute $q$ according to Eq. (21) and the overall dominance degree of the alternative $S_{{p,}}$ by Eq. (23).

Lastly, rank in a descending order (Table 16).

Table 16 The outcomes about PHF-PT-TODIM method

5.5 Comprehension Comparison

Contrast it with different methods in the same environment, the results have a little difference, and the optimal alternative is $S_{3}$. The principle of each approach may result in these fine distinctions. The classical TODIM method neglect to distinguish the negative and positive attributes but focus on MADM in real number. Besides, it regards the initial weight vector of the attributes as the ultima weight vector. While the PHFWA and the PHFWG operator focus on the entirety and unit separately, the TOPSIS method pays more attention to the disparity of the negative and positive ideal point, and the extended TODIM method based on CPT considers more about the psychological factors which influences the behavior of DMs. Moreover, the comparison between the TODIM in PT shows that there are differences in early standardization and distance measurement. Meanwhile, we take a different approach to model approach construction. The theory that Tian, Niu, Ma and Xu [48] used has some limitations about the range of application and concept of random dominance. Therefore, we applied the cumulative prospect theory which studied by Tversky and Kahneman [46] to solve the above limitations. With this comparison, we testify the practicability of this newly proposed method (Table 17).

Table 17 The sequence from different methods

6 Conclusions

The classical TODIM method which is developed from PT calculates the dominance degree to show the DMs’ different acceptance of risk and the weight of attributes is objective probability. However, the PT shows the positive and negative attitudes of DMs by the value function and gives the nonlinear transformed probability weight function. Thus, the classical TODIM method has not fully demonstrated the idea of the PT. Furthermore, the CPT gives the development of the original PT which solves the limitation of the PT in preference transitivity and random dominance. In this paper, we integrate the classical TODIM method and the CPT in probabilistic hesitant fuzzy environment. Besides we utilize the entropy information to calculate the original weight of attributes. After that, we used an example to compare the results of different methods to prove the effectiveness of the novel methods. I believe that in the near future, the new method can be applied to many more fields and examples.

One of the advantages of this paper is the combination of the classical TODIM method and the cumulative prospect theory which fills up the deficiency of the traditional scheme. Moreover, the circumstance of the PHF expresses the hesitation in uncertainty by probability making the environment more informative. In addition, the application of psychological theory such as CPT makes it more practical in a complex environment. Therefore, more effort should be put into the PHF environment and the combination of classical MCDM methods and CPT in the future. Besides this newly proposed method could also integrate other group decision making model [49, 50] to better solve group decision-making problems such as the green supplier selection, disaster management and emergency processing in complex environments [51,52,53,54,55,56,57,58].