Multiple Attribute Group Decision-Making Approach Based on Multi-granular Unbalanced Hesitant Fuzzy Linguistic Information

Abstract

Based on multi-granular hesitant linguistic theory and unbalanced linguistic information, this paper proposes multi-granular unbalanced hesitant fuzzy linguistic term set, which can better describe the fuzzy and uncertain information from multiple attribute group decision making (MAGDM). In order to solve decision-making problem with interrelated attributes (or decision makers), the multi-granular unbalanced hesitant fuzzy linguistic Choquet integral average operator is proposed, and some properties about this operator are investigated, then a novel group decision-making method by the proposed operator is developed, and an example is adopted to demonstrate the proceeding of this method. Finally, compared with two existing methods, the effectiveness of the proposed method in MAGDM is shown.

1 Introduction

Multiple attribute group decision making (MAGDM) can be considered as the process of ranking alternatives or selecting an optimal alternative by many decision makers (DMs) based on multiple criteria [1,2,3,4]. In real life, because of the complexity and uncertainty of objective factors, as well as the fuzziness of human thinking, it is difficult for the DMs to make judgments with precise numerical values, and they often directly reflect their own preferences in the form of linguistic information. The linguistic variables, proposed by Zadeh [5, 6], are widely used to describe evaluation information, especially qualitative information [7,8,9,10,11,12,13]. However, due to the limitations of personal cognition and experience, one DM may hesitate between different linguistic variables in the evaluation process. In such cases, it is unrealistic that using only one linguistic term accurately reflects the intention of DM, thus, Rodríguez [14] proposed a hesitant fuzzy linguistic term set (HFLTS) to deal with this problem. Of course, the HFLTS is also used to express the information by several DMs. In addition, as a group, different DMs may hesitate between different fuzzy linguistic variables. For example, DM1 thinks that the performance evaluation of a mobile phone is “good,” DM2 considers it is “very good,” and DM3 deems it is “general.” So the inconsistency of DMs usually leads to hesitation, which can be also expressed by HFLTS. Obviously, the HFLTS combines the hesitant fuzzy set and the linguistic fuzzy set, and it can effectively express the hesitation of DMs in the decision-making process.

Since the HFLTS was proposed, it has attracted researchers’ wide attention and discussion in decision-making domain [15,16,17]. The main researches focus on three respects. The first respect is relative to foundation theories, such as distance measures [18, 19], similarity degrees [20]; the second are aggregation operators [21]; and the third are decision-making methods [22]. Further, some scholars extended HFLTSs to some new forms, such as interval-valued hesitant fuzzy linguistic term sets [23], probabilistic hesitant fuzzy linguistic term sets [24], and multi-granularity hesitant fuzzy linguistic term sets (MGHFLTSs) [25]. MGHFLTSs consider the different knowledge backgrounds and decision-making habits of DMs, without requiring the DMs to give linguistic evaluation with the same linguistic term set. Especially in MAGDM, different DMs will use different fuzzy linguistic information for one attribute of the same decision problem, and DMs will hesitate to use different fuzzy linguistic information, so there will be multi-granularity hesitant fuzzy variables. The computing with words (CWW) can deal with MAGDM of MGHFLTS [26], and three CWW models have been proposed, including the semantic model [27], the symbolic model [28], and the 2-tuple fuzzy linguistic model [29]. Among these three models, the advantages of the 2-tuple fuzzy linguistic model are reduction in information loss and improvement of accuracy [29]. Wang and Hao [30] developed a new version of 2-tuple fuzzy linguistic representation model by proportional 2-tuple fuzzy linguistic representation, that is, DMs can use two adjacent linguistic variables with symbolic proportions to represent decision preferences. In proportional 2-tuple model [30], the numerical value is calculated by the canonical characteristic values (CCVs). Because of these advantages of proportional 2-tuple fuzzy linguistic model, we will adopt proportional 2-tuple fuzzy linguistic model to express the linguistic information.

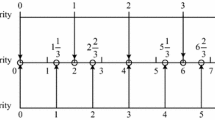
MGHFLTS is described on the assumption of linguistic variables that are distributed in uniform and symmetrical form; however, in realistic issues, the linguistic variables are not uniform or symmetrical [31]. Taking online course evaluation of China National Open University as an example, three groups of DMs (teachers, educational administrators, and teaching supervisions) do not evaluate all the courses with uniform and symmetrical linguistic term sets (shown in Fig. 1). Considering the advantages of unbalanced linguistic term set (ULTS), we will combine ULTS and MGHFLTS, and then to propose multi-granular unbalanced hesitant fuzzy linguistic term set (MGUHFLTS). At present, many researches based on ULTS [32, 33] and on MGHFLTS [23, 25, 34], respectively, have been achieved, but those achievements cannot deal with MGUHFLTS. Therefore, it is necessary to propose the novel concept of MGUHFLTS to solve some MAGDM problems. Based on MGUHFLTS, we will carry out some theory researches, such as operational rules, score function, expectation function, and comparison rules.

Fig. 1

On-line course grading system

In the process of MAGDM, the focus of the research is how to effectively integrate the evaluation information given by DMs. Presently, existing integration tools include arithmetic aggregation operator [32], geometric aggregation operator [35], generalized aggregation operator [36], etc. These operators are established under the condition that all the attributes (or DMs) are independent. However, in some MAGDM problems, attributes (DMs) are not completely independent, but interrelated and interacted. For example, there exists four attributes in online course evaluation: online course design ($C_{1}$), online teaching team ($C_{2}$), teaching support service ($C_{3}$), and teaching process monitoring ($C_{4}$). It is apparent that there is an interaction between $C_{1}$ and $C_{2}$. The fuzzy measures proposed by Sugeno [37] provide effective methods for dealing with the problem of interaction. Murofushi and Sugeno [38] used the nonadditivity of the fuzzy measures to explain the interaction between the attributes, put forward the Choquet integral, and discussed the rationality of it. Nowadays, Choquet integral has been developed to the interval neutrosophic linguistic [39,40,41], hesitant fuzzy linguistic [42], and granular computing [43]. Because the existing Choquet integral operators cannot solve MAGDM problem with MGUHFLTS, we will develop the multi-granular unbalanced hesitant fuzzy linguistic Choquet integral average (MGUHFLCA) operator to solve the decision problem under MGUHFLTS.

From the explanation above, the objectives and contributions of this paper are as follows:

• 1. To propose the concept of multi-granular unbalanced hesitant fuzzy linguistic term set (MGUHFLTS), and define operational rules, score function, expectation function, and comparison rules of MGUHFLTS.

• 2. To combine the MGUHFLEs with proportional 2-tuple fuzzy linguistic representation, and establish a transformation between ULTS and numerical data.

• 3. To develop the MGUHFLCA operator considering the relationship among attributes (or DMs).

• 4. To propose a novel MAGDM method based on the MGUHFLCA operator to deal with MAGDM problem in MGHFLTS.

• 5. By comparative analysis, the feasibility and advantages of the proposed MAGDM method are demonstrated.

The advantages of the proposed MAGDM method are that (1) it is more general in processing the fuzzy linguistic information because it can deal with the form of HFLTSs, HFLEs and proportional 2-tuple, and so on; (2) it is more convenient for DMs to select the different granular LTS based on their own cognition; (3) it is more practical for solving the MAGDM problem by multi-granularity HFLESs; (4) it is more reasonable by considering the relationship among attributes and DMs.

This paper is organized in the following structure. Sect. 2 introduces basic concepts of MGUHFLTS, the proportional 2-tuple fuzzy linguistic representation, and Choquet integral. In Sect. 3, the MGUHFLCA operator is proposed based on λ-fuzzy measure. In Sect. 4, a novel MAGDM approach based on proportional 2-tuple MGUHFLCA operator is developed. Section 5 compares the proposed method with the existing ones [44, 45] and discusses several CWW methodologies by proportional 2-tuple linguistic model. Section 6 is conclusion.

2 Preliminaries

In this section, some fundamental concepts are introduced, including the concept of fuzzy linguistic variables, the proportional 2-tuple fuzzy linguistic representation, the Choquet integral, and representation model of MGUHFLTS.

2.1 Linguistic Variables

2.1.1 The Concept of Linguistic Variables

Zadeh [6] presented the concept of linguistic variables (LVs). In the actual decision-making process, linguistic term set (LTS) is composed of odd linguistic terms (LTs). Let $S_{g} = \left\{ {s_{0} ,s_{1} , \ldots ,s_{g} } \right\}$ be a LTS, where $s_{i} \in S_{g}$ is called a LV,$i \in \left\{ {0,1, \cdots ,g} \right\}$, $g$ is finite even number, generally $g < 14$. $S_{g} = \left\{ {s_{0} ,s_{1} , \ldots ,s_{g} } \right\}$ needs to satisfy the following properties:

(1) Orderliness if $i > j$, then $s_{i} > s_{j}$;

(2) Negative operator if $j = g - i$, then $Neg\left( {s_{i} } \right) = s_{j}$ ($g + 1$ is the granularity of $S_{g}$);

(3) Maximization and minimization operator: if $s_{i} > s_{j}$, then $\hbox{max} \left( {s_{i} ,s_{j} } \right) = s_{i}$,$\hbox{min} \left( {s_{i} ,s_{j} } \right) = s_{j}$.

Example 1

Suppose the LTS $S_{6}$ consists of seven LTs:

$$S_{6} = \left\{ {s_{0} = {\text{nothing}},\;s_{1} = {\text{bad}},\;s_{2} = {\text{little}}\;{\text{bad}},\;s_{3} = {\text{medium}},\;s_{4} = {\text{little}}\;{\text{good}},\;s_{5} = {\text{good}},\;s_{6} = {\text{perfect}}} \right\},$$

and LTS $S_{4}$ consists of five LTs:

$$S_{4} = \left\{ {s_{0} = {\text{nothing}},\;s_{1} = {\text{bad}},\;s_{2} = {\text{medium}},\;s_{3} = {\text{good}},\;s_{4} = {\text{perfect}}} \right\}.$$

In the decision-making process, different DMs use different granularity LTSs called multi-granularity LTSs (MGLTSs) to describe their preferences. In example 1, LTS $S_{6}$ with granularity 7 and LTS $S_{4}$ with granularity 5 are MGLTSs, which are composed of $S_{6}$ and $S_{4}$.

2.1.2 Semantics of LVs

The semantic of LVs refers to the meaning of linguistic evaluation, which constitutes a LTS. This meaning is not the explanation of linguistic concepts, but the quantitative expression of linguistic evaluation by means of mathematical methods, in order to realize the correspondence between linguistic evaluation and numerical values. One of the commonly used methods of expressing linguistic semantics is membership function. In this paper, the trapezoidal membership functions are directly used to express to semantics of linguistic variables. Let trapezoidal fuzzy number $T\left[ {b - \gamma ,\;b,\;c,\;c + \gamma } \right]$ depict the semantics of the LTSs, then the semantic of $S_{i}$ is defined by $T_{{s_{i} }} \left[ {b_{i} - \gamma_{i} ,\;b_{i} ,\;c_{i} ,\;c_{i} + \gamma_{i} } \right]$.

2.2 The Proportional 2-Tuple Fuzzy Linguistic Representation

In order to compute with words (CWW), different linguistic computing models have been developed [46, 47]; among them, a fuzzy linguistic representation model was introduced by Herrera and Martínez [29], then based on this model, Wang and Hao [30] further proposed the proportional 2-tuple fuzzy linguistic representation model.

Definition 1

[30] Let $S_{g} = \left\{ {s_{0} ,s_{1} , \ldots ,s_{g} } \right\}$ be a LTS. $\alpha \in \left[ {0,1} \right]$, $s_{i} ,s_{i + 1} \in S_{g}$, then $\left( {\alpha s_{i} ,\left( {1 - \alpha } \right)s_{i + 1} } \right)$ is called proportional 2-tuple fuzzy linguistic model. The set of all ordinal proportional 2-tuple on LTS $S_{g}$ is denoted by

$$\overline{\overline{{S_{g} }}} = \left\{ {\left( {\alpha s_{i} ,\left( {1 - \alpha } \right)s_{i + 1} } \right)|\alpha \in \left[ {0,1} \right],i = 0,1, \ldots ,g - 1} \right\}$$

(1)

Theorem 1

[30] Let $\left( {\alpha s_{i} ,\left( {1 - \alpha } \right)s_{i + 1} } \right)$ and $\left( {\beta s_{j} ,\left( {1 - \beta } \right)s_{j + 1} } \right)$ be two proportional 2-tuple linguistic variables, the comparison rule between them is as follows:

• 1. if $i < j$, there are two situations:

  If $i = j - 1$, and $\alpha = 0$,$\beta = 1$, then $\left( {\alpha s_{i} ,\left( {1 - \alpha } \right)s_{i + 1} } \right)$ and $\left( {\beta s_{j} ,\left( {1 - \beta } \right)s_{j + 1} } \right)$ represent equivalent information, that is, $\left( {\alpha s_{i} ,\left( {1 - \alpha } \right)s_{i + 1} } \right) = \left( {\beta s_{j} ,\left( {1 - \beta } \right)s_{j + 1} } \right)$;

  Else if $\left( {\alpha s_{i} ,\left( {1 - \alpha } \right)s_{i + 1} } \right) < \left( {\beta s_{j} ,\left( {1 - \beta } \right)s_{j + 1} } \right)$;

• 2. if $i = j$, there are three situations:

  If $\alpha = \beta$, then $\left( {\alpha s_{i} ,\left( {1 - \alpha } \right)s_{i + 1} } \right)$ and $\left( {\beta s_{j} ,\left( {1 - \beta } \right)s_{j + 1} } \right)$ represent equivalent information, that is, $\left( {\alpha s_{i} ,\left( {1 - \alpha } \right)s_{i + 1} } \right) = \left( {\beta s_{j} ,\left( {1 - \beta } \right)s_{j + 1} } \right)$;

  If $\alpha > \beta$, then $\left( {\alpha s_{i} ,\left( {1 - \alpha } \right)s_{i + 1} } \right) < \left( {\beta s_{j} ,\left( {1 - \beta } \right)s_{j + 1} } \right)$;

  If $\alpha < \beta$, then $\left( {\alpha s_{i} ,\left( {1 - \alpha } \right)s_{i + 1} } \right) > \left( {\beta s_{j} ,\left( {1 - \beta } \right)s_{j + 1} } \right)$.

Wang and Hao [30] proposed a method based on canonical characteristic values (CCVs) to make the MGLTSs variables uniform. The essence of this method is a transformation, which is between CCVs and LTSs.

Definition 2

[30] Let trapezoidal fuzzy numbers $T_{{s_{i} }} \left[ {b_{i} - \gamma_{i} ,b_{i} ,c_{i} ,c_{i} + \gamma_{i} } \right]$ be defined as the semantic of $s_{i}$, the CCV of $s_{i}$ is as follows:

$${\text{CCV}}\left( {s_{i} } \right) = \frac{{b_{i} + c_{i} }}{2}.$$

(2)

Let $\overline{\overline{S}}$ be defined as proportional 2-tuple fuzzy linguistic model, $\forall \left( {\alpha s_{i} ,\left( {1 - \alpha } \right)s_{i + 1} } \right) \in \overline{\overline{S}}$, the function ${\text{CCV}}$ over $\overline{\overline{S}}$ is

$${\text{CCV}}\left( {\alpha s_{i} ,\left( {1 - \alpha } \right)s_{i + 1} } \right) = \alpha {\text{CCV}}\left( {s_{i} } \right) + \left( {1 - \alpha } \right){\text{CCV}}\left( {s_{i + 1} } \right) = \alpha \frac{{b_{i} + c_{i} }}{2} + \left( {1 - \alpha } \right)\frac{{b_{i + 1} + c_{i + 1} }}{2},$$

(3)

where $\alpha ,b_{i} ,c_{i} \in \left[ {0,1} \right]$,$i = 0,1 \ldots ,g - 1$.

The function ${\text{CCV}}$ is a bijection, and the inverse of ${\text{CCV}}$ is denoted by ${\text{CCV}}^{ - 1}$. By functions ${\text{CCV}}$ and ${\text{CCV}}^{ - 1}$, transformations between a proportional 2-tuple linguistic variable $\left( {\alpha s_{i} ,\left( {1 - \alpha } \right)s_{i + 1} } \right)$ and a numerical value can be achieved. A group of computational models have been developed for the proportional 2-tuple fuzzy linguistic representation model, such as a 2-tuple comparison operator [30], a 2-tuple negation operator [31], and a wide range of 2-tuple aggregation operators [48].

In most classical decision-making problems, LTS is usually assumed that LTs are uniformly and symmetrically distributed around the midterm. However, the LTS given by some DMs does not always satisfy this form, and then the concept of unbalanced linguistic term set (ULTS) is proposed.

2.3 Representation of MGUHFLTS

2.3.1 Unbalanced LTS

Definition 3

[48] Let LTS $S_{g}$ and CCV of $\overline{\overline{S}}_{g}$ be defined as before, $s^{*}$ be the midterm of $S_{g}$. $S_{g}$ is called balanced LTS, when the following conditions are met:

• 1. A unique constant $\xi > 0$ exists, and ${\text{CCV}}\left( {s_{i} } \right) - {\text{CCV}}\left( {s_{j} } \right) = \xi \left( {i - j} \right)$ for all $i,j = 0,1, \ldots ,g$;

• 2. Let $S^{R} = \left\{ {s|s \in S_{g} ,s > s^{*} } \right\}$ and $S^{L} = \left\{ {s|s \in S_{g} ,s < s^{*} } \right\}$. Let $\# \left( {S^{R} } \right)$ and $\# \left( {S^{L} } \right)$ be the cardinalities of $S^{R}$ and $S^{L}$, respectively, the $\# \left( {S^{R} } \right) = \# \left( {S^{L} } \right)$.

Otherwise, it is an ULTS. For convenience, the $S$ denotes ULTS in this paper.

$$S = \left\{ {s_{k} |k = 0,1, \ldots \tau } \right\},$$

(4)

where the granularity is $\left( {\tau + 1} \right)$, and $s_{k}$ satisfies $s_{i} > s_{j}$, iff $i > j$.

It is easy to see that new definition of ULTS is consistent with the previous two models.

2.3.2 The Hesitant Linguistic Term Set

Definition 4

[14] Let $S_{g}$ be a balanced LTS, then a HFLTS $H_{s}$ is an ordered subset of the consecutive linguistic terms of $S_{g}$.

Example 2

Let $S_{4} = \left\{ {s_{0} = {\text{nothing}},\;s_{1} = {\text{bad}},\;s_{2} = {\text{medium}},\;s_{3} = {\text{good}},\;s_{4} = {\text{perfect}}} \right\}$, then $\left\{ {s_{1} ,s_{2} ,s_{3} } \right\}$ is one of expressions of HFLTS.

When it comes to ULTS, the definition of unbalanced HFLTSs is shown as follows:

Definition 5

[44] Let $S = \left\{ {s_{0} ,s_{1} , \ldots ,s_{\tau } } \right\}$ be an ULTS. Then, an unbalanced HFLTS on $S$ is an ordered finite subset of consecutive linguistic terms of $S$.

2.3.3 MGUHFLTS

Generally, a MGUHFLTS is referred to a set of ULTSs with distinct granularities.

Definition 6

Let $x_{i} \in X$, $i = 1,2, \ldots ,N$, then $S^{\text{MG}} = \left\{ {S^{t} |t = 1, \ldots ,T} \right\}$ is called the MGULTSs, where $S^{t}$$\left( {t = 1, \ldots ,T} \right)$ is an ULTS by using the form of formula (4).

Suppose that $S^{t} = \left\{ {s_{0}^{t} ,s_{1}^{t} , \ldots ,s_{\tau }^{t} } \right\}$, then the granularity of $S^{t}$ is $\left( {\tau + 1} \right)$, and $s_{\alpha }^{t} \in S^{t}$ is the $\alpha$ th term of $S^{t}$,$\left( {t = 1, \ldots ,T} \right)$.

Then, the mathematical form of a MGUHFLTS on X is denoted by

$$\bar{H}_{S} = \left\{ { < x_{i} ,\overline{{h_{s} }} \left( {x_{i} } \right) > |x_{i} \in X} \right\},$$

(5)

where $\bar{h}_{s} \left( {x_{i} } \right):X \to S^{t}$ is a function defined on set X, for any element $x_{i} \in X$, there is a unique $\bar{h}_{s} \left( {x_{i} } \right)$ corresponding to it. $\overline{h}_{S} \left( {x_{i} } \right) = \left\{ {S_{{\delta_{j} }}^{{}} \left( {x_{i} } \right)|S_{{\delta_{j} }}^{{}} \left( {x_{i} } \right) \in S^{t} ,j = 1, \ldots ,L} \right\}$. L is the cardinal number of $\bar{h}_{s} \left( {x_{i} } \right)$, which represents the number of elements in set $\bar{h}_{s} \left( {x_{i} } \right)$, and $\delta_{j} \in \left\{ {0,1, \ldots ,\tau } \right\}$. So the granularity of $\bar{h}_{s} \left( {x_{i} } \right)$ is $\# \left( t \right)$. Then, $\bar{h}_{s} \left( {x_{i} } \right)$ is called multi-granularity unbalanced hesitate fuzzy linguistic element (MGUHFLE), so MGUHFLTS is the set of all MGUHFLEs.

Example 3

Let $S^{1} = \left\{ {s_{0}^{1} ,s_{1}^{1} ,s_{2}^{1} ,s_{3}^{1} ,s_{4}^{1} } \right\}$ be an ULTS with granularity 5, and $S^{2} = \left\{ {s_{0}^{2} ,s_{1}^{2} ,s_{2}^{2} ,s_{3}^{2} ,s_{4}^{2} ,s_{5}^{2} ,s_{6}^{2} } \right\}$ be an ULTS with granularity 7. Given $\bar{H}_{S} = \left\{ {\left\{ {s_{2}^{1} ,s_{3}^{1} ,s_{1}^{2} } \right\},\left\{ {s_{4}^{2} ,s_{5}^{2} } \right\}} \right\}$, then it is a MUHFLS, among which $\left\{ {s_{2}^{1} ,s_{3}^{1} ,s_{1}^{2} } \right\}$ and $\left\{ {s_{4}^{2} ,s_{5}^{2} } \right\}$ are two MGUHFLEs of $\bar{H}_{S}$. The granularity of $\bar{H}_{S}$ is 2.

Remark 1

With further study of the HFLTS, the discontinuous HFLTS has been expanded [49].

Definition 7

Let $S^{\text{MG}} = \left\{ {S^{t} |t = 1, \ldots ,T} \right\}$ be MGULTSs,$\bar{h}_{{S_{{}} }}^{{}}$,$\bar{h}_{{S_{1} }}^{{}}$, and $\bar{h}_{{S_{2} }}^{{}}$ be three MGUHFLEs, $\lambda$ be a real number. The followings are some operational laws:

$$(1)\quad \bar{h}_{{S_{1} }}^{{}} \oplus \bar{h}_{{S_{2} }} = {\text{CCV}}^{ - 1} \left( {\bigcup\limits_{{\gamma_{1} \in CCV\left( {\bar{h}_{{S_{1} }} } \right),\gamma_{2} \in CCV\left( {\bar{h}_{{S_{2} }} } \right)}} {\left\{ {\gamma_{1} + \gamma_{2} - \gamma_{1} \gamma_{2} } \right\}} } \right);$$

(6)

$$(2)\quad \bar{h}_{{S_{1} }}^{{}} \otimes \bar{h}_{{S_{2} }} = {\text{CCV}}^{ - 1} \left( {\bigcup\limits_{{\gamma_{1} \in CCV\left( {\bar{h}_{{S_{1} }} } \right),\gamma_{2} \in CCV\left( {\bar{h}_{{S_{2} }} } \right)}} {\left\{ {\gamma_{1} \gamma_{2} } \right\}} } \right);$$

(7)

$$(3)\quad \lambda \overline{h}_{S} = {\text{CCV}}^{ - 1} \left( {\bigcup\limits_{{\gamma \in CCV\left( {\bar{h}_{S} } \right)}} {\left\{ {1 - \left( {1 - \gamma } \right)^{\lambda } } \right\}} } \right);$$

(8)

$$(4)\quad \left( {\overline{h}_{S} } \right)^{\lambda } = {\text{CCV}}^{ - 1} \left( {\bigcup\limits_{{\gamma \in CCV\left( {\bar{h}_{S} } \right)}} {\left\{ {\gamma^{\lambda } } \right\}} } \right).$$

(9)

Remark 2

In the operational laws, $\bar{h}_{S}^{{}}$ can be converted to multi-granularity unbalanced hesitant proportional 2-tuple fuzzy linguistic expression $\left( {\alpha s_{i} ,\left( {1 - \alpha } \right)s_{i + 1} } \right)$, according to formula (3),

$${\text{CCV}}\left( {\overline{h}_{s} } \right) = \alpha {\text{CCV}}\left( {s_{i} } \right) + \left( {1 - \alpha } \right){\text{CCV}}\left( {s_{i + 1} } \right),$$

(10)

where ${\text{CCV}}\left( {s_{i} } \right) \le {\text{CCV}}\left( {\overline{h}_{s} } \right) \le {\text{CCV}}\left( {s_{i + 1} } \right)$.

By solving formula (10),

$$\begin{aligned} & {\text{CCV}}\left( {\overline{h}_{s} } \right) = \alpha {\text{CCV}}\left( {s_{i} } \right) + {\text{CCV}}\left( {s_{i + 1} } \right) - \alpha {\text{CCV}}\left( {s_{i + 1} } \right) \\ & \alpha {\text{CCV}}\left( {s_{i + 1} } \right) - \alpha {\text{CCV}}\left( {s_{i} } \right) = {\text{CCV}}\left( {s_{i + 1} } \right) - {\text{CCV}}\left( {\overline{h}_{s} } \right) \\ & \alpha = \frac{{{\text{CCV}}\left( {s_{i + 1} } \right) - {\text{CCV}}\left( {\overline{h}_{s} } \right)}}{{{\text{CCV}}\left( {s_{i + 1} } \right) - {\text{CCV}}\left( {s_{i} } \right)}}. \\ \end{aligned}$$

(11)

In the following, an example is given to verify the operational laws in Definition 7:

Example 4

Let $S^{1} = \left\{ {s_{0}^{1} ,s_{1}^{1} ,s_{2}^{1} ,s_{3}^{1} ,s_{4}^{1} } \right\}$,$S^{2} = \left\{ {s_{0}^{2} ,s_{1}^{2} ,s_{2}^{2} ,s_{3}^{2} ,s_{4}^{2} ,s_{5}^{2} ,s_{6}^{2} } \right\}$ be two MGUTSs, $h_{{S_{1} }} = \left\{ {s_{2}^{1} ,s_{3}^{1} ,s_{1}^{2} } \right\}$ and $h_{{S_{2} }} = \left\{ {s_{4}^{2} ,s_{5}^{2} } \right\}$ be two MGUHFLEs, $\lambda = 2$. Here,$h_{{S_{1} }}$ and $h_{{S_{2} }}$ can be converted to multi-granularity unbalanced hesitant proportional 2-tuple fuzzy linguistic expression, i.e., $h_{{S_{1} }} = \left\{ {s_{2}^{1} ,s_{3}^{1} ,s_{1}^{2} } \right\} = \left\{ {\left( {s_{2}^{1} ,0s_{3}^{1} } \right),\left( {s_{3}^{1} ,0s_{4}^{1} } \right),\left( {s_{1}^{2} ,0s_{2}^{2} } \right)} \right\}$ and $h_{{S_{2} }} = \left\{ {s_{4}^{2} ,s_{5}^{2} } \right\} = \left\{ {\left( {s_{4}^{2} ,0s_{5}^{2} } \right),\left( {s_{5}^{2} ,0s_{6}^{2} } \right)} \right\}$.The semantics of $S^{1}$ and $S^{2}$ are given by trapezoidal fuzzy numbers in [0,1] as follows: $s_{0}^{1} :T\left( {0,0,0,0} \right)$, $s_{1}^{1} :T\left( {0.2,0.32,0.3942,0.5142} \right)$, $s_{2}^{1} :T\left( {0.3,0.4,0.6,0.7} \right)$, $s_{3}^{1} :T\left( {0.45,0.6,0.8,0.95} \right)$, $s_{4}^{1} :T\left( {1,1,1,1} \right)$;$s_{0}^{2} :T\left( {0,0,0,0} \right)$, $s_{1}^{2} :T\left( {0,0.1,0.2,0.3} \right)$, $s_{2}^{2} :T\left( {0.2,0.3,0.35,0.45} \right)$, $s_{3}^{2} :T\left( {0.35,0.4,0.6,0.65} \right)$;$s_{4}^{2} :T\left( {0.6,0.65,0.7,0.75} \right)$;$s_{5}^{2} :T\left( {0.7,0.8,0.9,0.1} \right)$;$s_{6}^{2} :T\left( {1,1,1,1} \right)$. By the function (4), the CCVs of $S^{1}$ and $S^{2}$ can be calculated as ${\text{CCV}}\left( {s_{0}^{1} } \right) = 0$, ${\text{CCV}}\left( {s_{1}^{1} } \right) = 0.3571$, ${\text{CCV}}\left( {s_{2}^{1} } \right) = 0.5$, ${\text{CCV}}\left( {s_{3}^{1} } \right) = 0.7$, ${\text{CCV}}\left( {s_{4}^{1} } \right) = 1$; ${\text{CCV}}\left( {s_{0}^{2} } \right) = 0$, ${\text{CCV}}\left( {s_{1}^{2} } \right) = 0.15$, ${\text{CCV}}\left( {s_{2}^{2} } \right) = 0.325$, ${\text{CCV}}\left( {s_{3}^{2} } \right) = 0.5$, ${\text{CCV}}\left( {s_{4}^{2} } \right) = 0.675$, ${\text{CCV}}\left( {s_{5}^{2} } \right) = 0.85$, ${\text{CCV}}\left( {s_{6}^{2} } \right) = 1$, respectively. So ${\text{CCV}}\left( {h_{{S_{1} }} } \right) = \left\{ {0.5,0.7,0.1786} \right\}$, ${\text{CCV}}\left( {h_{{S_{2} }} } \right) = \left\{ {0.6607,0.8} \right\}$. In this case, $S^{1} = \left\{ {s_{0}^{1} ,s_{1}^{1} ,s_{2}^{1} ,s_{3}^{1} ,s_{4}^{1} } \right\}$ is selected as the basic LTS, the results should be displayed in the form of proportional 2-tuple fuzzy linguistic variables, which is based on $S^{1}$. In addition, we get

• 1.
  $$\begin{aligned} \bar{h}_{{S_{1} }}^{{}} \oplus \bar{h}_{{S_{2} }} & \\ &= {\text{CCV}}^{ - 1} \left( {\bigcup\limits_{{\gamma_{1} \in CCV\left( {\bar{h}_{{S_{1} }} } \right),\gamma_{2} \in CCV\left( {\bar{h}_{{S_{2} }} } \right)}} {\left\{ {\gamma_{1} + \gamma_{2} - \gamma_{1} \gamma_{2} } \right\}} } \right) = {\text{CCV}}^{ - 1} \left( {0.8304,0.9000,0.8982,0.9400,0.7213,0.8357} \right) \\ &= \left\{ {\left( {0.5655s_{3}^{1} ,0.4345s_{4}^{1} } \right),\left( {0.3333s_{3}^{1} ,0.6667s_{4}^{1} } \right),\left( {0.3393s_{3}^{1} ,0.6607s_{4}^{1} } \right),} \right. \\ & \left. {\left( {0.2000s_{3}^{1} ,0.8000s_{4}^{1} } \right),\left( {0.9290s_{3}^{1} ,0.0710s_{4}^{1} } \right),\left( {0.5476s_{3}^{1} ,0.4524s_{4}^{1} } \right)} \right\} \\ \end{aligned}$$
• 2.
  $$\begin{aligned} \bar{h}_{{S_{1} }}^{{}} \otimes \bar{h}_{{S_{2} }} & \\ &= {\text{CCV}}^{ - 1} \left( {\bigcup\limits_{{\gamma_{1} \in CCV\left( {\bar{h}_{{S_{1} }} } \right),\gamma_{2} \in CCV\left( {\bar{h}_{{S_{2} }} } \right)}} {\left\{ {\gamma_{1} \gamma_{2} } \right\}} } \right) = {\text{CCV}}^{ - 1} \left( {0.3304,0.4000,0.4625,0.5600,0.1180,0.1429} \right) \\ &= \left\{ {\left( {0.0749s_{0}^{1} ,0.9251s_{1}^{1} } \right),\left( {0.6998s_{1}^{1} ,0.3002s_{2}^{1} } \right),\left( {0.2625s_{1}^{1} ,0.7375s_{2}^{1} } \right),} \right. \\ & \left. {\left( {0.7000s_{2}^{1} ,0.3000s_{3}^{1} } \right),\left( {0.6696s_{0}^{1} ,0.3304s_{1}^{1} } \right),\left( {0.5999s_{0}^{1} ,0.40001s_{1}^{1} } \right)} \right\}. \\ \end{aligned}$$
• 3.
  $$\begin{aligned} \lambda h_{{S_{1} }} &= {\text{CCV}}^{ - 1} \left( {\bigcup\limits_{{\gamma \in CCV(\bar{h}_{S} )}} {\left\{ {1 - \left( {1 - \gamma } \right)^{\lambda } } \right\}} } \right) = {\text{CCV}}^{ - 1} \left( {1 - \left( {1 - 0.5} \right)^{2} ,1 - \left( {1 - 0.7} \right)^{2} ,1 - \left( {1 - 0.1786} \right)^{2} } \right) \\ &= {\text{CCV}}^{ - 1} \left( {0.7500,0.9100,0.3253} \right) \\ &= \left\{ {\left( {0.8333s_{3}^{1} ,0.1667s_{4}^{1} } \right),\left( {0.3000s_{3}^{1} ,0.7000s_{4}^{1} } \right),\left( {0.0890s_{0}^{1} ,0.9110s_{1}^{1} } \right)} \right\}. \\ \end{aligned}$$
• 4.
  $$\begin{aligned} \left( {h_{{S_{1} }} } \right)^{\lambda } &= {\text{CCV}}^{ - 1} \left( {\bigcup\limits_{{\gamma \in CCV\left( {\bar{h}_{S} } \right)}} {\left\{ {\gamma^{\lambda } } \right\}} } \right) = {\text{CCV}}^{ - 1} \left( {0.5^{2} ,0.7^{2} ,0.1786^{2} } \right) = {\text{CCV}}^{ - 1} (0.2500,0.4900,0.0319) \\ &= \left\{ {\left( {0.2999s_{0}^{1} ,0.7001s_{1}^{1} } \right),\left( {0.700s_{1}^{1} ,0.9300s_{2}^{1} } \right),\left( {0.9107s_{0}^{1} ,0.0893s_{1}^{1} } \right)} \right\}. \\ \end{aligned}$$

Furthermore, some properties of these operational laws are investigated as follows:

Theorem 2

Let $S^{MG} = \left\{ {S^{t} |t = 1, \ldots ,T} \right\}$ be MGULTSs,$\bar{h}_{S}^{{}}$,$\bar{h}_{{S_{1} }}^{{}}$ and $\bar{h}_{{S_{2} }}^{{}}$ be three MGUHFLEs, $\lambda$,$\lambda_{1}$ and $\lambda_{2}$ be three positive real numbers. Then,

• 1. $\bar{h}_{{S_{1} }}^{{}} \oplus \bar{h}_{{S_{2} }} = \bar{h}_{{S_{2} }} \oplus \bar{h}_{{S_{1} }}^{{}} ;$

• 2. $\bar{h}_{{S_{1} }}^{{}} \otimes \bar{h}_{{S_{2} }} = \bar{h}_{{S_{2} }} \otimes \bar{h}_{{S_{1} }}^{{}} ;$

• 3. $\lambda \left( {\bar{h}_{{S_{1} }}^{{}} \oplus \bar{h}_{{S_{2} }} } \right) = \lambda \bar{h}_{{S_{1} }} \oplus \lambda \bar{h}_{{S_{2} }} ;$

• 4. $\left( {\bar{h}_{{S_{1} }}^{{}} \otimes \bar{h}_{{S_{2} }} } \right)^{\lambda } = \left( {\bar{h}_{{S_{1} }} } \right)^{\lambda } \otimes \left( {\bar{h}_{{S_{2} }} } \right)^{\lambda } ;$

• 5. $\lambda_{1} \bar{h}_{S} \oplus \lambda_{2} \bar{h}_{S} = \left( {\lambda_{1} + \lambda_{2} } \right)\bar{h}_{S} ;$

• 6. $\left( {\bar{h}_{S} } \right)^{{\lambda_{1} }} \otimes \left( {\bar{h}_{S} } \right)^{{\lambda_{2} }} = \left( {\bar{h}_{S} } \right)^{{\lambda_{1} + \lambda_{2} }} ;$

• 7. $(\bar{h}_{{S_{1} }} \oplus \bar{h}_{{S_{2} }} ) \oplus \bar{h}_{{S_{3} }} = \bar{h}_{{S_{1} }} \oplus (\bar{h}_{{S_{2} }} \oplus \bar{h}_{{S_{3} }} );$

• 8. $(\bar{h}_{{S_{1} }} \otimes \bar{h}_{{S_{2} }} ) \otimes \bar{h}_{{S_{3} }} = \bar{h}_{{S_{1} }} \otimes (\bar{h}_{{S_{2} }} \otimes \bar{h}_{{S_{3} }} ).$

Proof

The properties of (1), (2), and (8) are easy to be proved, so the proofs can be omitted.

$$\begin{aligned} (3)\quad \lambda \left( {\bar{h}_{{S_{1} }} \oplus \bar{h}_{{S_{2} }} } \right) & \\ &= \lambda {\text{CCV}}^{ - 1} \left( {\bigcup\limits_{{\gamma_{1} \in CCV\left( {\bar{h}_{{S_{1} }} } \right),\gamma_{2} \in CCV\left( {\bar{h}_{S2} } \right)}} {\left\{ {\gamma_{1} + \gamma_{2} - \gamma_{1} \gamma_{2} } \right\}} } \right) = {\text{CCV}}^{ - 1} \left( {\bigcup\limits_{{\gamma_{1} \in CCV\left( {\bar{h}_{{S_{1} }} } \right),\gamma_{2} \in CCV\left( {\bar{h}_{S2} } \right)}} {\left\{ {1 - \left( {1 - \gamma_{1} } \right)^{\lambda } \left( {1 - \gamma_{2} } \right)^{\lambda } } \right\}} } \right) \\ &= {\text{CCV}}^{ - 1} \left( {\bigcup\limits_{{\gamma_{1} \in CCV\left( {\bar{h}_{{S_{1} }} } \right)}} {\left\{ {1 - \left( {1 - \gamma_{1} } \right)^{\lambda } } \right\}} } \right) \oplus {\text{CCV}}^{ - 1} \left( {\bigcup\limits_{{\gamma_{2} \in CCV\left( {\bar{h}_{{S_{2} }} } \right)}} {\left\{ {1 - \left( {1 - \gamma_{2} } \right)^{\lambda } } \right\}} } \right) = \lambda \bar{h}_{{S_{1} }} \oplus \lambda \bar{h}_{{S_{2} }} \\ \end{aligned}$$

$$\begin{aligned} (4)\quad \left( {\bar{h}_{{S_{1} }} \otimes \bar{h}_{{S_{2} }} } \right)^{\lambda } & \\ &= \left( {{\text{CCV}}^{ - 1} \left( {\bigcup\limits_{{\gamma_{1} \in CCV\left( {\bar{h}_{{S_{1} }} } \right),\gamma_{2} \in CCV\left( {\bar{h}_{{S_{2} }} } \right)}} {\left\{ {\gamma_{1} \gamma_{2} } \right\}} } \right)} \right)^{\lambda } = {\text{CCV}}^{ - 1} \left( {\bigcup\limits_{{\gamma_{1} \in CCV\left( {\bar{h}_{{S_{1} }} } \right)}} {\left\{ {\gamma_{1}^{\lambda } } \right\}} } \right) \otimes {\text{CCV}}^{ - 1} \left( {\bigcup\limits_{{\gamma_{2} \in CCV\left( {\bar{h}_{{S_{2} }} } \right)}} {\left\{ {\gamma_{2}^{\lambda } } \right\}} } \right) = \left( {\bar{h}_{{S_{1} }} } \right)^{\lambda } \otimes \left( {\bar{h}_{{S_{2} }} } \right)^{\lambda } \\ \end{aligned}$$

$$\begin{aligned} (5)\quad \lambda_{1} \bar{h}_{S} \oplus \lambda_{2} \bar{h}_{S} & \\ &= {\text{CCV}}^{ - 1} \left( {\bigcup\limits_{{\gamma \in CCV\left( {\bar{h}_{S} } \right)}} {\left\{ {1 - \left( {1 - \gamma } \right)^{{\lambda_{1} }} } \right\}} } \right) \oplus {\text{CCV}}^{ - 1} \left( {\bigcup\limits_{{\gamma \in CCV\left( {\bar{h}_{S} } \right)}} {\left\{ {1 - \left( {1 - \gamma } \right)^{{\lambda_{2} }} } \right\}} } \right) \\ &= {\text{CCV}}^{ - 1} \left( {\bigcup\limits_{{\gamma \in CCV\left( {\bar{h}_{S} } \right)}} {\left\{ {1 - \left( {1 - \gamma } \right)^{{\lambda_{1} }} + 1 - \left( {1 - \gamma } \right)^{{\lambda_{2} }} - \left( {1 - \left( {1 - \gamma } \right)^{{\lambda_{1} }} } \right)\left( {1 - \left( {1 - \gamma } \right)^{{\lambda_{2} }} } \right)} \right\}} } \right) \\ &= {\text{CCV}}^{ - 1} \left( {\bigcup\limits_{{\lambda \in CCV\left( {h_{S} } \right)}} {\left\{ {1 - \left( {1 - \gamma } \right)^{{\lambda_{1} + \lambda_{2} }} } \right\}} } \right) = \left( {\lambda_{1} \oplus \lambda_{2} } \right)\bar{h}_{S} \\ \end{aligned}$$

$$\begin{aligned} (6)\quad \left( {\bar{h}_{S} } \right)^{{\lambda_{1} }} \otimes \left( {\bar{h}_{S} } \right)^{{\lambda_{2} }} & \\ &= {\text{CCV}}^{ - 1} \left( {\bigcup\limits_{{\gamma \in CCV\left( {\bar{h}_{S} } \right)}} {\left\{ {\gamma_{{}}^{{\lambda_{1} }} } \right\}} } \right) \otimes {\text{CCV}}^{ - 1} \left( {\bigcup\limits_{{\gamma \in CCV\left( {\bar{h}_{S} } \right)}} {\left\{ {\gamma_{{}}^{{\lambda_{2} }} } \right\}} } \right) = {\text{CCV}}^{ - 1} \left( {\bigcup\limits_{{\gamma \in CCV\left( {\bar{h}_{S} } \right)}} {\left\{ {\gamma_{{}}^{{\lambda_{1} + \lambda_{2} }} } \right\}} } \right) = \left( {\bar{h}_{S} } \right)^{{\lambda_{1} + \lambda_{2} }} \\ \end{aligned}$$

$$\begin{aligned} (7)\quad (\bar{h}_{{S_{1} }} \oplus \bar{h}_{{S_{2} }} ) \oplus \bar{h}_{{S_{3} }} & \\ &= {\text{CCV}}^{ - 1} \left( {\bigcup\limits_{{\gamma_{1} \in CCV\left( {\bar{h}_{{S_{1} }} } \right),\gamma_{2} \in CCV\left( {\bar{h}_{{S_{2} }} } \right)}} {\left\{ {1 - \left( {1 - \gamma_{1} } \right)\left( {1 - \gamma_{2} } \right)} \right\}} } \right) \oplus \bar{h}_{{S_{3} }} \\ &= {\text{CCV}}^{ - 1} \left( {\bigcup\limits_{{\gamma_{1} \in CCV\left( {\bar{h}_{{S_{1} }} } \right),\gamma_{2} \in CCV\left( {\bar{h}_{{S_{2} }} } \right),\gamma_{3} \in CCV\left( {\bar{h}_{{S_{3} }} } \right)}} {\left\{ {1 - \left( {1 - \left( {1 - \left( {1 - \gamma_{1} } \right)\left( {1 - \gamma_{2} } \right)} \right)} \right)\left( {1 - \gamma_{3} } \right)} \right\}} } \right) \\ &= {\text{CCV}}^{ - 1} \left( {\bigcup\limits_{{\gamma_{1} \in CCV\left( {\bar{h}_{{S_{1} }} } \right),\gamma_{2} \in CCV\left( {\bar{h}_{{S_{2} }} } \right),\gamma_{3} \in CCV\left( {\bar{h}_{{S_{3} }} } \right)}} {\left\{ {1 - \left( {1 - \gamma_{1} } \right)\left( {1 - \gamma_{2} } \right)\left( {1 - \gamma_{3} } \right)} \right\}} } \right) = \bar{h}_{{S_{1} }} \oplus (\bar{h}_{{S_{2} }} \oplus \bar{h}_{{S_{3} }} ) \\ \end{aligned}$$

(Q.E.D.)

□

Definition 8

Let $S^{1} = \left\{ {s_{0}^{1} ,s_{1}^{1} , \ldots ,s_{{\tau_{1} }}^{1} } \right\}$ and $S^{2} = \left\{ {s_{0}^{2} ,s_{1}^{2} , \ldots ,s_{{\tau_{2} }}^{2} } \right\}$ be two ULTSs. The granularity of $S^{1}$ is $\left( {\tau_{1} + 1} \right)$, and the granularity of $S^{2}$ is $\left( {\tau_{2} + 1} \right)$. Let $\overline{H}_{{S_{1} }}$ and $\overline{H}_{{S_{2} }}$ be two MUHTSs on $S^{1}$ and $S^{2}$, then

• 1. The intersection $\overline{H}_{{S_{1} }} \cap \overline{H}_{{S_{2} }}$

  $$\overline{H}_{{S_{1} }} \cap \overline{H}_{{S_{2} }} = \left\{ {s_{k} |s_{k} \in \overline{H}_{{S_{1} }} \;{\text{and}}\;s_{k} \in \overline{H}_{{S_{2} }} } \right\};$$

• 2. The union $\overline{H}_{{S_{1} }} \cup \overline{H}_{{S_{2} }}$ of $\overline{H}_{{S_{1} }}$ and $\overline{H}_{{S_{2} }}$ is defined by $\overline{H}_{{S_{1} }}$ and $\overline{H}_{{S_{2} }}$ is defined by

  $$\overline{H}_{{S_{1} }} \cup \overline{H}_{{S_{2} }} = \left\{ {s_{k} |s_{k} \in \overline{H}_{{S_{1} }} \;{\text{or}}\;s_{k} \in \overline{H}_{{S_{2} }} } \right\}.$$

Definition 9

Let $S^{t} = \left\{ {s_{0}^{t} ,s_{1}^{t} , \ldots ,s_{\tau }^{t} } \right\}$ denote MGULTSs, the MGUHFLE on S is $\bar{h}_{S}$. Moreover, the score function of $\bar{h}_{S}$ is defined by

$$S\left( {\bar{h}_{S} } \right) = \frac{1}{{\# \left( {\bar{h}_{S} } \right)}}\sum\nolimits_{{s_{k}^{t} \in \bar{h}_{S} }} {{\text{CCV}}\left( {s_{k}^{t} } \right)} ,$$

(12)

where $\# \left( {\bar{h}_{S} } \right)$ is the number of the elements in $\bar{h}_{S}$.

Definition 10

Let $S^{t} = \left\{ {s_{0}^{t} ,s_{1}^{t} , \ldots ,s_{\tau }^{t} } \right\}$ denote MGULTSs, the MGUHFLE on S is $\bar{h}_{S}$. Moreover, the expectation of $\bar{h}_{S}$ is defined as follows:

$$E\left( {\bar{h}_{S} } \right) = \sum\nolimits_{k = 0}^{\tau } {\beta_{k}^{t} CCV\left( {s_{k}^{t} } \right)}$$

(13)

For two MGUHFLEs $\overline{h}_{{S_{1} }}$ and $\overline{h}_{{S_{2} }}$,

if $S\left( {\bar{h}_{{S_{1} }} } \right) > S\left( {\bar{h}_{{S_{2} }} } \right)$, then $\overline{h}_{{S_{1} }} > \overline{h}_{{S_{2} }}$;

if $S\left( {\bar{h}_{{S_{1} }} } \right) < S\left( {\bar{h}_{{S_{2} }} } \right)$, then $\overline{h}_{{S_{1} }} < \overline{h}_{{S_{2} }}$;

if $S\left( {\bar{h}_{{S_{1} }} } \right) = S\left( {\bar{h}_{{S_{2} }} } \right)$,

if $E\left( {\bar{h}_{{S_{1} }} } \right) > E\left( {\bar{h}_{{S_{2} }} } \right)$, then $\overline{h}_{{S_{1} }} > \overline{h}_{{S_{2} }}$;

if $E\left( {\bar{h}_{{S_{1} }} } \right) < E\left( {\bar{h}_{{S_{2} }} } \right)$, then $\overline{h}_{{S_{1} }} < \overline{h}_{{S_{2} }}$;

if $E\left( {\bar{h}_{{S_{1} }} } \right) = E\left( {\bar{h}_{{S_{2} }} } \right)$, then $\overline{h}_{{S_{1} }} = \overline{h}_{{S_{2} }}$.

2.4 λ-Fuzzy Measure and Choquet Integral

In order to solve the MAGDM problems where there exists relationship among the attributes or decision makers, we need use the λ-fuzzy measure and Choquet integral which are introduced as follows.

2.4.1 λ-Fuzzy Measure

Sugeno [50] first proposed another set function, i.e., the fuzzy measure (nonadditive measure) to replace additivity with weaker monotonicity and continuity, and among various types of fuzzy measure, because there are the advantages of its simple structure and a few parameters in λ-fuzzy measure, it is widely used in MAGDM.

Definition 11

[50] If the fuzzy measure $g$ satisfies the following additional properties: if $A \cap B = \phi$,

$$g\left( {A \cup B} \right) = g\left( A \right) + g\left( B \right) + \lambda g\left( A \right)g\left( B \right)$$

(14)

where $\lambda \in \left( { - 1,\infty } \right)$, then $g$ is called λ-fuzzy measure ($g_{\lambda }$).

$g_{\lambda }$ has the following characteristics:

• 1. Additivity if $\lambda = 0$, then $g_{\lambda } \left( {A \cup B} \right) = g_{\lambda } \left( A \right) + g_{\lambda } \left( B \right)$;

• 2. Sub-additivity if $\lambda < 0$, then $g_{\lambda } \left( {A \cup B} \right) < g_{\lambda } \left( A \right) + g_{\lambda } \left( B \right)$;

• 3. Super-additivity if $\lambda > 0$, then $g_{\lambda } \left( {A \cup B} \right) > g_{\lambda } \left( A \right) + g_{\lambda } \left( B \right)$.

Theorem 3

Let $X = \left\{ {x_{1} ,x_{2} , \ldots ,x_{n} } \right\}$ be a finite set and the fuzzy density function of $x_{i}$ is $g_{\lambda } \left( {x_{i} } \right)$ , then $g_{\lambda }$ can be expressed as follows:

$$g_{\lambda } \left( X \right) = g_{\lambda } \left( {\bigcup\limits_{i = 1}^{n} {x_{i} } } \right) = \left\{ {\begin{array}{*{20}l} {\frac{1}{\lambda }\left( {\prod\limits_{i = 1}^{n} {\left( {1 + \lambda g\left( {x_{i} } \right)} \right) - 1} } \right),} \hfill & {\lambda \ne 0} \hfill \\ {\sum\limits_{i = 1}^{n} {g\left( {x_{i} } \right),} } \hfill & {\lambda = 0} \hfill \\ \end{array} } \right.$$

(15)

Theorem 4

Since $g_{\lambda } \left( X \right) = 1$ , when $\lambda \ne 0$ , the value of $\lambda$ is determined according to the following formula:

$$\lambda + 1 = \prod\limits_{i = 1}^{n} {\left( {1 + \lambda g\left( {x_{i} } \right)} \right)}$$

(16)

2.4.2 Choquet Integral

Fuzzy integral is a kind of nonlinear function defined on the fuzzy measure, including Suggeon fuzzy integral [37], Weber fuzzy integral [51], Choquet fuzzy integral [38], and so on. At present, Choquet integral is widely used to solve the MAGDM problems [41, 53, 54], which is defined as follows:

Definition 12

[52] Let $f$ be a nonnegative function defined on $X = \left\{ {x_{1} ,x_{2} , \ldots ,x_{m} } \right\}$, $\mu$ be a fuzzy measure on $X$, then the discrete Choquet integral $f$ with respect to the fuzzy measure $\mu$ be as follows:

$$CI_{u} \left( {f\left( {x_{1} } \right),f\left( {x_{2} } \right), \ldots ,f\left( {x_{m} } \right)} \right) = \sum\limits_{j = 1}^{m} {f\left( {\left( {x_{\sigma \left( j \right)} } \right)} \right)} \left[ {\mu \left( {A_{\sigma \left( j \right)} } \right) - \mu \left( {A_{{\sigma \left( {j + 1} \right)}} } \right)} \right]$$

(17)

where $\sigma \left( 1 \right),\sigma \left( 2 \right), \ldots ,\sigma \left( m \right)$ is a permutation of $\left( {1,2, \ldots ,m} \right)$, satisfying $0 \le f(x_{\sigma (1)} ) \le f(x_{\sigma (1)} ) \le \cdots , \le f(x_{\sigma (m)} )$, and $A_{\sigma \left( j \right)} = \left\{ {x_{\sigma \left( j \right)} ,x_{{\sigma \left( {j + 1} \right)}} , \ldots ,x_{\sigma \left( m \right)} } \right\}$,$A_{{\sigma \left( {m + 1} \right)}} = \emptyset$,$f\left( {x_{\sigma \left( 0 \right)} } \right) = 0$.

3 Multi-granularity Unbalanced Hesitate Fuzzy Average Choquet Integral

Based on the MGUHFLE and the Choquet integral, the ${\text{MGUHFLCA}}$ operator based on λ-fuzzy measure is proposed, which can deal with the interactions among the attributes.

Definition 13

Let $\bar{h}_{{S_{j} }} \left( {j = 1,2, \ldots ,m} \right)$ be a collection of MGUHFLEs, $X$ be the set of attributes and $\mu$ be fuzzy measure on X, then the MGUHFLCA operator is defined as follows:

$${\text{MGUHFLCA}}_{\mu } \left( {\bar{h}_{{S_{1} }} ,\bar{h}_{{S_{2} }} , \ldots ,\bar{h}_{{S_{m} }} } \right) = \mathop \oplus \limits_{j = 1}^{m} \left( {\left( {\mu \left( {\bar{H}_{{S_{\left( j \right)} }} } \right) - \mu \left( {\bar{H}_{{S_{{\left( {j + 1} \right)}} }} } \right)} \right)\bar{h}_{{S_{\left( j \right)} }} } \right)$$

(18)

where $\left( {\left( 1 \right),\left( 2 \right), \ldots ,\left( m \right)} \right)$ is a permutation of $\left( {1,2, \ldots ,m} \right)$, satisfying $\bar{h}_{{S_{\left( 1 \right)} }} \le \bar{h}_{{S_{\left( 2 \right)} }} \le \cdots \le \bar{h}_{{S_{\left( m \right)} }}$ and $\bar{H}_{{S_{\left( j \right)} }} = \left\{ {\bar{h}_{{S_{\left( j \right)} }} ,\bar{h}_{{S_{{\left( {j + 1} \right)}} }} , \ldots ,\bar{h}_{{S_{\left( m \right)} }} } \right\}$, $j = 1,2, \cdots ,m$, $\bar{H}_{{S_{{\left( {m + 1} \right)}} }} = \emptyset$.

Theorem 5

Let $\bar{h}_{{S_{j} }} \left( {j = 1,2, \ldots ,m} \right)$ be a collection of MGUHFLEs, then the aggregated value obtained by the MGUHFLCA operator is shown as follows:

$${\text{MGUHFLCA}}_{\mu } \left( {\bar{h}_{{S_{1} }} ,\bar{h}_{{S_{2} }} , \ldots ,\bar{h}_{{S_{m} }} } \right) = \mathop \oplus \limits_{j = 1}^{m} \left( {\left( {\mu \left( {\bar{H}_{{S_{\left( j \right)} }} } \right) - \mu \left( {\bar{H}_{{S_{{\left( {j + 1} \right)}} }} } \right)} \right)\bar{h}_{{S_{\left( j \right)} }} } \right) = {\text{CCV}}^{ - 1} \left( {\bigcup\limits_{{\gamma_{{S_{\left( j \right)} }} \in {\text{CCV}}\left( {\bar{h}_{{S_{\left( j \right)} }} } \right)}} {\left\{ {1 - \prod\limits_{j = 1}^{m} {\left( {1 - \gamma_{{S_{\left( j \right)} }} } \right)}^{{\mu_{{S_{\left( j \right)} }} }} } \right\}} } \right)$$

(19)

where $\mu_{{S_{\left( j \right)} }} = \mu \left( {\bar{H}_{{S_{\left( j \right)} }} } \right) - \mu \left( {\bar{H}_{{S_{{\left( {j + 1} \right)}} }} } \right)$.

Proof

Theorem 5 can be proved by mathematical induction.□

• a. For $m = 1$, since

  ${\text{MGUHFLCA}}_{\mu } \left( {\bar{h}_{{S_{1} }} } \right) = \left( {\mu \left( {\bar{H}_{{S_{\left( 1 \right)} }} } \right) - \mu \left( \emptyset \right)} \right)\bar{h}_{{S_{\left( 1 \right)} }} = \bar{h}_{{S_{\left( 1 \right)} }}$.

  Obviously, Eq. (19) holds for $m = 1$.

• b. For $m = 2$, since

  $$\mu_{{S_{\left( 1 \right)} }} \bar{h}_{{S_{\left( 1 \right)} }} = {\text{CCV}}^{ - 1} \left( {\bigcup\limits_{{\gamma_{{S_{\left( 1 \right)} }} \in {\text{CCV}}\left( {h_{{S_{\left( 1 \right)} }} } \right)}} {\left\{ {1 - \left( {1 - \gamma_{{S_{\left( 1 \right)} }} } \right)} \right\}} } \right),$$

  and $\mu_{{S_{\left( 2 \right)} }} \bar{h}_{{S_{\left( 2 \right)} }} = {\text{CCV}}^{ - 1} \left( {\bigcup\limits_{{\gamma_{{S_{\left( 2 \right)} }} \in {\text{CCV}}\left( {h_{{S_{\left( 2 \right)} }} } \right)}} {\left\{ {1 - \left( {1 - \gamma_{{S_{\left( 2 \right)} }} } \right)} \right\}} } \right)$,

  then get

  $${\text{MGUHFLCA}}_{\mu } \left( {\bar{h}_{{S_{1} }} ,\bar{h}_{{S_{2} }} } \right) = \mu_{{S_{\left( 1 \right)} }} \bar{h}_{{S_{\left( 1 \right)} }} \oplus \mu_{{S_{\left( 2 \right)} }} \bar{h}_{{S_{\left( 2 \right)} }} = {\text{CCV}}^{ - 1} \left( {\bigcup\limits_{{\gamma_{{S_{\left( j \right)} }} \in {\text{CCV}}\left( {\bar{h}_{{S_{\left( j \right)} }} } \right)}} {\left\{ {1 - \left( {1 - \gamma_{{S_{\left( 1 \right)} }} } \right)^{{\mu_{{S_{\left( 1 \right)} }} }} \left( {1 - \gamma_{{S_{\left( 2 \right)} }} } \right)^{{\mu_{{S_{\left( 2 \right)} }} }} } \right\}} } \right).$$

  Thus, Eq. (19) holds for $m = 2$.

• c. If Eq. (19) holds for $m = k$, then

  $${\text{MGUHFLCA}}_{\mu } \left( {\bar{h}_{{S_{1} }} ,\bar{h}_{{S_{2} }} , \ldots ,\bar{h}_{{S_{k} }} } \right) = \mathop \oplus \limits_{j = 1}^{k} \mu_{{S_{\left( j \right)} }} \bar{h}_{{S_{\left( j \right)} }} = {\text{CCV}}^{ - 1} \left( {\bigcup\limits_{{\gamma_{{S_{\left( j \right)} }} \in {\text{CCV}}\left( {\bar{h}_{{S_{\left( j \right)} }} } \right)}} {\left\{ {1 - \prod\limits_{j = 1}^{k} {\left( {1 - \gamma_{{S_{\left( j \right)} }} } \right)}^{{\mu_{{S_{\left( j \right)} }} }} } \right\}} } \right),$$

  then when $m = k + 1$, for $\forall \gamma_{{S_{\left( j \right)} }} \in CCV\left( {\bar{h}_{{S_{\left( j \right)} }} } \right)$, we have,

  $$\begin{aligned} {\text{MGUHFLCA}}_{\mu } \left( {\bar{h}_{{S_{1} }} ,\bar{h}_{{S_{2} }} , \ldots ,\bar{h}_{{S_{k + 1} }} } \right) &= \mathop \oplus \limits_{j = 1}^{k + 1} \mu_{{S_{\left( j \right)} }} \bar{h}_{{S_{\left( j \right)} }} \\ &= {\text{CCV}}^{ - 1} \left( {\bigcup\limits_{{\gamma_{{S_{\left( j \right)} }} \in {\text{CCV}}\left( {\bar{h}_{{S_{\left( j \right)} }} } \right)}} {\left\{ {1 - \prod\limits_{j = 1}^{k} {\left( {1 - \gamma_{{S_{\left( j \right)} }} } \right)}^{{\mu_{{S_{\left( j \right)} }} }} } \right\}} } \right) \oplus {\text{CCV}}^{ - 1} \left( {\bigcup\limits_{{\gamma_{{S_{{\left( {k + 1} \right)}} }} \in {\text{CCV}}\left( {\bar{h}_{{S_{{\left( {k + 1} \right)}} }} } \right)}} {\left\{ {1 - \left( {1 - \gamma_{{S_{{\left( {k + 1} \right)}} }} } \right)^{{\mu_{{S_{{\left( {k + 1} \right)}} }} }} } \right\}} } \right) \\ &= {\text{CCV}}^{ - 1} \left( {\bigcup\limits_{{\gamma_{{S_{\left( j \right)} }} \in {\text{CCV}}\left( {\bar{h}_{{S_{\left( j \right)} }} } \right)}} {\left\{ {1 - \prod\limits_{j = 1}^{k + 1} {\left( {1 - \gamma_{{S_{\left( j \right)} }} } \right)}^{{\mu_{{S_{\left( j \right)} }} }} } \right\}} } \right). \\ \end{aligned}$$

  i.e., Equation (19) holds for $m = k + 1$, thus we confirm Eq. (19) holds for all $m$. Q.E.D

Theorem 6

According to the definition of MGUHFLCA operator and the operational rules of MGUHFLEs, the MGUHFLCA operator has the following desirable properties:

• 1. (Boundedness) Let $\bar{h}^{ - }_{S} = {\text{CCV}}^{ - 1} \left( {\hbox{min} \left\{ {\gamma_{{S_{j} }} } \right\}} \right)$,$\bar{h}^{ + }_{S} = {\text{CCV}}^{ - 1} \left( {\hbox{max} \left\{ {\gamma_{{S_{j} }} } \right\}} \right)$, so

$$\bar{h}_{S}^{ - } \le {\text{MGUHFLCA}}_{\mu } \left( {\bar{h}_{{S_{1} }} ,\bar{h}_{{S_{2} }} , \cdots ,\bar{h}_{{S_{m} }} } \right) \le \bar{h}_{S}^{ + }$$

Proof

Since $y = x^{a}$$\left( {0 < a < 1} \right)$ is a monotone increasing function, when $x > 0$, it holds

$$1 - \prod\limits_{j = 1}^{m} {\left( {1 - \hbox{min} \left\{ {\gamma_{{S_{j} }} } \right\}} \right)}^{{\left( {\mu \left( {\bar{H}_{{S_{j} }} } \right) - \mu \left( {\bar{H}_{{S_{j + 1} }} } \right)} \right)}} \le 1 - \prod\limits_{j = 1}^{m} {\left( {1 - \gamma_{{S_{j} }} } \right)}^{{\left( {\mu (\bar{H}_{{S_{j} }} ) - \mu (\bar{H}_{{S_{j + 1} }} )} \right)}} \le 1 - \prod\limits_{j = 1}^{m} {\left( {1 - \hbox{max} \left\{ {\gamma_{{S_{j} }} } \right\}} \right)}^{{\left( {\mu (\bar{H}_{{S_{j} }} ) - \mu (\bar{H}_{{S_{j + 1} }} )} \right)}} ,$$

which is equivalent to

$$1 - \left( {1 - \hbox{min} \left\{ {\gamma_{{S_{j} }} } \right\}} \right)^{{\sum\limits_{j = 1}^{m} {\left( {\mu (\bar{H}_{{S_{j} }} ) - \mu (\bar{H}_{{S_{j + 1} }} )} \right)} }} \le 1 - \prod\limits_{j = 1}^{m} {\left( {1 - \gamma_{{S_{j} }} } \right)}^{{\left( {\mu (\bar{H}_{{S_{j} }} ) - \mu (\bar{H}_{{S_{j + 1} }} )} \right)}} \le 1 - \left( {1 - \hbox{max} \left\{ {\gamma_{{S_{j} }} } \right\}} \right)^{{\sum\limits_{j = 1}^{m} {\left( {\mu (\bar{H}_{{S_{j} }} ) - \mu (\bar{H}_{{S_{j + 1} }} )} \right)} }} ,$$

i.e., $\hbox{min} \left\{ {\gamma_{{S_{j} }} } \right\} \le 1 - \prod\limits_{j = 1}^{m} {\left( {1 - \gamma_{{S_{j} }} } \right)}^{{\left( {\mu (\bar{H}_{{S_{j} }} ) - \mu (\bar{H}_{{S_{j + 1} }} )} \right)}} \le \hbox{max} \left\{ {\gamma_{{S_{j} }} } \right\}.$

since $T\left( {\bar{h}_{S}^{ - } } \right) \le T\left( {\bar{h}_{S} } \right) \le T\left( {\bar{h}_{S}^{ + } } \right)$, namely, $\bar{h}_{S}^{ - } \le MGUHFLCA_{\mu } \left( {\bar{h}_{{S_{1} }} ,\bar{h}_{{S_{2} }} , \ldots ,\bar{h}_{{S_{m} }} } \right) \le \bar{h}_{S}^{ + }$. Q.E.D

• 2. (Commutativity) If $\left\{ {\bar{h}^{\prime}_{{S_{1} }} ,\bar{h}^{\prime}_{{S_{2} }} , \ldots ,\bar{h}^{\prime}_{{S_{m} }} } \right\}$ is a permutation of $\left\{ {\bar{h}_{{S_{1} }} ,\bar{h}_{{S_{2} }} , \ldots ,\bar{h}_{{S_{m} }} } \right\}$, then

  $${\text{MGUHFLCA}}_{\mu } \left( {\bar{h}_{{S_{1} }} ,\bar{h}_{{S_{2} }} , \ldots ,\bar{h}_{{S_{m} }} } \right) = {\text{MGUHFLCA}}_{\mu } \left( {\bar{h}^{\prime}_{{S_{1} }} ,\bar{h}^{\prime}_{{S_{2} }} , \ldots ,\bar{h}^{\prime}_{{S_{m} }} } \right).$$

  □

Proof

Suppose $\left( {\left( 1 \right),\left( 2 \right), \ldots ,\left( m \right)} \right)$ be a permutation of both $\left\{ {\bar{h}^{\prime}_{{S_{1} }} ,\bar{h}^{\prime}_{{S_{2} }} , \ldots ,\bar{h}^{\prime}_{{S_{m} }} } \right\}$ and $\left\{ {\bar{h}_{{S_{1} }} ,\bar{h}_{{S_{2} }} , \ldots ,\bar{h}_{{S_{m} }} } \right\}$, such that $\bar{h}_{{S_{\left( 1 \right)} }} \le \bar{h}_{{S_{\left( 2 \right)} }} \le \cdots \le \bar{h}_{{S_{\left( m \right)} }}$,$\bar{H}_{{S_{\left( j \right)} }} = \left\{ {\bar{h}_{{S_{\left( 1 \right)} }} ,\bar{h}_{{S_{\left( 2 \right)} }} , \ldots ,\bar{h}_{{S_{\left( m \right)} }} } \right\}$, then

$${\text{MGUHFLCA}}_{\mu } \left( {\bar{h}_{{S_{1} }} ,\bar{h}_{{S_{2} }} , \ldots ,\bar{h}_{{S_{m} }} } \right) = {\text{MGUHFLCA}}_{\mu } \left( {\bar{h}^{\prime}_{{S_{1} }} ,\bar{h}^{\prime}_{{S_{2} }} , \ldots ,\bar{h}^{\prime}_{{S_{m} }} } \right) = \mathop \oplus \limits_{j = 1}^{m} \left( {\left( {\mu \left( {\bar{H}_{{S_{\left( j \right)} }} } \right) - \mu \left( {\bar{H}_{{S_{{\left( {j + 1} \right)}} }} } \right)} \right)\bar{h}_{{S_{\left( j \right)} }} } \right)$$

(Q.E.D)

• 3. (Monotonity) If $\bar{h}_{{S_{j} }} \le \bar{h}^{\prime}_{{S_{j} }}$ for $\forall j \in \left\{ {1,2, \ldots ,m} \right\}$, then,

  $${\text{MGUHFLCA}}_{\mu } \left( {\bar{h}_{{S_{1} }} ,\bar{h}_{{S_{2} }} , \ldots ,\bar{h}_{{S_{m} }} } \right) \le {\text{MGUHFLCA}}_{\mu } \left( {\bar{h}^{\prime}_{{S_{1} }} ,\bar{h}^{\prime}_{{S_{2} }} , \ldots ,\bar{h}^{\prime}_{{S_{m} }} } \right).$$

  □

Proof

Considering $\bar{h}_{{S_{j} }} \le \bar{h}^{\prime}_{{S_{j} }}$ for $\forall j \in \left\{ {1,2, \ldots ,m} \right\}$, we have

$$\gamma = 1 - \prod\limits_{j = 1}^{m} {\left( {1 - \gamma_{{S_{j} }} } \right)}^{{\left( {\mu \left( {\bar{H}_{{S_{j} }} } \right) - \mu (\bar{H}_{{S_{j + 1} }} )} \right)}} \le 1 - \prod\limits_{j = 1}^{m} {\left( {1 - \gamma^{\prime}_{{S_{j} }} } \right)}^{{\left( {\mu (S_{j} ) - \mu (\bar{H}_{{S_{j + 1} }} )} \right)}} = \gamma^{\prime},$$

since $T\left( {\bar{h}_{{S_{j} }} } \right) \le T\left( {\bar{h}^{\prime}_{{S_{j} }} } \right)$, namely

$${\text{MGUHFLCA}}_{\mu } \left( {\bar{h}_{{S_{1} }} ,\bar{h}_{{S_{2} }} , \ldots ,\bar{h}_{{S_{m} }} } \right) \le {\text{MGUHFLCA}}_{\mu } \left( {\bar{h}^{\prime}_{{S_{1} }} ,\bar{h}^{\prime}_{{S_{2} }} , \ldots ,\bar{h}^{\prime}_{{S_{m} }} } \right)$$

(Q.E.D)

□

4 A Novel MAGDM Approach Based on Proportional 2-Tuple MGUHFLCA Operators

In this section, a novel MAGDM approach with the information of MGHFLTEs is proposed on the basis of proportional 2-tuple MGUHFLCA operator.

4.1 The MAGDM Method Based on MGUHFLCA Operators

For a linguistic MAGDM problem, DMs may use different granularity linguistic term sets to give their evaluation, how to select granularity depends on DMs’ familiarity with the problem. The more familiar with the situation DMs are, the finer granularity is used; conversely, the rougher granularity is used.

In this section, we use the MGUHFLCA operator to solve the MAGDM with MGHFLTEs. Let $G = \left\{ {G_{1} ,G_{2} , \ldots ,G_{q} } \right\}$ be a set of groups of DMs,$A = \left\{ {A_{1} ,A_{2} , \ldots ,A_{m} } \right\}$ be a set of alternatives and $C = \left\{ {C_{1} ,C_{2} , \ldots ,C_{n} } \right\}$ be a set of attributes. Let $S^{\text{MG}} = \left\{ {S^{t} |t = 1, \ldots ,T} \right\}$, $S^{t} = \left\{ {s_{0}^{t} ,s_{1}^{t} , \ldots ,s_{\tau }^{t} } \right\}$, $s_{\alpha }^{t} \in S^{t}$ be the ULTS which is expressed by $S^{k} = \left\{ {s_{0}^{k} ,s_{1}^{k} , \ldots ,s_{g\left( k \right)}^{k} } \right\}$ and the ${\text{CCV}}$ function on $S^{k}$ is ${\text{CCV}}^{k}$$k = 1,2, \ldots ,p$. Suppose that the evaluation value of group $G_{k}$ under attribute $C_{j}$ of alternative $A_{i}$ is expressed as $\bar{h}_{ij}^{k}$, then the decision matrix given is $\bar{H}^{k} = \left[ {\bar{h}_{ij}^{k} } \right]_{m \times n}$,$i = 1,2, \ldots ,m$,$j = 1,2, \ldots ,n$,$k = 1,2, \ldots ,q$.

Based on the introduced MGUHFLCA operator, a novel MAGDM method is given by the following steps.

• Step 1 Selecting a basic ULTS $S^{B}$ from $\left\{ {S^{1} ,S^{2} \ldots ,S^{q} } \right\}$.

  The ranking results will not be affected by the selection of the basic LTS.

• Step 2 Constructing decision matrices of the MGHFLTEs $\left[ {\bar{h}_{ij}^{k} } \right]_{m \times n}$$\left( {k = 1,2, \cdots ,q} \right)$.$h_{ij}^{k}$ can be transformed to the proportional 2-tuple sets $\bar{h}_{ij}^{k}$ in terms of formula (1).

• Step 3 Determining the fuzzy measure of group of DMs.

• Step 4 Integrating each group of DMs, assessment by MGUHFLCA operator to obtain the overall information $\overline{H}^{B} = \left[ {\bar{h}_{ij}^{B} } \right]_{m \times n}$.

• Step 5 Determining the fuzzy measure $\mu_{C}$ of attributes.

• Step 6 Using the MGUHFLCA operator to integrate the attributes’ values of each alternative into a collective assessment $\bar{h}_{i}^{B}$.

• Step 7 For each alternative, calculating the score value and expected value.

• Step 8 According to defined score function, the best alternative is obtained by ranking the alternatives $A_{i} \left( {i = 1,2, \cdots ,m} \right)$.

In the next subsection, we will apply the posed MAGDM method to deal with the “Online Courses Assessment” with MGUHFLEs information.

4.2 Illustrative Example

An example about the online courses assessment of China National Open University is used to illustrate the application of the proposed MAGDM method.

China National Open University is characterized by online courses, which is the unique teaching resources based on modern information technology and adopting mobile learning mode. Assume that there are four alternatives, i.e., four online courses $A = \left\{ {A_{1} ,A_{2} ,A_{3} ,A_{4} } \right\}$ in China National Open University. In order to accurately reflect the real situation of the courses, the online courses are assessed according to four attributes, i.e., online course design ($C_{1}$), online teaching team ($C_{2}$), teaching support service ($C_{3}$), teaching process monitoring ($C_{4}$). Assume that there are three groups of DMs, i.e., three teachers ($G_{1}$), three educational administrators ($G_{2}$), three teaching supervisions ($G_{3}$), and they provided their assessments with MGUHFLEs. The groups of DMs are independent of each other, and the weight vector is as follows: $W_{G} = \left\{ {0.2,0.3,0.5} \right\}$. The ULTSs used by three groups of DMs are given below:

$S^{1} = \left\{ {s_{0}^{1} = {\text{extremely}}\;{\text{bad}},\;s_{1}^{1} = {\text{very}}\;{\text{bad}},\;s_{2}^{1} = {\text{a}}\;{\text{little}}\;{\text{good}};\;s_{3}^{1} = {\text{bad}},\;s_{4}^{1} = {\text{medium}},\;s_{5}^{1} = {\text{good}},\;s_{6}^{1} = {\text{a}}\;{\text{little}}\;{\text{good}},\;s_{7}^{1} = {\text{very}}\;{\text{good}},\;s_{8}^{1} = {\text{extremely}}\;{\text{good}}} \right\}$,$S^{2} = \left\{ {s_{0}^{2} :{\text{extremely}}\;{\text{bad}},\;s_{1}^{2} :{\text{very}}\;{\text{bad}},\;s_{2}^{2} :{\text{bad}},\;s_{3}^{2} :{\text{medium}},\;s_{4}^{2} :{\text{good}},\;s_{5}^{2} :{\text{very}}\;{\text{good}},\;s_{6}^{2} :{\text{extremely}}\;{\text{good}}} \right\}$,$S^{3} = \left\{ {s_{0}^{3} :{\text{very}}\;{\text{bad}},\;s_{1}^{3} :{\text{bad,}}\;s_{2}^{3} :{\text{medium}},s_{3}^{3} :{\text{good,}}\;s_{4}^{3} :{\text{very}}\;{\text{good}}} \right\}$. The semantics of the ULTSs are shown in Tables 1, 2 and 3.

Table 1 ${\text{CCVs}}$ and semantics of $S^{1}$

Table 2 ${\text{CCVs}}$ and semantics of $S^{2}$

Table 3 ${\text{CCVs}}$ and semantics of $S^{3}$

The assessment values of each course given by three groups of DMs with MGUHFLEs are shown in Tables 4, 5 and 6. Among them, group $G_{1}$ choose assessment information in $S^{1}$ and $S^{2}$, group $G_{2}$ choose assessment information in $S^{2}$ and $S^{3}$, and group $G_{3}$ choose assessment information in $S^{1}$,$S^{2}$ and $S^{3}$.

Table 4 Assessment value of different attributes of four online courses given by $G_{1}$

Table 5 Assessment value of different indicators of four online courses given by $G_{2}$

Table 6 Assessment value of different indicators of four online courses given by $G_{3}$

• Step 1 In this example, there are three ULTSs. Without loss of generality, $S^{3}$ is chosen as the basic LTS $S^{B}$.

• Step 2 The assessment information provided by groups of DMs with MGUHFLEs is transformed to the proportional 2-tuple sets. The decision matrices $\bar{H}^{k} = \left( {\bar{h}_{ij}^{k} } \right)_{4 \times 4} \left( {k = 1,2,3} \right)$ in the form of proportional 2-tuple sets are shown as follows:

  $$\bar{H}^{1} = \left[ {\begin{array}{*{20}l} {\left\{ {\left( {s_{7}^{1} ,0s_{8}^{1} } \right),\left( {s_{7}^{1} ,0s_{8}^{1} } \right)} \right\}} \hfill & {\left\{ {\left( {s_{7}^{1} ,0s_{8}^{1} } \right)} \right\}} \hfill & {\left\{ {\left( {s_{6}^{1} ,0s_{7}^{1} } \right),\left( {s_{7}^{1} ,0s_{8}^{1} } \right)} \right\}} \hfill & {\left\{ {\left( {s_{6}^{1} ,0s_{7}^{1} } \right),\left( {s_{7}^{1} ,0s_{8}^{1} } \right),\left( {s_{5}^{2} ,0s_{6}^{2} } \right)} \right\}} \hfill \\ {\left\{ {\left( {s_{6}^{1} ,0s_{7}^{1} } \right),\left( {s_{4}^{2} ,0s_{5}^{2} } \right)} \right\}} \hfill & {\left\{ {\left( {s_{5}^{1} ,0s_{6}^{1} } \right),\left( {s_{6}^{1} ,0s_{7}^{1} } \right),\left( {s_{4}^{2} ,0s_{5}^{2} } \right)} \right\}} \hfill & {\left\{ {\left( {s_{4}^{1} ,0s_{5}^{1} } \right)} \right\}} \hfill & {\left\{ {\left( {s_{3}^{1} ,0s_{4}^{1} } \right),\left( {s_{3}^{2} ,0s_{4}^{2} } \right)} \right\}} \hfill \\ {\left\{ {\left( {s_{5}^{1} ,0s_{6}^{1} } \right),\left( {s_{6}^{1} ,0s_{7}^{1} } \right)} \right\}} \hfill & {\left\{ {\left( {s_{6}^{1} ,0s_{7}^{1} } \right),\left( {s_{5}^{2} ,0s_{6}^{2} } \right)} \right\}} \hfill & {\left\{ {\left( {s_{6}^{1} ,0s_{7}^{1} } \right),\left( {s_{7}^{1} ,0s_{8}^{1} } \right),\left( {s_{4}^{2} ,0s_{5}^{2} } \right)} \right\}} \hfill & {\left\{ {\left( {s_{4}^{1} ,0s_{5}^{1} } \right)} \right\}} \hfill \\ {\left\{ {\left( {s_{2}^{1} ,0s_{3}^{1} } \right)} \right\}} \hfill & {\left\{ {\left( {s_{3}^{1} ,0s_{4}^{1} } \right),\left( {s_{4}^{1} ,0s_{5}^{1} } \right),\left( {s_{3}^{2} ,0s_{4}^{2} } \right)} \right\}} \hfill & {\left\{ {\left( {s_{2}^{2} ,0s_{3}^{2} } \right)} \right\}} \hfill & {\left\{ {\left( {s_{3}^{1} ,0s_{4}^{1} } \right),\left( {s_{3}^{1} ,0s_{4}^{1} } \right)} \right\}} \hfill \\ \end{array} } \right]$$
  $$\bar{H}^{2} = \left[ {\begin{array}{*{20}l} {\left\{ {\left( {s_{3}^{3} ,0s_{4}^{3} } \right)} \right\}} \hfill & {\left\{ {\left( {s_{4}^{2} ,0s_{5}^{2} } \right),\left( {s_{5}^{2} ,0s_{6}^{2} } \right)} \right\}} \hfill & {\left\{ {\left( {s_{4}^{2} ,0s_{5}^{2} } \right)} \right\}} \hfill & {\left\{ {\left( {s_{4}^{2} ,0s_{5}^{2} } \right),\left( {s_{3}^{3} ,0s_{4}^{3} } \right)} \right\}} \hfill \\ {\left\{ {\left( {s_{3}^{2} ,0s_{4}^{2} } \right),\left( {s_{3}^{3} ,0s_{4}^{3} } \right)} \right\}} \hfill & {\left\{ {\left( {s_{3}^{2} ,0s_{4}^{2} } \right)} \right\}} \hfill & {\left\{ {\left( {s_{2}^{2} ,0s_{3}^{2} } \right),\left( {s_{2}^{2} ,0s_{3}^{2} } \right),\left( {s_{2}^{3} ,0s_{3}^{3} } \right)} \right\}} \hfill & {\left\{ {\left( {s_{2}^{2} ,0s_{3}^{2} } \right),\left( {s_{3}^{2} ,0s_{4}^{2} } \right)} \right\}} \hfill \\ {\left\{ {\left( {s_{4}^{2} ,0s_{5}^{2} } \right)} \right\}} \hfill & {\left\{ {\left( {s_{3}^{2} ,0s_{4}^{2} } \right),\left( {s_{3}^{3} ,0s_{4}^{3} } \right)} \right\}} \hfill & {\left\{ {\left( {s_{3}^{2} ,0s_{4}^{2} } \right)} \right\}} \hfill & {\left\{ {\left( {s_{5}^{2} ,0s_{6}^{2} } \right),\left( {s_{3}^{3} ,0s_{4}^{3} } \right)} \right\}} \hfill \\ {\left\{ {\left( {s_{2}^{2} ,0s_{3}^{2} } \right),\left( {s_{2}^{2} ,0s_{3}^{2} } \right),\left( {s_{2}^{3} ,0s_{3}^{3} } \right)} \right\}} \hfill & {\left\{ {\left( {s_{1}^{2} ,0s_{2}^{2} } \right)} \right\}} \hfill & {\left\{ {\left( {s_{2}^{2} ,0s_{3}^{2} } \right),\left( {s_{1}^{3} ,0s_{2}^{3} } \right)} \right\}} \hfill & {\left\{ {\left( {s_{2}^{2} ,0s_{3}^{2} } \right),\left( {s_{3}^{2} ,0s_{4}^{2} } \right)} \right\}} \hfill \\ \end{array} } \right]$$
  $$\bar{H}^{3} = \left[ {\begin{array}{*{20}l} {\left\{ {\left( {s_{4}^{2} ,0s_{5}^{2} } \right),\left( {s_{3}^{3} ,0s_{4}^{3} } \right)} \right\}} \hfill & {\left\{ {\left( {s_{3}^{3} ,0s_{4}^{3} } \right)} \right\}} \hfill & {\left\{ {\left( {s_{6}^{1} ,0s_{7}^{1} } \right),\left( {s_{5}^{2} ,0s_{6}^{2} } \right),\left( {s_{3}^{3} ,0s_{4}^{3} } \right)} \right\}} \hfill & {\left\{ {\left( {s_{6}^{1} ,0s_{7}^{1} } \right)} \right\}} \hfill \\ {\left\{ {\left( {s_{4}^{1} ,0s_{5}^{1} } \right)} \right\}} \hfill & {\left\{ {\left( {s_{3}^{1} ,0s_{4}^{1} } \right),\left( {s_{3}^{2} ,0s_{4}^{2} } \right)} \right\}} \hfill & {\left\{ {\left( {s_{3}^{1} ,0s_{4}^{1} } \right),\left( {s_{3}^{3} ,0s_{4}^{3} } \right)} \right\}} \hfill & {\left\{ {\left( {s_{2}^{3} ,0s_{3}^{3} } \right)} \right\}} \hfill \\ {\left\{ {\left( {s_{4}^{2} ,0s_{5}^{2} } \right),\left( {s_{2}^{3} ,0s_{3}^{3} } \right)} \right\}} \hfill & {\left\{ {\left( {s_{4}^{1} ,0s_{5}^{1} } \right)} \right\}} \hfill & {\left\{ {\left( {s_{5}^{1} ,0s_{6}^{1} } \right),\left( {s_{3}^{2} ,0s_{4}^{2} } \right)} \right\}} \hfill & {\left\{ {\left( {s_{6}^{1} ,0s_{7}^{1} } \right),\left( {s_{3}^{3} ,0s_{4}^{3} } \right)} \right\}} \hfill \\ {\left\{ {\left( {s_{1}^{3} ,0s_{2}^{3} } \right)} \right\}} \hfill & {\left\{ {\left( {s_{2}^{1} ,0s_{3}^{1} } \right),\left( {s_{2}^{3} ,0s_{3}^{3} } \right)} \right\}} \hfill & {\left\{ {\left( {s_{3}^{2} ,0s_{4}^{2} } \right),\left( {s_{2}^{3} ,0s_{3}^{3} } \right)} \right\}} \hfill & {\left\{ {\left( {s_{3}^{1} ,0s_{4}^{1} } \right)} \right\}} \hfill \\ \end{array} } \right]$$

• Step 3 Determining the fuzzy measure (weight) of each group of DMs. Assume that the fuzzy measure of each group is as follows:

  $\mu \left( \emptyset \right) = 0$,$\mu \left( {G_{1} } \right) = 0.2$,$\mu \left( {G_{2} } \right) = 0.3$,$\mu \left( {G_{3} } \right) = 0.5$. In this example, the groups of DMs are independent of each other, $\lambda_{G} = 0$; according to Formula (15), we get

  $$\mu \left( {G_{1} ,G_{2} } \right) = 0.5,\quad \mu \left( {G_{1} ,G_{3} } \right) = 0.7,\quad \mu \left( {G_{2} ,G_{3} } \right) = 0.8,\quad \mu \left( {G_{1} ,G_{2} ,G_{3} } \right) = 1.$$

• Step 4 Integrating each group’s assessment by ${\text{MGUHFLCA}}$ operator to obtain the comprehensive information. The comprehensive attribute values of the alternative $A_{i} \left( {i = 1,2,3,4} \right)$ given by three groups under attribute $C_{j} \left( {j = 1,2,3,4} \right)$ are obtained by the ${\text{MGUHFLCA}}$ operator, $\bar{H}^{B} = \bar{h}_{ij}^{B} \left( {i = 1,2,3,4;j = 1,2,3,4} \right)$.

  For example,

  $$\bar{H}_{11}^{B} = \left\{ {\left( {0.7274s_{3}^{3} ,0.2726s_{4}^{3} } \right),\left( {0.7274s_{3}^{3} ,0.2726s_{4}^{3} } \right),\left( {0.6988s_{3}^{3} ,0.3012s_{4}^{3} } \right),\left( {0.6988s_{3}^{3} ,0.3012s_{4}^{3} } \right)} \right\}.$$

  The other results are omitted here.

• Step 5 Determining the fuzzy measure of each attribute and attribute set. Assume that the fuzzy measure of each attribute is as follows:

  $\mu \left( \emptyset \right) = 0,\mu \left( {C_{1} } \right) = 3/9,\mu \left( {C_{2} } \right) = 4/9,\mu \left( {C_{3} } \right) = 2/9,\mu \left( {C_{4} } \right) = 3/9$, according to Formula (16), $\lambda_{C} = - 0.578$. According to Formula (15), all the fuzzy measures of each attribute are as follows:

  $\mu \left( {C_{1} ,C_{2} } \right) = 0.692$, $\mu \left( {C_{1} ,C_{3} } \right) = 0.513$,$\mu \left( {C_{1} ,C_{4} } \right) = 0.602$,$\mu \left( {C_{2} ,C_{3} } \right) = 0.610$,$\mu \left( {C_{2} ,C_{4} } \right) = 0.692$,$\mu \left( {C_{3} ,C_{4} } \right) = 0.513$,$\mu \left( {C_{1} ,C_{2} ,C_{3} } \right) = 0.825$,$\mu \left( {C_{1} ,C_{2} ,C_{4} } \right) = 0.892$,$\mu \left( {C_{1} ,C_{3} ,C_{4} } \right) = 0.747$,$\mu \left( {C_{2} ,C_{3} ,C_{4} } \right) = 0.825$,$\mu \left( {C_{1} ,C_{2} ,C_{3} ,C_{4} } \right) = 1$.

• Step 6 Using the ${\text{MGUHFLCA}}$ operator to integrate the attribute values of each alternative into a collective assessment $\bar{H}_{i}^{B}$, here $\bar{H}_{i}^{B}$ is a proportional 2-tuple fuzzy linguistic variable on $S^{B}$. After calculation by Formula (19), $\bar{H}_{i}^{B}$ can be obtained.

  For example,

  $$\bar{H}_{1}^{B} = \left\{ {\left( {0.6790s_{3}^{3} ,0.3210s_{4}^{3} } \right),\left( {0.6311s_{3}^{3} ,0.3689s_{4}^{3} } \right),\left( {0.6988s_{3}^{3} ,0.3012s_{4}^{3} } \right), \ldots ,\left( {0.6023s_{3}^{3} ,0.3977s_{4}^{3} } \right),\left( {0.6481s_{3}^{3} ,0.3519s_{4}^{3} } \right)} \right\}.$$

• Step 7 Calculating the score function for each alternative,

  $$S\left( {\bar{H}_{1} } \right) = 0.808,\quad S\left( {\bar{H}_{2} } \right) = 0.556,,\quad S\left( {\bar{H}_{3} } \right) = 0.699,\quad S\left( {\bar{H}_{4} } \right) = 0.350.$$

• Step 8 According to values of score function, the ranking of the alternatives is:$A_{1} \succ A_{3} \succ A_{2} \succ A_{4}$.

  So the best alternative is $A_{1}$.

5 Comparison Analysis and Discussion

In Sect. 5, a comparison analysis is given between MGUHFLCA operator and the other two operators [44, 45], and then several CWW methodologies by proportional 2-tuple linguistic model are summarized to prove the improvement of our MAGDM method.

5.1 Comparison Analysis

With the aim of validating the feasibility of the MAGDM method in Sect. 4, a comparison analysis is made.

Example 5

Assume that a university assesses four colleges $A_{1} ,A_{2} ,A_{3}$ and $A_{4}$, i.e., college of computer science ($A_{1}$), college of accounting ($A_{2}$), college of economics and management ($A_{3}$) and college of international education ($A_{4}$). In order to accurately reflect the real situation of each college, the assessment is mainly based on three attributes, i.e., teaching ($C_{1}$), scientific research ($C_{2}$) and service ($C_{3}$). Meanwhile, assume that there are three DMs $D_{1}$,$D_{2}$ and $D_{3}$. Given that the attributes are independent and the weight vector is $\omega_{C} = \left( {0.3,0.45,0.25} \right)$, and the three DMs are independent of each other and the weight vector is $\lambda_{D} = \left( {0.25,0.35,0.4} \right)$. They provide their assessments with unbalanced HFLTSs, and the ULTSs used are as follows: $S^{1} = \left\{ {s_{0}^{1} :{\text{extremely}}\;{\text{bad}},\;s_{1}^{1} :{\text{very}}\;{\text{bad}},s_{2}^{1} :{\text{bad}},s_{3}^{1} :{\text{medium}},s_{4}^{1} :{\text{good}},s_{5}^{1} :{\text{very}}\;{\text{good}},s_{6}^{1} :{\text{extremely}}\;{\text{good}}} \right\}$, $S^{2} = S^{1} = \left\{ {s_{0}^{1} ,s_{1}^{1} ,s_{2}^{1} ,s_{3}^{1} ,s_{4}^{1} ,s_{5}^{1} ,s_{6}^{1} } \right\}$,$S^{3} = \left\{ {s_{0}^{3} :{\text{very}}\;{\text{bad,}}s_{1}^{3} :{\text{bad}},s_{2}^{3} :{\text{medium}},s_{3}^{3} :{\text{good}},s_{4}^{3} :{\text{very}}\;{\text{good}}} \right\}$. The semantics of the ULTSs are the same as Tables 2 and 3. Further assume that the decision matrices $\bar{H}^{k} = \left( {\bar{h}_{ij}^{k} } \right)_{4 \times 3} \left( {k = 1,2,3} \right)$ given by $D_{1}$,$D_{2}$ and $D_{3}$ are shown in Tables 7, 8, 9, respectively.

Table 7 Decision matrix $\bar{H}^{1}$ from Example 5 given by $D_{1}$

Table 8 Decision matrix $\bar{H}^{2}$ from Example 5 given by $D_{2}$

Table 9 Decision matrix $\bar{H}^{3}$ from Example 5 given by $D_{3}$

By using the method proposed in this paper, we can get the score functions $S\left( {\bar{H}_{1} } \right) = 0.616$,$S\left( {\bar{H}_{2} } \right) = 0.535$,$S\left( {\bar{H}_{3} } \right) = 0.7$,$S\left( {\bar{H}_{4} } \right) = 0.423$, so the ranking result is $A_{3} \succ A_{1} \succ A_{2} \succ A_{4}$.

Then, the MAGDM method based on $UHFLWA$ operator by Yu et al. [44], and proportional 2-tuple weighted average operator by Li and Dong [45] are used to solve the same problem, and the ranking results are identical: $A_{3} \succ A_{1} \succ A_{2} \succ A_{4}$. The detail result values of the three operators are illustrated in Table 10.

Table 10 A comparison of different operators with independent DMs for Example 5

The results obtained by the three operators are the same, that is, $A_{3}$ is the optimal alternative. So the feasibility and validity of the proposed operator can be verified. Three operators are feasible.

The limits of Yu et al. [44] and Li and Dong [45]’s operators are that they are only used to solve the MAGDM problem with independent attributes. On the contrary, the advantage of MGUHFLCA operator not only solves MAGDM problem with independent attributes (or DMs), but also with interrelated attributes (or DMs).

In Example 5, the three attributes, teaching ($C_{1}$), scientific research ($C_{2}$), and service ($C_{3}$), are interrelated to each other in real life. When “scientific research” develops well, it will be helpful to “teaching”; meanwhile, better “service” will promote “teaching” and “scientific research.” However, Yu et al. [44] and Li and Dong [45] do not consider this interrelation. Although the result of ranking from Yu et al. [44] and Li and Dong [45] are the same as ours, MGUHFLCA operator is much better. Example 6 will prove the advantage of it.

Example 6

Assume that the three DMs in Example 5 are related to each other, the weight vector of the DMs is $S\left( {\bar{H}_{4} } \right) = 0.382$, and other assumptions remain unchanged.

$\mu \left( \emptyset \right) = 0$,$\mu \left( {D_{1} } \right) = 0.2$,$\mu \left( {D_{2} } \right) = 0.1$,$\mu \left( {D_{3} } \right) = 0.2$, according to Formula (16), $\lambda_{D} = 5$. According to Formula (15), all the fuzzy measures of each DM are as follows:

$$\mu \left( {D_{1} ,D_{2} } \right) = 0.4,\quad S\left( {\bar{H}_{3} } \right) = 0.655,\quad S\left( {\bar{H}_{4} } \right) = 0.382,\quad \mu \left( {D_{1} ,D_{2} ,D_{3} } \right) = 1.$$

By using the proposed method in this paper, we can get the score functions $S\left( {\bar{H}_{1} } \right) = 0.587$,$S\left( {\bar{H}_{2} } \right) = 0.476$,$S\left( {\bar{H}_{3} } \right) = 0.655$,$S\left( {\bar{H}_{4} } \right) = 0.382$, the ranking result is unchanged: $A_{3} \succ A_{1} \succ A_{2} \succ A_{4}$.

Then, the MAGDM methods based on ${\text{UHFLWA}}$ operator by Yu et al. [44] and proportional 2-tuple weighted average operator by Li and Dong [45] are used to solve the same problem, and the ranking results are not the same. The detail result values of the three operators are illustrated in Table 11.

Table 11 A comparison of different operators with dependent DMs for Example 6

According to Table 11, the slightly different rankings can be found, and then reason is that the assumptions of DMs’ relationships by Yu et al. [44] and Li and Dong [45] are equalities:$\mu \left( {D_{i} ,D_{j} } \right) = \mu \left( {D_{i} } \right) + \mu \left( {D_{j} } \right)$, $\mu \left( {D_{i} ,D_{j} ,D_{k} } \right) = \mu \left( {D_{i} } \right) + \mu \left( {D_{j} } \right) + \mu \left( {D_{k} } \right)$$\left( {i,j,k = 1,\;2,\;3;i \ne j \ne k} \right)$; however, the preconditions of DMs’ relationships in Example 6 are inequalities: $\mu \left( {D_{1} ,D_{2} } \right) = 0.4 > \mu \left( {D_{1} } \right) + \mu \left( {D_{2} } \right) = 0.3$,$\mu \left( {D_{1} ,D_{3} } \right) = 0.6 > \mu \left( {D_{1} } \right) + \mu \left( {D_{3} } \right) = 0.4$,$\mu \left( {D_{2} ,D_{3} } \right) = 0.4 > \mu \left( {D_{2} } \right) + \mu \left( {D_{3} } \right) = 0.3$. That means the relationships between $D_{1}$ and $D_{2}$,$D_{1}$ and $D_{3}$,$D_{2}$ and $D_{3}$ are complementary. It is unreasonable to get the ranking results by Yu et al. [44] and Li and Dong [45] in Example 6.

5.2 Discussion

In the following, we will give a comparison of characteristics in our proposed method with Wang and Hao’s method [30], Dong et al.’s method [48], Yu et al.’s method [44], and Li and Dong’s method [45], which are listed in Table 12, and detailed explanations are shown as follows.

Table 12 A comparison of characteristics of different CWW methodologies by proportional 2-tuple

(1) Both Wang and Hao’s method [30] and Li and Dong’s method [45] used the simple weighted average operator, which cannot deal with the problem of multi-granularity, nor can it solve the problem of assessment form HFLTSs.

(2) Both Dong et al.’s method [48] and Yu et al.’s method [44] can solve multi-granularity unbalanced MAGDM problems, but they do not consider the relationship among attributes or/and DMs, while the proposed method in this paper can deal with the relationship among attributes or/and DMs of MAGDM problems.

(3) Both Dong et al. [48] and Yu et al. [44] ’s methods allow DMs to select assessment information from different granularity LTSs, but it cannot solve the MAGDM problem with multi-granularity HFLESs.

(4) The shortcomings mentioned above can be overcome by the proposed MGUHFLCA operator when there are complementary or redundant interactions among attributes (or DMs) in MAGDM problems. Moreover, the proposed method also allows the DMs to choose assessment information from multi-granularity linguistic term sets freely.

6 Conclusion

This paper studied the method of MAGDM problems with MGUHFLEs by means of proportional 2-tuple fuzzy linguistic aggregation operator, and proposed a MGUHFLCA operator, which could consider the relationship among attributes (or DMs). By comparing MGUHFLCA operator and the other two operators, the feasibility and advantages of the proposed method have been verified. The main works and conclusions are shown as follows. Firstly, the concept of MGUHFLTS was defined, and the operational rules, score function, expectation function, and comparison rules of MGUHFLTS were proposed. Secondly, a connection between MGUHFLEs and proportional 2-tuple fuzzy linguistic representation was given, and a transformation between ULTS and numerical data was developed. Finally, a MGUHFLCA operator was proposed, which cannot only deal with the independent attributes (or DMs), but also dependent attributes (or DMs).

In the future studies, we will apply the proposed method to investment evaluation and product development.