1 Introduction

Fuzzy sets introduced by Zadeh [1] in 1965 have revolutionalized many research fields. Decision-making processes are modeled more efficiently using fuzzy preference relations [2, 3]. Fuzzy preference relations [4], multiplicative fuzzy preference relations [5–7], and linguistic fuzzy preference relations [8] are useful in dealing with uncertainty and ambiguity in decision-making problems.

Literature presents different ideals to combat vagueness. Building on Zadeh’s fuzzy sets, Torra [9, 10] introduced hesitant fuzzy sets as an innovative tool to handle inaccuracy in situations where vagueness appears in two or more sources of information simultaneously. Stating the exact degree of membership of an element may lead to complications. Hesitant fuzzy sets are flexible in the sense that they permit the membership of an element to a set to be represented by several possible values between 0 and 1.

Hesitant fuzzy preference relations are useful in dealing with uncertainty that may arise in complex decision-making problems. Recently, much attention has been paid to build the theory of hesitant fuzzy preference relations and in highlighting its application. Hesitant fuzzy preference relations add flexibility to the uncertainty representation problem. Xia and Xu [11] and Beg and Rashid [12] defined hesitant fuzzy element along with certain operations on them. With respect to the linguistic environment, Hererra et al. [13] introduced the hesitant fuzzy linguistic term set and highlighted the flexibility and usefulness of these sets in dealing with linguistic information. Relevant work on linguistic information can be found in [14, 15]. Furthermore, a group decision-making model based on hesitant fuzzy linguistic information was presented in [16].

Incomplete information is a real-world problem and has been attentively studied by many researchers over the past decade [3, 17–22]. Recently, Zhu and Xu [23] proposed a method to cater for incomplete hesitant fuzzy preference relations. Some methods discard decision makers with incomplete information and base their decision on the given preference relations that are complete. Discarding such pieces of information may result in loss of some important data. Some methods estimate missing values using preferences of other experts. However, methods that consider expert’s own preferences to estimate the missing information are considered more appropriate by researchers. Using transitivity to resolve the problem of incompleteness is currently popular among the researchers. However, using additive transitivity to tackle the incompleteness leads to estimated preferences that are beyond the decided range of decision makers. Outliers do not have any interpretation. Transformation functions have been defined to bring back the outlying preferences. The same method has been generalized for incomplete hesitant fuzzy preference relations in [23]. This paper stresses that using transformation functions to edit the estimated preferences that outlie the defined range voids the originality of the preferences provided by the decision maker. Therefore, it is comparatively better to restrict the experts before incomplete information is provided rather than changing the given information later. It is only realistic to imagine cases where decision makers fail to abide by the upper bound condition presented to them. Such cases may be dealt with using two methods. The first method suggests that the decision maker who fails to abide by the upper bound condition be withdrawn from the panel of decision makers. The second method, which is proposed and agreed to in this article suggests that inspite of excluding the decision maker from the panel, minimum possible preferences must be revised. However, revisions are not encouraged which is why we propose the condition to decision makers before the decision-making process begins. But in unavoidable circumstances, we prefer to revise instead of eliminating the expert from the panel. To ensure minimum possible revisions, we propose an algorithm. We discussed the latter case and propose an algorithm which displays that if upper bound condition is met then additive transitivity for hesitant fuzzy preference relations must be used to estimate missing preferences. If the condition is not met, then revisions are proposed to the decision maker which is followed by estimation of missing preferences.

This paper focuses on incompleteness of hesitant fuzzy preference relations using additive transitivity. This property may lead to outlying estimated preferences which has no interpretation in decision-making problem. In order to overcome this problem, we propose an upper bound condition, (hubc) property, which is based on the decision maker’s least and greatest preference intensity. Property (hubc) promises that the estimated values will lie inside the desired range. This article also deals with the situation when decision makers fail to satisfy property (hubc) and in spite of dropping such judges from the panel of experts, this article proposes an algorithm to undertake minimal possible revision of preferences. Also, the algorithm is sensitive to the choice of left end limit and right end limit of the interval that is to be revised and does not alter both if either of the two abides by (hubc). This algorithm results in incomplete hesitant fuzzy preference relations that satisfy condition (hubc). Hence, such relations are completed by estimating preferences that are promised to lie inside the defined domain and hence are expressible. Once incompleteness is taken care of, we propose a ranking method inspired from Borda and fuzzy Borda rule [24]. The ranking method is named HF-Borda count which we introduce and use to rank hesitant fuzzy preference relations. We extend this method to deal with situation of ties between alternatives.

This paper is stated in the following manner. Section 2 presents some basic definitions that are used in the sequel. In Sect. 3, we formulate an upper bound condition, property (hubc), for experts who intend on providing incomplete information. If the condition is respected then the estimated preferences will be expressible. Moreover, in this section, an algorithm is defined to tackle the case when an experts fails to satisfy property (hubc). Section 4 presents HF-Borda count to rank hesitant fuzzy preference relations. This method deals with probable ties between alternatives. Section 5 concludes the paper and proposes future directions.

2 Preliminaries

Definition 2.1

[1] A fuzzy set A on a set of nonempty alternatives X is characterized by a membership function \(\mu _{A}:X\rightarrow [0,1],\) where \(\mu _{A}(x)\) is defined as the degree of membership of element x in fuzzy set A for each x \(\in X.\)

Definition 2.2

[25] A fuzzy preference relation P on X is characterized by a function \(\mu _{P}:X\times X\rightarrow [0,1],\) where \(\mu _{P}(x_{i},x_{j})=p_{ij}\) indicates the preference intensity with which alternative \(x_{i}\) is preferred over \(x_{j}\). According to Orlovsky [25], fuzzy preference relation P is

  1. i.

    Additive reciprocal if for all i, j it satisfies \(p_{ij}+p_{ji}=1\);

  2. ii.

    Additive transitive if \(p_{ij}=p_{ik}+p_{kj}-0.5\) for all i, j, k.

Definition 2.3

[9] Let X be a fixed nonempty set, a hesitant fuzzy set on X is represented by a function h that applies to X and returns a finite subset of \(\ [0,1]\). Mathematically [11],

$$\begin{aligned} E=\{<x,h_{E}(x)>:x\in X\} \end{aligned},$$

where \(h_{E}(x)\) , hesitant fuzzy element, is a set of values in [0, 1],  representing the probable membership degrees of the element \(x\in X\) to the set E.

Definition 2.4

[10, 11] Consider \(h,h_{1},\) and \(h_{2}\) to be three hesitant fuzzy elements. Then the following operations are defined:

  1. i.

    \(h^{c}=\cup _{\gamma \in h}\{1-\gamma \},\)

  2. ii.

    \(h_{1}\oplus h_{2}=\cup _{\gamma _{1}\in h_{1},\gamma _{2}\in h_{2}}\{\gamma _{1}+\gamma _{2}-\gamma _{1}\gamma _{2}\},\)

  3. iii.

    \(h_{1}\otimes h_{2}=\cup _{\gamma _{1}\in h_{1},\gamma _{2}\in h_{2}}\{\gamma _{1}\gamma _{2}\}.\) Further, the following operations are defined by Zhu and Xu [23] for hesitant fuzzy elements \(h_{1}\) and \(h_{2}\) and a real number b, 

  4. iv.

    \(h_{1}\widetilde{+}h_{2}=\cup _{\gamma _{1}\in h_{1},\gamma _{2}\in h_{2}}\{\gamma _{1}+\gamma _{2}\},\)

  5. v.

    \(h\widetilde{-}b=\cup _{\gamma \in h}\{\gamma -b\}.\)

Definition 2.5

[11] Score of a hesitant fuzzy element h is defined as

$$\begin{aligned} s(h)=\frac{1}{l_{h}}\sum _{\gamma \in h}\gamma \end{aligned},$$

where \(l_{h}\) is the number of values in h.

Definition 2.6

[11] Variance of a hesitant fuzzy element h is defined as

$$\begin{aligned} v(h)=\frac{1}{l_{h}}\sqrt{\sum _{\gamma _{i},\gamma _{j}\in h}(\gamma _{i}-\gamma _{j})^{2}} \end{aligned},$$

where \(l_{h}\) is the cardinality of h.v(h) is also called the deviation degree of h. This reflects the standard deviation among all pairs of elements in a hesitant fuzzy element of h.

Definition 2.7

[11] Consider two hesitant fuzzy elements \(h_{1}\) and \(h_{2}\), if \(s(h_{1})<s(h_{2})\) then \(h_{1}<h_{2\text { }}.\) In case \(s(h_{1})=s(h_{2})\) and

  1. i.

    If \(v(h_{1})>v(h_{2})\) then \(h_{1}<h_{2}.\)

  2. ii.

    If \(v(h_{1})=v(h_{2})\) then \(h_{1}=h_{2}.\)

Remark 2.8

[26] A hesitant fuzzy preference relation H on X is represented in matrix form as \(H=(h_{ij})_{n\times n}\subset X\times X,\) where \(h_{ij}=\{h_{ij}^{s},s=1,2,\ldots ,l_{h_{ij}}\}\) is a hesitant fuzzy element indicating all probable degrees to which the alternative \(x_{i}\) is preferred to the alternative \(x_{j}.\) Furthermore, the following conditions must be satisfied for \(i,j=1,2,\ldots n.\)

  1. i.

    \(h_{ii}=\{0.5\}\)

  2. ii.

    \(h_{ij}^{\sigma (s)}+h_{ij}^{\sigma (l_{h_{ij}}-s+1)}=1\)

  3. iii.

    \(l_{h_{ij}}=l_{h_{ji}}\) Here \(h_{ij}^{\sigma (s)}\) and \(h_{ij}^{\sigma (l_{h_{ij}}-s+1)}\) are the s-th and \((l_{h_{ij}}-s+1)\)th smallest values in \(h_{ij}\), respectively.

Remark 2.9

[23, 26] Some of the transitivity properties on a hesitant fuzzy preference relation \(H=(h_{ij})_{n\times n}\subset X\times X\) are stated in the following:

  1. i.

    H satisfies the triangle condition if \(h_{ij}\le h_{ik}\oplus h_{kj}\) for all \(i,j,k=1,2,\ldots,n.\)

  2. ii.

    H is weakly transitive if \(h_{ik}\ge \{0.5\}\) and \(h_{kj}\ge \{0.5\}\) imply \(h_{ij}\ge \{0.5\}\) for all \(i,j,k=1,2,\ldots ,n.\)

  3. iii.

    H is max–min transitive if \(h_{ij}\ge \min \{h_{ik},h_{kj}\}\) for all \(i,j,k=1,2,\ldots ,n.\)

  4. iv.

    H is max–max transitive if \(h_{ij}\ge \max \{h_{ik},h_{kj}\}\) for all \(i,j,k=1,2,\ldots ,n.\)

  5. v.

    Furthermore, \(H\,\)is additive transitive if \(h_{ij}=h_{ik} \widetilde{+}h_{kj}\widetilde{-}0.5\) for all \(i,j,k=1,2,\ldots ,n.\)

Borda count [27–29] chooses the alternative which stands highest on average in the agents’ preference ordering. Recently, Borda rule was further extended to fuzzy Borda rule for fuzzy preference relations by Nurmi [30] and Gracia et al. [24].

Definition 2.10

[30] Let \(R=(r_{ij})_{n\times n}\) represent a fuzzy preference relation then the rank assigned to each alternative is defined as \(r(x_{i})=\sum _{j=1,r_{ij}>0.5}^{n}r_{ij}\) for \(i,j\in \{1,2,\ldots ,n\}.\) According to the fuzzy borda rule, \(x_{i}\succ x_{j}\) only if \(r(x_{i})\succ r(x_{j}).\)

3 Hesitant Upper Bound Condition (hubc) for Incomplete Information

In real-world problems as cardinality of X and the complexity of the criteria involved increases, it becomes less likely for all experts involved in the decision-making process to be able to express their preferences over given alternatives. As stated by Zhu and Xu [23], transitivity is a handy tool to estimate missing preferences. It has been mentioned that additive consistency may produce unreasonable results.

In this paper, we stress that if additive consistency is used appropriately then it will not lead to unreasonable solutions. Let M[0, 1] denote the collection of all possible finite subsets of [0, 1]. A hesitant fuzzy preference value is called expressible if it belongs to M[0, 1]. Estimated preferences that do not belong to M[0, 1] are called nonexpressible in this study. They are nonexpressible because they cannot be interpreted in decision-making models. There are two cases that are widely considered in literature while dealing with incompleteness. If \(h_{ik}\) and \(h_{kj}\) are provided by decision makers, then using transitivity properties, \(h_{ij}\) can be easily found. More interesting is the case where decision maker is certain about his preferences for a particular alternative over other alternatives in X. This is the case where a complete row or a complete column of preference intensities is provided by the decision maker. In the study to follow, we consider the case when expert exhibits preference intensities of \(x_{k}\) over \(x_{i}\), where k is fixed and \(i\ne k\in \{1,2,\ldots ,n\}.\)

Example 3.1

Let \(X=\{x_{1},x_{2},x_{3},x_{4}\}\) be the set of four alternatives. Consider an incomplete hesitant fuzzy preference relation provided by a decision maker as follows:

$$\begin{aligned} H=\left[ \begin{array}{llll} \{0.5\} &{} - &{} - &{} - \\ \{0.3,0.5,0.9\} &{} \{0.5\} &{} \{0.1,0.6,0.9,1\} &{} \{0.4,0.6,0.9\} \\ - &{} - &{} \{0.5\} &{} - \\ - &{} - &{} - &{} \{0.5\} \end{array} \right] \end{aligned}.$$

Clearly, the decision maker is capable of comparing alternative \(x_{2}\) with the set of alternatives present in X. The first step is to identify the crucial preference \(h_{23}\). We assert that if the crucial preference is estimated to be expressible then the other missing preferences can also be estimated to be expressible. We use additive consistency to estimate the missing preference \(h_{13}.\) According to the property of additive transitivity, \(h_{13}=h_{12}\widetilde{+}h_{23}\widetilde{-}0.5.\) Now, \(h_{13}=\{0.1,0.5,0.7\}\,\) because of additive reciprocity. Similarly, \(h_{23}=\{-0.3,0.2,0.3,0.1,0.5,0.7,0.9\}\) and \(h_{24}= \{0,0.2,0.4,0.5,0.6,0.8,0.9,1.1\}\). It should be noted that \(h_{23}\),\(h_{24}\notin M[0,1].\)

If the estimated preferences are nonexpressible then such a completed relation will have no interpretation. Moreover, consistency cannot be determined in such a preference relation. In order to complete an incomplete hesitant fuzzy preference relation with expressible preferences, we need to focus on the hesitant fuzzy element with the least and greatest element.

Theorem 3.3 states a condition that needs to be satisfied by the decision makers prior to proposing incomplete information. Suppose that the preferences provided are \(h_{kj},\) where k is fixed and j varies from 1 to n. Let the smallest left end limit present in any hesitant fuzzy element \(h_{kj}\) where k is fixed, be denoted by \(\epsilon _{h}\) and the largest right end limit be denoted by \(\delta _{h}\). That is, let \(\epsilon _{h}=\min (\min _{j}(h_{kj}))\) and \(\delta _{h}=\max (\max _{j}(h_{kj})).\)Then the upper bound condition or property (hubc) is defined as \(\delta _{h}\le 0.5+\epsilon _{h}.\) If property (hubc) is satisfied by the incomplete hesitant fuzzy preference relation provided by a decision maker then the missing preferences can be estimated using consistency. Moreover, the estimated preferences will be expressible.

Lemma 3.2

If the missing crucial preference of an n by n incomplete hesitant fuzzy preference relation is expressible then so are the remaining preferences that are to be estimated.

Proof

Suppose that \(n\,\)preferences \(h_{kj}\) where k is fixed and \(j\in \{1,2,\ldots ,n\}\) are provided by a decision maker in the k-th row. Let \(h_{ij}\) be the crucial hesitant fuzzy element such as \(h_{ij}\) is expressible, that is, \(h_{ij}\in M[0,1].\) Now, let \(h_{sj}\) denote any other missing hesitant fuzzy element with the least and greatest element denoted by \(h_{sj}^{l}\) and \(h_{sj}^{g}\). Then,

$$\begin{aligned} h_{sj}=h_{sk}\widetilde{+}h_{kj}\widetilde{-}0.5 \end{aligned},$$

which implies that, \(h_{sj}^{l}=h_{sk}^{l}\widetilde{+}h_{kj}^{l}\widetilde{- }0.5.\) Moreover,

$$\begin{aligned} h_{sj}^{l}<(1-h_{ks}^{g})+h_{kj}^{l}-0.5 \end{aligned}$$
(3.1)

Since, \(0\le h_{kj}^{g}\le 0.5+h_{ki}^{l}\) therefore, 3.1 can be written as

$$\begin{aligned} h_{sj}^{l}<(1-h_{ks}^{g})+(h_{kj}^{g}-0.5)<(1-h_{ks}^{g})+h_{ki}^{l} \end{aligned}.$$

We know that \(h_{ki}^{l}\le h_{ks}^{l}\le h_{ks}^{g}\le h_{kj}^{g}\) . Equivalently, \(1-h_{ki}^{l}\geqslant 1-h_{ks}^{l}\geqslant 1-h_{ks}^{g}\geqslant 1-h_{kj}^{g}.\) Therefore,

$$\begin{aligned} h_{sj}^{l}\le h_{ik}^{g}+h_{ki}^{l}=1 \end{aligned},$$

which proves that \(h_{sj}^{l}\le 1.\) Similarly,

$$\begin{aligned} h_{sj}^{g}=h_{sk}^{g}+h_{kj}^{g}-0.5\le (1-h_{ks}^{l})+h_{ki}^{l} \end{aligned}$$

Also, \(h_{ki}^{l}\le h_{ks}^{l}\le h_{kj}^{g}\) which is equivalent to \(1-h_{ki}^{l}\geqslant 1-h_{ks}^{l}\geqslant 1-h_{kj}^{g}\). Therefore,

$$\begin{aligned} h_{sj}^{g}\le (1-h_{ki}^{l})+h_{ki}^{l}=1 \end{aligned}.$$

Similarly, it can be proved that \(h_{sj}^{l},h_{sj}^{g}\geqslant 0.\) Therefore, if the crucial preference is expressible then other estimated preference \(h_{sj}\) will also be expressible. That is, if \(h_{ij}\in M[0,1]\) then \(h_{sj}\in M[0,1].\) \(\square\)

Theorem 3.3

Assume that n preferences of a decision maker in an \(n\times n\) incomplete hesitant fuzzy preference relation are given by \(h_{kj},\) where k is fixed and \(j\in \{1,2,\ldots ,n\}.\) If \(h_{kj}\) satisfies property (hubc) then the missing preferences can be estimated. Moreover, the estimated preferences are expressible.

Proof

Suppose that n preferences \(h_{kj},\) where k is fixed and \(j\in \{1,2,\ldots ,n\}\) are provided by a decision maker in the k-th row. Further suppose that the least element of all hesitant fuzzy elements lies in the hesitant fuzzy element \(h_{ki}\) and is denoted as \(h_{ki}^{l}\). Whereas the greatest of all hesitant fuzzy elements lies in \(h_{kj}\) and is denoted as \(h_{kj}^{g}.\) Since property (hubc) is satisfied, therefore,

$$\begin{aligned} 0\le h_{kj}^{g}\le 0.5+h_{ki}^{l} \end{aligned}.$$
(3.2)

Also, \(h_{ki}^{l}\le h_{ki}^{g}.\) So, \(0\le h_{kj}^{g}\le 0.5+h_{ki}^{g}.\) Hence,

$$\begin{aligned} 0\le h_{kj}^{l}\le h_{kj}^{g}\le 0.5+h_{ki}^{g} \end{aligned}.$$
(3.3)

According to the definition of a crucial preference, \(h_{ij}\) qualifies as the crucial missing hesitant fuzzy element. Lemma 3.2 proves that if \(h_{ij}\) is expressible then so are other missing preferences. So, we need to prove that the crucial preference \(h_{ij}\) is expressible. We know that \(h_{ij}=h_{ik}\widetilde{+}h_{kj}\widetilde{-}0.5\) . It implies that

$$\begin{aligned} h_{ij}^{l}= & {} h_{ik}^{l}+h_{kj}^{l}-0.5=(1-h_{ik}^{g})+h_{kj}^{l}-0.5 \\= & {} (h_{kj}^{l}-h_{ki}^{g})+0.5 \end{aligned}$$

Equation (3.3) implies that \(h_{kj}^{l}-h_{ki}^{g}\le 0.5.\) Therefore, \(h_{ij}^{l}\le 1.\) Similarly,

$$\begin{aligned} h_{ij}^{g}=h_{ik}^{g}+h_{kj}^{g}-0.5=(1-h_{ki}^{l})+h_{kj}^{g}-0.5 \end{aligned}.$$

Because of Eq. (3.2) we have

$$\begin{aligned} h_{ij}^{g}=(1-h_{ki}^{l})+h_{kj}^{g}-0.5=(h_{kj}^{g}-h_{ki}^{l})+0.5\le 1 \end{aligned}.$$

Similarly, it can be proved that \(h_{ij}^{l},h_{ij}^{g}\geqslant 0.\) Therefore, the crucial preference \(h_{ij}\in M[0,1].\) \(\square\)

It has been proven that (hubc) ensures estimation of missing preferences in an incomplete hesitant fuzzy preference relation. Moreover, additive consistency along with (hubc) leads to expressible estimated preferences. Examples provided by Xu et al. [23] are based on hesitant fuzzy elements with cardinality not more than three. Moreover, the estimated preferences do not have cardinality greater than three either. This leaves ambiguity in the use of additive consistency. Consider the following 4 by 4 incomplete hesitant fuzzy preference relation (in Example 3.4) where the first row has been provided by the decision maker. The example is elaborative and self explanatory in the use of additive consistency along with (hubc) and it cannot be worked out using the method of Xu et al. [23].

Example 3.4

Suppose that Adam, panel member of a decision-making committee is adamant on proposing incomplete information. Adam has been asked to abide by property (hubc). Considerate of this property, Adam presents information that is stated in the form of following hesitant fuzzy preference relation:

$$\begin{aligned} H_\mathrm{Adam}= \left[\begin{array}{llll} \{0.5\}&\{0.3,0.4,0.5\}&\{0.2,0.6\}&\{0.2,0.3,0.6\} \\ \{0.5,0.6,0.7\}&\{0.5\}&- & - \\ \{0.4,0.8\}&- & \{0.5\}&- \\ \{0.4,0.7,0.8\}&- & -&[0.5\} \end{array} \right]\end{aligned}$$

The missing values are estimated as follows: \(H_\mathrm{Adam}=\)

$$\begin{aligned} \begin{bmatrix} \{0.5\}&\{0.3,0.4,0.5\}&\{0.2,0.6\}&\{0.2,0.3,0.6\} \\ \{0.5,0.6,0.7\}&\{0.5\}&\begin{array}{l} \{0.2,0.3,0.4, \\ 0.6,0.7,0.8\} \end{array}&\begin{array}{l} \{0.2,0.3,0.4, \\ 0.5,0.6,0.7,0.8\} \end{array} \\ \{0.4,0.8\}&\begin{array}{l} \{0.2,0.3,0.4, \\ 0.6,0.7,0.8\} \end{array}&\{0.5\}&\begin{array}{l} \{0.1,0.2,0.5, \\ 0.6,0.9\} \end{array} \\ \{0.4,0.7,0.8\}&\begin{array}{l} \{0.2,0.3,0.4, \\ 0.5,0.6,0.7,0.8\} \end{array}&\begin{array}{l} \{0.1,0.4,0.5 \\ 0.8,0.9\} \end{array}&\{0.5\} \end{bmatrix} \end{aligned}$$

It needs to be noted that in the completed hesitant fuzzy preference relation all estimated preferences are expressible. Moreover, the completed relation satisfies consistency property.

Although we have proposed a property for decision makers expressing incomplete information but we have not as yet catered for the situation where decision makers are unable or not willing to abide by it. This situation is pertinent to decision-making problems and therefore must not be neglected. There are two ways to deal with the decision maker who does not abide by the (hubc). Excluding this decision maker from the panel is one method which may result in loss of important information. The other method is to revise minimum possible information provided by the decision maker. In this paper, we proceed with the latter approach in which we revise the least possible amount of information provided by the decision maker.

Suppose n preferences \(h_{i^{\prime }j}\) for fixed \(i^{\prime }\) and \(j\in \{1,2,\ldots ,n\}\) are provided by a decision maker. Let \(\flat = \{h_{i^{\prime }1}^{(1)},h_{i^{\prime }1}^{(2)},\ldots h_{i^{\prime }1}^{(l_{1})},h_{i^{\prime }2}^{(1)},h_{i^{\prime }2}^{(2)},\ldots ,h_{i^{\prime }2}^{(l_{2})},\ldots h_{i^{\prime }k}^{(1)},h_{i^{\prime }k}^{(2)},\ldots h_{i^{\prime }k}^{(l_{k})},\ldots ,h_{i^{\prime }n}^{(1)},\)

\(h_{i^{\prime }n}^{(1)},\ldots h_{i^{\prime }n}^{(l_{n})}\},\) where \(k\ne i^{\prime }\) be the collection of all preference intensities in each hesitant fuzzy element. Here, \(h_{i^{\prime }k}^{(t)}\) represents t-th member of the hesitant fuzzy element \(h_{i^{\prime }k}\) and \(l_{k}\) denotes cardinality of the hesitant fuzzy element \(h_{i^{\prime }k}.\)

Let \(\daleth \subseteq \flat\) be a collection of elements that satisfy property (hubc). As mentioned earlier, we intend to undertake minimum possible revisions. Therefore, the algorithm is divided into two cases. Consider \(\mid \daleth \mid\) and \(\mid \flat \mid\) to represent cardinality of \(\daleth\) and \(\flat :\)

Case 1: If \(\mid \daleth \mid \ge \lceil \frac{\mid \flat \mid -1}{2} \rceil :\)

Then let \(\gamma _{k},k\ne i^{\prime },\) represent k-th hesitant fuzzy element in the \(i^{\prime }\) row where \(k\in \{1,2,\ldots ,n\}\).

For \(\gamma _{k}\) If \(h_{i^{\prime }1}^{(s)}\in \daleth\) where \(s\in \{1,2,\ldots ,s_{1}-1\}\) then no change required. Otherwise, if \(h_{i^{\prime }1}^{(s_{1})}\notin \daleth\) then \(h_{i^{\prime }1}^{(s_{1})}=0.5+\inf (\flat ).\) Moreover, \(h_{i^{\prime }1}^{(s_{1}+1)}=h_{i^{\prime }1}^{(s_{1}+2)}=\cdots =h_{i^{\prime }1}^{l_{1}}=0.5+\inf (\flat ).\)

Let \(\gamma _{2}\) be the second hesitant fuzzy element in the \(i^{\prime }\) row then if \(h_{i^{\prime }2}^{(s)}\in \daleth\) for \(s\in \{1,2,\ldots ,s_{2}-1\}\) then no change is required. However, \(h_{i^{\prime }2}^{(s_{2}+1)}=0.5+\inf (\flat ).\) Also, \(h_{i^{\prime }2}^{(s_{2}+1)}=h_{i^{\prime }2}^{(s_{2}+2)}= \cdots=h_{i^{\prime }2}^{l_{2}}=0.5+\inf (\flat ).\)

Let \(\gamma _{n}\) be the n-th hesitant fuzzy element in the \(i^{\prime }\) row then if \(h_{i^{\prime }n}^{(s)}\in \daleth\) for \(s\in \{1,2,\ldots ,s_{n}-1\}\) then no change is required. However, \(h_{i^{\prime }n}^{(s_{n}+1)}=0.5+\inf (\flat ).\) Also, \(h_{i^{\prime }n}^{(s_{n}+1)}=h_{i^{\prime }n}^{(s_{n}+2)}=\cdots =h_{i^{\prime }n}^{l_{n}}=0.5+\inf (\flat ).\)

Case 2: If \(\mid \daleth \mid <\lceil \frac{\mid \flat \mid -1}{2} \rceil :\)

Then it means that lesser members of hesitant fuzzy elements satisfy property (hubc). Therefore, in order to make minimum possible revisions, the smallest element must be changed.

Let \(\inf (\flat )=\xi _{1}\) and \(\sup (\flat )=\delta .\) If \(\xi _{1}<\delta -0.5\) then leave as is. Otherwise, \(\xi _{1}=\xi _{1}^{*}\) where \(\xi _{1}^{*}=\delta -0.5.\) Now,

\(\inf (\flat /\xi _{1})=\xi _{2}.\) If \(\xi _{2}<\delta -0.5\) then leave as is. Otherwise, \(\xi _{2}=\xi _{2}^{*}\) where \(\xi _{2}^{*}=\delta -0.5.\)

\(\inf (\flat /\xi _{{\rm card}(\daleth )})=\xi _{\daleth }.\) If \(\xi _{\daleth }<\delta -0.5\) then leave as it is. Otherwise, \(\xi _{\daleth }=\xi _{\daleth }^{*}\) where \(\xi _{\daleth }^{*}=\delta -0.5.\)

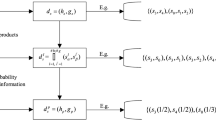
Consider the flow chart in Fig. 1. If the incomplete information provided by decision makers already fulfills (hubc) then this algorithm will stop after the first iteration. Otherwise, this algorithm will perform minimal possible revisions.

Fig. 1
figure 1

Flowchart

Full size image

To illustrate, we discuss the following case where decision maker presents incomplete information. Moreover, the decision maker is unable to abide by property (hubc). Hence, algorithm 1 is used to revise minimal possible information. Afterwards, the incomplete information is estimated to be expressible and therefore it is useable in decision-making models.

Example 3.5

Consider a set of commodities \(X=\{x_{1},x_{2},x_{3},x_{4}\}\). Suppose that the decision maker is to present incomplete information. The decision maker is capable of expressing preference intensities of the second alternative over other alternatives such that \(h_{21}=\{0.1,0.65,0.7\},h_{23}= \{0.2,0.6,0.9\}\) and \(h_{24}=\{0.2,0.3,0.4,0.5\dot{\}}.\) Clearly, the decision maker does not abide by property (hubc), and therefore, the estimated preferences will not be expressible. For instance, \(1.3\in h_{13}\) cannot be interpreted in preference modeling since it outlies the defined domain. We use algorithm 1, to solve this problem. Accordingly, \(\flat =\{0.1,0.2,0.3,0.4,0.5,0.6,0.65,0.7,0.9\}\) and \(\daleth =\{0.65,0.7,0.9\}\). Since, \(\mid \daleth \mid <\lceil \frac{\mid \flat \mid -1}{2}\rceil\), therefore, case 2 is to be followed. Accordingly, the least value \(\inf (\flat )=\xi _{1}=0.1\) which is revised to be \(\xi _{1}^{*}=0.4\) where \(\delta =0.7.\) For the second iteration, \(\inf (\flat /\xi _{1})=\xi _{2}=0.2\) which does not satisfy \(\xi _{2}<\delta -0.5\) where \(\delta =0.9.\) Therefore, according to the algorithm, \(\xi _{2}\) is revised to be \(\xi _{2}^{*}=0.4.\) Similarly, \(\xi _{3}^{*}\) is revised to be 0.4. The algorithm stops here because \(\inf (\flat /\xi _{3})=\xi _{4}<\delta -0.5\). Therefore, the revised hesitant fuzzy elements are \(h_{21}=\{0.4,0.65,0.7 \},h_{23}=\{0.4,0.6,0.7\}\) and \(h_{24}=\{0.4,0.5\dot{\}}.\) Algorithm 1 has helped in undertaking minimal possible revisions that result in hesitant fuzzy elements that satisfy property (hubc). Accordingly, the missing preferences are estimated and the completed hesitant fuzzy preference relation is stated as follows:

$$\begin{aligned} \begin{bmatrix} \{0.5\}&\mathbf {\{0.3,0.35,0.6\}}&\begin{array}{l} \{0.2,0.25,0.4,0.45, \\ 0.5,0.55,0.7,0.8\} \end{array}&\begin{array}{l} \{0.2,0.25,0.3, \\ 0.35,0.5,0.6\} \end{array} \\ \mathbf {\{0.4,0.65,0.7\}}&\mathbf {\{0.5\}}&\mathbf {\{0.4,0.6,0.7\}}&\mathbf {\{0.4,0.5\dot{\}}} \\ \begin{array}{l} \{0.2,0.3,0.45,0.5, \\ 0.55,0.6,0.75,0.8\} \end{array}&\mathbf {\{0.3,0.4,0.6\}}&\{0.5\}&\begin{array}{l} \{0.2,0.3,0.4, \\ 0.5\} \end{array} \\ \begin{array}{l} \{0.4,0.5,0.65, \\ 0.7,0.75,0.8\} \end{array}&\mathbf {\{0.5,0.6}\}&\{0.5,0.6,0.7,0.8\}&\{0.5\} \end{bmatrix} \end{aligned}$$

4 Hesitant Fuzzy Borda Rule (HF-Borda Rule)

In Sect. 3, we proposed a method to estimate missing information for which property (hubc) was formulated for decision makers. This property promises expressible estimated preference values. Moreover, an algorithm to deal with decision makers incapable of abiding by property (hubc) was stated. The procedure is summarized using a flowchart. We build on this study and assume that incomplete information has been completed using methods defined in Sect. 2. Therefore, in this section, we will be delivering a ranking method for incomplete hesitant fuzzy preference relations provided by m decision makers. For this purpose, we state HF-Borda count which is inspired by fuzzy borda count. While ranking alternatives, we also discuss the case of probable ties among alternatives and we discuss possible way of breaking these ties.

Let \(h_{ij}^{k}\) represent degree of confidence with which the decision maker \(k\in \{1,2,\ldots,m\}\) prefers \(x_{i}\) to \(x_{j}.\) Then the final value assigned by the expert k to each alternative \(x_{i}\) is as follows:

$$\begin{aligned} \widehat{h}_{k}(x_{i})=\sum _{j=1,s(h_{ij}^{k})>0.5}^{n}s(h_{ij}^{k}) \end{aligned}$$
(4.1)

which coincides with the sum of scores of all preferences with individual score greater than 0.5 in the i-th row in the hesitant fuzzy preference relation. Therefore, the definitive HF-Borda count for an alternative \(x_{i}\) is obtained as the sum of the values assigned by each expert as follows:

$$\begin{aligned} \widehat{r}(x_{i})=\sum _{k=1}^{m}\widehat{r}_{k}(x_{i}) \end{aligned}.$$
(4.2)

Alternative with lower scores are ranked lower as compared to alternatives with higher scores. Accordingly, the alternative with the greatest score, is most preferred. Also, \(x_{i}\prec x_{j}\) if and only if \(\widehat{h}(x_{i})< \widehat{h}(x_{j}).\) Similarly, \(x_{i}\simeq x_{j}\) if and only if \(\widehat{ h}(x_{i})=\widehat{h}(x_{j}).\) In case when there is indifference between two alternatives, then the standard deviation among all pairs of elements of a hesitant element are to be noted. Sum of deviations of all hesitant fuzzy elements in a row are added. Mathematically, if

$$\begin{aligned} \widehat{h}(x_{i})= & {} \widehat{h}(x_{j})\text { for }i\ne jt \end{aligned}$$
(4.3)
$$\begin{aligned} \overline{\widehat{h}}_{k}(x_{i})= & {} \sum _{j=1,s(h_{ij}^{k})>0.5}^{n}v(h_{ij}^{k}) \end{aligned}$$
(4.4)

represents sum of variance of hesitant fuzzy elements in a row with score greater than 0.5. Also,

$$\begin{aligned} \overline{\widehat{h}}(x_{i})=\sum _{k=1}^{m}\overline{\widehat{h}}_{k}(x_{i}) \end{aligned}$$
(4.5)

denoting sum of variance of an alternative by each expert. The smaller the variance, the preferred the alternative will be. For instance, to break the tie between \(x_{i}\) and \(x_{j}.\) Given \(x_{i}\simeq x_{j},\) if \(\overline{ \widehat{h}}(x_{i})<\overline{\widehat{h}}(x_{j}),\) then \(x_{j}\prec x_{i}\). With the help of variance, we will able to break ties between alternatives.

Consider the following example where three decision makers provide incomplete information represented in bold. The following hesitant fuzzy preference relations are completed using method defined in Sect. 3. The completed relations are then ranked using HF-Borda count.

Example 4.1

Consider the set of three decision makers \(E=\{e_{1},e_{2},e_{3}\}\). Suppose that the decision makers present the following information written in bold over the set of four alternatives \(X=\{x_{1},x_{2},x_{3},x_{4}\}.\) After estimating the missing information using theorem 3.3, the relations are completed and stated as follows:

$$\begin{aligned} H_{e_{1}}= \begin{bmatrix} \mathbf {\{0.5\}}&\begin{array}{l} \mathbf {\{0.45,0.5,0.7,} \\ \mathbf {0.73\}} \end{array}&\mathbf {\{0.6,0.64,0.67\}}&\mathbf {\{0.28,0.51,0.54\}} \\ \begin{array}{l} \mathbf {\{0.27,0.3,} \\ \mathbf {0.5,0.55\}} \end{array}&\{0.5\}&\begin{array}{l} \{0.27,0.3,0.35, \\ 0.37,0.47,0.5, \\ 0.53,0.55,0.6, \\ 0.7,0.73,0.75, \\ 0.78\} \end{array}&\begin{array}{l} \{0.05,0.08,0.28, \\ 0.33,0.28,0.31 \\ 0.55,0.56,0.31, \\ 0.35,0.54,0.59\} \end{array} \\ \begin{array}{l} \mathbf {\{0.33,0.36,} \\ \mathbf {0.4\}} \end{array}&\begin{array}{l} \{0.22,0.25,0.27, \\ 0.3,0.4,0.45, \\ 0.47,0.5,0.53 \\ 0.63,0.65,0.7, \\ 0.73\} \end{array}&\{0.5\}&\begin{array}{l} \{0.11,0.14,0.18, \\ 0.34,0.37,0.4, \\ 0.41,0.44\} \end{array} \\ \begin{array}{l} \mathbf {\{0.46,0.49,} \\ \mathbf {0.72\}} \end{array}&\begin{array}{l} \{0.41,0.46,0.65, \\ 0.69,0.44,0.45 \\ 0.69,0.72,0.67 \\ 0.72,0.92,0.95\} \end{array}&\begin{array}{l} \{0.56,0.59,0.6, \\ 0.63,0.66,0.82, \\ 0.86,0.89\} \end{array}&\{0.5\} \end{bmatrix} \end{aligned}$$

Hesitant fuzzy preference relation \(H_{e_{2}}\) of the second expert \(e_{2}\) is as follows:

$$\begin{aligned} H_{e_{2}}= \begin{bmatrix} \{0.5\}&\begin{array}{l} \mathbf {\{0.48,0.52,} \\ \mathbf {0.54\}} \end{array}&\begin{array}{l} \{0.35,0.39,0.41, \\ 0.45,0.49,0.5, \\ 0.51,0.53,0.55, \\ 0.56,0.57,0.59, \\ 0.6\} \end{array}&\begin{array}{l} \{0.03,0.06,0.07, \\ 0.09,0.1,0.17, \\ 0.26,0.29,0.3, \\ 0.32,0.33,0.35, \\ 0.52,0.53,0.54, \\ 0.56,0.57,0.58, \\ 0.59\} \end{array} \\ \mathbf {\{0.46,0.48,0.52\}}&\mathbf {\{0.5\}}&\begin{array}{l} \mathbf {\{0.37,0.47,0.51,} \\ \mathbf {0.52,0.55\}} \end{array}&\begin{array}{l} \mathbf {\{0.05,0.08,0.28,} \\ \mathbf {0.31,0.54,0.55\}} \end{array} \\ \begin{array}{l} \{0.4,0.41,0.43, \\ 0.44,0.45,0.47, \\ 0.49,0.5,0.51, \\ 0.55,0.59,0.65\} \end{array}&\begin{array}{l} \mathbf {\{0.45,0.48,} \\ \mathbf {0.49,} \\ \mathbf {0.53,0.63\}} \end{array}&\{0.5\}&\begin{array}{l} \begin{array}{l} \{0,0.03,0.04, \\ 0.06,0.07,0.08, \\ 0.11,0.18,0.21, \\ 0.23,0.26,0.27, \\ 0.29,0.3,0.31, \\ 0.34,0.41,0.44, \\ 0.49,0.5,0.52, \\ 0.53,0.54,0.57, \\ 0.58,0.67,0.68\} \end{array} \end{array} \\ \begin{array}{l} \{0.4,0.42,0.44, \\ 0.46,0.48,0.65, \\ 0.67,0.68,0.7, \\ 0.71,0.74,0.88, \\ 0.9,0.94, \\ 0.91,0.93,0.97\} \end{array}&\begin{array}{l} \mathbf {\{0.45,0.46,} \\ \mathbf {0.69,0.72,} \\ \mathbf {0.92,0.95\}} \end{array}&\begin{array}{l} \{0.32,0.33,0.42, \\ 0.43,0.47,0.48, \\ 0.5,0.51,0.56, \\ 0.59,0.66,0.69, \\ 0.71,0.74,0.77, \\ 0.79,0.82,0.93, \\ 0.94,0.96,0.97,1\} \end{array}&\{0.5\} \end{bmatrix} \end{aligned}$$

Hesitant fuzzy preference relation of the third expert \(e_{3}\) is stated as follows:

$$\begin{aligned} H_{e_{3}}= \begin{bmatrix} \mathbf {\{0.5\}}&\mathbf {\{0.3\}}&\mathbf {\{0.2,0.6\}}&\mathbf {\{0.6\}} \\ \mathbf {\{0.7\}}&\{0.5\}&\{0.4,0.8\}&\{0.8\} \\ \mathbf {\{0.4,0.8\}}&\{0.2,0.6\}&\{0.5\}&\{0.5,0.9\} \\ \mathbf {\{0.4\}}&\{0.2\}&\{0.1,0.5\}&\{0.5\} \end{bmatrix} \end{aligned}$$

Then the final value assigned by the expert \(e_{1}\) to alternative \(x_{1}\) is 1.2316. Similarly,

$$\begin{aligned} \widehat{h}_{e_{1}}(x_{2})= \sum _{j=1,s(h_{ij}^{e_{1}})>0.5}^{4}s(h_{ij}^{e_{1}})=0.53076,\,\widehat{h} _{e_{1}}(x_{3})=0\,\,\text { and }\,\,\widehat{h}_{e_{1}}(x_{4})=0.623. \end{aligned}$$

Also, according to the second and third experts, \(e_{2}\) and \(e_{3},\) \(\widehat{h}_{e_{2}}(x_{1})=0.5133,\) \(\widehat{h}_{e_{2}}(x_{2})=0,\) \(\widehat{h}_{e_{2}}(x_{3})=0.516,\) \(\widehat{h}_{e_{2}}(x_{4})=2.06033,\) \(\widehat{h}_{e_{3}}(x_{1})=0.6,\) \(\widehat{h}_{e_{3}}(x_{2})=2.1,\) \(\widehat{ h}_{e_{3}}(x_{3})=1.3,\) respectively. Score of the hesitant fuzzy elements can be stated in the form of following matrices. Here \(x_{i}^{k}\) represents the degree with which expert k prefers alternative i over the rest of the alternatives.

$$\begin{aligned} \begin{array}{l} \begin{array}{l} x_{1}^{e_{1}} \\ x_{2}^{e_{1}} \\ x_{3}^{e_{1}} \\ x_{4}^{e_{1}} \end{array} \begin{pmatrix} - &{} 0.595 &{} 0.636666 &{} 0 \\ 0 &{} - &{} 0.53076 &{} 0 \\ 0 &{} 0 &{} - &{} 0 \\ 0.55666 &{} 0.6475 &{} 0.62333 &{} - \end{pmatrix} \mathop {\left( \begin{array}{l} 1.2316\\ 0.53076\\ 0 \\ 1.82749 \end{array} \right) }\limits ^{\sum \limits _{j=1,s(h_{ij}^{k})>0.5}^{n}s(h_{ij}^{k})} \end{array} \end{aligned}$$

According to the second expert,

$$\begin{aligned} \begin{array}{l} \begin{array}{l} x_{1}^{e_{2}} \\ x_{2}^{e_{2}} \\ x_{3}^{e_{2}} \\ x_{4}^{e_{2}} \end{array} \begin{pmatrix} - &{} 0.51333 &{} 0 &{} 0 \\ 0 &{} - &{} 0 &{} 0 \\ 0 &{} 0.516 &{} - &{} 0 \\ 0.69882 &{} 0.698333 &{} 0.6631818 &{} - \end{pmatrix} \mathop {\left( \begin{array}{l} 0.51333\\ 0\\ 0.516 \\ 2.0603348 \end{array} \right) }\limits ^{\sum \limits _{j=1,s(h_{ij}^{k})>0.5}^{n}s(h_{ij}^{k})} \end{array} \end{aligned}$$

Lastly, according to the third expert,

$$\begin{aligned} \begin{array}{l} \begin{array}{l} x_{1}^{e_{3}} \\ x_{2}^{e_{3}} \\ x_{3}^{e_{3}} \\ x_{4}^{e_{3}} \end{array} \begin{pmatrix} - &{} 0 &{} 0 &{} 0.6 \\ 0.7 &{} - &{} 0.6 &{} 0.8 \\ 0.6 &{} 0 &{} - &{} 0.7 \\ 0 &{} 0 &{} 0 &{} - \end{pmatrix} \mathop {\left( \begin{array}{l} 0.6\\ 2.1\\ 1.3 \\ 0 \end{array} \right) }\limits ^{\sum \limits _{j=1,s(h_{ij}^{k})>0.5}^{n}s(h_{ij}^{k})} \end{array} \end{aligned}$$

Now, the HF-Borda count for alternative \(x_{1}\) is \(\widehat{h} (x_{1})=\sum _{k=1}^{m}\widehat{h}_{k}(x_{1})=2.3448,\widehat{h} (x_{2})=2.63076,\) \(\ \widehat{h}(x_{3})=1.816,\) \(\ \widehat{h} (x_{4})=3.8878248.\) Accordingly, \(x_{1}\prec x_{3}\prec x_{2}\prec x_{4}.\) Hence, an incomplete hesitant fuzzy preference relation has been completed and ranked.

Consider the following example, where HF-Borda count results in a tie between two alternatives. The above-mentioned method helps resolve the tie and rank the two alternatives explicitly.

Example 4.2

Consider the following 3 by 3 hesitant fuzzy preference relation that needs to be ranked using HF-Borda count.

$$\begin{aligned} H= \begin{bmatrix} \mathbf {\{0.5\}}&\mathbf {\{0.3\}}&\mathbf {\{0.2,0.4\}}&\mathbf {\{0.6\}} \\ \mathbf {\{0.7\}}&\{0.5\}&\{0.4,0.6\}&\{0.8\} \\ \mathbf {\{0.4,0.6\}}&\{0.2,0.4\}&\{0.5\}&\{0.5,0.7\} \\ \mathbf {\{0.4\}}&\{0.2\}&\{0.3,0.5\}&\{0.5\} \end{bmatrix} \begin{pmatrix} \begin{array}{l} 0.6 \end{array} \\ \begin{array}{l} 1.5 \end{array} \\ 0.6 \\ 0 \end{pmatrix} \end{aligned}$$

According to the HF-Borda count, \(x_{4}\prec x_{3}\simeq x_{1}\prec x_{2}.\) Therefore, to break the tie, sum of variance of the relevant hesitant fuzzy elements in each row is added. \(\overline{\widehat{h}}(x_{1})=0\) and \(\overline{\widehat{h}}(x_{3})=0.1.\) Therefore, the tie is broken and the two alternatives are ranked as \(x_{1}\prec x_{3}.\)

Similarly, if m decision makers provide incomplete hesitant fuzzy preference relations then the relations can be completed and ranked. Moreover, if there are any ties among the alternatives then the ties may be dissolved using the proposed method.

5 Conclusion and Future Work

Additive transitivity has been used to cater for incompleteness in hesitant fuzzy preference relations. It often leads to outlying estimations that void the defined domain. Literature uses transformation functions to translate the outliers back in the domain but at the cost of voiding originality of the information provided by decision makers. The aim of this paper is to take care of the problem of outlying estimated preferences.

This paper proposes property (hubc) which is coupled with additive transitivity to handle incomplete informations. Property (hubc) promises to estimate missing information that is expressible, which means that the estimated values lie inside the domain. Moreover, because of (hubc), the originality of information provided by the expert is not voided. We also consider the situation where decision maker is unable to abide by (hubc). Instead of discarding this expert, we propose an algorithm that undertakes minimal possible revisions. The resultant information satisfies property (hubc) and consequently, the incomplete information is completed.

The second emphasis of this article is on ranking of hesitant fuzzy preference relations. For this purpose, an extension of fuzzy Borda rule is defined in this article. This new method is denoted as HF-Borda rule. This rule is further modified to take care of probable ties that may persist between alternatives. A strong assumption in this paper is the absence of influence. In future, consensus of incomplete hesitant fuzzy preference relations in the presence of influence may be studied and compared to the work of Cabrerizo et al. [22, 31, 32].