1 Introduction

Industrial development has caused the increase in the consumption of electrical energy. This increasing of required energy has prompted several studies to search new kinds of source of energy. However, several kinds of clean energies have been discovered such as photovoltaic energy. It is well known that the operating point depends on the load characteristic and some climatic parameters such as temperature and irradiation. To increase the efficiency of the PV array panel system, it is crucial to operate the PV panel energy conversion system at the most near to the maximum power point.

Therefore, the tracking control of the maximum power point is a very difficult problem because the PV panel energy conversion system has a nonlinear behavior. To overcome these difficulties, many tracking control strategies have been proposed such as perturb and observe [1–4], incremental conductance [1–3, 5, 6], neural network [7], neural fuzzy techniques [8], and Mamdani-type fuzzy logic controller [9–13]. Other researchers have combined classical with new theories such as: Takagi–Sugeno (T–S) with fractional algorithms [14], augmented system with T–S fuzzy system [15].

The main contribution of this work, which deals with maximum power point tracking (MPPT) for photovoltaic panel, consists of developing a new algorithm based on T–S-type fuzzy system, whereas most of papers using Mamdani-type fuzzy system. In this paper, the PV array panel energy conversion system has been modeled by T–S-type fuzzy system. A reference model has been computed every time based on the measurement of climatic variables such as temperature and irradiation. Also, the MPPT algorithm has been developed based on a new parallel distributed compensation (PDC) method which was designed for T–S fuzzy systems. This paper is organized as follows. In Sect. 2, we recall in the first part the model of photovoltaic cell, then we show the influence of climatic parameters such as temperature and irradiation on the electrical characteristic of the PV array panel. In the second part, we describe the photovoltaic energy system by a state model.

In the third section, we recall the T–S fuzzy-type system, and then we present the average T–S fuzzy model for photovoltaic energy system. In Sect. 4, we describe the control strategy, which includes three blocks. The first part is reserved for computing the reference model, whereas the second part is reserved for the T–S fuzzy controller and stability analysis. The fuzzy controller which represents the MPPT algorithm is based on a modified PDC, it includes two terms. The controller parameters are computed based on linear matrices inequalities (LMI). In Sect. 5, simulation results of photovoltaic energy system show performances of the proposed MPPT algorithm tracker. Conclusions are drawn in the final section.

2 Photovoltaic Energy System

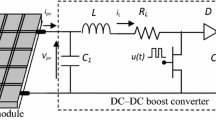
The photovoltaic energy system is given by Fig. 1, it consists of a photovoltaic array panel connected to a DC–DC converter which provides the power to the load. Also, the converter controls indirectly the operating point of the PV array panel and consequently its power generation by adjusting the duty cycle of the DC/DC converter. However, we can regulate the panel voltage V pv to the V MPP which, therefore, affects the output power of the PV array module.

Fig. 1
figure 1

Photovoltaic energy conversion system

Full size image

In the first stage, we recall the most popular model of photovoltaic cells which is proposed by Singer [16], it is given by the following Fig. 2.

Fig. 2
figure 2

Equivalent circuit for PV cell

Full size image

The equivalent circuit of PV cell includes a current generator which depends essentially on temperature (T) and irradiation (G). It has also a diode, connected to an internal parallel and series resistor namely respectively, R sh and R s.

The PV cell model is described by the following equations [16]:

$$I_{\text{pv}} = I_{\text{ph}} - I_{\text{s}} \left[ {\exp \left( {q\left( {\frac{{V_{\text{pv}} + R_{\text{s}} I}}{{n_{\text{s}} kT}}} \right)} \right) - 1} \right] - \frac{{\left( {V_{\text{pv}} + R_{\text{s}} I} \right)}}{{R_{\text{sh}} }}.$$
(1)

The expression of current which is generated by the photovoltaic panel varies with temperature and irradiation. It is expressed by the following equation:

$$I_{\text{ph}} = \left( {I_{{{\text{ph,}}n}} + K_{\text{I}} \varDelta T} \right)\frac{G}{{G_{n}}},$$
(2)

I ph,n is the rated current generated by the PV panel under standard condition of temperature and irradiation (T = 25 °C and G n  = 1000 w/m2).

$$V_{\text{oc}} = n_{\text{s}} \frac{KT}{q}{\text{Log}}\left( {\frac{{I_{\text{sc}} + I_{\text{s}} }}{{I_{\text{s}} }}} \right)$$
(3)
$$V_{\text{pv}} = n_{\text{s}} \frac{KT}{q}{\text{Log}}\left( {\frac{{I_{\text{sc}} + I_{\text{s}} - I_{\text{pv}} }}{{I_{\text{s}} }}} \right),$$
(4)

where V oc is the open-circuit voltage, I s is a reverse saturation current, and I sc is the short-circuit current.

It is straightforward to verify that the above equations, which describe relations between electrical variables of photovoltaic panel, are nonlinear. They depend on temperature and irradiation. The following Figs. 3 and 4 show respectively, the evolution of the power–voltage characteristics of a photovoltaic panel, at a given fixed temperature for variable irradiations and at given fixed irradiation for variable temperatures.

Fig. 3
figure 3

PV power curves with different T

Full size image
Fig. 4
figure 4

PV power curves with different G

Full size image

From the curves of Figs. 3 and 4 we can affirm that for each PV curve, there exists only one MPP. In order to extract the maximum power from the PV array panel, the MPP must be reached using a specific algorithm tracker.

In the second stage, we present the modeling of the photovoltaic conversion system which can be presented by Fig. 1.

The average dynamic model of the photovoltaic system can be expressed in continuous conduction by the following equations:

$$\left\{ {\begin{array}{ll} {\frac{{{\text{d}}V_{{{\text{pv}}}} }}{{{\text{d}}t}} = } & {\frac{1}{{C_{1} }}\left( {I_{{{\text{pv}}}} - I_{{\text{L}}} } \right)} \\ {\frac{{{\text{d}}I_{{\text{L}}} }}{{{\text{d}}t}}\,\, = } & {\frac{1}{L}\left[ {V_{{{\text{pv}}}} - \left( {1 - \mu } \right)V_{{{\text{c2}}}} } \right]} \\ {\frac{{{\text{d}}V_{{{\text{c2}}}} }}{{{\text{d}}t}} = } & {\frac{1}{{C_{2} }}\left[ {(1 - \mu )I_{{\text{L}}} - \frac{{V_{{{\text{c2}}}} }}{{R_{{\text{L}}} }}} \right]} \\ \end{array} } \right.$$
(5)

where µ represents the duty cycle.

It is clear that the system described by Eq. (5) can be presented in the following form:

$$\dot{x}(t) = A(x)x(t) + B(x)u(t),$$
(6)

where \(x(t) = \left[ {\begin{array}{*{20}c} {V_{\text{pv}} } & {I_{L} } & {V_{\text{c2}} } \\ \end{array} } \right]^{T}\) is the state vector, A is the state matrix, and B is the input vector. They are given as follows:

$$A = \left[ {\begin{array}{*{20}c} {\frac{{I_{\text{pv}} }}{{V_{\text{pv}} C_{1} }}} & { - \frac{1}{{C_{1} }}} & 0 \\ \frac{1}{L} & 0 & { - \frac{1}{L}} \\ 0 & {\frac{1}{{C_{2} }}} & {\frac{ - 1}{{R_{L} C_{2} }}} \\ \end{array} } \right],\quad B = \left[ {\begin{array}{*{20}c} 0 \\ {\frac{{V_{\text{c2}} }}{L}} \\ { - \frac{{I_{L} }}{{C_{2} }}} \\ \end{array} } \right],$$

and u = µ represents the duty cycle.

We note that the state matrix A and the input vector B include a nonlinear term. However, many approaches can be used to study this system such as neural networks or fuzzy systems. In this work we use T–S-type fuzzy system for modeling the later system and to develop the MPPT algorithm.

3 T–S Fuzzy Model of Photovoltaic Energy Conversion System

Several studies have shown that the continuous nonlinear system (6) can be presented by a T–S fuzzy-type dynamic model. It is expressed by a combination of linear local models or sub models. Each one of them is described by a fuzzy rule, characterizing local input–output relations of sub models [17, 18]. The ith rule of the fuzzy model has the following form:

ith Plant rule:

$$\begin{aligned} {\text{IF }}z_{1} {\text{ is }}M_{i1} {\text{ and }}z_{2} {\text{ is }}M_{i2} {\text{ and}} \ldots {\text{and }}z_{n} {\text{ is }}M_{in} \hfill \\ {\text{THEN }} \dot{x}(t) = A_{i} x(t) + B_{i} u(t);\quad i = 1,2, \ldots c, \hfill \\ \end{aligned},$$
(7)

where \(\left\{ {M_{ij} } \right\}\) are the fuzzy sets, \(x(t) \in R^{n}\) is the state vector, u(t) is the input vector, \(A_{i} \in R^{n \times n}\) is the state matrix, \(B_{i} \in R^{n \times m}\) is the input matrix, \(\left\{ {z_{ 1} (t), \ldots ,z_{n} (t)} \right\}\) are the premise variables. \(y(t) \in {\text{R}}^{m}\) is the output vector; c is the number of fuzzy rules. The global fuzzy model of the system has the following form:

$$\dot{x} (t )= \frac{{\sum\nolimits_{j = 1}^{c} {w_{i} (z (t ) )\left[ {A_{i} x (t )+ B_{i} u (t )} \right]} }}{{\sum\nolimits_{i = 1}^{c} {} w_{i} (z(t))}}.$$
(8)

For each rule R i is attributed a weight w i (z(t)) which depends on the grade of membership function of premise variables z j (t) in fuzzy sets M ij :

$$w_{i} \left( {z(t)} \right) = \prod\limits_{j = 1}^{n} {M_{ij} \left( {z_{j} (t)} \right)},$$

where M ij (z j (t)) is the grade of membership of z j (t) to the fuzzy set M ij .

Let \(h_{j} (z (t ) )= \frac{{w_{j} (z (t ) )}}{{\sum\nolimits_{i = 1}^{c} {w_{i} (z (t ) )} }},\) with w i (z(t)) > 0;

for i = 1, …, c.

$$\begin{aligned} &\sum\limits_{i = 1}^{c} {w_{i} (z (t ) )> 0,} \quad 0 < h_{i} (z(t)) < 1,\quad i = 1,\ldots,c, \hfill \\ &\sum\limits_{i = 1}^{c} {h_{i} } (z (t ) )= 1. \hfill \\ \end{aligned}$$

The T–S fuzzy state model is given by the following equation:

$$\dot{x} (t )= \sum\limits_{i = 1}^{c} {h_{i} } (z (t ) )\left[ {A_{i} x (t )+ B_{i} u (t )} \right].$$
(9)

The fuzzy premise variables are chosen as:

$$z_{ 1} = V_{\text{pv}} ,z_{ 2} = I_{\text{pv}} ,z_{ 3} = {\text{I}}_{L} ,z_{ 4} = V_{\text{s}},$$

where V pv represents the PV voltage, I pv the PV current, I L the inductor current, and V s the output voltage.

Each premise variable belongs to a bounded interval such as: \(z_{k} (t) \in \left[ {z_{\hbox{min} ,k} \quad z_{\hbox{max} ,k} } \right],\) where z min,k and z max,k are the lower and upper bounds of the variable z k .

However, each nonlinear term can be transformed under the following shape:

$$z_{k} (t )= M_{\hbox{min} ,k} \left( {z_{k} (t)} \right) \cdot z_{\hbox{max} ,k} + M_{\hbox{max} ,k} \left( {z_{k} (t)} \right) \cdot z_{\hbox{min} ,k},$$
(10)

where the membership functions are defined as follows:

$$\begin{aligned}M_{\hbox{min} ,k}^{{}} (z_{k} (t))& = M_{1,k}^{{}} (z_{k} (t)) = \frac{{z_{k} (t) - z_{\hbox{min} ,k} }}{{z_{\hbox{max} ,k} - z_{\hbox{min} ,k} }} \hfill \\ M_{\hbox{max} ,k}^{{}} (z_{k} (t))& = M_{2,k}^{{}} (z_{k} (t)) = \frac{{z_{\hbox{max} ,k} - z_{k} (t)}}{{z_{\hbox{max} ,k} - z_{\hbox{min} ,k} }}. \hfill \\ \end{aligned}$$
(11)

The plant includes some nonlinearities from I PV, I L , V PV, and V c2. We note that there is a relationship between the magnitudes of current I PV and I L and voltage magnitudes V PV, and V c2. However, the structure of the state matrices A i and B i of each local model of the T–S fuzzy model of the energy conversion system are described as follow:

$$A_{i} = \left[ {\begin{array}{lll} {\frac{{\alpha _{i} }}{{C_{1} }}} & { - \frac{1}{{C_{1} }}} & 0 \\ {\frac{1}{L}} & 0 & { - \frac{1}{L}} \\ 0 & {\frac{1}{{C_{2} }}} & {\frac{{ - 1}}{{R_{L} C_{2} }}} \\ \end{array} } \right],\,B_{i} = \left[\begin{array}{l} 0 \\ {\frac{{V_{{{\text{c}}2i}} }}{L}} \\ { - \frac{{I_{{Li}} }}{{C_{2} }}}\\\end{array}\right],$$

where \(\alpha_{i} = \frac{{I_{{{\text{pv}}i}} }}{{V_{{{\text{pv}}i}}}}\)

The premise variables, z k (t), have been chosen as: I Li and V c2i . Each of them belongs to the interval \(\left[ {z_{\hbox{min} ,k} \quad z_{\hbox{max} ,k} } \right]\). Basis of Eq. (10), the T–S-type fuzzy model must include four local models:

$$A_{1} = \left[ {\begin{array}{lll} {\frac{{\alpha_{\hbox{max} } }}{{C_{1} }}} & { - \frac{1}{{C_{1} }}} & 0 \\ \frac{1}{L} & 0 & { - \frac{1}{L}} \\ 0 & {\frac{1}{{C_{2} }}} & {\frac{ - 1}{{R_{L} C_{2} }}} \\ \end{array} } \right],\quad B_{1} = \left[ {\begin{array}{l} 0 \\ {\frac{{V_{{{\text{c}}2\hbox{max} }} }}{L}} \\ { - \frac{{I_{L\hbox{max} } }}{{C_{2} }}} \\ \end{array} } \right];$$
$$A_{2} = \left[ {\begin{array}{lll} {\frac{{\alpha_{\hbox{max} } }}{{C_{1} }}} & { - \frac{1}{{C_{1} }}} & 0 \\ \frac{1}{L} & 0 & { - \frac{1}{L}} \\ 0 & {\frac{1}{{C_{2} }}} & {\frac{ - 1}{{R_{L} C_{2} }}} \\ \end{array} } \right],\quad B_{2} = \left[ {\begin{array}{l} 0 \\ {\frac{{V_{{{\text{c}}2\hbox{min} }} }}{L}} \\ { - \frac{{I_{L\hbox{max} } }}{{C_{2} }}} \\ \end{array}}\right];$$
$$A_{3} = \left[ {\begin{array}{lll} {\frac{{\alpha_{\hbox{min} } }}{{C_{1} }}} & { - \frac{1}{{C_{1} }}} & 0 \\ \frac{1}{L} & 0 & { - \frac{1}{L}} \\ 0 & {\frac{1}{{C_{2} }}} & {\frac{ - 1}{{R_{L} C_{2} }}} \\ \end{array} } \right],\quad B_{3} = \left[ {\begin{array}{l} 0 \\ {\frac{{V_{{{\text{c}}2\hbox{min} }} }}{L}} \\ { - \frac{{I_{L\hbox{min} } }}{{C_{2} }}} \\ \end{array} } \right];$$
$$A_{4} = \left[ {\begin{array}{lll} {\frac{{\alpha_{\hbox{min} } }}{{C_{1} }}} & { - \frac{1}{{C_{1} }}} & 0 \\ \frac{1}{L} & 0 & { - \frac{1}{L}} \\ 0 & {\frac{1}{{C_{2} }}} & {\frac{ - 1}{{R_{L} C_{2} }}} \\ \end{array} } \right],\quad B_{4} = \left[ {\begin{array}{l} 0 \\ {\frac{{V_{c2\hbox{max} } }}{L}} \\ { - \frac{{I_{L\hbox{min} } }}{{C_{2} }}} \\ \end{array} } \right]$$

In this case, the membership functions are defined as follows:

$$\begin{aligned} M_{11}^{{}} (z_{1} (t)) = M_{31}^{{}} (z_{1} (t)) = \frac{{z_{\hbox{max} ,1} - z_{1} (t)}}{{z_{\hbox{max} ,1} - z_{\hbox{min} ,1} }}; \hfill \\ M_{21}^{{}} (z_{1} (t)) = M_{41}^{{}} (z_{1} (t)) = \frac{{z_{1} (t) - z_{\hbox{min} ,1} }}{{z_{\hbox{max} ,1} - z_{\hbox{min} ,1} }} \hfill \\ \end{aligned}$$
$$\begin{aligned} M_{12}^{{}} (z_{2} (t)) = M_{42}^{{}} (z_{2} (t)) = \frac{{z_{\hbox{max} ,2} - z_{2} (t)}}{{z_{\hbox{max} ,2} - z_{\hbox{min} ,2} }}; \hfill \\ M_{22}^{{}} (z_{2} (t)) = M_{32}^{{}} (z_{2} (t)) = \frac{{z_{2} (t) - z_{\hbox{min} ,2} }}{{z_{\hbox{max} ,2} - z_{\hbox{min} ,2} }} \hfill \\ \end{aligned}$$

4 Control Strategy

The control strategy that we suggest is given by Fig. 5.

Fig. 5
figure 5

Control strategy

Full size image

The control strategy consists of three blocks: T–S fuzzy reference model, controller, and plant.

4.1 T–S Fuzzy Reference Model

The T–S fuzzy reference model is computed on the basis of T–S-type fuzzy model, where the temperature T and the irradiation G have been used as fuzzy premise variables, Z R1 = T and Z R2 = G. It is possible to compute, at any time, the desired state variables, consequently the maximum power of the PV array panel which can be generated.

The nonlinear reference model can be described by the following T–S fuzzy model:

ith reference rule:

$$\begin{aligned} {\text{IF }}z_{1R} {\text{ is }}\lambda_{i1} {\text{ and }}z_{2R} {\text{ is }}\lambda_{i2} {\text{ and}} \, \ldots \, {\text{and }}z_{nR} {\text{ is }}\lambda_{in} \, \hfill \\ {\text{THEN}} \left\{ \begin{array}{l} \dot{x}_{R} (t) = D_{i} x_{R} (t) \, \hfill \\ y_{R} (t) = C_{Ri} x_{R} (t),\quad i = 1,2, \ldots ,cr, \hfill \\ \end{array} \right. \hfill \\ \end{aligned},$$
(12)

where \(\left\{ {\lambda_{ij} } \right\}\) are the fuzzy sets, \(x_{R} (t) = \left[ {V_{{{\text{pv}}r}} \quad I_{Lr} \quad V_{{{\text{c}}2r}} } \right]^{T}\) is the state reference variable vector, and \(D_{i} \in R^{n \times n}\) is the local reference state matrix, \(\left\{ {z_{ 1R} (t), \ldots ,z_{nR} (t)} \right\}\) are the premise variables. \(y(t) \in R^{m}\) is the output vector; cr is the number of fuzzy rules. Then, the T–S fuzzy reference model is given by the following equation:

$$\dot{x}_{R} (t )= \sum\limits_{i = 1}^{cr} {\eta_{i} (z (t ) )\,D_{i} x_{R} (t )},$$
(13)

With,

$$D_{i} = \left[ {\begin{array}{*{20}c} {\frac{{I_{{{\text{MPP}}i}} }}{{V_{{{\text{MPP}}i}} C_{1} }}} & { - \frac{1}{{C_{1} }}} & 0 \\ \frac{1}{L} & 0 & { - \frac{{(1 - \mu_{{{\text{op}}i}} )}}{L}} \\ 0 & {\frac{{(1 - \mu_{{{\text{op}}i}} )}}{{C_{2} }}} & {\frac{ - 1}{{R_{L} C_{2} }}} \\ \end{array} } \right],$$

with: \(\mu_{{{\text{op}}i}} = 1 - \sqrt {\frac{{V_{{{\text{MPP}}i}} }}{{R_{L} I_{{{\text{MPP}}i}} }}}\) [19].

4.2 T–S Fuzzy Controller and Stability Analysis

From the T–S fuzzy model of photovoltaic energy conversion system, we design the T–S fuzzy controller which represents the MPPT algorithm. The controller provides the value of the corresponding duty cycle which guarantees stability of the system and allows modifying the operating point to extract the maximum energy from the panel. The most popular state feedback T–S fuzzy controller is based on parallel distributed compensation (PDC) technique, which is proposed by Kang and Sugeno. The PDC controller and the fuzzy model share the same fuzzy sets in the premise parts [20, 21]. Basis of the T–S fuzzy models, the PDC fuzzy controller is designed as follows:ith controller rule:

$$\begin{aligned} {\text{IF}}\,z_{1}\,{\text{is}}\,M_{i1}\,{\text{and}}\,z_{2}\,{\text{is}}\,M_{i2}\, {\text{and}}\,\ldots \, {\text{and}}\,z_{n}\,{\text{ is}}\,M_{in} {\text{ THEN}} \hfill \\ u(t) = - \;K_{i} x(t)\,,\quad i = 1,2, \ldots c. \hfill\\\end{aligned}$$
(14)

The global fuzzy controller is represented by,

$$u(t) = - \;\sum\limits_{i = 1}^{c} {h_{i} } (z)K_{i} x(t).$$
(15)

In this paper, a new PDC controller is proposed in [22]. The main difference with the ordinary PDC controller in [20–23] is to have a term for the feedback signal of x R (t). In this case, the PDC controller is insufficient to cancel the static tracking errors. However, an integral action is added to the new PDC fuzzy controller.

The control input has two terms as follows:

$$u(t) = - \;\sum\limits_{i = 1}^{c} {h_{i} } (z)K_{i} e(t) + u_{I} (t)$$
(16)

where,

$$u_{I} (t) = - \;\sum\limits_{i = 1}^{c} {h_{i} } (z)K_{i} e_{I} (t)$$
(17)

Then,

$$u(t) = - \sum\limits_{i = 1}^{c} {h_{i} } (z)\left[ {K_{i} \quad K_{i} } \right]\left[ {\begin{array}{*{20}c} {e(t)} \\ {e_{I} (t)} \\ \end{array} } \right],$$

where the feedback gains K i will be related to an LMI problem.

Theorem

Consider the reference model ( 13 ) which is used to give the reference state variables, the nonlinear system ( 6 ) which can be represented by the T–S fuzzy model ( 9 ) and the controller ( 16 ) based on the PDC techniques. If there exists a common symmetric positive definite matrix Q > 0 and feedback gains M i which satisfy the following LMI ( 18 ) and ( 19 ), then the closed loop system is asymptotically stable and the tracking error converges toward zero.

$$\left[ {\begin{array}{*{20}c} {QA_{i}^{T} + A_{i} Q - B_{i} M_{i} - M_{i}^{T} B_{i}^{T} } & { - B_{i} M_{i} } & {(A_{i} - D_{k} )Q} \\ { - M_{i}^{T} B_{i}^{T} } & { - I} & 0 \\ {Q(A_{i} - D_{k} )^{T} } & 0 & { - \rho^{2} I} \\ \end{array} } \right] < 0,\quad {\text{for}}\;i{ = 1,} \ldots {\text{c}}\;{\text{and}}\;k{ = 1,} \ldots cr,$$
(18)
$$\left[ {\begin{array}{*{20}c} {QA_{i}^{T} + A_{i} Q - B_{i} M_{j} - M_{j}^{T} B_{i}^{T} } & { - B_{i} M_{j} } & {(A_{i} - D_{k} )Q} \\ { - M_{j}^{T} B_{i}^{T} } & { - I} & 0 \\ {Q(A_{i} - D_{k} )^{T} } & 0 & { - \rho^{2} I} \\ \end{array} } \right] < 0,\quad {\text{for}}\;i{ = 1,} \ldots ,c, \,j = 1, \ldots c,\;i \ne j\;{\text{and}}\;k = 1, \ldots ,cr.$$
(19)

Proof

The state tracking error is given by,

$$e(t) = x_{R} (t) - x(t)$$
(20)

In order to compute the feedback gains K i and to verify the system stability, we choose the following quadratic Lyapunov candidate function, definite positive.

$$V(e) = e^{T} (t)Pe(t) + \frac{1}{{\rho^{2} }}\int\limits_{0}^{t} {x_{R}^{T} (\tau )} x_{R} (\tau ){\text{d}}\tau + \int\limits_{0}^{t} {e_{I}^{T}(\tau )e_{I} (\tau ){\text{d}}\tau }.$$
(21)

The system is asymptotically stable if we prove that: \(\dot{V}(e) < 0\).

$$\dot{V}(e) = \dot{e}_{{}}^{T} Pe + e_{{}}^{T} P\dot{e} + \frac{1}{{\rho^{2} }}x_{R}^{T} x_{R} + e_{I}^{T} e_{I},$$
(22)
$$\dot{e} (t )= \sum\limits_{i = 1}^{c} {\sum\limits_{k = 1}^{cr} {h_{i} (z)} } \eta_{k} (z )\left[ {A_{i} e (t )+ B_{i} u (t ) { + }\left( {A_{i} - D_{k} } \right)x_{R} (t )} \right],$$
(23)
$$\begin{aligned} \dot{e} (t )& = \sum\limits_{i = 1}^{c} {\sum\limits_{j = 1}^{c} {\sum\limits_{k = 1}^{cr} {h_{i} (z)} } } h_{j} (z)\eta_{k} (z )\left[ {A_{i} e (t )- B_{i} \left( {K_{j} e + K_{j} e_{I} } \right)} \right] \\ & \quad { + }\sum\limits_{i = 1}^{c} {\sum\limits_{j = 1}^{c} {\sum\limits_{k = 1}^{cr} {h_{i} (z)} } } h_{j} (z)\eta_{k} (z )\left( {A_{i} - D_{k} } \right)x_{R} (t ) ,\\ \end{aligned}$$
(24)
$$\begin{aligned} \dot{V}(e) = & \sum\limits_{i = 1}^{c} {\sum\limits_{j = 1}^{c} {\sum\limits_{k = 1}^{cr} {h_{i} (z)h_{j} (z)} } \eta_{k} (z )} \\ \times & \left( \begin{array}{l} \left( {\left( {A_{i} - B_{i} K_{j} } \right) e (t )- B_{i} K_{j} e_{I} (t )} \right)^{T} Pe \hfill \\ +\, \left( {\left( {A_{i} - D_{k} } \right)x_{R} (t )} \right)^{T} Pe \hfill \\ + \,e_{{}}^{T} P\left( {\left( {A_{i} - B_{i} K_{j} } \right) e (t )- B_{i} K_{j} e_{I} (t )} \right) \hfill \\ +\, e_{{}}^{T} P\left( {\left( {A_{i} - D_{k} } \right)x_{R} (t )} \right) \hfill \\ \end{array} \right) \\ + & \frac{1}{{\rho^{2} }}x_{R}^{T} x_{R} + e_{I}^{T} e_{I} \\ \end{aligned}$$
(25)
$$\begin{aligned} \dot{V}(e) = & \sum\limits_{i = 1}^{c} {\sum\limits_{j = 1}^{c} {\sum\limits_{k = 1}^{cr} {h_{i} (z)h_{j} (z)} } \eta_{k} (z )} \\ \times & \left( \begin{array}{l} e^{T} \left( {A_{i} - B_{i} K_{j} } \right)^{T} Pe{ + }e^{T} P\left( {A_{i} - B_{i} K_{j} } \right) e \hfill \\ - e_{I}^{T} K_{J}^{T} B_{i}^{T} Pe - e_{{}}^{T} PB_{i} K_{j} e_{I} \hfill \\ + x_{R}^{T} \left( {A_{i} - \;D_{k} } \right)^{T} Pe + e_{{}}^{T} P\left( {A_{i} - \;D_{k} } \right)x_{R} \hfill \\ \end{array} \right) \\ & + \frac{1}{{\rho^{2} }}x_{R}^{T} x_{R} + e_{I}^{T} e_{I} \\ \end{aligned}$$
(26)
$$\begin{aligned} {\dot{V}}(e) = & \sum\limits_{i = 1}^{c} {\sum\limits_{\begin{array}{l} k = 1 \\ k \ne i \end{array}}^{cr} {h_{i}^{2} (z )} \eta_{k} (z )} \times & \left( \begin{array}{l} e^{T} \left( {A_{i} - B_{i} K_{i} } \right)^{T} Pe + e^{T} P\left( {A_{i} { - }B_{i} K_{i} } \right) e \\ - e_{I}^{T} K_{i}^{T} B_{i}^{T} Pe - e_{{}}^{T} PB_{i} K_{i} e_{I} \\ { + }x_{R}^{T} \left( {A_{i} - D_{k} } \right)^{T} Pe + e_{{}}^{T} P\left( {A_{i} - D_{k} } \right)x_{R} \\ + \frac{1}{{\rho^{2} }}x_{R}^{T} x_{R} + e_{I}^{T} e_{I} \\ \end{array} \right) & \quad + \sum\limits_{\begin{array}{l} i = 1 \\ i \ne j \end{array} }^{c} {\sum\limits_{j = 1}^{c} {\sum\limits_{\begin{array}{l} k = 1 \\ k \ne i \end{array} }^{cr} {h_{i} (z)h_{j} (z)} } } \eta_{k} (z ) \times & \left( \begin{array}{l} e^{T} \left( {A_{i} - B_{i} K_{j} } \right)^{T} Pe + e^{T} P\left( {A_{i} { - }B_{i} K_{j} } \right) e \\ - e_{I}^{T} K_{J}^{T} B_{i}^{T} Pe - e_{{}}^{T} PB_{i} K_{j} e_{I} \\ { + }x_{R}^{T} \left( {A_{i} - D_{k} } \right)^{T} Pe + e_{{}}^{T} P\left( {A_{i} - D_{k} } \right)x_{R} \\ + \frac{1}{{\rho^{2} }}x_{R}^{T} x_{R} + e_{I}^{T} e_{I} \\ \end{array} \right) \\ \end{aligned}$$
(27)

We note in this analysis that the feedback gains and stability will be related to an LMI problem. Therefore, we obtain the inequality \(\dot{V}(e) < 0\) when the following conditions are satisfied:

$$\left\{ \begin{array}{l} e^{T} \left( {A_{i} - B_{i} K_{i} } \right)^{T} Pe + e^{T} P\left( {A_{i} - B_{i} K_{i} } \right) e - e_{I}^{T} K_{i}^{T} B_{i}^{T} Pe \hfill \\ - \, e_{{}}^{T} PB_{i} K_{i} e_{I} { + }x_{R}^{T} \left( {A_{i} - D_{k} } \right)^{T} Pe + e_{{}}^{T} P\left( {A_{i} - D_{k} } \right)x_{R} \hfill \\ + \frac{1}{{\rho^{2} }}x_{R}^{T} x_{R} + e_{I}^{T} e_{I} < 0, \, \hfill \\ {\text{for }}i{ = 1,} \ldots c\quad {\text{and}}\quad k{ = 1,} \ldots ,cr \hfill \\ e^{T} \left( {A_{i} - B_{i} K_{j} } \right)^{T} Pe + e^{T} P\left( {A_{i} - B_{i} K_{j} } \right) e \hfill \\ -\, e_{I}^{T} K_{J}^{T} B_{i}^{T} Pe - e_{{}}^{T} PB_{i} K_{j} e_{I} { + }x_{R}^{T} \left( {A_{i} - D_{k} } \right)^{T} Pe \hfill \\ + \, e_{{}}^{T} P\left( {A_{i} - D_{k} } \right)x_{R} + \frac{1}{{\rho^{2} }}x_{R}^{T} x_{R} + e_{I}^{T} e_{I} < 0, \hfill \\ {\text{for }}i{ = 1,} \ldots ,c\quad \, j{ = 1,} \ldots ,{\text{c}}\quad i \ne j{\text{ and }}k{ = 1,} \ldots ,cr \hfill \\ \end{array} \right.$$
(28)

Using the Schur complement [17], the inequality in (28) can be written as,

$$\begin{aligned} \left[ {\begin{array}{*{20}c} {A_{i}^{T} P + PA_{i} - PB_{i} K_{i} - K_{i}^{T} B_{i}^{T} P} & { - PB_{i} K_{i} } & {P(A_{i} - D_{k} )} \\ { - K_{i}^{T} B_{i}^{T} P} & { - I} & 0 \\ {(A_{i} - D_{k} )^{T} P} & 0 & { - \rho^{2} I} \\ \end{array} } \right] < 0,\quad {\text{for }}i{ = 1,} \ldots ,c\quad {\text{and }}k{ = 1,} \ldots ,cr \hfill \\ \left[ {\begin{array}{*{20}c} {A_{i}^{T} P + PA_{i} - PB_{i} K_{j} - K_{j}^{T} B_{i}^{T} P} & { - PB_{i} K_{j} } & {P(A_{i} - D_{k} )} \\ { - K_{j}^{T} B_{i}^{T} P} & { - I} & 0 \\ {(A_{i} - D_{k} )^{T} P} & 0 & { - \rho^{2} I} \\ \end{array} } \right] < 0,\quad {\text{for }}i{ = 1,} \ldots ,c ,\quad \, j{ = 1,} \ldots ,c ,\quad i \ne j\quad {\text{and}}\quad k{ = 1,} \ldots ,cr. \hfill \\ \hfill \\ \end{aligned}$$
(29)

Since these inequalities contain coupled elements such as PB i K i , then these inequalities are BiLMIs. However, we must transform them to the LMIs. So, we perform a congruence transformation by \({\text{diag}}\left[ {\begin{array}{*{20}c} {[P^{ - 1} } & I & I \\ \end{array} } \right]\) to (29) and considering Q = P −1, \(M_{i} = K_{i} P^{ - 1} = K_{i} Q\), we obtain the following matrices in the LMI form:

$$\left[ {\begin{array}{lll} {QA_{i}^{T} + A_{i} Q - B_{i} M_{i} - M_{i}^{T} B_{i}^{T} } & { - B_{i} M_{i} } & {(A_{i} - D_{k} )Q} \\ { - M_{i}^{T} B_{i}^{T} } & { - I} & 0 \\ {Q(A_{i} - D_{k} )^{T} } & 0 & { - \rho^{2} I} \\ \end{array} } \right] < 0,\quad {\text{for }}i{ = 1,} \ldots ,c\quad {\text{and}}\quad k{ = 1,} \ldots ,cr,$$
(30)
$$\left[ {\begin{array}{lll} {QA_{i}^{T} + A_{i} Q - B_{i} M_{j} - M_{j}^{T} B_{i}^{T} } & { - B_{i} M_{j} } & {(A_{i} - D_{k} )Q} \\ { - M_{j}^{T} B_{i}^{T} } & { - I} & 0 \\ {Q(A_{i} - D_{k} )^{T} } & 0 & { - \rho^{2} I} \\ \end{array} } \right] < 0,\quad {\text{for }}i{ = 1,} \ldots ,c ,\; \, j{ = 1,} \ldots ,c , { }\;i \ne j\quad {\text{and}}\quad k{ = 1,} \ldots ,cr.$$
(31)

5 Simulation Results

In this section, we use Matlab to simulate the behavior of the energy conversion system. The characteristics of the PV array panel are given by the following Table 1.

Table 1 Characteristics of the PV array panel
Full size table

The matrices P and Q, and feedback gains K 1, K 2, K 3 and K 4 are obtained by solving the appropriate LMIs.

$$P = 1000\left[ {\begin{array}{*{20}c} {3.7874} & { - 1.1007} & {0.0182} \\ { - 1.1007} & {1.3710} & { - 0.0231} \\ {0.0182} & { - 0.0231} & {0.0023} \\ \end{array} } \right]$$
$$Q = \left[ {\begin{array}{*{20}c} {0.0003} & {0.0003} & {0.0001} \\ {0.0003} & {0.0011} & { - 0.0087} \\ {0.0001} & {0.0087} & {0.5134} \\ \end{array} } \right]$$
$$K_{1} = \left[ {\begin{array}{*{20}c} { - 0.3439} & {0.2438} & { - 0.0041} \\ \end{array} } \right],$$
$$K_{2} = \left[ {\begin{array}{*{20}c} { - 0.3920} & {0.2742} & { - 0.0046} \\ \end{array} } \right],$$
$$K_{3} = \left[ {\begin{array}{*{20}c} { - 3.1551} & {2.5099} & { - 0.0424} \\ \end{array} } \right],$$
$$K_{4} = \left[ {\begin{array}{*{20}c} { - 1.1744} & {0.9936} & { - 0.0168} \\ \end{array} } \right]$$

To demonstrate the performance of the proposed MPPT control approach, we apply a sudden variation of temperature or solar irradiation as shown in the Figs. 6 and 7.

Fig. 6
figure 6

Evolution of temperature

Full size image
Fig. 7
figure 7

Evolution of irradiation

Full size image

In this test, we have chosen five pairs of irradiation and temperature. We know that for each pair there exists only one optimal operating point which can be determined from the power–voltage characteristics of the PV array panel which is not always available for each pair (G,T). It is important to mention that it is not possible to know the appropriate coordinates of the ideal optimal operating point (V MPP, I MPP) for all pairs (G,T) as there are infinite number of pairs (G,T).

In the following Table 2, we give the ideal corresponding values (V MPPR, I MPPR) of operating point for each pair of temperature and irradiation, and the computed values (V MPP, I MPP) by our algorithm.

Table 2 Coordinate for each operating point
Full size table

The following Figs. 8, 9, 10, 11, 12, 13, 14, 15, and 16 show respectively the evolution of the V MPP voltage, the error of V MPP voltage, output voltage of converter, error of output voltage of converter, panel current, error of panel current delivered power, error of delivered power, and the duty cycle.

Fig. 8
figure 8

Evolution of output voltage

Full size image
Fig. 9
figure 9

Evolution of error output voltage

Full size image
Fig. 10
figure 10

Evolution of the V MPP voltage

Full size image
Fig. 11
figure 11

Evolution of error V MPP voltage

Full size image
Fig. 12
figure 12

Evolution of the inductance current

Full size image
Fig. 13
figure 13

Evolution of the error inductance current

Full size image
Fig. 14
figure 14

Evolution of the power

Full size image
Fig. 15
figure 15

Evolution of the error power

Full size image
Fig. 16
figure 16

Evolution of the duty cycle

Full size image

In Figs. 9, 10, 11, 12, 14, 15, and 16, we observe momentary peaks; they are due to sudden and significant change in temperature and irradiation. Actually, the changes in temperature and irradiation are not made this way as given in Figs. 6 and 7, but we have used it to show the performance of the proposed algorithm. It is clear that at the steady state, the errors tend toward zero and the state variables reach the reference one. Also, it is visible that the computed coordinates, of optimal operating point, based on the proposed algorithm, are almost the same as the ideal optimal operating point. This allows demonstrating the performance of the proposed algorithm.

6 Conclusion

In this paper, a new intelligent control strategy based on the Takagi–Sugeno-type fuzzy system has been proposed for the MPPT of a PV energy system. All the PV system has been modeled by T–S fuzzy system. Based on the measurement of temperature and irradiation, we deduce the coordinates of the desired optimal operating point which corresponds to the maximum power. The MPPT algorithm is based on a modified PDC method. The controller parameters have been computed based on the LMI. The stability of system has been proved based on Lyapunov approach. The simulation results show that the proposed algorithm tracks quickly the optimal operating point despite sudden variations of temperature and irradiation. It is worth noting that there are no oscillations in the various figures.