1 Introduction

The wave-piercing catamaran (WPC) is a high-performance ship. A WPC is capable of reaching navigation speeds of 35–40 knots due to its special hull structure, by which wave resistance is greatly reduced when the ship is sailing at high speed. However, it is reported (Castiglione et al. 2011) that WPCs will produce rocking motions in high sea states. These rocking motions may inflict negative effects on the seakeeping performance of fast catamarans, such as seasickness, speed loss, and low maneuverability. The wave-encounter frequency increases when the ship velocity increases. Consequently, the vertical oscillation (heave and pitch motion) becomes a serious problem for catamarans (Soars 1993). Improving the seakeeping performance of WPCs is essential to the control of ship motion. The most commonly used stabilizer for improving the vertical oscillation of ships is the passive fin under the bow, which generates lift and damping for the hull—the former slightly raises the ship’s bow and reduces the wet hull area, thereby reducing drag and lightening the wave impact, while the latter counteracts the heaving force and pitching moment. The passive fin can reduce heave/pitch motion. But some researches indicate that active fins may be more effective in improving vertical oscillations.

Thomas (1998) performed sea trials on a ride control system (RCS) based on a generalized predictive controller. Compared to experimental data, the control system was effective (Thomas 1998). They also studied the effect of slamming and whipping on the fatigue life of a high-speed catamaran (Thomas et al. 2006). Haywood et al. highlighted the importance of fluid mechanics emulation during RCS design. They introduced the design process of a controller and verified the anti-pitch effect of the RCS on a mini-type high-speed ship (Haywood et al. 1995). In a simulation of a trimaran, they proved that a controlled hydrofoil mounted on a high-speed ship can reduce the resistance and expand the navigation area (Haywood and Schaub 2006). Esteban et al. (2005), De la Cruz et al. (2004), Muñoz-Mansilla et al. (2009), and Giron-Sierra et al. (2002) studied seakeeping improvements for fast monohulled ferries using T-foils and trim tabs. After 10 years of research, they made significant achievements and proved the feasibility of genetic algorithm-based PID control of T-foils and trim tabs. A Japanese ferry company studied a 112-m wave yacht developed by the Australian company INCAT and collaborated with the Osaka Prefecture University in Japan to study the seaworthiness of the ship (Yoshiho et al. 2008). Qiang (2008) researched scheme optimization for the stabilizing fin and longitudinal motion control of a small waterplane area twin hull (SWATH) vehicle and obtained an optimized layout for the stabilizing fin and designed an effective H∞ controller for vertical motions.

For WPC, T-foils and trim tabs are chosen as the anti-vertical equipment. Although proportional-derivative (PD) control effects are stable, the system can be further improved based on modern intelligent control theory and strategy. The most significant impediments to performance are the uncertainties of the ship and external interference. These will affect the high-precision operation of the control system and even the instability of the system. They cannot be eliminated by improving the accuracy of the model, so the design of the system should accommodate the uncertainties of the model. This study focuses on the application of robust control in a high-speed WPC RCS. Aiming at the characteristics of a ship’s vertical motion control system—such as parameter uncertainty and external disturbance—it is easy to generate unmodeled dynamic uncertainties. An uncertain model of ship vertical motion is thereby established, and the controller is designed with an H∞ control method based on μ-synthesis theory. The RCS input consists of two angles: T-foil fin angle, αT, and trim tab angle, αF. A real-time decision-making system for these angles is proposed in this paper, and optimized by an improved genetic algorithm. Finally, using the catamaran as an example, a simulation analysis of the control effect is conducted.

2 Model of the coupled heave/pitch motion of a catamaran

The motion of a vessel can be divided into six degrees of freedom (DOF): heave, pitch, yaw, roll, surge, and sway. Among them, pitch and heave are vertical motions, which are usually coupled. Roll, sway, and yaw are lateral motions. Because the plates on both sides of a catamaran have the same shape, and the hull is symmetrical in the vertical section of the middle line, coupling usually does not occur between the transverse and vertical motions.

When analyzing the motions of a wave-piercing boat sailing in waves, it is generally necessary to use linear potential theory. At this time, the following assumptions are to be made: the catamaran is a rigid body; the waves acting on the catamaran have small steepness and amplitudes; the catamaran’s motion is slight, and the motions and forces satisfy the superposition principle; the error caused by the surface tension of water is not calculated, and the water is assumed to be incompressible; the underwater hull structure of the catamaran satisfies all the hydrodynamic parameters required by the strip theory. The frequency domain 6-DOF motion equations of a catamaran can be written as (Lloyd 1989)

$$(M + A_{kj}^{{}} )\ddot{\xi }_{j} + B_{kj} \dot{\xi } + C_{kj}^{{}} \xi_{k} = F_{jk} \;k,j = 1, \ldots ,6,$$
(1)

where \(\xi ,\dot{\xi } ,\ddot{\xi }\) represent the displacement, velocity, and acceleration of the vessel; the indices “k” and “j” represent the j-mode oscillatory motion caused by the k-direction force; M is the rigid body mass matrix; \(A,B\) are the added mass and damping matrix, respectively; C is the restoring matrix; and F is the excitation force.

For heave and pitch, the coupled 2-DOF equations are written as

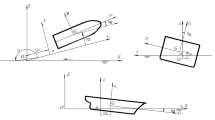
$$\begin{aligned} (M_{{}} + A_{33}^{{}} )\ddot{\xi }_{3} + C_{33}^{{}} \xi_{3} + B_{33}^{{}} \dot{\xi } + A_{35}^{{}} \ddot{\xi }_{5} + C_{35}^{{}} \xi_{5} + B_{35}^{{}} \dot{\xi }_{5} = F_{3} {\text{e}}^{{iw_{e} t}} \hfill \\ (I_{55} + A_{55}^{{}} )\ddot{\xi }_{5} + C_{55}^{{}} \xi_{5} + B_{55}^{{}} \dot{\xi }_{5} + A_{53}^{{}} \ddot{\xi }_{3} + C_{53}^{{}} \xi_{3} + B_{53}^{{}} \dot{\xi }_{3} = F_{5} {\text{e}}^{{iw_{e} t}} . \hfill \\ \end{aligned}$$
(2)

In this study, a 2.5D numerical method was used to predict the vertical motion performance of a high-speed catamaran. The parameters of the target ship are shown in Table 1 and Fig. 1 shows a body plan of the vessel.

Table 1 WPC principle parameters
Full size table
Fig. 1
figure 1

3D model of the WPC

Full size image

The hydrodynamic coefficients in the above equations are mainly related to three factors: the static buoyancy effect of the ship, the potential flow motion by the disturbance with free water surface, and the effect of the viscous flow on the naked hull.

The hydrodynamic coefficients that are related to the static buoyancy of ships can be easily obtained, while those caused by the potential flow are mainly calculated by the panel method (Faltinsen et al. 1991; Salvesen et al. 1970; Ma 2005; Ma et al. 2016). Calculations of the hydrodynamic coefficients produced by the viscosity and actuators are based on experimental data and the semi empirical. Finally, the calculation formula for the total hydrodynamic coefficient can be obtained by adding all three parts of the hydrodynamic coefficients. Only C in this equation is a constant; A and B depend on the wave-encounter frequency.

In this study, we used the WPC ship model described in Table 1 as an example and calculated its hydrodynamic coefficients at five different speeds using 2.5D theory. By this method, the wave-force model, the hydrodynamic coefficients were obtained. With those data, the force–motion model can be obtained.

Compared to the experimental data obtained by the Harbin Engineering University towing tank, the heave and pitch response amplitude operators (RAOs) at different wavelength–ship length ratios are shown in Fig. 2.

Fig. 2
figure 2

Heave and pitch RAOs at different speeds: a 1.952 m/s; b 2.469 m/s; c 3.086 m/s; d 3.704 m/s

Full size image

It can be seen from Fig. 2 that the numerical calculation results were in good agreement with those of the model tests. The variation trend of the hull motion–wavelength ratio was consistent with that of the model test. The average error of the prediction results for pitch and heave motion was between 8 and 10%, which is within the acceptable range. Therefore, this method can be used to predict the vertical motion of catamaran.

3 Model of the T-foil and trim tab

T-foils are significant in improving the seakeeping performance of WPCs. The T-foil is small relative to the ship’s hull, but—with a reasonable installation—increases the damping of the ship and its resistance to wave-induced forces and moments and reduces vertical motions. The vertical acceleration is usually produced by heave and pitch and affects the seaworthiness of the ship.

Tables 2 and 3 show the principle parameters of the T-foil and trim tab, respectively; Figs. 3 and 4 show the structure of the actuators (von Sicard 2002).

Table 2 T-foil principle parameters
Full size table
Table 3 Trim tab principle parameters
Full size table
Fig. 3
figure 3

Structure of T-foil with flap

Full size image
Fig. 4
figure 4

Structure of trim tab

Full size image

The motion of the trim tabs is limited upward, while the fin of the T-foil can move freely upward and downward.

The design of the actuators was based on the dimensions of the ship and hydraulic cylinder capabilities, and the relevant physics dictated the boundaries. The T-foil fins were trapezoidal with a 3-m span, 2.5 maximum chord, 13.5°/s maximum rotational speed, and ± 15° maximum angle. The fin flaps also had a 13.5°/s maximum rotational speed and ± 15° maximum angle. The trim tabs were rectangular with a 4.8-m span, 1.1 chord, 13.5°/s maximum rotational speed, and − 15° maximum angle. The actuators offer lift force at the price of drag and other degrading phenomena, such as cavitation and turbulence. As mentioned, the T-foil can produce both upward and downward forces, while the trim tab can only generate an upward force. As such, the T-foil plays the leading role in anti-vertical control, while the trim tab plays a supplementary role in anti-vertical control. The lift force is a function of the actuator angle α and the fluid speed U given by (Esteban et al. 2005)

$$\begin{aligned} F_{T} &= \frac{1}{2}\rho (A_{T} + A_{TF} )C_{LT} \left( {\alpha_{T} ,\alpha_{TF} } \right)U^{2} \\ F_{F} &= \frac{1}{2}\rho A_{F} C_{LF} (\alpha_{F} )U^{2} \\ M_{T} &= \frac{1}{2}l_{T} \rho A_{T} C_{LT} \left( {\alpha_{T} } \right)U^{2} \\ F_{F} &= \frac{1}{2}l_{F} \rho A_{F} C_{LF} (\alpha_{F} )U^{2} , \\ \end{aligned}$$
(3)

where lT and lF are the locations of the T-foil and trim tab on the ship, respectively; CLT and CLF are the lift coefficients of the T-foil and trim tab, respectively; αT is the T-foil fin angle of attack; αF is the trim tab angle of attack; AT is the area of the T-foil; AF is the area of trim tab; ρ is the fluid density; and U is the ship velocity. From the experiment, the relationships between the fin angles and the T-foil/trim tab lift coefficients are shown in Fig. 5. A sketch of the WPC with T-foils and trim tabs is shown in Fig. 6.

Fig. 5
figure 5

Relationships between fin angles and T-foil/trim tab lift coefficients

Full size image
Fig. 6
figure 6

Sketch of WPC with RCS

Full size image

The T-foil lift coefficient, CLT, is a two-variable function of αT and αTF and can be obtained by a regression analysis (Thomas 1998) using experimental data.

The stability of the WPC with RCS is herein defined as: after the WPC is disturbed by external or ride control forces, it deviates from its original equilibrium position; when the same force is canceled, the boat has the ability to return to its original equilibrium state. We obtained an inequality with data in this design:

$$l_{F} \rho A_{F} C_{LF} (\alpha_{F\hbox{max} } )U^{2} + l_{T} \rho A_{T} C_{LT} \left( {\alpha_{T\hbox{max} } } \right)U^{2} < \nabla \mathop {GM}\limits^{\_\_\_\_} \xi_{5\hbox{max} } ,$$

where αFmax, αTmax, and ξ5max are the maximum angles of the T-foil, trim tab, and pitch motion, respectively.

This means that the maximum moment generated by the RCS cannot exceed the restore moment of the ship with a maximum pitch angle—that is, the RCS will not affect the stability of the hull.

4 H∞ controller design

4.1 Linear fractional transformation model of the coupled heave/pitch motion of a catamaran with T-foils and trim tabs

For the parameter perturbation system, it is generally considered that the uncertainty is linear with the coefficient matrix of the state equation. However, the relationship between the parameters and coefficient matrix of the state equation is not linear in practical problems. Therefore, for general situations, the object model of the parametric perturbation system is described by linear fractional transformation (LFT).

The closed-loop control system is described as

$$\begin{aligned} (M_{{}} + A_{33}^{{}} )\ddot{\xi }_{3} + C_{33}^{{}} \xi_{3} + B_{33}^{{}} \dot{\xi } + A_{35}^{{}} \ddot{\xi }_{5} + C_{35}^{{}} \xi_{5} + B_{35}^{{}} \dot{\xi }_{5} = F_{3} {\text{e}}^{{iw_{e} t}} + F_{u} \hfill \\ (I_{55} + A_{55}^{{}} )\ddot{\xi }_{5} + C_{55}^{{}} \xi_{5} + B_{55}^{{}} \dot{\xi }_{5} + A_{53}^{{}} \ddot{\xi }_{3} + C_{53}^{{}} \xi_{3} + B_{53}^{{}} \dot{\xi }_{3} = F_{5} {\text{e}}^{{iw_{e} t}} + M_{u} . \hfill \\ \end{aligned}$$
(4)

The space representation of the equation is

$$\begin{aligned} \dot{x} \left( t \right) &= \left[ {\begin{array}{*{20}c} { - A_{1}^{ - 1} B_{1} } &\quad { - A_{1}^{ - 1} C_{1} } \\ {I_{2 \times 2} } &\quad {0_{2 \times 2} } \\ \end{array} } \right]x\left( t \right) + \left[ {\begin{array}{*{20}c} {A_{1}^{ - 1} } \\ {0_{2 \times 2} } \\ \end{array} } \right]F\left( t \right) + \left[ {\begin{array}{*{20}c} {A_{1}^{ - 1} } \\ {0_{2 \times 2} } \\ \end{array} } \right]u\left( t \right) \\ A_{1} &= \left[ {\begin{array}{*{20}c} {M + A_{33} } &\quad {A_{35} } \\ {A_{53} } &\quad {I_{5} + A_{33} } \\ \end{array} } \right] \\ B_{1} &= \left[ {\begin{array}{*{20}c} {B_{33} } &\quad {B_{35} } \\ {B_{53} } &\quad {B_{55} } \\ \end{array} } \right],C_{1} = \left[ {\begin{array}{*{20}c} {C_{33} } &\quad {C_{35} } \\ {C_{53} } &\quad {C_{55} } \\ \end{array} } \right] \\ y &= Cx\left( t \right) \\ \mathop {\dot{x} \left( t \right)}\limits^{.} &= \left[ {\begin{array}{*{20}c} {\mathop {\xi_{3} }\limits^{..} \left( t \right)} \\ {\mathop {\xi_{5} }\limits^{..} \left( t \right)} \\ {\mathop {\xi_{3} }\limits^{.} \left( t \right)} \\ {\mathop {\xi_{5} }\limits^{.} \left( t \right)} \\ \end{array} } \right],x\left( t \right) = \left[ {\begin{array}{*{20}c} {\mathop {\xi_{3} }\limits^{.} \left( t \right)} \\ {\mathop {\xi_{5} }\limits^{.} \left( t \right)} \\ {\mathop {\xi_{3} }\limits^{{}} \left( t \right)} \\ {\mathop {\xi_{5} }\limits^{{}} \left( t \right)} \\ \end{array} } \right] \\ F\left( t \right) &= \left[ {\begin{array}{*{20}c} {F_{3} } \\ {F_{5} } \\ \end{array} } \right],u\left( t \right) = \left[ {\begin{array}{*{20}c} {F_{u} } \\ {M_{u} } \\ \end{array} } \right], \\ \end{aligned}$$
(5)

where x is the state vector, y is the output vector, u is the input vector (total control forces and moments generated by T-foils and trim tabs and need to be allocation and optimization for T-foil and trim tab), F is the disturbance vector, and E and A are the coefficient matrix for the nominal system.

The state variables x1 generated by control and x2 generated by waves are separated as

$$\begin{aligned} \dot{x}_{1} \left( t \right) &= \left[ {\begin{array}{*{20}c} { - A_{1}^{ - 1} B_{1} } & { - A_{1}^{ - 1} C_{1} } \\ {I_{2 \times 2} } & {0_{2 \times 2} } \\ \end{array} } \right]x_{1} \left( t \right) + \left[ {\begin{array}{*{20}c} {A_{1}^{ - 1} } \\ {0_{2 \times 2} } \\ \end{array} } \right]u\left( t \right) \\ \dot{x}_{2} \left( t \right) &= \left[ {\begin{array}{*{20}c} { - A_{1}^{ - 1} B_{1} } & { - A_{1}^{ - 1} C_{1} } \\ {I_{2 \times 2} } & {0_{2 \times 2} } \\ \end{array} } \right]x_{2} \left( t \right) + \left[ {\begin{array}{*{20}c} {A_{1}^{ - 1} } \\ {0_{2 \times 2} } \\ \end{array} } \right]F\left( t \right) \\ y &= Cx_{1} \left( t \right) + Cx_{2} \left( t \right). \\ \end{aligned}$$
(6)

In this way, the output, y, of the system will become two parts: the first is the pitch and heave value caused by the stabilization device; the second is the pitch and heave value caused by wave interference.

Let \(\omega = Cx_{2} \left( t \right)\) be the interference. The system can then be transformed into a non-singular standard control problem

$$\begin{aligned} \dot{x}_{1} \left( t \right) &= \left[ {\begin{array}{*{20}c} { - A_{1}^{ - 1} B_{1} } & { - A_{1}^{ - 1} C_{1} } \\ {I_{2 \times 2} } & {0_{2 \times 2} } \\ \end{array} } \right]x_{1} \left( t \right) + \left[ {\begin{array}{*{20}c} {A_{1}^{ - 1} } \\ {0_{2 \times 2} } \\ \end{array} } \right]u\left( t \right) \\ y &= Cx_{1} \left( t \right) + \omega . \\ \end{aligned}$$
(7)

Let \(q_{1} = \left( {A_{33} ,A_{35} ,A_{53} ,A_{55} } \right)\), \(q_{2} = \left( {B_{33} ,B_{35} ,B_{53} ,B_{55} } \right)\), \(q = \left( {q_{1} ,q_{2} } \right)\). According to the state equation, \(M\left( q \right) = \left[ {\begin{array}{*{20}c} {A\left( q \right)} & {B\left( q \right)} \\ {C\left( q \right)} & {D\left( q \right)} \\ \end{array} } \right]\). Thus, by means of factorization, \(M\left( q \right) = F_{u} \left( {P_{M} ,\Delta } \right)\), where \(\Delta = {\text{diag}}\left( {A_{33} ,A_{35} ,A_{53} ,A_{55} ,B_{33} ,B_{35} ,B_{53} ,B_{55} } \right)\), and

$$P_{M} = \left[ {\begin{array}{*{20}c} {P_{M11} } & {P_{M12} } \\ {P_{M21} } & {P_{M22} } \\ \end{array} } \right].$$

The perturbation range of the model coefficients is set as 20%, and \(\Delta = F_{u} \left( {P_{\Delta } ,\Delta_{\delta } } \right)\) is obtained, where \(\Delta_{\delta } = {\text{diag}}\left( {\delta_{1} ,\delta_{2} ,\delta_{3} ,\delta_{4} ,\delta_{5} ,\delta_{6} ,\delta_{7} ,\delta_{8} } \right)\), \(\left| {\delta_{i} } \right| \le 1\), and \(P_{\Delta } = \left[ {\begin{array}{*{20}c} {P_{\Delta 11} } & {P_{\Delta 12} } \\ {P_{\Delta 21} } & {P_{\Delta 22} } \\ \end{array} } \right]\).

A standard LFR of M(q) can be obtained by star product calculation

$$M\left( \delta \right) = F_{u} \left( {P,\Delta_{\delta } } \right),$$
(8)

where

$$P = \left[ {\begin{array}{*{20}c} {F_{l} \left( {P_{\Delta } ,P_{M11} } \right)} & {P_{\Delta 12} \left( {I - P_{M11} P_{\Delta 22} } \right)^{ - 1} P_{M12} } \\ {P_{M21} \left( {I - P_{\Delta 22} P_{M11} } \right)^{ - 1} P_{\Delta 21} } & {F_{u} \left( {P_{M} ,P_{\Delta 22} } \right)} \\ \end{array} } \right].$$

4.2 Design of H∞ controller based on μ synthesis

A schematic diagram of the anti-vertical motion robust control system is shown in Fig. 7.

Fig. 7
figure 7

Schematic diagram of the anti-vertical motion robust control system

Full size image

In the figure, Wp is the performance weight function and Wr is the control weight function, which are determined according to the physical meaning after repeated selection.

Because the actual WPC vertical motion control system is highly complex and non-linear, the general method for controller design is to transform it into a linear system under the assumption of small disturbances. However, the disturbances of this system cannot be treated as small. Therefore, it is necessary to consider the effects of external disturbances, parameter uncertainties, and unmodeled dynamics when designing a controller based on linear systems. For this, μ synthesis is a powerful tool. It is not only mature in theory, but also less conservative (Doyle 2002).

The aim of μ synthesis is to find a controller, K, to minimize \(\mu_{\Delta } \left( M \right)\).

$$\mu_{\Delta } \left( M \right) = \frac{1}{{\hbox{min} \left\{ {\bar{ \sigma} \left( \Delta \right)\left| {\Delta \in \bar{\Delta} ,\det \left( {I - M\Delta } \right) = \left. 0 \right\}} \right.} \right.}},$$
(9)

where \(\bar{\sigma } \left( \Delta \right)\) is the maximum singular value of \(\Delta\). If we assume that M and \(\Delta\) are stable, when \(\Delta = 0\) and \(\det \left( {I - M\Delta } \right) = 1 \ne 0\), the system is stable. With the increase of \(\bar{\sigma } \left( \Delta \right)\), the continuity of the poles shows that there must be an initial value of \(\bar{\sigma} \left( \Delta \right) = 1/\mu_{\Delta } \left( M \right)\) such that \(\det \left( {I - M\Delta } \right) = 0\). It can be seen that the smaller the \(\mu_{\Delta } \left( M \right)\), the larger the permissible perturbation range of the system.

Subsequently, the design was conducted using the μ-toolbox in MATLAB, and the μ-synthesis controller of the system was obtained using D–K iteration.

5 Decision-making system for T-foil and trim tab

After obtaining the H∞ anti-vertical controller, the output forces and moments are generated by the two T-foils and two trim tabs. Based on Eq. (3), the RCS three angle inputs could be countless. As such, the optimization and allocation of the control angles are proposed in this section. The T-foil and the trim tab are independently. The energy consumption that RCS turn its fins with can be the optimization target. To achieve the minimum energy consumption, it is necessary to first establish the driving energy model.

The angles of the T-foil fin, flap, and trim tab at k and k + 1 instant are \(\alpha_{T} (k),\alpha_{F} (k)\) and \(\alpha_{T} (k + 1),\alpha_{F} (k + 1)\), respectively. The servo system driving moment of the T-foil and trim tab is MTT, MTFT, and MFT. The driving energy of the system from the k to k + 1 instant can be expressed as follows:

$$\Delta J\left( {k + 1} \right) = \int_{{\alpha_{T} (k)}}^{{\alpha_{T} (k + 1)}} {M_{TT} (\theta )} {\text{d}}\theta + \int_{{\alpha_{TF} (k)}}^{{\alpha_{TF} (k + 1)}} {M_{TFT} (\theta )} {\text{d}}\theta + \int_{{\alpha_{F} (k)}}^{{\alpha_{F} (k + 1)}} {M_{FT} (\theta )} {\text{d}}\theta .$$
(10)

When the T-foil fin turns, the servo system needs to overcome four moments: MTR generated by the hydrodynamic force to the fin axis, MTj produced by the fin speed changes, the recovery moment MTh, and the friction moment MTf. Based on the moment balance principle, the total moment MTT can be obtained

$$M_{TT} = - (M_{TR} + M_{Tj} + M_{Th} + M_{Tf} ).$$
(11)

MTR is the main part of MTT.

$$M_{TR} = - \frac{1}{2}\rho A_{T} \frac{{\partial C_{MT} }}{{\partial \alpha_{T} }}U^{2} \alpha_{T} l_{p} ,$$
(12)

where CMT is the T-foil torque coefficient and LP is the distance from the hydrodynamic point of action to the fin shaft.

$$M_{Tj} = - j\omega ,$$
(13)

where j is the moment of inertia of the fin around the shaft and ω is the angular acceleration.

$$M_{Th} = h\alpha_{T} ,$$
(14)

where h is the recovery coefficient of the fin. The friction moment MTf is 10% of the other three moments:

$$M_{{T{\text{f}}}} = 0.1 \times (M_{TR} + M_{Tj} + M_{Th} ).$$
(15)

Similarly, it is easy to find the driving moment of the trim tab, MFT:

$$M_{FT} = - (M_{FR} + M_{Fj} + M_{Fh} + M_{Ff} ),$$
(16)

where

$$M_{FR} = - \frac{1}{2}\rho A_{F} \frac{{\partial C_{FF} }}{{\partial \alpha_{F} }}U^{2} \alpha_{F} l_{q} ,$$
(17)
$$M_{Fj} = - j_{F} \omega_{F} ,$$
(18)
$$M_{Fh} = h_{F} \alpha_{F} ,$$
(19)
$$M_{{F{\text{f}}}} = 0.1 \times (M_{FR} + M_{Fj} + M_{Fh} ).$$
(20)

In summary, the expression of the system driving energy model is obtained

$$\begin{aligned} \Delta J\left( {k + 1} \right) &= \frac{1}{2}\rho A_{T} U^{2} l_{p} \int_{{\alpha_{T} (k)}}^{{\alpha_{T} (k + 1)}} {C_{MT} (\theta )} {\text{d}}\theta - (M_{Tj} + M_{Th} + M_{Tf} ) \times [\alpha_{T} (k + 1) - \alpha_{T} (k)] \\ & + \frac{1}{2}\rho A_{F} U^{2} l_{q} \int_{{\alpha_{F} (k)}}^{{\alpha_{F} (k + 1)}} {C_{MF} (\theta )} {\text{d}}\theta - (M_{Fj} + M_{Fh} + M_{Ff} ) \times [\alpha_{F} (k + 1) - \alpha_{F} (k)]. \\ \end{aligned}$$
(21)

To get the T-foil angle αT(k + 1) and trim tab angle αF(k + 1) with minimized energy consumption, we need to optimize (αT(k + 1), αF(k + 1)). The vertical righting force and moment calculated by the controller are F(k + 1) and M(k + 1), respectively, and the function of the distribution rules of the T-foil and trim tab is to determine αT(k + 1) and αF(k + 1) for the k + 1 instant. There are many methods for parameter optimization, such as the simplex and gradient methods. However, the simplex method easily falls to a local optimal solution, and the gradient method can only be used to continuous-differential performance index function; hence, they are not suitable for our case. According to the excellent convergence effect of the simple genetic algorithm (SGA) (Deb and Goldberg 1989; Michalewicz 1996) and the fast convergence speed of pattern search method (PSM), an improved genetic algorithm combining the two is proposed. The basic idea is to optimize the initial scheme using the genetic algorithm of adaptive crossover operator and mutation operator. The optimized scheme is then used as the initial scheme of the pattern search method for fast convergence optimization, so that the global optimal solution with the best effect and the highest efficiency can be obtained.

The genetic algorithm is generally applied to unconstrained optimization, so the penalty function P(X, γ) is used to transform the constrained problem into an unconstrained problem. The penalty function and corresponding augmented fitness function are shown in formula (24).

$$\begin{aligned} P\left( {X,\gamma } \right) &= \gamma \left\{ {\sum\limits_{i = 1}^{N} {\left| {h_{i} \left( X \right)} \right|} + \sum\limits_{j = 1}^{M} {\left| {\hbox{min} \left[ {0,g_{j} \left( X \right)} \right]} \right|} } \right\} \\ \hbox{min} F\left( {X,\gamma } \right) &= f\left( X \right) + P\left( {X,\gamma } \right). \\ \end{aligned}$$
(22)

In the formula, \(\gamma\) is the penalty factor, hi(X) is the partial function of equality, and gj(X) is the partial function of inequality.

The pattern search algorithm is a direct optimization method, which is easy to calculate and does not require solving of the reciprocal of the objective function. It uses local test information of search points to find the descending direction of the objective function and uses two search methods—exploratory movement and pattern movement—to reduce the number of iterations. Exploratory movement is in the advantageous direction of axial detection and mode movement is in the advantageous direction of accelerated movement. The optimization effect of the pattern search method is closely related to the convergence of the initial solution of the algorithm it relies on, and the judgment of the motor scheme is determined only by an increase or decrease of the value of a single optimization variable, rather than a change of the value of multiple optimization variables. As such, it is difficult for the pattern search method to achieve a global optimal solution. If the simple genetic algorithm is used to obtain the initial solution and the pattern search method is then applied, the optimization will be better.

For the minimum problem, the crossover operator, Pc, and mutation operator, Pv, of the simple genetic algorithm are

$$\begin{aligned} P_{c} &= \left\{ {\begin{array}{*{20}c} {P_{c1} ,_{{}} f' > f_{\text{avg}} } \\ {(f_{\hbox{min} } - f')P_{c1} /(f_{\hbox{min} } - f_{\text{avg}} ),_{{}} f' \le f_{\text{avg}} } \\ \end{array} } \right. \\ P_{v} &= \left\{ {\begin{array}{*{20}c} {P_{v1} ,_{{}} f' > f_{\text{avg}} } \\ {(f_{\hbox{min} } - f')P_{v1} /(f_{\hbox{min} } - f_{\text{avg}} ),_{{}} f' \le f_{\text{avg}} } \\ \end{array} } \right.. \\ \end{aligned}$$
(23)

In Formula (23), the values of Pc1 and Pv1 are between 0 and 1, fmin is the minimum fitness in the population, favg is the average fitness in each generation, f′ is the smaller fitness of two individuals to cross, and f is the fitness of individuals to mutate. For the constrained allocation optimization problem of the RCS, we can see from Formula (23) that the search speed of the genetic operators is slow in the initial stage of evolution, and it is easy to converge to the local optimal solution in the later stage of evolution, and the evolution algebra is independent of the crossover and mutation rates. Therefore, the adaptive crossover and mutation rates must be improved. The accuracy and efficiency of the crossover and mutation rates of the genetic algorithm depend on the fitness of the individual population. As such, when the fitness is high, to reduce the probability of gene damage, individuals will adopt smaller crossover and mutation rates. When the fitness is low, to ensure that the search area is enlarged, individuals will adopt larger crossover and mutation rates. Therefore, the operators of the improved genetic algorithm are as follows:

$$\begin{aligned} P_{c} &= \left\{ {\begin{array}{*{20}c} {P_{c1} ,_{{}} f' > f_{\text{avg}} } \\ {\frac{{P_{c1} - P_{c2} }}{2}\cos \left( {\frac{{f - f_{\text{avg}} }}{{f_{\hbox{min} } - f_{\text{avg}} }}\pi } \right) + \frac{{P_{c1} + P_{c2} }}{2},_{{}} f' \le f_{\text{avg}} } \\ \end{array} } \right. \\ P_{v} &= \left\{ {\begin{array}{*{20}c} {P_{v1} ,_{{}} f' > f_{\text{avg}} } \\ {\frac{{P_{v1} - P_{v2} }}{2}\cos \left( {\frac{{f - f_{\text{avg}} }}{{f_{\hbox{min} } - f_{\text{avg}} }}\pi } \right) + \frac{{P_{v1} + P_{v2} }}{2},_{{}} f' \le f_{\text{avg}} } \\ \end{array} } \right.. \\ \end{aligned}$$
(24)

The objective function is

$${ \hbox{min} }\Delta J\left( {k + 1} \right).$$
(25)

The constraint conditions are

$$\begin{aligned} &F_{u} ({\text{k}} + 1) = F_{T} (\alpha_{T} ,\alpha_{TF} ) + F_{F} (\alpha_{F} ) \hfill \\ &M_{u} ({\text{k}} + 1) = M_{T} (\alpha_{T} ,\alpha_{TF} ) + M_{F} (\alpha_{F} ) \hfill \\ &\left| {\alpha_{T} (k + 1)} \right| \le \alpha_{T\hbox{max} } \hfill \\ &0 \le \alpha_{F} (k + 1) \le \alpha_{F\hbox{max} } \hfill \\ &\left| {\frac{{\alpha_{T} (k + 1) - \alpha_{T} (k)}}{\Delta t}} \right| \le \dot{\alpha}_{T\hbox{max} } \hfill \\ &\left| {\frac{{\alpha_{F} (k + 1) - \alpha_{F} (k)}}{\Delta t}} \right| \le \dot{\alpha}_{F\hbox{max} } . \hfill \\ \end{aligned}$$
(26)

The population size was 100, Tstart was 0.4, and Tend was 0.8. The proportional selection, single point crossover, and basic bit mutation strategies were applied for optimization. The ratio value was 0.25, and the initial crossover and mutation values were 0.3 and 0.2, respectively. The termination condition was set as the average fitness difference of five successive generations less than 0.01. The optimization flowchart is shown in Fig. 8.

Fig. 8
figure 8

Flowchart of the optimization model

Full size image

6 Simulation and results

With the controller and optimization, a simulation of the intelligent robust control system for the T-foil/trim tab for the vertical motion of the ship was conducted. To reflect the advance of the algorithm, we added a normal PD controller in the simulation and compared it with the proposed controller. The simulated sea condition was as follows: the sea state number (SSN) was 5, the significant wave height was 5 m, the wave direction was 180°, and the ship speed was 4.497 m/s. Figure 9 shows a structure block diagram of the system principle. Figures 10 and 11 show the simulation results.

Fig. 9
figure 9

Structure block diagram of the system

Full size image
Fig. 10
figure 10

Simulation results of the vessel: a heave displacement; b pitch angle; c heave velocity; d pitch velocity; e heave acceleration; f pitch acceleration

Full size image
Fig. 11
figure 11

Angles of the T-foils and trim tabs (significant wave height = 3 m)

Full size image

Additionally, to conserve space, the experimental results of other voyage conditions are given in Table 4. The experiment was performed in the Harbin Engineering University College of Automation’s towing pool. We used four different SSNs and ship speeds to verify the feasibility of the controller.

Table 4 Vertical motion of WPC in irregular waves
Full size table

From the simulation results in Figs. 10 and 11, we can see that the RCS could not only stabilize the vertical motion, but also suppress the external disturbances and improve the vertical motion performance. With the proposed controller, the actuator reactions to the wave forces were evidently faster than those with the normal PID controller and had more reasonable allocation than with normal PID control. The pitch and heave motions were both reduced effectively with the proposed controller, and its anti-heave and anti-pitch effects were superior to those of the PID controller. The H∞ robust controller was used to design the joint control system for the T-foils and trim tabs. The uncertainty of the system model, the randomness of the disturbances, and the driving energy of the RCS were considered such that the anti-vertical motion effect and robust performance of the system could be obtained, and the control signals were well allocated to the RCS.

7 Conclusion

This paper presented a calculation method for the force/moment generated by T-foils and trim tabs and established an LFT model for WPC vertical motions with parameter perturbation. After obtaining the closed-loop model, an H∞ controller based on μ-synthesis theory was designed. Due to the multi-component composition of the RCS, a T-foil/trim tab decision-making system was established by an improved genetic algorithm with pattern search algorithm. From the simulation results, it has a good effect on improving the vertical motion performance of the ship and it can meet the robust performance requirements of the system.