Development of a Wave Energy Converter with Mechanical Power Take-Off via Supplementary Inertia Control

Abstract

To reduce environmental pollution, alternative renewable energy resources have been explored for decades. Wave energy has a high energy density, high utilization time and no fuel costs, so it is considered as the most promising alternative to the fossil fuel resources. The number of studies of wave energy converters (WECs) has rapidly increased. This paper proposes a new method to achieve the resonant behavior of a point absorber floating buoy type of WEC using a mechanical power take-off system. By using the inertia characteristics of a hydraulic flywheel accumulator-based electro-hydraulic actuator to change the corresponding supplementary mass of the floating buoy, the total mass of the buoy was close to a match with the relatively low frequency of the wave, so that the buoy was in resonance with the wave. The specifications of the hydraulic flywheel accumulator system were proposed and studied. The working principle was analyzed, and a mathematical model was then derived to investigate the system operation. An experimental set-up was implemented to validate the mathematical model. Numerical simulation using MATLAB/Simulink was done to evaluate the operation of the system.

1 Introduction

Wave energy resources have been exploited since 1973 due to the oil crisis. It is sustainable, persistent and significantly greater in power density (2–3 kW/m²) compared to solar (0.1–0.3 kW/m²) or wind [1,2,3,4,5] (about 0.5 kW/m²) energy. Thousands of patents for wave energy converters (WECs) have been recorded [6]. Wave energy utilization was examined by Falcão [7] to investigate the conception, construction and deployment into the sea of WEC prototypes. According to Iraide [8], the most suitable locations to exploit the global resource using WECs have been identified, and the different types of WECs along with their features and working principles have been described in detail. The point absorber type or oscillating body system has received more attention for use in converters because it is less complex and expensive than other technologies. Under a wave form, a device is forced to move up and down in a heaving motion. Then, the movement of this device can be transmitted into a rotary or linear motion of the generator to generate electricity [8].

There are four main methods used by the oscillating body system or point absorber type to capture wave energy in the heave mode of motion. The first method involves smart material. Dielectric polymers can be used to convert mechanical energy from ocean waves into electrical energy [9,10,11,12]. The second type involves a direct drive linear generator [13,14,15,16,17], which has a drawback of inducing high forces at low velocity compared to the rated speed of a generator. The third type involves the use of hydraulic power take-off (PTO), which has gained more attention due to its flexible connection in the larger systems [18,19,20,21,22]. In addition, the mechanical PTO types are an efficient low-cost method for extracting wind or wave energy [23,24,25,26,27,28,29]. Among them, the WECs using mechanical PTO have been developed for a long time due to their simple structure and scale down capacity, whereas many of the other current technologies have shown undesirable qualities such as low efficiency, complex structures and expensive devices. Moreover, the mechanical PTO could be a good candidate for using the exploitable wave energy resource in the nearshore whose characteristics have been analyzed in [30], which has benefits including low costs for maintenance and repair as well as electricity transmission lines to the shore. Several studies have been carried out on the point absorber types to indicate the performance and the power absorption of WEC; the problem of maximizing the extraction energy has been addressed either by suitably choosing the hydrodynamic and mechanical characteristics of the devices to achieve resonant motion or by applying specific control strategies to properly guide the motion of the floating buoy. The optimal movement of a buoy (maximal velocity and position) occurs when the natural frequency of the buoy is the same as the frequency of the incoming wave.

This paper studies the optimal control of a WEC using a mechanical PTO system. The WEC can absorb wave energy by converting the bidirectional motion of ocean waves into the one-way rotation of an electric generator with high efficiency. The hydrodynamics of the WEC was modeled in the time domain and validated by experiments which were carried out in the Research Institute of Small and Medium Shipbuilding under different regular waves. Based on the validated model, a supplementary mass was incorporated to change the natural frequency of the system. A conceptual design of the inertia supplementary device is presented. Here, a hydraulic flywheel accumulator-based electro-hydraulic actuator (HFW-EHA) was employed to adjust the equivalent inertia of the WEC. The natural frequency could be tuned to resonance with the wave frequencies. Then, the hydrodynamics of the WEC was controlled by adjusting the HFW-EHA. A fuzzy proportional–integral–derivative (PID) controller was designed to improve the working performance and the absorbed energy. The working stroke limitation of the buoy motion was constrained by the mechanical design [31]. Based on the physical limitations or mechanical limitations of the real device, the supplementary mass closed-loop control was applied to maximize the absorbed energy. Finally, a simulation was carried out in MATLAB/Simulink to investigate the performance of the WEC. Consequently, the performance of the WEC was improved to increase the capture width ratio and the overall efficiency significantly.

2 Configuration and Working Principle of Mechanical PTO WEC

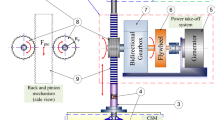
The general configuration of the mechanical PTO WEC is shown in Fig. 1, which consists of three main components: a hemispherical floating buoy, a bidirectional gearbox (BG) coupled with a flywheel, and an electric generator. The basic working principle has already been presented in the authors’ previous work [32].

Fig. 1

Configuration of the WEC with mechanical PTO

Under the water level of the incident wave, the floating buoy is forced to oscillate upward and downward. The floating buoy motion is transmitted directly to a main shaft. The main shaft is coupled with the BG by a rack and pinions. Two pinions are fixed to two input shafts coupled with two driving gears by one-way bearings. The two driving gears are engaged with the driven gear to convert bidirectional motion into one-way rotary motion. Then, the output shaft of the BG is fixed to the driven gear. Thus, the upward and downward motions of the floating buoy are transferred to the one-way rotation of the output shaft. Moreover, the rotational speed of the output shaft can be amplified by the gear ratio of the BG. The flywheel fixed to the output shaft is used to store and release rotational kinetic energy. It keeps the speed of the output shaft smooth although the input shafts work discontinuously. Finally, the electric generator driven by the speed of the output shaft generates the electricity. The output energy is then received by an external load or a storage device.

3 Optimum Control Strategy

According to Falnes [33], two conditions must be satisfied to optimize the absorbed power. These are the “resonance condition” or the “optimum phase control” and the “optimum load resistance” or “damping coefficient”. Optimum load resistance control has been applied easily due to a simple procedure. However, resonance condition control is more complicated due to the control mechanism. The inertia of the floating buoy structure must be tuned to values that bring the natural frequency of the device close to the wave spectrum frequencies (resonance behavior). The natural frequency of the buoy is commonly larger than the incident wave frequencies. Therefore, a neutral mass is added to increase the inertia of the buoy. Silvia [17] and Alves [34] tuned the natural frequency of the buoy to be in resonance with the given incident wave by adding a deeply submerged mass with enough neutral mass. The buoy can be split into two parts; one is close to the water surface to have good radiation capabilities, and the other one is submerged deep enough not to affect the radiated wave from the surface buoy. Vantorre [35] has controlled the inertia of the buoy by coupling it with a supplementary mass. Binh [36] has controlled the floating mass by pumping sea water into the chamber.

Previous works have contributed to the investigation of methods that can increase the inertia of the buoy. Although these methods are suitable in the laboratory, it is difficult to control supplementary mass under realistic conditions. When wave spectrum frequencies are changed, the inertia of the buoy also needs to be tuned to adapt the performance of the WEC device. Moreover, the stroke limitation of the buoy motion is set by its mechanical design. It can be claimed that the maximum useful stroke can absorb the maximum power. Therefore, the new control strategy is to maximize the absorbed power by applying mass control.

Figure 2 illustrates the working principle of WEC with controllable inertia in three dimensions (Fig. 2a) and in a diagram (Fig. 2b). The HFW-EHA system is employed to control the inertia of the buoy. Here, the rotational inertia of the HFW-EHA is translated into translational inertia (i.e., mass) by a rack and pinion mechanism. To change the inertia of the HFW-EHA, the oil volume inside the hydraulic flywheel is adjusted by controlling the EHA system. The HFW-EHA configuration is shown in Fig. 3. The special asymmetric design of the flywheel and piston offers a significant change in the amount of fluid volume inside it with respect to the change in the piston position. The EHA system, which is known as a power-shift system, is employed to control the position of the hydraulic flywheel piston directly by the oil flow rate. An electric motor drives the hydraulic pump, which supplies the oil flow rate throughout the rotary union [37] (as shown in Fig. 4) at both ends of the flywheel’s shaft to drive the piston in both left and right motions. For example, the inertia of the HFW is increased/decreased when the flow is supplied in the left/right hydraulic chamber. When the desired position is achieved, the EHA is turned off, and the hydraulic circuit locks the current axial positions of the piston, and then keeps the inertia constant without consuming energy.

Fig. 2

Configuration of the proposed WEC with controllable inertia hydraulic flywheel based electro-hydraulic actuator: 1—buoy; 2—main shaft; 3—generator; 4—conventional flywheel; 5—bidirectional gearbox; 6—piston; 7—controllable inertia hydraulic flywheel; 8—EHA system; 9—fluid lines; 10—rack and pinions; 11—rotary union; 12—frame

Fig. 3

HFW-EHA system: 1—rotary union; 2—hydraulic flywheel; 3—bearing; 4—pilot check valve; 5—relief valve; 6—check valve; 7—oil filter; 8—servo motor; 9—oil pump

Fig. 4

Rotary union component allows fluid to be pumped into chamber with rotating shaft [37]

4 Mathematical Model

4.1 Mechanical PTO WEC Model

As shown in the schematic diagram in Fig. 5, the analytical model is calculated according to hydrodynamic behavior and the resistive force from the PTO system. The motion of the floating buoy is usually simulated in the frequency domain using boundary integral equation methods; however, it is also modeled in time domain originally by Cummins [38]. The dynamics model of the WEC was discussed and verified in detail in the previous work [32]. The following equations briefly explain the system dynamic model.

Fig. 5

The schematic diagram for the dynamic model of the PTO

The forces acting on a point-absorbing WEC are due to both the forces from the external pressures on the buoy and the forces from the PTO [33]. The governing equation can be expressed as:

$$ m \cdot \ddot{z} = f_{h} + f_{pto} = f_{e} + f_{r} + f_{hs} + f_{v} + f_{pto} $$

(1)

where z is the buoy displacement in the vertical direction, m is the buoy mass, f_h is the hydrodynamic force acting on the buoy and f_pto is the force induced by the PTO, and f_h is the sum of the excitation force f_e, the radiation force f_r, the hydrostatic force f_hs and the viscous damping force f_v. These forces can be expressed as:

$$ f_{e} = f_{3} A\sin (\omega \,t + \alpha ) $$

(2a)

where f₃ and A are the excitation force and wave amplitude, respectively, and ω and α are the wave frequency and phase difference between the wave and the excitation force, respectively

$$ f_{r} = - m_{a} \ddot{z} - R_{r} \dot{z} $$

(2b)

where m_a is the added mass at infinite frequency and R_r is the radiation damping coefficient

$$ f_{hs} = - \rho gA_{b} z $$

(2c)

where ρ and A_b are the seawater density and the projected area of the buoy perpendicular to the direction of z, respectively, and g is the acceleration due to gravity

$$ f_{v} = - \frac{1}{2}\rho C_{d} A_{b} (\dot{z} - \dot{\eta })\left| {\dot{z} - \dot{\eta }} \right| $$

(2d)

where C_d is the viscous damping (drag) coefficient.

The hydrodynamic forces and coefficients can be calculated by using the WAMIT commercial software (version 7.0) [39].

The reactive force from the PTO system is comprised of two components and is presented in the following equation:

$$ f_{pto} = - f_{trans} - f_{f} $$

(3)

where f_trans is the transmission force and f_f is the friction force.

The transmission force can be calculated by:

$$ f_{trans} = \frac{{T_{g} }}{{r_{p} }}k_{g} $$

(4)

where r_p is the pinion radius and k_g is the gearbox ratio. The transmission torque or the resistive torque T_g is the torque induced from the generator. In this paper, a magneto-rheological (MR) brake was employed to simulate the resistive torque of the generator instead of using a real one so that we can adjust the load or driven torque easily in the experiment. The resistive torque is given in Eq. (5a) as a function of the angular velocity $\dot{\theta},$ the static friction torque T_br, the Coulomb friction torque T_c and the transition approximation coefficient c_vt, which is identified by the curve fitting the results of (5a) with measurement values [40]. Among them, the load resistive coefficient R_u is selected to apply torque control

$$ T_{g} = \left(T_{c} + (T_{br} - T_{c} )e^{{( - c_{vt} \left| {\dot{\theta }} \right|)}} \right)sign(\dot{\theta }) + R_{u} \dot{\theta } $$

(5a)

$$ \dot{\theta } = \frac{{\dot{z}}}{{r_{p} }}k_{g} . $$

(5b)

Then, the flywheel motion is obtained by using Newton’s second law for a rotational body. It can be assumed that the flywheel inertia represents the body inertia which includes that of the flywheel coupled with the generator. The rotational motion of the flywheel is determined by combining the driving torque and resistive torque in Eq. (6)

$$ T_{out} - T_{g} = I_{fl} \ddot{\theta } $$

(6a)

$$ I_{fl} = \frac{1}{2}m_{fl} r_{fl}^{2} . $$

(6b)

The driving torque T_out is induced by the hydrodynamic force on the floating buoy in both upward and downward movement, and it can be expressed as follows:

$$ T_{out} = T_{in} /k_{g} = \left| {f_{h} } \right| \times r_{p} $$

(7)

The second term on the right side of Eq. (3) represents the friction forces acting on the floating buoy which can be modeled using a method proposed by Armstrong [40]. Then, the friction force is rewritten in Eq. (8), where F_c is the Coulomb friction that opposes motion with a constant force at any velocity; F_br is the breakaway friction force, which is the sum of the Coulomb and static frictions at zero velocity; F_v is the viscous friction coefficient and c_vf is the transition approximation coefficient, which is used for the approximation of the transition between the static and the Coulomb frictions

$$ f_{f} = \left(F_{c} + (F_{br} - F_{c} )e^{{( - c_{vf} \left| {\dot{z}} \right|)}} \right)sign(\dot{z}) + F_{v} \dot{z}. $$

(8)

The generated power and energy are obtained in Eqs. (9) and (10) respectively

$$ P_{g} = T_{g} \dot{\theta } $$

(9)

$$ E_{g} = \int\limits_{0}^{t} {P_{g} } dt. $$

(10)

4.2 HFW-EHA Model

The instantaneous inertia of the hydraulic flywheel is the combination of the initial inertia (i.e., without fluid) and the inertia caused by the amount of fluid V_f pumped into the hydraulic chamber as shown in Fig. 6; this depends on the piston displacement x and is calculated by [41]:

$$ \begin{aligned} I_{fl} & = I_{0} + I_{add} = I_{0} + \frac{{\rho_{oil} V_{f} R^{2} }}{2}\, + \frac{{\rho_{oil} V_{r} r^{2} }}{2} \\ & = I_{0} + \frac{{\rho_{oil} x\pi R^{4} }}{2}\, + \frac{{\rho_{oil} (L - x)\pi r^{4} }}{2} \\ \end{aligned} $$

(11)

where V_r is the amount of fluid in the small rod chamber.

Fig. 6

Hydraulic flywheel device

Hence, determining the fluid inside the accumulator means determining the inertia of the flywheel. The volume of fluid depends on the position of the piston displacement. By using Newton’s second law and hydraulic-system principles, the dynamics of an EHA (Fig. 3) can be described by the following equations:

$$ \left\{ {\begin{array}{*{20}l} {\ddot{x} = \frac{1}{{m_{eq} }}\left( {A_{R} P_{R} - A_{r} P_{r} } \right)} \hfill \\ {P_{R} = \frac{{\beta_{e} }}{{V_{0R} + A_{R} x}}\left( {Q_{v1} - k_{leak} \left( {P_{R} - P_{r} } \right) - A_{R} \dot{x}} \right)} \hfill \\ {P_{r} = \frac{{\beta_{e} }}{{V_{0r} - A_{r} x}}\left( {Q_{v2} + k_{leak} \left( {P_{R} - P_{r} } \right) + A_{r} \dot{x}} \right)} \hfill \\ {Q_{v1} = D\omega_{m} - Q_{v3} + Q_{v5} } \hfill \\ {Q_{v2} = - D\omega_{m} - Q_{v4} + Q_{v6} } \hfill \\ \end{array} } \right. $$

(12)

where P_R and P_r are the pressure values of the two chambers, respectively; m_eq is the equivalent mass; A_R and A_r are the actuating areas; V_0R and V_0r are the original total volumes of the two chambers, respectively; D is the displacement of the pump; ω_m is the speed of the servo-driven pump system; k_leak is the leakage constant; β_e is the Bulk modulus and Q_vi (i = 1, …, 6) are the flow rates from the i supplemental-check valves or relief valves, respectively.

Thus, the piston position is adjusted by the speed of the bidirectional pump driven by a direct current (DC) servo motor. Given the desired trajectory x_d, the objective is the determination of the speed command for the DC servo motor ω_m, in order to control the track of the output position x to be as close as possible to x_d. The development of the position controller is described in the following section.

5 Control Design

Reacting to the given incident wave and specifications of the PTO system, the supplementary inertia was determined to bring the natural frequency close or far from the wave spectrum. A desired mass closed-loop control was applied to improve the performance by changing the hydrodynamics of the WEC device. Figure 7 illustrates the schematic control diagram for mass closed-loop control. Once wave profiles were determined, the hydrodynamic parameters were pre-computed by the WAMIT software. An analytical model was built to investigate the buoy elevation. Then, the responded stroke was obtained by measuring in the haft of the cycle and compared to the stroke limitation. Mass closed-loop control with respect to maximum stroke (not higher than the limit value) was applied to generate the required supplementary inertia. Here, the relative error between the desired mass and the actual one was sent to the fuzzy PID controller. The controller sent the output signal to generate the required inertia from the HFW. The supplementary mass was calculated and sent to the analytical model.

Fig. 7

Schematic control diagram for supplementary mass closed-loop control

The PID controller is well known due to its simple structure and easy design [42]. However, conventional PID controllers cannot work well over a wide range of operating conditions due to the fixed gains used. To widen the working conditions, a fuzzy PID controller was applied to control the buoy mass or supplementary inertia. The control signal is expressed in the time domain as:

$$ u\left( t \right) = K_{P} e\left( t \right) + K_{I} \int\limits_{0}^{t} {e\left( t \right)dt + K_{D} \frac{de\left( t \right)}{dt}} $$

(13)

where e(t) is the error between the desired set point and the output, de(t) is the derivation of error, u(t) is the control signal used to control the DC servo motor speed ω_m, K_P is the proportional gain, K_I is the integral gain and K_D is the derivative gain.

The PID parameters were tuned by fuzzy inferences which provided a nonlinear mapping from the error and derivation of error to the PID parameters. These parameters were changed within the initial parameter boundaries

$$ K_{n} \left( t \right) = K_{n{\mathrm{min}} } + U_{n} \left( t \right)\Delta K_{n} ,\,\,U_{n} \left( t \right) \in \left[ {0,1} \right] $$

(14)

where n is a notation of P, I or D; U_n(t) is a parameter obtained from the fuzzy n tuner; ΔK_n = K_nmax–K_nmin is the allowable deviation of K_n and K_nmin and K_nmax are the minimum and maximum values, respectively, of the K_n determined from experiments.

For the fuzzy designs, triangular membership functions (MFs) were used to represent the partitions of fuzzy inputs and outputs. A fuzzy controller was applied using local inferences. In this study, the fuzzy reasoning results of outputs were gained by aggregation operations of fuzzy sets of inputs and designed fuzzy rules, where the max–min aggregation method and centroid defuzzification method were used. The fuzzy inference system was established based on fuzzy set theory, so it was first necessary to carry out the fuzzification of the input and output variables, which transformed the input and output data into proper semantic values. The inputs were chosen as absolute scales of the system control error |e(t)| and its derivative |de(t)|, which were forced into the same range from 0 to 1 by using suitable scaling factors chosen from the system specifications. Then, the fuzzy range of inputs and outputs was separated into five semantic variables, and the corresponding fuzzy subsets were [SS; MS; MM; BM; BB]. Here, SS is small; MS is medium small; MM is medium; BM is medium big, and BB is big. The input MFs had uniform shapes, and their centroids were positioned at the same intervals as in Fig. 8a, while the output MFs were set at the same intervals as in Fig. 8b. Based on the above fuzzy sets of the input and output variables, rules for computing the fuzzy reasoning results, U_n, were established as in Table 1.

Fig. 8

MF design for the inputs and output of the fuzzy controller

Table 1 Rule table of the fuzzy controller

For each of the fuzzy P/I/D input variables, the MFs can be expressed as follows

$$ f_{j} \left( {x_{i} } \right) = \left\{ {\begin{array}{*{20}l} {1 + \frac{{\left( {x_{i} - a_{ij} } \right)}}{{b_{ji}^{ - } }}} \hfill & {IF:\,\left( { - b_{ij}^{ - } } \right) \le \left( {x_{i} - a_{ij} } \right) \le 0} \hfill \\ {1 - \frac{{\left( {x_{i} - a_{ij} } \right)}}{{b_{ij}^{ + } }}} \hfill & {IF:0 \le \left( {x_{i} - a_{ij} } \right) \le \left( {b_{ij}^{ + } } \right)} \hfill \\ 0 \hfill & {Otherwises} \hfill \\ {( {i = 1,2;}} \hfill & {j = 1,2, \ldots ,N}) \hfill \\ \end{array} } \right. $$

(15)

where x_i is an input value (x₁ ≡ |e(t)|; x₂ ≡ |de(t)|) and a_ij, b ⁻ _ij , b ⁺ _ij , and N are the centroid, left half-width and right half-width of the jth MF and the MF number of the ith input, respectively.

Each of the fuzzy P, I and D tuners has one output: U_fP, U_fI and U_fD, respectively, which can be computed corresponding to a pair of the input values

$$ U_{fn} = \frac{{\sum\nolimits_{m = 1}^{M} {mf\left( {w_{m} } \right)w_{m} } }}{{\sum\nolimits_{m = 1}^{M} {mf\left( {w_{m} } \right)} }} $$

(16)

where w_m is the weight of the control output, M is the MF number and mf (w_m) is the fuzzy output function given by

$$ mf\left( {w_{m} } \right) = \sum\limits_{j,k} {mf_{jk} \left( {w_{m} } \right)} $$

(17)

where mf_jk (w_m) is the consequent fuzzy output function when the first and second inputs are in the jth and kth classes, respectively.

$$ mf_{jk} \left( {w_{m} } \right) = \delta_{jk} \mu_{jk} $$

(18)

where δ_jk is a factor activated when inputs x₁ and x₂ are in classes jth and kth and μ_jk is the height of the consequent fuzzy function obtained from the input classes jth and kth

$$ \mu_{jk} = \hbox{min} \left[ {f_{j} \left( {x_{1} } \right),f_{k} \left( {x_{2} } \right)} \right] $$

(19)

The fuzzy output U_fn contains single output values that are initially set at the same intervals. Consequently, factor U_n can be obtained from U_fn using the sigmoid activation function

$$ U_{n} = \frac{1}{{1 + e^{{ - U_{fn} }} }},\quad U_{n} \in \left( {0,1} \right) $$

(20)

By using Eqs. (13)–(20), the main control signal, u(t), can be obtained.

6 Model Validation

The validation tests were performed to verify the modeling of the mechanical PTO WEC under different regular waves. A prototype system was designed, fabricated and assembled in the Research Institute of Small and Medium Shipbuilding. A complete layout of the test bench is described in Fig. 9. It consisted of a buoy, the PTO system and the peripheral interface devices. As shown in Fig. 10, the PTO system consisted of an MR brake, a torque transducer and a BG. The MR brake was closed-loop controlled to simulate the torque induced by an electric generator. The induced torque and speed of the MR brake were measured continuously by the torque transducer along with the speed sensor MP-981. A thrust shaft fixed to the buoy was employed to transmit the power from the buoy to the BG via the rack and pinion gear power transmission. Consequently, the translational motion of the rack was converted to the one-way rotary motion of the flywheel. A simpler testbench can be performed as follow Lim [43] or Lee [44].

Fig. 9

Layout of the tests in the wave tank

Fig. 10

Configuration of the PTO system

To carry out the tests, some setting parameters of the working conditions and specifications of the device were required to be defined in advance. Three different regular waves were generated by the wave simulator system. Their different amplitudes and frequencies are shown in Table 2.

Table 2 Setting working conditions for simulation

Specifications of the PTO system are given in Table 3. These parameters were obtained by direct measurement. Based on the working conditions and specifications of the PTO system, the hydrodynamic parameters were obtained using the WAMIT software and were plotted in Fig. 11. The hydrodynamic parameters including the added mass, the radiation damping, the excitation coefficient and the phase angle are plotted in the frequency domain in the range of 2.0–3.5 rad/s.

Table 3 Specifications of PTO system

Fig. 11

The hydrodynamic parameters were obtained by the WAMIT software

For each test, the wave and the buoy elevation were measured for comparison with the simulation results. The generating torque and speed of the generator were also recorded to calculate the generated power. It can be seen in Fig. 12 that there was reasonable agreement between the test results and the simulation model in all cases. For each case, the best resistive load coefficient, which absorbs the largest generated energy, was selected for the comparison. Although there was some disturbance at the peak of torque and speed due to imprecision in the mechanical structure, the measured average energy is in good agreement with that of the model. Imprecision in the mechanical structure can be due to some handmade parts. Some flashbacks occurred in locations where the relative speed direction of the transmitted parts has changed, which may change the friction behavior and the twisted torque. Also, the nonlinear characteristics of hydrodynamic behavior were not incorporated into the analytical model. Therefore, the most significant differences can be found by locating the largest or smallest value compared to that of the model in these cases. However, mean values are approximated with the model. In general, the model can be validated based on reasonable agreement between the simulation and test results.

Fig. 12

Elevation comparisons between simulation and test results for three wave cases

7 Simulation Results and Discussion

Simulations were carried out to compare the performance of the WEC device with and without the HFW-EHA inertia/mass-controlled under regular wave case 2, which had absorbed the highest energy among the three wave tests. The result is plotted in Fig. 13. The elevations of the buoy increased during the first 20–30 s (transient state) to calculate the wave parameters and to reach the desired mass; after that, it was stable (steady state) for all of the remaining time. The response torque and speed also increased, and then the output energy was increased compared to the uncontrolled case. Compared with the working time of the system, the required time in the transient state was acceptable.

Fig. 13

Response comparisons between uncontrolled and mass-controlled systems in regular wave case 2

Moreover, simulations under irregular waves were performed to demonstrate the applicability of the proposed system for real sea conditions. Here, the wave profile was developed using the Pierson and Moskowitz wave spectral formulation for fully developed wind-generated seas from analyses of wave spectra in the North Atlantic Ocean [33] as:

$$ S(\omega ) = A\omega^{ - 5} \exp ( - B\omega^{ - 4} ) $$

(21)

where A = 8.1 × 10⁻³ g², $B = 0.74\left( {\frac{g}{{V_{19.4} }}} \right)^{4}$ and V_19.4 is the wind speed at the height of 19.4 m.

The wind speed at 3 m/s with respect to an angular frequency range of 1.5–4.0 rad/s was chosen to generate the random incident wave field. The irregular wave covered all of the three wave cases tested in Table 2. The wave profile is plotted in the top of Fig. 14, and the simulated responses of the system are presented in the same figure.

Fig. 14

Response comparisons between uncontrolled and mass-controlled systems in irregular wave case

Table 4 shows the energy absorption and comparison between uncontrolled and mass-controlled cases. The absorbed energy in the mass-controlled case was larger than that of the uncontrolled case, because the natural frequency of the buoy was tuned to be close to the wave frequency. Consequently, the buoy elevations were larger, and the buoy mass reached the desired value. Finally, the output energy increased about 18% compared to that of the uncontrolled system in regular wave case and about 12% in the irregular case.

Table 4 Comparisons of energy absorption

8 Conclusions

This paper developed an innovative WEC for the extraction of ocean wave energy. A basic conceptual design of a WEC using a mechanical PTO was presented. A combined hydrodynamic and mechanical simulation of the WEC based on the time domain using pre-computed hydrodynamic coefficients was used to investigate the system operation. The analytical model was validated by verification tests under different regular wave conditions. Next, an optimum control strategy was proposed to improve the response of the WEC system under realistic conditions.

Supplementary inertia closed-loop control using a fuzzy PID controller was applied to increase the absorbed power. The proposition of the HFW-EHA was presented to change the inertia of the buoy. Consequently, the energy generation increased about 18% compared to the best working conditions of the uncontrolled system. The proposed WEC was designed for laboratory testing. A simple structure to reduce the cost and to install easily was chosen. In the near future, a complete system will be built up and verified under real sea conditions. The rack and pinion mechanism will be replaced by a cable and timing belt. With this new design, the buoy can capture energy in both heave and surge modes. Moreover, the shear problem can be solved. This new system also includes a safety mechanism. Future works involve setting up bench tests for verification of the proposed model in a water tank. Then, a model predictive control for irregular waves can also be studied to investigate the WEC’s adaptability with realistic requirements.