An improved updated Lagrangian SPH method for structural modelling

Abstract

This paper presents a set of novel refined schemes to enhance the accuracy and stability of the updated Lagrangian SPH (ULSPH) for structural modelling. The original ULSPH structure model was first proposed by Gray et al. (Comput Methods Appl Mech Eng 190:6641–6662, 2001) and has been utilised for a wide range of structural analyses including metal, soil, rubber, ice, etc., although the model often faces several drawbacks including unphysical numerical damping, high-frequency noise in reproduced stress fields, presence of several artificial terms requiring ad hoc tunings and numerical instability in the presence of tensile stresses. In these regards, this study presents a set of enhanced schemes corresponding to (1) consistency correction on discretisation schemes for differential operators, (2) a numerical diffusive term incorporated in the continuity or the density rate equation, (3) tuning-free stabilising term based on Riemann solution and (4) careful control/switch of stress divergence differential operator model under tensile stresses. Qualitative/quantitative validations are conducted through several well-known benchmark tests.

Graphical abstract

1 Introductions

Particle methods [1] are potentially robust computational methods that have been drawing great interest these days. Particle methods have Lagrangian and meshfree features that lead to advantages in simulating problems characterised by highly deformed interfaces including free surfaces, large material deformations or fractures often appearing in a variety of engineering fields, as summarised in some review papers [2,3,4,5]. Smoothed particle hydrodynamics (SPH) is one of the most famous particle methods, which was originally proposed for astrophysical applications by Gingold and Monaghan [6] and Lucy [7]. Since its proposal, the SPH has been applied to various engineering fields including fluid mechanics and structural analysis.

Due to its Lagrangian meshfree nature, the SPH method has been often adopted for simulations of free surface fluid flows. The first application of SPH towards free surface fluid flows was conducted by Monaghan [8] with weakly compressible SPH (WCSPH) method [9] along with stabilisation by an artificial viscosity (AV) term [10]. For reliable simulations, continuous efforts have been devoted to enhancement of stability and accuracy of SPH for fluid modelling. Specifically, the δ-SPH method [11, 12] is one of the most popular and effective enhanced schemes in the WCSPH framework. This scheme can result in effective suppression of high-frequency acoustic noise and reliable reproduction of smooth pressure field through incorporation of a numerical density diffusion term (δ-term) in the continuity equation. The other branch of improved WCSPH fluid model is the incorporation of Riemann solution in the WCSPH context, resulting in the Riemann SPH method [13, 14]. The Riemann SPH improves accuracy and stability of WCSPH by providing theoretically minimum required dissipation on the system based on the solution of Riemann problem.

In general, SPH fluid models experience a so-called tensile instability. Indeed, in fluid models where the stress tensor is isotropic and the pressure is a function of density, i.e. those that incorporate a polytropic equation of state, the Hessian operator in continuum level fails to satisfy the stability condition in the presence of tension [15]. In addition, in discrete level, utilisation of an Eulerian kernel with respect to current configuration for the estimation of kinematics of Lagrangian moving particles would also trigger instabilities in tension [16]. Moreover, the Lagrangian nature of particle motions would likely form anisotropic irregular particle distributions. A lot of efforts have been devoted to tackling these challenges and a number of enhanced schemes have been proposed, including an artificial stress (AS) term [17], a tensile instability control (TIC) scheme for fluids [18], the so-called XSPH [19] and the particle shifting scheme [20]. As a result, the δ-SPH and the Riemann SPH fluid models together with enhanced schemes have been successfully applied to a wide range of hydrodynamic problems accompanied by free surfaces (e.g. [21, 22]).

Another important category of SPH applications corresponds to structural analyses. The advantage of SPH method in handling complex boundary conditions has been proven to be effective towards modelling of complex shaped structures and their deformations (e.g. [23,24,25]). Considering the application of SPH to large deformations including topological changes and material fracture, the updated Lagrangian SPH (ULSPH) formulation would be justifiable, resulting in the so-called ULSPH structure models (e.g. [26]).

Regarding the ULSPH structure model developments, the model by Gray et al. [1] is the one of the most widely adopted models as found in the literature (e.g. [27,28,29,30,31,32,33,34]). Their model is configured in the updated Lagrangian framework with incorporation of numerical stabilisers including XSPH, artificial viscosity and artificial stress terms. Although this model has been shown to provide relatively fine results in a wide range of applications [27,28,29,30,31,32,33,34] and has been directly adopted in several recent works [29, 31,32,33], there are several serious issues that require careful enhancements. These issues include pseudo unphysical decrease of material stiffness or increase of damping [35], inclusion of several tuning parameters in incorporated artificial stabilisers [35] and amplification of spurious high-frequency noise in stress field due to the rank deficiency [36, 37] and the explicit solution process of the stress tensor.

With regard to the artificial stabilisers in the ULSPH framework, their incorporation is mainly linked with rank deficiency [36, 37] due to the collocated nature of SPH approximations (as field variables and their derivatives are calculated at the same calculation points) as well as the so-called tensile instability [15, 16] or more precisely unphysical modes in tensile stress states due to growth of small-scale perturbations in particle motions. To be more specific, an artificial viscous term is often applied to stabilise the momentum equation and an artificial stress term is utilised to minimise the presence of unphysical modes in tensile stress states. With regard to the unphysical modes in tensile stress states, the instability may arise at the continuum level where a hypoelastic model is used for moderate or large strains or for problems that include physical instabilities. Even if the hypoelastic model is stable within the considered range of strains, from the SPH discretisation standpoint, the use of an Eulerian kernel function at the current nodal positions may trigger tensile instabilities. This is because the discretisation of tangent stiffness matrix depends on the current nodal positions which may potentially lead to negative eigenvalues [15, 38]. The so-called TLSPH (total Lagrangian SPH) [39, 40] or updated reference Lagrangian SPH [41, 42] for structural modelling are free from tensile instability because the kernel and its derivative remain constant with respect to a constant reference configuration.

Apart from the issue of artificial stabilisers, the ULSPH model of Gray et al. [1] faces two more challenges corresponding to incompleteness of approximations [43, 44] and pressure instability due to an explicit solution of an equation of state from approximated densities at discrete calculation points. Hence, enhanced schemes can be proposed with respect to (1) incompleteness, (2) pressure instability, (3) rank deficiency and (4) unphysical modes in tensile stress states or tensile instability.

Regarding the issue of incompleteness, consistency-related corrections [43, 44] can be effectively utilised to improve the completeness or the reproducibility of kernel-based approximations of the gradient operator models. As for the issue of pressure instability, conservative diffusive terms can be incorporated in the continuity or the density rate equation to enhance the continuity and smoothness of the density and thus, the pressure field. In this regard, incorporation of the δ-SPH scheme [11, 12], which is a second-order accurate scheme in space, is considered as a proper choice.

As for the issue of rank deficiency, a relevant approach corresponds to the incorporation of stress points [45]. This approach can stabilise the simulations by incorporating a set of additional computational points referred to as stress points so that field variables and their derivatives will be calculated at separate computational points, resulting in staggered integrations rather than collocated ones. However, this approach leads to a complex coding process and increase of computational cost. In addition, calculation of optimum positions of stress points, especially in case of complex structural geometries, would bring an additional challenge. Another approach corresponds to inclusion of a supplementary set of conservation laws for geometric strain measures along with appropriate involutions [41, 46,47,48]. This approach provides notably accurate, stable and efficient results, however, along with an increased level of complexity in coding and implementation. In order to deal with the issue of rank deficiency in a simple yet effective manner, a possible approach is to replace the artificial viscosity term by a Riemann-based diffusive term in the momentum equation, in a manner consistent with the δ-term in the density rate equation, as the δ-term can be closely linked to a Riemann term. Accordingly, the new Riemann-based stabilisation term would be free of tuning parameters and effectively stabilise the discretised momentum equation.

As for the challenge corresponding to unphysical modes in tensile stress states, the artificial stress term proposed by Gray et al. [1] was set through adding tuning-required repulsive interparticle forces if the principal stresses were tensile. Instead of using tuning-required artificial stresses, we may simply incorporate a tensile instability control or a switch analogous to that incorporated in the context of SPH for fluids referred to as TIC (tensile instability control) [18]. In such a case, in evaluation of divergence of stress tensor, for tensile principal stresses, instead of use of an antisymmetric and momentum-conservative scheme, we utilise a Taylor-series consistent scheme to recover the reproducibility, attaining a more accurate approximation of kinematics (accelerations) and thus, minimising the unphysical perturbations prone to be induced and intensified in tensile stress states.

This study aims at showing step-by-step enhancements of stability and accuracy for the ULSPH structure model by focusing on the aspects of (i) incompleteness, (ii) pressure instability, (iii) rank deficiency and (iv) tensile instability. Accordingly, four enhanced schemes are proposed for the ULSPH structure model: (1) incorporation of a corrective matrix in discretisations related to divergence of velocity and stress, as well as velocity gradient tensor, (2) a second-order numerical diffusive term (δ-term) incorporated in the continuity or the density rate equation for stabilisation of pressure field, (3) a tuning-free second-order Riemann term (in place of the tuning-required artificial viscosity scheme) for stabilisation of the discretised momentum equation and (4) a tensile instability control scheme (in place of the tuning-required artificial stress term) to mitigate the issue of tensile instability. The accuracy and robustness of the proposed schemes are investigated and validated by reproducing some benchmark tests, namely dynamic response of a free oscillating cantilever plate [1], high speed rotation of an elastic square plate [49], wave propagation in a homogeneous elastic cable [50], collision of two homogeneous elastic rings [1], elastic wave propagation in heterogeneous cable [27, 51, 52] and collision of two composite elastic rings.

2 Numerical method

2.1 Principal equations for the structure model

The principal equations of the structure model correspond to the continuity and Cauchy’s equations [1], which are described as:

$$ \frac{{{\text{D}}\rho }}{{{\text{D}}t}} = - \rho \nabla \cdot {\varvec{u}} $$

(1)

$$ \frac{{{\text{D}}{\varvec{u}}}}{{{\text{D}}t}} = \frac{1}{\rho }\nabla \cdot {{\varvec{\sigma}}} $$

(2)

where u denotes velocity vector, ρ signifies density, t represents time, and σ implies the Cauchy’s stress tensor; the operator $\nabla$ represents the gradient evaluated at the current configuration. Note that in Eq. (2), the body force in the linear momentum equation has been neglected due to the absence of body force in all the benchmark tests performed in this paper.

In the ULSPH structure model, the stress tensor ${\varvec{\sigma}}$ is decomposed into spherical and deviatoric parts, i.e.

$$ {{\varvec{\sigma}}} = - p{\varvec{I}} + {\varvec{S}} $$

(3)

$$ p = - \left( {\lambda + \frac{2}{3}\mu } \right){\text{tr}}\left( {{\varvec{\varepsilon}}} \right);\quad {\varvec{S}} = 2\mu \left( {{{\varvec{\varepsilon}}} - \frac{1}{3}{\text{tr}}\left( {{\varvec{\varepsilon}}} \right){\varvec{I}}} \right) $$

(4)

where p represents the pressure (the spherical part of the stress tensor), S denotes the deviatoric part of the stress tensor, ε signifies the strain tensor, I denotes the unit tensor, and λ and μ indicate the Lame’s constants.

The pressure can be linked to the density through the EOS (equation of state), which can be written as:

$$ p = c_{0}^{2} \left( {\rho - \rho_{0}^{{}} } \right);\quad c_{0}^{{}} = \sqrt {\frac{K}{{\rho_{0}^{{}} }}} ;\quad K = \lambda + \frac{2}{3}\mu $$

(5)

where c₀ is speed of sound, ρ₀ denotes the reference density, and K represents the bulk modulus. Density is evolved in time through application of the continuity equation (Eq. 1).

The deviatoric part of the stress tensor would be updated in time as an incremental form of the presented Hooke’s law with the use of Jaumann stress rate, i.e.

$$ \frac{{{\text{D}}{\varvec{S}}}}{{{\text{D}}t}} = 2\mu \left( {{\dot{\varvec{\varepsilon }}} - \frac{1}{3}{\text{tr}}\left( {{\dot{\varvec{\varepsilon }}}} \right){\varvec{I}}} \right) + {{\varvec{\varOmega}}} \cdot {\varvec{S}} - {\varvec{S}} \cdot {{\varvec{\varOmega}}} $$

(6)

$$ {\dot{\varvec{\varepsilon }}} = \frac{1}{2}\left( {\nabla {\varvec{u}} + \left( {\nabla {\varvec{u}}} \right)^{{\text{T}}} } \right);\quad {{\varvec{\varOmega}}} = \frac{1}{2}\left( {\nabla {\varvec{u}} - \left( {\nabla {\varvec{u}}} \right)^{{\text{T}}} } \right) $$

(7)

where ${\dot{\varvec{\varepsilon }}}$ is the strain rate tensor and ${{\varvec{\varOmega}}}$ signifies the spin tensor; the superscript T stands for the transpose of a tensor.

2.2 Updated Lagrangian SPH (ULSPH) structure model

The principal equations presented in Sect. 2.1 are discretised and solved based on the updated Lagrangian SPH (ULSPH) framework. The ULSPH structure model was originally developed by Gray et al. [1]. The governing equations are discretised as follows:

$$ \frac{{{\text{D}}\rho_{i}^{{}} }}{{{\text{D}}t}} = - \rho_{i}^{{}} \sum\limits_{j} {\hat{\user2{u}}_{ij}^{{}} \cdot \nabla_{i}^{{}} w_{ij} V_{j} } $$

(8)

$$ \frac{{{\text{D}}{\varvec{u}}_{i}^{{}} }}{{{\text{D}}t}} = \sum\limits_{j} {m_{j}^{{}} \left( {\frac{{{{\varvec{\sigma}}}_{j}^{{}} + {{\varvec{\sigma}}}_{i}^{{}} }}{{\rho_{i}^{{}} \rho_{j}^{{}} }}} \right) \cdot \nabla_{i}^{{}} w_{ij} } + {{\varvec{\varPi}}}_{i}^{{{\text{AV}}}} + {{\varvec{\varGamma}}}_{i} $$

(9)

$$ \frac{{{\text{D}}{\varvec{r}}_{i}^{{}} }}{{{\text{D}}t}} = \hat{\user2{u}}_{i}^{{}} $$

(10)

where $\hat{\user2{u}}_{ij} = \user2{\hat{u}}_{j} - \hat{\user2{u}}_{i}$; V and m, respectively, signify volume and mass; $\hat{\user2{u}}$ is the transport/advection velocity; the subscripts i and j, respectively, represent a target particle i and its typical neighbouring particle j. The Cauchy’s stress tensor is obtained from summation of pressure and deviatoric stress tensors as shown in Eq. (3).

For the kernel function w, a fifth-order C2 Wendland kernel is adopted [53]:

$$ w_{ij} = \left\{ {\begin{array}{*{20}l} {\alpha_{{D_{s} }}^{{2{\text{D}}}} \left( {1 - \frac{q}{2}} \right)^{4} \left( {2q + 1} \right)} \hfill & {\quad \left( {0 \le q \le 2} \right)} \hfill \\ 0 \hfill & {\quad \left( {q > 2} \right)} \hfill \\ \end{array} } \right. $$

(11)

$$ \alpha_{{D_{s} }}^{{2{\text{D}}}} = \frac{7}{{4\pi h^{2} }};\quad q = \frac{{\left| {{\varvec{r}}_{ij} } \right|}}{h} $$

(12)

where r_ij = r_j − r_i; h stands for the smoothing length (in the whole computational domain, a constant smoothing length of h = 1.2 d₀ is considered in this study: d₀ = particle diameter or initial particle spacing).

For calculation of the Cauchy’s stress tensor or the deviatoric part of stress tensor, approximation of the velocity gradient tensor is necessary, which is obtained as follows:

$$ \left\langle {\nabla {\varvec{u}}} \right\rangle_{i} = \sum\limits_{j} {\hat{\user2{u}}_{ij}^{{}} \otimes \nabla_{i}^{{}} w_{ij} V_{j} } $$

(13)

The transport velocity $\hat{\user2{u}}$ is obtained from the XSPH scheme [19] to ensure the robustness of simulations.

$$ \hat{\user2{u}}_{i}^{{}} = {\varvec{u}}_{i}^{{}} + \delta {\varvec{u}}_{i}^{{}} ;\quad \delta {\varvec{u}}_{i}^{{}} = \varepsilon^{{{\text{XSPH}}}} \sum\limits_{j} {{\varvec{u}}_{ij}^{{}} \frac{{2m_{j} }}{{\rho_{j} + \rho_{i} }}w_{ij} } $$

(14)

where $\varepsilon^{{{\text{XSPH}}}}$ is tuning parameter, which is recommended to be set in the range of [0, 0.5] [19]. The transport $\hat{\user2{u}}$ becomes equivalent to actual velocity u when $\varepsilon^{{{\text{XSPH}}}} = 0$. In this study, $\varepsilon^{{{\text{XSPH}}}} = 0.5$ is used as recommended in [19]. Note that more precise discussion on arbitrary Lagrangian Eulerian (ALE)-based implementation of transport velocity is presented in Michel et al. [54]; however, in this study for simplicity we do not include advected velocity-related terms in the momentum equation similar to Gray et al. [1] and Zhang et al. [55] by considering the fact that the effect of transport velocity-related terms in momentum equation is negligible in structure analysis [55].

In the ULSPH discretised momentum equation [1], for stabilisation of simulations with respect to the rank deficiency and the tensile instability, several numerical stabilisers including the artificial viscosity Π^AV and the artificial stress Γ are incorporated. The artificial viscosity Π^AV is formulated as:

$$ {{\varvec{\varPi}}}_{i}^{{{\text{AV}}}} = \sum\limits_{j} {m_{j}^{{}} \Pi_{ij}^{{{\text{AV}}}} \nabla_{i}^{{}} w_{ij} } $$

(15)

$$ \Pi_{ij}^{{{\text{AV}}}} = \left\{ {\begin{array}{*{20}l} {\frac{{\alpha^{{{\text{AV}}}} hc_{ij}^{{}} }}{{\rho_{ij}^{{}} }}\frac{{{\varvec{u}}_{ij} \cdot {\varvec{r}}_{ij} }}{{\left| {{\varvec{r}}_{ij} } \right|^{2} + \left( {0.1h} \right)^{2} }}} \hfill & {\left( {{\varvec{u}}_{ij} \cdot {\varvec{r}}_{ij} < 0} \right)} \hfill \\ 0 \hfill & {\left( {{\varvec{u}}_{ij} \cdot {\varvec{r}}_{ij} \ge 0} \right)} \hfill \\ \end{array} } \right.;\quad \rho_{ij}^{{}} = \frac{{\rho_{i}^{{}} + \rho_{j}^{{}} }}{2},\quad c_{ij}^{{}} = \frac{{c_{i}^{{}} + c_{j}^{{}} }}{2} $$

(16)

where α^AV is the tuning parameter for artificial viscosity term (α^AV = 1.0, in this study) and c denotes the speed of sound.

The artificial stress term ${{\varvec{\varGamma}}}$ is written as:

$$ {{\varvec{\varGamma}}}_{i} = \sum\limits_{j} {m_{j}^{{}} \frac{{f_{ij} \left( {{\varvec{R}}_{j} + {\varvec{R}}_{i} } \right)}}{{\rho_{i}^{{}} \rho_{j}^{{}} }} \cdot \nabla_{i}^{{}} w_{ij} } ;\quad f_{ij} = \varepsilon \left( {\frac{{w_{ij} }}{{w\left( {d_{0} } \right)}}} \right)^{n} $$

(17)

where ε and n are the tuning parameters for artificial stress term, which are set as ε = 0.15 and n = 8, in this study for the numerical investigations unless otherwise stated. The parameter settings on ε and n are known to have large effect on the stability and accuracy, and even bring several adverse effects on the obtained results [35], and thus a careful tuning process is necessary based on the target phenomena [56]. In addition, a serious issue related to the artificial stress term is related to the absence of consistency, i.e. this term is not necessarily diminished as the spatial resolution is continually refined. Therefore, incorporation of this artificial stress term would likely affect the convergence properties of the ULSPH structure model. In Eq. (17), the tensor R is obtained through diagonalisation of the Cauchy’s stress tensor [1], i.e. for the 2D case,

$$ \left\{ {\begin{array}{*{20}l} {R_{i}^{xx} = \overline{R}_{i}^{xx} \cos^{2} \theta_{i} + \overline{R}_{i}^{yy} \sin^{2} \theta_{i} } \hfill \\ {R_{i}^{yy} = \overline{R}_{i}^{xx} \sin^{2} \theta_{i} + \overline{R}_{i}^{yy} \cos^{2} \theta_{i} } \hfill \\ {R_{i}^{xy} = R_{i}^{yx} = \sin \theta_{i} \cos \theta_{i} \left( {\overline{R}_{i}^{xx} + \overline{R}_{i}^{yy} } \right)} \hfill \\ \end{array} } \right. $$

(18)

$$ \overline{R}_{i}^{\alpha \beta } = \left\{ {\begin{array}{*{20}l} { - \overline{\sigma }_{i}^{\alpha \beta } } \hfill & {\quad \left( {\overline{\sigma }_{i}^{\alpha \beta } > 0} \right)} \hfill \\ 0 \hfill & {\quad \left( {{\text{otherwise}}} \right)} \hfill \\ \end{array} } \right. $$

(19)

$$ \left\{ {\begin{array}{*{20}l} {\overline{\sigma }_{i}^{xx} = \sigma_{i}^{xx} \cos^{2} \theta_{i} + \sigma_{i}^{yy} \sin^{2} \theta_{i} + 2\sigma_{i}^{xy} \sin \theta_{i} \cos \theta_{i} } \hfill \\ {\overline{\sigma }_{i}^{yy} = \sigma_{i}^{xx} \sin^{2} \theta_{i} + \sigma_{i}^{yy} \cos^{2} \theta_{i} - 2\sigma_{i}^{xy} \sin \theta_{i} \cos \theta_{i} } \hfill \\ \end{array} } \right. $$

(20)

$$ \theta_{i} = \frac{1}{2}\arctan \left( {\frac{{2\sigma_{i}^{xy} }}{{\sigma_{i}^{xx} - \sigma_{i}^{yy} }}} \right) $$

(21)

where superscripts x and y stand for x and y coordinates and superscripts α and β mean x or y coordinates. In the diagonalisation process, the symmetric property of the Cauchy’s stress tensor ($\sigma_{i}^{xy} = \sigma_{i}^{yx}$) is considered. Indeed, tensor R can be regarded as the transformed tensile principal stress tensor and the artificial stress Γ is added to reproduce repulsive interparticle forces when the principal stresses are tensile.

2.3 Time stepping

For the time stepping scheme, the first-order Euler explicit scheme is adopted in this study, i.e.

$$ \rho^{k + 1} = \rho^{k} + \left( {\frac{{{\text{D}}\rho }}{{{\text{D}}t}}} \right)^{k} \Delta t $$

(22)

$$ {\varvec{u}}^{k + 1} = {\varvec{u}}^{k} + \left( {\frac{{{\text{D}}{\varvec{u}}}}{{{\text{D}}t}}} \right)^{k} \Delta t $$

(23)

$$ {\varvec{S}}^{k + 1} = {\varvec{S}}^{k} + \left( {\frac{{{\text{D}}{\varvec{S}}}}{{{\text{D}}t}}} \right)^{k} \Delta t $$

(24)

$$ {\varvec{r}}^{k + 1} = {\varvec{r}}^{k} + \left( {\frac{{{\text{D}}{\varvec{r}}}}{{{\text{D}}t}}} \right)^{k} \Delta t $$

(25)

where Δt is the time step size, which is set by the CFL condition:

$$ \Delta t \le C_{{{\text{CFL}}}} \frac{h}{{c_{0}^{{}} }} $$

(26)

where C_CFL denotes the Courant number (C_CFL = 1.0, in this study). Note that the accuracy of time advancement can be enhanced by implementing high-order schemes (e.g. [1]); however, in this study, a simple scheme is adopted for the sake of simplicity and to prove the applicability of proposed refined schemes even with a simple time integration scheme.

3 Step-by-step improvement of ULSPH structure model

3.1 Incorporation of a corrective matrix in discretisation schemes

For enhancement of accuracy and ensuring the first-order completeness of approximations, a kernel gradient correction [43] is implemented, i.e. the consistency-related corrective matrix L_i is multiplied onto the gradient of kernel function $\nabla_{i}^{{}} w_{ij}$. This correction is applied in discretisations of the velocity and stress divergence, in the continuity and linear momentum equations, respectively, as well as the velocity gradient tensor in calculation of deviatoric part of the Cauchy’s stress tensor. Accordingly, as the first-step improvement, Eqs. (8), (9) and (13) corresponding to the original ULSPH [1] are modified as follows:

$$ \frac{{{\text{D}}\rho_{i}^{{}} }}{{{\text{D}}t}} = - \rho_{i}^{{}} \sum\limits_{j} {\hat{\user2{u}}_{ij}^{{}} \cdot \left( {{\varvec{L}}_{i} \cdot \nabla_{i}^{{}} w_{ij} V_{j} } \right)} $$

(27)

$$ \frac{{{\text{D}}{\varvec{u}}_{i}^{{}} }}{{{\text{D}}t}} = \sum\limits_{j} {m_{j}^{{}} \left( {\frac{{{{\varvec{\sigma}}}_{j}^{{}} \cdot {\varvec{L}}_{j} + {{\varvec{\sigma}}}_{i}^{{}} \cdot {\varvec{L}}_{i} }}{{\rho_{i}^{{}} \rho_{j}^{{}} }}} \right) \cdot \nabla_{i}^{{}} w_{ij} } + {{\varvec{\varPi}}}_{i}^{{{\text{AV}}}} + {{\varvec{\varGamma}}}_{i} $$

(28)

$$ \left\langle {\nabla {\varvec{u}}} \right\rangle_{i} = \sum\limits_{j} {\hat{\user2{u}}_{ij}^{{}} \otimes \left( {{\varvec{L}}_{i} \cdot \nabla_{i}^{{}} w_{ij} V_{j} } \right)} $$

(29)

Note that in Eq. (28), divergence of stress is discretised with the corrective matrix in a similar manner to the TLSPH structure model by Ganzenmüller [57] or Lee et al. [46]. That is, before applying kernel correction, we reformulate the divergence of stress as

$$ \begin{aligned} \left\langle {\frac{1}{\rho }\nabla \cdot {{\varvec{\sigma}}}} \right\rangle_{i} & = \sum\limits_{j} {m_{j} \left( {\frac{{{{\varvec{\sigma}}}_{j} + {{\varvec{\sigma}}}_{i} }}{{\rho_{i} \rho_{j} }}} \right) \cdot \nabla_{i} w_{ij} } \\ & = \sum\limits_{j} {m_{j} \left( {\frac{{{{\varvec{\sigma}}}_{j} \cdot \nabla_{i} w_{ij} + {{\varvec{\sigma}}}_{i} \cdot \nabla_{i} w_{ij} }}{{\rho_{i} \rho_{j} }}} \right)} \\ & = \sum\limits_{j} {m_{j} \left( {\frac{{ - {{\varvec{\sigma}}}_{j}^{{}} \cdot \nabla_{j} w_{ij} + {{\varvec{\sigma}}}_{i} \cdot \nabla_{i} w_{ij} }}{{\rho_{i} \rho_{j} }}} \right)} \\ \end{aligned} $$

(30)

and then apply L_i and L_j to $\nabla_{i}^{{}} w_{ij}$ and $\nabla_{j}^{{}} w_{ij}$, respectively. In this formulation, the even function property of kernel gradient is considered ($\nabla_{i}^{{}} w_{ij} = - \nabla_{j}^{{}} w_{ij}$). In addition, when the artificial stress term is considered, the kernel correction is adopted in a similar manner to that in the stress divergence term, i.e.

$$ {{\varvec{\varGamma}}}_{i} = \sum\limits_{j} {m_{j} \frac{{f_{ij} \left( {{\varvec{R}}_{j} \cdot {\varvec{L}}_{j} + {\varvec{R}}_{i} \cdot {\varvec{L}}_{i} } \right)}}{{\rho_{i} \rho_{j} }} \cdot \nabla_{i} w_{ij} } $$

(31)

3.2 Inclusion of a density diffusive term in the density rate equation

In explicit SPH fluid models, it is common to add a density diffusive term into the continuity equation for obtaining a smooth pressure field. This concept was originally proposed by Molteni and Colagrossi [58], and then, Antuono et al. [11] proposed a refined and well-known form of this diffusive term referred to as the δ-SPH scheme. This scheme can well suppress the numerical high-frequency noise in the density and thus the pressure fields.

In this study, the structural analyses are conducted with respect to an updated Lagrangian framework including a density rate equation with respect to the continuity equation for a continuum. The structure model does not consider an artificial reduction of sound speed as commonly adopted in the WCSPH fluid model; however, the pressure is obtained explicitly from an EOS as a function of the density field updated in time with respect to the density rate equation. Due to this fact, the described ULSPH structure model would also suffer from high-frequency acoustic perturbations in the pressure and thus the stress fields. To remove such spurious noises, a density diffusive term comprising Laplacian and bi-Laplacian operators, and thus being second-order accurate in space, is newly incorporated into the continuity or structural density rate equation:

$$ \frac{{{\text{D}}\rho_{i}^{{}} }}{{{\text{D}}t}} = - \rho_{i}^{{}} \sum\limits_{j} {\hat{\user2{u}}_{ij}^{{}} \cdot \left( {{\varvec{L}}_{i} \cdot \nabla_{i}^{{}} w_{ij} V_{j} } \right)} + D_{i} $$

(32)

$$ D_{i} = \delta hc_{0}^{{}} \sum\limits_{j} {\psi_{ij} \frac{{{\varvec{r}}_{ij} \cdot \nabla_{i}^{{}} w_{ij} }}{{\left| {{\varvec{r}}_{ij} } \right|^{2} }}V_{j} } $$

(33)

$$ \psi_{ij} = 2\rho_{ij} - \left( {\left\langle {\nabla \rho } \right\rangle_{i} + \left\langle {\nabla \rho } \right\rangle_{j} } \right) \cdot {\varvec{r}}_{ij} $$

(34)

$$ \left\langle {\nabla \rho } \right\rangle_{i} = \sum\limits_{{j \in \Omega_{\chi } }} {\rho_{ij} {\varvec{L}}_{i} \cdot \nabla_{i}^{{}} w_{ij} V_{j} } $$

(35)

where δ is the density diffusive coefficient. The Ω_χ signifies the phase that the particle i belongs to, which restricts the density diffusion only among the same phases in simulations of composite materials, similar to application of the δ-SPH fluid model to multiphase phenomena [59]. By incorporating this diffusive term, a smooth pressure field and thus an improved stress field are expected to be achieved. Following the name “δ-SPH”, we name the present structure model as δ-ULSPH structure model. Density diffusive coefficient δ is adjusted as δ = 0.002 in this study from our numerical tests including the preliminary results presented in [60]. Note that in this study, as shown in the above equations, the density diffusive term is effective only on the spherical part of stress tensor, and therefore, the deviatoric part is still straightforwardly updated by using Eqs. (6) and (24) with the Jaumann stress rate formulation.

3.3 Replacement of artificial viscosity with a second-order Riemann SPH-based diffusive term

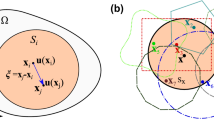
As shown in Eq. (15), the artificial viscosity term requires tuning on the parameter α^AV (or two parameters α^AV and β^AV, as shown in [9, 29] for example). Such ad hoc tuning coefficient is preferable to be removed. For this purpose, in this study, a second-order Riemann SPH-based diffusive term is newly incorporated into the momentum equation in place of the artificial viscosity term. In the context of Riemann SPH, the discontinuity interface is defined between particles i and j along with their relative unit vector, as shown in Fig. 1a. Then, the Riemann solution leads to three waves emanating from the discontinuity, as shown in Fig. 1b. Herein, the quantities of left and right states, L and R, are expressed based on the ones at particles i and j, respectively:

$$ \left\{ {\begin{array}{*{20}l} {\left( {\rho_{{\text{L}}} ,u_{{\text{L}}} ,p_{{\text{L}}} } \right) = \left( {\rho_{i} ,u_{i}^{{}} ,p_{i} } \right)} \hfill \\ {\left( {\rho_{{\text{R}}} ,u_{{\text{R}}} ,p_{{\text{R}}} } \right) = \left( {\rho_{j} ,u_{j}^{{}} ,p_{j} } \right)} \hfill \\ \end{array} } \right. $$

(36)

$$ u_{i} = {\varvec{u}}_{i} \cdot \frac{{{\varvec{r}}_{ij} }}{{\left| {{\varvec{r}}_{ij} } \right|}};\quad u_{j} = {\varvec{u}}_{j} \cdot \frac{{{\varvec{r}}_{ij} }}{{\left| {{\varvec{r}}_{ij} } \right|}} $$

(37)

Fig. 1

a Construction of 1D-Riemann problem along with the relative vector between particles i and j, b Riemann problem with two intermediate states

and also the quantities of left and right star regions (intermediate states) are assumed to satisfy $p_{{\text{L}}}^{*} = p_{{\text{R}}}^{*} = p_{{}}^{*}$ and $u_{{\text{L}}}^{*} = u_{{\text{R}}}^{*} = u_{{}}^{*}$, where $p_{{}}^{*}$ and $u_{{}}^{*}$ are obtained from a Riemann solver along with an assumption of $p_{{\text{L}}}^{*} + p_{{\text{R}}}^{*} \simeq 2p_{{}}^{*}$ and $u_{{\text{L}}}^{*} + u_{{\text{R}}}^{*} \simeq 2u_{{}}^{*}$ [22].

In this study, this concept is applied for the structural analyses.

First, as shown in Eq. (3), the Cauchy’s stress tensor of particle i is described as:

$$ {{\varvec{\sigma}}}_{i} = - p_{i} {\varvec{I}} + {\varvec{S}}_{i} $$

(38)

As discussed in Meng et al. [50], in the Riemann SPH scheme with Roe’s approximation, an assumption of $p_{i} + p_{j} \simeq 2p^{*}$ is introduced and then pressure interaction between particles i and j is determined based on the Riemann solution $p^{*}$, which is obtained by:

$$ p^{*} = \frac{1}{2}\left\{ {p_{i} + p_{j} + p_{{}}^{**} } \right\} $$

(39)

$$ p_{{}}^{**} = C_{ij} \left( {u_{i} - u_{j} } \right) $$

(40)

$$ C_{ij} = \frac{{c_{i} \rho_{i} \sqrt {\rho_{i} } + c_{j} \rho_{j} \sqrt {\rho_{j} } }}{{\sqrt {\rho_{i} } + \sqrt {\rho_{j} } }} $$

(41)

Combining Eqs. (38) and (39) and the assumption of $p_{i} + p_{j} \simeq 2p^{*}$, we have,

$$ {{\varvec{\sigma}}}_{i} = - \left( {2p^{*} - p_{j} } \right){\varvec{I}} + {\varvec{S}}_{i} = - p_{i} {\varvec{I}} + {\varvec{S}}_{i} - p_{{}}^{**} {\varvec{I}} $$

(42)

Herein, the newly appeared term, i.e. $p^{**}$, corresponds to the minimum required diffusion for stabilisation calculated based on the Riemann solution. If we write this diffusive term in a consistent form with the artificial viscosity term, we have:

$$\begin{aligned} {{\varvec{\varPi}}}_{i}^{R} &= \sum\limits_{j} m_{j}^{{}} \left({\frac{{ - 2p_{{}}^{**} }}{{\rho_{i}^{{}} \rho_{j}^{{}} }}}\right) \nabla_{i}^{{}} w_{ij}\\ &= \sum\limits_{j} {m_{j}^{{}}\left( {\frac{{2C_{ij} \left( {u_{j} - u_{i} }\right)}}{{\rho_{i}^{{}} \rho_{j}^{{}} }}} \right)\nabla_{i}^{{}}w_{ij} } \end{aligned}$$

(43)

In this study, as further enhancement, Eq. (37) corresponding to the linear reconstruction of variables is modified with respect to a second-order reconstruction as follows:

$$ \begin{aligned}u_{i} &= \left( {{\varvec{u}}_{i} + \frac{1}{2}\left\langle {\nabla {\varvec{u}}} \right\rangle_{i}^{c} \cdot {\varvec{r}}_{ij} } \right) \cdot \frac{{{\varvec{r}}_{ij} }}{{\left| {{\varvec{r}}_{ij} } \right|}};\\ u_{j} &= \left( {{\varvec{u}}_{j} - \frac{1}{2}\left\langle {\nabla {\varvec{u}}} \right\rangle_{j}^{c} \cdot {\varvec{r}}_{ij} } \right) \cdot \frac{{{\varvec{r}}_{ij} }}{{\left| {{\varvec{r}}_{ij} } \right|}}\end{aligned} $$

(44)

$$ \left\langle {\nabla {\varvec{u}}} \right\rangle_{i}^{c} = \sum\limits_{j} {{\varvec{u}}_{ij}^{{}} \otimes \left( {{\varvec{L}}_{i} \cdot \nabla_{i}^{{}} w_{ij} V_{j} } \right)} $$

(45)

In these equations, superscript c on the velocity gradient tensor is added to highlight that the discretisation is performed using a pure Lagrangian velocity vector with corrective matrix (rather than the transport velocity) and thus, to distinguish Eq. (45) from Eq. (29). It should be noted that the second-order reconstruction in Eq. (44) does not include slope limiter functions (e.g. [61, 62]) since for the considered test cases of this study clear improvements by the limiters have not been observed and the simplicity of the formulation is preferred here. However, the limiter functions are expected to become important for test cases that include steeper variations of variables either in kinematics or dynamics, and thus, detailed investigation of the contribution of limiters on the accuracy will be conducted in our future works.

3.4 Mitigation of artificial stress by a tensile instability control scheme

In the momentum equation, several numerical stabilisers corresponding to artificial viscosity Π^AV and artificial stress ${{\varvec{\varGamma}}}$ are incorporated. Such artificial terms are indeed necessary for stabilisation of simulations as previously discussed, although they may bring adverse effects [35] and require parameter tuning, in general. Therefore, mitigation of the effects of these terms would lead to improved reproductions of structural responses.

In the previous subsection, the tuning-required artificial viscosity term Π^AV was replaced by a second-order Riemann term Π^R. In this subsection, the focus will be on reduction of the adverse effects of the artificial stress term. To achieve this purpose, we need to recall that the artificial stress term [1] was proposed to minimise the unphysical perturbations in particle motions in tensile stress states through introduction of a short-range and tuning-required repulsive force between two particles. Instead of applying tuning-required artificial stress term, we may simply incorporate a so-called tensile instability control or a switch analogous to that applied in SPH for fluids [18]. The key purpose of this switch is to enhance the approximated kinematics (accelerations) and thus, minimise the unphysical perturbations in particle motions in tensile stress states. In compressive stress states, an antisymmetric and thus momentum-conservative (pressure) gradient or (stress) divergence scheme is often preferred because for a regular particle distribution and in the presence of a full kernel compact support, the first-order consistency would be automatically recovered. This is because, for instance, in case of pressure gradient in SPH, we can rewrite the Taylor-series consistent scheme as follows, resulting in a momentum-conservative and antisymmetric type pressure gradient model.

$$ \left\langle {\nabla p} \right\rangle_{i}^{{}} = \sum\limits_{j} {V_{j}^{{}} \left( {p_{j}^{{}} - p_{i}^{{}} } \right)\nabla_{i}^{{}} w_{ij} } + \sum\limits_{j} {V_{j}^{{}} \left( {2p_{i} } \right)\nabla_{i}^{{}} w_{ij} } $$

(46)

The second term on the right-hand side would vanish for a perfectly regular particle distribution and in the absence of truncated kernel domains. For irregular particle distributions and with compressive stress states, i.e. positive pressure, the second term would have a regulating effect on the particle distribution. In tensile stress states, or in case of negative pressure, however, this term would aggravate the regularity of particle distributions as well as the perturbations in particle motions. For this reason, Sun et al. [18] introduced a so-called TIC (tensile instability control) scheme to simply switch from a momentum-conservative, antisymmetric pressure gradient scheme to a Taylor-series consistent one for negative pressures, i.e.

$$ \left\langle {\frac{1}{\rho }\nabla p} \right\rangle_{i}^{{}} = \sum\limits_{j} {m_{j}^{{}} \left( {\frac{{p_{j}^{{}} + p_{i}^{{}} }}{{\rho_{i}^{{}} \rho_{j}^{{}} }}} \right)\nabla_{i}^{{}} w_{ij} } - \sum\limits_{j} {m_{j}^{{}} \left( {\frac{{F\left( {p_{i} } \right)}}{{\rho_{i}^{{}} \rho_{j}^{{}} }}} \right)\nabla_{i}^{{}} w_{ij} } $$

(47)

$$ F\left( {p_{i} } \right) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {\quad \left( {p_{i} \ge 0 \cup i \notin \Omega_{{{\text{IN}}}} } \right)} \hfill \\ {2p_{i} } \hfill & {\quad \left( {p_{i} < 0 \cap i \in \Omega_{{{\text{IN}}}} } \right)} \hfill \\ \end{array} } \right. $$

(48)

where $\Omega_{{{\text{IN}}}}$ stands for the inner region of the continuum. The first term on the right-hand side in Eq. (47) is the original summation-type pressure gradient component and the second term of right-hand side in Eq. (47) is the TIC term. The TIC term is activated only for particles in negative pressure located in the inner continuum region.

In the case of structural analyses, the momentum equation will include the divergence of the Cauchy’s stress, including both volumetric and deviatoric stresses. Tensile instability is aggravated by − 2R_i corresponding to the positive components of stress tensor of particle i, rather than negative pressure 2p_i, and therefore, − 2R_i should be subtracted from the original summation-type antisymmetric stress divergence model. Therefore, the stress divergence model adopting the TIC concept can be written as:

$$ \left\langle {\frac{1}{\rho }\nabla \cdot {{\varvec{\sigma}}}} \right\rangle_{i}^{{}} = \sum\limits_{j} {m_{j}^{{}} \left( {\frac{{{{\varvec{\sigma}}}_{j}^{{}} + {{\varvec{\sigma}}}_{i}^{{}} }}{{\rho_{i}^{{}} \rho_{j}^{{}} }}} \right) \cdot \nabla_{i}^{{}} w_{ij} } - \sum\limits_{j} {m_{j}^{{}} \left( {\frac{{{\varvec{F}}\left( {{\varvec{R}}_{i}^{{}} } \right)}}{{\rho_{i}^{{}} \rho_{j}^{{}} }}} \right) \cdot \nabla_{i}^{{}} w_{ij} } $$

(49)

$$ {\varvec{F}}\left( {{\varvec{R}}_{i}^{{}} } \right) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {\quad \left( {i \notin \Omega_{{{\text{IN}}}} } \right)} \hfill \\ { - 2{\varvec{R}}_{i}^{{}} } \hfill & {\quad \left( {i \in \Omega_{{{\text{IN}}}} } \right)} \hfill \\ \end{array} } \right. $$

(50)

From Eq. (49), for principal tensile stresses of a target particle i, i.e. for positive components of R_i, a more accurate approximation of corresponding kinematics (accelerations) would be achieved, resulting in minimisation of unphysical modes in tensile stress states. Indeed, the TIC scheme can be regarded as a switch in approximation of stress divergence for the principal tensile stresses rather than a stabilisation scheme. Bonet and Kulasegaram [15] have also shown that for constant or linear tensile stress fields, incorporation of first-order consistent SPH gradient or divergence operator would alleviate the tensile instability.

If the TIC scheme is adopted, robust calculations are achievable without the use of the artificial stress term ${{\varvec{\varGamma}}}$ for the inner domain of the continuum. On the other hand, for the surface and surface-vicinity particles, due to the absence of a complete kernel support and inaccuracies associated with incomplete SPH approximations [63], utilisation of the momentum-conservative form of the stress divergence becomes important to avoid unphysical accelerations and thus, ensure the stability. In particular, unlike fluid simulations where p_i has negligible values at and in the vicinity of free surfaces (truncated kernel domains), stress components may have large values near structural surfaces and the issue of incompleteness, even with first-order consistency corrections, becomes prominent. Once the momentum-conservative form of stress divergence is utilised, in the presence of tensile stresses, slight perturbations in particle motions can be amplified and thus, the artificial stress term needs to be utilised to suppress such unphysical tensile stress modes. Therefore, the artificial stress term is still necessary for particles located at structural surfaces to ensure a perfect control of tensile stress modes. With corrective matrix being incorporated, the final form of the momentum equation with the TIC control becomes:

$$ \frac{{{\text{D}}{\varvec{u}}_{i}^{{}} }}{{{\text{D}}t}} = \left\{ {\begin{array}{*{20}l} {\sum\limits_{j} {m_{j}^{{}} \left( {\frac{{{{\varvec{\sigma}}}_{j}^{{}} \cdot {\varvec{L}}_{j} + {{\varvec{\sigma}}}_{i}^{{}} \cdot {\varvec{L}}_{i} }}{{\rho_{i}^{{}} \rho_{j}^{{}} }}} \right) \cdot \nabla_{i}^{{}} w_{ij} } + {{\varvec{\varPi}}}_{i}^{R} + {{\varvec{\varGamma}}}_{i} } \hfill & {\quad \left( {i \notin \Omega_{{{\text{IN}}}} } \right)} \hfill \\ {\sum\limits_{j} {m_{j}^{{}} \left( {\frac{{{{\varvec{\sigma}}}_{j}^{{}} \cdot {\varvec{L}}_{j} + {{\varvec{\sigma}}}_{i}^{{}} \cdot {\varvec{L}}_{i} }}{{\rho_{i}^{{}} \rho_{j}^{{}} }}} \right) \cdot \nabla_{i}^{{}} w_{ij} } - \sum\limits_{j} {m_{j}^{{}} \left( {\frac{{ - 2{\varvec{R}}_{i}^{{}} \cdot {\varvec{L}}_{i} }}{{\rho_{i}^{{}} \rho_{j}^{{}} }}} \right) \cdot \nabla_{i}^{{}} w_{ij} } + {{\varvec{\varPi}}}_{i}^{R} } \hfill & {\quad \left( {i \in \Omega_{{{\text{IN}}}} } \right)} \hfill \\ \end{array} } \right. $$

(51)

Here, it should be noted that the parameters of (ε, n) = (0.15, 8) are used for the artificial stress term in Eq. (51), which is used only for the surface and surface-vicinity particles.

Regarding the categorization of particle types, structural surface particles can be simply detected by:

$$ C_{i} < 0.9;\quad C_{i} = \sum\limits_{j} {w_{ij} V_{j} } $$

(52)

where C is the colour function. When a target particle i satisfies the above condition, it is considered as a surface particle. Then, the particles adjacent to the detected surface particles (|r_ij|< 1.2 d₀) are set as vicinity particles. Others are regarded as the inner region particles. Note that since the benchmark tests in this paper do not include considerable change or splitting/merging process of structural surfaces, the current simple detection scheme will work well; however, for test cases including considerable deformations or topological changes of surface boundaries, more refined detection schemes such as parachute-shape detection algorithm [64] should be considered.

4 Numerical validations and investigations

The performances of the proposed enhanced schemes are verified through a set of numerical examples, namely, dynamic response of a free oscillating cantilever plate [1], high speed rotation of an elastic square plate [49], wave propagation in a homogeneous elastic cable [50], collision of two homogeneous elastic rings [1], elastic wave propagation in a heterogeneous cable [27, 51, 52] and collision of two composite elastic rings.

Figure 2 portrays a conceptual presentation of the enhancements proposed in this study. As this figure illustrates, four refined schemes are proposed so as to address four corresponding challenges in the original ULSPH structure model [1]. The enhancing effect by each proposed scheme will be illustrated in a step-by-step manner in this section. The enhanced ULSPH which benefits from four enhancements will be abbreviated as δ-ULSPH-R-TIC, which includes consistency-related corrections, a second-order δ-term or density diffusive term in the density rate equation, a second-order Riemann term in the momentum equation and a tensile stress instability control (TIC) scheme. Table 1 is presented to list the abbreviations of the applied and proposed schemes used for descriptions of structure models in this study.

Fig. 2

Conceptual presentation of the enhancements proposed in this study

4.1 Dynamic response of a free oscillating cantilever plate

First verification test is a classical benchmark corresponding to the dynamic response of a free oscillating cantilever plate [1, 65,66,67]. Figure 3 presents the computational set-up. The plate is subjected to an initial velocity distribution of u_y(x). In this figure, k_w is the wave number (k_wL = 1.875); ξ is a velocity amplification factor (ξ = 0.01). Particle diameter is set as d₀ = 1.0E−3 m.

Table 1 Concise descriptions of the abbreviations used in this study

Fig. 3

Schematic sketch of computational set-up—dynamic response of a free oscillating cantilever plate

First, the effect of incorporation of the consistency-related corrective matrix (Sect. 3.1) is investigated. Figure 4 demonstrates the deflection time histories measured at the free end of cantilever plate reproduced by ULSPH-AV-AS without corrective matrix (h = 1.2 d₀ or 1.8 d₀), ULSPH-AV-AS (with corrective matrix) (h = 1.2 d₀) and δ-ULSPH-AV-AS (h = 1.2 d₀). It is clear from this figure that the ULSPH models incorporating the consistency-related corrective matrix (Eqs. 27, 28 and 29) could well suppress the unphysical damping of deflection and provide closer results to the analytical solution in comparison with the models without the corrective matrix. In addition, according to this figure, the model using δ-term (or density diffusive term) shows consistent result with respect to the one without δ-term, indicating that the inclusion of δ-term with the value of δ = 0.002 does not bring serious adverse effects such as numerical damping of energy.

Fig. 4

Deflection time histories at the edge of plate by ULSPH-AV-AS without corrective matrix (h = 1.2 d₀ or 1.8 d₀), ULSPH-AV-AS (with corrective matrix) (h = 1.2 d₀) and δ-ULSPH-AV-AS (h = 1.2 d₀)—dynamic response of a free oscillating cantilever plate

In this work, for the tuning parameters of the AS term (ε and n), we adopt ε = 0.15 and n = 8. In order to explain the properness of this tuning parameter setting, in Fig. 5, (a) deflection time histories at the free end of cantilever plate and (b) total energy time histories by ULSPH-AV-AS with a set of different AS tuning parameters are plotted. In this figure, parameters of (ε, n) = (0.30, 4) (recommended values in [1]), (ε, n) = (0.15, 8.00) (recommended values in [56]), (ε, n) = (0.15, 8) and (ε, n) = (0.5, 8) are presented. As this figure shows, the setting of (ε, n) = (0.15, 8) has resulted in the closest deflection curve with respect to the theoretical solution with minimum unphysical energy variations.

Fig. 5

a Deflection time histories at the edge of plate and b total energy time histories by ULSPH-AV-AS with a set of different AS tuning parameters—dynamic response of a free oscillating cantilever plate

Figure 6 plots (a) deflection time histories at the free end of cantilever plate and (b) total energy time histories simulated by δ-ULSPH-AV-AS, δ-ULSPH-R-AS and δ-ULSPH-R-TIC. This figure portrays that the replacement of AV term with R term does not deteriorate the accuracy and stability of the model and the use of TIC instead of AS could lead to improved estimation of both deflection curve and energy time variation. In other words, the tuning-required AV could be successfully replaced by a second-order accurate Riemann term in the momentum equation and the TIC could be implemented instead of the AS term, resulting in enhanced accuracy in terms of deflection and energy variation.

Fig. 6

a Deflection time histories at the edge of plate and b total energy time histories by δ-ULSPH-AV-AS, δ-ULSPH-R-AS and δ-ULSPH-R-TIC—dynamic response of a free oscillating cantilever plate

Figure 7 shows the deflection time histories at the free end of cantilever plate by δ-ULSPH-R-TIC with a set of different particle diameters (d₀ = 2.0E−3 m, 1.0E−3 m and 5.0E−4 m). From the presented figure, refinement of the spatial resolution has resulted in improved estimations of the deflection curve with respect to the theoretical solution, portraying that δ-ULSPH-R-TIC possesses a good convergence property. Table 2 presents RMSE (root mean square error) and NRMSE (normalised RMSE) with respect to the analytical solution corresponding to Fig. 7, where gradual convergence of the numerical results to the reference solution is confirmed and the convergence property of the proposed model is validated quantitatively.

Fig. 7

Deflection time histories at the edge of plate by δ-ULSPH-R-TIC with a set of different particle diameters—dynamic response of a free oscillating cantilever plate

Table 2 RMSE (root mean square error) and NRMSE (normalised RMSE) corresponding to the deflection time histories in dynamic response of free oscillating cantilever plate with respect to the analytical solution reproduced by δ-ULSPH-R-TIC for 1 s of physical time corresponding to Fig. 7—dynamic response of a free oscillating cantilever plate

4.2 High speed rotation of an elastic square plate

To investigate the stability of the proposed method under the continuous tensile stresses, a second benchmark test corresponding to a high speed rotation of an elastic square plate [49] is performed. Figure 8 represents the initial condition of simulation. An elastic square plate with a length of 1.0 m (L = 1.0 m) is subjected to a rotational motion with the angular velocity of ω = 105.0 s⁻¹. The physical properties of the square plate, namely, density, Young’s modulus and Poisson’s ratio are, respectively, set as ρ = 1.1E+3 kg/m³, E = 17.0E+6 Pa and ν = 0.45. The horizontal and vertical motions of the reference point at (x,y) = (0.5L, 0.5L) are measured. The particle diameter is set as d₀ = 4.0E−2 m.

Fig. 8

Schematic sketch of computational set-up—high speed rotation of an elastic square plate

Figure 9 presents snapshots of particles illustrating the pressure field (p) at t = 0.09 s and 0.15 s by δ-ULSPH-R-AS with a set of different AS tuning parameters and δ-ULSPH-R-TIC. As shown in this figure, the accuracy of the model using AS is highly dependent on the selection of tuning parameters, and stress noises cannot be fully eliminated in all tested parameter cases. On the other hand, the model with the TIC scheme could provide stable and noiseless stress field at both instants t = 0.09 s and 0.15 s.

Fig. 9

Snapshots of particles illustrating pressure field (p) at t = 0.09 s and 0.15 s by δ-ULSPH-R-AS with a set of different AS tuning parameters and δ-ULSPH-R-TIC—high speed rotation of an elastic square plate

Figure 10 shows snapshots of particles together with the pressure field (p) at t = 0.15 s related to a set of different spatial resolutions of d₀ = 8.0E−2 m, 4.0E−2 m and 2.0E−2 m, by δ-ULSPH-R-AS with two different AS tuning parameters and δ-ULSPH-R-TIC. From the presented figure, through refinement of spatial resolution, the noise in pressure field is aggravated for structure models using the AS term, while, for the model benefitting from the TIC scheme, such unphysical outcome is not found.

Fig. 10

Snapshots of particles illustrating pressure field (p) at t = 0.15 s by δ-ULSPH-R-AS with different AS tuning parameters and δ-ULSPH-R-TIC under different spatial resolutions—high speed rotation of an elastic square plate

To assess the accuracy of δ-ULSPH-R-TIC, the same simulation of plate rotation is carried out by a well-developed and rigorously validated FVM code [68, 69]. The FVM simulation is performed by using a second-order vertex-centred finite volume algorithm combined with an explicit Runge–Kutta time integrator as well as using an acoustic Riemann solver together with linear reconstruction for the evaluation of the numerical fluxes [68, 69]. In the FVM simulation, the plate was discretised by linear triangular elements with a spatial resolution of 25 × 25 × 2 (676 nodes/1250 elements). Figure 11 demonstrates snapshots of particles illustrating the pressure field (p) at t = 0.09 s and 0.15 s by either FVM or δ-ULSPH-R-TIC. For the δ-ULSPH-R-TIC simulation d₀ = 4.0E−2 m, corresponding to a spatial resolution of 25 × 25. According to the presented figure, the rotated plate and the pressure distributions reproduced by δ-ULSPH-R-TIC are in good agreement with respect to the results by the FVM code [68, 69].

Fig. 11

Snapshots of particles illustrating pressure field (p) at t = 0.09 s and 0.15 s by either FVM or δ-ULSPH-R-TIC—spatial resolutions are 25 × 25 × 2 (676 nodes/1250 elements) for FVM and 25 × 25 (d₀ = 4.0E−2 m) for δ-ULSPH-R-TIC—high speed rotation of an elastic square plate

Figure 12 plots time histories of x- and y-positions at the edge point of square plate originally located at (x, y) = (0.5L, 0.5L) simulated by δ-ULSPH-R-TIC. According to this figure, the square plate is quantitatively shown to rotate smoothly.

Fig. 12

Time histories of x- and y-positions at the edge point of square originally located at (x, y) = (0.5L, 0.5L) reproduced by δ-ULSPH-R-TIC—high speed rotation of an elastic square plate

Figure 13 shows a comparison among δ-ULSPH-R-TIC without (a) and with (b) the artificial stress (AS) term for the surface and surface-vicinity particles. The presented figure portrays the incidence of tensile instability at the surface region when the AS term is excluded for the surface and surface-vicinity particles. In order to completely eliminate the use of AS term, we may use virtual (ghost) particles at the surface region along with the TIC scheme.

Fig. 13

Snapshots of particles illustrating pressure field (p) at t = 0.09 s and 0.15 s by δ-ULSPH-R-TIC without/with AS term for the surface and surface-vicinity particles—high speed rotation of an elastic square plate

4.3 Wave propagation in a homogeneous elastic cable

The third considered benchmark is wave propagation in a homogeneous elastic cable [50]. The initial configuration is presented in Fig. 14. An elastic cable with geometry of L = 10 m × H = 0.2 m is attached onto a fixed wall boundary on the left. The quarter region of the cable from the right free end is subjected to an initial constant rightward velocity U₀ = 5.0 m/s. The physical quantities of the cable are set as ρ = 8.0E+3 kg/m³ in density, E = 2.0E+11 Pa in Young’s modulus and ν = 0.0 in Poisson’s ratio. The particle diameter is set as d₀ = 2.5E−2 m.

Fig. 14

Schematic sketch of computational set-up—wave propagation in a homogeneous elastic cable

Figure 15 shows displacement time histories at the edge of the cable simulated by δ-ULSPH-AV-AS, δ-ULSPH-AV-TIC and δ-ULSPH-R-TIC. As shown in this figure and its enlarged part, the use of TIC in place of AS has resulted in an improved estimation of displacement. In addition, replacement of the AV with the R term has resulted in suppression of the spike noise.

Fig. 15

Displacement time histories at the edge of cable by δ-ULSPH-AV-AS, δ-ULSPH-AV-TIC and δ-ULSPH-R-TIC—wave propagation in a homogeneous elastic cable

The improvement by the R term is more evident in Fig. 16, where the velocity time histories at the edge of cable by δ-ULSPH-AV-AS, δ-ULSPH-AV-TIC and δ-ULSPH-R-TIC are shown. The figure and its enlarged portions demonstrate that the spike noises appearing in the models with the AV term are well eliminated by using the R term.

Fig. 16

Velocity time histories at the edge of cable by δ-ULSPH-AV-AS, δ-ULSPH-AV-TIC and δ-ULSPH-R-TIC—wave propagation in a homogeneous elastic cable

Figure 17 plots (a) displacement and (b) velocity time histories at the edge of cable by δ-ULSPH-R-TIC with a set of different particle diameters (d₀ = 5.0E−2 m, 2.5E−2 m and 1.25E−2 m). From the presented figure, gradual approach of the numerical results to the theoretical solution by refinement of spatial resolution can be confirmed, indicating the convergence property of δ-ULSPH-R-TIC.

Fig. 17

a Displacement and b velocity time histories at the edge of cable by δ-ULSPH-R-TIC with a set of different particle diameters—wave propagation in a homogeneous elastic cable

Figure 18 plots displacement time histories at the edge of cable by (a) δ-ULSPH-R-TIC and (b) δ-ULSPH-R-AS with a set of different particle diameters (d₀ = 5.0E−2 m, 2.5E−2 m and 1.25E−2 m). From this figure, refinement of spatial resolution in case of δ-ULSPH-R-AS has not resulted in clear improvement of results. On the other hand, use of TIC instead of AS has clearly improved the convergence property of ULSPH. Table 3 shows RMSE and NRMSE corresponding to Fig. 18, quantitatively confirming the superior convergence property of δ-ULSPH-R-TIC in comparison with δ-ULSPH-R-AS. From Fig. 18 and Table 3, the issue of absence of consistency of the AS term discussed in Sect. 2.2 can be confirmed.

Fig. 18

Displacement time histories at the edge of cable by a δ-ULSPH-R-TIC and b δ-ULSPH-R-AS with a set of different particle diameters—wave propagation in a homogeneous elastic cable

Table 3 RMSE (root mean square error) and NRMSE (normalised RMSE) corresponding to the displacement time histories in wave propagation in a homogeneous elastic cable with respect to the theoretical solution reproduced by (a) δ-ULSPH-R-TIC and (b) δ-ULSPH-R-AS for 0.01 s of physical time corresponding to Fig. 18—wave propagation in a homogeneous elastic cable

4.4 Collision of two homogeneous elastic rings

As the fourth benchmark, the test case of collision of two homogeneous elastic rings [1] is considered. Figure 19 illustrates the computational set-up of this benchmark test. Two elastic rings with inner/outer diameters of 0.03 m/0.04 m are subject to initial horizontal approaching velocities of U₀ = 1.0 m/s, eventually resulting in a strong collision of the rings. In this test case, acoustic pressure noises would become dominant due to the presence of material impact, leading to severe noise in stress field and numerical instability, and thus, the effect of density diffusive term is expected to be clearly observed. The physical properties of the rings are set as ρ = 1.0E+3 kg/m³ in density, E = 2.0E+6 Pa in Young’s modulus and ν = 0.495 in Poisson’s ratio. The rings are discretised in a cylindrical arrangement with a particle diameter of d₀ = 1.0E−3 m.

Fig. 19

Schematic sketch of computational set-up—collision of two homogeneous elastic rings

Since the assumption of continuum material is true for single ring and rigorously not true for interaction between two different rings, interaction between rings should be treated as contact of two different materials, rather than SPH analysis including both rings. For this sake, SPH interactions between particles belonging to different rings are switched off and the interaction of two rings is modelled by using the following contact force [70]:

$$ {\varvec{a}}_{i}^{{{\text{col}}}} = \frac{{{\varvec{F}}_{i}^{{{\text{col}}}} }}{{m_{i} }} = \frac{1}{{m_{i} }}\sum\limits_{j} {{\varvec{f}}_{ij}^{{{\text{col}}}} } $$

(53)

$$ {\varvec{f}}_{ij}^{{{\text{col}}}} = \left\{ {\begin{array}{*{20}l} {\frac{1}{\Delta t}\frac{{m_{i} m_{j} }}{{m_{j} + m_{i} }}\frac{{{\varvec{u}}_{ij} \cdot {\varvec{r}}_{ij} }}{{\left| {{\varvec{r}}_{ij} } \right|}}\frac{{{\varvec{r}}_{ij} }}{{\left| {{\varvec{r}}_{ij} } \right|}}} \hfill & {\quad \left( {{\varvec{u}}_{ij} \cdot {\varvec{r}}_{ij} < 0} \right)} \hfill \\ {\mathbf{0}} \hfill & {\quad \left( {{\varvec{u}}_{ij} \cdot {\varvec{r}}_{ij} \ge 0} \right)} \hfill \\ \end{array} } \right. $$

(54)

The collision acceleration term ${\varvec{a}}_{i}^{{{\text{col}}}}$ is added into the momentum equation.

Figure 20 shows snapshots of particles illustrating stress field (σ_xx) at t = 0.013 s, 0.023 s and 0.034 s by ULSPH-R-TIC and δ-ULSPH-R-TIC. According to the figure, the severe noises in stress fields observed in the ULSPH-R-TIC results are effectively suppressed in δ-ULSPH-R-TIC results, thanks to the incorporated density diffusive term (δ-term).

Fig. 20

Snapshots of particles illustrating stress field (σ_xx) at t = 0.013 s, 0.023 s and 0.034 s by ULSPH-R-TIC and δ-ULSPH-R-TIC—collision of two homogeneous elastic rings

Figure 21 demonstrates snapshots of particles illustrating the stress field (σ_xy) at t = 0.013 s by ULSPH-R-TIC and δ-ULSPH-R-TIC, where both results show almost consistent stress fields. It should be recalled that the density diffusion term in δ-ULSPH is directly effective on the spherical part of stress tensor and theoretically does not have any smoothing effect on the deviatoric part.

Fig. 21

Snapshots of particles illustrating stress field (σ_xy) at t = 0.013 s by ULSPH-R-TIC and δ-ULSPH-R-TIC—collision of two homogeneous elastic rings

Figure 22 presents snapshots of particles illustrating the stress field (σ_xx) at t = 0.013 s and 0.034 s by ULSPH-R-TIC and δ-ULSPH-R-TIC with a refined particle diameter of d₀ = 5.0E−4 m. The figure portrays the enhancing effect of the δ-term in a fine resolution case, especially during the rings impact. Comparing Fig. 22 with Fig. 20, refinement of resolution has resulted in a smoother stress field (σ_xx) by the δ-ULSPH-R-TIC.

Fig. 22

Snapshots of particles illustrating stress field (σ_xx) at t = 0.013 s and 0.034 s by ULSPH-R-TIC and δ-ULSPH-R-TIC with particle diameter of d₀ = 0.0005 m—collision of two homogeneous elastic rings

Figure 23 plots (a) time histories of elastic strain, kinetic and total energies reproduced by δ-ULSPH-R-TIC and (b) total energy time histories by ULSPH-R-TIC and δ-ULSPH-R-TIC. From Fig. 23a, the total energy is shown to largely dissipate after collision takes place, which is due to the irreversible dissipation by numerical stabilising terms in the momentum equation. After the rings collide, some amount of kinetic energy is converted to elastic strain energy and vice versa as the collision process proceeds. According to Fig. 23b, the δ-ULSPH-R-TIC shows almost consistent energy time variation in comparison with that of ULSPH-R-TIC. In other words, the δ-term effectively suppresses the high-frequency acoustic noises in density, pressure and thus stress fields without serious adverse effects on the energy conservation property.

Fig. 23

a Time histories of elastic strain, kinetic and total energies reproduced by δ-ULSPH-R-TIC and b total energy time histories by ULSPH-R-TIC and δ-ULSPH-R-TIC—collision of two homogeneous elastic rings

For further validation of δ-ULSPH-R-TIC, the simulation of elastic rings impact is repeated by using an FVM code [68, 69], which is proven to be reliably applicable to structural mechanics problems including those characterised by material impact [71]. Figure 24 portrays snapshots of particles illustrating stress field (σ_xx) at t = 0.013 s, 0.023 s and 0.034 s by either δ-ULSPH-R-TIC or FVM. The spatial resolutions are set as d₀ = 1.0E−3 m (4386 particles) for δ-ULSPH-R-TIC and 2728 nodes/4960 elements for FVM. From the presented figure, the configuration of rings and the stress distributions reproduced by δ-ULSPH-R-TIC agree well with the results by the FVM code [68, 69].

Fig. 24

Snapshots of particles illustrating stress field (σ_xx) at t = 0.013 s, 0.023 s and 0.034 s by either δ-ULSPH-R-TIC or FVM—spatial resolutions are d₀ = 1.0E−3 m (4386 particles) for δ-ULSPH-R-TIC and 2728 nodes/4960 elements for FVM—collision of two homogeneous elastic rings

4.5 Elastic wave propagation in a heterogeneous cable

In order to investigate the applicability of the proposed schemes in simulations of composite materials that include discontinuity of material properties [72], the benchmark test of elastic wave propagation in heterogeneous cable [27, 51, 52] is conducted as the fifth validation test case. This test involves material discontinuity at the centre of the cable between aluminium and copper, as shown in the schematic sketch of this test in Fig. 25.

Fig. 25

Schematic sketch of computational set-up—elastic wave propagation in heterogeneous cable

The aluminium and copper cables with 1 m length are connected, resulting in a composite cable of 2 m long. The physical properties of the aluminium are set as ρ = 2.785E+3 kg/m³ in density, E = 79.1E+9 Pa in Young’s modulus and ν = 0.43 in Poisson’s ratio, while those of the copper are set as ρ = 8.930E+3 kg/m³ in density, E = 138.1E+9 Pa in Young’s modulus and ν = 0.48 in Poisson’s ratio.

For generation of stress wave on the system, a monochromatic axial displacement is imposed at its left extremity as follows:

$$ u_{d} \left( {0,t} \right) = A_{1} \left( {1 - \cos \omega t} \right);\quad 0 \le t \le 1.0 \times 10^{ - 4} $$

(55)

where u_d(x,t) is the axial displacement, A₁ = 5.0 × 10⁻⁵ m is the amplitude, and ω = π × 10⁴ rad/s is the frequency. In the simulation code, to impose this condition, the left extremity particles are enforced to have the following velocity condition:

$$ \frac{{{\text{D}}u_{d} \left( {0,t} \right)}}{{{\text{D}}t}} = A_{1} \omega \sin \omega t;\quad 0 \le t \le 1.0 \times 10^{ - 4} $$

(56)

After t = 1.0 × 10⁻⁴ s, the left boundary particles are released and begin to act as free extremity. Also, since the analytical solution is obtained based on a 1D elastic wave propagation problem, the speed of sound for the 1D problem is used instead, similar to Oger et al. [27] as:

$$ c_{0}^{{}} = \sqrt {\frac{E}{\rho }} $$

(57)

The derivation of analytical solution for this benchmark test will be described in detail in “Appendix A”.

Figure 26 shows snapshots of particles illustrating stress field (σ_xx) reproduced by δ-ULSPH-R-TIC. From the snapshots, it is clear that the proposed model could result in a smooth stress field. Propagation of stress wave is well simulated, and focusing on the material interface, reflecting/transmitting processes of the stress wave are robustly reproduced.

Fig. 26

Snapshots of particles together with stress field (σ_xx) reproduced by δ-ULSPH-R-TIC—elastic wave propagation in heterogeneous cable

Figure 27 presents the stress (σ_xx) profiles at t = 1.0E−4 s, 1.5E−4 s, 2.0E−4 s, 2.5E−4 s, 3.0E−4 s and 3.5E−4 s reproduced by δ-ULSPH-AV-AS, δ-ULSPH-AV-TIC and δ-ULSPH-R-TIC along with the corresponding analytical solution. It can be seen from the presented figure and its enlarged portions that the model using the TIC scheme has provided almost consistent results with respect to the analytical solution compared to the one using the AS term. In addition, from Fig. 27, incorporation of the R term has been effective in suppressing the unphysical stress noises.

Fig. 27

Stress (σ_xx) profiles at t = 1.0E−4 s, 1.5E−4 s, 2.0E−4 s, 2.5E−4 s, 3.0E−4 s and 3.5E−4 s reproduced by δ-ULSPH-AV-AS, δ-ULSPH-AV-TIC and δ-ULSPH-R-TIC along with analytical solution—elastic wave propagation in heterogeneous cable

Figure 28 presents stress (σ_xx) profiles at t = 1.0E−4 s, 1.5E−4 s, 2.0E−4 s, 2.5E−4 s, 3.0E−4 s and 3.5E−4 s reproduced by δ-ULSPH-R-TIC with a set of different particle diameters (d₀ = 4.8E−3 m, 2.4E−3 m and 1.2E−3 m). According to the figure, the refinement of spatial resolution has resulted in enhanced reproductions of the stress profile with respect to the reference solution, in specific, in terms of the magnitudes of peak stresses.

Fig. 28

Stress (σ_xx) profiles at t = 1.0E−4 s, 1.5E−4 s, 2.0E−4 s, 2.5E−4 s, 3.0E−4 s and 3.5E−4 s reproduced by δ-ULSPH-R-TIC under a set of different particle diameters along with analytical solution—elastic wave propagation in heterogeneous cable

4.6 Collision of two composite elastic rings

The sixth conducted benchmark is the collision of two composite elastic rings. This test case involves material and shock discontinuities where acoustic pressure noises would be dominant, resulting in severe noise in the stress field and likely, instability of the calculation. Figure 29 presents the initial set-up of this benchmark test. Basic calculation settings are the same as the homogeneous case in Sect. 4.4, except for the presence of material discontinuity and difference in the Young’s modulus. The two elastic rings with inner and outer diameters of 0.03 m and 0.04 m have the approaching horizontal velocity of 1.0 m/s. The density and Poisson’s ratio are ρ = 1.0E+3 kg/m³ and ν = 0.495. Composite elastic rings with the Young’s modulus of E_A = 10E_B = 5.0E+6 Pa are considered, where each ring consists of material A (outer) and B (inner) as half and half in the thickness direction. The rings are discretised in a cylindrical arrangement with a particle diameter of d₀ = 1.0E−3 m.

Fig. 29

Schematic sketch of computational set-up—collision of two composite elastic rings

Figure 30 shows snapshots of particles illustrating stress field (σ_xx) at t = 0.014 s, 0.022 s and 0.040 s reproduced by ULSPH-R-TIC and δ-ULSPH-R-TIC. From the figure, through the comparison of the reproduced stress fields by ULSPH-R-TIC and δ-ULSPH-R-TIC, the density diffusive term (δ-term) is proven to work well in suppression of the severe stress noises in the impact problem of composite materials.

Fig. 30

Snapshots of particles illustrating stress field (σ_xx) at t = 0.014 s, 0.022 s and 0.040 s by ULSPH-R-TIC and δ-ULSPH-R-TIC—collision of two composite elastic rings

Figure 31 shows the plots of (a) time histories of elastic strain, kinetic and total energies reproduced by δ-ULSPH-R-TIC and (b) total energy time histories by ULSPH-R-TIC and δ-ULSPH-R-TIC. Overall results and tendencies are shown to be consistent with the ones in homogeneous ring impact in Sect. 4.4, i.e. the use of δ-term (density diffusive term) does not deteriorate the method’s conservation properties of energy. In addition, from the presented results the structure model benefitting from four proposed enhancements, namely, δ-ULSPH-R-TIC has been shown to be capable of reproducing structural mechanics problems corresponding to both homogeneous and composite materials.

Fig. 31

a Time histories of elastic strain, kinetic and total energies reproduced by δ-ULSPH-R-TIC and b total energy time histories by ULSPH-R-TIC and δ-ULSPH-R-TIC—collision of two composite elastic rings

The discontinuity in the material properties for the composite elastic ring impact corresponded to the Young’s modulus only (Fig. 29). The same test case is repeated by considering an additional discontinuity in the materials’ densities as depicted in Fig. 32a. The ratios of the materials’ densities and the Young’s moduli are both set as 1:10. Figure 32b shows typical snapshots illustrating the stress field (σ_xx) at t = 0.014 s, 0.023 s and 0.036 s, reproduced by ULSPH-R-TIC and δ-ULSPH-R-TIC. The figure illustrates the effect of δ term as well as the robustness of δ-ULSPH-R-TIC in reproducing the collision of composite rings with discontinuities in both density and Young’s modulus. Figure 33 plots (a) elastic strain, kinetic and total energy time variations reproduced by δ-ULSPH-R-TIC and (b) total energy time histories by ULSPH-R-TIC and δ-ULSPH-R-TIC, where a similar tendency of energy time variations is seen for Young’s modulus and density discontinuities with respect to the results of homogeneous elastic rings and composite ones of only Young’s modulus discontinuity.

Fig. 32

a Schematic sketch of computational set-up for the case of both Young’s modulus and density discontinuities; b snapshots of particles illustrating stress field (σ_xx) at t = 0.014 s, 0.023 s and 0.036 s by ULSPH-R-TIC and δ-ULSPH-R-TIC—collision of two composite elastic rings

Fig. 33

a Time histories of elastic strain, kinetic and total energies reproduced by δ-ULSPH-R-TIC and b total energy time histories by ULSPH-R-TIC and δ-ULSPH-R-TIC under both Young’s modulus and density discontinuities—collision of two composite elastic rings

5 Concluding remarks

In this study, four numerical aspects or shortcomings related to a commonly applied updated Lagrangian SPH (ULSPH) structure model are targeted. These aspects include: (i) incompleteness of approximations, (ii) pressure instability, (iii) rank deficiency and (iv) tensile instability control. For aspects (i) and (ii), no consideration was considered in the original ULSPH structure model [1]. For aspects (iii) and (iv), the original ULSPH [1], respectively, incorporated artificial viscosity and artificial stress terms that include tuning parameters. In this paper, step-by-step enhancements for the ULSPH structure model are presented through a systematic consideration of these four aspects, and proposal of simple, yet effective schemes.

The first enhancement corresponds to incorporation of a consistency-related corrective matrix to ensure the first-order consistency of approximations related to the velocity divergence (in the continuity equation), stress divergence (in the momentum equation) and the velocity gradient tensor (in calculation of deviatoric part of the Cauchy’s stress tensor). The second enhancement is inclusion of a second-order diffusive term (δ-term) into the continuity or density rate equation to tackle the issue of pressure instability. The third improvement corresponds to incorporation of a second-order Riemann term in place of the artificial viscosity or the AV term in the momentum equation with regard to the issue of rank deficiency. The third enhancement is consistent with the second one, as δ-term can be regarded as a Riemann diffusive term. The fourth improvement focuses on enhanced approximations of kinematics (accelerations) for the principal tensile stresses in order to mitigate the tensile stress instability or growth of unphysical perturbations in tensile stress states. Through incorporation of a switch in estimation of the stress divergence, referred to as the TIC (tensile instability control) scheme, we have shown that the artificial stress or the AS term which includes several tuning-required parameters, can be eliminated at least for inner structural particles that have a full kernel compact support.

A total number of six benchmark tests are conducted for a scrupulous and systematic validation of proposed enhancements. The results show that step-by-step improvements are achievable through incorporation of the proposed enhanced schemes. In specific, the refined structure model which benefits from all four enhancements, namely, δ-ULSPH-R-TIC, is shown to provide reliable results even for challenging problems that include structural impacts in the presence of material discontinuities.

In our future works, a detailed and theoretical investigation of the optimum diffusive parameter δ will be conducted similar to the one performed by Antuono et al. [73]. The extension of the present enhanced ULSPH method to 3D as well as its comprehensive comparisons with other advanced SPH structure methods [41] is also among our future targets. Furthermore, the development of variationally consistent [47, 72] ULSPH formulations should also be targeted especially when possession of excellent features in both conservation and consistency are of interest. In addition, specific focus will be devoted to extension of the enhanced ULSPH structure model for reproduction of dynamics of viscoelastic or elastoplastic materials as well as damage/fracture modelling. The development of an entirely Lagrangian meshfree FSI solver with incorporation of the enhanced ULSPH structure model is also among our future works.

Appendices

Appendix A. Theoretical solution of elastic wave propagation (Sect. 4.5)

In this appendix, the analytical solution of 1D elastic wave propagation corresponding to the benchmark test in Sect. 4.5 is derived based on the elementary rod theory [52]. In this theory, the rod is assumed to be long and slender so that the lateral contraction could be negligibly small.

The equation of motion is obtained as follows. Let us consider an element inside a rod. Let q(x,t) be the external force per unit volume, u(x,t) be the displacement in x-direction, A be the area of cross section, Δx be the length of the element in x-direction as an infinitesimal value, ρ be the density of the rod, and F be the force acting on the face of cross section, as shown in Fig. 

Fig. 34

An element of a rod with subjected loads

34.

Considering the force balance for an element of the rod as:

$$ \left( {\rho A\Delta x} \right)\frac{{\partial^{2} u}}{{\partial t^{2} }} = - F + \left( {F + \frac{\partial F}{{\partial x}}\Delta x} \right) + qA\Delta x $$

(A.1)

where ρA denotes the mass per unit length of the rod. The above momentum equation can be expressed as:

$$ \frac{\partial F}{{\partial x}} = \rho A\frac{{\partial^{2} u}}{{\partial t^{2} }} - qA $$

(A.2)

The relationship between the strain ε and displacement u can be written as:

$$ \varepsilon = \frac{\partial u}{{\partial x}} $$

(A.3)

The Hooke’s law in one-dimensional form can be described as:

$$ \sigma = \frac{F}{A} = E\varepsilon $$

(A.4)

where $\sigma$ stands for stress. Substituting Eqs. (A.3) and (A.4) into Eq. (A.2), we obtain Eq. (A.5) as:

$$ \frac{\partial }{\partial x}\left( {EA\frac{\partial u}{{\partial x}}} \right) = \rho A\frac{{\partial^{2} u}}{{\partial t^{2} }} - qA $$

(A.5)

If the external force q(x,t) does not exist and the rod is a homogeneous material, we can obtain the below wave equation:

$$ \frac{{\partial^{2} u}}{{\partial t^{2} }} - C^{2} \frac{{\partial^{2} u}}{{\partial x^{2} }} = 0;\quad C = \sqrt {\frac{E}{\rho }} $$

(A.6)

where C represents the speed of sound corresponding to the velocity of the propagating wave. We can solve this wave equation under the provided initial conditions and boundary conditions.

For a composite rod, i.e. a rod consisting of physically different materials with clear phase interface, we consider general d’Alembert solution of Eq. (A.6) for each material phase. In case of the test case in Sect. 4.5, left component (phase 1: aluminium) and right component (phase 2: copper) are connected at the centre of the rod with a clear material interface. The wave reflects at the interface due to the discontinuity of materials. Considering that displacement and stress are continuous across the material interface, we can find the reflection coefficient $A_{1}^{{{\text{ref}}}}$ and transmission coefficient $A_{2}^{{{\text{inc}}}}$.

For phase 1, the displacement and the stress induced by the incident wave (coefficient of $A_{1}^{{{\text{inc}}}}$) can be written with using angular frequency ω and wave number k as:

$$ u_{1}^{{{\text{inc}}}} \left( {x,t} \right) = A_{1}^{{{\text{inc}}}} \exp \left( {i\left( {\omega t - k_{1} x} \right)} \right) $$

(A.7)

$$ \sigma_{1}^{{{\text{inc}}}} \left( {x,t} \right) = E_{1}^{{}} \frac{{\partial u_{1}^{{{\text{inc}}}} }}{\partial x} = - A_{1}^{{{\text{inc}}}} E_{1}^{{}} k_{1}^{{}} \exp \left( {i\left( {\omega t - k_{1} x} \right)} \right) $$

(A.8)

The displacement and the stress occurred by reflection wave are obtained as:

$$ u_{1}^{{{\text{ref}}}} \left( {x,t} \right) = A_{1}^{{{\text{ref}}}} \exp \left( {i\left( {\omega t + k_{1} x} \right)} \right) $$

(A.9)

$$ \sigma_{1}^{{{\text{ref}}}} \left( {x,t} \right) = E_{1}^{{}} \frac{{\partial u_{1}^{{{\text{ref}}}} }}{\partial x} = A_{1}^{{{\text{ref}}}} E_{1}^{{}} k_{1}^{{}} \exp \left( {i\left( {\omega t + k_{1} x} \right)} \right) $$

(A.10)

For phase 2, the displacement and the stress can be calculated as:

$$ u_{2}^{{{\text{inc}}}} \left( {x,t} \right) = A_{2}^{{{\text{inc}}}} \exp \left( {i\left( {\omega t - k_{2} x} \right)} \right) $$

(A.11)

$$ \sigma_{2}^{{{\text{inc}}}} \left( {x,t} \right) = E_{2}^{{}} \frac{{\partial u_{2}^{{{\text{inc}}}} }}{\partial x} = - A_{2}^{{{\text{inc}}}} E_{2}^{{}} k_{2}^{{}} \exp \left( {i\left( {\omega t - k_{2} x} \right)} \right) $$

(A.12)

Since the displacement and stress are continuous across the material interface, the following relationship would hold:

$$ A_{1}^{{{\text{inc}}}} + A_{1}^{{{\text{ref}}}} = A_{2}^{{{\text{inc}}}} $$

(A.13)

$$ - A_{1}^{{{\text{inc}}}} E_{1}^{{}} k_{1}^{{}} + A_{1}^{{{\text{ref}}}} E_{1}^{{}} k_{1}^{{}} = - A_{2}^{{{\text{inc}}}} E_{2}^{{}} k_{2}^{{}} $$

(A.14)

Thus, the reflection coefficient and transmission coefficient can be obtained as:

$$ A_{1}^{{{\text{ref}}}} = A_{1}^{{{\text{inc}}}} \frac{{E_{1}^{{}} k_{1}^{{}} - E_{2}^{{}} k_{2}^{{}} }}{{E_{1}^{{}} k_{1}^{{}} + E_{2}^{{}} k_{2}^{{}} }} $$

(A.15)

$$ A_{2}^{{{\text{inc}}}} = 2A_{1}^{{{\text{inc}}}} \frac{{E_{1}^{{}} k_{1}^{{}} }}{{E_{1}^{{}} k_{1}^{{}} + E_{2}^{{}} k_{2}^{{}} }} $$

(A.16)

Since the components would have difference in both Young’s modulus and density, Eqs. (A.15) and (A.16) will be further formulated to the form including density. We now consider the continuity of angular frequency across material interface as:

$$ \omega = k_{1}^{{}} C_{1}^{{}} = k_{2}^{{}} C_{2}^{{}} $$

(A.17)

We obtain the relationship of wave numbers between two phases as:

$$ \frac{{k_{1}^{{}} }}{{k_{2}^{{}} }} = \frac{{C_{2}^{{}} }}{{C_{1}^{{}} }} = \sqrt {\frac{{E_{2}^{{}} \rho_{1}^{{}} }}{{E_{1}^{{}} \rho_{2}^{{}} }}} $$

(A.18)

Equation (A.15) can be rewritten by substituting Eq. (A.18) as:

$$ \begin{aligned} A_{1}^{{{\text{ref}}}} & = A_{1}^{{{\text{inc}}}} \frac{{E_{1}^{{}} k_{1}^{{}} - E_{2}^{{}} k_{2}^{{}} }}{{E_{1}^{{}} k_{1}^{{}} + E_{2}^{{}} k_{2}^{{}} }} \\ & = A_{1}^{{{\text{inc}}}} \frac{{1 - \frac{{E_{2}^{{}} k_{2}^{{}} }}{{E_{1}^{{}} k_{1}^{{}} }}}}{{1 + \frac{{E_{2}^{{}} k_{2}^{{}} }}{{E_{1}^{{}} k_{1}^{{}} }}}} \\ & = A_{1}^{{{\text{inc}}}} \frac{{1 - \sqrt {\frac{{E_{2}^{{}} \rho_{2}^{{}} }}{{E_{1}^{{}} \rho_{1}^{{}} }}} }}{{1 + \sqrt {\frac{{E_{2}^{{}} \rho_{2}^{{}} }}{{E_{1}^{{}} \rho_{1}^{{}} }}} }} \\ & = A_{1}^{{{\text{inc}}}} \frac{{1 - \alpha_{r} }}{{1 + \alpha_{r} }} \\ \end{aligned} $$

(A.19)

$$ \alpha_{r} = \sqrt {\frac{{E_{2}^{{}} \rho_{2}^{{}} }}{{E_{1}^{{}} \rho_{1}^{{}} }}} $$

(A.20)

Substituting Eq. (A.19) into Eq. (A.13), we can obtain the amplitude of the transmission wave as:

$$ \begin{aligned} A_{2}^{{{\text{inc}}}} & = A_{1}^{{{\text{inc}}}} + A_{1}^{{{\text{ref}}}} \\ & = A_{1}^{{{\text{inc}}}} + A_{1}^{{{\text{inc}}}} \frac{{1 - \alpha_{r} }}{{1 + \alpha_{r} }} \\ & = A_{1}^{{{\text{inc}}}} \frac{2}{{1 + \alpha_{r} }} \\ \end{aligned} $$

(A.21)

Appendix B. Discussion on the similarity among Riemann diffusive term, artificial viscosity and δ-SPH

The continuity equation including the δ or the density diffusive term can be written as (also discussed in Sect. 3.2):

$$ \frac{{{\text{D}}\rho_{i}^{{}} }}{{{\text{D}}t}} = - \rho_{i}^{{}} \sum\limits_{j} {{\varvec{u}}_{ij}^{{}} \cdot \nabla_{i}^{{}} w_{ij} V_{j} } + D_{i} $$

(B.1)

$$ D_{i} = \delta hc_{0}^{{}} \sum\limits_{j} {\psi_{ij} \frac{{{\varvec{r}}_{ij} \cdot \nabla_{i}^{{}} w_{ij} }}{{\left| {{\varvec{r}}_{ij} } \right|^{2} }}V_{j} } $$

(B.2)

$$ \psi_{ij}^{{{\text{0th}}}} = 2\rho_{ij} $$

(B.3)

$$ \psi_{ij}^{{{\text{1st}}}} = 2\rho_{ij} - \left( {\left\langle {\nabla \rho } \right\rangle_{i} + \left\langle {\nabla \rho } \right\rangle_{j} } \right) \cdot {\varvec{r}}_{ij} $$

(B.4)

Equations (B.3) and (B.4) correspond to zeroth- and first-order corrected functions (Refs. [12, 58], respectively).

In Riemann SPH, for the case of linear reconstruction of variables, the continuity equation is written as:

$$ \frac{{{\text{D}}\rho_{i}^{{}} }}{{{\text{D}}t}} = - 2\rho_{i}^{{}} \sum\limits_{j} {\left( {{\varvec{u}}_{{}}^{*} - {\varvec{u}}_{i}^{{}} } \right) \cdot \nabla_{i}^{{}} w_{ij} V_{j} } $$

(B.5)

$$ {\varvec{u}}_{{}}^{*} = u_{{}}^{*} \frac{{{\varvec{r}}_{ij} }}{{\left| {{\varvec{r}}_{ij} } \right|}} + \left\{ {\frac{{{\varvec{u}}_{i}^{{}} + {\varvec{u}}_{j}^{{}} }}{2} - \frac{{u_{i}^{{}} + u_{j}^{{}} }}{2}\frac{{{\varvec{r}}_{ij} }}{{\left| {{\varvec{r}}_{ij} } \right|}}} \right\} $$

(B.6)

$$ u_{{}}^{*} = \frac{1}{2}\left[ {u_{i} + u_{j} + \frac{1}{{C_{ij} }}\left( {p_{i} - p_{j} } \right)} \right] $$

(B.7)

$$ u_{i}^{{}} = {\varvec{u}}_{i}^{{}} \cdot \frac{{{\varvec{r}}_{ij} }}{{\left| {{\varvec{r}}_{ij} } \right|}}_{{}} ;\quad u_{j}^{{}} = {\varvec{u}}_{j}^{{}} \cdot \frac{{{\varvec{r}}_{ij} }}{{\left| {{\varvec{r}}_{ij} } \right|}} $$

(B.8)

$$ C_{ij} = \frac{{c_{i} \rho_{i} \sqrt {\rho_{i} } + c_{j} \rho_{j} \sqrt {\rho_{j} } }}{{\sqrt {\rho_{i} } + \sqrt {\rho_{j} } }} $$

(B.9)

From the equation of state, we have:

$$ p_{i}^{{}} = c_{0}^{2} \left( {\rho_{i}^{{}} - \rho_{0}^{{}} } \right) $$

(B.10)

Reformulating equations by substituting Eqs. (B.6) to (B.10) into Eq. (B.5), then:

$$ \frac{{{\text{D}}\rho_{i}^{{}} }}{{{\text{D}}t}} = - \rho_{i}^{{}} \sum\limits_{j} {{\varvec{u}}_{ij}^{{}} \cdot \nabla_{i}^{{}} w_{ij} V_{j} } + \rho_{i}^{{}} \sum\limits_{j} {\frac{{c_{0}^{2} \rho_{ij} }}{{C_{ij} }}\frac{{{\varvec{r}}_{ij} }}{{\left| {{\varvec{r}}_{ij} } \right|}} \cdot \nabla_{i}^{{}} w_{ij} V_{j} } $$

(B.11)

Comparing Eqs. (B.1) and (B.11), the density diffusion by Riemann solution D^R can be written as:

$$ D_{i}^{{\text{R}}} = hc_{0}^{{}} \sum\limits_{j} {\left( {\frac{{\rho_{i}^{{}} c_{0}^{{}} }}{{C_{ij} }}\frac{{\left| {{\varvec{r}}_{ij} } \right|}}{h}} \right)\psi_{ij}^{{\text{R}}} \frac{{{\varvec{r}}_{ij} \cdot \nabla_{i}^{{}} w_{ij} }}{{\left| {{\varvec{r}}_{ij} } \right|^{2} }}V_{j} } $$

(B.12)

$$ \psi_{ij}^{{\text{R}}} = 2\rho_{ij} $$

(B.13)

Therefore, the density diffusion by Riemann solution has close similarity with the δ-SPH diffusion term without a first-order correction [58].

Linear momentum equation with the artificial viscosity term can be written as:

$$ \frac{{{\text{D}}{\varvec{u}}_{i}^{{}} }}{{{\text{D}}t}} = \sum\limits_{j} {m_{j}^{{}} \left( {\frac{{{{\varvec{\sigma}}}_{j}^{{}} + {{\varvec{\sigma}}}_{i}^{{}} }}{{\rho_{i}^{{}} \rho_{j}^{{}} }}} \right) \cdot \nabla_{i}^{{}} w_{ij} } + {{\varvec{\varPi}}}_{i}^{{{\text{AV}}}} $$

(B.14)

$$ {{\varvec{\varPi}}}_{i}^{{{\text{AV}}}} = \sum\limits_{j} {m_{j}^{{}} \Pi_{ij}^{{{\text{AV}}}} \nabla_{i}^{{}} w_{ij} } $$

(B.15)

$$ \Pi_{i}^{{{\text{AV}}}} = \left\{ {\begin{array}{*{20}l} {\frac{{\alpha^{{{\text{AV}}}} hc_{ij}^{{}} }}{{\rho_{ij}^{{}} }}\frac{{{\varvec{u}}_{ij} \cdot {\varvec{r}}_{ij} }}{{\left| {{\varvec{r}}_{ij} } \right|^{2} + \left( {0.1h} \right)^{2} }}} \hfill & {\quad \left( {{\varvec{u}}_{ij} \cdot {\varvec{r}}_{ij} < 0} \right)} \hfill \\ 0 \hfill & {\quad \left( {{\varvec{u}}_{ij} \cdot {\varvec{r}}_{ij} \ge 0} \right)} \hfill \\ \end{array} } \right.;\quad \rho_{ij}^{{}} = \frac{{\rho_{i}^{{}} + \rho_{j}^{{}} }}{2},\quad c_{ij}^{{}} = \frac{{c_{i}^{{}} + c_{j}^{{}} }}{2} $$

(B.16)

In the Riemann SPH, linear momentum continuity equation is written as (see Sect. 3.3):

$$ \frac{{{\text{D}}{\varvec{u}}_{i}^{{}} }}{{{\text{D}}t}} = \sum\limits_{j} {m_{j}^{{}} \left( {\frac{{{{\varvec{\sigma}}}_{j}^{{}} + {{\varvec{\sigma}}}_{i}^{{}} }}{{\rho_{i}^{{}} \rho_{j}^{{}} }}} \right) \cdot \nabla_{i}^{{}} w_{ij} } + {{\varvec{\varPi}}}_{i}^{{\text{R}}} $$

(B.17)

$$ {{\varvec{\Pi}}}_{i}^{{\text{R}}} = \sum\limits_{j} {m_{j}^{{}} \left( {\frac{{2C_{ij} \left( {u_{j} - u_{i} } \right)}}{{\rho_{i}^{{}} \rho_{j}^{{}} }}} \right)\nabla_{i}^{{}} w_{ij} } $$

(B.18)

$$ C_{ij} = \frac{{c_{i} \rho_{i} \sqrt {\rho_{i} } + c_{j} \rho_{j} \sqrt {\rho_{j} } }}{{\sqrt {\rho_{i} } + \sqrt {\rho_{j} } }} $$

(B.19)

$$ u_{i} = {\varvec{u}}_{i} \cdot \frac{{{\varvec{r}}_{ij} }}{{\left| {{\varvec{r}}_{ij} } \right|}};\quad u_{j} = {\varvec{u}}_{j} \cdot \frac{{{\varvec{r}}_{ij} }}{{\left| {{\varvec{r}}_{ij} } \right|}} $$

(B.20)

$$ \begin{aligned}u_{i} &= \left( {{\varvec{u}}_{i} + \frac{1}{2}\left\langle {\nabla {\varvec{u}}} \right\rangle_{i}^{c} \cdot {\varvec{r}}_{ij} } \right) \cdot \frac{{{\varvec{r}}_{ij} }}{{\left| {{\varvec{r}}_{ij} } \right|}};\quad\\ u_{j} &= \left( {{\varvec{u}}_{j} - \frac{1}{2}\left\langle {\nabla {\varvec{u}}} \right\rangle_{j}^{c} \cdot {\varvec{r}}_{ij} } \right) \cdot \frac{{{\varvec{r}}_{ij} }}{{\left| {{\varvec{r}}_{ij} } \right|}} \end{aligned}$$

(B.21)

where Eqs. (B.20) and (B.21) correspond to linear and second-order constructions of variables. Here, considering linear construction of variables (Eq. B.20), since we have

$$ u_{j} - u_{i} = {\varvec{u}}_{ij} \cdot \frac{{{\varvec{r}}_{ij} }}{{\left| {{\varvec{r}}_{ij} } \right|}} $$

thus, we can reformulate Eq. (B.18) as:

$$ {{\varvec{\Pi}}}_{i}^{{\text{R}}} = \sum\limits_{j} {m_{j}^{{}} \Pi_{ij}^{{\text{R}}} \nabla_{i}^{{}} w_{ij} } $$

(B.22)

$$ \Pi_{ij}^{{\text{R}}} = \left( {\frac{{2\left| {{\varvec{r}}_{ij} } \right|C_{ij} }}{{\rho_{i}^{{}} \rho_{j}^{{}} }}} \right)\left( {\frac{{{\varvec{u}}_{ij} \cdot {\varvec{r}}_{ij} }}{{\left| {{\varvec{r}}_{ij} } \right|^{2} }}} \right) $$

(B.23)

Therefore, one can see that the AV term and the Riemann term have similarity. Indeed, Meng et al. [22] discussed this similarity and proposed a limiter function for Riemann stabilisation term in order to avoid excessive dissipation. Note that a concise summary of δ versus Riemann density diffusive terms as well as artificial viscosity versus Riemann momentum diffusive terms is presented in Fig. 

Fig. 35

A concise summary of δ versus Riemann density diffusive terms as well as artificial viscosity versus Riemann momentum diffusive terms

35.