Abstract
In this paper, a consistent meshfree Lagrangian approach for numerical analysis of incompressible flow with free surfaces, named least squares moving particle semi-implicit (LSMPS) method, is developed. The present methodology includes arbitrary high-order accurate meshfree spatial discretization schemes, consistent time integration schemes, and generalized treatment of boundary conditions. LSMPS method can resolve the existing major issues of widely used strong-form particle method for incompressible flow—particularly, the lack of consistency condition for spatial discretization schemes, difficulty in enforcing consistent Neumann boundary conditions, and serious instability like unphysical pressure oscillation. Applications of the present proposal demonstrate remarkable enhancements of stability and accuracy.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Today the finite element method (FEM) [101], the finite volume method (FVM) [98], and the finite difference method (FDM) [87] based computational mechanics play a conspicuous role in technology advancement. A noteworthy feature of them is that they divide a continuum domain into discrete subdivision usually called mesh/grid, which requires connectivity based on a topological map; however, the characteristic of them is not always suitable. For instance, in order to adapt topological and geometric changes undergone by the real material, such as simulations of fluid flow or large strain continuum deformation, Lagrangian description (i.e. moving mesh/grid) could be applied; however, one would face distortion of mesh/grid which results in either termination of the computation or severe deterioration in numerical accuracy. Arbitrary Lagrangian Eulerian (ALE) formulations [26, 36] have been developed to overcome the difficulty caused by distortion of mesh/grid, of which objective is to move mesh/grid independently from actual motion of material so that distortion could be minimized; nevertheless, distortion of mesh/grid still remains and causes overwhelming errors in numerical solutions.
Under these circumstances, meshfree methods and/or particle methods, which discretize a continuum by only a set of nodal points or particles, have been sought in order to find better discretization procedures without mesh/grid constraints. Since the connectivity among nodes can be generated anytime desired and can change with time, meshfree/particle methods can easily handle simulations of very large deformations, even with the changes of the topological structure and fragmentation–coalescence of continuum.
In general, according to computational modelings and formulations, meshfree/particle methods can be categorized into two different classifications as well: the weak form formulations of Partial Differential Equations (PDEs); and the strong form formulations of PDEs. The first class of meshfree/particle methods is used with various weak formulations such as Galerkin methods, for example, diffuse element method (DEM) [73], element free Gelerkin (EFG) method [11, 13–15, 67], reproducing Kernel particle method (RKPM) [21, 63–65], h-p cloud method [27, 28, 58, 74], partition of unity method (PUM) [7–9, 69], meshless local Petrov–Gelerkin (MLPG) method [2–6], finite point method (FPM) [75–77, 80], particle finite element method (P-FEM) [38, 78, 79], reproducing Kernel element method (RKEM) [56, 62, 66, 86]. The second category of meshfree/particle methods is used to approximate the strong form PDEs discretized by specific collocation techniques, for instance, smoothed particle hydrodynamics (SPH) method [31, 60, 68, 71, 72], moving particle semi-implicit (MPS) method [48, 49], meshfree finite difference method [57, 59], finite pointset method (FPM) [95–97].
In various weak form meshfree/particle methods, shape functions, or more general meshfree interpolants, are constructed based on the so-called “partition of unity”, then consistency conditions, polynomial completeness, or reproducing conditions are satisfied. On the other hand, although the strong form particle methods such as the SPH method and the MPS method have been shown to be useful widely in engineering applications especially in fluid dynamics, their standard formulae of spatial discretization schemes are not consistent except under very limited conditions, and do not hold polynomial completeness/reproducing conditions or differential completeness/reproducing conditions. According to the Lax’s equivalence theorem [51], this major issue must never be overlooked. Moreover, this matter yields adverse effects for both computational accuracy and stability. Some correction methods for resolving the lack of polynomial completeness or reproducing conditions on the spatial discretization schemes (which will be discussed in Chap. 3) have been proposed; however, they are far from adequate in terms of the compatibility with satisfaction of higher order consistency conditions and numerical stability. Strong form meshfree/particle methods still have a difficulty relating to procedures of enforcing boundary conditions, especially Neumann boundary conditions. Hence, prevailing strong form particle methods, whose advantage is that they can handily run numerical analysis of continuum with large deformation, even with the changes of topological structure and fragmentation–coalescence, are inadequately studied as an accurate mathematical computation.
With taking particular note to controversies described above, we develop a new consistent fully Lagrangian meshfree particle method, named least squares moving particle semi-implicit (LSMPS) method, for numerical analysis of incompressible fluid flow with free surfaces. As its name suggests, LSMPS method is based on the method of weighted “Least Squares” procedure, and follows fundamentals of the MPS method [48, 49]: “Moving Particle” means meshfree fully Lagrangian approach, and “Semi-implicit” represents the type of time integration algorithm for incompressible flow which is well-known as the projection method [33]. LSMPS method succeeds the name of the existing MPS method; however, all of LSMPS formulae are different from of the current MPS method.
In this paper, we introduce a new methodology and formulae as a meshfree Lagrangian approach (particle method), including arbitrary high order accurate meshfree spatial discretization schemes, consistent time integration schemes, and generalized treatment of boundary conditions. Additionally, some numerical demonstrations compared with the conventional MPS solutions show drastic improvement of accuracy and stability.
2 Preliminary
2.1 Notation
In order to expedite the presentation, we introduce some preliminaries for notations. Throughout this paper, the letter \(d\) is a positive integer and denotes the spatial dimension. \(\varOmega \subseteq \mathbb {R}^d\) is a nonempty, open, bounded, and connected set. \(\partial \varOmega \) denotes the boundary of \(\varOmega \), and \(\partial \varOmega \) is assumed to be Lipschitz continuous or smoother, as the case may be.
\(\mathbb {N}_0\) denotes the set of non negative integers. If
is an \(d\)-tuple of non negative integers, we call \(\varvec{\alpha }\) a multi-index. Then, the quantity
is defined to be the length of \(\varvec{\alpha }\). We also use the following conventions:
If \(\varvec{\alpha }, \varvec{\beta } \in \mathbb {N}_0^d\), we say \(\varvec{\beta } \le \varvec{\alpha }\) provided
By the same token,
If \(\mathbf{x} := (x_1, \ldots , x_d)^T \in \mathbb {R}^d\) and \({\varvec{\alpha }} \in \mathbb {N}_0^d\), then \(\mathbf{x}^{{\varvec{\alpha }}}\) is defined as follows:
If \(f(\mathbf{x})\) is a real valued function on an open subset of \(\mathbb {R}^d\), \({\varvec{\alpha }} \in \mathbb {N}_0^d\) and smoothness of \(f\) is assumed enough, then \(D_\mathbf{x}^{{\varvec{\alpha }}}f(\mathbf{x})\) denotes the \({\varvec{\alpha }}\)th order Fréchet derivative of \(f\) as follows:
If \(\mathbf{x} = (x_1, \ldots , x_d)^T\) is an arbitrary point of \(\mathbb {R}^d\), then
denotes the Euclidian norm of \(\mathbf{x}\), and we usually use \(\Vert \mathbf{x}\Vert \) as abridged notation.
2.2 Consistency, completeness, reproducing condition, and the partition of unity
In order to advance concrete discussions on the study of convergence, according to Belytschko et al. [12], three terms are frequently used: (i) Consistency [90] : a property of the discretization schemes for partial differential equations, which is usually utilized in Finite Difference approximations, (ii) Reproducing conditions [64, 65]: the ability of the approximation to reproduce specified functions, which are usually polynomials, (iii) Completeness [37]: polynomial completeness or completeness , which is usually discussed in the FEM.
2.2.1 Consistency
Strikwerda [90] defines the consistency condition of particular operators for approximating derivatives as follows:
Theorem 2.1
(Consistency [12, 90]) A scheme \(L_hu=f\) that is consistent with the differential equation \(Lu=f\) is accurate (consistent) of order p if for any sufficiently smooth function \(v\)
In the above definition, a parameter \(h\) denotes the refinement of mesh/grid and \(p\) refers to the order of consistency. Obviously, it is necessary for convergence that \(p>0\), and we require that \(p \ge 1\) for the efficient numerical calculation.
According to the well-known Lax-Richtmyer equivalence theorem [51], a consistent finite difference scheme for a well-posed partial differential equation is convergent if and only if it is stable. Consequently, any discretization scheme must satisfy the \(p\)th order \((p>0)\) consistency condition to obtain convergence. The consistency is straightforward to verify and stability is typically much easier to show than convergence; therefore, the convergence is usually studied via the Lax-Richtmyer equivalence theorem.
2.2.2 Completeness, reproducing condition, and the partition of unity–nullity
Since ascertaining whether meshfree interpolants are consistent for irregularly distributed nodes is significantly more difficult than examining whether finite difference schemes for a uniform structured grid, the completeness or reproducing conditions which play the same role [12] as the consistency conditionsFootnote 1 are explored, instead.
The reproducing conditions or the completeness are the ability of the approximation to reproduce specified functions which are usually polynomials. One can say that an approximation \(f^h(\mathbf{x})\) is complete to order \(p\) if any given polynomial up to order \(p\) can be reproduced exactly. If an approximation \(f^h(\mathbf{x})\) is given by
where \(\{ \varPhi _i(\mathbf{x}) \}_{1\le i \le N}\) are the interpolant functions and \(\{ f(\mathbf{x}_i) \}_{1\le i \le N}\) are given nodal values for the set of nodes \(\{\mathbf{x}_i\}_{1\le i \le N}\) , then the completeness or the reproducing conditions can be defined as follows:
Theorem 2.2
(\(p\)th order completeness/reproducing condition) For a multi index \(\varvec{\alpha }\in \mathbb {N}_0^d:\,0 \le |\varvec{\alpha }|\le p\), an interplant function \(\varPhi _i(\mathbf{x})\in \mathbb {R}\) holds the \(p\)th order polynomial completeness/reproducing condition if it satisfies:
or equivalently,
Some meshfree discretization schemes are formulated to satisfy alternatives, the differential completeness or the differential reproducing conditions which are requirement that the derivatives of a polynomial field be reproduced correctly. They can be defined directly from Theorem 2.2 by taking derivatives of Eqs. (11) and (12), i.e.
Theorem 2.3
(\(p\)th order differential completeness/reproducing condition) Let an interplant function \(\varPhi _i(\mathbf{x}) \in C^k(\mathbb {R}^d)\). For multi indicies \(\varvec{\alpha }, \varvec{\beta }\in \mathbb {N}_0^d:\,0 \le |\varvec{\alpha }|\le p, 0 \le |\varvec{\beta }|\le k(\le p)\), an interplant function \(\varPhi _i(\mathbf{x})\) holds the \(p\)th order differential completeness/reproducing condition if it satisfies:
or equivalently,
It should be noted that the Theorem 2.2 and 2.3 are similar to \(p\)th order consistency condition and \(p\)th order differential consistency condition for RKPM shape function [55, 65], respectively.
If \(\varvec{\alpha } = \mathbf{0}\), Eqs. (11) and (12) become
and if \(\varvec{\alpha } \ne \mathbf{0}\), Eq. (11) does
These are the origin of the name “The Partition of Unity”, and “The Partition of Nullity”. These properties are closely related with not only meshfree interpolant [65] but also mesh-based one. Obviously, since FEM interpolant functions, called shape functions satisfy the Kronecker delta property, they are constructed based on the partition of unity–nullity. Moreover, weighting coefficients of linear combination on the finite difference schemes are built on the partition of unity–nullty to obtain certain order of consistency.
Interestingly, Liu et al. [65] showed that least squares based interpolants provide achievement of polynomial completeness/reproducing conditions, or so-called the partition of unity–nullity—vice versa, corrected interpolant formulae to fulfill the polynomial completeness/reproducing conditions are quite identical to the production derived from least squares procedures. Chakravarthy [17] showed the fundamental concept of the finite difference schemes that to determine unknowns emerged from Taylor expansion or polynomial approximation is generalization of finite difference operator. Also, it yields normal equations which is the very idea of the linear least squares approaches.
With focusing attention to a close relationship of consistency, completeness/reproducing conditions, and the partition of unity–nullity, and leveraging the fact that the least squares schemes contribute achievement of arbitrary high-order consistency conditions for meshfree spatial discretization schemes, we develop new formulae in the next section.
3 Meshfree spatial discretization schemes
3.1 An overview of the existing meshfree spatial discretization schemes
As mentioned it in the introduction, various meshfree and/or particle methods have been sought, in order to discretize a domain without mesh/grid constraints. There are a lot of discretization schemes for meshfree interpolants and meshfree finite difference. One of the most prevalent particle methods is the SPH method which discretizes partial differential equations by a integral representation collocation technique. Even though the SPH method has achieved a lot of success in computational mechanics, it has not been viewed as an accurate mathematical computation which stems from the fact that it lacks a rigorous convergence theory as well as a successive refinement procedure [81].
The early SPH interpolants do not satisfy the discrete partition of unity and nullity [63] except under very limited conditions. This means the defection of SPH interpolants 0th or higher order completeness/reproducing conditions in general particle distribution, which results in incapability of representing rigid body motion correctly, even though it is Galilean invariant (rigid body translation only). Also, the primal SPH gradient operator and Laplace operator generally have analogous problem. In order to solve this matter, several correction schemes have been proposed, for example, Monaghan’s symmetrization on derivative approximation [70, 71], Johnson–Beissel correction [41], Randles–Libersky correction [82], Krongauz–Belytschko correction [12], Chen–Beraun correction [18–20], Bonet-Kulasegaram integration correction [16], Aluru’s collocation RKPM [1], Zhang–Batra correction [99, 100]. They correct SPH kernel interpolant to satisfy completeness/reproducing condition in the interpolation field, or equivalently, to modify SPH derivative approximation operators directly to meet derivative completeness/reproducing condition in the derivative of the interpolants. It must be mentioned that almost all 1st or higher order consistent corrected formulae as listed above are based on the least squares methods, for instance, the most widely used 1st order consistent gradient approximation operator for the SPH method developed by Randles–Libersky [82] is one of the least squares based discretizations.
Least squares procedures are excellent with meshfree interpolants or meshfree finite difference schemes. Liu et al. [65] demonstrate that moving least squares (MLS) [50] approximation is equivalent to reproduced Kernel (RK) interpolant [65] which are corrected kernel approximation based on the reproducing conditions. MLSRK interpolant can provide arbitrary high order consistency condition, and is the contemporary version of the classical MLS one since the basic concept of reproducing kernel, or more generally speaking, the fundamentals of the partition of unity–nullity incubates various derivation of meshfree interpolants [54, 61, 62] . With taking particular note of the SPH kernel interpolant inconsistency, Dilts [24, 25] utilizes MLS interpolant [50] to improve the accuracy of the SPH kernel approximation, so-called moving least squares particle hydrodynamics (MLSPH). Since MLS can construct sufficiently smoothed interpolation globally with optional order of polynomial completeness/reproducing conditions, it is widely used in meshfree/particle methods, such as various Galerkin meshfree approach listed in Introduction (e.g. DEM, EFGM, RKPM, etc. ).
Since the early MPS gradient operator and Laplace operator [49] generally lack 1st or higher order differential completeness/reproducing condition except under very limited conditions (e.g. regular particle distribution is assumed), varied correction techniques have been proposed in order to enhance the accuracy of the MPS method. For instance, Khayyer–Gotoh gradient operator anti-symmetrization [42], Khayyer–Gotoh divergence operator correction [43], Khayyer–Gotoh Laplace operator correction [44], Khayyer–Gotoh gradient operator correction [45], and Suzuki gradient operator correction [39, 91] are proposed. Only Suzuki method based on weighted least squares technique can achieve 1st order consistency for gradient operator; however, others do not hold differential completeness/reproducing conditions in general case. In other words, they are far from satisfaction of high order accuracy. Of course, similar to adopting least squares approach into SPH method, least squares based formulae can be introduced to the MPS method. Koh et al. [46] utilize two dimensional second order generalized finite difference schemes [57, 59] based on weighted least squares to the MPS method. Tamai et al. [93] formulate generalized finite difference schemes based on the weighted least squares for the MPS method, which provides arbitrary high order consistency and can be applied for arbitrary dimension.
Consistent least squares based spatial discretization finite difference schemes [46, 57, 59, 91, 93] resolve the rack of polynomial completeness/reproducing conditions on the MPS method so that high order consistency conditions are fulfilled and absolute enhancement of accuracy would be given; however, utilizing least squares based scheme raise a new problem—normal equations derived from the least squares procedures will be ill-conditioned problems which results in either serious deterioration in numerical accuracy and stability or termination of the computation. Selecting neighborhood stenciles [59] to circumvent this ill-conditioned problems is proposed; however, this technique can not be the fundamental solution since the condition numbers of coefficient matrices derived from the least squares, so-called the “moment matrices”, are not independent from characteristic length of calculation points spacing.
In order to overcome the weakness of the least squares based spatial discretization schemes that normal equations shall be ill-conditioned and to obtain high order consistency conditions from them, we reformulate the least squares based schemes in the next section.
3.2 A new meshfree spatial discretization schemes based on the weighted least squares procedure
3.2.1 Stone–Weierstrass theorem of locally compact version
Let \(f : \mathbb {R}^d \rightarrow \mathbb {R}\) be a sufficiently smooth functionFootnote 2 that is defined on a simply connected open set \(\varOmega \subseteq \mathbb {R}^d\). According to the Stone-Weirestrass theorem of locally compact version [84, 88, 89], for a fixed point \(\bar{\mathbf{x}} \in \bar{\varOmega }\), one should always be able to approximate \(f(\mathbf{x})\) by a polynomial series locally. Thus, we can define a local function
where
If the function \(f(\mathbf{x})\) is smooth enough as assumed, there exists a local operator \(L_{\bar{\mathbf{x}}} : C^0 (B(\bar{\mathbf{x}})) \rightarrow C^p (B(\bar{\mathbf{x}}))\) s.t.
where
is \(p\)th order complete polynomial basis, and \(\mathbf{a}(\bar{\mathbf{x}})\) is coefficient vector. Utilizing Taylor expansion of approximated polynomial function around \(\mathbf{x}_i\) with nearby point \(\mathbf{x}_j \in B(\bar{\mathbf{x}})\) yields
where
is the residual of local polynomial approximation. Equation (21) is a well-known form of Taylor expansion, and we use it several times in this paper without special note again.
3.2.2 Weight function
We use the weighted least squares procedures for new spatial discretization schemes formulae, then the weight(window) function which satisfy the following conditions is defined.
where \(r_e\) is the dilation parameter and the radius of compact support of the weight function. In the LSMPS method, singular weight function like
which is usually used in the MPS method, could be applied; therefore, the condition of non-singularity (Eq. 24) is not necessarily for the weight function. For obtaining stable calculation, however, application of non-singular weight functions is highly recommended.
3.2.3 Standard scheme type-A
We define new meshfree spatial discretization schemes with arbitrary high order consistency conditions.
Derivation:
According to the Stone–Weierstrass theorem discussed in the Sect. 3.2.1, and utilizing Taylor expansion of local polynomial approximation, one can obtain
If we use weighted least squares technique to minimize weighted squared residuals
associated with the residual \( R_{ij}^{p+1}\) and weight function \(w_{ij}\), normal equations equivalent to the existing spatial discretization formulae [59, 93] based on the weighted least squares procedure are provided; however, they must be ill-conditioned if \(p \ge 2\) as discussed in Sect. 3.1. In order to fix this issue, we now introduce adroit variable transformation for unknowns s.t.
where \(r_s : 0 < r_s \le r_e\) is the scaling parameter, then Eq. (36) can be equivalently transformed into
One can transliterate this equation with symbols \(\mathbf{D}_\mathbf{x},H_{r_s},\mathbf{p}(\mathbf{x})\) defined by Eqs. (30), (31), and (34),
and applicate the weighted least squares procedures. If we define a discrete functional associated with \(R_{ij}^{p+1}\),
normal equations can be provided by minimizing functional \(J\), i.e.
One can transliterate the above with symbols \(\mathbf{M}_i,\mathbf{b}_i\) defined by Eqs. (32) and (33),
Thus, if the moment matrix \(\mathbf{M}_i\) is not singular, solutions \(H_{r_s}^{-1}\mathbf{D}_{\mathbf{x}}f^h(\mathbf{x}_i)\) are uniquely determined by solving normal equations,
Finally, since the scaling matrix \(H_{r_S}\) defined by Eq. (31) is always non-singular and invertible, we can obtain the Standard LSMPS scheme formulae type-A,
Remark 3.2
Introducing scaling for the basis is not a brand new technique since MLSRK interpolant [65] already installed it; however, it must be mentioned that there exists a concrete difference. MLSRK basis utilizes dilation parameter \(\varrho ( = r_e)\) for scaling the basis. On the other hand, LSMPS formulae employs another parameter \(r_s : 0 < r_s \le r_e = \varrho \) for scaling. This minor change results in major alteration in the condition number of moment matrices, which will be investigated in later.
Since the standard LSMPS schemes type-A are derived from the weighted least squares method, heritages from the past studies related to the least squares one could be applied.
Definition 3.3
(\((r_e,p)\)-regularity on the standard LSMPS scheme type-A) A family of particle distribution \(\{\mathbf{x}_i\}_{ 1 \le i \le N }\) is said to be \((r_e,p)\)-regular, if there exists a constant \(C\) s.t.
When \(\{\mathbf{x}_i\}_{1 \le i \le N}\) is \((r_e,p)\)-regular, the condition number of \(\mathbf{M}_i\), which is equal to \(\Vert \mathbf{M}_i \Vert \Vert \mathbf{M}_i^{-1} \Vert \) will be uniformly bounded. It must be mentioned that the definition of \((r_e,p)\)-regularity above is nearly accordance with the concept of \((\varrho ,p)\)-regularity, which has been introduced by Han and Meng [34] for the RKPM.
Definition 3.4
(Admissible particle distribution on the standard LSMPS scheme type-A) For a given particle distribution \(\{\mathbf{x}_i\}_{1 \le i \le N}\), let \(\bar{B}(\mathbf{x}, r) := \left\{ \mathbf{x}' \in \mathbb {R}^d\ \ | \ \Vert \mathbf{x} - \mathbf{x}' \Vert \le r \right\} \), fill distance : \(h_{\mathbf{x}, \varOmega } := \displaystyle \sup _{\mathbf{x} \in \varOmega } \min _{1 \le i \le N} \Vert \mathbf{x} - \mathbf{x}_i \Vert \), and separation distance : \(\eta _\mathbf{x} := \frac{1}{2}\displaystyle \min _{j \ne i} \Vert \mathbf{x}_j - \mathbf{x}_i \Vert \), then admissible particle distribution on the standard scheme type-A is defined as follows:
Theorem 3.5
(Consistency of the Standard LSMPS scheme type-A) Let \(f : \mathbb {R}^d \rightarrow \mathbb {R}\) be a sufficiently smooth function that is defined on a open set \(\varOmega \subset \mathbb {R}^d\), and assume that \(f(\mathbf{x}) \in C^{p+1}(\varOmega )\). For multi-index \(\varvec{\alpha }: 1\le |\varvec{\alpha }| \le p\), there exists a constant \(C : 0 \le C <\infty \), then Standard LSMPS scheme type-A holds the following consistency condition.
Proof
Utilizing Taylor expansion of \(f(\mathbf{x}) \in C^{p+1}(\varOmega )\) yields
where
then one can obtain
Now we can transliterate the above equation with symbols \(\mathbf{D}_\mathbf{x}, H_{r_s}, \mathbf{p}(\mathbf{x})\) defined by Eqs. (30), (31), and (34)
Multiplying \(\mathbf{p}\left( (\mathbf{x}_j - \mathbf{x})/r_s\right) \) to lead normal equations provides
and multiplying compactly supported weight function \(w:\mathbb {R}^d \rightarrow \mathbb {R}\) and taking summation of index \(j : j \in B(\bar{\mathbf{x}})\) makes
Hence, if \((r_e, p)\)-regularity is assumed,
Consequently,
As a result,
\(\square \)
3.2.4 Standard scheme type-B
We can derive another meshfree spatial discretization scheme with slight change from the standard schemes type-A, as named Standard LSMPS schemes type-B which satisfies arbitrary high order consistency conditions.
Derivation:
Similar to the derivation of the standard scheme type-A, according to the Stone–Weierstrass theorem discussed in the Sect. 3.2.1, and with utilizing Taylor expansion of local polynomial approximation, one can obtain
In order to resolve the problem that normal equations derived from the least squares procedure shall be ill-conditioned, we introduce astute variable transformation for unknowns s.t.
where \(r_s : 0 < r_s \le r_e\) is the scaling parameter, then Eq. (72) can be equivalently transformed into
One can transliterate this equation with symbols \(\widehat{\mathbf{D}_\mathbf{x}},\widehat{H_{r_s}},\widehat{\mathbf{p}}(\mathbf{x})\) defined by Eq. (66), (67), and (70),
and adopt the weighted least squares procedures. If we define a discrete functional associated with \(\widehat{R_{ij}^{p+1}}\),
normal equations can be provided by minimizing functional \(J\), i.e.
One can transliterate the above with symbols \({\widehat{\mathbf{M}}_i},\widehat{\mathbf{b}_i}\) defined by Eq. (68) and (69),
Thus, if the moment matrix \(\widehat{\mathbf{M}_i}\) is not singular, solutions \(\widehat{H_{r_s}}^{-1}\widehat{\mathbf{D}_{\mathbf{x}}}f^h(\mathbf{x}_i)\) are uniquely determined by solving normal equations, then
Finally, since the scaling matrix \(\widehat{H_{r_s}}\) defined by Eq. (67) is always non-singular, we can obtain the standard LSMPS scheme formulae type-B,
Remark 3.7
The difference between the standard scheme type-A and type-B is degree of freedoms of a linear system derived from the weighted least squares method. The standard scheme type-B can provide interpolation of function \(f\) on each point \(\mathbf{x}_i\). Obviously, interpolated \(f^h(\mathbf{x}_i)\) is not equal to a value \(f(\mathbf{x}_i)\) which calculation point \(\mathbf{x}_i\) holds in general. Additionally, standard LSMPS scheme type-B is a special case of the moving least squares formulae [50] with introducing scaling parameter for the basis. Consequently, we can get some modification of MLS interpolant as the following.
Definition 3.8
(Modified Moving Least Squares interpolant (Continuous form)) Let \(f : \mathbb {R}^d \rightarrow \mathbb {R}\) be a sufficiently smooth functionFootnote 3 that is defined on a simply connected open set \(\varOmega \subset \mathbb {R}^d\). There exists a global mapping operator \(G : C^0(\varOmega ) \rightarrow C^p(\varOmega )\) s.t.
Definition 3.9
(Modified Moving Least Squares interpolant (Discrete form)) Let \(f : \mathbb {R}^d \rightarrow \mathbb {R}\) be a sufficiently smooth function that is defined on a simply connected open set \(\varOmega \subset \mathbb {R}^d\). There exists a global mapping operator \(G : C^0(\varOmega ) \rightarrow C^p(\varOmega )\) s.t.
Definition 3.10
(Modified Moving Least Squares Reproducing Kernel interpolant (Discrete form)) Let \(f : \mathbb {R}^d \rightarrow \mathbb {R}\) be a sufficiently smooth function that is defined on a simply connected open set \(\varOmega \subset \mathbb {R}^d\). There exists a global mapping operator \(G : C^0(\varOmega ) \rightarrow C^p(\varOmega )\) s.t.
Definition 3.11
(\((r_e,p)\)-regularity on the standard LSMPS scheme type-B) A family of particle distribution \(\{\mathbf{x}_i\}_{ 1 \le i \le N }\) is said to be \((r_e,p)\)-regular, if there exists a constant \(C\) s.t.
Definition 3.12
(Admissible particle distribution on the standard LSMPS scheme type-B) For a given particle distribution \(\{\mathbf{x}_i\}_{1 \le i \le N}\), let \(\bar{B}(\mathbf{x}, r) := \left\{ \mathbf{x}' \in \mathbb {R}^d\ \ | \ \Vert \mathbf{x} - \mathbf{x}' \Vert \le r \right\} \), fill distance : \(h_{\mathbf{x}, \varOmega } := \displaystyle \sup _{\mathbf{x} \in \varOmega } \min _{1 \le i \le N} \Vert \mathbf{x} - \mathbf{x}_i \Vert \), and separation distance : \(\eta _\mathbf{x} := \frac{1}{2}\displaystyle \min _{j \ne i} \Vert \mathbf{x}_j - \mathbf{x}_i \Vert \), then admissible particle distribution on the standard scheme type-B is defined as follows:
Theorem 3.13
(Consistency of the Standard LSMPS scheme type-B) Let \(f : \mathbb {R}^d \rightarrow \mathbb {R}\) be a sufficiently smooth function that is defined on a open set \(\varOmega \subset \mathbb {R}^d\), and assume that \(f(\mathbf{x}) \in C^{p+1}(\varOmega )\). For multi-index \(\varvec{\alpha }: 1\le |\varvec{\alpha }| \le p\), there exists a constant \(C : 0 \le C <\infty \), then Standard LSMPS scheme type-B holds the following consistency condition.
Proof
Since proof of this theorem can be demonstrated with almost the same strategy as the theorem 3.5 for the standard scheme type-A, we will omit it.\(\square \)
3.2.5 Meshfree compact scheme
In the FDM, spatial discretization schemes can be categorized as explicit schemes or implicit schemes so-called compact schemes [53]. The former can be expressed as linear combination of functional value, i.e. \(\alpha \)th order derivative of sufficiently smooth function \(f\) is approximated by
where coefficient \(C_j\) is determined by the partition of unity–nullity to achieve a certain order of consistency condition. On the other hand, the later schemes so-called compact schemes utilize not only functional value but also derivatives to approximate derivatives; therefore, \(\alpha \)th order derivative of sufficiently smooth function \(f\) is approximated by
where coefficient \(C_{j,k}\) is also determined by the partition of unity–nullity to achieve a certain order of consistency condition. Noteworthy characteristics of compact schemes is achievement of higher accuracy and resolution compared with the same order accurate explicit finite difference schemes. Although compact schemes require solving a linear system, their higher accuracy and resolution provide reduction of total calculation cost. Various higher order accurate schemes with higher resolution have been sought to obtain both more accurate solutions and retrenchment of calculation cost [10, 53].
Since the compact schemes utilized in the FDMs are designed for one dimensional uniform structured grid, they cannot be applied for arbitrary unstructured gird or meshfree framework. Hence, we develop novel arbitrary high order accurate compact schemes that can be applied for arbitrary unstructured grids and meshfree framework in optional dimensions.
Derivation:
According to the Stone–Weierstrass theorem discussed in the Sect. 3.2.1, and utilizing Taylor expansion of \(p+q\)th order local polynomial approximation, one can obtain
For a multi index \(\varvec{\beta }: 0 \le |\varvec{\beta }| \le q\), if \(D_{\mathbf{x}}^{\varvec{\beta }} f(\mathbf{x}) \in C^{0} (\varOmega )\) is assumed, one can define \(p+q-|\varvec{\beta }|\)th order local polynomial approximation of \(D_\mathbf{x}^{\varvec{\beta }} f(\mathbf{x})\) with the Stone–Weierstrass theorem. Due to this, utilizing Taylor expansion for approximated \(L_{\bar{\mathbf{x}}}D_\mathbf{x}^{\varvec{\beta }}f (\mathbf{x})\) yields
Now, we try to eliminate the second summation in the Eq. (104)
by utilizing linear combination of Eq. (105), in order to achieve an extra higher order truncation limits than standard explicit schemes. This is the fundamental concept of the compact schemes that additional degrees of freedom of derivatives are utilized to cancel out higher order truncation errors. Specifically, for multi indices \({\varvec{\alpha }} : 0 \le |\varvec{\alpha }| \le p, {\varvec{\beta }} : 1\le |\varvec{\beta }| \le q \le p\), the identity of \( D_\mathbf{x}^{\varvec{\alpha }} f^h (\mathbf{x}_i)\) s.t.
completes the purpose. Solving the above identity provides coefficients \(C(\varvec{\beta }, p, q)\), s.t.
Multiplying this coefficient to Eq. (105) and taking summation for multi-index \(\varvec{\beta }: 0 \le |\varvec{\beta }| \le q\) yields
where \(C({\varvec{\beta }}, p, q)(\mathbf{x}_j - \mathbf{x}_i)^{\varvec{\beta }}\widehat{R_{ij, \varvec{\beta }}^{p+q+1-|\varvec{\beta }|}} := \widetilde{R_{ij, \varvec{\beta }}^{p+q+1}} \) is the residuals of polynomial approximation which satisfy \(\forall \varvec{\beta }: 0 \le |\varvec{\beta }| \le q, \quad \widehat{R_{ij, \varvec{\beta }}^{p+q+1}}= \fancyscript{O}(\Vert \mathbf{x}_j - \mathbf{x}_i\Vert ^{p+q+1})\). One can transliterate this equation with symbols \(\widehat{H_{r_s}'},\widehat{ \mathbf{D}_\mathbf{x}}, \widehat{\mathbf{p}(\mathbf{x}})\) defined by Eq. (96), (97) and (101),
and adopt the weighted least squares procedures. If we define a discrete functional associated with \(\widetilde{R_{ij, {\varvec{\beta }}}^{p+q+1}}\),
normal equations can be provided by minimizing functional \(J'\), i.e.
One can transliterate the above with symbols \(\widehat{\mathbf{M}_i}, \widehat{\mathbf{b}_i''}\) defined by Eq. (98), and (100),
Thus, if the moment matrix \(\widehat{\mathbf{M}_i}\) is not singular, solutions \(\widehat{H_{r_s}'}^{-1}\widehat{\mathbf{D}_{\mathbf{x}}}f^h(\mathbf{x}_i)\) are uniquely determined by solving normal equations, so
Finally, since the scaling matrix \(\widehat{H_{r_s}'}\) defined by Eq. (97) is always non-singular, we can obtain the meshfree compact schemes formulae,
Remark 3.14
Although we defined two types of standard schemes, meshfree compact scheme are limited to only a type-B formulation if the condition \(p=q\) is satisfied. This is attributed to rank deficiency of scaling matrix for type-A formulae, s.t.
If \(p=q\),
thereby, rank deficiency of scaling matrix \(H_{r_s}'\) occurs. If \(q < p\), this problem for type-A formulation does not arise; however, a condition \(p=q\) provides the highest \(2p\)th order consistency with \(p\)th order polynomial basis. In consequence, we defined only type-B formulae of meshfree compact schemes since rank deficiency of scaling matrix for type-B defined by Eq. (97) does not happen. This mean that
thus, the scaling matrix \(\widehat{H_{r_s}'}\) is always invertible.
Theorem 3.15
(Consistency of the meshfree compact scheme) Let \(f(\mathbf{x}) \in C^{p+q+1}(\varOmega )\) that is defined on a simply connected open set \(\varOmega \subset \mathbb {R}^d\). For multi-index \(\varvec{\alpha }: 1\le |\varvec{\alpha }| \le p\), there exists a constant \(C : 0 \le C <\infty \), then meshfree compact scheme holds the following consistency condition.
Proof
Since proof of this theorem can be demonstrated with almost the same strategy as the standard scheme type-A and type-B, it will not be discussed.
Similar to the relationship between the standard schemes type-B and the MLS interpolant, meshfree compact schemes can provide MLS-like interpolant function. Since utilizing derivatives for interpolant is based on the Hermite interpolation technique, we can define Hermite-type MLS interpolant function as follows:
Definition 3.16
(Hermite-type Moving Least Squares interpolant (Discrete form)) Let \(f : \mathbb {R}^d \rightarrow \mathbb {R}\) be a sufficiently smooth function that is defined on a simply connected open set \(\varOmega \subset \mathbb {R}^d\). There exists a global mapping operator \(G:C^0(\varOmega ) \rightarrow C^p(\varOmega ) \) s.t.
Note that this interpolant function is completely different from the Generalized MLS(GMLS) [2], since GMLS formulae cannot achieve an extra higher order truncation limit than the order of polynomial basis.
3.3 Numerical demonstrations
In this section, we would like to show the advantages of new schemes.
3.3.1 Calculation conditions
In order to compare accuracy and convergence rates of schemes, derivatives of the following non-linear function [29, 30]
defined on a domain \(\varOmega := \{ (x,y) \in \mathbb {R}^2 \ | \ [0,1] \times [0,1] \}\), is calculated. A set of calculation points \(\{ \mathbf{x}_i \}_{1 \le i \le N}\) is distributed quasi-randomly by the following generation process; (i) : distribute nodal points \(\{ \mathbf{x}_i ' \}_{1 \le i \le N}\) on the two dimensional uniformly structured square lattice with width \(h\), (ii) : give relative perturbation \(\{ \delta \mathbf{x}_i \}_{1 \le i \le N}\) by two dimensional normal distribution with parameters \(\mu =0, \sigma = 0.10\), where \(\mu , \sigma \) denote the expectation of the distribution and the standard deviation, respectively. Consequently, positions of irregularly arranged calculation points \(\{ \mathbf{x}_i \}_{1 \le i \le N} = \{\mathbf{x}_i ' + \delta \mathbf{x}_i \}_{1 \le i \le N}\). As a measure of accuracy, discrete relative nodal supreme error norm
is utilized. Furthermore, in order to confirm an effectiveness of introducing scaling parameter \(r_s\) to resolve ill-conditioned system, the maximum condition number of moment matrices
and averaged condition number of moment matrices
are exploited. In this analysis, MLS interpolant [50] with consistent derivative, MLSRKPM interpolant [65] with consistent derivative, standard LSMPS scheme type-A, standard LSMPS scheme type-B, and meshfree compact scheme are appropriated. On the least squares based schemes, 2nd order, 3rd order, and 4th order polynomial basis are used, respectively. 4th order spline function (\(w \in C_0^2 (\mathbb {R}^d)\)) is chosen as a weight function for all schemes. Dilation parameters and scaling parameters used in this numerical tests are shown in Table 1. Note that numerical experiments performed by Tamai et al. [93] showed that a gradient operator and a Laplace operator of the existing MPS method [49] do not converge with constant dilation parameter for the compact support of the weight functions.
3.3.2 Calculation results
Convergence rates of \(e_{\infty }^{(1,0)}, e_{\infty }^{(0,1)}\) Footnote 4 are shown in Figs. 1 and 2, and comparison of condition numbers of moment matrices are displayed in Figs. 3, 4, 5, 6, 7, and 8. Figures 1 and 2 show that the existing MLS, MLSRKPM, and present standard LSMPS schemes type-A/B achieve almost the same accuracy and convergence rate with the same order polynomial basis up to certain order \(p\); however, it is notable that standard LSMPS schemes do not require complicated differentiation of interpolant functions since standard LSMPS schemes calculate derivatives directly. For this reason, standard LSMPS schemes provide reduction of calculation cost for strong-form meshfree spatial discretization with arbitrary high order accuracy. Standard LSMPS schemes type-A and type-B are equally matched in terms of accuracy and convergence rate, whereas calculation waits of them are clearly different. Since number of unknowns in normal equations of type-A formulation is just one less than type-B, from a perspective of calculation cost we can conclude that type-A formulae are preferable to type-B. Incidentally, inversion of accuracy between schemes \(p=3\) and \(p=4\) occurs partially. This phenomena is attributed to choice of dilation parameter. On the explicit spatial discretization schemes, a larger dilation parameter is required for higher order approximation which results in increase of calculation time.
Convergence rates of \(e_{\infty }^{(1,0)}\) (MLS, MLSRKPM, Standard LSMPS-A/B schemes, and 4th order meshfree compact scheme)
Convergence rates of \(e_{\infty }^{(0,1)}\) (MLS, MLSRKPM, Standard LSMPS-A/B schemes, and 4th order meshfree compact scheme)
Averaged condition number of moment matrices (MLS, MLSRKPM, LSMPS) \((p = 2)\)
Averaged condition number of moment matrices (MLS, MLSRKPM, LSMPS) \((p = 3)\)
Averaged condition number of moment matrices (MLS, MLSRKPM, LSMPS) \((p = 4)\)
Maximum condition number of moment matrices (MLS, MLSRKPM, LSMPS) \((p = 2)\)
Maximum condition number of moment matrices (MLS, MLSRKPM, LSMPS) \((p = 3)\)
Maximum condition number of moment matrices (MLS, MLSRKPM, LSMPS) \((p = 4)\)
Worthy of special mention is excellent accuracy of meshfree compact scheme. Drawing a comparison between 2nd-order explicit schemes and 4th-order meshfree compact scheme with the same dilation parameter and the same order basis demonstrates higher accuracy of the compact scheme, and it beyonds comparison. Moreover, comparing between 4th-order explicit schemes and 4th-order meshfree compact scheme shows the advantage of meshfree compact scheme from the standpoint of accuracy. Note that if 4th-order polynomial basis is utilized for least squares approximation, meshfree compact scheme can achieve up to 8th order consistency for the first derivatives. Although meshfree compact schemes require several times iterative procedure, they can contribute astonishingly higher accuracy and higher order convergence rate than existing explicit meshfree spatial discretization schemes.
Figures 3, 4, 5, 6, 7, and 8 demonstrate that the effects of introducing scaling parameter \(r_s\) for the basis of the weighted least squares method are significant. Condition numbers of MLS moment matrix are not bounded, in other words, smaller calculation point spacing makes larger condition number of moment matrix.Footnote 5 This is extremely dangerous case in numerical calculation. On the other hand, maximum condition numbers of MLSRK moment matrces and LSMPS moment matrices are uniformly bounded; however, condition numbers of MLSRK moment matrixces are certainly larger than LSMPS’s. As discussed in Remark 3.2, introducing scaling parameter \(r_s\) instead of dilation parameter \(r_e\) is a slight change from the idea of MLSRK basis; however, it makes an enormous difference for the condition number. Lower condition number provided by the present technique yields avoidance of ill-conditioned problem which results in enhancement of stability and accuracy in practical numerical calculations.Footnote 6
4 Time integration scheme and boundary conditions
4.1 The rotational pressure-correction projection method
The classical projection scheme of Chorin [22] based on the Helmholtz decomposition theorem and its derivations are commonly utilized for numerical analyses of incompressible flow. Consider the incompressible flow governed by the Navier–Stokes equations and the mass conservation
where \(\mathbf{u},\, \rho ,\, \nu ,\, P,\, \mathbf{f}\) denotes velocity vector, density, kinematic viscosity, pressure, and body force, respectively. There are a lot of derivations of projection scheme. For instance, assume that \(\mathbf{u}\) be a sufficiently smooth function, the pressure-correction schemes can be written into the following generalized form [33]:
1st Step :
with boundary condition
2nd Step :
with boundary conditions
where \(\varGamma \) denotes the boundary of a domain, and modified pressure \(\phi \) is defined as follows:
Although \(s\)th order backward difference formulae that approximate \(D\mathbf{u}/Dt\) are applied in the above equations, other consistent time discretization schemes are perfectly acceptable.Footnote 7 \(\chi \) is a user-defined coefficient that equal to \(0\) or \(1\). The choice \(\chi = 0\) yields the standard pressure-correction projection schemes, whereas \(\chi = 1\) gives the rotational pressure-correction schemes. An important difference between the standard pressure-correction schemes and the rotational forms appear in the Neumann boundary condition for pressure Poisson equations. The former enforce the homogeneous Neumann boundary condition, s.t.
this non-physical inconsistent Neumann boundary conditions enforced on the pressure introduces the numerical boundary layer which limits the accuracy of time integration schemes [33, 83]. The later, the rotational schemes, however, enforce the non-homogeneous Neumann boundary condition, s.t.
which, unlike Eq. (140), is a consistent pressure boundary condition derived from a velocity boundary condition \(\mathbf{u}\cdot \mathbf{n}|_{\varGamma }\). This is the origin of the name of “rotational” projection method.Footnote 8 Therefore, we adopt the rotational pressure-correction projection scheme in order to obtain consistent time integration for LSMPS method.
Since LSMPS method will treat incompressible flow with free surfaces and boundary walls, we now modify and reformulate the rotational pressure-correction schemes as follows:
In Definition 4.1, \(\varGamma _D,\, \varGamma _D',\, \varGamma _N'\) denotes Dirichlet boundary (boundary wall) on the velocity, Dirichlet boundary (free surface) on the pressure, and Neumann boundary (boundary wal) on the pressure, respectively. Taking divergence of Eq. (146) and utilizing divergence free condition of the velocity \(\nabla \cdot \mathbf{u}^{k+1} =0\) yield modified pressure Poisson equations, s.t.
with boundary conditions
It should be noticed that if Dirichlet boundary condition on the pressure \(P^{k+1}|_{\varGamma _D'} = 0\) were enforced, Dirichlet boundary condition on the modified pressure would be \(\phi ^{k+1}|_{\varGamma _D'} = \mu \nabla \cdot \tilde{\mathbf{u}}\). On the free surfaces, incompressible condition \(\nabla \cdot \tilde{\mathbf{u}} = 0\) must be satisfied, then Dirichlet boundary condition on the modified pressure would be \(\phi ^{k+1}|_{\varGamma _D'} = 0\). Note that solving modified pressure Poisson equation (153) is equivalent to calculating consistent pressure Poisson equations s.t.
with consistent non-homogeneous Neumann boundary condition. One can observe from Eq. (153) and (156) that source term of consistent Poisson equation is simplified by the introduction of the rotational forms.
Note that time discretization schemes applied on the moving particle steps and the velocity evolution steps can be replaced any other higher order time discretization schemes.
4.2 Generalized Neumann boundary conditions enforcement
In numerical calculations, treatment of boundary conditions plays a role as important as consistency and stability of discretization schemes. In order to consummate LSMPS method as a numerical method for solving partial differential equations, we have to consider both Dirichlet and Neumann boundary conditions on the velocity or the pressure.
Since LSMPS method is based on the strong-form formulations, Dirichlet boundary conditions can be easily treated by substitutiing of boundary values. On the other hand, Neumann boundary condition enforcing is relatively difficult. This seems to be commonality in the strong-form numerical methods. For instance, in the FDM, utilizing higher order spatial discretization schemes yields more complicated formulations of “one-sided finite difference schemes” to enforce Neumann boundary conditions. This problem is a remarkable tendency in two or three dimensional analysis which results in difficulty of programming code implementation and maintenance.
In the existing particle method with semi-implicit algorithm for incompressible fluid such as projection SPH method [23], incompressible SPH method [85], and MPS method [49, “dummy particle” approach for boundary walls is usually applied, and homogeneous pressure Neumann boundary condition is implemented with modification procedures of coefficient matrix for the discretized Laplace operator of the pressure Poisson equations; however, they are inconsistent as long as their discrete Laplace operator schemes and the homogeneous pressure boundary condition enforcement are inconsistent.
In order to construct a generalized procedure to enforce consistent Neumann boundary conditions, we define a new constrained scheme based on the weighted least squares method.
Recall that we introduced variable transformations to avoid ill-conditioned linear system derived from the least squares procedures s.t.
to formulate Standard LSMPS schemes type-A/B, and assume that outer normal unit vector \(\mathbf{n}\) is uniquely defined on the boundary of the domain \(\varGamma \) and Neumann boundary condition of sufficiently smooth function \(f\) is given by
This Neumann boundary condition can be rewritten equivalently as
where
and \(r_s>0\) is the scaling parameter. Equations (161) and (162) can be viewed as one of the equations that constructs normal equations derived from the weighted least squares method since unknowns are common. Thus, if we define a discrete functional associated with \(R_{ij}^{p+1}, \widehat{R_{ij}^{p+1}}\) , Eqs. (161) and (162), s.t.
they provide normal equations. The choice of weight \(w_N (\mathbf{x}_i, r_e)\) for Neumann boundary condition enforcement is arbitrary. In this study, we utilize the following:
Note that this choice requires non-singular weight function usage. Then, if moment matrices of normal equations provided by minimizing Eqs. (166) and (168) are non-singular, we can obtain constraint LSMPS schemes type-A/B to enforce arbitrary Neumann boundary condition as follows:
Remark 4.4
Since moment matrices of linear systems are changed with additional terms \(\mathbf{N}_i, \widehat{\mathbf{N}_i}\), the conditions of moment matrix invertibility are relaxed. In other words, adscititious outer normal vector \(\mathbf{n}\) for the moment matrix acts as the position of the additive virtual calculation point. Moreover, it moves “the center of gravity of particles”, minifies the condition number of moment matrix, and provides an improvement of accuracy near the domain boundary.
4.3 Surface boundary particle detection algorithm
In order to run analyses of fluid flow with free surfaces with Lagrangian description, dynamic algorithm to detect surface boundary particles is required. In the MPS method [49], a very simple algorithm is utilized. Let \(n_i\) be a parameter called “particle number density”Footnote 9 of particle \(\mathbf{x}_i\) defined by
and \(n_i^*,\, n^0\) denotes a particle number density pre-solving pressure Poisson equations and a reference particle number density, respectively. The MPS surface boundary detection algorithm is that, if a particle \(\mathbf{x}_i\) satisfies
then it will be judged as a particle on the surface boundary; otherwise, it will be treated as a particle in interior of domain. \(\beta \) is a user-defined tuning parameter, and is usually chosen to be in the range of \(\beta = 0.80-0.97\). Very similar algorithm is introduced for incompressible SPH method [85] that the condition is
where \(\rho \) denotes the density that is defined by
These algorithm are very simple, however, erroneous decision of surface boundary particle, which yields unphysical oscillation of pressure fields, often occurs. Various proposal to solve this problem have been sought, for instance, alternative or additive conditions such as usage of the center of gravity of the particles [32], gradient of the particle number density [40], and divergence of particle position [52] are introduced; however, incorrect judgements remains.
Boundary detection algorithm based on the particular geometrical conditions are also proposed, for example, “Arc method” for the MLSPH method [24, 25] provides excellent results. Koh et al. also utilize Arc method for the MPS method [46]; however, it has a deal killer that extension of the algorithm for three dimensional surface boundary detection must be severely complex. Actually, Haque and Dilts constructed the methodology of three dimensional arc method [35]; however, it is exceedingly complicated and requires high computational cost.
Under these circumstances, we propose a new precisive surface boundary particle detection algorithm with unified simple implementation for arbitrary dimension. A new one consists of three steps.
First step is similar to the existing MPS algorithm. If a particle \(\mathbf{x}_i\) satisfies the condition governed by Eq. (197), then a particle get the next step decision. Otherwise, a particle \(\mathbf{x}_i\) will be treated as one in the interior of domain and the second or the final steps are skipped. It should be noticed that, unlike the MPS method, LSMPS particle number density is defined by
where \(\varLambda _i := \{ j \ | \ 0 \le \Vert \mathbf{x}_j - \mathbf{x}_i \Vert < r_e \}\), since non-singular weight functions are utilized for LSMPS method.
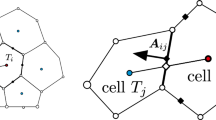
On the second step, for particles \(\mathbf{x}_i\), eigenvalues \(\lambda _k; 1 \le k \le d\) of 1st order moment matrix defined by
are utilized for the surface boundary screening. If a condition
is satisfied, then a particle \(\mathbf{x}_i\) is located on the surface boundary of the domain, and the final step will be omitted. If a condition
is fulfilled, then a particle \(\mathbf{x}_i\) goes to the final judgement. If a condition
is held, then a particle \(\mathbf{x}_i\) lies in the interior of the domain. The reason to utilize the minimum eigenvalue of 1st order moment matrixFootnote 10 is that near or on the surface boundary, the minimum eigenvalue of 1st order moment matrix will be smaller, on the other hand, in the interior of the domain, it will be closer to 1. Obviously, if particle distribution is on the uniform structured grid, the minimum eigenvalue of 1st order moment matrix is 1. \(\beta , \beta _1, \beta _2\) are user-defined tuning parameters, and \(\beta = 0.90, \beta _1 = 0.20, \beta _2=0.80\) are chosen in this study, respectively.
On the final judgement, only particular geometrical informations of particle distribution are capitalized; therefore, no tuning parameter is utilized. The final decision whether a particle \(\mathbf{x}_i\) is on the free surface boundary or not is performed by searching other particle or particles in the scanning region. Schematic diagram of the final-step is showed in Fig. 9, and definition of the searching region is displayed in Fig. 10. If conditions
or
are satisfied, a particle \(\mathbf{x}_i\) is judged to be in the interior of the domain; otherwise, it is considered to be on the free surface boundary. In the above conditions, \(l_0\) denotes the averaged particle distance at the initial state, and \(\mathbf{n}\) is a normalized eigenvector associated with the minimum eigenvalue, which plays the same role as an outer unit normal vector near or on the free surfaces since an eigenvector associated with the minimum eigenvalue face in the direction that particle distribution is poor. Hence, we can get outer unit normal vectors \(\mathbf{n}\) as a byproduct of the second step of the present algorithm and this reduces calculation cost. Note that a portion of searching region
is important to avoid fallacious decision that “two layers” of surface boundary is produced.
Schematic diagram of final-stage judgement algorithm to detect particles on the free surface
Geometric diagram definition of searching region for final-stage judgement algorithm to detect particles on the free surface
The advantages of present methodology are simplicity of implementation, unified formulae for arbitrary number of dimension, and an exclusion of tuning parameter in the final step. Although this technique utilizes geometrical information of particle distribution, unlike arc method [24, 25, 35], three dimensional surface boundary detection algorithm never becomes complicated.
4.4 Modification of source term of the Poisson equation
As discussed in the Sect. 4.1, modified pressure Poisson equation
should be solved in the LSMPS rotational pressure-correction scheme. This is a consistent formulation if consistent spatial discretization schemes are applied; however, this yields accumulation of numerical errors derived from space-time discretization error that appears in a long time numerical simulation. The reason comes from the fact that the source term \(\beta _s \frac{\rho }{\varDelta t}\nabla \cdot \tilde{\mathbf{u}}\) cannot reflect particle overcrowding and depopulation. In other words, number of particles per typical volume must be overlooked, though incompressibility manifested by the divergence free condition of the velocity field \(\nabla \cdot \mathbf{u} = 0\) is well satisfied. In contrast, in the existing MPS method and Incompressible SPH method, the following pressure Poisson equations are solved.
On the MPS and Incompressible SPH source term formulae, numerical errors of particle number density or density, which means number of particles per typical volume, must be estimated at every time step and never vanish; however, this type of formulations yields overwhelming oscillation of pressure fields. Thus, divergence free (DF) type source term (Eq. 207) and density invariant (DI) type source term (Eq. 208) have their advantages and disadvantages.
In order to combine the advantages of DF-type and DI-type source term formulations, mixed source term formulae are developed. Tanaka and Masunaga [94] and Kondo and Koshizuka [47] proposed two-term or three-term mixed source term for the MPS method, respectively. Their proposal could provide smoother pressure fields and keeping particle density to be constant; however, time-step \((\varDelta t)\) dependent tuning parameters that restrict the use of variable time-stepping and are difficult to chose in general are required. Khayyer and Gotoh [45] also utilized three-term mixed source term without time-step dependent tuning parameters; however, their accuracy is 0th or less since they adopted non-renormalized SPH divergence operator to approximate time derivative of particle number density.
Our present approach is an improvement of Kondo and Koshizuka’s [47] proposal without any access to the time-step dependent tuning parameters that time derivatives of density in Kondo and Koshizuka’s formulae are replaced by divergence of velocity via continuity equation to enhance accuracy. Note that particle number density and density estimation defined by Eqs. (196) and (199) utilize the lack of 0th order completeness/reproducing condition. Consequently, the accuracy of particle number density or density are 0th or less, in general. On the other hand, divergence of velocity calculated with consistent spatial discretization schemes can achieve arbitrary high order accuracy; therefore, we utilize divergence of intermediate velocity \(\tilde{\mathbf{u}}\) as a major component of source term and add feed-backing terms of particle distribution error as follows:
The second term of Eq. (208) is a error correction term of divergence free condition, and \(| (n^k - \hat{n^0})/\hat{n^0}|\) is a non-dimensional semi-positive coefficient. The third term is a error adjustment term of particle number density invariant, and \(|\nabla \cdot \mathbf{u}^k|\) is a semi-positive coefficient chosen to have appropriate dimension. Note that successive refinement procedures of time-space subdivisions make \(\nabla \cdot \mathbf{u}^k\) to be zero; therefore, error correction terms must vanish when incompressibility of the fluid is numerically satisfied. \(\widehat{n^0}\) is the modified reference of particle number density defined by
In the above equation, the coefficient \(N_{\text {Filled cell}}/N_{\text {Total cell}}\) is a remediation factor for the lack of 0th to approximate particle number density defined by Eq. (196). Consider a uniform structured local background cell with spacing \(l_0\). Schematic diagram is shown in Fig.11. \(N_{\text {Total cell}}\) is the total number of local background cells, which must be well-adopted for the dilation parameter \(r_e\) and number of dimension \(d\).Footnote 11 \(N_{\text {Filled cell}}\) is the number of local background cells occupied by a particle or particles. \(N_{\text {Filled cell}}\) count increment is different for each particle types. Fluid particles in the interior of the domain are counted with weight \(1\), and fluid particles on the free surface boundary or wall boundary are enumerated with weight \(1/2\). If two or more particles exist in a cell, the maximum count of this cell is limited to be 1. This simple procedures should be perfumed not to all but particles that includes boundary particle in their own support of weight function. This present modification must enhance accuracy of particle number density approximation dramatically near or on the boundaries.
Schematic diagram of particle number density modification with utilizing temporary local background cell
5 Numerical example
In order to demonstrate the advantage of the present LSMPS method comparing with the existing MPS method, two dimensional dam-collapse (dam-break) problem is chosen as a benchmark problem. Since dam-collapse problem includes free surfaces (Dirichlet boundary on the pressure and Neumann boundary on the velocity), boundary wall (Dirichlet boundary on the velocity and Neumann boundary on the pressure), and topological changes and fragmentations of continuum, it is a comprehensive benchmark of incompressible flow with free surfaces.
5.1 Calculation conditions
The governing equations are the Navier–Stokes equations with gravity acceleration (Eq. 131) and the continuity equation (Eq. 130). Initial state (shape) of fluid and fixed solid boundary wall is illustrated in Fig. 12. Physical parameters are chosen as follows: density \(\rho = 1.0\times 10^3\;\mathrm{kg/m^3}\), kinematic viscosity \(\nu = 1.0 \times 10^{-6}\; \mathrm{m^2/s}\), norm of gravity acceleration \(\Vert \mathbf{g} \Vert = 9.8\; \mathrm{m/s^2}\), and the following numerical parameters are used: averaged particle spacing at the initial state \(l_0 = 5.0\times 10^{-3}\; \mathrm{m}\), dilation parameter \(r_e = 4.1l_0\), and scaling parameter \(r_s = 1.3l_0\). The following weight function is utilized for both LSMPS and MPS methods.
For the LSMPS method, the standard LSMPS scheme type-A and the constrained LSMPS scheme type-A with 2nd order polynomial basis is utilized for spatial discretization, and for time integration scheme, \((r, s) = (0, 1)\) is selected; therefore, the order of LSMPS time integration scheme is similar to the existing MPS one.Footnote 12 It must be emphasized that no stabilization techniques are introduced for the LSMPS calculation. On the other hand, for the MPS method, some stabilization procedures are adopted since calculation of the existing MPS without stabilization results in terminating computation in early times of numerical simulation. In particular, stabilization method such as collision model [47], gradient operator modification [48], and pressure modification that negative pressure is corrected to be zero, are introduced only for the MPS method.
Schematic diagram of initial state of fluid and fixed boundary wall for the two dimensional dam collapse problem
5.2 Calculation results
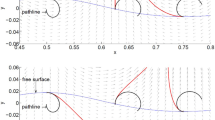
Snapshots of calculation results \((t=0.2, \ldots , 1.2)\) with contour plot of pressure fields are shown in Figs. 13, 14, 15, 16, 17, and 18, and the time evolutions of pressure observed on a sampling points A and B are displayed in Figs. 19 and 20. Figures 13, 14, 15, 16, 17, and 18 shows that the existing MPS solutions suffered from unphysical pressure oscillation. In contrast, LSMPS solutions provide smoother pressure field without numerical oscillation. One can observe from Figs. 13, 14, 15, 16, 17, and 18 that clarity of free surface boundary is demonstrably different. Smoother pressure field contributes to stable motions of particles, which results in unambiguity of deformable fluid interfaces. Moreover, Figs. 19 and 20 demonstrate that LSMPS solutions produce smooth pressure evolution in both space and time. Now we can gain release from problem such as serious numerical pressure oscillation.
Calculation result of dam collapse problem with pressure contour color map (Top Existing MPS method, Bottom Present LSMPS method, \(t=0.2\))
Calculation result of dam collapse problem with pressure contour color map (Top Existing MPS method, Bottom Present LSMPS method, \(t=0.4\))
Calculation result of dam collapse problem with pressure contour color map (Top Existing MPS method, Bottom Present LSMPS method, \(t=0.6\))
Calculation result of dam collapse problem with pressure contour color map (Top Existing MPS method, Bottom Present LSMPS method, \(t=0.8\))
Calculation result of dam collapse problem with pressure contour color map (Top Existing MPS method, Bottom Present LSMPS method, \(t=1.0\))
Calculation result of dam collapse problem with pressure contour color map (Top Existing MPS method, Bottom Present LSMPS method, \(t=1.2\))
Time evolution of pressure on a sampling point A
Time evolution of pressure on a sampling point B
The major differences between the MPS method and the LSMPS method in this analysis are the order of spatial discretization schemes, pressure Neumann boundary condition, pressure source term of Poisson equation, and surface boundary particle detection algorithm. We have to mention that this more accurate and stable calculation can be obtained only by an introduction of the combination of new proposals. In other words, implementation of one improvement would be frustrated by a variety of factors. Since LSMPS formulae presented in this study can achieve arbitrary high order accuracy, more accurate solution can be widely expected from an application of higher order schemes.
6 Conclusion
In this paper, a new consistent meshfree-Lagrangian approach for incompressible flow with free surfaces, named Least Squares Moving Particle Semi-implicit (LSMPS) method is developed. This methodology includes arbitrary high order consistent meshfree spatial discretization schemes, time integration schemes with consistent boundary conditions, and generalized treatment of Neumann boundary conditions. Application of new proposals to benchmark problem demonstrates conspicuous enhancement of stability and accuracy. Excellent accuracy of new meshfree compact schemes generalized for arbitrary dimension and high order of consistency is worthy of special mention. They are applicable for not only incompressible flows but also any targets governed by partial differential equations in meshfree framework; therefore, this new meshfree method can be utilized as one of the powerful tools to obtain high order accurate numerical solutions.
Notes
\(p\)th order polynomial completeness conditions or reproducing conditions is sufficient condition of \(p\)th order consistency.
At least, \(f(\mathbf{x}) \in C^0(\bar{\varOmega })\).
At least, \(f(\mathbf{x}) \in C^0({\varOmega })\).
\(e_{\infty }^{(1,0)} , e_{\infty }^{(0,1)}\) mean \( e_{\infty }^{\varvec{\alpha }}|_{\alpha = (1,0)} , e_{\infty }^{\varvec{\alpha }}|_{\alpha = (0,1)}\), respectively.
Order of MLS moment matrix’s condition number is evaluated as \(\fancyscript{O}(r_e^{-2p})\), see [92]
In practical numerical analyses, there exist not only round-off errors of floating-point arithmetics but also numerical errors. In this numerical convergence study, exact functional values \(\{f(\mathbf{x}_i)\}_{1 \le i \le n}\) are substituted into the right hand side vectors \(\{\mathbf{b}(\mathbf{x}_i)\}_{1 \le i \le n}\), then they contain only round-off errors; however, in practical simulation of continuum, the right hand side vectors must have numerical errors (e.g. numerical errors of pressure, velocity.). Ill-conditioned problems will enlarge these errors; therefore, keeping linear systems to be well-conditioned with lower condition number is crucially important.
For instance, in our experience, The well-known Crank–Nicolson scheme provides excellent results in terms of calculation cost and numerical accuracy.
Note that the identity \(\mu \nabla ^2 \mathbf{u}^{k+1} = - \mu \nabla \times \nabla \times \mathbf{u}^{k+1}\) is used.
It should be called “weight function density” for more accurate description.
Note that linear transformation \(\dfrac{( \mathbf{x}_j - \mathbf{x}_i)}{\Vert \mathbf{x}_j - \mathbf{x}_i\Vert } \dfrac{( \mathbf{x}_j - \mathbf{x}_i)^T}{\Vert \mathbf{x}_j - \mathbf{x}_i\Vert }\) is the orthogonal projection matrix onto the relative particle position \({( \mathbf{x}_j - \mathbf{x}_i)}/{\Vert \mathbf{x}_j - \mathbf{x}_i\Vert }\); therefore, 1st order moment matrices defined by Eq. (201) are also “averaged orthogonal projection matrices” and their eigenvector associated with the minimum eigenvalue face in the direction that particle distribution around \(\mathbf{x}_i\) is poor.
For example, if \(r_e = 3.1 \approx 3\) and \(d=2\) are chosen, \(N_{\text {Total cell}} = (2 \times r_e)^2 \approx 6^2 = 36\). If \(r_e = 3.1 \approx 3\) and \(d=3\) are chosen, \(N_{\text {Total cell}} = (2 \times r_e)^3 \approx 6^3 = 216\). Determination of \(N_{\text {Total cell}}\) must be flexible for the choice of dilation parameter.
Of course, as would be expected empirically, high order time integration schemes provide more accurate numerical solution. There are a lot of time discretization schemes, therefore, investigation of time integration schemes applied for LSMPS method would be interesting work in future.
References
Aluru N (2000) A point collocation method based on reproducing Kernel approximations. Int J Numer Methods Eng 47(6):1083–1121
Atluri S, Cho J, Kim HG (1999) Analysis of thin beams, using the meshless local Petrov–Galerkin method, with generalized moving least squares interpolations. Comput Mech 24(5):334–347
Atluri S, Zhu T (1998) A new meshless local Petrov–Galerkin (mlpg) approach in computational mechanics. Comput Mech 22(2):117–127
Atluri S, Zhu T (2000) New concepts in meshless methods. Int J Numer Methods Eng 47(1–3):537–556
Atluri S, Zhu TL (2000) The meshless local Petrov–Galerkin (mlpg) approach for solving problems in elasto-statics. Comput Mech 25(2–3):169–179
Atluri SN, Kim HG, Cho JY (1999) A critical assessment of the truly meshless local Petrov–Galerkin (mlpg), and local boundary integral equation (lbie) methods. Comput Mech 24(5): 348–372
Babuska I, Melenk JM (1995) The partition of unity finite element method. Tech. rep, DTIC Document
Babuska I, Melenk JM (1996) The partition of unity method. Int J Numer Methods Eng 40(1):727–758
Babuška I, Zhang Z (1998) The partition of unity method for the elastically supported beam. Comput Methods Appl Mech Eng 152(1):1–18
Balsara DS, Shu CW (2000) Monotonicity preserving weighted essentially non-oscillatory schemes with increasingly high order of accuracy. J Comput Phys 160(2):405–452
Belytschko T, Gu L, Lu Y (1994) Fracture and crack growth by element free Galerkin methods. Modell Simul Mater Sci Eng 2(3A):519
Belytschko T, Krongauz Y, Dolbow J, Gerlach C (1998) On the completeness of meshfree particle methods. Int J Numer Methods Eng 43(5):785–819
Belytschko T, Lu Y, Gu L (1995) Crack propagation by element-free Galerkin methods. Eng Fract Mech 51(2):295–315
Belytschko T, Lu Y, Gu L, Tabbara M (1995) Element-free Galerkin methods for static and dynamic fracture. Int J Solids Struct 32(17):2547–2570
Belytschko T, Lu YY, Gu L (1994) Element-free Galerkin methods. Int J Numer Methods Eng 37(2):229–256
Bonet J, Kulasegaram S (2000) Correction and stabilization of smooth particle hydrodynamics methods with applications in metal forming simulations. Int J Numer Methods Eng 47(6):1189–1214
Chakravarthy SR (1970) Some new approaches to grid generation, discretization, and solution methods for cfd. In: Proceedings of 4th international symposium computational fluid dynamics 14, pp. 403–420
Chen J, Beraun J (2000) A generalized smoothed particle hydrodynamics method for nonlinear dynamic problems. Comput Methods Appl Mech Eng 190(1):225–239
Chen J, Beraun J, Carney T (1999) A corrective smoothed particle method for boundary value problems in heat conduction. Int J Numer Methods Eng 46(2):231–252
Chen J, Beraun J, Jih C (1999) Completeness of corrective smoothed particle method for linear elastodynamics. Comput Mech 24(4):273–285
Chen JS, Pan C, Wu CT, Liu WK (1996) Reproducing Kernel particle methods for large deformation analysis of non-linear structures. Comput Methods Appl Mech Eng 139(1):195–227
Chorin AJ (1968) Numerical solution of the Navier–Stokes equations. Math Comput 22(104):745–762
Cummins SJ, Rudman M (1999) An sph projection method. J Comput Phys 152(2):584–607
Dilts GA (1999) Moving-least-squares-particle hydrodynamics. Consistency and stability. Int J Numer Methods Eng 44(8):1115–1155
Dilts GA (2000) Moving least-squares particle hydrodynamics ii: conservation and boundaries. Int J Numer Methods Eng 48(10):1503–1524
Donea J, Giuliani S, Halleux J (1982) An arbitrary Lagrangian–Eulerian finite element method for transient dynamic fluid–structure interactions. Comput Methods Appl Mech Eng 33(1):689–723
Duarte CA, Oden JT (1996) An h-p adaptive method using clouds. Comput Methods Appl Mech Eng 139(1):237–262
Duarte CA, Oden JT (1996) Hp clouds-an hp meshless method. Numer Methods Partial Differ Equ 12(6):673–706
Franke R (1979) A critical comparison of some methods for interpolation of scattered data. Tech. rep, DTIC Document
Franke R (1982) Scattered data interpolation: tests of some methods. Math Comput 38(157):181–200
Gingold RA, Monaghan JJ (1977) Smoothed particle hydrodynamics-theory and application to non-spherical stars. Mon Noti R Astron Soc 181:375–389
Gotoh H, Khayyer A, Hori C (2009) New assessment criterion of free surface for stabilizing pressure field in particle method. Jpn Soc Civil Eng Series B2 (Coastal Eng) 2:21–25
Guermond J, Minev P, Shen J (2006) An overview of projection methods for incompressible flows. Comput Methods Appl Mech Eng 195(44):6011–6045
Han W, Meng X (2001) Error analysis of the reproducing Kernel particle method. Comput Methods Appl Mech Eng 190(46):6157–6181
Haque A, Dilts GA (2007) Three-dimensional boundary detection for particle methods. J Comput Phys 226(2):1710–1730
Hirt C, Amsden AA, Cook J (1974) An arbitrary lagrangian-eulerian computing method for all flow speeds. J Comput Phys 14(3):227–253
Hughes TJ (2012) The finite element method: linear static and dynamic finite element analysis. Dover Publications, Mineola
Idelsohn SR, Oñate E, Pin FD (2004) The particle finite element method: a powerful tool to solve incompressible flows with free-surfaces and breaking waves. Int J Numer Methods Eng 61(7):964–989
Iribe T, Nakaza E (2010) A precise calculation method of the gradient operator in numerical computation with the mps. J Jpn Soc Civil Eng B 66(1):46–50
Itori S, Iribe T, Nakaza E. An improvement of dirichlet boundary conditions in numerical simulations using mps method. Japan Soc Civil Eng B2 (Coastal Eng)
Johnson GR, Beissel SR (1996) Normalized smoothing functions for sph impact computations. Int J Numer Methods Eng 39(16):2725–2741
Khayyer A, Gotoh H (2008) Development of cmps method for accurate water-surface tracking in breaking waves. Coast Eng J 50(02):179–207
Khayyer A, Gotoh H (2009) Modified moving particle semi-implicit methods for the prediction of 2d wave impact pressure. Coast Eng 56(4):419–440
Khayyer A, Gotoh H (2010) A higher order Laplacian model for enhancement and stabilization of pressure calculation by the mps method. Appl Ocean Res 32(1):124–131
Khayyer A, Gotoh H (2011) Enhancement of stability and accuracy of the moving particle semi-implicit method. J Comput Phys 230(8):3093–3118
Koh C, Gao M, Luo C (2012) A new particle method for simulation of incompressible free surface flow problems. Int J Numer Methods Eng 89(12):1582–1604
Kondo M, Koshizuka S (2011) Improvement of stability in moving particle semi-implicit method. Int J Numer Methods Fluids 65(6):638–654
Koshizuka S, Nobe A, Oka Y (1998) Numerical analysis of breaking waves using the moving particle semi-implicit method. Int J Numer Methods Fluids 26(7):751–769
Koshizuka S, Oka Y (1996) Moving-particle semi-implicit method for fragmentation of incompressible fluid. Nucl Sci Eng 123(3):421–434
Lancaster P, Salkauskas K (1981) Surfaces generated by moving least squares methods. Math Comput 37(155):141–158
Lax PD, Richtmyer RD (1956) Survey of the stability of linear finite difference equations. Commun Pure Appl Math 9(2):267–293
Lee ES, Moulinec C, Xu R, Violeau D, Laurence D, Stansby P (2008) Comparisons of weakly compressible and truly incompressible algorithms for the sph mesh free particle method. J Comput Phys 227(18):8417–8436
Lele SK (1992) Compact finite difference schemes with spectral-like resolution. J Comput Phys 103(1):16–42
Li S, Liu WK (1999) Reproducing Kernel hierarchical partition of unity, part iformulation and theory. Int J Numer Methods Eng 45(3):251–288
Li S, Liu WK (2004) Meshfree particle methods, vol 11. Springer, Dordrecht
Li S, Lu H, Han W, Liu WK, Simkins DC (2004) Reproducing Kernel element method part ii: globally conforming \(i^m/c^n\) hierarchies. Comput Methods Appl Mech Eng 193(12):953–987
Liszka T (1984) An interpolation method for an irregular net of nodes. Int J Numer Methods Eng 20(9):1599–1612
Liszka T, Duarte C, Tworzydlo W (1996) hp-meshless cloud method. Comput Methods Appl Mech Eng 139(1):263–288
Liszka T, Orkisz J (1980) The finite difference method at arbitrary irregular grids and its application in applied mechanics. Comput Struct 11(1):83–95
Liu GGR, Liu M (2003) Smoothed particle hydrodynamics: a meshfree particle method. World Scientific, Singapore
Liu WK, Chen Y, Uras RA, Chang CT (1996) Generalized multiple scale reproducing Kernel particle methods. Comput Methods Appl Mech Eng 139(1):91–157
Liu WK, Han W, Lu H, Li S, Cao J (2004) Reproducing kernel element method. Part 1: theoretical formulation. Comput Methods Appl Mech Eng 193(12):933–951
Liu WK, Jun S, Li S, Adee J, Belytschko T (1995) Reproducing Kernel particle methods for structural dynamics. Int J Numer Methods Eng 38(10):1655–1679
Liu WK, Jun S, Zhang YF (1995) Reproducing Kernel particle methods. Int J Numer Methods Fluids 20(8–9):1081–1106
Liu WK, Li S, Belytschko T (1997) Moving least-square reproducing Kernel methods (i) methodology and convergence. Comput Methods Appl Mech Eng 143(1):113–154
Lu H, Li S, Simkins DC Jr, Kam Liu W, Cao J (2004) Reproducing kernel element method part iii: generalized enrichment and applications. Comput Methods Appl Mech Eng 193(12):989–1011
Lu Y, Belytschko T, Gu L (1994) A new implementation of the element free Galerkin method. Comput Methods Appl Mech Eng 113(3):397–414
Lucy LB (1977) A numerical approach to the testing of the fission hypothesis. Astron J 82:1013–1024
Melenk JM, Babuška I (1996) The partition of unity finite element method: basic theory and applications. Comput Methods Appl Mech Eng 139(1):289–314
Monaghan JJ (1988) An introduction to sph. Comput Phys Commun 48(1):89–96
Monaghan JJ (1992) Smoothed particle hydrodynamics. Ann Rev Astron Astrophys 30:543–574
Monaghan JJ (2005) Smoothed particle hydrodynamics. Rep Prog Phys 68(8):1703
Nayroles B, Touzot G, Villon P (1992) Generalizing the finite element method: diffuse approximation and diffuse elements. Comput Mech 10(5):307–318
Oden J, Duarte C, Zienkiewicz O (1998) A new cloud-based hp finite element method. Comput Methods Appl Mech Eng 153(1):117–126
Oñate E, Idelsohn S (1998) A mesh-free finite point method for advective-diffusive transport and fluid flow problems. Comput Mech 21(4–5):283–292
Oñate E, Idelsohn S, Zienkiewicz O, Taylor R (1996) A finite point method in computational mechanics. applications to convective transport and fluid flow. Int J Numer Methods Eng 39(22):3839–3866
Oñate E, Idelsohn S, Zienkiewicz O, Taylor R, Sacco C (1996) A stabilized finite point method for analysis of fluid mechanics problems. Comput Methods Appl Mech Eng 139(1):315–346
Oñate E, Idelsohn SR, Celigueta MA, Rossi R (2008) Advances in the particle finite element method for the analysis of fluid-multibody interaction and bed erosion in free surface flows. Comput Methods Appl Mech Eng 197(19):1777–1800
Oñate E, Idelsohn SR, Del Pin F, Aubry R (2004) The particle finite element methodan overview. Int J Comput Methods 1(02):267–307
Oñate E, Perazzo F, Miquel J (2001) A finite point method for elasticity problems. Comput Struct 79(22):2151–2163
Quinlan NJ, Basa M, Lastiwka M (2006) Truncation error in mesh-free particle methods. Int J Numer Methods Eng 66(13):2064–2085
Randles P, Libersky L (1996) Smoothed particle hydrodynamics: some recent improvements and applications. Comput Methods Appl Mech Eng 139(1):375–408
Rannacher R (1992) On Chorin’s projection method for the incompressible Navier–Stokes equations. Springer, Berlin
Rudin W (1976) Principles of mathematical analysis (International Series in Pure & Applied Mathematics). McGraw-Hill, New York
Shao S, Lo EY (2003) Incompressible sph method for simulating Newtonian and non-Newtonian flows with a free surface. Adv Water Resour 26(7):787–800
Simkins DC Jr, Li S, Lu H (2004) Kam Liu, W.: Reproducing kernel element method. part iv: globally compatible cn (n 1) triangular hierarchy. Comput Methods Appl Mech Eng 193(12):1013–1034
Smith G (1985) Numerical solution of partial differential equations: finite difference methods. Oxford applied mathematics and computing science series. Clarendon Press, Oxford
Stone MH (1937) Applications of the theory of boolean rings to general topology. Trans Am Math Soc 41(3):375–481
Stone MH (1948) The generalized weierstrass approximation theorem. Math Mag 21(5):237–254
Strikwerda J (2007) Finite difference schemes and partial differential equations. SIAM, Philadelphia
Suzuki Y (2007) Ph.D. thesis, The University of Tokyo, Japan
Tamai T (2014) Development of least squares moving particle semi-implicit method. Master’s Thesis, The University of Tokyo, Japan
Tamai, T, Shibata K, Koshizuka S (2013) Development of the higher-order mps method using the taylor expansion. Trans Jpn Soc Comput Eng Sci 2013 (20130003)
Tanaka M, Masunaga T (2010) Stabilization and smoothing of pressure in mps method by quasi-compressibility. J Comput Phys 229(11):4279–4290
Tiwari S, Kuhnert J (2003) Finite pointset method based on the projection method for simulations of the incompressible navier-stokes equations. Meshfree methods for partial differential equations. Springer, Berlin, pp 373–387
Tiwari S, Kuhnert J (2005) A numerical scheme for solving incompressible and low mach number flows by the finite pointset method. Meshfree methods for partial differential equations II. Springer, Berlin, pp 191–206
Tiwari S, Kuhnert J (2007) Modeling of two-phase flows with surface tension by finite pointset method (fpm). J Comput Appl Math 203(2):376–386
Versteeg H, Malalasekera W (2007) An introduction to computational fluid dynamics: the finite volume method. Pearson Education Limited, Singapore
Zhang G, Batra R (2004) Modified smoothed particle hydrodynamics method and its application to transient problems. Comput Mech 34(2):137–146
Zhang G, Batra R (2009) Symmetric smoothed particle hydrodynamics (ssph) method and its application to elastic problems. Comput Mech 43(3):321–340
Zienkiewicz OC, Taylor RL (1977) The finite element method, vol 3. McGraw-Hill, London
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Tamai, T., Koshizuka, S. Least squares moving particle semi-implicit method. Comp. Part. Mech. 1, 277–305 (2014). https://doi.org/10.1007/s40571-014-0027-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40571-014-0027-2