Inverse Model for Simultaneously Estimating Material Parameters and Absorption Coefficient in a Laser-Irradiated Sheet

Abstract

In this work, a heuristic inverse method for simultaneous estimation of thermal conductivity, specific heat, density and absorptivity in a laser-irradiated sheet is proposed. A fast forward model, which can predict the temperature evolution during laser heating is built as the foundation of the inverse model. The forward model comprises of a proper analytical modelling considering three-dimensional heat conduction equation with coupled conduction–convection boundary conditions. The proposed inverse method tries to change the unknown parameters in each step till the predicted temperature close to the recorded temperature. Two different examples of a heating process on aluminium alloy (Al 6061-T6) are considered to demonstrate the efficacy of the inverse method. The accuracy of the inverse method is assessed by simulated experimental temperatures considering temperature-dependent properties in the forward model. The results show that the inversely recovered parameters are sufficiently accurate in calculating the surface temperature at different process conditions. The suggested heuristic inverse method has the potential for the fast computation of parameters for a desired laser heating temperature without needing arduous experiments and unproductive finite element method (FEM) analysis.

Introduction

Laser irradiation effect is the basis of many different laser technology applications, e.g., machining, forming, heat treating, welding and surface alloying [1,2,3,4,5]. The overall performance of various high-power laser beam applications is significantly dependent on thermal effects, which in turn reveal the laser-metal interaction mechanism [6]. Currently, there are numerous studies on the thermal effects of laser irradiation of sheet materials, some of which are based on experimental measurements and others on theoretical modelling. Theoretical modelling can reduce the time-consuming experimental efforts, and provide an alternative possible way to attain the real insight into the problem. In literature [7,8,9] the physical process of laser heating was simulated by finite element-based models and the corresponding physical concept was also revealed. The literature [10,11,12,13] deals with the analytical modelling method to study the thermal behaviour of target materials during laser heating process. The analytical model can directly build an intuitive functional relation between the parameters and the findings, which is of great importance for elucidating the physical phenomenon of solid material generated by laser radiation.

In many practical problems, when a solid material is irradiated by a high-intensity laser beam, the parameters of the material are often unknown, but the surface temperature of the material can be measured. At this point, if the material parameters can be retrieved by sensing the temperature, the laser-based manufacturing processes can be optimised significantly [23, 24]. The experimental methods like hot wire method [14], plane source [15], 3-omega [16], and, laser flash method [17] have been used to estimate the thermal properties of the material. However, the certainty of these methods is highly dependent on the nature of heat transfer process and the test samples. Therefore, in the last few decades, inverse estimation methods have been adopted by engineers and scientists. For a known effect (temperature data), inverse methods can be effectively used to estimate the parameters influencing that effect (material parameters). Ozisik [18] presented the fundamental concepts of inverse heat transfer and details of solution technique using various inverse methods. Colaco et al. [19] provides fundamental understanding of various inverse and optimization problems and implementations of various algorithms for handling inverse heat transfer problems.

The forward problem is the pillar of the inverse problem, and its solution must be inexpensive to compute so that it may be efficiently implemented on real-time machine tools. The forward problem in laser heating is relatively complex and is studied either by an analytical model or a numerical model. Zhang et al. [20] proposed a methodology to estimate the absorption and reflection coefficients for the surface of laser irradiated metallic sheets. The inverse problem was solved via the conjugate gradient method, with the forward model being analytically formulated as a one-dimensional heat conduction problem. A sensitivity study was used to confirm the validity of the inverse method. Mishra and Dixit [21] simultaneously estimated the thermal diffusivity and absorptivity of the heated sheet by solving three-dimensional forward problem created using analytical model. However, their solution did not focus on the influence of convective boundary conditions at all surfaces of the substrate. These create a limit for the effectiveness of analytical problem for the thermal analysis in laser line heating and reduces the practicability of the developed model in industrial applications. Sun [22] proposed a hybrid DFIM-SQP (decentralized fuzzy interface method-sequential quadratic programming) technique for the determination of time-dependent heat flux, absorption coefficient, scattering coefficient, and thermal conductivity in a participating medium simultaneously. The technique requires surface temperature and radiative intensity for the inverse analysis. Cui et al. [23] developed a method to predict the temperature-dependent thermal conductivity and the boundary heat flux. The method uses the solution of a two-dimensional transient heat conduction problem. Sun et al. [24] used the improved krill herd (IKH) algorithm to simultaneously determine the temperature-dependent thermal conductivity and heat capacity of a material. Kant et al. [25] proposed a combined finite element scheme and an artificial neural network based inverse method to obtain the absorptivity of the heated surface. In this work, the authors have implemented finite element method (FEM) as forward model for inverse estimation. Kumar et al. [26] adopted a method to simultaneously predict the average values of three parameters viz., thermal conductivity, absorptivity and heat transfer coefficient of the laser irradiated sheet. With the help of forward model temperatures at the irradiated surface, unknown parameters were estimated. In their study, the finite element scheme has been used to calculate forward model temperatures. In the next work Kumar et al. [27] estimated the average values of thermal conductivity, specific heat capacity and absorptivity at the heated surface. The authors used literature results to support the estimation process and results highlighted that the estimated values of thermal conductivity and specific heat capacity has a deviation of 6.5% and –14%, respectively. However, it is noted that only three unknown parameters can be estimated simultaneously in this manner. They also suggested that an efficient inverse method is needed to determine the density of the material during laser-based manufacturing that are challenging to identify through experiments.

The method for solving the forward problem is a crucial aspect to address the inverse problem, and its solution is of utmost importance. Although numerical approaches have been implemented in the field of inverse heat transfer, they are too computationally expensive to be employed for finding the optimal solution. On the other hand, analytical approaches have been reported to have a higher computing efficiency than numerical approaches, which can further broaden the use of this analytical modelling approach. To this end, the solution of the forward problem using the analytical model enabling faster and cheaper estimation of transient 3D temperature evolution in laser material processing is lacking, especially in terms of properly defining boundary conditions. Therefore, developing an inverse method using the fast forward model is needed for simultaneously estimate unknown parameters in a finite-sized workpiece induced by laser.

In this paper, a novel inverse thermal method for simultaneous estimation of four unknown parameters, i.e., thermal conductivity, specific heat, density and absorptivity for a laser-irradiated material has been proposed. The fast forward model is formulated as a transient three-dimensional heat conduction in a finite slab to which a combined conduction–convection boundary conditions are imposed. Then, the sensitivity analysis is carried out by perturbing the relevant parameters and examining the ensuing variations in measured fields. The inverse method is based on the simple heuristic technique and utilizes the temperature data of the laser-irradiated sheet for parameters retrieval. Two different application-based examples of a heating process on aluminium alloy (Al 6061-T6) have been used to test the robustness of the proposed inverse method. The method proposed herein tries to change the unknown parameters in each step till the predicted temperature close to the recorded temperature and thus proved to be an effective technical means for the undertaken task.

Method of the Inverse Processing

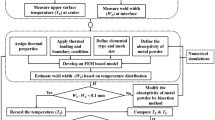
The schematic of the proposed method for the identification of unknown parameters is presented in Fig. 1. Laser heating is applied by a continuous wave heat source at the top surface of the metal sheet. The experienced temperature evolution at its scanned side is registered by thermal camera. A 1.5 mm thick aluminium alloy (Al 6061-T6) sheet is selected as work specimen among others available on the market which has wide applications in automobile, aerospace and marine engineering. Inverse problem aims at recovering unknown parameters (material parameters and absorptivity) of the laser-irradiated sheet from the measured surface temperature. Determining the material parameters to ensure the resulting surface temperature can considerably aid in achieving the desired deformation, microstructure evolution and residual stress of the workpiece. To solve the thermal inverse problem, a suitable inverse technique is proposed. The inverse technique tries to change the unknown parameters in each step till the predicted temperature close to the desired temperature. The methodology for solving the inverse problem is based on forward model able to virtually replicate the observed thermal scene. Once the unknown process parameters have been correctly estimated, inverse variation of temperature evolution in the laser heated sheet can also be obtained.

Fig. 1

Schematic representation of the proposed inverse method

Fast Forward Model

In general, a forward model is required to solve the inverse parameter estimation problem. In this paper, a physics-based analytical model that provides deep understanding of the physical concept of laser heating process is considered as a fast forward model to facilitate faster calculation of inverse solution.

Formulation and Solution of the Forward Model

The purpose of the forward model here is to calculate the 3D temperature evolution in the laser-irradiated sheet that varies with space and time. Consider a three-dimensional finite-sized sheet of length L, width B, and thickness H, as shown in Fig. 2. In reference to the figure, the temperature in the laser-irradiated sheet can be calculated by solving the differential equation of heat conduction in the x, y and z coordinates with boundary conditions as given from Eqs. (1, 2a, b, c, d, e, f, 3):

$$\frac{{\partial }^{2}T}{\partial {x}^{2}}+\frac{{\partial }^{2}T}{\partial {y}^{2}}+\frac{{\partial }^{2}T}{\partial {z}^{2}}+\frac{\dot{Q}\left(x,y,z,t\right)}{k}=\frac{1}{\alpha }\frac{\partial T}{\partial t}$$

(1)

with the following boundary conditions:

$$\begin{array}{ccc}-k\frac{\partial T}{\partial x}+h\left(T-{T}_{\infty }\right)=0& \mathrm{for}& x=0\end{array}$$

(2a)

$$\begin{array}{ccc}k\frac{\partial T}{\partial x}+h\left(T-{T}_{\infty }\right)=0& \mathrm{for}& x=L\end{array}$$

(2b)

$$\begin{array}{ccc}-k\frac{\partial T}{\partial y}+h\left(T-{T}_{\infty }\right)=0& \mathrm{for}& y=0\end{array}$$

(2c)

$$\begin{array}{ccc}k\frac{\partial T}{\partial y}+h\left(T-{T}_{\infty }\right)=0& \mathrm{for}& y=B\end{array}$$

(2d)

$$\begin{array}{ccc}-k\frac{\partial T}{\partial z}+h\left(T-{T}_{\infty }\right)=0& \mathrm{for}& z=0\end{array}$$

(2e)

$$\begin{array}{ccc}k\frac{\partial T}{\partial z}+h\left(T-{T}_{\infty }\right)=0& \mathrm{for}& z=H\end{array}$$

(2f)

and with the following initial condition:

$$\begin{array}{ccc}T=F\left(x,y,z\right)={T}_{0}& \mathrm{for}& t=0\end{array}$$

(3)

where $T=T\left(x,y,z,t\right)$ is the temperature at time t, $\dot{Q}\left(x,y,z,t\right)$ the heat supply, $\alpha =k/\rho {c}_{p}$ the thermal diffusivity of the workpiece material, k the thermal conductivity, ρ the density, c_p the heat capacity, $F\left(x,y,z\right)$ the expression of non-uniform initial temperature of the workpiece, ${T}_{0}$ the workpiece initial bulk temperature, and ${T}_{\infty }$ the environment temperature.

Fig. 2

Schematic representation of 3D thermal model of heat flux

The solution to the stated homogeneous heat conduction problem is obtained by using the integral transform technique [28]. Thus, the temperature evolution in the laser-irradiated sheet at any time and location can be expressed as [13]:

$$T\left(x,y,z,t\right)=\sum_{m=1}^{\infty }\sum_{n=1}^{\infty }\sum_{p=1}^{\infty }\frac{{X}_{m}\left({\beta }_{m},x\right){Y}_{n}\left({\gamma }_{n},y\right){Z}_{p}\left({\eta }_{p},z\right)}{{N}_{x}\left({\beta }_{m}\right){N}_{y}\left({\gamma }_{n}\right){N}_{z}\left({\eta }_{p}\right)}\left\{\begin{array}{l}\widehat{\overline{\widetilde{F}} }\left({\beta }_{m},{\gamma }_{n},{\eta }_{p}\right)\mathrm{exp}\left(-\alpha \left({{\beta }_{m}}^{2}+{{\gamma }_{n}}^{2}+{{\eta }_{p}}^{2}\right)t\right)\\ +\frac{\widehat{\overline{\widetilde{\dot{Q}}} }\left({\beta }_{m},{\gamma }_{n},{\eta }_{p},t\right)}{k\left({{\beta }_{m}}^{2}+{{\gamma }_{n}}^{2}+{{\eta }_{p}}^{2}\right)}\left\{1-\mathrm{exp}\left(-\alpha \left({{\beta }_{m}}^{2}+{{\gamma }_{n}}^{2}+{{\eta }_{p}}^{2}\right)t\right)\right\}\end{array}\right\}$$

(4)

where β_m, γ_n and η_p, $\left(m=n=p=\mathrm{1,2},3,...,\right)$ are the positive roots of the following transcendental equations

$$\begin{array}{cc}\left\{\beta_m^2-\left(\frac hk\right)^2\right\}\tan\left(\beta_mL\right)-2\left(\frac{h\beta_m}k\right)=0&\mathrm{for}\;x\;\mathrm{direction}\end{array}$$

(5)

$$\begin{array}{cc}\left\{\gamma_n^2-\left(\frac hk\right)^2\right\}\tan\left(\gamma_nW\right)-2\left(\frac{h\gamma_n}k\right)=0&\mathrm{for}\;y\;\mathrm{direction}\end{array}$$

(6)

and

$$\begin{array}{cc}\left\{\eta_p^2-\left(\frac hk\right)^2\right\}\tan\left(\eta_pH\right)-2\left(\frac{h\eta_p}k\right)=0&\mathrm{for}\;z\;\mathrm{direction}\end{array}$$

(7)

The functions ${X}_{m}\left({\beta }_{m},x\right),{Y}_{n}\left({\gamma }_{n},y\right),{Z}_{p}\left({\eta }_{p},z\right),{N}_{x}\left({\beta }_{m}\right),{N}_{y}\left({\gamma }_{n}\right),{N}_{z}\left({\eta }_{p}\right)\text{ and }\widehat{\overline{\widetilde{F}} }\left({\beta }_{m},{\gamma }_{n},{\eta }_{p}\right)$ are given in Appendix. A more detailed derivation is given in the paper of Nath and Yadav [13]. In the forward problem model, the heat flux generated $\widehat{\overline{\widetilde{\dot{Q}}} }\left({\beta }_{m},{\gamma }_{n},{\eta }_{p},t\right)$ at the workpiece surface is taken as Gaussian distribution and is given by following relationship:

$$\widehat{\overline{\widetilde{\dot{Q}}} }\left({\beta }_{m},{\gamma }_{n},{\eta }_{p},t\right)=\frac{0.865\eta P}{\pi {r}_{b}^{2}}\left\{\begin{array}{l}\left(\frac{h}{k}\left(\frac{\mathrm{cos}\left({\beta }_{m}{x}_{n}\right)-\mathrm{cos}\left({\beta }_{m}{x}_{p}\right)}{{\beta }_{m}}\right)-\mathrm{sin}\left({\beta }_{m}{x}_{n}\right)+\mathrm{sin}\left({\beta }_{m}{x}_{p}\right)\right)\\ \times \left(\frac{h}{k}\left(\frac{\mathrm{cos}\left({\gamma }_{n}{y}_{n}\right)-\mathrm{cos}\left({\gamma }_{n}{y}_{p}\right)}{{\gamma }_{n}}\right)-\mathrm{sin}\left({\gamma }_{n}{y}_{n}\right)+\mathrm{sin}\left({\gamma }_{n}{y}_{p}\right)\right)\\ \times \left({\eta }_{p}\mathrm{cos}\left({\eta }_{p}H\right)-\frac{h}{k}\mathrm{sin}\left({\eta }_{p}H\right)\right)\end{array}\right\}$$

(8)

where $\eta$ is the absorptivity of the work specimen, P the laser power, r_b the laser beam radius, (${x}_{n},{x}_{p},{y}_{n}\text{ and }{y}_{p}$) the transient position of the laser spot on a linear trajectory.

It is worth mentioning that process variables such as beam power, scan speed, beam radius, etc.have a significant influence on material properties in the irradiated sheet since it may change the predicted temperature [29]. Since the property parameters are correlated with temperature, the temperature-dependent material properties are taken into account in the forward problem model. The thermophysical material data of aluminium alloy (Al 6061-T6) shown in Table 1 [30] are used in this study.

Table 1 Relevant material data used for forward problem model [30]

Validation of the Forward Model

Prior to incorporating the forward problem model into the inverse processing, its accuracy must be proven. To achieve this, experimental tests were conducted in which the effect of laser-material interaction in the form of temperature was provided by the thermal camera. The specimen, which is an aluminium sheet of size (100 × 50 × 1.5) mm³ has been subjected to laser irradiation on the platform shown in Fig. 3, where a 1 kW fiber laser system (ABRO) was used. After being cleaned, the specimens were coated with graphite spray in the same manner as described in [13]. The heating over the specimen along the linear trajectory was performed using a laser source with radius equal to 2 mm. The irradiated surface temperature of the specimen was measured by thermal camera (FLIR) described by the following parameters: image frequency of 60 Hz, spectral range of 7.5–13 µm, and maximum temperature range of 2000 ºC. To ensure the repeatability, three replicates were done to measure the temperature at each set of experiments.

Fig. 3

Experimental setup: (a) conceptual representation and (b) photograph of real-time

The comparison between the predicted and measured temperature variations along the beam path at the top surface of the sheet is presented in Fig. 4. This indicates a good agreement between forward problem model results and experimental test results. The errors of the maximum temperature of the selected points are within 6% for different test conditions. This suggests that the forward heat conduction model can be retained accurate enough in order to predict the temperature evolution in a laser-irradiated sheet, which is a good foundation for the inverse problem.

Fig. 4

Comparison between calculated temperature using the forward problem model with experimental temperature (a) V = 1500 mm/min and (b) V = 2000 mm/min

Sensitivity Analysis and Inference for Inverse Modelling

The concept of the sensitivity analysis is used to study the effect of parameters viz. thermal conductivity, specific heat, density, and absorptivity in the forward model (Eq. 4). This analysis demonstrates the efficacy of the forward problem model as an effective technical means for assessing the laser heating process for a specific material. The surface temperatures for Al 6061-T6 aluminium sheet during laser heating process are measured at two locations (at P₁ and P₂): 25 mm and 45 mm away from the laser start point lying on the scanning path. Figure 5a depicts the relationship between surface temperature and thermal conductivity (k). It is observed that the magnitude of the temperature is strongly dependent on the thermal conductivity. In addition, the difference in temperature between the two locations increases as k decreases. Figure 5b illustrates the influence of the specific heat (c_p) on the surface temperature. The obtained temperature profile is found to have a different pattern from that of k. This can be ascertained by comparing Fig. 5a with Fig. 5b. The material’s density (ρ) also decides the surface temperature when the material is irradiated by an identical quantity of heat. Figure 5c shows the influence of the density on the surface temperature. It is observed that the temperature of the upper surface decreases with an increasing density. Figure 5d shows the relationship between material absorptivity (η) and the surface temperature. Here, the temperatures at two locations are greatly varied with the absorptivity. Sensitivity assessment as outlined here plays a crucial role in the inverse estimation of parameters. A parameter with a high sensitivity is desirable since it may aid in obtaining an accurate estimation result. In contrast, small sensitivity parameters are preferred for other parameters in order to minimise estimation error.

Fig. 5

Results for the effects of (a) thermal conductivity, (b) specific heat, (c) density and (d) absorptivity on surface temperature (P = 600 W, V = 1500 mm/min and r_b = 2 mm)

Inverse Problem

In the inverse problem, four unknown parameters are retrieved for the target temperature of the irradiated aluminium sheet. The unknown parameters are following: thermal conductivity (k), specific heat (c_p), density (ρ) and absorptivity (η). Meanwhile, the effect of the measurement location on the accuracy of inverse estimation is taken into account. It is found that the parameters like surface temperature, bend angle and microstructure evolution can be used to calculate the objective functions. However, the surface temperature of irradiated sample is the most convenient form in a practical point of view. The present inverse problem relies on the measured temperature values and the results of the forward problem obtained for guessed values of the unknown parameters at two locations (at P₁ and P₂) of the sheet. The problem of retrieval of unknown parameters is considered as an optimization problem wherein the following objective functions are minimised [31]:

$${F}_{1}=\frac{1}{n}\times {\sum_{i=1}^{n}\left(\frac{{T}_{im}-{T}_{ic}}{{T}_{im}}\right)}^{2}$$

(9)

$${F}_{2}=\frac{1}{n}\times {\sum_{j=1}^{n}\left(\frac{{T}_{jm}-{T}_{jc}}{{T}_{jm}}\right)}^{2}$$

(10)

where ${T}_{im}$ and ${T}_{jm}$ represent measured temperatures at two locations i.e., at P₁ and P₂. The corresponding calculated temperatures are represented by ${T}_{ic}$ and ${T}_{jc}$ and n is the number of observations. To solve the defined inverse problem, the iterative process based on the heuristic technique [26, 31] is used. The framework of the solution methodology is depicted in Fig. 6. The conclusion from the sensitivity analysis aided in the designing simulated experiments in which data were not taken from physical experiments, but generated based on the forward model that use temperature-dependent material properties. As the forward model has already been validated, such undertaken treatment is enough to establish the robustness of the proposed method.

Fig. 6

Framework of the inverse algorithm based on heuristic method

The methodology for solving the stated inverse problem is summarised below.

• Step 1: Generate suitable ranges of unknown parameters k, c_p, ρ and η.

• Step 2: The range for each parameter is divided into three distinct linguistic zones, labelled low (L), medium (M), and high (H), as illustrated in Fig. 7 for two of the parameters. As a result, the entire domain is divided up into 3⁴ separate cells, totalling 81.

• Step 3: At the beginning of the algorithm, select the middle (M) value as the initial guess of all unknown parameters.

• Step 4: Compute the objective functions F₁ and F₂ from Eqs. (9) and (10), respectively.

• Step 5: Set three other parameters (c_p, ρ and η) fixed, conduct a one-dimensional search for the optimal value of k as follows:

  • In cases where F₁ and F₂ are increased by jumping k into the centre of an adjacent cell, the value of k should be left unchanged.

  • In cases where F₁ and F₂ are decreased by jumping k into the centre of the adjacent cell, the value of k should be set to the middle value of that cell.

  • If none of these apply, do not change the value of k.

• Step 6: For the optimization of the remaining parameters c_p, ρ and η, the same methodology as in Step 5 is repeated. The search domain is reduced to a single cell following an iteration consisting of four one-dimensional searches.

• Step 7: The procedure described in Step 2 is repeated for the subsequent iteration in order to further divide the optimal cell. Figure 7 illustrates how the single optimal cell is reduced to three linguistic zones. The procedure continues till F₁ and F₂ are less than 0.001.

Fig. 7

Illustration of the linguistic zones during search procedure

Results of Inverse Estimation

Performance of the Estimation Algorithm

This section evaluates the performance of the method for solving the inverse problem using a heuristic-based optimization algorithm. Two different application-based examples have been used to test the robustness of the proposed inverse method. The aluminium alloy Al 6061-T6 is selected for the examples. The simulated experimental data obtained in both the examples using temperature-dependent values of material properties are set as the benchmark. The inverse methodology is applied to estimate the average values of material properties (k, c_p, and ρ) and absorption coefficient (η).

A. Example 1

In the first example, the dimension of the workpiece is (100 × 50 × 1.5) mm³, absorptivity is 0.4, laser power is 500 W, scan speed is 1500 mm/min and beam radius is 2 mm. The initial guess range of k, c_p, and ρ are taken as (180 − 223) W/(m·ºC), (876 − 1154) J/(kg·ºC) and (2705 − 2609.5) kg/m³, respectively [30]. The range of η is taken as (0.1 − 0.9). The computation is carried out using mid-range values of k, c_p, ρ and η to calculate the objective functions F₁ and F₂. With the fixed mid-range values of c_p, ρ and η, the value of k is updated to get the optimum cell using the proposed approach. Following the approach, the value of c_p, ρ and η are updated. The convergence is met after three iterations. The final results after convergence of k, c_p, ρ and η are k = 222.2 W/(m·ºC), c_p = 1148.83 J/(kg·ºC), ρ = 2685.43 kg/m³ and η = 0.5 corresponds to F₁ = 0.00089 and F₂ = 0.00076. All together 25 simulations were carried out to recover the unknown parameters that took about 20 min of total screen time. The simulation results obtained using the heuristic optimization algorithm for selected steps are shown in Table 2. The variations of temperature at both the locations P₁ and P₂ including initial guess, simulated experiment and final estimation for the considered example is shown in Fig. 8. The proposed model tries to change the unknown parameters in each step till the model predicts the closest temperature to the desired temperature. It is seen that the distribution of temperature obtained inversely is in good agreement with the simulated experimental data.

Table 2 Simulation results of selected steps for estimating k, c_p, ρ and η (P = 500 W, V = 1500 mm/min, r_b = 2 mm)

Fig. 8

Comparison between calculated temperature using the estimated values of k, c_p, ρ and η with actual temperature at points (a) P₁ and (b) P₂ (P = 500 W, V = 1500 mm/min and r_b = 2 mm)

B. Example 2

In the second example, the dimension of the workpiece is (100 × 50 × 3) mm³, absorptivity is 0.6, laser power is 600 W, scan speed is 2000 mm/min and beam radius is 3.5 mm. A procedure similar to Example 1 is followed to calculate the objective functions F₁ and F₂. Following the procedure, the value of k, c_p, ρ and η are updated and the convergence is obtained in two iterations. The final results after convergence of k, c_p, ρ and η are k = 182.38 W/(m·ºC), c_p = 891.45 J/(kg·ºC), ρ = 2636.03 kg/m³ and η = 0.58 corresponds to F₁ = 0.000079 and F₂ = 0.000068. All together 17 simulations were performed to recover the unknown parameters that took about 15 min of total screen time. The simulation results of the inverse estimation of four unknown parameters for selected steps are presented in Table 3. In Fig. 9 one can see the distribution of temperature at the heated surface for initial guess, simulated experiment, and final estimation. The matching is good, indicating that heuristic technique has effectively minimized the error. The method proved to be effective in the undertaken task.

Table 3 Simulation results of selected steps for estimating k, c_p, ρ and η (P = 600 W, V = 2000 mm/min, r_b = 3.5 mm)

Fig. 9

Comparison between calculated temperature using the estimated values of k, c_p, ρ and η with actual temperature at points (a) P₁ and (b) P₂ (P = 600 W, V = 2000 mm/min and r_b = 3.5 mm)

In examples 1 and 2, the convergence is obtained at a very short number of iterations i.e., in 17–25 function evaluations. Following the inverse procedure, the example 1 converges after three number of iterations and the example 2 converges after two number of iterations which shows the efficacy of the proposed inverse method.

Error Analysis

To ensure accuracy, the estimated k, c_p and ρ are compared to the actual values of k (= 209.51 W/(m·ºC)), c_p (= 1085.02 J/(kg·ºC)) and ρ (= 2630 kg/m³) from Zhu et al. [32], corresponding to the average sample temperature (329.82 ºC). The average temperature is assumed to be the average of the maximum temperature at 3 locations along the beam path at the upper and lower surfaces of the irradiated sheet. An error margin of 6.06% in k, 5.88% in c_p, 2.11% in ρ is observed. This comparison shows that the thermal parameters of the heated sheet can be recovered in an acceptable accuracy.

The accuracy of the presented procedure is further evaluated at different operating conditions selected from Nath and Yadav [33]. The dimension of the workpiece in these operating conditions is taken as (100 × 50 × 1.5) mm³. Once the unknown process parameters have been correctly estimated, inverse variation of temperature evolution at the laser-irradiated sheet can also be obtained. By varying the laser power and scan speed, the maximum temperature data from the inversely estimated process parameters and the simulated experiment are shown in Figs. 10 and 11. The results show that the inversely obtained unknown parameters are sufficiently accurate in calculating the surface temperature at different operating conditions. The estimated surface temperatures at two locations: P₁ and P₂ tend to be higher than the simulated experimental values. The error in the maximum temperature of the heated body predicted with inversely estimated parameters and simulated experiments are listed in Table 4. The main reason for these errors arises from the gap between the analytical modelling method and experimental measurements in the forward analysis. The maximum error in temperature prediction is for Case number 5, which is 6.55% at point P₁ and 6.30% at point P₂. It can be also found that the inverse accuracy improves slightly as the measurement location moves away from the laser start point.

Fig. 10

Inverse variation of maximum temperature with laser power after heating 100 mm × 50 mm × 1.5 mm aluminium sheet at points (a) P₁ and (b) P₂

Fig. 11

Inverse variation of maximum temperature with scan speed after heating 100 mm × 50 mm × 1.5 mm aluminium sheet at points (a) P₁ and (b) P₂

Table 4 Relative error distribution obtained using the heuristic based inverse method compared with the actual results

To assess the robustness of the method for solving the inverse problem, additive white Gaussian noise (AWGN) is added in temperature data obtained from the simulated experiment using AWGN inbuilt MATLAB function. As a fundamental noise model in information theory, AWGN is often used to mimic the results of various naturally occurring random processes. The temperature data that is generated with AWGN accurately represents the findings of the physical experiments. Figure 12 compares the estimated temperature using the material parameters obtained by inverse method with experimental data. It is found that the inversely estimated unknown parameters indicate a good potential and shop floor applicability of the developed inverse method.

Fig. 12

Comparison between inversely estimated temperature with the simulated experimental data (obtained by AWGN) corresponding the inversely estimated values (k = 182.38 W/(m·ºC), c_p = 891.45 J/(kg·ºC), ρ = 2636.03 kg/m.³ and η = 0.58) at point P₁

Conclusions

In this work, a heuristic inverse method for determining the average values of material parameters and absorptivity during laser heating process is proposed. A fast forward model, created using proper analytical modelling, which can predict the temperature evolution in a laser-irradiated sheet is built as the foundation of the inverse problem. The inverse method employs a simple heuristic technique that utilizes the temperature data of the laser-irradiated sheet for parameters retrieval. Two different application-based examples of a heating process on aluminium are considered to illustrate the performance of the inverse method. The accuracy of the inverse method is assessed with the aid of simulated experiments in which data are generated based on the forward model that use temperature-dependent material properties. The results show that the inversely obtained unknown parameters are sufficiently accurate in calculating the surface temperature at different process conditions. The method proposed herein achieves the closest temperature to the desired heating temperature by optimizing the unknown parameters in a reasonable number of iterations, which shows the efficiency of the inverse method. This study has shown the feasibility of use of the proposed inverse method that considers the physics-based analytical model for quick and inexpensive determination.

Appendix

Following expressions are used in solution:

$${X}_{m}\left({\beta }_{m},x\right)={\beta }_{m}\mathrm{cos}\left({\beta }_{m}x\right)+\left(\frac{h}{k}\right)\mathrm{sin}\left({\beta }_{m}x\right)$$

(A.1)

$${Y}_{n}\left({\gamma }_{n},y\right)={\gamma }_{n}\mathrm{cos}\left({\gamma }_{n}y\right)+\left(\frac{h}{k}\right)\mathrm{sin}\left({\gamma }_{n}y\right)$$

(A.2)

$${Z}_{p}\left({\eta }_{p},z\right)={\eta }_{p}\mathrm{cos}\left({\eta }_{p}z\right)+\left(\frac{h}{k}\right)\mathrm{sin}\left({\eta }_{p}z\right)$$

(A.3)

$$N_x\left(\beta_m\right)=\frac12\left\{\left(\beta_m^2+\left(\frac hk\right)^2\right)\left(L+\frac{\displaystyle\frac hk}{\left(\beta_m^2+\left(\frac hk\right)^2\right)}\right)+\frac hk\right\}$$

(A.4)

$$N_y\left(\gamma_n\right)=\frac12\left\{\left(\gamma_m^2+\left(\frac hk\right)^2\right)\left(W+\frac{\displaystyle\frac hk}{\left(\gamma_m^2+\left(\frac hk\right)^2\right)}\right)+\frac hk\right\}$$

(A.5)

$$N_z\left(\eta_p\right)=\frac12\left\{\left(\eta_m^2+\left(\frac hk\right)^2\right)\left(W+\frac{\displaystyle\frac hk}{\left(\eta_m^2+\left(\frac hk\right)^2\right)}\right)+\frac hk\right\}$$

(A.6)

$$\widehat{\overline{\widetilde{F}} }\left({\beta }_{m},{\gamma }_{n},{\eta }_{p}\right)={T}_{0}\left[\begin{array}{l}\left\{\frac{h}{k{\beta }_{m}}\left(1-\mathrm{cos}\left({\beta }_{m}L\right)\right)+\mathrm{sin}\left({\beta }_{m}L\right)\right\}\left\{\frac{h}{k{\gamma }_{n}}\left(1-\mathrm{cos}\left({\gamma }_{n}W\right)\right)+\mathrm{sin}\left({\gamma }_{n}W\right)\right\}\\ \times \left\{\frac{h}{k{\eta }_{p}}\left(1-\mathrm{cos}\left({\eta }_{p}H\right)\right)+\mathrm{sin}\left({\eta }_{p}H\right)\right\}\end{array}\right]$$

(A.7)