1 Introduction

It is a common misconception that the Heisenberg uncertainty principle applies both to the variances of two complementary observables in a quantum state, and to the relation between the precision in a measurement of one of the observables and the resulting disturbance to the complementary observable. Specifically, the rigorously proved “Robertson relationship” [1–3]

$$\begin{aligned} \Delta {X}\Delta {P} \ge \frac{\hbar }{2} \end{aligned}$$
(1)

(also commonly known as the Heisenberg uncertainty principle) has been taken to imply that any measurement with precision \(\Delta {X}\) must invariably lead to a momentum disturbance of at least \({\hbar }/(2\Delta {X})\) in magnitude. However, it was shown by Ozawa in 2003 that this common interpretation of the uncertainty principle is actually incorrect [4]. Erhart et al. [5] and we [6] independently provided experimental confirmations of Ozawa’s modified error–disturbance relationship.

Recently, a paper by Busch et al. [7] appeared claiming to invalidate this work, arguing in favour of a different set of definitions of error and disturbance, and proving that Heisenberg’s original expression was in fact rigorously correct by these definitions. In what follows, we will clarify the origin of this seeming contradiction. In short, our reading of [7] is that the disturbance of Busch et al. is a property of the measurement device (being maximized over all input states) and is thus “state independent”. As a result, their work shows that any measurement which is capable of achieving a measurement precision of \(\Delta {X}\) must impart a momentum disturbance of \({\hbar }/(2\Delta {X})\) on some state; however, there are many states which could pass through the measurement apparatus undisturbed. Ozawa’s result, on the other hand, demonstrates that when a measurement is done on a particular state, with a precision of \(\Delta {X}\), the momentum disturbance to that state need not be as large as \({\hbar }/(2\Delta {X})\)—i.e. it is “state dependent”.

It is important to make the distinction between state-dependent and independent relationships for several reasons. First, the original Robertson relation is state dependent. By this we mean that the variance of both observables (\(\Delta {X}\) and \(\Delta {P}\)), and in general the right-hand side of the relationship (the expectation value of their commutator, \(\langle [\hat{X},\hat{P}]\rangle \)) is calculated for a given state—and not maximized over all states as are Busch et al.’s definitions of error and disturbance. As such, it might be expected that an error–disturbance formulation of Heisenberg’s ideas would also be state dependent. Second, in a quantum key distribution setting, entropic forms of the Robertson relation have been used in security proofs of certain protocols [8, 9]. In such scenarios, a state-dependent form of the relationship is essential, since the performance of a protocol must be quantified on a given run. This is not to say that a state-independent formulation has no use, but it is why a state-dependent error–disturbance relationship could prove essential. Such a state-dependent relationship is what we [6], the Hasegawa group [5], and now several others [10–14] have confirmed experimentally. The point of our present paper is to explain clearly how the difference of definitions arises. We will also point to some specific examples of disturbance which we argue are better captured by Ozawa’s definition than by Busch et al.’s.

2 Busch et al.’s disturbance

Busch et al. first define the disturbance to \( \hat{P}\), for a given state, to be some measure of difference between the probability distribution over \({P}\) before and after the measurement. Note that this definition of disturbance, using a measure of difference between probability distributions, is different from conventional notions of disturbance, which would refer to the difference in the individual values of \({P}\) before and after the measurement. As we will see in the next section, Ozawa’s disturbance clearly addresses this problem using an operator formalism instead of classical statistics. After defining the disturbance to a given state, Busch et al. go further and maximize this disturbance over all localized momentum states, arriving at their final disturbance, \(\eta _\mathrm{B}(\hat{P})\). They have a similar definition for the error of an \(\hat{X}\) measurement, \(\epsilon _\mathrm{B}(\hat{X})\), where this error is maximized over all localized position states. It is these two maximized quantities that they prove are constrained by the relationship

$$\begin{aligned} \epsilon _\mathrm{B}(\hat{X})\eta _\mathrm{B}(\hat{P}) \ge \frac{\hbar }{2}, \end{aligned}$$
(2)

which has the same form as the Robertson relationship (Eq. 1). However, in general, the disturbance is maximized for one state (a state localized in momentum and spread out in position) and the measurement error for another (a state localized in position). So, their relationship cannot be used to describe how much a state will be disturbed by a measurement. What they actually quantify is not how much the state that one measures is disturbed, but rather how much “disturbing power” the measuring apparatus has—i.e., how much it could disturb the momentum distribution of some hypothetical state. In other words, their work implies that any device which could for some states measure position to an accuracy of \(\Delta {X}\) must be able to disturb the momentum of some state by at least \(\Delta {P}={\hbar }/(2\Delta {X})\) (while other states could be disturbed significantly less). On physical grounds, it is clear that this must be the case: if a state begins in a momentum eigenstate and \(\hat{X}\) is then measured to a precision of \(\Delta {X}\), the final state would be required to possess an uncertainty in momentum, and that uncertainty could only come from the measurement. Ozawa instead asks whether or not a measuring device must disturb the momentum of every state by such a large amount. As has been shown experimentally, it need not do so [5, 6, 10–12].

3 Ozawa’s disturbance

The idea of disturbance as defined by Ozawa [4] is quite straightforward. We simply wish to know how much the momentum \(\hat{P}\) of a given state changes due to some process \(\hat{U}\). We can assume \(\hat{U}\) is unitary, but it may act on a larger Hilbert space, thus appearing non-unitary on the system sub-space (this allows measurement to be treated naturally in terms of a von Neumann system-probe coupling). Then a good, classically-motivated measure of the disturbance to a state is the root-mean squared (RMS) difference between \(\hat{P}\) before and after the process, \(\hat{U}\):

$$\begin{aligned} \eta _\mathrm{o}(\hat{P})= \langle (\hat{U}^\dag \hat{P} \hat{U}-\hat{P})^2\rangle ^\frac{1}{2}. \end{aligned}$$
(3)

Although it has been argued that such a definition has no physical meaning [15], Lund and Wiseman [16] showed that this definition can be understood by comparing the value of a weak measurement made prior to the process with that of a strong measurement after it. Additionally, Ozawa’s definition of disturbance can be used to quantify types of disturbance which are “missed” by Busch et al.’s definition.

Consider the position-disturbance of a process (not necessarily a measurement) which simply flips a particle’s position wave function, taking \(\hat{X}\) to \(-\hat{X}\). Ozawa’s definition, applied to position, is \(\eta _\mathrm{o}(\hat{X})= \langle (\hat{U}^\dag \hat{X} \hat{U}-\hat{X})^2\rangle ^\frac{1}{2}\). For this process, \(\hat{U}^\dag \hat{X}\hat{U}=-\hat{X}\), so we have \(\eta _\mathrm{o}(\hat{X})=2\langle \hat{X}^2\rangle ^\frac{1}{2}\). This is at least equal to \(2\Delta {X}\). (The exact equality holds if \(\langle \hat{X}\rangle =0\).) But note that in the case of a symmetric wavefunction the position probability distribution will not change, therefore, the unmaximized disturbance defined by Busch et al. will be zero. This is reminiscent of the debate over the momentum disturbance required (or not) to destroy double-slit interference [17, 18]; our group recently applied weak measurements in that case to show how non-zero disturbance can exist even when measures of “average disturbance” vanish [19].

To make it clear why it can be useful to have a measure of disturbance which does not vanish in such cases, imagine a related but more complicated situation: a symmetric, localized, one-dimensional position wavefunction, in the presence of dispersion. Due to the dispersion, this wavefunction will broaden, and after some time the higher momentum components will be predominantly on one side of the wavefunction and the lower momentum components near the other side. If nothing is done, the wavefunction will continue to broaden. However, if this wavefunction is flipped about its center, it will begin to narrow: clearly an observable effect. However, immediately after the process (of flipping the wavefunction) both the position and the momentum probability distributions are unchanged. While these distribution-based measures vanish, there is clearly a sense in which individual particles must have had their positions and/or momenta disturbed in order for their future evolution to be modified; this disturbance is captured by Ozawa’s definition.

4 Ozawa’s relationship

To derive an error–disturbance relationship, the error of a position measurement, \(\epsilon _\mathrm{o}(\hat{X})\), must also be defined. This is done in a manner analogous to the definition of disturbance in Eq. (3). Now, we imagine that \(\hat{U}\) describes a von Neumann coupling between the position of the particle and some probe. The error of a measurement is then the RMS difference between the value of \(\hat{X}\) on the system and the value of \(\hat{X}\) read off of the probe:

$$\begin{aligned} \epsilon _\mathrm{o}(\hat{X})= \langle (\hat{U}^\dag \hat{X}_{\mathrm{probe}}\hat{U}-\hat{X}_{\mathrm{system}})^2\rangle ^\frac{1}{2}. \end{aligned}$$
(4)

This definition of measurement error has also recently been used to investigate complementarity relations [10], and similar definitions have been used to study the effect of correlations existing prior to the measurement between the system and probe [20]. Based on these definitions (Eqs. 3 and 4), Ozawa showed that the error and the disturbance must obey

$$\begin{aligned} \epsilon _\mathrm{o}(\hat{X})\eta _\mathrm{o}(\hat{P}) +\epsilon _\mathrm{o}(\hat{X})\Delta {P} + \eta _\mathrm{o}(\hat{P})\Delta {X} \ge \frac{\hbar }{2}, \end{aligned}$$
(5)

where \(\Delta {X}\) and \(\Delta {P}\) are the usual uncertainties pertaining to the state, those appearing in the Robertson relationship. This relationship is very similar to Eq. (2), but with two additional terms. Since both terms are positive-definite, this inequality is strictly weaker than the Heisenberg expression—it may be satisfied while the latter is violated. (Recently, a tighter relationship—still weaker than the Heisenberg expression—was derived[21, 22], and experimentally demonstrated [12].)

To understand Ozawa’s relationship (Eq. 5), let us first consider why it is that Eqs. 2 and 1 are often confused—a confusion coming from an understandable mistake. If we measure the position of a particle with some associated error, \(\epsilon (\hat{X})\), the post-measurement state is collapsed into a state having a wavefunction with a spread of at most \(\epsilon (\hat{X})\). If this is the case, then since the state must satisfy Eq. (1), it must have a width in momentum of \(\Delta {P} \ge {\hbar }/(2\epsilon (\hat{X}))\). The mistake is to assume that this momentum uncertainty is all due to the measurement disturbance (i.e., \(\eta (\hat{P}) = \Delta {P}\)); then Eq. (2) follows immediately. What this argument misses is that the final state may possess momentum uncertainty from the initial state as well as from the measurement interaction. If the particle’s momentum is already sufficiently uncertain to satisfy the Robertson relationship, then there is no obvious requirement for the measurement to disturb it further.

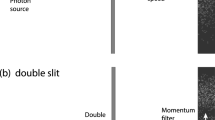
Let us present an extreme example to clarify the effects of this error in reasoning. Consider a particle which starts in a wavefunction which is strictly localized between \(x_1\) and \(x_2\) (i.e. it has compact support), such that \(\Delta {X}< x_2-x_1\). Now imagine carrying out an imprecise measurement of position by checking whether the particle passes through a slit of width \(\epsilon (\hat{X})\) (Fig. 1). If \(\epsilon (\hat{X})>\Delta {X}\) and the measurement succeeds, then the particle’s wavefunction never encountered the slit, and is undisturbed; that is \(\eta (\hat{P})=0\) Footnote 1 (Fig. 1a). So, we see that we can perform a measurement with finite \(\epsilon (\hat{X})\) which does not disturb the particle’s momentum and thus \(\epsilon (\hat{X})\eta (\hat{P})=0\), in contradiction with Eq. (2). Although the final momentum uncertainty must satisfy the Robertson relation (with the small post-measurement position uncertainty), some of this final uncertainty may come from the initial uncertainty (\(\Delta P\)) rather than relying on a contribution from the measurement (\(\eta (\hat{P})\)).

Fig. 1
figure 1

A simple position measurement: a particle’s position is measured to an accuracy \(\epsilon (\hat{X})\) by attempting to pass it through a slit. a If the slit is wider that the spread in the particle’s wavefunction (i.e. the particle’s wavefunction is strictly zero outside of the slit), \(\Delta {X} < \epsilon (\hat{X})\), the particle is not disturbed, as shown in a’. b If the slit is narrow compared to the particle’s wavefunction, \(\Delta {X} > \epsilon (\hat{X})\), then the particle is disturbed and it is collapsed to a post-measurement state with \(\Delta {X} \approx \epsilon (\hat{X})\) shown in b’

Full size image

5 Conclusions

In summary, we have discussed Ozawa and Busch et al.’s different definitions of error and disturbance, and their resulting constraints. Busch et al.’s definitions are maximized over all states and are thus state-independent, while Ozawa’s definitions are state-dependent, applying to any state that is measured. The reason for the different definitions may depend on the point of view: Ozawa’s state-dependent definition is more appropriate when considering the disturbance a given quantum state will experience, while the state-independent approach of Busch et al. may be more natural for characterizing a measurement apparatus without reference to specific states. When applied to the disturbance, Busch et al.’s state-dependent definition describes the disturbing power of a measuring device, quantifying how much the measurement could disturb some hypothetical state. We have also pointed to a situation which Busch et al.’s unmaximized disturbance would assign a value of zero, but that Ozawa’s disturbance would better quantify. Finally, we contend that Ozawa’s definition is closer in spirit to the disturbance typically associated with Heisenberg’s microscope than the definition of Busch et al.

Since the original submission of this paper (to another journal, which rejected it based on the criticisms of the very workers with whose work we were taking issue and whom we had requested not be used as referees, and despite our responses thereto), several other works have appeared attempting to clarify the different definitions of precision and disturbance and their role in discussions of the interpretation of the uncertainty principle and measurement–disturbance relations; see for instance [23–26].