Experimentally robustness improvement of DC motor speed control optimization by H-infinity of mixed-sensitivity synthesis

Abstract

Speed control of DC motor needs excellent robustness to guarantee its function to work properly against uncertainty and disturbance. The uncertainty may occur because of mechatronic component degradation, sensor noise, and environmental effect. Overload and accident have the possibility to be a significant disturbance. The performance of the DC motor is related to its stability and accuracy, which becomes a robust control goal. Robustness is an essential criterion for DC motor applications, from electronic household appliances to electric vehicles. This research aims to improve the robustness of DC motor speed control by H-infinity optimization of mixed-sensitivity synthesis technique to deal with uncertainty and disturbance. Comparison of theoretical modeling of mechatronics principle and experimental identification model is used for finding the best plant model to be processed by mixed-sensitivity synthesis. The proposed controller’s singular values are successfully dropped significantly twice due to robustness improvement from the experimental data. The optimization controller design is robustly stable due to loaded mass as disturbance assessment. The robustness performance improves significantly because the proposed plan has better overshoot errors and smother signal. In addition, the Lyapunov stability assessment on eigenvalues and graphical method proves that the proposed controller design is asymptotically stable. Although the proposed design has significant higher order, it can easily improve DC motor speed control through personal computer (PC)-based control. The calculation of mixed-sensitivity H-infinity control is proven scientifically in this work for the DC motor plant experiment.

1 Introduction

The safety and comfort of the most electric vehicle are related to the DC motor as its actuator. The excellent quality of DC motor performance is need by electric cars and motorcycles to copter drones [1] for running well. DC motor also has an urgent role in the convenience of the use of electronic household appliances. The robustness of DC motor speed control [2, 3] ensures the system can work appropriately against not only uncertainty but also disturbance. The best stability of the plant is the purpose of a robust control study. Moreover, the accuracy of an electronic product-based DC motor [4] is influenced by its robustness (Table 1).

Table 1 Nomenclature description

The stability and accuracy of the system are influenced by the uncertainty and disturbance of the DC motor plant. DC motor characteristics, particularly the nonlinearity of speed and torque, may generate uncertainty to the rotational speed control system [5, 6]. Moreover, the quality reduction of the mechatronics component, such as resistor, inductor, and capacitor, to the time must have caused its uncertainty. The overloaded and environmental circumstances may generate significant disturbance. The sensitivity of the position sensor has the possibility to cause uncertainty, particularly in noise cases. The robust control [7,8,9] offers the controller design research to bargain with uncertainty. However, the adaptive control may contrast or combine with a robust paradigm [10, 11]. The H-infinity method gives a mathematical optimization problem to be solved as stabilization assurance [12, 13] which becomes an alternative way to other robust techniques such as $H_2$ [14] and sliding mode control [15]. The technique of mixed-sensitivity synthesis [16, 17] utilizes the cutoff frequency condition of the plant to optimize robustness through weighting filters and augmented plant.

The purpose of this research is to increase the robustness of DC motor speed control by implementing H-infinity optimization control of mixed-sensitivity synthesis [18] method in the experiment. These strategies guarantee the stability performance of the DC motor from uncertainty and disturbance. The facilities of the DC motor are a valuable experimental tool to implement an investigation for rotational speed control via PC [19, 20]. Hence, the actual behavior of the DC motor from the experiment should be used to design the identification model to compare with the theoretical of mechatronics model for searching the best fit plant model. The transfer function, which illustrates the relation between signal control input of motor voltage and output of rotation speed in the time domain, can be used to build the H-infinity mixed-sensitivity synthesis controller. Not only assessment of singular values of optimization model but also experimentally loaded mass will be used to analyze the robustness performance of the proposed controller design before and after applying the H-infinity controller. The overshoot error also should be examined. Furthermore, the stability of the proposed method could be investigated by Lyapunov stability analysis. Besides those contributions, this paper wants to test and implement the knowledge of H-infinity of mixed-sensitivity synthesis in the real experiment of DC motor speed control as a novelty. Our proposed experimental procedures with the detailed descriptions of the real implementation of the concept of H-infinity robust control through the synthesis method of mixed sensitivity on DC motor rotational speed provide a major scientific contribution to this paper.

2 Robust control design

2.1 Robust control of H-infinity method

The robust control theory provides the controller design method to deals with uncertainty and disturbance of the system. The worst controller circumstances for a robust performance under model, signal, or performance uncertainties are designed on robust control studies [13]. The possibility of multiple sources of uncertainties, noises, and disturbances on a control system consideration is compromised by robust control methods to provide a properly function [12]. The robust control criteria occur when infimum of singular values from the overall transfer function of the system does not exceed from 1, which can be formulated below:

$$\begin{aligned} \parallel H_\omega \parallel =\frac{1}{\inf _\omega \sigma (H(j\omega ))}<1 \end{aligned}$$

(1)

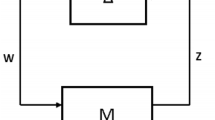
The peak gain across all frequencies and all input directions is the norm of H-infinity [21]. The H-infinity method has controllers to meet stabilization by guaranteeing robust performance. The H-infinity methods provide the problem solving of calculated mathematical optimization [22] of controller design in Fig. 1.

Fig. 1

Controller design of H-infinity method

The parameters are as follows: w = the disturbance inputs; u = the control inputs; z = the error outputs to be kept small; y = the measurement outputs provided to the controller; and P and K are matrices. The formula is written as follows:

$$\begin{aligned} \begin{bmatrix} z \\ v \\ \end{bmatrix} = P(s) \begin{bmatrix} w \\ u \\ \end{bmatrix} = \begin{bmatrix} P_{11}(s) &{} P_{12}(s) \\ P_{21}(s) &{} P_{22}(s) \\ \end{bmatrix} \begin{bmatrix} w \\ u \\ \end{bmatrix} \end{aligned}$$

(2)

$$\begin{aligned} u=K(s)v \end{aligned}$$

(3)

The expression of dependency of z on w as:

$$\begin{aligned} z=H_{(P,K)}w \end{aligned}$$

(4)

The lower linear fractional transformation is as follows:

$$\begin{aligned} H_{(P,K)}=P_{11}+P_{22}K(I-P_{22})^{-1}P_{21} \end{aligned}$$

(5)

The infinity norm to find the controller K is defined as the supremum of the maximum singular value $\sigma$ of the frequency response of a dynamic system for the matrix below:

$$\begin{aligned} \parallel H_{(P,K)}\parallel _\infty =\sup \sigma (H_{(P,K)}(j\omega )) <\alpha \end{aligned}$$

(6)

$\alpha$ is a nonnegative scalar of controller performance. Furthermore, controller K supposes to be included in the system to solve the mathematical optimization problem; therefore, the controller design can guarantee its performance robustly from an uncertainty. The optimization uses the two-Riccati formula with loop shifting H-infinity controller that maximizes an entropy $\zeta$ integral relating to the point $S_0$ by $H_{(P,K)}(j\omega )=H_\omega$ for solving Eq. (7).

$$\begin{aligned} \zeta = \frac{\alpha ^2}{2\pi }\int _{-\infty }^{\infty } \ln \mid \det I-\alpha ^{2}H_\omega 'H_\omega \mid \left[ \frac{S_0^2}{S_0^2+\omega ^2}\right] {\text {d}}\omega \end{aligned}$$

(7)

That equation uses a standard $\alpha$-iteration method to determine the optimal value of the performance level $\alpha$. The bisection algorithm of $\alpha$-iteration which starts with high and low estimates of $\alpha$ and iterates on $\alpha$ values to approach the optimal H-infinity control design. Optimization design using H-infinity robust control is particularly challenging to be implemented in DC motor plants [23, 24].

2.2 DC speed control modeling

The optimization model of DC motor speed control should be not only investigated but also validated in the real experiments. The QUBE-Servo 2 product of Quanser Consulting Inc. [19, 25] in Fig. 2 helps research to test its design comfortably and accurately because this platform eases the implementation of a control system based on PC, especially on Simulink/MATLAB.

Fig. 2

Experimental tool of DC motor

The first principles modeling [26] is studied in this research which observes both electrical and mechanical (mechatronics) of DC motor component. This theoretical model is illustrated in the diagram of the connection between the load hub and disk hub below.

Fig. 3

Diagram of mechatronics parameter of DC motor

Electronics components such as resistor and inductor are electrified due to the electric voltage through the DC motor in Fig. 3. Electrical energy through electromotive voltage (back-EMF) is converted into motion energy in the form of rotation speed.

$$\begin{aligned} E_{\text {b}}=K_{\text {m}} \omega \end{aligned}$$

(8)

The rotational speed is the change in angle over time.

$$\begin{aligned} \omega =\frac{{\text {d}}\theta }{{\text {d}}t} \end{aligned}$$

(9)

DC motor, which has mechanical components such as inertia, also rotates the two gears with their respective inertia values (see Fig. 2). The moment of inertia can also be calculated from the mass and radius of the gear, for example, the following connecting gear:

$$\begin{aligned} J_{\text {a}}=\frac{1}{2} \times m_{\text {a}} \times r_{\text {a}}^2 \end{aligned}$$

(10)

Those conditions are the same with the load gear inertia. Therefore, the effective moment of inertia of the DC motor control system is proportional to the resultant.

$$\begin{aligned} J_{\text {ef}} = J_{\text {m}}+J_{\text {a}}+J_{\text {b}} \end{aligned}$$

(11)

The torque of a DC motor is related to its inertia and its derivative of angular speed.

$$\begin{aligned} \tau =J_{\text {ef}}\frac{d\omega }{{\text {d}}t} \end{aligned}$$

(12)

The electric current that flows is also proportional to the torque produced.

$$\begin{aligned} \tau =K_{\text {m}} \times i \end{aligned}$$

(13)

According to Kirchhoff’s second law in a closed circuit, the total potential or voltage difference is zero.

$$\begin{aligned} \sum V=0 \end{aligned}$$

(14)

In other words, the amount of electric motion (EMF) and the amount of voltage drop are also zero. This means that no electrical energy is lost in the circuit or that all electrical energy is used, reinforced by the law of conservation of energy.

$$\begin{aligned} \sum E+i \times R=0 \end{aligned}$$

(15)

The closed electrical circuit in Fig. 3 is analyzed by Kirchhoff’s second law as follows :

$$\begin{aligned} V-i \times R-L \times \frac{{\text {d}}i}{{\text {d}}t}-E_{\text {b}}=0 \end{aligned}$$

(16)

$E_{\text {b}}$ is substituted by Eq. (8)

$$\begin{aligned} V-i \times R-L \times \frac{{\text {d}}i}{{\text {d}}t}-K_{\text {m}} \times \omega =0 \end{aligned}$$

(17)

The input of V is combined with the output of $\omega$ on the left side.

$$\begin{aligned} V-K_{\text {m}} \times \omega =i \times R+L \times \frac{{\text {d}}i}{{\text {d}}t} \end{aligned}$$

(18)

The model from mechatronics principle of DC motor in Eq. (18) is applied as theoretical of mechatronics model in this research. The mathematical model of control systems design for analysis is usually used a state space model which apply state variables to describe a system by a set of first-order differential or difference equations in Eq. (19) and Fig. 4.

$$\begin{aligned} {\dot{x}}=Ax+Bu; y=Cx+Du \end{aligned}$$

(19)

where x = state vector; y = output vector; u = input vector; A = state matrix; B = input matrix; C = output matrix; and D = feedforward matrix.

Fig. 4

State space model

The transfer function is the ratio of the output to the input of a system in the Laplace domain [27], which is also applied for control systems design (Fig. 5).

$$\begin{aligned} H(s)=\frac{Y(s)}{X(s)} \end{aligned}$$

(20)

The parameters are as follows:

Fig. 5

Transfer function block diagram

X(s) = input signal; H(s) = transfer function; Y(s) = output signal; s = complex frequency;

Transfer function or state space can be obtained from system identification procedure which uses statistical methods to build mathematical models of dynamical systems from the relation between both input and output measured data [28]. The system identification method offers the optimal design of experiments for an efficient model [29]. The statistical technique of the system identification estimates the model by minimizing the error between the model output, $Y_{\text {model}}$ and the measured experimental results, $Y_{meas}$.

$$\begin{aligned} Y_{\text {model}}(t) = H \times u(t) \end{aligned}$$

(21)

Therefore, the difference between the output model and the measured results or error, e, becomes minimal as possible using statistical calculations by MATLAB software of System Identification Toolbox.

$$\begin{aligned} e(t)= Y_{\text {meas}}(t)- Y_{\text {model}}(t) \rightarrow 0 \end{aligned}$$

(22)

The identification model is built by these technique. Both models would be compared to search for the most accurate plant model to experimental results.

3 Modeling and experiment method

The theoretical model from the first principle of the mechatronics component in Eq. (18) is used to develop a model for robust optimization. On the other hand, the experimental modeling by the system identification method is another accurate option approximation problem solver for DC motor plant. The voltage input of the DC motor signal is applied by amplifier-based PC control. Furthermore, the encoder sensor measures the angular rotation of the DC motor as output. Both technique modeling would be compared in this work.

The proportional–integral–derivative (PID) controller by best observation coefficient ($K_{\text {P}}=1.4$, $K_{\text {I}}=0.005$, and $K_{\text {D}}=0.001$) is used as an example controller to build a model for this research. The block diagram of the experimental method is shown in Fig. 6.

Fig. 6

Experimental closed-loop method diagrams

The block diagram is shown in Fig. 7 to observe this closed-loop [30] modeling for control system model from experimental data of DC motor speed control due to formula (20) and Fig. 6.

Fig. 7

The block diagram for DC motor speed control from experiment data by system identification way

The methodology of mixed-sensitivity synthesis for constructing the robust controller K is essentially based on the choice of the so-called weight matrices $W_1(s)$, $W_2(s)$, $W_3(s)$ [13] (Fig. 8).

Fig. 8

Weight matrices of H-infinity mixed-sensitivity synthesis

The parameters are as follows: $W_1(s)$ = first weight matrices, which regulates the medium- and low-frequency response of the open-loop optimized system; $W_2(s)$ = second weight matrices, which corresponds to the forecast (upper estimate) for additive perturbations of the form; and $W_3(s)$ = third weight matrices, which corresponds to the forecast (upper estimate) for multiplicative perturbations of the form.

Thus, the weight matrices expand the control plant; they add additional structural-parametric uncertainty to the mathematical description. Suppose the controller K ensures the high-quality functioning of the system with an expanded plant. In that case, it is guaranteed to ensure the efficient operation of the nominal plant. The value of $\gamma$ ($0\le \gamma \le 0.5$) is the degree for calculation of first weight matrices. $\omega _c$ is selected due to cutoff frequency from each selected period.

$$\begin{aligned} \omega _c=\root 3 \of {j} \end{aligned}$$

(23)

j is cutoff frequency number.

a). $W_1(s)$ selection:

Fig. 9

Bode plot of plant transfer function

Equations can be generated from Fig. 9 to build first weight matrices.

$$\begin{aligned}&\Delta H=20 \times \log (\omega _1/\omega _2) \end{aligned}$$

(24)

$$\begin{aligned}&20 \times \log (\omega _1/\omega _2)=20 \times \log (\gamma ^{-1}) \end{aligned}$$

(25)

Hence, the function inside the logarithm of both sides is equal.

$$\begin{aligned} \omega _1=\gamma \times \omega _2 \end{aligned}$$

(26)

The period is the reciprocal of the frequency.

$$\begin{aligned}&T_1=\omega _1^{-1} \end{aligned}$$

(27)

$$\begin{aligned}&T_2=\omega _2^{-1} \end{aligned}$$

(28)

The construction of the first weight matrices is made from both first and second periods calculation.

$$\begin{aligned} W_1(s)=\frac{(T_2s+1)^m}{\gamma \times (T_1s+1)^n} \end{aligned}$$

(29)

Note : $n,m\ge 1,n\ge m$

b). $W_2(s)$ selection: It is assumed that the multiplicative uncertainty, for example, perturbations, absorbs by the additive one, and only the first one is taken into account. Thus, for $W_2(s)$, the condition $W_2(s) \approx$ 0 or very small value is chosen.

c). $W_3(s)$ selection: It is analogous to the first weight matrices, and then, the third weight matrices can be made from the period of the points.

$$\begin{aligned}&T_3=\omega _3^{-1} \end{aligned}$$

(30)

$$\begin{aligned}&T_4=\omega _4^{-1} \end{aligned}$$

(31)

$$\begin{aligned}&W_3(s)=\frac{(T_4s+1)^m}{\gamma \times (T_3s+1)^n} \end{aligned}$$

(32)

For simple case, the cutoff frequency can be used to develop the third weight matrices below.

$$\begin{aligned} W_3(s)=\frac{s^n}{W_2+\beta \times \omega _c^n} \end{aligned}$$

(33)

where: $\beta \in [0..10]$

The Robust Control Toolbox of MATLAB [31] is applied due to the formula from (1) and (7) to compute H-infinity optimal controller. That software also draws its singular value to investigate each robust criteria.

4 Results and discussion

Besides implementing the first principle of the mechanics and electronics component of the DC motor as theoretical of mechatronics model (see Eq. (18)), the experimental data from closed-loop PID control in Fig. 6 are used to develop an identification model shown in Fig. 7. Here, model from the system identification technique in first- and second-order transfer function is given as follows (see Fig. 5 and Eq. (20))

$$\begin{aligned}&H_1(s)= \frac{-0.09442s+60.02}{s+ 18.81} \end{aligned}$$

(34)

$$\begin{aligned}&H_2(s)= \frac{-27.9s + 627.8}{ s^2 + 75.15s + 199.2 } \end{aligned}$$

(35)

Here are described the comparison results between mechatronics and identification model in Fig. 10. The experiment results are used to validate those models.

Fig. 10

Validation of models by experiment result

Figure 10 shows that the identification model of second order (see Eq.(35)) has a closer step response to the experimental results. On the other hand, the identification model of the first order from Eq. (34) is the farthest overshoot by approximately 8.3 rad/s to the experimental validation. The middle overshoot by around 6 rad/s occurred on the mechatronics model of Eq. (18). Because of the similarity to the experiment reference, Eq. (35) of the second-order transfer function is selected for the plant model. This chosen model would be used to build an H-infinity optimization controller by the mixed-sensitivity synthesis method.

The number of constants on the denominator of Eq. (35) is used to observe cutoff frequency conditions of equation (21).

$$\begin{aligned} \omega _c=\root 3 \of {199.2}=5.8\approx 6 \end{aligned}$$

From the $\omega _c=6$ rad/s, it can be chosen the value of $\omega _2=4$. The second period of (28) is calculated as follows.

$$\begin{aligned} T_2=\frac{1}{4}=0.25 \end{aligned}$$

We option the value of $\gamma$ by 0.3. So its calculation follows (26).

$$\begin{aligned} \omega _1=0.3\times 4=1.2 \end{aligned}$$

Thus, the first period of (27) can be calculated as follows.

$$\begin{aligned} T_1=\frac{1}{1.2}=0.833 \end{aligned}$$

The first weight matrices (29) can be formed from calculated data before. $W_2 = 0.0001$ is selected the value of second weight matrices. The simple way is used through $\omega _c$ value to calculate the third weight matrices. All weighting matrices are described in Fig. 11.

Fig. 11

The option of selected weight matrices

Whole calculated weight matrices ($W_1, W_2, W_3$) are augmented in model plant to construct an optimization design. The singular value of the transfer function of the selected plant model of formula (35) in Fig. 12 is drawn to check the robust criteria of H-infinity.

Fig. 12

The singular values of the plant model

Fig. 13

Graphs of singular values of proposed controller K design of H-infinity optimization

Although the Infinium of singular values decreased until -50 dB at $10^4$ rad/s, it started to form around 10 dB. The robust control criteria of the plant model are not satisfied (see Eq. (1)). Therefore, the plant model should be optimized by the H-infinity calculation method. The calculated controller K on the transfer function of the plant model from formula (5) (Fig. 6) is described in the transfer function (Eq. (36)):

$$\begin{aligned} \frac{1.085e07 s^3 + 1.738e12 s^2 + 2.934e14 s + 6.617e15}{s^4 + 2.705e09 s^3 + 6.929e12 s^2 + 3.024e15 s + 1.083e16 }\nonumber \\ \end{aligned}$$

(36)

That transfer function of controller K design (36) is plotted in Fig. 13 to research its singular value.

Figure 13 illustrates that the robust control criteria of controller K design are satisfied. Moreover, its singular values began from around – 4 dB ($<1$) and then it dropped to -80 dB after $10^{10}$ rad/s. That proposed controller K transfer function would be included in the plant model shown in Fig. 1. Therefore, the optimal design controller by H-infinity calculation (Eq. (6), (7)) develops the complex transfer function of the closed-loop system in Eq. (37).

The singular values of the closed-loop transfer function of controller design as Eq. (37) must be assessed to analyze the robust criteria in formula (1) and the norm of H-infinity in formula (5). The graphs of singular values of the closed-loop transfer function of the proposed design optimization are shown in Fig. 14:

$$\begin{aligned} \frac{-3.027e08 s^4 - 4.847e13 s^3 - 7.094e15 s^2 - 3.862e14 s + 4.154e18}{s^6 + 2.705e09 s^5 + 7.132e12 s^4 + 3.545e15 s^3 + 2.395e17 s^2 + 1.416e18 s + 2.157e18} \end{aligned}$$

(37)

Fig. 14

Graphs of singular values of proposed controller design

Even though the singular values of the closed-loop transfer function started by approximately 5 dB, it was better than before (10 dB in Fig. 13). The singular values reached 0 dB at 3 rad/s, and then, it declined to – 160 dB after $10^6$ rad/s. The proposed design has successfully declined the starting of singular values by two times, while the conditions of $\parallel H_\omega \parallel <1$ and $\parallel H_{(P,K)}\parallel _\infty <\alpha$ are not really satisfied. Because of those reasons, the proposed optimization controller design has increased its robustness. The proposed design is tested experimentally, and the results are compared with the plant without controller K; comparison graphs are shown in Fig. 15.

The experiment graphs of the optimization design in Fig. 15 showed marvelous results. It described robust control signal visually and improved its robustness than before applying the proposed controller K. In addition, the overshoot error dropped as time response. The robust control gets the step response to smoother.

Fig. 15

Comparison results of step response between before and after optimization

To analyze the robustness of the proposed controller design, the assessment of the mass loaded is conducted (see Fig. 16). Those diagrams illustrated the dealing from overload disturbance and other uncertainties, which are derived from Fig. 1. Both devaluing of the electronic and mechanic components also environmental effects take on those uncertainties. The noise of the encoder sensor caused uncertainty through measurement output.

Fig. 16

External disturbance by mass loaded

Weight and bar in Fig. 17 were added to the top of motor gear to test its performance against load disturbance. The mass loaded was around 220 g.

Fig. 17

Mass loaded as external disturbance

The image magnification in Fig. 18 indicated that mass loaded had increased the overshoot only by 0.05 rad/s. Although this external disturbance gives a small effect, it can test the robustness performance of the proposed optimization design experimentally.

Fig. 18

The effect of mass loaded to the plant

Once again, the proposed method from optimization produced perfect robust control of step response under mass-loaded disturbance. Almost without overshoot errors happened to optimization results. The stability of the proposed design can be analyzed by Lyapunov theory [32] to ensure its performance. The graph of optimization controller by H-infinity in Fig. 19 showed obviously that it is close to the desired rotational speed at 3 rad/s due to running time. In addition, the error (e) tends to zero as time runs to unlimited. The condition of $\lim _{t \rightarrow \infty }\left\| e \right\| =0$ proves that the step response of the optimization controller by H-infinity is asymptotically stable.

Fig. 19

Optimization results of mass-loaded plant

The alternative way to investigate the stability of the proposed controller design (see Eq. (37)) is by calculating the eigenvalues of A matrix in state space formula (19) and Fig. 4 on its closed-loop model. The results of the state matrix of closed-loop controller design are shown in Eq. (38):

$$\begin{aligned} A= \end{aligned}$$

$$\begin{aligned} \begin{bmatrix} -75&{}-12&{}0.00&{}-236&{}-829&{}348\\ 16.00&{}0.00&{}0.00&{}0.00&{}0.00&{}0.00\\ 3.49&{}-4.90&{}-1.20&{}0.00&{}0.00&{}0.00\\ 0.00&{}0.00&{}0.00&{}-311&{}-842&{}348\\ 0.00&{}0.00&{}0.00&{}16.00&{}0.00&{}0.00\\ 3.49&{}-4.90&{}0.00&{}0.00&{}0.00&{}-1.20\\ \end{bmatrix} \end{aligned}$$

(38)

A is the matrix with an 6 $\times$ 6 dimension. The calculation of 6 eigenvalues ($\lambda$) is shown below:

$$\begin{aligned} \lambda = \begin{bmatrix} -1.20 \\ -265.57 \\ -2.75 \\ -3.79 \\ -43.17 \\ -72.40 \\ \end{bmatrix} \end{aligned}$$

(39)

The 6 $\times$ 1 matrix of eigenvalues indicates that all real parts of the eigenvalues of the A matrix are negative. Because of $\lambda (real) < 0$ conditions, the state space of optimization closed-loop controller by H-infinity has asymptotic stability [33].

Investigation of the control input voltage, u or V on DC motors stated in both the mechatronics principle (Eq. (18)) and the identification model (Fig. 7), can be carried out to determine how H-infinity optimization through the K controller improves robustness, accuracy, and stability. The voltage comparison in Fig. 20 showed that the controller K changed the initial voltage from around 4 V to 2.5 V. Moreover, it made the voltage signal smoother.

Fig. 20

Comparison of the control input voltage

The H-infinity optimization controller designs could build the control more robustness to deal with uncertainty. However, the proposed optimal transfer function design has more complex, around three times higher order both the numerator and denominator (see Eq. (35) and (37)). Figure 21 shows that controller K has a more significant order than the DC speed motor model plant, which caused the order of optimization transfer function to enhance dramatically. However, the development of processors grew rapidly, creating high-performance computing products both in minicomputers and personal computers to quickly solve the computation of high-order transfer function for control system application.

Fig. 21

Increase in transfer function order through optimization

Fig. 22

Proposed experimental procedure to synthesis technique of mixed sensitivity for H-infinity robust optimization

In summary, the optimization of controller design achieves robustness improvement because it declined successfully singular values of the transfer function of the proposed method. Moreover, it got asymptotic stability. This optimization can minimize the possibility of multiple sources of uncertainties [34], noises, and disturbances, such as the degradation of electronics, mechanical items, and encoders sensing [35] and also overloaded disturbance. The implementation of the H-infinity mixed-sensitivity synthesis method has scientifically proven to improve the robustness of DC motor speed control in the true experiment.

The astonishing success in implementing the H-infinity robust control principle for controlling the rotational speed of a DC motor using the mixed-sensitivity synthesis technique prompted us to propose the experimental procedure in Fig. 22 to enrich this research’s scientific benefits. All DC model plants that can be modeled into a transfer function should surely apply this experimental procedure. The transfer function model was preferred because it is comfortable to utilize the corner frequency value to validate the H-infinity calculation employing the mixed-sensitivity synthesis method.

5 Conclusion

The development of controller optimization on DC motor speed control by H-infinity mixed-sensitivity synthesis technique is successfully constructed due to improved robustness performance. The theoretical modeling from first principle of electrical and mechanical components has the worse on the similarity step response than identification model to experiment reference. The decline of singular values of transfer function of proposed closed-loop design indicated the robustness enhancement. Fascinating results of optimization step response happened because of the perfect robust control signal both before and after mass-loaded disturbance. The robustness improvement occurred on the proposed controller design by declining overshoot error to the time response and getting smother signal. The results of the proposed method achieve the asymptotic stability because of satisfaction on graphical analysis and eigenvalues investigation. Although the proposed controller increased the order of transfer function around three times significantly, it could be solved using personal computer’s performance.

The application of mechatronic components and position sensor also mass-loaded disturbance on DC motor speed control may cause the sources of uncertainties, noises, and disturbances which can be neglected by the controller optimization by H-infinity mixed-sensitivity synthesis of robust control method. The experiment proved the proposed technique scientifically that the successful implementation of robustness increment happened on the DC motor speed control plant. Our proposed experimental procedure can inspire other researchers and contribute to the implementation of control theory.