A robust control strategy for a self-excited induction generator wind turbine system

Abstract

In this paper, a new control strategy of a variable speed based SEIG wind energy conversion is presented. Nonlinear control strategy is proposed to extract maximum available energy from the wind turbine and regulate the rotor flux magnitude of SEIG and the DC-link voltage in the generator side as well as the load voltage magnitude in the inverter load side under wind speed, load and rotor/stator resistances variations. The proposed nonlinear adaptive controller is robust given its insensitivity to SEIG variation of the rotor and stator resistances. The global convergence and stability analysis taking into account the interconnections between the stator electrical angular position, the rotor flux and rotor resistance estimators and the nonlinear controller have been proved by using the separation principle. Another contribution of this paper is the robustness of the proposed method with respect to the variation of the driven speed and relatively low wind speed operation. Thus, the proposed stand-alone variable speed based SEIG wind energy conversion system can be used in remote and isolated areas where the mean value of the wind speed profile is relatively low.

1 Introduction

1.1 Antecedents and motivations

The self-excited induction generator (SEIG) has emerged from among the well known generators as a suitable candidate to be driven by wind turbine. The main advantages of the SEIG are small size and weight, low cost and simplicity of construction, absence of separate source for excitation and reduced maintenance cost but its main drawback is its inherently poor voltage regulation. The fact that the induction machine (IM) is a multivariable, nonlinear and highly coupled process with time-varying parameters, has motivated a lot of work in the control community during the last decade [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17]. The most popular method is the field-oriented control (F.O.C.) which provides a means to obtain high-performance control of IM. But F.O.C. methodology requires knowledge of the rotor flux which is not usually measured [14]. Traditionally, observers are used to estimate the rotor flux. However, the flux observers used in the currently IM control rely on a good knowledge of the rotor resistance.

Fig. 1

Global structure of the control system

It is well known in literature (e.g. see [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17]) that the rotor resistance and the stator resistance may vary up to $100\%$ and $50\%$ of their nominal values, respectively, during operation of the IM due to rotor heating. Standard methods for the estimation of IM parameters include the blocked rotor test, the no-load test and the standstill frequency response test. But, these methods cannot be used online during normal operation of the machine. The most natural solution is to online identify the time-varying parameters. The problem of the online identification of the induction machine parameters has been addressed by several papers in the literature [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17].

But in the self-excited generator mode operation of the IM, different approaches for voltage regulation have been developed [18,19,20] without taking into account the fact that the rotor resistance required for the rotor flux estimation is time-varying. In [19] the technique and limitation of varying the flux in the induction generator to regulate the generated voltage under variation of the rotor speed are discussed. In [18], standard sliding mode control associated to the flux oriented control technique is applied to the dc-bus voltage regulation of SEIG. The control strategy proposed in [18] is difficult to implement online because this method used the rotor flux and the rotor resistance which varies with the operating conditions. In [20], fuzzy logic based voltage controller has been proposed for voltage source pulse width modulation (PWM) converter connected to SEIG to regulate the dc-bus voltage. In the above contributions, the investigation of the variation of the electrical parameters (e.g. stator and rotor resistance) has not been discussed.

1.2 Main contributions

In this paper, a new control strategy of a stand-alone variable speed based SEIG wind energy conversion is presented. The main objective of the proposed adaptive nonlinear control strategy is to extract maximum available energy from the wind turbine and regulate the rotor flux magnitude of SEIG and the DC-link voltage in the generator side as well as the load voltage magnitude in the inverter load side under wind speed, load and rotor/stator resistances variations. To this end, adaptive nonlinear controllers are designed. In order to avoid the chattering effect, we used an approximation of the $\hbox {sign}$ function of the well known sliding mode control technique which has proved to be particularly appropriate for nonlinear systems control, presenting robust features with respect to system parameter uncertainties and external disturbances [21].

The proposed nonlinear adaptive controller is robust given its insensitivity to SEIG variation of the rotor resistance and stator resistance. The global convergence and stability analysis taking into account the interconnections between the stator electrical angular position, the rotor flux and rotor resistance estimators and the nonlinear controller have been proved by using the separation principle. The resulting nonlinear controllers can be easily implemented in practice since finite time estimators for the rotor resistance, rotor flux and stator electrical angular position required for the adaptation of the controller are provided.

Another contribution of this paper is the robustness of the proposed method with respect to the variation of the driven speed and relatively low wind speed operation. Consequently, the proposed stand-alone variable speed based SEIG wind energy conversion system can be used in remote and isolated areas where the mean value of the wind speed profile is relatively low.

1.3 Structure of the paper

The paper is organized as follows. In Sect. 2, global structure and control objective are presented. In Sect. 3, generator side control strategy is described while in Sect. 4, load side inverter control strategy design is introduced. In Sect. 5, simulation results using the proposed nonlinear controller and conventional P.I. controllers are reported and some concluding remarks are given in Sect. 6.

2 Global structure and control objective

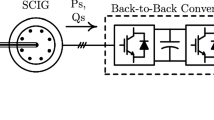
The control structure of a SEIG based variable speed wind turbine is shown in Fig. 1. This structure consists of the SEIG connected to a variable speed wind turbine through a step-up gear box, a PWM controlled converter and a vector controlled PWM voltage source inverter which is used to supply the loads through LC filter. It can be noticed that the output of a variable speed SEIG can not be used without transformation as it varies in amplitude and frequency due to fluctuating wind. Thus, a constant dc-voltage is required for direct use, storage or conversion to AC via an inverter.

Initially, the dc-bus voltage is assumed to be zero and the battery on the dc-bus side of the inverter provides the initial excitation through the diode. When the rotor flux reaches the desired level, the dc-bus voltage increases and becomes greater than the battery voltage; Then the diode cuts off the battery from the dc-bus and the generator supplies itself the necessary energy to control the voltage across the compensator dc-capacitor and the reactive power required by the SEIG is provided by the three-phase control converter.

The goal of this work is to use a simple maximum power point tracking strategy to extract the optimal torque of the variable speed turbine and design the dc-voltage and rotor flux controllers as well as the load side frequency and voltage regulators assuming that the measured outputs are the rotor speed, stator currents, load-side currents and voltages despite large variation of the stator/rotor resistances.

3 Generator side control strategy

The control task in this section is to extract the maximum power from the wind turbine and regulate the rotor flux and the dc-bus voltage.

3.1 Modeling of the wind turbine

The mechanical power extracted from wind turbine can be expressed as:

$$\begin{aligned} P_t= & {} \dfrac{1}{2}\pi \rho R^2C_p(\lambda )v^3 \end{aligned}$$

(1)

where $\rho$ is the air density, R is the radius of the turbine, v is the wind speed, $C_p(\lambda )$ is the power coefficient and $\lambda$ is the tip-speed ratio (TSR). This TSR is given by the relation

$$\begin{aligned} \lambda= & {} \dfrac{R\omega _{mt}}{v}=\dfrac{R\omega _{m}}{n_gv} \end{aligned}$$

(2)

where $\omega _{mt}$ is the turbine rotor speed, $\omega _{m}$ is the generator rotor speed and ${n_g}$ is the gearbox ratio. The general characterization of $C_p$ depends on $\lambda$ and the blade pitch angle $\beta$. In the literature, many authors have proposed different methods to characterize the expression of $C_p(\lambda )$ [22, 23]. All the analysis in this work is done considering the angle of the blade pitch $\beta$ settled to zero, i.e. $\beta \equiv 0$. The following characterization taken from [23] is used.

$$\begin{aligned} C_p(\lambda )= & {} \left( \dfrac{C_2}{\lambda }-C_3\right) e^{-\frac{C_1}{\lambda }}+C_4\lambda . \end{aligned}$$

(3)

Maximum power can be extracted from the wind turbine when it operates at maximum $C_p$ (i.e at $C_p^*$) [23]. This is achieved if the rotor speed is kept at an optimal value of the TSR $\lambda ^*$. The optimal rotor speed can be obtained by solving Eq. (2) for $\omega _{mt}$:

$$\begin{aligned} \omega _{mt}^*= & {} \dfrac{\lambda ^* v}{R}. \end{aligned}$$

(4)

Therefore, for a given wind speed, the main control objective is to regulate the rotor speed to its optimal value.

The rotor dynamic of wind turbine system is given by:

$$\begin{aligned} J_t\frac{d\omega _m}{dt}= & {} \frac{T_t}{n_g}-T_e-f\omega _m, \end{aligned}$$

(5)

where $J_t$ is the turbine total inertia, $T_t$ is the aerodynamic torque, and f is the turbine total external damping. The wind turbine characteristics used in this work is given in “Appendix 4”.

3.2 Modeling of the induction generator

Assuming that the rotor flux is oriented such the quadrature component $\phi _{rq}=0$, the dynamic model of the induction generator associated to PWM converter in the synchronously rotating reference frame d and q axis is given by [18, 24]:

$$\begin{aligned}&{\dot{i}}_{sd} = -\gamma _1i_{sd}+\omega _si_{sq}+\gamma _2\phi _r+\nu v_{sd} \end{aligned}$$

(6)

$$\begin{aligned}&{\dot{i}}_{sq} = -\omega _si_{sd}-\gamma _1i_{sq}-\gamma _3\omega \phi _r+\nu v_{sq} \end{aligned}$$

(7)

$$\begin{aligned}&{\dot{\phi }}_r = \frac{L_m}{\tau _r}i_{sd}-\frac{1}{\tau _r}\phi _r \end{aligned}$$

(8)

$$\begin{aligned}&\omega _s = \omega +\omega _r,\quad \omega _r=\frac{L_m}{\tau _r}\frac{i_{sq}}{\phi _r},\quad \theta _s=\int \omega _s dt \end{aligned}$$

(9)

$$\begin{aligned}&v_{sd} = \frac{1}{2}S_dv_{dc},\quad v_{sq} = \frac{1}{2}S_qv_{dc},\quad T_e=n_p\frac{L_m}{L_r}\phi _ri_{sq} \end{aligned}$$

(10)

$$\begin{aligned}&{\dot{v}}_{dc} = -\frac{1}{2C}(S_di_{sd}+S_qi_{sq})-\frac{Sv_{dc}}{R_LC}-\frac{i_i}{C}\nonumber \\&\hbox {with}\; \sigma = 1-\frac{L_m^2}{L_sL_r},\quad \tau _s=\frac{L_s}{R_s},\quad \tau _r=\frac{L_r}{R_r},\quad \nu =\frac{1}{\sigma L_s}\nonumber \\&\gamma _1 = \frac{1}{\sigma \tau _s}+\frac{1-\sigma }{\sigma \tau _r},\quad \gamma _2=\frac{1-\sigma }{L_m\sigma \tau _r},\quad \hbox {and}\quad \gamma _3=\frac{1-\sigma }{L_m\sigma }.\nonumber \\ \end{aligned}$$

(11)

The first expression of (9) represents the relation between the stator voltages/ currents electrical angular frequency $\omega _s$ and the rotor currents electrical angular frequency $\omega _r$ while the last expression is the stator electrical angular position $\theta _s$. The notation for the nonlinear dynamics of induction generator is given in “Appendix 7”. The measured variable is $\omega$, while $(i_{sd},i_{sq})$, $\phi _r$ and $R_r$ are not measurable. The control inputs are the stator voltages ($v_{sd}, v_{sq}$) and the outputs to be controlled are the rotor flux $\phi _r$, the generator rotor speed $\omega _m$ and the dc-voltage $v_{dc}$ in the dc-side.

Note that the rotor and stator winding resistances are typically uncertain because $R_r$ and $R_s$ may vary up to $100\%$ and $50\%$ of their nominal values, respectively due to stator and rotor heating.

The following assumptions will be considered until further notice.

• (i) The stator current and voltage are bounded signals.

• (ii) The rotor resistance $R_r\in \Omega _{R_r}$, where $\Omega _{R_r}$ is a compact set of ${\mathbb {R}}$.

• (iii) It is also assumed that the rate of variation of the stator/rotor inductances ($L_m$, $L_s$, $L_r$) and rotor resistance are negligible compared to the dynamic of the stator currents and the rotor flux.

The control objectives of the generator side can be summarized as follows:

• Achievement of the maximum energy extraction by regulating the the rotor speed to its optimal value,

• Regulation of the dc-bus voltage and rotor flux,

for any unknown but bounded $R_r$, despite uncertainties on the stator resistance.

Remark 1

The values of ($i_{sd},i_{sq}$) can be computed using the measurements of the stator currents ($i_{sa},i_{sb},i_{sc}$), the estimation of the stator electrical angular position $\theta _s$ and the (a, b, c) coordinate frame $\rightarrow$ (d, q) coordinate frame transformation. The expression used for the estimation of $\theta _s$ is given in Sect. 3.4.2 and the (a, b, c) coordinate frame $\rightarrow$ (d, q) coordinate frame transformation is given in “Appendix 8”.

3.3 Non-adaptive control strategy

Since Eqs. (5) and (8) do not contain the stator voltage explicitly as an input, in the following analysis, some transformations will be done to make the stator voltage components $v_{sd}$ and $v_{sq}$ appear explicitly as inputs in both equations.

Under assumptions (i)–(iii), we first compute the second time-derivative of $\phi _r$ and then use (6) and (8) to derive the dynamic equation for the rotor flux containing the stator voltage component $v_{sd}$ as a control input. We then obtain

$$\begin{aligned}&\frac{d^2\phi _r}{dt^2}=f_{\phi _r}+a_4v_{sd}\nonumber \\&\hbox {with}\quad f_{\phi _r} = a_1 i_{sd}+a_2 i_{sq}+a_3\phi _r,\nonumber \\&a_1=-\left( \frac{L_m\gamma _1}{\tau _r}+\frac{L_m}{\tau _r^2}\right) , a_2=\frac{L_m\omega _s}{\tau _r},\nonumber \\&~~~~~~\quad \times \, a_3=\frac{L_m\gamma _2}{\tau _r^2}+\frac{1}{\tau _r^2}, a_4=\frac{\nu L_m}{\tau _r}. \end{aligned}$$

(12)

To derive the dynamic equation for the rotor speed containing the stator voltage component $v_{sq}$ as a control input, let us rewrite (5) as follows.

$$\begin{aligned} \frac{d\omega _m}{dt}= & {} \frac{T_t}{J_tn_g}-\frac{T_e}{J_t}-\frac{f}{J_t}\omega _m, \end{aligned}$$

(13)

Since the aerodynamic torque $T_t$ is not measurable and the control strategy is to derive the controller that ensures optimal torque tracking in finite time, we exploit the work of [25] and replace $T_t$ in (13) by the following expression:

$$\begin{aligned} T_{t_{op}}= & {} k_{op}(\omega _m)^2\quad \hbox {with}\quad k_{op}=\frac{\rho \pi R^5C_p^*}{2\lambda ^{*3}n_g^2}. \end{aligned}$$

(14)

The dynamic equation for the rotor speed containing the stator voltage component as a control input is derived by computing the second time-derivative of $\omega _m$ and using (13), (7) and (10). This leads to

$$\begin{aligned}&\frac{d^2\omega _m}{dt^2}=f_{\omega _m}+b_9v_{sq},\nonumber \\&\hbox {with } f_{\omega _m}=b_1\omega _m^3+b_2\omega _m^2+b_3\omega _m+b_4\omega _m\phi _ri_{sq}\nonumber \\&~~~~~~~~~~~~~~~~\quad +\,b_5\phi _ri_{sq}+b_6i_{sd}i_{sq}+b_7\omega _s\phi _ri_{sd} +b_8\omega _m\phi _r^2, \nonumber \\&b_1=\frac{2k_{op}^2}{J_t^2n_g^2},\quad b_2=\frac{3fk_{op}}{J_t^2n_g},\quad b_3=\frac{f^2}{J_t^2}, \nonumber \\&b_4=\frac{-2n_pL_mk_{op}}{J_t^2n_gL_r},\quad b_5=\frac{n_pL_m}{J_tL_r}\left( \frac{f}{J_t}+\frac{1}{\tau _r}+\gamma _1\right) \nonumber \\&b_6=\frac{-n_pL_m^2}{J_tL_r\tau _r},\quad b_7=\frac{n_pL_m}{J_tL_r},\quad b_8=\frac{n_p^2\gamma _3L_m}{J_tL_r},\nonumber \\&b_9=\frac{-n_pL_m\nu \phi _r}{J_tL_r}. \end{aligned}$$

(15)

Remark 2

Since $v_{sd}$ and $v_{sq}$ given by (12) and (15) are responsible for the flux magnitude control and rotor speed control, respectively, the control goals can now be viewed as a decoupling problem.

Assuming that the rate of variation of the rotor flux and rotor speed references signals are negligible compared to other existing dynamics, the rotor flux and rotor speed tracking error dynamics are given by

$$\begin{aligned} {\ddot{e}}_{\phi _r}= & {} -f_{\phi _r}-a_4v_{sd} \end{aligned}$$

(16)

$$\begin{aligned} {\ddot{e}}_{\omega _m}= & {} -f_{v_{dc}}-b_9v_{sq}. \end{aligned}$$

(17)

Under the assumption that the rotor flux and rotor resistance are available, let us choose the switching surfaces [26] ($c_{\phi _r}>0$ and $c_{\omega _m}>0$ are tuning parameters)

$$\begin{aligned} s_{\phi _r}= & {} \frac{de_{\phi _r}}{dt}+c_{\phi _r}e_{\phi _r} \end{aligned}$$

(18)

$$\begin{aligned} s_{\omega _m}= & {} \frac{de_{\omega _m}}{dt}+c_{\omega _m}e_{\omega _m},\hbox {with} e_{\omega _m}=\omega ^*_m-\omega _m \end{aligned}$$

(19)

and the Lyapunov candidate function

$$\begin{aligned} W= & {} \frac{1}{2}( a_4s_{\phi _r}^2+b_9s_{\omega _m}^2) \end{aligned}$$

(20)

whose time-derivative is:

$$\begin{aligned} {\dot{W}}= & {} a_4s_{\phi _r}\dot{s}_{\phi _r}+b_9s_{\omega _m}\dot{s}_{\omega _m}. \end{aligned}$$

(21)

By choosing ($k_{v_{sd}}$ and $k_{v_{sq}}$ are positive design parameters)

$$\begin{aligned} v_{sd}= & {} {v_{sd}}_{eq}-k_{v_{sd}} \hbox {sign}(s_{\phi _r}) \end{aligned}$$

(22)

$$\begin{aligned} v_{sq}= & {} {v_{sq}}_{eq}-k_{v_{sq}} \hbox {sign}(s_{\omega _m}) \end{aligned}$$

(23)

where

$$\begin{aligned} v_{{sd}_{eq}}= & {} \frac{1}{a_4}\left[ f_{\phi _r} +c_{\phi _r}\left( \frac{L_m}{\tau _r}i_{sd}-\frac{1}{\tau _r}\phi _r\right) \right] ,\end{aligned}$$

(24)

$$\begin{aligned} v_{{sq}_{eq}}= & {} -\frac{1}{b_9}[f_{\omega _m}+c_{\omega _m}(k_{opt}\omega _m^2-\frac{n_pL_m}{L_r}\phi _ri_{sq}-f\omega _m)]\nonumber \\ \end{aligned}$$

(25)

are equivalent control terms [27] and are the unique solutions of $\dot{s}_{\phi _r}=0$ and $\dot{s}_{\omega _m}=0$ respectively, the time-derivative of W becomes

$$\begin{aligned} \dot{W}= & {} -k_{v_{sd}}a_4|s_{\phi _r}|-k_{v_{sq}}b_9|s_{\omega _m}|. \end{aligned}$$

(26)

Therefore, $|s_{\phi _r}|\rightarrow 0$ and $|s_{\omega _m}|\rightarrow 0$ which implies that $|e_{\phi _r}|$ and $|e_{\omega _m}|$ converge to zero. Consequently, maximum energy extraction from wind turbine is achieved by virtue of relation (4).

To prove the finite time convergence of $s_{\phi _r}$ to zero and $s_{\omega _m}$ to zero, we rewrite (20) as follows

$$\begin{aligned}&W =W_1+W_2\nonumber \\&\hbox { with } W_1=\frac{1}{2} a_4s_{\phi _r}^2\quad \hbox {and}\quad W_2=\frac{1}{2}b_9s_{\omega _m}^2. \end{aligned}$$

(27)

By taking into account (22)–(23) and (24)–(25), we obtain

$$\begin{aligned} s_{\phi _r}\dot{s}_{\phi _r}= & {} -k_{v_{sd}}|s_{\phi _r}|\quad \hbox {and}\quad s_{\omega _m}\dot{s}_{\omega _m}=-k_{v_{sq}}|s_{\omega _m}|. \end{aligned}$$

(28)

The above equations can be rewritten as

$$\begin{aligned} \dot{W}_1\!=\!-\!\sqrt{2}k_{v_{sd}}\sqrt{W_1(s_{\phi _r})}\quad \hbox {and}\quad \dot{W}_2\!=\!-\sqrt{2}k_{v_{sq}}\!\sqrt{W_2(s_{\omega _m})}.\nonumber \\ \end{aligned}$$

(29)

Thus, there exists finite times $t_{\phi _r}$ and $t_{v_{sq}}$ such that inequalities (30)–(31) hold

$$\begin{aligned} t_{\phi _r}< & {} \frac{|s_{\phi _r}(0)|}{k_{v_{sd}}} \end{aligned}$$

(30)

$$\begin{aligned} t_{v_{sq}}< & {} \frac{|s_{\omega _m}(0)|}{k_{v_{sq}}}. \end{aligned}$$

(31)

The reference rotor flux linkage required at any speed is calculated using the relationship between rotor speed and rotor flux linkage as follows [19].

$$\begin{aligned} \phi _r^*= & {} \frac{\omega _{m_{min}}}{\omega _m}\phi _{r_{max}} \end{aligned}$$

(32)

Note that when the rotor speed decreases to a value lower than $\omega _{m_{min}}$, theoretically the flux linkage should increase to a value higher that $\phi _{r_{max}}$. However, in an induction machine, once the saturation level is reached, the controller forces more direct axis current $i_{sd}$ to produce more flux. The magnitude of the exciting current can exceed the rated current of the machine without approaching the required reference flux. As a result the magnitude of the generated voltage drops.

Remark 3

To avoid the effect of the measurement noise, the time-derivatives of $e_{\phi _r}$ in (18) and $e_{\omega _m}$ in (19) can be computed using (8) and (5).

Note that the above nonlinear control is not implementable in practice since the slide manifold $s_{\phi _r}$, the equivalent control terms (24) and (25) are not available due to the fact that the rotor flux and rotor resistance are not online measurable. Furthermore, the stator electrical angular position $\theta _s$ depends upon the rotor flux and the rotor resistance which is assumed to be unknown time-varying parameter. Consequently, on-line adaptation laws for $R_r$, $\theta _s$ and observer for $\phi _r$ are required to achieve the practical implementation of the above nonlinear controller.

3.4 Adaptive design

In this section, online estimators for the rotor resistance, rotor flux and stator electrical angular position required to achieve the implementation of the above nonlinear controller (22)–(23) are derived.

3.4.1 Rotor resistance estimation algorithm

In our approach, we adopt the dynamics of a balanced induction generator, expressed in a fixed reference frame $\alpha$-$\beta$ attached to the stator [3, 28]:

$$\begin{aligned} \dot{i}_{s\alpha }= & {} \frac{1}{\gamma _4}(-L_rR_si_{s\alpha }+L_m^{2}\omega i_{s\beta }+L_mR_ri_{r\alpha }{+}L_rL_m\omega i_{r\beta }\nonumber \\&+\,L_rv_{s\alpha }) \end{aligned}$$

(33)

$$\begin{aligned} \dot{i}_{s\beta }= & {} \frac{1}{\gamma _4}(-L_m^{2}\omega i_{s\alpha }-L_rR_si_{s\beta }-LrL_m\omega i_{r\alpha }{+}L_mR_ri_{r\beta }\nonumber \\&+\,L_rv_{s\beta }) \end{aligned}$$

(34)

$$\begin{aligned} \dot{i}_{r\alpha }= & {} \frac{1}{\gamma _4}(L_mR_si_{s\alpha }-L_mL_s\omega i_{s\beta }-L_sR_ri_{r\alpha }{-}L_sL_r\omega i_{r\beta }\nonumber \\&-\,L_mv_{s\alpha }) \end{aligned}$$

(35)

$$\begin{aligned} \dot{i}_{r\beta }= & {} \frac{1}{\gamma _4}(L_mL_s\omega i_{s\alpha }+L_mR_si_{s\beta }+L_sL_r\omega i_{r\alpha }{-} L_sR_ri_{r\beta }\nonumber \\&-\,L_mv_{s\beta }) \end{aligned}$$

(36)

where $\gamma _4=L_sL_r-L_m^{2}$.

We can now consider the following observer ($K>0$ is a constant designed parameter):

$$\begin{aligned} \dot{{\hat{i}}}_{s\alpha }= & {} \frac{1}{\gamma _4}(-L_rR_si_{s\alpha }+L_m^{2}\omega i_{s\beta }+L_m{\hat{R}}_r{\hat{i}}_{r\alpha }+L_mL_r\omega {\hat{i}}_{r\beta }\nonumber \\&+\,L_rv_{s\alpha }+\,K \hbox {sign}(i_{s\alpha }-{\hat{i}}_{s\alpha })) \end{aligned}$$

(37)

$$\begin{aligned} \dot{{\hat{i}}}_{s\beta }= & {} \frac{1}{\gamma _4}(-L_m^{2}\omega i_{s\alpha }- L_rR_si_{sb}-L_mL_r\omega {\hat{i}}_{r\alpha }\nonumber \\&\quad +\,L_m{\hat{R}}_r{\hat{i}}_{r\beta }{+}L_rv_{s\beta }+K \hbox {sign}(i_{s\beta }-{\hat{i}}_{s\beta })) \end{aligned}$$

(38)

$$\begin{aligned} \dot{{\hat{i}}}_{r\alpha }= & {} \frac{1}{\gamma _4}(L_mR_si_{s\alpha }-L_sL_m\omega i_{s\beta }-L_s{\hat{R}}_r{\hat{i}}_{r\alpha }\nonumber \\&\quad -\,L_sL_r\omega {\hat{i}}_{r\beta }{+} u_{\alpha }-L_mv_{s\alpha }) \end{aligned}$$

(39)

$$\begin{aligned} \dot{{\hat{i}}}_{r\beta }= & {} \frac{1}{\gamma _4}(L_sL_m\omega i_{s\alpha }+L_mR_si_{s\beta }\nonumber \\&\quad +\,L_sL_r\omega {\hat{i}}_{r\alpha }- L_s{\hat{R}}_r{\hat{i}}_{r\beta }{+}u_{\beta }-L_mv_{s\beta }) \end{aligned}$$

(40)

where $u_\alpha$ and $u_\beta$ are additional signals yet to be designed and $\hbox {sign}$ is the well known $\hbox {sign}$ function. The estimated quantities are shown as ${\hat{x}}$ while the error quantities are given as follows ${\tilde{x}}=x-{\hat{x}}$ (e.g., ${\tilde{i}}_{s\alpha }=i_{s\alpha }-{\hat{i}}_{s\alpha }$, ${\tilde{i}}_{s\beta }=i_{s\beta }-{\hat{i}}_{s\beta }$, ${\tilde{i}}_{r\alpha }=i_{r\alpha }-{\hat{i}}_{r\alpha }$, ${\tilde{i}}_{r\beta }=i_{r\beta }-{\hat{i}}_{r\beta }$, ${\tilde{R}}_r=R_r-{\hat{R}}_r$).

The dynamics of the observer error can be computed using (33)–(36) and (37)–(40) as

$$\begin{aligned} \dot{{\tilde{i}}}_{s\alpha }= & {} \frac{1}{\gamma _4}(L_mR_r{\tilde{i}}_{r\alpha }+L_m{\tilde{R}}_r{\hat{i}}_{r\alpha }+L_mL_r\omega {\tilde{i}}_{r\beta }){-}K \hbox {sign}({\tilde{i}}_{s\alpha })\nonumber \\ \end{aligned}$$

(41)

$$\begin{aligned} \dot{{\tilde{i}}}_{s\beta }= & {} \frac{1}{\gamma _4}(-L_mL_r\omega {\tilde{i}}_{r\alpha }+L_mR_r{\tilde{i}}_{r\beta }+L_m{\tilde{R}}_r{\hat{i}}_{r\beta }){-}K \hbox {sign}({\tilde{i}}_{s\beta })\nonumber \\ \end{aligned}$$

(42)

$$\begin{aligned} \dot{{\tilde{i}}}_{r\alpha }= & {} \frac{1}{\gamma _4}(-L_sR_r{\tilde{i}}_{r\alpha }-L_s{\tilde{R}}_r{\hat{i}}_{r\alpha }-L_sL_r\omega {\tilde{i}}_{r\beta }-u_{\alpha }) \end{aligned}$$

(43)

$$\begin{aligned} \dot{{\tilde{i}}}_{r\beta }= & {} \frac{1}{\gamma _4}(L_sL_r\omega {\tilde{i}}_{r\alpha }-L_sR_r{\tilde{i}}_{r\beta }-L_s{\tilde{R}}_r{\hat{i}}_{r\beta }-u_{\beta }) \end{aligned}$$

(44)

To achieve the design of the rotor resistance identifier the following additive assumption is required.

Assumption (iv) It is assumed that the following rotor resistance identifiability condition holds:

$$\begin{aligned} |i_{r\alpha }(t)|&\ge 0&\quad \hbox {and}\quad |i_{r\beta }(t)|\ge 0\quad \forall t\ge 0. \end{aligned}$$

(45)

By considering the following Lyapunov candidate function

$$\begin{aligned} V_1= & {} \frac{1}{2}{\tilde{i}}_{s\alpha }^{2}+\frac{1}{2}{\tilde{i}}_{s\beta }^{2} \end{aligned}$$

(46)

and computing its time-derivative along the trajectories of (41) and (42), we obtain

$$\begin{aligned} \dot{V}_1= & {} \frac{1}{\gamma _4}(L_mL_r{\tilde{i}}_{r\beta }{\tilde{i}}_{s\alpha }+L_mR_r{\tilde{i}}_{r\alpha }{\tilde{i}}_{s\alpha }+L_m{\tilde{R}}_r{\hat{i}}_{r\alpha }{\tilde{i}}_{s\alpha } \nonumber \\&-K|{\tilde{i}}_{s\alpha }|-L_mL_r\omega {\tilde{i}}_{r\alpha }{\tilde{i}}_{s\beta }+L_mR_r{\tilde{i}}_{r\beta }{\tilde{i}}_{s\beta }+L_m{\tilde{R}}_r\nonumber \\&{\hat{i}}_{r\beta }{\tilde{i}}_{s\beta }-K|{\tilde{i}}_{s\beta }|) \end{aligned}$$

(47)

From (47), by taking into account assumptions (i) and (ii), the following inequalities hold:

$$\begin{aligned} \dot{V}_1\le & {} \frac{1}{\gamma _4}(-|{\tilde{i}}_{s\alpha }|\Big [K- (L_mL_r\omega |{\tilde{i}}_{r\beta }|+L_mR_r|{\tilde{i}}_{r\alpha }|\nonumber \\&+\,L_m{\tilde{R}}_r\mid {\hat{i}}_{r\alpha }\mid )\Big ] -|{\tilde{i}}_{s\beta }|\Big [K-(L_mL_r\omega \mid {\tilde{i}}_{r\alpha }\mid \nonumber \\&+\,L_mR_r\mid {\tilde{i}}_{r\beta }\mid +L_m{\tilde{R}}_r\mid {\hat{i}}_{r\beta }\mid )\Big ]). \end{aligned}$$

(48)

Assuming that the estimate ${\hat{R}}_r$, ${\hat{i}}_{r\alpha }$, and ${\hat{i}}_{r\beta }$ are bounded,¹ let positive constants $\xi _{\alpha }$ and $\xi _{\beta }$ be available such that

$$\begin{aligned} \xi _{\alpha }= & {} \frac{1}{\gamma _4}(L_mL_r\omega |{\tilde{i}}_{r\beta }|_m+L_mR_r|{\tilde{i}}_{r\alpha }|_m+L_m{\tilde{R}}_r\mid {\hat{i}}_{r\alpha }\mid _m) \nonumber \\\end{aligned}$$

(49)

$$\begin{aligned} \xi _{\beta }= & {} \frac{1}{\gamma _4}(L_mL_r\omega \mid {\tilde{i}}_{r\alpha }\mid _m+L_mR_r\mid {\tilde{i}}_{r\beta }\mid _m+L_m{\tilde{R}}_r\mid {\hat{i}}_{r\beta }\mid _m)\nonumber \\ \end{aligned}$$

(50)

where $|.|_m$ denotes the maximum value of |.|. By choosing

$$\begin{aligned} K> & {} \hbox {sup}(\xi _{\alpha },\xi _{\beta }) \end{aligned}$$

(51)

the derivative of $V_1$ will be negative definite $\forall$ ${\tilde{i}}_{s\alpha }\ne 0$ and ${\tilde{i}}_{s\beta }\ne 0$. Therefore, the observer errors ${\tilde{i}}_{s\alpha }$ and ${\tilde{i}}_{s\beta }$ converge to 0 in finite time if the gain K is chosen such that condition (51) is satisfied.

Remark 4

Since the rotor signals are not measurable in the case of squirrel cage induction machine, the gain K in (51) can be selected by trial and error method.

We now consider the following quadratic function of the rotor current observer error and rotor resistance estimation error:

$$\begin{aligned} V_2= & {} \frac{1}{2}{\tilde{i}}_{r\alpha }^{2}+\frac{1}{2}{\tilde{i}}_{r\beta }^{2}+\frac{1}{2}{\tilde{R}}_r^{2}. \end{aligned}$$

(52)

Its time-derivative along the trajectories of (43) and (44) yields

$$\begin{aligned} \dot{V}_2= & {} \frac{1}{\gamma _4}(-L_sR_r{\tilde{i}}_{r\alpha }^{2}-L_s{\tilde{R}}_r{\hat{i}}_{r\alpha }{\tilde{i}}_{r\alpha }-u_{\alpha }{\tilde{i}}_{r\alpha }-L_sR_r{\tilde{i}}_{r\beta }^{2} \nonumber \\&{-}L_s{\tilde{R}}_r{\hat{i}}_{r\beta }{\tilde{i}}_{rb}-u_{\beta }{\tilde{i}}_{r\beta }+{\tilde{R}}_r\dot{{\tilde{R}}}_r). \end{aligned}$$

(53)

If we choose $u_{\alpha }$, $u_{\beta }$ and $\dot{{\tilde{R}}}_r$ as follows ($K_{R_r}$ is a designed parameter):

$$\begin{aligned} u_{\alpha }= & {} -L_s{\tilde{R}}_r{\hat{i}}_{r\alpha }\nonumber \\ u_{\beta }= & {} -L_s{\tilde{R}}_r{\hat{i}}_{r\beta }\nonumber \\ \dot{{\tilde{R}}}_r= & {} \dot{{\hat{R}}}_r=-K_{R_r} \hbox {sign}({\tilde{R}}_r) \end{aligned}$$

(54)

$\dot{V}_2$ becomes

$$\begin{aligned} \dot{V}_2= & {} -\frac{L_sR_r}{\gamma _4}({\tilde{i}}_{r\alpha }^{2}+{\tilde{i}}_{r\beta }^{2})-K_{R_r}\mid {\tilde{R}}_r\mid . \end{aligned}$$

(55)

Consequently, under the identifiability condition (45) and if the auxiliary variables $u_{\alpha }$, $u_{\beta }$ and $\dot{{\tilde{R}}}_r$ are chosen as in (54), $\dot{V}_2$ will be negative definite $\forall {\tilde{i}}_{r\alpha }\ne 0$, $\forall {\tilde{i}}_{r\beta }\ne 0$ and $\forall {\tilde{R}}_r\ne 0$. Thus, ${\hat{i}}_{r\alpha }$, ${\hat{i}}_{r\beta }$ and ${\hat{R}}_r$ converge in finite time to their nominal values $i_{r\alpha }$, $i_{r\beta }$ and $R_r$ with the convergence rate $\frac{L_sR_r}{\gamma _4}$ and $K_{R_r}$, respectively.

Remark 5

If $\displaystyle K_{R_r}>\frac{L_sR_r}{\gamma _4}$, the rotor resistance convergence will be faster than that of the rotor current. In contrary, if $\displaystyle K_{R_r}<\frac{L_sR_r}{\gamma _4}$, the rotor current convergence will be faster than that of the rotor resistance. The case $\displaystyle K_{R_r}=\frac{L_sR_r}{\gamma _4}$ is difficult to implement in practice since $R_r$ is assumed to be unknown and is time-varying but verifies in normal operation of the SEIG $R_{r_{min}}\le R_r\le R_{r_{max}}$.

To achieve the design of the rotor resistance estimator, implementable expression for ${\tilde{R}}_r$ is required. Under condition (51), a sliding-mode occurs in finite time on the manifold

$$\begin{aligned} \dot{{\tilde{i}}}_{s\alpha }= & {} {\tilde{i}}_{s\alpha }=0\nonumber \\ \dot{{\tilde{i}}}_{s\beta }= & {} {\tilde{i}}_{s\beta }=0. \end{aligned}$$

(56)

The equivalent injection terms [27] can be computed by solving the equation

$$\begin{aligned} \dot{{\tilde{i}}}_{s\alpha }= & {} 0 \nonumber \\ \dot{{\tilde{i}}}_{s\beta }= & {} 0. \end{aligned}$$

(57)

Consequently, (41) and (42) can be rewritten as

$$\begin{aligned}&\frac{1}{\gamma _4}(L_mL_r\omega {\tilde{i}}_{r\beta }+L_mR_r{\tilde{i}}_{r\alpha }+L_m{\tilde{R}}_r{\hat{i}}_{r\alpha })-W_{\alpha eq}=0 \end{aligned}$$

(58)

$$\begin{aligned}&\frac{1}{\gamma _4}(-L_mL_r\omega {\tilde{i}}_{r\alpha }+L_mR_r{\tilde{i}}_{r\beta }+L_m{\tilde{R}}_r{\hat{i}}_{r\beta })-W_{\beta eq}=0\nonumber \\ \end{aligned}$$

(59)

where $W_{\alpha eq}=K \hbox {sign}({\tilde{i}}_{s\alpha })$ and $W_{\beta eq}=K \hbox {sign}({\tilde{i}}_{s\beta })$. The expressions of the equivalent injection terms can be deduced from (58) and (59) but these expressions cannot be implemented in practice since ${\tilde{i}}_{r\alpha }$, ${\tilde{i}}_{r\beta }$ and ${\tilde{R}}_r$ are not available.² To overcome this problem, the equivalent injection terms are approximated using first order low-pass filters as in [27]. If the design parameter $K_{R_r}$ is chosen such that

$$\begin{aligned} 0<&K_{R_r}&< \frac{L_sR_{rmin}}{\gamma _4}, \end{aligned}$$

(60)

the rotor current convergence will be faster than that of the rotor resistance. Under this assumption and identifiability condition (45), the implementable expression of the rotor resistance estimation error ${\tilde{R}}_r$ can be derived from (58) and (59) by neglecting the terms containing the rotor current estimation error. We then obtain

$$\begin{aligned} {\tilde{R}}_r= & {} \frac{\gamma _4({\hat{i}}_{r\alpha }W_{\alpha eq}+{\hat{i}}_{r\beta }W_{\beta eq})}{L_m({\hat{i}}_{r\alpha }^{2}+{\hat{i}}_{r\beta }^{2})}. \end{aligned}$$

(61)

Finally, the overall simplified rotor resistance estimator can be summarized as follows:

$$\begin{aligned} \dot{{\hat{i}}}_{s\alpha }= & {} \frac{1}{\gamma _4}(-L_rR_si_{s\alpha }+L_m^{2}\omega i_{s\beta }+L_m{\hat{R}}_r{\hat{i}}_{r\alpha }+L_mL_r\omega {\hat{i}}_{r\beta }\nonumber \\&+\,L_rv_{s\alpha })-K \hbox {sign}({\tilde{i}}_{s\alpha })\nonumber \\ \dot{{\hat{i}}}_{s\beta }= & {} \frac{1}{\gamma _4}(-L_m^{2}\omega i_{s\alpha }-L_rR_si_{s\beta }-L_mL_r\omega {\hat{i}}_{r\alpha }\nonumber \\&+\, L_m{\hat{R}}_r {\hat{i}}_{r\beta }{+}L_rv_{s\beta })-K \hbox {sign}({\tilde{i}}_{s\beta })\nonumber \\ \dot{{\hat{i}}}_{r\alpha }= & {} \frac{1}{\gamma _4}(L_mR_si_{s\alpha }-L_mL_s\omega i_{s\beta }-L_s{\hat{R}}_r{\hat{i}}_{r\alpha }\nonumber \\&-\,L_sL_r\omega {\hat{i}}_{r\beta }{+}u_\alpha -L_mv_{s\alpha })\nonumber \\ \dot{{\hat{i}}}_{r\beta }= & {} \frac{1}{\gamma _4}(L_mL_s\omega i_{s\alpha }+L_mR_si_{s\beta }+L_sL_r\omega {\hat{i}}_{r\alpha }\nonumber \\&-\, L_s{\hat{R}}_r{\hat{i}}_{r\beta }{+}u_\beta -L_mv_{s\beta })\nonumber \\ u_{\alpha }= & {} -L_s{\tilde{R}}_r{\hat{i}}_{r\alpha },\quad u_{\beta }=-L_s{\tilde{R}}_r{\hat{i}}_{r\beta }\nonumber \\ \dot{{\hat{R}}}_r= & {} -K_{R_r} \; \hbox {sign}({\tilde{R}}_r) \; \hbox {with} \; {\tilde{R}}_r=\frac{\gamma _4({\hat{i}}_{r\alpha }W_{\alpha eq}+{\hat{i}}_{rb}W_{\beta eq})}{L_m({\hat{i}}_{r\alpha }^{2}+{\hat{i}}_{r\beta }^{2})}.\nonumber \\ \end{aligned}$$

(62)

3.4.2 Rotor flux and stator electrical angular position estimation algorithms

Rotor flux observer design

Let us now consider the following observer for $\phi _r$

$$\begin{aligned} \dot{{\hat{\phi }}}_r= & {} \frac{L_m{\hat{R}}_r}{L_r}i_{sd}-\frac{{\hat{R}}_r}{L_r}{\hat{\phi _r}} \end{aligned}$$

(63)

and let ${\tilde{e}}_{\phi _r}=\phi _r-{\hat{\phi }}_r$ be the rotor flux observer error. By taking into account (8), the observer error dynamic equation may be computed as follows:

$$\begin{aligned} \dot{{\tilde{e}}}_{\phi _r}= & {} \frac{{\tilde{R}}_r}{L_r}(L_mi_{sd}-\phi _r)-\frac{{\hat{R}}_r}{L_r}{\tilde{e}}_{\phi _r} \end{aligned}$$

(64)

From the fact that ${\tilde{R}}_r$ converges to the neighborhood of 0 in finite time, the observer error ${\tilde{e}}_{\phi _r}$ converges to the neighborhood of 0 which immediately implies that ${\hat{\phi }}_r$ converges to $\phi _r$.

Stator electrical angular position estimation algorithm

Assuming that the estimates of the rotor resistance and rotor flux converge in finite time to their nominal values, the estimation of the stator electrical angular position can be achieved by using (9) as follows.

$$\begin{aligned} {\hat{\omega }}_s= & {} \omega +\frac{L_m{\hat{R}}_r}{L_r}\frac{i_{sq}}{{\hat{\phi }}_r},\quad {\hat{\theta }}_s=\int {\hat{\omega }}_s dt+{\hat{\theta }}_s(0). \end{aligned}$$

(65)

Remark 6

The proposed adaptive nonlinear control is not a direct current control. To limit the reference value of $v_{sd}$ and $v_{sq}$ (which implicitly limits the current reference value), saturated functions have been used. However, in the practice, the SEIG based system should be equipped with a fast over current protection unit.

3.5 Global convergence and stability analysis

To achieve the global convergence and stability analysis, let us recall the non-adaptive nonlinear controller (22)–(23):

$$\begin{aligned} v_{sd}= & {} {v_{sd}}_{eq}-k_{v_{sd}} \hbox {sign}(s_{\phi _r}) \end{aligned}$$

(66)

$$\begin{aligned} v_{sq}= & {} {v_{sq}}_{eq}-k_{v_{sq}}\text{ sign }(s_{\omega _m}) \end{aligned}$$

(67)

where

$$\begin{aligned} v_{{sd}_{eq}}= & {} \frac{1}{a_4}\left[ f_{\phi _r}-{\ddot{\phi }}^*_r-c_{\phi _r}{\dot{\phi }}^*_r +c_{\phi _r}\left( \frac{L_m}{\tau _r}i_{sd}-\frac{1}{\tau _r}\phi _r\right) \right] , \nonumber \\\end{aligned}$$

(68)

$$\begin{aligned} v_{{sq}_{eq}}= & {} -\frac{1}{b_9}[f_{\omega _m}+c_{\omega _m}(k_{opt}\omega _m^2-\frac{n_pL_m}{L_r}\phi _ri_{sq}-f\omega _m)]\nonumber \\ \end{aligned}$$

(69)

Note that it has been proved in section 3.3 that the above non-adaptive controller achieves finite time convergence of the tracking errors to zero of the rotor speed and rotor flux of SEIG associated to PWM converter.

In practice, the adaptive controller is used because the rotor flux $\phi _r$ is not measurable and the observer of the rotor flux depends up-on the rotor resistance $R_r$ which is assumed to be unknown time-varying parameter. In addition, the equivalent terms (68)–(69) and the stator electrical angular position $\theta _s$ require the knowledge of the rotor flux and rotor resistance. In this case, $\theta _s$, $R_r$ and $\phi _r$ are substituted in the above non-adaptive controller by their estimates.

The global convergence and stability analysis taking into account the interconnections between $R_r$, $\phi _r$ and $\theta _s$ estimators and the nonlinear controller are based on the separation principle theorem. The finite-time convergence of the estimation algorithms allows to design the estimators and the nonlinear control law separately, i.e., the separation principle is satisfied [29, 30]. The only requirement for its implementation is the boundedness of the states of the system [assumptions (i)–(iii), the identifiability condition (45), conditions (51) and (60)] in the operational domain.

3.6 DC-link voltage control strategy design

In order to regulate the dc-link voltage, an electronic load controller (ELC) is proposed. This ELC consists of an insulated gate bipolar transistor IGBT operating as a chopper connected in series with a dump load resistance $R_L$. This dump load is designed such that when the duty cycle of the chopper is unity (during fault or over-generation), it should consume the maximum output power of the generator. The dump load can be a heater load or a battery charging load. Using the power balance principle, the dynamic behavior of the dc-bus voltage is given by [31]

$$\begin{aligned} \frac{C}{2}\frac{dv_{dc}^2}{dt}= & {} \omega _mT_e-\frac{Sv_{dc}^2}{R_L}-P_{in} \end{aligned}$$

(70)

where $P_{in}$ is the input power of the inverter. We rewrite (70) as follows.

$$\begin{aligned} \frac{dv_{dc}}{dt}= & {} f_{v_{dc}}+g_{v_{dc}}v_\alpha ,\text{ with }\quad v_\alpha =Sv_{dc} \end{aligned}$$

(71)

$$\begin{aligned} f_{v_{dc}}= & {} \frac{\omega _mT_e}{Cv_{dc}}-\frac{P_{in}}{Cv_{dc}},\text{ and }\quad g_{v_{dc}}=-\frac{1}{R_LC}. \end{aligned}$$

(72)

The expression for the DC-link voltage control of $v_{dc}$ can be easily computed as in the case of $\phi _r$ and $\omega _m$ control strategy (Sect. 3.3) as follows

$$\begin{aligned} v_\alpha ^*= & {} -\frac{1}{g_{dc}}(f_{dc}+k_{i_{dc}}e_{dc})-k_{p_{dc}}\text{ sign }(S_{dc}),\nonumber \\&\quad \text{ where } \quad S_{dc}=e_{dc}+k_{i_{dc}}\int e_{dc}, \quad e_{dc}=v_{dc}-v_{dc}^*.\nonumber \\ \end{aligned}$$

(73)

4 Load side inverter control strategy design

The control objective in the load side inverter is the regulation of the AC load voltage magnitude. Note that the frequency of the load voltages and currents is imposed by the frequency of the load $\omega _e$ used in the (a, b, c) coordinate frame $\rightarrow$ (d, q) coordinate frame transformation.

4.1 Modeling of voltage source inverter and LC filter

The voltage source inverter is connected to the AC load through an LC filter. In the synchronously rotating reference frame d and q axis, the voltage equations are given by [31]:

$$\begin{aligned} \dot{i}_{id}= & {} -\frac{R_f}{L_f}i_{id}+\omega _e i_{iq}+\frac{1}{L_f}v_{id}-\frac{1}{L_f}v_{d} \end{aligned}$$

(74)

$$\begin{aligned} \dot{i}_{iq}= & {} -\frac{R_f}{L_f}i_{iq}-\omega _e i_{id}+\frac{1}{L_f}v_{iq}-\frac{1}{L_f}v_{q} \end{aligned}$$

(75)

$$\begin{aligned} \dot{v}_{d}= & {} \frac{1}{C_f}i_{id}-\frac{1}{C_f}i_{Ld} \end{aligned}$$

(76)

$$\begin{aligned} \dot{v}_{q}= & {} \frac{1}{C_f}i_{iq}-\frac{1}{C_f}i_{Lq} \end{aligned}$$

(77)

The notation for the above nonlinear dynamics is given in “Appendix 7”. The methodology used to obtain the filter parameters is described in [32] and is given in “Appendix 8”.

Assuming that the load side inverter currents in the synchronously rotating reference frame d and q axis are constants, the equations used for the derivation of the control law in this section can be computed using the differentiation of (76) and (77) combined with (74) and (75). This leads to:

$$\begin{aligned} {\ddot{v}}_{d}= & {} \frac{1}{C_f}\left( -\frac{R_f}{L_f}i_{id}+\omega _ei_{iq}+\frac{1}{L_f}v_{id}-\frac{1}{L_f}v_{d}\right) \end{aligned}$$

(78)

$$\begin{aligned} {\ddot{v}}_{q}= & {} \frac{1}{C_f}\left( -\frac{R_f}{L_f}i_{iq}-\omega _e i_{id}+\frac{1}{L_f}v_{iq}-\frac{1}{L_f}v_{q}\right) \end{aligned}$$

(79)

Assuming that the load side voltage reference values in the synchronously rotating reference frame d and q axis are constants, the expressions for the load side inverter control of $v_d$ and $v_q$ can be easily computed as in the case of $\phi _r$ and $\omega _m$ control strategy (Sect. 3.3) as follows

$$\begin{aligned} v_{i_d}^*= & {} {v_{id}}_{eq}-k_{v_{id}}\text{ sign }(s_{v_{d}}) \end{aligned}$$

(80)

$$\begin{aligned} v_{i_q}^*= & {} {v_{iq}}_{eq}-k_{v_{iq}}\text{ sign }(s_{v_{q}}) \end{aligned}$$

(81)

where

$$\begin{aligned} {v_{id}}_{eq}= & {} \left( R_f-L_fC_{v_{d}}\right) i_{id}-\omega _eL_fi_{iq}\nonumber \\&+\,v_d+L_fC_{v_{d}}i_{Ld},\quad s_{v_{d}}=\left( \frac{d}{dt}+C_{v_{d}}\right) (v_{d}-v_{d}^*) \nonumber \\\end{aligned}$$

(82)

$$\begin{aligned} v_{{iq}_{eq}}= & {} \left( R_f-L_fC_{v_q}\right) i_{iq}+\omega _eL_fi_{id}\nonumber \\&+\,v_q+L_fC_{v_{q}}i_{Lq},\quad s_{v_{q}}=\left( \frac{d}{dt}+C_{v_{q}}\right) (v_q-v_q^*).\nonumber \\ \end{aligned}$$

(83)

Remark 7

To reduce the chattering phenomenon on the proposed controllers, the sign function has been approximated as [33]

$$\begin{aligned} \text{ sign }(.)= & {} \frac{(.)}{|(.)|+\epsilon }\quad \text{ with }\quad 0<\epsilon <1. \end{aligned}$$

(84)

The structure of the proposed nonlinear controllers is depicted in Fig. 2.

Fig. 2

Structure of the proposed adaptive nonlinear controllers

4.2 Controller parameters tuning

It is worth observing that, in order to increase the tracking performance of the above controllers, a rigorous methodology for the optimal tuning of the controller design parameters is required. However, it is difficult to define such a methodology, since the overall adaptive control is nonlinear with time-varying adaptive parameters. In this section, some guidelines for the selection of controller parameter values (i.e. $c_{\omega _m}$, $c_{\phi _r}$, $k_{v_{sq}}$, $k_{v_{sd}}$ in Sect. 3.3) are given.

The following considerations have to be taken into account.

• $c_{\omega _m}$ and $c_{\phi _r}$ should be chosen sufficiently smaller than the frequency (in rad/s) of the lowest unmodeled dynamics.

• the larger $c_{\omega _m}$, $c_{\phi _r}$, $k_{v_{sq}}$ and $k_{v_{sd}}$, the worse the effect of noise present in the input of the adaptive controller;

• in real-time implementation using DSP, $c_{\omega _m}$ and $c_{\phi _r}$ should be chosen sufficiently smaller than the sampling frequency (in rad/s).

Hence the values of $c_{\omega _m}$, $c_{\phi _r}$, $k_{v_{sq}}$ and $k_{v_{sd}}$ should be chosen using the above guidelines in order to obtain a trade-off between the signal content preservation and the noise reduction.

5 Simulation results

The effectiveness of the proposed nonlinear controller (NC) has been verified by numerical simulations within the Matlab/Simulink environment software with sampling time of $40\mu ~s$. This sampling time is real-time implementable using actual commercial DSP1104 [34]. The parameters of the induction machine, generator side converter and load side inverter used in the simulation are given in “Appendices 1, 2 and 3”, respectively.

Two sets of simulation have been performed. For comparison, these simulations have been performed using both nonlinear controllers and conventional P.I regulators. The structures of the P.I regulators are given in Figs. 3 and 4.

Fig. 3

Structure of the PI regulators in the generator side

Fig. 4

Structure of the PI regulators in the load side

In all simulations, the capacitive load RC, inductive load RL, and the RLC load have been applied at time $t=0\,\mathrm{s}$, $t=1.5\mathrm{s}$ and $2.5\,\mathrm{s}$, respectively. The values of the different loads have been chosen as follows.

Capacitive load RC: $R=150\Omega$, $C=30\,\mathrm{mF}$. Inductive load RC: $R=150\Omega$, $L=50\,\mathrm{mH}$. Combined inductive-capacitive load RLC: $R=150\Omega$, $L=50\,\mathrm{mH}$, $C=30\,\mathrm{mF}$. The frequency of the load is $\omega _e=100\pi$.

The tuning parameters of the nonlinear controllers selected according to the procedure described in Sect. 4.2, have been chosen as follows.

Rotor flux magnitude and rotor speed controllers gains: $c_{\omega _{m}}=200$, $k_{v_{sq}}=30$, $c_{\phi _r}=300$ and $k_{v_{sd}}=50$. DC-link voltage regulation gains: $k_{i_{dc}}=2$ and $k_{p_{dc}}=10$.

Load side inverter nonlinear controllers gains: $c_{v_{d}}=10$, $k_{v_d}=10$, $c_{v_q}=20$ and $k_{v_q}=10$. The gains of the rotor resistance identifier are $K=50$ and $K_{R_r}=35$. The equivalent injection terms have been approximated using first order low-pass filter with time-constant of $3.5\,\mathrm{ms}$ and the $\text{ sign }$ function in the controller (66)–(67) has been approximated using (84) with $\epsilon =0.01$. Note that the value of $K_{R_r}$ verifies condition (60) since $\frac{L_sR_{rmin}}{L}=128.2\,\mathrm{s}^{-1}$. The initial value of $\theta _s$ is $0.01~\mathrm{rad}$. The parameters of the LC filter used in the load side inverter are: $L_f=40\,\mathrm{mH}$, $C_f=10\,\upmu F$ and $R_f=0.1\Omega$.

The tuning parameters of the PI regulators selected according to the procedure described in “Appendix 5”, have been chosen as follows.

Generator converter side

Rotor flux regulator: $k_{p\varphi _r}=110$, $k_{i\varphi _r}=1660$.

Rotor speed regulator: $k_{p\omega _m}=4$, $k_{i\omega _m}=1$.

Stator current components $i_{sd}$ and $i_{sq}$ regulators: $k_{pi_{sd}}=k_{pi_{sq}}=100$, $k_{ii_{sd}}=k_{ii_{sq}}=600$.

Grid inverter side

Load voltage direct axis component PI regulators gains: $k_{pv_d}=0.45$, $k_{iv_d}=1.2$, $k_{pi_{d}}=10$ and $k_{ii_{d}}=5$.

Load voltage quadrature axis component PI regulators gains: $k_{pv_q}=10$, $k_{iv_q}=5$, $k_{pi_{q}}=5$ and $k_{ii_{q}}=2.5$.

To verify the effectiveness and robustness of the proposed method, all simulations have been carried out with SEIG driven by variable wind speed turbine and under noise condition when the magnitude of the noise reaches about $3.75\%$ of the maximum values of the measurable stator currents (Figs. 5, 6, 7, 8, 9, 10, 11, 12, 13, 14).

Fig. 5

First set of simulation: Comparative performances when the stator resistance is assumed to be constant under online variation of the rotor resistance (variation starts at time $t=1\,\mathrm{s}$ and reaches $100\%$ at time $t=2\,\mathrm{s}$). a DC-bus voltage (i), rotor flux magnitude (ii), and rotor resistance (iii). b Wind speed (i), rotor speed (ii), and power coefficient (iii)

Fig. 6

First set of simulation: Comparative performances when the stator resistance is assumed to be constant under online variation of the rotor resistance (variation starts at time $t=1\,\mathrm{s}$ and reaches $100\%$ at time $t=2\,\mathrm{s}$). a DC-bus voltage regulation error (i), rotor flux magnitude tracking error (ii) and rotor speed tracking error (iii). b d-axis load voltage component (i), and q-axis load voltage component (ii), d-axis load voltage component regulation error (iii)

Fig. 7

First set of simulation: Performance when the stator resistance is assumed to be constant under online variation of the rotor resistance (variation starts at time $t=1\,\mathrm{s}$ and reaches $100\%$ at time $t=2\,\mathrm{s}$). a Control signal during transient periods in the case of the NC (i, ii and iii); control signal during transient periods in the case of the PI regulator (i, ii and iii). b SEIG stator current component $i_{sa}$ in the case of the NC (i); SEIG stator current component $i_{sa}$ in the case of the PI regulator (ii)

Fig. 8

First set of simulation: Performance when the stator resistance is assumed to be constant under online variation of the rotor resistance (variation starts at time $t=1\,\mathrm{s}$ and reaches $100\%$ at time $t=2\,\mathrm{s}$). a Load voltage component $v_a$ during transient periods in the case of the NC (i and ii); load voltage component $v_a$ during transient periods in the case of the PI regulator (i and ii). b Load current component $i_a$ during transient periods in the case of the NC (i and ii); load current component $i_a$ during transient periods in the case of the PI regulator (i and ii)

Fig. 9

First set of simulation: Performance when the stator resistance is assumed to be constant under online variation of the rotor resistance (variation starts at time $t=1\,\mathrm{s}$ and reaches $100\%$ at time $t=2\,\mathrm{s}$). a Zoom in Fig. 5a, iii for $R_r$, zoom of the rotor current component ${\hat{i}}_{r\alpha }$ and zoom in Fig. 5b, iii for $C_p$ during transient periods. b Zoom in Fig. 6a

In the first set of simulation, the stator resistance is assumed to be constant while the rotor resistance is assumed to be time-varying. This variation starts at time $t=1\,\mathrm{s}$ and reaches $100\%$ of the nominal value of $R_r$ at time $t=2\,\mathrm{s}$. The results are depicted in Figs. 5, 6, 7, 8, 9 and 10.

It can be noticed from these figures the good performance of the proposed nonlinear control and the poor performance of the P.I regulators under online variation of the rotor resistance and when the wind speed varies from 9 to $6.5~\mathrm{m/s}$ at time $t=3.5\,\mathrm{s}$. The steady state errors obtained when the wind speed varies from 9 to $6.5~\mathrm{m/s}$ at time $t=3.5\,\mathrm{s}$ show that the results obtained using the nonlinear controller are more precise than those provided by PI regulators. During transient periods, the performance obtained using PI regulators exhibits higher overshoot values than the performance provided by the nonlinear controllers (Figs. 9b, 14b). One can also notice that the convergence times of the rotor current and rotor resistance are 0.015, and $0.14\,s$, respectively. Thus the assumption that the rotor current convergence must be faster than the convergence time of the rotor resistance is satisfied. Under load variations, both controllers provided good performance as shown in Figs. 6b and 12b. One can also notice that the control signal value in the case of the PI regulators is greater than the value obtained in the case of the adaptive nonlinear control when rotor resistance variation occurs at time $t=1\,\mathrm{s}$ and when the wind speed varies from 9 to $6.5~\mathrm{m/s}$ at time $t=3.5\,\mathrm{s}$.

Fig. 10

First set of simulation: Performance when the stator resistance is assumed to be constant under online variation of the rotor resistance (variation starts at time $t=1\,\mathrm{s}$ and reaches $100\%$ at time $t=2\,\mathrm{s}$). Estimate of the electrical angular frequency $\omega _s$ during transient (i, ii and iii) required for the implementation of both nonlinear control and PI regulators in the generator side

In the second set of simulation, the performance of both controllers under $50\%$ variation of the stator resistance (this variation occurs at time $t=2.5\,\mathrm{s}$) has been investigated while the rotor resistance is assumed to be time-varying as in the first set of simulation. In this case, the obtained results are shown in Figs. 11, 12, 13 and 14.

The remarks made for the previous case are also valid for the present case. It can be noticed the robustness of both controllers with respect to stator resistance variation.

The convergence times of the estimation of the rotor current component, the rotor resistance, rotor flux, stator angular position (via the electrical angular frequency $\omega _s$) and the convergence time of the rotor speed and dc-link voltage have been estimated during the start-up period of the control system in the generator side and are given in Table 1 (all these convergence times are taken from the initial start-up time $t_0=0$). From this table, one can notice that the convergence time of the rotor speed ($0.04\,\mathrm{s}$) is less than the convergence time of the rotor resistance ($0.14\,\mathrm{s}$) due to the robustness of the proposed control with respect to parameter uncertainties. The convergence time of the proposed control algorithm is the maximum convergence time of the control outputs (convergence time of the dc-link voltage: $0.11\,\mathrm{s}$).

Finally, the comparative results show globally that the nonlinear control algorithm provided better performance than the P.I regulators in the generator side control strategy while in the load side inverter control strategy, both nonlinear controller and P.I regulators achieved satisfactorily performance.

Fig. 11

Second set of simulation: Comparative performances under online variation of the rotor resistance (variation starts at time $t=1\,\mathrm{s}$ and reaches $100\%$ at time $t=2\,\mathrm{s}$) and $50\%$ stator resistance variation at $t=2.5\,\mathrm{s}$. a DC-bus voltage (i), rotor flux magnitude (ii), and rotor resistance (iii). b Wind speed (i), rotor speed (ii), and power coefficient (iii)

Fig. 12

Second set of simulation: Comparative performances under online variation of the rotor resistance (variation starts at time $t=1\,\mathrm{s}$ and reaches $100\%$ at time $t=2\,\mathrm{s}$) and $50\%$ stator resistance variation at $t=2.5\,\mathrm{s}$. a DC-bus voltage regulation error (i), rotor flux magnitude tracking error (ii) and rotor speed tracking error (iii). b d-axis load voltage component (i), and q-axis load voltage component (ii), load voltage magnitude regulation error (iii)

Fig. 13

Second set of simulation: Comparative performances under online variation of the rotor resistance (variation starts at time $t=1\,\mathrm{s}$ and reaches $100\%$ at time $t=2\,\mathrm{s}$) and $50\%$ stator resistance variation at $t=2.5\,\mathrm{s}$. a Control signal during transient periods in the case of the NC (i, ii and iii); Control signal during transient periods in the case of the PI regulator (i, ii and iii). b SEIG stator current component $i_{sa}$ in the case of the NC (i); SEIG stator current component $i_{sa}$ in the case of the PI regulator (ii)

Fig. 14

Second set of simulation: Comparative performances under online variation of the rotor resistance (variation starts at time $t=1\,\mathrm{s}$ and reaches $100\%$ at time $t=2\,\mathrm{s}$) and $50\%$ stator resistance variation at $t=2.5\,\mathrm{s}$. a Zoom in Fig. 11a, iii for $R_r$, zoom of the rotor current component ${\hat{i}}_{r\alpha }$ and zoom in Fig. 11b, iii for $C_p$ during transient periods. b Zoom in Fig. 6a

6 Conclusion

In this paper, a new control strategy of a stand-alone variable speed based SEIG wind energy conversion has been investigated. Maximum extraction of available energy from the wind turbine and regulation of the rotor flux magnitude and DC-link voltage in the generator side as well as the regulation of the load voltage magnitude in the inverter load side under wind speed, load and rotor/stator resistances variations have been achieved using adaptive nonlinear controller and PI regulators. Comparative results show globally that the nonlinear control algorithm provided better performance than the P.I regulators in the generator side control strategy while both nonlinear controller and P.I regulators achieved satisfactorily performance in the load side inverter control strategy. Finally, the proposed stand-alone variable speed based SEIG wind energy conversion systems can be used in remote and isolated areas where the mean value of the wind speed profile is relatively low.

Table 1 Convergence times for $R_r$, $\Phi _r$, $\omega _s$ and $\omega _m$ during the start-up period of the control system in the generator side

Appendices

Appendix 1: Induction machine parameters [19]

Power: $3.5~\mathrm{kw}$; Rated speed: $1450~\text{ rpm }$; Rated field current: $7.8~\mathrm{A}$; $n_p=2$; $L_r=L_s=191.4~\text{ mH }$; $L_m=180~\text{ mH }$; $R_s=1.66~\Omega$; $R_r=2.75~\Omega$.

Appendix 2: Parameters of the generator side converter

Switching frequency: $6~\text{ kHz }$; DC link capacitor: $2000~\mu \text{ F }$

Appendix 3: Parameters of the load side inverter

Switching frequency: $6~\text{ kHz }$; $R_f=0.1\Omega$, $C_f=10\upmu \text{ F }$ and $L_f=40\text{ mH }$.

Appendix 4: Wind turbine characteristics

Density of air $\rho =1.225$, Area swept by blades, $A=19.635\,\mathrm{m}^2$, Optimum coefficient, $k_{op}=0.0037 \mathrm{Nm/(rad/s)}^{2}$, $C_{pmax}=0.48$, Cut-in wind speed $v_{min}=3.5\,\mathrm{m/s}$, Cut-out wind speed $v_{max}=25\,\mathrm{m/s}$, Gearbox ratio $n_g=\frac{\omega _m}{\omega _{mt}}=6.25$, Turbine total inertia, $J_t=3\,\mathrm{kg}\,\mathrm{m}^2$, Turbine total external damping, $f=0.0027 \,\mathrm{Nm/(rad/s)}$.

Appendix 5: Method for the determination of PI controller parameters

1.1 Design of the rotor flux PI regulators

The open loop transfer function of the subsystem described by (8) is given by:

$$\begin{aligned} \frac{\varphi _r(s)}{i_{sd}(s)}= & {} \frac{\frac{L_mR_r}{L_r}}{s+\frac{R_r}{L_r}}. \end{aligned}$$

(85)

where $s=d/dt$ is the Laplace operator.

Two PI regulators are required to regulate the rotor flux. The first regulator provides the reference stator current component $i_{sd}^*$ while the second one is used for the control of the stator current component $i_{sd}$. Let us denote $C_{\phi _r}(s)$ the transfer function of the first PI regulator. Its expression is:

$$\begin{aligned} C_{\phi _r}(s)= & {} \frac{k_{p\phi _r}\left( \frac{k_{i\phi _r}}{k_{p\phi _r}}+s\right) }{s}. \end{aligned}$$

(86)

where $k_{p\phi _r}$ and $k_{i\phi _r}$ are positive tuning gains. The open loop transfer function $G_{{OC}_{\phi _r}}(s)$ taking into account the PI regulator is:

$$\begin{aligned} G_{{OC}_{\phi _r}}(s)= & {} \frac{k_{p\phi _r}L_mR_r}{L_r}\times \frac{\frac{k_{i\phi _r}}{k_{p\phi _r}}+s}{s(s+\frac{R_r}{L_r})}. \end{aligned}$$

(87)

The compensation of the pole of $G_{{OC}_{\phi _r}}(s)$ by the zero of the PI regulator yields

$$\begin{aligned} \frac{k_{i\phi _r}}{k_{p\phi _r}}= & {} \frac{R_r}{L_r} \end{aligned}$$

(88)

$$\begin{aligned} \text{ and } G_{{OC}_{\phi _r}}(s)= & {} \frac{L_mk_{p\phi _r}R_r}{L_rs}. \end{aligned}$$

(89)

The closed-loop transfer function $F_{{OC}_{\phi _r}}(s)$ can be computed as:

$$\begin{aligned} F_{{OC}_{\phi _r}}(s)= & {} \frac{1}{\frac{L_r}{R_rL_mk_{p\phi _r}}s+1}. \end{aligned}$$

(90)

The above closed-loop transfer function represents a standard first-order system with time-constant $\tau _{\phi _r}=\frac{L_r}{R_rL_mk_{p\phi _r}}$.

It is well known that after three time constants, the first-order unit step response is within 95 percent of its steady state value. Thus the settling time $t_{S(5\%)}$ typically defined to be the time at which the response enters and remains within a $\pm 5$ percent band about the steady-state value can be approximated in the case of first-order system by

$$\begin{aligned} t_{S_{\phi _r}(5\%)}= & {} 3\tau _{\phi _r}. \end{aligned}$$

(91)

Consequently, given a desired settling time $t_{S_{\phi _r}(5\%)}$, from (88) and (91), we can deduce the expressions for $k_{p\phi _r}$ and $k_{i\phi _r}$ as:

$$\begin{aligned} k_{p\phi _r}= & {} \frac{3L_r}{R_rL_mt_{S_{\phi _r}(5\%)}} \end{aligned}$$

(92)

$$\begin{aligned} k_{i\phi _r}= & {} \frac{3}{L_mt_{S_{\phi _r}(5\%)}}. \end{aligned}$$

(93)

The same procedure can be applied to design the second PI regulator for the rotor flux control loop and others PI regulators used in this work.

Appendix 6: Relation between the nominal value $v_{{dc}_n}$ and the nominal line-to-line RMS supply voltage $v_{n_{sac}}$

This relation is given by [35]:

$$\begin{aligned} v_{{dc}_n}= & {} \frac{2\sqrt{2}}{\sqrt{3}} v_{n_{sac}}. \end{aligned}$$

The application of this relation to the control system used in this work yields:

$$\begin{aligned} v_{{dc}_n}= & {} 677{,}69~\mathrm{V}. \end{aligned}$$

The reference value of the $v_{dc}$ verifies the following inequality.

$$\begin{aligned} v_{dc}^*< & {} v_{{dc}_n}. \end{aligned}$$

In this work, the reference value of $600\,\mathrm{V}$ has been used.

Appendix 7: System nomenclature

$\phi _r=\phi _{rd}$ :

Rotor flux magnitude (Wb)

$i_{sd}$,$i_{sq}$ :

Stator currents components in in (d, q) coordinate frame (A)

$v_{sd}$, $v_{sq}$ :

Stator voltages in (d, q) coordinate frame (V)

$n_p$ :

Number of pole pairs

$\omega$ :

Rotor electrical angular frequency (rad/s)

$\omega _m=\omega /n_p$ :

Mechanical rotor speed (rad/s)

$\omega _s$ :

Electrical angular frequency of the voltages and currents of stator windings (rad/s)

$\omega _r$ :

Electrical angular frequency of the currents of rotor windings (rad/s)

$\theta _s$ :

Stator electrical angular position (rad)

$R_r,R_s$ :

Rotor and stator resistances ($\Omega$)

$L_r,L_s$ :

Rotor and stator inductances (H)

$L_m$ :

Mutual inductance (H)

$R_L$ :

Dump load resistance ($\Omega$)

C :

DC-link capacitor (F)

$i_i$ :

Current at the input of the inverter (A)

$v_{dc}$ :

DC-link voltage (V)

$T_e$ :

Electromagnetic torque (Nm)

$i_{s\alpha }$, $i_{s\beta }$ :

Stator currents components in $(\alpha ,\beta )$ coordinate frame (A)

$i_{r\alpha }$, $i_{r\beta }$ :

Rotor currents components in $(\alpha ,\beta )$ coordinate frame (A)

$v_{s\alpha }$, $v_{s\beta }$ :

Stator voltages components in $(\alpha ,\beta )$ coordinate frame (V)

S :

Switching functions of PWM technique of Electronic Load Control (ELC)

$S_a$, $S_b$ and $S_c$ :

Switching functions of PWM technique

$S_d$, $S_q$ :

Switching functions of PWM technique in (d, q) coordinate frame

$\omega _e$ :

Pulsating frequency of the AC load (rad/s)

$v_{id}$, $v_{iq}$ :

Inverter output voltages components in (d, q) coordinate frame (V)

$v_{d}$, $v_{q}$ :

AC load voltages components in (d, q) coordinate frame (V)

$i_{id}$, $i_{iq}$ :

Inverter output currents components in (d, q) coordinate frame (A)

$i_{Ld}$, $i_{Lq}$ :

Load currents components in (d, q) coordinate frame (A)

$R_f$ :

LC-filter resistor in Inverter side ($\Omega$)

$L_f$ :

LC-filter inductor in Inverter side (H)

$C_f$ :

LC-filter capacitor in Inverter side (F)

$x^*$ :

Reference signals for x.

Appendix 8

(a, b, c) coordinate frame $\rightarrow$ $(\alpha ,\beta )$ coordinate frame equations [36].

$$\begin{aligned} \left[ \begin{array}{c}x_\alpha \\ x_\beta \end{array}\right]= & {} \sqrt{\frac{2}{3}}\left[ \begin{array}{ccc}1&{}-\frac{1}{2}&{}-\frac{1}{2}\\ 0&{}\frac{\sqrt{3}}{2}&{}-\frac{\sqrt{3}}{2}\end{array}\right] \quad \left[ \begin{array}{c}x_a\\ x_b\\ x_c\end{array}\right] \end{aligned}$$

$(\alpha ,\beta )$ coordinate frame $\rightarrow$ (d, q) coordinate frame equations.

$$\begin{aligned} \left[ \begin{array}{c}x_d\\ x_q\end{array}\right]= & {} \left[ \begin{array}{cc}\cos \theta _s &{}\sin \theta _s\\ -\sin \theta _s&{}\cos \theta _s\end{array}\right] \left[ \begin{array}{c}x_\alpha \\ x_\beta \end{array}\right] \end{aligned}$$

(d, q) coordinate frame $\rightarrow$ $(\alpha ,\beta )$ coordinate frame equations.

$$\begin{aligned} \left[ \begin{array}{c}x_\alpha \\ x_\beta \end{array}\right]= & {} \left[ \begin{array}{cc}\cos \theta _s &{}-\sin \theta _s\\ \sin \theta _s&{}\cos \theta _s\end{array}\right] \left[ \begin{array}{c}x_d\\ x_q\end{array}\right] \end{aligned}$$

$(\alpha ,\beta )$ coordinate frame $\rightarrow$ (a, b, c) coordinate frame equations.

$$\begin{aligned} \left[ \begin{array}{c}x_a\\ x_b\\ x_c\end{array}\right]= & {} \sqrt{\frac{2}{3}}\left[ \begin{array}{ccc}1&{}0&{}\\ -\frac{1}{2}&{}\frac{\sqrt{3}}{2}&{}\\ -\frac{1}{2}&{}-\frac{\sqrt{3}}{2}\end{array}\right] \left[ \begin{array}{c}x_\alpha \\ x_\beta \end{array}\right] \end{aligned}$$

Appendix 9

Design methodology for LC filter.

The transfer function of the second order low pass LC filter is

$$\begin{aligned} T(s)= & {} \frac{1}{1+R_fC_fs+L_fC_fs^2}. \end{aligned}$$

The cut-off angular frequency of this filter is:

$$\begin{aligned} \omega _0= & {} \frac{1}{\sqrt{L_fC_f}} \end{aligned}$$

The cut-off frequency is then equal to:

$$\begin{aligned} f_0= & {} \frac{1}{2\pi \sqrt{L_fC_f}} \end{aligned}$$

The values of the LC filter can be chosen such that the central frequency of the first harmonic packet to be eliminated is equal to $5f_0$.