1 Introduction

Chaos is an interesting phenomenon that has gained wide attention in many areas of engineering. The fundamental characteristic of a chaotic system is its sensitive dependence on initial conditions; which means, a small shift in the initial states can lead to extraordinary perturbation in the system states [1]. Discovery of chaos goes back to times when Lorenz was simulating the weather models [2]. Lorenz found a 3-dimensional autonomous system, which could exhibit two-scroll chaos attractor. Now, there are many systems reported in the literature related to chaotic behavior and chaos synchronization [3–15].

Since the concept of master-slave synchronization for coupled chaotic systems was proposed in [16], much attention has been paid on control and synchronization of chaotic systems due to its potential applications in secure communication, biological systems, information science, etc., [17–27]. Many approaches are proposed to deal with this problem such as adaptive control [28–30], sliding mode control [31–33], active control [34–37], optimal control [38] and backstepping design [39, 40]. Notice that in practice there are always some unknown factors, which affect the chaotic systems and deteriorate the performance of synchronization schemes. Thus, it is better to implement robust controllers to realize synchronization.

Fractional calculus is a 300-years-old topic. However, applying fractional-order calculus to dynamic systems control is just a recent focus of interest. In fact, during the last years, fractional calculus has been used increasingly for control systems; its ability has been recognized in improving the performance of controllers especially in the area of robust control.

Most of the above-mentioned strategies guarantee the asymptotic stability of the resulted synchronization error dynamic. It means that, the state trajectories of the slave system can reach to the state trajectories of the master system within an infinite settling time. However, in practical application it is more valuable to synchronize master–slave chaotic systems in a given finite time.

With the above motivations, in this paper we investigate application of fractional-order sliding mode control for robust synchronization of chaotic systems. Sliding mode control is a control method for robustly control of uncertain systems [41]. It provides both advantages of sliding mode and fractional-order controllers simultaneously. The idea behind this control strategy is utilizing fractional-order sliding surfaces instead of traditional ones. Several comparative studies are reported in the recent literature, which have stated that fractional-order sliding mode outperforms conventional sliding mode controllers [42–46]. The proposed fractional adaptive sliding mode controller has the advantage of combining the tracking facilities of the adaptive control with the robustness of the sliding mode control.

However, most of the above-mentioned researches on chaos synchronization have focused on fractional-order or integer-order chaotic systems. To the best of our knowledge, there has been very little information about the control methods which can be used for both fractional-order and integer-order chaotic systems.

There are some advantages, which make our proposed method attractive. First, a novel fractional active sliding surface is presented in this paper. Fractional order derivative makes the more degree of freedom in sliding surface. Second, our proposed method can be used for both fractional-order and integer-order chaotic systems. It can also be used for both identical and non-identical chaotic systems. Third, the method is designed for a wide class of chaotic systems, which means its universal applicability. Fourth, the proposed method synchronizes master–slave chaotic systems in a given finite time.

In spite of intensive researches, the stability of fractional-order systems remains an open problem. Stability of fractional order nonlinear dynamic systems are studied in [47, 48]. LMI stability conditions for fractional order systems are investigated in [49]. In [50] an extension of Lyapunov–Krasovskii theorem for the fractional nonlinear systems is proposed. An extension of Lyapunov direct method for fractional-order systems using Bihari’s and Bellman–Gronwall’s inequality and a proof of comparison theorem for fractional-order systems are proposed in [51].

We develop our controller design in such a way that stability of the closed-loop system can be studied easily. We show that our proposed method can guarantee the system asymptotic stability for both integer-order and fractional-order chaotic systems in the presence of system uncertainties and external disturbances. Numerical simulations are verifying our theoretical results.

This paper is organized as follows: in Sect. 2 basic definitions of fractional calculus are included. Section 3 deals with controller design for synchronization of integer-order chaotic systems. Synchronization of fractional-order systems is presented in Sect. 4 and finally, the concluding remarks are given in Sect. 4.3.

2 Fractional calculus

Let us first introduce definitions and results needed here with respect to fractional calculus which will be used later.

Definition 1

The fractional integral \(\mathbf{I}_{0,\mathrm{t}}^\mathrm{q}\) with fractional order \(q\in R^{+}\) of function \(f(t)\) is defined as

$$\begin{aligned} \mathbf{I}_{0,\mathrm{t}}^{\mathrm{q}} \;f(t)=\frac{1}{\Gamma (q)}\int _0^{t} {(t-\tau )^{q-1}f(\tau )d\tau } \end{aligned}$$
(1)

In this definition, the initial time is set to zero.

Definition 2

The Riemann–Liouville derivative of fractional order \(q\in R^{+}\) with function \(f(t)\) is defined as

$$\begin{aligned} _{{\mathsf {RL}}} \mathbf{D}_{0,\mathrm{t}}^{\mathrm{q}}\, f(t)= & {} \frac{d^{m}}{dt^{m}}\mathbf{I}_{0,\mathrm{t}}^{\mathrm{m-q}}f(t) \nonumber \\= & {} \frac{1}{\Gamma (m-q)}\frac{d^{m}}{dt^{m}}\int _0^t {(t-\tau )^{m-q-1}f(\tau )d\tau }\qquad \end{aligned}$$
(2)

where \(m-1<q<m\in R^{+}\).

Definition 3

The Caputo derivative of fractional order \(q\in R^{+}\) with function \(f(t)\) is defined as

$$\begin{aligned} _{{\mathsf {C}}} \mathbf{D}_{0,\mathrm{t}}^\mathrm{q} \;\;f(t)= & {} \mathbf{I}_{0,\mathrm{t}}^{\mathrm{m-q}} \frac{d^{m}}{dt^{m}} f(t)\nonumber \\= & {} \frac{1}{\Gamma (m-q)}\int _0^t {(t-\tau )^{m-q-1}f^{(m)}(\tau )d\tau } \end{aligned}$$
(3)

where \(m-1<q<m\in R^{+}\) [52].

Theorem 1

[47, 48] Let \(x = 0\) be an equilibrium point for either Caputo or Riemann–Liouville fractional non-autonomous system

$$\begin{aligned} \mathbf{D}^{\alpha }x=f\left( {x,t} \right) \end{aligned}$$
(4)

where \(f(x,t)\) satisfies the Lipschitz condition with Lipschitz constant \(l> 0\) and \(\alpha \in (0,1)\). Assume that there exists a Lyapunov function \(V(t,x(t))\) satisfying

$$\begin{aligned} \alpha _{1} \Vert x\Vert ^{a}\le & {} V (t,x) \le \alpha _{2}\Vert x\Vert \\ \dot{V}(t,x)\le & {} -\alpha _{3}\Vert x\Vert \end{aligned}$$

where \(\alpha _1, \alpha _2,\alpha _3\) and \(a\) are positive constants and \(\Vert .\Vert \) denotes an arbitrary norm. Then the equilibrium point of the system (4) is Mittag–Leffler (asymptotic) stable.

Remark 1

In the rest of this paper, we use the Caputo’s definition of fractional derivative. For the sake of simplicity the notations \(\mathbf{I}^{\mathrm{q}}\) and \(\mathbf{D}^{\mathrm{q}}\) denote fractional integral and derivative respectively.

3 Synchronization of integer-order chaotic systems

3.1 Problem statement

Dynamics of many problems of practical interest could be represented by practical form (5), such as: the motion of a non-autonomous symmetric gyroscope [9], the horizontal platform system [14], the Vander pol chaotic system [41], Inverted pendulum [41] and so on.

Consider an integer-order chaotic system described by the following second-order nonlinear differential equations

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{y}_1 =y_2 \\ \dot{y}_2 =f(\mathbf{y},t)+\Delta f(\mathbf{y},t)+d_y (t)+u(t) \\ \end{array}} \right. \end{aligned}$$
(5)

where \(\mathbf{y}(t)=\left[ {y_1 (t),y_2 (t)} \right] ^{T}\) denotes state vector, \(f(\mathbf{y},t)\) is a nonlinear function of \(\mathbf{y}\) and \( {\textit{t}}, \Delta f(\mathbf{y},t)\) represents additive uncertain term of the chaotic system, \(d_y (t)\) models external disturbances and \(u(t)\) specifies the control input. Without loss of generality, we can assume that \(\Delta f(\mathbf{y},t)\) and \(d_y (t)\) are bounded by some positive constants i.e. \(\left| {\Delta f(\mathbf{y},t)} \right| \le \Delta _f\) and \(\left| {d_y (t)} \right| \le D_y \). In addition, it is assumed that \(\Delta f(\mathbf{y},t)\) satisfies the conditions required to ensure that the system defined in (5) has a unique solution in the time interval \(\left[ {t_0, +\infty } \right) ,\;t_0 >0\) for any given initial condition. In order to realize a synchronization state between two chaotic systems, the control problem is deriving an appropriate control law in such a way that the states of chaotic system (5) track the states of another chaotic system, which is described as follows

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{x}_1 =x_2 \\ \dot{x}_2 =g(\mathbf{x},t)+\Delta g(\mathbf{x},t)+d_x (t) \\ \end{array}} \right. \end{aligned}$$
(6)

where \(\mathbf{x}(t)=\left[ {x_1 (t),x_2 (t)} \right] ^{T}\) denotes state vector and \(g(\mathbf{x},t)\) is a nonlinear function of \(\mathbf{x}\) and \(t\), we can also assume that \(\Delta g(\mathbf{x},t)\) and \(d_x (t)\) are bounded by some positive constants i.e. \(\left| {\Delta g(\mathbf{x},t)} \right| \le \Delta _g, \left| {d_x (t)} \right| \le D_x \).

Assumption 1

With the above discussion, one can obtain that:

$$\begin{aligned} \left| {d_y (t)-d_x (t)} \right| \le \mu \quad \hbox {and}\quad \left| {\Delta f(\mathbf{y},t)-\Delta g(\mathbf{x},t)} \right| \le \sigma \end{aligned}$$

where \(\mu \) and \(\sigma \) are positive constants.

Definition 4

For the master system (6) and the slave system (5) it is said that synchronization state is realized, if there exists a control input \(u(t)\) such that

$$\begin{aligned} \mathop {\lim }\limits _{\mathrm{t}\rightarrow \infty } \left\| {\mathbf{e}(t)} \right\| =\mathop {\lim }\limits _{\mathrm{t}\rightarrow \infty } \left\| {\mathbf{y}(t)-\mathbf{x}(t)} \right\| =0 \end{aligned}$$
(7)

where \(\left\| .\right\| \) is the Euclidean norm and \(\mathbf{e}(t)=\left[ {e_1 (t),e_2 (t)} \right] ^{T}\)is called the state error. Then the problem of chaos synchronization reduces to a stabilization problem. The controller has the duty to keep \(\left\| {\mathbf{e}(t)} \right\| \) to zero. From (5) and (6), one can obtain the error dynamics as follows

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{e}_1 =e_2 \\ \dot{e}_2 =f(\mathbf{y},t)-g(\mathbf{x},t)+\Delta f(\mathbf{y},t)-\Delta g(\mathbf{x},t)+d_y (t)\\ \qquad \quad -\,d_x (t)+u(t) \\ \end{array}} \right. \end{aligned}$$
(8)

A control strategy will be proposed in the next section to deal with this problem.

3.2 Controller design

In order to design a fractional-order sliding mode controller the first and most critical step is constructing an appropriate sliding surface, hence the following fractional sliding surface is proposed

$$\begin{aligned} S\left( t \right) =k_1 e_1 \left( t \right) +k_2 \mathbf{D}^{\alpha }e_1 \left( t \right) +k_3 \dot{e}_1 \left( t \right) \end{aligned}$$
(9)

where \(\alpha \in \left( {0,1} \right) \) and \(k_i, i=1,2,3\) are design parameters which should be chosen such that (9) be Hurwitz. As it is well-known in sliding mode control theory, we use \(\dot{S}=0\) to obtain the equivalent control law.

$$\begin{aligned} \dot{S}\left( t \right) =k_1 \dot{e}_1 \left( t \right) +k_2 \frac{d}{dt}\left( {\mathbf{D}^{\alpha }e_1 \left( t \right) } \right) +k_3 \ddot{e}_1 \left( t \right) \end{aligned}$$
(10)

by substituting the error dynamics (8) into (10), one has

$$\begin{aligned} \dot{S}\left( t \right)= & {} k_1 e_2 +k_2 \frac{d}{dt}\mathbf{D}^{\alpha }e_1 +k_3 \left[ f(\mathbf{y},t)-g(\mathbf{x},t)\right. \nonumber \\&\left. +\Delta f(\mathbf{y},t)-\,\Delta g(\mathbf{x},t)+d_y (t)-d_x (t)+u(t) \right] \nonumber \\ \end{aligned}$$
(11)

We assume the following equivalent control law

$$\begin{aligned} u_{eq} (t)= & {} -\left( {f(Y,t)-g(X,t)} \right) \nonumber \\&-\,k_3^{-1} \left( {k_1 \dot{e}_1 \left( t \right) +k_2 \frac{d}{dt}\left( {\mathbf{D}^{\alpha }e_1 \left( t \right) } \right) } \right) \end{aligned}$$
(12)

The fractional order term in control signal i.e. \(\mathbf{D}^{\alpha }e_1 \left( t \right) \), enhanced the controller robustness. Due to adding the extra degree of freedom, fractional order sliding mode controller can achieve better control performance than integer order sliding mode controller. Since in practical applications, the system uncertainty terms \(\Delta f(\mathbf{y},t)\) and \(\Delta g(\mathbf{x},t)\) and external disturbances \(d_{x}(t)\) and \(d_{y}(t)\) are unknown, and according to Assumption 1, in order to improve the robustness against uncertainties, we employ the following discontinuous reaching law

$$\begin{aligned} u_{sw} (t)=-\lambda _{s}S(t)-\left( {k_s +\sigma +\mu } \right) \hbox {sgn}(S(t)) \end{aligned}$$
(13)

where \(\lambda _s\) and \(k_s\) are positive constants and will be determined later. Hence, the overall control law becomes

$$\begin{aligned} u(t)= & {} -\left( {f(Y,t)-g(X,t)} \right) \nonumber \\&-\,k_3^{-1} \left( {k_1 \dot{e}_1 \left( t \right) +k_2 \frac{d}{dt}\left( {\mathbf{D}^{\alpha }e_1 \left( t \right) } \right) } \right) \nonumber \\&-\,\left[ {\lambda _{s} S(t)+\left( {k_{s} +\sigma +\mu } \right) \hbox {sgn}(S(t))} \right] \end{aligned}$$
(14)

Theorem 2

Consider the synchronization error system (8). If, this system is controlled by the control law \(u(t)\) in (14), then the system trajectories will converge to the sliding surface \(S(t) = 0\).

Proof

Consider a positive definite Lyapunov function candidate in the following form:

$$\begin{aligned} V\left( t \right) =\left| {S\left( t \right) } \right| \end{aligned}$$
(15)

Taking derivative of both sides of (15) with respect to time, one has

$$\begin{aligned} \dot{V}\left( t \right)= & {} \dot{S}\left( t \right) \times \hbox {sgn}\left( {S\left( t \right) } \right) \nonumber \\= & {} \left( {k_1 \dot{e}_1 \left( t \right) +k_2 \frac{d}{dt}\left( {\mathbf{D}^{\alpha }e_1 \left( t \right) } \right) +k_3 \ddot{e}_1 \left( t \right) } \right) \nonumber \\&\times \, \hbox {sgn}\left( {S\left( t \right) } \right) \nonumber \\= & {} \left( k_1 \dot{e}_1 \left( t \right) +k_2 \frac{d}{dt}\left( {\mathbf{D}^{\alpha }e_1 \left( t \right) } \right) \right. \nonumber \\&\left. +\,k_3 \left( {\begin{array}{l} f(Y,t)-g(X,t)+ \\ \Delta f(Y,t)-\Delta g(X,t)+d_y (t)\\ \quad -d_x (t)+u(t) \\ \end{array}} \right) \right) \nonumber \\&\times \, \hbox {sgn}\left( {S\left( t \right) } \right) \end{aligned}$$
(16)

Substituting (14) into (16) yields

$$\begin{aligned} \dot{V}\left( t \right)= & {} k_3 \left( { \begin{array}{l} \Delta f(Y,t)-\Delta g(X,t)+d_y (t)-d_x (t) \\ -\left[ {\lambda _s S(t)+\left( {k_s +\sigma +\mu } \right) \hbox {sgn}(S(t))} \right] \\ \end{array}} \right) \nonumber \\&\times \, \hbox {sgn}\left( {S\left( t \right) } \right) \nonumber \\ \dot{V}\left( t \right)\le & {} k_3 \left( {\left| {\Delta f(Y,t)-\Delta g(X,t)} \right| +\left| {d_y (t)-d_x (t)} \right| } \right) \nonumber \\&-\,k_3 \left( {\lambda _s \left| {S(t)} \right| +\left( {k_s +\sigma +\mu } \right) } \right) \nonumber \\ \dot{V}\left( t \right)\le & {} -k_3 \left( {\lambda _s \left| {S(t)} \right| +k_s } \right) \le -\eta \left| {S(t)} \right| \end{aligned}$$
(17)

where \(\eta =\min \left\{ {k_3 \lambda _s,k_3 k_s} \right\} \)

It implies that the asymptotic stability of the system is guaranteed. Therefore, the fractional-order sliding mode control law (14) is verified. Hence, according to Theorem 2, the state trajectories of the error system (8) will converge to \(S(t) = 0\) asymptotically. \(\square \)

Theorem 3

Consider the nonlinear tracking error system (8). If this system is controlled by the fractional sliding surface (9), then its state trajectories will converge to the proposed fractional sliding surface in finite time.

Proof

We can obtain the reaching time as follows:

From inequality (17), we have

$$\begin{aligned} \dot{V}\left( t \right)\le & {} -k_3 \left( {\lambda _s \left| {S(t)} \right| +k_s } \right) \nonumber \\ \dot{V}\left( t \right)= & {} \frac{d\left| {S\left( t \right) } \right| }{dt}\le -\left( {k_3 \lambda _s \left| {S(t)} \right| +k_3 k_s } \right) \end{aligned}$$
(18)

It is clear that

$$\begin{aligned} dt\le -\frac{1}{k_3 k_s }\frac{d\left| {S\left( t \right) } \right| }{\left( {{\lambda _s }\Big /{k_s }} \right) \left| {S(t)} \right| +1} \end{aligned}$$
(19)

Taking integral of both sides of (19) from 0 to \(t_{r}\) and letting \(S(t_{r}) = 0\), we have

$$\begin{aligned} t_r\le & {} -\frac{1}{k_3 k_s }\int _{S\left( 0 \right) }^{S\left( {t_r } \right) } {\frac{d\left| {S\left( t \right) } \right| }{\left( {{\lambda _s }\Big /{k_s }} \right) \left| {S(t)} \right| +1}} \nonumber \\= & {} \frac{1}{k_3 \lambda _s }\ln \left( {\left( {{\lambda _s }\Big /{k_s }} \right) \left| {S(0)} \right| +1} \right) \end{aligned}$$
(20)

Therefore, the state trajectories of the error system (8) will converge to \(S(t) = 0\) in the finite time \(t_{r}\). This completes the proof. \(\square \)

Theorem 4

Consider the sliding mode dynamics (9), If Laplace transform of the error, \(E(s) = L\{ e(t)\}\) is bounded, then the state trajectories of the system (8) will converge to zero as \(t \rightarrow \infty \).

Proof

Using the Laplace transform of the Caputo derivative for (9), and assuming \(E(s) = L\{ e(t)\}\) one has

$$\begin{aligned} k_1 E\left( s \right) +k_2 s^{\alpha }E\left( s \right) -k_2 s^{\alpha -1}e\left( 0 \right) +k_3 sE\left( s \right) -k_3 e\left( 0 \right) =0 \end{aligned}$$
(21)

Using the final-value theorem of the Laplace transformation one can obtain:

$$\begin{aligned} e\left( \infty \right)= & {} \mathop {\lim }\limits _{t\rightarrow \infty } e\left( t \right) =\mathop {\lim }\limits _{s\rightarrow 0} sE\left( s \right) \nonumber \\= & {} \mathop {\lim }\limits _{s\rightarrow 0} s\times \frac{k_2 s^{\alpha -1}e\left( 0 \right) +k_3 e\left( 0 \right) }{k_1 +k_2 s^{\alpha }+k_3 s}=0 \end{aligned}$$
(22)

Assuming \(|e(t)| < \beta <\infty \) it can be concluded that \(\mathop {\lim }\limits _{t\rightarrow \infty }e(t)=0\). This shows the convergence of the error system trajectories to the fractional sliding surface (9).

In the next section, we derive the adaption law for the proposed controller. \(\square \)

3.3 Adaptation law synthesis

We have designed an active sliding mode controller for synchronization of non-identical chaotic systems with uncertainty and disturbance. In the previous sections, it has been shown knowing the bounds of disturbances is vital to guarantee the system stability. However, in practice it is not simple to determine these bounds precisely. In what follows, we develop an adaptation law to overcome this problem.

Lemma 1

to tackle the unknown parameters, the following adaptation laws are proposed.

$$\begin{aligned}&\begin{array}{l} \dot{\hat{{\sigma }}}=k_3 \xi _1 \left| {S\left( t \right) } \right| \\ \dot{\hat{{\mu }}}=k_3 \xi _2 \left| {S\left( t \right) } \right| \\ \end{array}\end{aligned}$$
(23)
$$\begin{aligned}&\begin{array}{l} \dot{\hat{{\lambda }}}_s =k_3 \xi _3 S^{2}(t) \\ \dot{\hat{{k}}}_s =k_3 \xi _4 \left| {S\left( t \right) } \right| \\ \end{array} \end{aligned}$$
(24)

where \(\hat{{\sigma }}, \hat{{\mu }},\hat{{\lambda }}_s\) and \(\hat{{k}}_s\) are estimations for \(\sigma ,\mu ,\lambda _s\) and \(k_s\) respectively; and \(\xi _1,\xi _2,\xi _3\) and \(\xi _4\) are positive constants.

Proof

choose a Lyapunov function as follows

$$\begin{aligned} V\left( t \right) =\frac{1}{2}S^{2}\left( t \right) +\xi _1^{-1} (\tilde{\sigma })^{2}+\xi _2^{-1} (\tilde{\mu })^{2}+\xi _3^{-1} (\tilde{\lambda }_s )^{2}+\xi _4^{-1} (\tilde{k}_s )^{2} \end{aligned}$$
(25)

where \(\tilde{k}_{s}=\hat{k}_{s}-k_{s}\), \(\tilde{\mu }=\hat{{\mu }}-\mu , \tilde{\sigma }=\hat{{\sigma }}-\sigma \) and \(\tilde{\lambda }_{s}=\hat{\lambda }_{s}-\lambda _{s}\) taking derivative of both sides of (25) with respect to time yields:

$$\begin{aligned} V\left( t \right)= & {} S\left( t \right) \dot{S}\left( t \right) +\xi _1^{-1} \tilde{\sigma }(\dot{\hat{{\sigma }}})+\xi _2^{-1} (\tilde{\mu })\dot{\hat{{\mu }}}+\xi _3^{-1} \tilde{\lambda }_s (\dot{\hat{{\lambda }}}_s )\nonumber \\&+\,\xi _4^{-1} \tilde{k}_s (\dot{\hat{{k}}}_s ) \end{aligned}$$
(26)

Using the control input (14)

$$\begin{aligned} \dot{V}\left( t \right)= & {} S( t )\!\left( \! {k_3 \!\left( \! {\begin{array}{l} \Delta f(Y,t)-\Delta g(X,t) \\ +d_y (t)-d_x (t) \\ -\left[ {\hat{{\lambda }}_s S(t)\!+\!\left( {\hat{{k}}_s \!+\!\hat{{\sigma }}\!+\!\hat{{\mu }}} \right) \hbox {sgn}\left( {S(t)} \right) } \right] \\ \end{array}} \right) }\! \right) \nonumber \\&+\,\left( {\begin{array}{l} \xi _1^{-1} \tilde{\sigma }(\dot{\hat{{\sigma }}})+\xi _2^{-1} (\tilde{\mu })\dot{\hat{{\mu }}} \\ +\xi _3^{-1} \tilde{\lambda }_s (\dot{\hat{{\lambda }}}_s )+\xi _4^{-1} \tilde{k}_s (\dot{\hat{{k}}}_s ) \\ \end{array}} \right) \nonumber \\ \dot{V}\left( t \right)\le & {} k_3 \left( {\begin{array}{l} \left( {\begin{array}{l} \left| {\Delta f(Y,t)-\Delta g(X,t)} \right| \\ +\left| {d_y (t)-d_x (t)} \right| \\ \end{array}} \right) \left| {S\left( t \right) } \right| \\ -\hat{{\lambda }}_s S^{2}(t)-S\left( t \right) \left( {\hat{{k}}_s +\hat{{\sigma }}+\hat{{\mu }}} \right) \hbox {sgn}\left( {S(t)} \right) ) \\ \end{array}} \right) \nonumber \\&+\,\left( {\begin{array}{l} \xi _1^{-1} \tilde{\sigma }(\dot{\hat{{\sigma }}})+\xi _2^{-1} (\tilde{\mu })\dot{\hat{{\mu }}} \\ +\xi _3^{-1} \tilde{\lambda }_s (\dot{\hat{{\lambda }}}_s )+\xi _4^{-1} \tilde{k}_s (\dot{\hat{{k}}}_s ) \\ \end{array}} \right) \nonumber \\ \dot{V}\left( t \right)\le & {} k_3 \left( {\begin{array}{l} \sigma \left| {S\left( t \right) } \right| +\mu \left| {S\left( t \right) } \right| -\hat{{\lambda }}_s S^{2}(t) \\ -S\left( t \right) \left( {\hat{{k}}_s +\hat{{\sigma }}+\hat{{\mu }}} \right) \hbox {sgn}\left( {S(t)} \right) \\ \end{array}} \right) \nonumber \\&+\,\left( {\begin{array}{l} \xi _1^{-1} \tilde{\sigma }(\dot{\hat{{\sigma }}})+\xi _2^{-1} (\tilde{\mu })\dot{\hat{{\mu }}} \\ +\xi _3^{-1} \tilde{\lambda }_s (\dot{\hat{{\lambda }}}_s )+\xi _4^{-1} \tilde{k}_s (\dot{\hat{{k}}}_s ) \\ \end{array}} \right) \nonumber \\ \dot{V}\left( t \right)\le & {} k_3 \left( {\begin{array}{l} \left( {\sigma +\mu } \right) \left| {S\left( t \right) } \right| -\hat{{\lambda }}_s S^{2}(t) \\ -S\left( t \right) \left( {\hat{{k}}_s +\hat{{\sigma }}+\hat{{\mu }}} \right) \hbox {sgn}\left( {S(t)} \right) \\ \end{array}} \right) \nonumber \\&+\,\left( {\begin{array}{l} \xi _1^{-1} \tilde{\sigma }(\dot{\hat{{\sigma }}})+\xi _2^{-1} (\tilde{\mu })\dot{\hat{{\mu }}} \\ +\xi _3^{-1} \tilde{\lambda }_s (\dot{\hat{{\lambda }}}_s )+\xi _4^{-1} \tilde{k}_s (\dot{\hat{{k}}}_s ) \\ \end{array}} \right) \end{aligned}$$
(27)

Introducing the adaptation laws (23) into the right hand of (27), one obtains

$$\begin{aligned} \dot{V}\left( t \right)\le & {} k_3 \left( \left( {\hat{{\sigma }}+\hat{{\mu }}} \right) \left| {S\left( t \right) } \right| -\hat{{\lambda }}_s S^{2}(t)-\left| {S\left( t \right) } \right| \left( {\hat{{\sigma }}+\hat{{\mu }}} \right) \right. \nonumber \\&\left. -\,\hat{{k}}_s \left| {S\left( t \right) } \right| \right) +\xi _3^{-1} \tilde{\lambda }_s (\dot{\hat{{\lambda }}}_s )+\xi _4^{-1} \tilde{k}_s (\dot{\hat{{k}}}_s ) \end{aligned}$$
(28)

Using the adaptation laws (24) into the right hand of (28), one obtains

$$\begin{aligned} \dot{V}\left( t \right) \le -k_3 \left( {k_s \left| {S\left( t \right) } \right| +\lambda _s S^{2}(t)} \right) \end{aligned}$$

This implies that stability of the system is guaranteed.

One of the major contributions of the proposed controller is as follows:

Utilizing these adaptation laws allows us to gain a high-performance synchronization of non-identical chaotic systems with uncertainty and disturbance. The proposed method does not need the knowledge of disturbance bounds. Switching gains have a capability to adapt themselves automatically to stabilize the system perturbed by any unknown disturbances and uncertainty. \(\square \)

3.4 Example 1: synchronization of \(\Phi ^{6}\)-Van der Pol and Duffing–Holmes systems

In this section, an illustrative example has been presented to verify the effectiveness of the proposed controller.

The \(\Phi ^{6}\)-Van der Pol system is described as a master system by the following equations

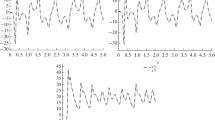
$$\begin{aligned} \dot{x}_1= & {} x_2 \nonumber \\ \dot{x}_2= & {} \mu (1-x_1^2 )x_2 +\zeta x_1 +\delta x_1^3 +\rho x_1^5 +f_0 \cos \left( {\omega \;t} \right) \nonumber \\&+\,\Delta g\left( {x_1,x_2 } \right) +d_x \left( t \right) \end{aligned}$$
(29)

where \(\mu =0.4,\zeta =-0.26,\delta =-1,\rho =-0.1,\omega =0.86\) and \(f_o =4.5\) yield chaotic trajectory. The chaotic behavior of this system has been depicted in Fig. 1.

Fig. 1
figure 1

Chaotic attractor of \(\Phi ^{6}\)-Van der Pol system

Full size image

For the \(\Phi ^{6}\)-Van der Pol system the initial conditions are set as \(x_1 (0)=0.2\), \(x_2 (0)=0.5\). It is assumed that this system is perturbed by \(\Delta g\left( {x_1,x_2 } \right) =0.2\sin (x_1)\cos (x_2 )\) and \(d_x \left( t \right) =0.12\cos (3t)\).

The Duffing–Homes system is described as a slave system as follows:

$$\begin{aligned} \dot{y}_1= & {} y_2 \nonumber \\ \dot{y}_2= & {} y_1 -ay_2 -y_1^3 +b\cos t+\Delta f(y_1,y_2 )+d_y \left( t \right) +u\left( t \right) \nonumber \\ \end{aligned}$$
(30)

where \(a=0.25\) and \(b=0.3\) yield chaotic motion. For the purpose of numerical simulations we set the initial conditions as \(y_1 (0)=-0.1, y_2 (0)=-0.3\). It is also assumed that the slave is perturbed by \(d_y \left( t \right) =0.1\cos (2t)\) and \(\Delta f(y_1 ,y_2 )=0.3\sin (y_1 )\sin (y_2)\).

The controller parameters are assumed as \(\hat{{\mu }}\left( 0 \right) =0.5,\hat{{\delta }}\left( 0 \right) =0.5\), \(\hat{{k}}_s \left( 0 \right) =0.5, \hat{{\lambda }}_s \left( 0 \right) =0.5\), \(\alpha =0.9, k_1 =15,k_2 =3,k_3 =1\). The control input is applied at \(t=2\) s.

Simulation results are illustrated in Fig. 2, which shows that the proposed controller provides a robust synchronization state between master and slave in the presence of uncertainties and disturbances.

Fig. 2
figure 2figure 2

Simulation results for Example 1. a State trajectories of the first states of synchronized systems (29) and (30). b State trajectories of the second state of synchronized systems (29) and (30). c State trajectories of the controlled synchronization error of (29) and (30). d Time response of the update parameters for (29) and (30). e Time history of the applied control input for (30)

Full size image

4 Synchronization of fractional-order chaotic systems

So far, design of fractional-order sliding mode controller for synchronization of two integer-order chaotic systems is presented. This section deals with developing fractional-order sliding mode controller for fractional-order chaotic systems.

4.1 Problem statement

Consider a fractional-order chaotic system described as follows

$$\begin{aligned} \mathbf{D}^{\alpha }y_1 (t)= & {} y_2 (t) \nonumber \\ \mathbf{D}^{\alpha }y_2 (t)= & {} f(\mathbf{y},t)+\Delta f(\mathbf{y},t)+d_y (t)+u(t) \end{aligned}$$
(31)

where \(\alpha \in \left( {0,1} \right) \), \(\left| {\Delta f(\mathbf{y},t)} \right| \le \Delta _f \) and \(\left| {d(t)_y } \right| \le D_y\). Considering the system (31) as slave, one can define the master as follows

$$\begin{aligned} \mathbf{D}^{\alpha }x_1 (t)= & {} x_2 (t) \nonumber \\ \mathbf{D}^{\alpha }x_2 (t)= & {} g(\mathbf{x},t)+\Delta g(\mathbf{x},t)+d_x (t) \end{aligned}$$
(32)

where \(\left| {\Delta g(\mathbf{x},t)} \right| \le \Delta _2\) and \(\left| {d(t)_x } \right| \le D_x\). Defining the state errors as (8), the error dynamics become

$$\begin{aligned} \mathbf{D}^{\alpha }e_1 (t)= & {} e_2 (t) \nonumber \\ \mathbf{D}^{\alpha }e_2 (t)= & {} f(\mathbf{y},t)-g(\mathbf{x},t)+\Delta f(\mathbf{y},t)\nonumber \\&-\,\Delta g(\mathbf{x},t)+d_y (t)-d_x (t)+u(t) \end{aligned}$$
(33)

The controller should be designed such that \(\left\| \mathbf{e} \right\| \rightarrow 0\) as \(t\rightarrow \infty \).

Assumption 2

The uncertainty terms and external disturbances are assumed to satisfy the following inequalities

$$\begin{aligned} \left| {\mathbf{D}^{1-\alpha }\left( {\Delta f(\mathbf{y},t)\!-\!\Delta g(\mathbf{x},t)} \right) } \right|\le & {} \sigma _\alpha , \left| {\mathbf{D}^{1-\alpha }\left( {d_y (t)\!-\!d_x (t)} \right) } \right| \\\le & {} \mu _\alpha \end{aligned}$$

4.2 Controller design

In order to design a fractional-order sliding mode controller, the following fractional order sliding surface is proposed

$$\begin{aligned} S\left( t \right) =k_1 e_1 \left( t \right) +k_2 \mathbf{D}^{\alpha }e_1 \left( t \right) +k_3 \dot{e}_1 \left( t \right) \end{aligned}$$
(34)

Taking the first derivative from both sides of (34) with respect to time yields the following expression

$$\begin{aligned} \dot{S}\left( t \right)= & {} k_1 \dot{e}_1 \left( t \right) +k_2 \frac{d}{dt}\left( {\mathbf{D}^{\alpha }e_1 \left( t \right) } \right) +k_3 \ddot{e}_1 \left( t \right) =k_1 \dot{e}_1 \left( t \right) \nonumber \\&+\,k_2 \dot{e}_2 \left( t \right) +k_3 \ddot{e}_1 \left( t \right) = k_1 \dot{e}_1 \left( t \right) \nonumber \\&+\,k_2 \mathbf{D}^{1-\alpha }\left( f(\mathbf{y},t)-g(\mathbf{x},t)\!+\!\Delta f(\mathbf{y},t)\!-\!\Delta g(\mathbf{x},t)\right. \nonumber \\&\left. +\,d_y (t)-d_x (t) \right) +k_2 \mathbf{D}^{1-\alpha }u(t)+k_3 \ddot{e}_1 \left( t \right) \end{aligned}$$
(35)

By eliminating the uncertain terms from (35), we assume the following equivalent control law

$$\begin{aligned} u_{eq} (t)= & {} -k_2^{-1} \mathbf{D}^{\alpha -1}\left( {k_1 \dot{e}_1 \left( t \right) +k_3 \ddot{e}_1 \left( t \right) } \right) \nonumber \\&-\,\left( {\begin{array}{l} f(\mathbf{y},t)-g(\mathbf{x},t)+\Delta f(\mathbf{y},t)-\Delta g(\mathbf{x},t) \\ +d_y (t)-d_x (t) \\ \end{array}} \right) \nonumber \\ \end{aligned}$$
(36)

Since in practical applications, the system uncertainty terms \(\Delta f({\mathbf {y}},t)\) and \(\Delta g({\mathbf {x}},t)\) and external disturbances \(d_{x} (t)\) and \(d_{y} (t)\) are unknown, and according to Assumption 2, in order to deteriorate the uncertain terms in (33), the switching control law is proposed

$$\begin{aligned} u_{sw} (t)=-\mathbf{D}^{\alpha -1}\left( {\lambda _s S(t)+\left( {k_s +\sigma _\alpha +\mu _\alpha } \right) \hbox {sgn}(S(t))} \right) \end{aligned}$$
(37)

In practical application, the external disturbances and the system uncertainties are unknown then the control law becomes

$$\begin{aligned} u(t)= & {} u_{^{eq}} (t)+u_{sw} (t)= -k_2^{-1} \mathbf{D}^{\alpha -1}\left( {k_1 \dot{e}_1 \left( t \right) +k_3 \ddot{e}_1 \left( t \right) } \right) \nonumber \\&-\,f(\mathbf{y},t)+g(\mathbf{x},t)-\mathbf{D}^{\alpha -1} \left[ \lambda _s S(t)\right. \nonumber \\&\left. +\,\left( {k_s +\sigma _\alpha +\mu _\alpha } \right) \hbox {sgn}(S(t)) \right] \end{aligned}$$
(38)

Theorem 5

Consider the synchronization error system (33). If, this system is controlled by the control law \(u(t)\) in (38), then the system trajectories will converge to the sliding surface \(S(t) = 0\).

Proof

Consider a positive definite Lyapunov function candidate in the following form:

$$\begin{aligned} V\left( t \right) =\left| {S\left( t \right) } \right| \end{aligned}$$
(39)

Taking derivative of both sides of (15) with respect to time, one has

$$\begin{aligned} \dot{V}\left( t \right)= & {} \dot{S}\left( t \right) \times \hbox {sgn}\left( {S\left( t \right) } \right) \nonumber \\= & {} \begin{array}{l} \left( {k_1 \dot{e}_1 \left( t \right) +k_2 \mathbf{D}^{1-\alpha }\left( {\begin{array}{l} f(\mathbf{y},t)-g(\mathbf{x},t)+\Delta f(\mathbf{y},t) \\ -\Delta g(\mathbf{x},t)+d_y (t)-d_x (t)+u(t) \\ \end{array}} \right) +k_3 \ddot{e}_1 \left( t \right) } \right) \end{array} \times \, \hbox {sgn}\left( {S\left( t \right) } \right) \nonumber \\&\times \,{\begin{array}{l} \left( {k_2 \mathbf{D}^{1-\alpha }\left( {\begin{array}{l} +\Delta f(\mathbf{y},t)-\Delta g(\mathbf{x},t)+d_y (t)-d_x (t) \\ -\mathbf{D}^{\alpha -1}\left[ {\lambda _s S(t)+\left( {k_s +\sigma _\alpha +\mu _\alpha } \right) \hbox {sgn}(S(t))} \right] \\ \end{array}} \right) } \right) \end{array}}\times \, \hbox {sgn}\left( {S\left( t \right) } \right) \end{aligned}$$
(40)

Substituting (38) into (40) yields

$$\begin{aligned} \dot{V}\left( t \right)= & {} \left( k_2 \mathbf{D}^{1-\alpha }\left( {\Delta f(\mathbf{y},t)-\Delta g(\mathbf{x},t) }\right) \right. \nonumber \\&\quad +\,k_2 \mathbf{D}^{1-\alpha }\left( {d_y (t)-d_x (t)} \right) \nonumber \\&\quad \left. -\,k_2 \left[ {\begin{array}{l} \lambda _s S(t) \\ +\left( {k_s +\sigma _\alpha +\mu _\alpha } \right) \hbox {sgn}(S(t)) \\ \end{array}} \right] \right) \nonumber \\&\quad \times \, \hbox {sgn}\left( {S\left( t \right) } \right) \nonumber \\&\quad \dot{V}\left( t \right) \le k_2 \left| {\mathbf{D}^{1-\alpha }\left( {\Delta f(\mathbf{y},t)-\Delta g(\mathbf{x},t) } \right) } \right| \nonumber \\&\quad +\,k_2 \left| {\mathbf{D}^{1-\alpha }\left( {d_y (t)-d_x (t)} \right) } \right| \nonumber \\&\quad -\,k_2 \left[ {\lambda _s \left| {S(t)} \right| +\left( {k_s +\sigma _\alpha +\mu _\alpha } \right) } \right] \nonumber \\&\quad \dot{V}\left( t \right) \le -k_2 \left( {\lambda _s \left| {S(t)} \right| +k_s } \right) \le -\eta \left| {S(t)} \right| \end{aligned}$$
(41)

which implies asymptotic stability.

Similar to the Theorem 3, the state trajectories of the error system (33) will converge to \(S(t)=0\) in the finite time \(t_r\):

$$\begin{aligned} t_r \le \frac{1}{k_2 \lambda _s }\ln \left( {\left( {{\lambda _s }\Big /{k_s }} \right) \left| {S(0)} \right| +1} \right) \end{aligned}$$
(42)

Also similar to the Theorem 4, using the Laplace transform of the Caputo derivative for (34), it can be concluded that \(\mathop {\lim }\limits _{\mathrm{t}\rightarrow \infty }e(t)=0\). This shows the convergence of the error system trajectories to the fractional sliding surface (34). \(\square \)

Lemma 2

to tackle the unknown parameters, the following adaptation laws are proposed.

$$\begin{aligned} \dot{\hat{{\sigma }}}_\alpha= & {} k_2 \xi _1\left| {S\left( t \right) } \right| \end{aligned}$$
(43)
$$\begin{aligned} \dot{\hat{{\mu }}}_\alpha= & {} k_2 \xi _2 \left| {S\left( t \right) } \right| \nonumber \\ \dot{\hat{{k}}}_s= & {} k_2 \xi _4 \left| {S\left( t \right) } \right| \nonumber \\ \dot{\hat{{\lambda }}}_s= & {} k_2 \xi _3 S^{2}(t) \end{aligned}$$
(44)

where \(\hat{{\sigma }}_\alpha ,\hat{{\mu }}_\alpha ,\hat{{\lambda }}_s\) and \(\hat{{k}}_s\) are estimations for \(\sigma _\alpha , \mu _\alpha ,\lambda _s\) and \(k_s\) respectively; and \(\xi _1, \xi _2, \xi _3\) and \(\xi _4\) are positive constants.

Proof

choose a Lyapunov function as follows

$$\begin{aligned} V\left( t \right)= & {} \frac{1}{2}S^{2}\left( t \right) +\xi _1^{-1} (\tilde{\sigma }_\alpha )^{2}+\xi _2^{-1} (\tilde{\mu }_\alpha )^{2}+\xi _3^{-1} (\tilde{\lambda }_s )^{2}\nonumber \\&+\,\xi _4^{-1} (\tilde{k}_s)^{2} \end{aligned}$$
(45)

where \(\tilde{k}_{s}=\hat{k}_{s}-k_{s}\),\(\tilde{\mu }_\alpha =\hat{{\mu }}_\alpha -\mu _\alpha \), \(\tilde{\sigma }_\alpha =\hat{{\sigma }}_\alpha -\sigma _\alpha \) and \(\tilde{\lambda }_{s}=\hat{\lambda }_{s}-\lambda _{s}\) taking derivative of both sides of (45) with respect to time yields:

$$\begin{aligned} V\left( t \right)= & {} S\left( t \right) \dot{S}\left( t \right) +\xi _1^{-1} \tilde{\sigma }_\alpha (\dot{\hat{{\sigma }}}_\alpha )+\xi _2^{-1} (\tilde{\mu }_\alpha )\dot{\hat{{\mu }}}_\alpha \nonumber \\&+\,\xi _3^{-1} \tilde{\lambda }_s (\dot{\hat{{\lambda }}}_s )+\xi _4^{-1} \tilde{k}_s (\dot{\hat{{k}}}_s ) \end{aligned}$$
(46)

Using the control input (38)

$$\begin{aligned} \dot{V}\left( t \right)= & {} S\left( t \right) \left( { \begin{array}{l} k_2 \mathbf{D}^{1-\alpha }\left( {\Delta f(\mathbf{y},t)-\Delta g(\mathbf{x},t)} \right) \\ +k_2 \mathbf{D}^{1-\alpha }\left( {d_y (t)-d_x (t)} \right) \\ -k_2 \left[ {\lambda _s S(t)+\left( {\hat{{k}}_s \!+\!\hat{{\sigma }}_\alpha \!+\!\hat{{\mu }}_\alpha } \right) \hbox {sgn}(S(t))} \right] \\ \end{array}}\! \right) \nonumber \\&+\,\left( { \begin{array}{l} \xi _1^{-1} \tilde{\sigma }_\alpha (\dot{\hat{{\sigma }}}_\alpha )+\xi _2^{-1} (\tilde{\mu }_\alpha )\dot{\hat{{\mu }}}_\alpha \\ +\xi _3^{-1} \tilde{\lambda }_s (\dot{\hat{{\lambda }}}_s )+\xi _4^{-1} \tilde{k}_s (\dot{\hat{{k}}}_s ) \\ \end{array}} \right) \nonumber \\ \dot{V}\left( t \right)\le & {} k_2 \left( {\begin{array}{l} \left( {\begin{array}{l} \left| {\mathbf{D}^{1-\alpha }\left( {\Delta f(\mathbf{y},t)-\Delta g(\mathbf{x},t)} \right) } \right| \\ +\left| {\mathbf{D}^{1-\alpha }\left( {d_y (t)-d_x (t)} \right) } \right| \\ \end{array}} \right) \left| {S\left( t \right) } \right| \\ -\hat{{\lambda }}_s S^{2}(t)-S\left( t \right) \left( {\hat{{k}}_s \!+\!\hat{{\sigma }}_\alpha \!+\!\hat{{\mu }}_\alpha } \right) \hbox {sgn}\left( {S(t)} \right) ) \\ \end{array}} \!\right) \nonumber \\&+\,\left( {\begin{array}{l} \xi _1^{-1} \tilde{\sigma }_\alpha (\dot{\hat{{\sigma }}}_\alpha )+\xi _2^{-1} (\tilde{\mu }_\alpha )\dot{\hat{{\mu }}}_\alpha \\ +\xi _3^{-1} \tilde{\lambda }_s (\dot{\hat{{\lambda }}}_s )+\xi _4^{-1} \tilde{k}_s (\dot{\hat{{k}}}_s ) \\ \end{array}} \right) \nonumber \\ \dot{V}\left( t \right)\le & {} k_2 \left( { \begin{array}{l} \left( {\sigma _\alpha +\mu _\alpha } \right) \left| {S\left( t \right) } \right| -\hat{{\lambda }}_s S^{2}(t) \\ -S\left( t \right) \left( {\hat{{k}}_s +\hat{{\sigma }}_\alpha +\hat{{\mu }}_\alpha } \right) \hbox {sgn}\left( {S(t)} \right) \\ \end{array}} \right) \nonumber \\&+\,\left( {\begin{array}{l} \xi _1^{-1} \tilde{\sigma }_\alpha (\dot{\hat{{\sigma }}}_\alpha )+\xi _2^{-1} (\tilde{\mu }_\alpha )\dot{\hat{{\mu }}}_\alpha \\ +\xi _3^{-1} \tilde{\lambda }_s (\dot{\hat{{\lambda }}}_s )+\xi _4^{-1} \tilde{k}_s (\dot{\hat{{k}}}_s ) \\ \end{array}} \right) \end{aligned}$$
(47)

Introducing the adaptation laws (43) into the right hand of (47), one obtains

$$\begin{aligned} \dot{V}\left( t \right)\le & {} k_2 \left( \!\left( {\hat{{\sigma }}_\alpha \!+\!\hat{{\mu }}_\alpha } \right) \left| {S\left( t \right) } \right| -\hat{{\lambda }}_s S^{2}(t)-\left| {S\left( t \right) } \right| \!\left( {\hat{{\sigma }}_\alpha +\hat{{\mu }}_\alpha } \right) \right. \nonumber \\&\left. -\,\hat{{k}}_s \left| {S\left( t \right) } \right| \right) +\xi _3^{-1} \tilde{\lambda }_s (\dot{\hat{{\lambda }}}_s )+\xi _4^{-1} \tilde{k}_s (\dot{\hat{{k}}}_s ) \end{aligned}$$
(48)

Inserting the adaptation laws (44) into the right hand of (48), one obtains

$$\begin{aligned} \dot{V}\left( t \right) \le -k_2 \left( {k_s \left| {S\left( t \right) } \right| +\lambda _s S^{2}(t)} \right) \end{aligned}$$
(49)

This implies that stability of the system is guaranteed. \(\square \)

4.3 Example 2: Synchronization of two fractional-order Duffing–Holmes and Gyro systems

Let us assume that the fractional-order version of Duffing–Holmes system (master system) can be described by

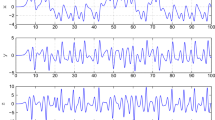
$$\begin{aligned} \mathbf{D}^{\alpha }x_1= & {} x_2 \nonumber \\ \mathbf{D}^{\alpha }x_2= & {} x_1 -ax_2 -x_1^3 +b\cos t+\Delta g\left( {x_1,x_2 } \right) +d_x \left( t \right) \nonumber \\ \end{aligned}$$
(50)

where \(a=0.25\) and \(b=0.3\) yield chaotic motion. Chaotic attractor of this system is illustrated in Fig. 3 for \(\alpha =0.98\). For the purpose of numerical simulations we set the initial conditions as \(x_1 (0)=0.3\), \(x_2 (0)=-0.2\). It is also assumed that the master is perturbed by \(\Delta g\left( {x_1, x_2 } \right) =0.1\sin (x_2 )\cos (x_1 )\) and \(d_x \left( t \right) =0.1\cos (3t)\).

Fig. 3
figure 3

Chaotic attractor of fractional-order Duffing–Holmes system

Full size image

The equation governing the motion of a symmetric gyro mounted on a vibrating base in terms of the rotation angle \(\theta \) (i.e. the angle between the spin axis of the gyro and the vertical axis), is given by [9]

$$\begin{aligned} \ddot{\theta }+\varepsilon ^{2}\frac{\left( {1-\cos \theta } \right) ^{2}}{\sin ^{3}\theta }-\beta \sin \theta +c_1 \dot{\theta }+c_2 \dot{\theta }^{3}=f\sin (\omega t)\sin \theta \end{aligned}$$
(51)

where the term \(f\sin (\omega t)\) represents a parametric excitation, \(c_1\) and \(c_2\) are linear and nonlinear damping terms, respectively. The term \(\varepsilon ^{2}{\left( {1-\cos \theta } \right) ^{2}}/{\sin ^{3}\theta }-\beta \sin \theta \) is a nonlinear resilience force. Choosing the state variables as \(y_1 =\theta \) and \(y_2 =\dot{\theta }\), Eq. (51) becomes:

$$\begin{aligned} \dot{y}_1= & {} y_2 \nonumber \\ \dot{y}_2= & {} -\varepsilon ^{2}\frac{\left( {1-\cos y_1 } \right) ^{2}}{\sin ^{3}y_1 }-\beta \sin y_1 -c_1 y_1 \nonumber \\&-\,c_2 y_2^3 +\left( {\beta +f\sin \omega t} \right) \sin y_1 +u\left( t \right) \end{aligned}$$
(52)

where \(\varepsilon =10,\;\beta =1,\;c_1 =0.5,\;c_2 =0.05,\;\omega =2\) and \(32<f<36\) yield chaotic behavior. Let us assume that the fractional-order version of Gyros system can be described by

$$\begin{aligned} \mathbf{D}^{\alpha }y_1= & {} y_2 \nonumber \\ \mathbf{D}^{\alpha }y_2= & {} -\varepsilon ^{2}\frac{\left( {1-\cos y_1 } \right) ^{2}}{\sin ^{3}y_1 }-\beta \sin y_1 -c_1 y_1 -c_2 y_2^3\nonumber \\&+\,\left( {\beta +f\sin \omega t} \right) \sin y_1 +\Delta f\left( {y_1 ,y_2 } \right) \nonumber \\&+\,u\left( t \right) +d_y (t) \end{aligned}$$
(53)

The system (51) exhibits chaotic behavior as shown in Fig. 4 for \(q=0.98\). In the numerical simulations we set \(f=35, y_1 (0)=-0.1, y_2 (0)=0.2\), \(d_y (t)=0.2\cos (t),\Delta f=0.4\sin (y_1 )\sin (y_2)\). The design parameters are chosen as \(\alpha =0.98,k_1 =20,k_2 =5\) and \(k_3 =2\) and \(\hat{{\mu }}\left( 0 \right) =1,\hat{{\delta }}\left( 0 \right) =1,\hat{{k}}_s \left( 0 \right) =1, \hat{{\lambda }}_s \left( 0 \right) =1\).

Fig. 4
figure 4

Chaotic attractor of fractional-order Gyros system

Full size image

The simulation results are presented in Fig. 5, which show that the master and slave are synchronized magnificently after a transient state.

Fig. 5
figure 5figure 5

Simulation results for Example 2. a State trajectories of the first states of synchronized systems (50) and (53). b State trajectories of the second state of synchronized systems (50) and (53). c State trajectories of the controlled synchronization error of (50) and (53). d Time response of the update parameters for (50) and (53). e Time history of the applied control input for (53)

Full size image

From the simulation results, it is shown that our theoretical results are feasible and efficient for synchronization of two non-identical fractional-order chaotic systems. Simulation results in Fig. 5 show the feasibility of the proposed controller in synchronizing of two fractional-order Duffing–Holmes and Gyros systems.

5 Conclusion

This paper studied the use of fractional-order sliding mode control in synchronization of both integer and fractional order chaotic systems. Using the fractional Lyapunov stability theory, the finite-time stability and robustness of the proposed scheme are mathematically proved. Simulation results illustrate the proposed method is feasible and efficient for synchronization of two non-identical fractional/integer order chaotic systems. Numerical simulations show this controller can synchronize master and slave systems even in the presence of external disturbance.