Parametric design of turbocharger rotor system under exhaust emission loads via surrogate model

Abstract

The common failure modes of a turbocharger rotor are bearing wear, impeller-casing rub events and shaft cracks due to high thermal currents. A reliable design of such rotors is therefore essential in order to avoid the vibration-based failure incidents during operation. The dynamic response gives vital information about the rotor condition as well as it helps in the inverse modelling to predict the optimum parameters. Present work deals with dynamic analysis and optimum design of a turbocharger rotor system subjected to ideal exhaust gas emission loads. The exhaust emission loads at the turbine in radial direction are modelled as Muszynska’s nonlinear seal forces, while the axial gas emission loads are treated as periodic blade passing excitations. The critical vibration characteristics of the rotor system running at uniform speed are analysed using the finite element model by considering nonlinear floating ring bearing forces and are initially validated with an experimental work performed on a turbocharger test-rig. Furthermore, the effects of gas load as well as floating ring bearing parameters on the critical frequencies and amplitudes are studied in detail. The effective input–output relationships are established using counter-propagation neural network (CPNN) learning scheme. Surrogate model using an improved Cuckoo search optimization in-conjunction with trained CPNN model in function evaluations is employed to predict the optimum values of the bearing parameters and relative emission load data. The relative output frequency response with optimized parameters is presented and  effectiveness of the approach over the finite element based function evaluation scheme is illustrated.

1 Introduction

Turbocharger is an important component in modern automobiles. Unlike carburettor engines, turbochargers facilitate in utilizing the balance energy of expanded exhaust gases from the engine. It is a tiny assembly possessing an outer casing within which an internal shaft with turbine and compressor discs at its two ends is mounted. The rotor system is supported on two floating ring bearings and one thrust foil bearing close to the compressor side [1]. In principle, the exhaust emission loads from the engine enter into the turbocharger casing at the turbine side and revolve the rotor system usually at very high speeds using expanding gas energy conversion. Due to integral shaft system, the compressor at the other end also revolves at the same speed and the inlet air entering through the diffuser gets pressurized sufficiently. This extra high-pressure inlet air enters the engine continuously and participates in the combustion process leading to a higher engine efficiency. The cycle of operations drastically reduces the polluting gases leaving the turbocharger exhaust. The principal component here is the rotor shaft, undergoing different kinds of loads including transients in the start-up and shut-down periods, high-temperature stresses, fluid-induced aerodynamic loads, etc. The common failure mode of the rotor is from the induced fatigue stresses due to cyclic loads [2]. Therefore, special attention is needed to estimate the vibration response accurately. Several earlier works [3,4,5,6] studied the free and forced vibration analysis of turbocharger rotors. The stability and bifurcation behaviour of the turbocharger rotor were presented with bearing parameter uncertainties [7, 8]. Bonello [9] included the nonlinear dynamics of floating ring bearings in the finite element model of the turbocharger rotor and studied the self-excited vibration responses for both full and semi-floating ring bearings. An approach to monitoring the turbocharger bearing clearance variations from the oil film pressure using the Reynolds equation has been presented by Zhang et al.[10]. Characteristics of a turbocharger with different types of bearing designs were presented with the nonlinear transient response and the optimal values for bearing dimensions were suggested by Chen [11]. Kirk et al.[12] explained the rotor instabilities in the turbocharger with the jump phenomenon. Effects of bearing outer clearance, unbalance, and engine excitations on the dynamic behaviour of turbocharger supported on floating ring bearings were thoroughly studied [13, 14]. Alsaeed et al. [15] investigated the influences of radial aerodynamic forces in compressor and turbine casings on the dynamic stability with the help of the rotor-bearing finite element model of the turbocharger. Dynamic characteristics of the rotor system with respect to floating ring bearing manufacturing tolerances were studied by Wang et al. [16]. Chatzisavvas et al. [17] presented the nonlinear vibrations and bifurcation behaviour of turbocharger supported on floating ring bearings with thrust bearing considerations. Cao et al. [18] described the bearing design and nonlinear transient characteristics of an industrial turbocharger supported on semi-floating bush bearings. Keshavarz et al. [19] presented transient dynamic simulations of SI engine turbocharger with GT-Power software. Lee et al. [20] obtained the axial thrust load from both numerical and experimental approaches during the turbocharger operation. In a more recent work, Peixoto and Cavalca [21] illustrated the effects of thrust bearing on the lateral vibration behaviour of a turbocharger rotor.

Optimum design of rotor-bearing parameters in high-speed machinery is one of the challenging issues in rotor dynamics. In particular, in turbocharger rotors where highly nonlinear bearing forces are involved, several parameters are to be optimally selected under various constraints [22, 23]. Some common criteria considered in the design are improving the stability [24], minimizing the rotor weight, and vibration amplitudes [25, 26], maximizing the critical frequencies of the system, minimizing the induced stresses. By adjusting the bearing stiffness, the critical speeds, and by setting the proper unbalance masses, the dynamic responses of turbocharger rotor can be modified [27]. Zhang et al. [28] recently presented a radial clearance adjustment mechanism in bearing for minimization of critical and sub-critical vibration response amplitudes as well as sub-synchronous oil whip instability.

During the design stage, the optimum parameters are predicted by repeating the complex dynamic analysis simulations several times. In order to save the time and computational memory, surrogate models are effectively used [29]. Many applications of surrogate models in engineering practice have been observed during the last one decade. Han et al. [30] illustrated an approach of identifying bearing parameters and unbalance in a three-disc rotor-bearing system using Kriging surrogate model integrated with genetic algorithms by minimizing the unbalance response. Nonlinear rotor-bearing parameter identification was also illustrated with an improved Kriging surrogate model [31]. Several other works were also reported the effectiveness of surrogate models as an alternative approach to computational fluid mechanics simulations, Recently, Lu et al. [32] proposed a surrogate model for the reliability analysis of turbine bladed disc deformations. For creating surrogate models, neural networks are commonly employed. Pantelelis et al. [33] utilized a neural network approach for fault identification in the navel turbocharger system using measured vibration response. Zhang and Su [34] presented an approach for turbo generator vibration faults using neural networks. Koutsovasilis et al. [35] implemented a numerical optimization scheme to predict the optimum shaft bearing geometry and wheel shaft parameters in a turbocharger for minimization of sub-synchronous responses in the start-up operations. In recent works, different kinds of neural network models have been reported for fault diagnosis [e.g. 36]. In turbocharger rotor dynamic simulations, the transient vibration response behaviour under exhaust gas emission loads with bearing nonlinearities is not considered in literature. The principal objective of the present study is to develop an effective numerical simulation platform for understanding the interaction effects of the floating ring bearing parameters and exhaust emission load factors simultaneously on the rotor frequency response and subsequent optimization of the system. The nonlinearities in radial components of exhaust emission loads are considered with the Muszynska seal force model, while the axial component is represented with turbine blade passing excitation. The unbalance response from the proposed finite element model is initially validated with an experiment on the turbocharger test-rig. Further, the model transient responses with exhaust emission loads are obtained by varying the important bearing parameters and load factors. The functional relationship between the five crucial parameters influencing the critical frequency and amplitude is established by the use of counter propagation neural network model. The surrogate model is then constructed by employing an improved Cuckoo search (CS) metaheuristic optimization method that makes use of trained CPNN for function evaluations. The effectiveness of the approach in comparison with regular function evaluation scheme is illustrated. The remaining part of the paper is organized as follows: Section-2 describes the mathematical modelling of the rotor system along with the different force models considered in the simulations. Section-3 presents the description of proposed approach, surrogate modelling and improved Cuckoo search optimization. Results and discussions are given in section-4.

2 Mathematical model of rotor system

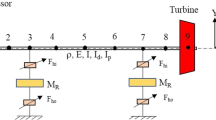
A turbocharger rotor consists of a tiny complex non-uniform flexible stepped turbo-compressor shaft supported on two floating ring bearings. Figure 1 shows the finite element model of an equivalent rotor system  on the floating ring bearings.

Fig. 1

Finite element model of rotor-bearing system

The flexible shaft is discretized into two node beam elements, with each node having five degrees of freedom (DOF) including axial deformation w and two bending deflections (u, v) and corresponding slopes (θ_x, θ_y).The turbine and compressor are considered as lumped masses mounted at the first and last nodes which contribute to inertial and gyroscopic matrices of the discs, while the bearings are located at nodes 3 and 7 for this configuration with m_R as the ring mass. The assembled equations of motion of rotor system can be written as:

$${\tilde{\mathbf{M}}}_{{\mathbf{s}}} \ddot{q} + \left( {{\tilde{\mathbf{C}}}_{{\mathbf{s}}} + \Omega {\tilde{\mathbf{G}}}_{{\mathbf{s}}} } \right)\dot{q} + {\tilde{\mathbf{K}}}_{{\mathbf{s}}} q = \tilde{F}_{{{\text{ug}}}} + \tilde{F}_{{{\text{hi}}}} + \tilde{g}_{{{\text{force}}}}$$

(1)

Here ${\tilde{\mathbf{M}}}_{{\mathbf{s}}}$ is the global mass matrix of the shaft, ${\tilde{\mathbf{C}}}_{{\mathbf{s}}}$ and ${\tilde{\mathbf{G}}}_{{\mathbf{s}}}$ denote, respectively, the damping and gyroscopic matrices, while ${\tilde{\mathbf{K}}}_{{\mathbf{s}}}$ represents the overall shaft stiffness. The displacement vector is denoted as q. The over dot indicates the time derivative. The right-hand side term $\tilde{F}_{{{\text{ug}}}}$ denotes the unbalance and gravity force vector, while $\tilde{F}_{hi} = [\begin{array}{*{20}c} {F_{{{\text{ix}}}} } & {F_{{{\text{iy}}}} ]^{T} } \\ \end{array}$ and $\tilde{g}_{{{\text{force}}}}$ are the inner oil film force vector and the exhaust gas excitation force vectors, respectively. It is assumed that the floating ring moves only in lateral directions and has a constant rotational speed Ω_R and has mass m_r. The motion of the equation of the rotating floating ring is written as:

$${\tilde{\mathbf{M}}}_{{\mathbf{r}}} \ddot{q}_{r} = \tilde{F}_{{{\text{ho}}}} - \tilde{F}_{{{\text{hi}}}}$$

(2)

where the displacement vector of the ring (eight left or right bearing) is denoted as q_r = [X_rY_r]^T and ${\tilde{\mathbf{M}}}_{{\mathbf{r}}}$ = diag(m_r,m_r) indicates the mass matrix of the ring. Also, $\tilde{F}_{{{\text{ho}}}} = [\begin{array}{*{20}c} {F_{{{\text{ox}}}} } & {F_{{{\text{oy}}}} ]^{T} } \\ \end{array}$ represents the outer film oil force vector. The resulting assembled equations of the motion for rotor and bearing can be obtained by combining eqs. (1) and (2) as:

$${\mathbf{M}}\ddot{q} + {\mathbf{C}}q + {\mathbf{K}}q = F$$

(3)

where

${\mathbf{M}} = \left[ {\begin{array}{*{20}c} {{\tilde{\mathbf{M}}}_{{\mathbf{s}}} } & 0 \\ 0 & {{\tilde{\mathbf{M}}}_{{\mathbf{r}}} } \\ \end{array} } \right],$${\mathbf{C}} = \left[ {\begin{array}{*{20}c} {{\tilde{\mathbf{C}}}_{{\mathbf{s}}} + \Omega {\tilde{\mathbf{G}}}_{{\mathbf{s}}} } & 0 \\ 0 & 0 \\ \end{array} } \right],$${\mathbf{K}} = \left[ {\begin{array}{*{20}c} {{\tilde{\mathbf{K}}}_{{\mathbf{s}}} } & 0 \\ 0 & 0 \\ \end{array} } \right]$ are the square matrices, while the final displacement vector is written in terms of shaft and ring degrees of freedom as $q = [\begin{array}{*{20}c} {q_{s} } & {q_{{r - {\text{left}}}} \begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {q_{{r - {\text{right}}}} } \\ \end{array} } \\ \end{array} ]^{T} } \\ \end{array}$ . Also, the resultant force vector is:

$$F = \left[ {\begin{array}{*{20}c} {\tilde{F}_{{{\text{ug}}}} + \tilde{F}_{{{\text{hi}}}} + \tilde{g}_{{{\text{force}}}} } & {\tilde{F}_{{{\text{ho}}}} - \tilde{F}_{{{\text{hi}}}} } \\ \end{array} } \right]^{T} = F_{{{\text{ug}}}} + F_{{{\text{bearing}}}}$$

(4)

2.1 Bearing forces

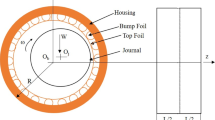
A floating ring bearing has a ring or bush inserted between the journal and sleeve and develops two thin lubricant films called inner and outer films, respectively. The ring consists of feed holes which allow the oil circulation from inner film to outer film. The notations and coordinates of the bearing are shown in Fig. 2.

Fig. 2

Floating ring bearing coordinate system and notation

Bearing forces are obtained from the instantaneous bearing pressures, which are derived by solving the Reynolds equations with appropriate boundary conditions. If the subscript j denotes the journal and p, μ and Ω are, respectively, film pressure, oil viscosity, and rotational speed, then the inner and outer fluid film Reynolds equations for both the films can be expressed as [37]:

$$\frac{1}{{R_{{\text{j}}} }}\frac{\partial }{{\partial \theta_{i} }}\left( {\frac{{h_{{\text{i}}}^{3} }}{{12\mu_{i} }}\frac{{\partial p_{i} }}{{\partial \theta_{i} }}} \right) + \frac{\partial }{{\partial z_{i} }}\left( {\frac{{h_{{\text{i}}}^{3} }}{{12\mu_{i} }}\frac{{\partial p_{i} }}{{\partial z_{i} }}} \right) = \frac{{(\Omega_{j} + \Omega_{r} )}}{2}\frac{{\partial h_{{\text{i}}} }}{{\partial \theta_{i} }} + \frac{{\partial h_{{\text{i}}} }}{\partial t}$$

(5)

$$\frac{1}{{R_{{\text{o}}} }}\frac{\partial }{{\partial \theta_{o} }}\left( {\frac{{h_{{\text{o}}}^{3} }}{{12\mu_{o} }}\frac{{\partial p_{o} }}{{\partial \theta_{o} }}} \right) + \frac{\partial }{{\partial z_{o} }}\left( {\frac{{h_{{\text{o}}}^{3} }}{{12\mu_{o} }}\frac{{\partial p_{o} }}{{\partial z_{o} }}} \right) = \frac{{\Omega_{r} }}{2}\frac{{\partial h_{o} }}{{\partial \theta_{o} }} + \frac{{\partial h_{{\text{o}}} }}{\partial t}$$

(6)

where R_j, R_i, and R_o represent, respectively, the journal radius, inner and outer radii of the ring, while the oil film thicknesses are denoted as h_i and h_o which can be written in terms of radial clearances of inner and outer films C₁, C₂ as follows:

$$h_{{\text{i}}} = C_{1} - x_{{\text{j}}} \cos \theta_{i} - y_{{\text{j}}} \sin \theta_{i}$$

(7)

$$h_{{\text{o}}} = C_{2} - X_{{\text{r}}} \cos \theta_{o} - Y_{{\text{r}}} \sin \theta_{o}$$

(8)

where O_r(X_r,Y_r) is the ring centre position, while $x_{{\text{j}}} = X_{{\text{j}}} - X_{{\text{r}}}$, $y_{{\text{j}}} = Y_{{\text{j}}} - Y_{{\text{r}}}$ and $\dot{x}_{{\text{j}}} = \dot{X}_{{\text{j}}} - \dot{X}_{{\text{r}}}$,$\dot{y}_{{\text{j}}} = \dot{Y}_{{\text{j}}} - \dot{Y}_{{\text{r}}}$ are relative displacements and velocities of the journal with respect to X–Y plane. Also, Ω_j and Ω_r are the angular speeds of the journal and floating ring, respectively. By considering infinitely short bearing approximation, the resultant partial differential equations can be simplified and the expressions for the pressures at inner and outer films are derived as

$$\begin{aligned} p_{{\text{i}}} = & \frac{{3\mu _{i} }}{{h_{{\text{i}}}^{3} }}\left( {z_{i}^{2} - \frac{{L_{i}^{2} }}{4}} \right)\left\{ {\left[ {\left( {\Omega _{{\text{j}}} + \Omega _{{\text{r}}} } \right)x_{{\text{j}}} - 2\dot{y}_{{\text{j}}} \sin \theta _{{\text{i}}} } \right],} \right. \\ & \left. { - \left[ {\left( {\Omega _{{\text{j}}} + \Omega _{{\text{r}}} } \right)y_{{\text{j}}} + 2\dot{x}_{{\text{j}}} } \right]\cos \theta _{i} } \right\}, \\ \end{aligned}$$

(9)

$$p_{{\text{o}}} = \frac{{3\mu_{o} }}{{h_{{\text{o}}}^{3} }}\left( {z_{o}^{2} - \frac{{L_{o}^{2} }}{4}} \right)\left[ {\left( {\Omega_{{\text{r}}} X_{{\text{r}}} - 2\dot{Y}\Omega_{{\text{r}}} } \right)\sin \theta_{o} - \left( {\Omega_{{\text{r}}} Y_{{\text{r}}} + 2\dot{X}_{{\text{r}}} } \right)\cos \theta_{o} } \right]$$

(10)

The detailed expressions for the time-varying bearing forces are obtained as surface integrals of the pressures [38] and the resultant component forces in vector form is:

$$\left\{ \begin{gathered} F_{{\text{ix}}} \hfill \\ F_{{\text{iy}}} \hfill \\ \end{gathered} \right\} = \mu_{i} (\Omega_{j} + \Omega_{r} )R_{j} L_{i} \left( {\frac{{R_{j} }}{{C_{1} }}} \right)^{2} \left( {\frac{{L_{i} }}{{2R_{j} }}} \right)^{2} \left\{ \begin{gathered} f_{{\text{ix}}} \hfill \\ f_{{\text{iy}}} \hfill \\ \end{gathered} \right\}$$

(11)

$$\left\{ \begin{gathered} F_{{\text{ox}}} \hfill \\ F_{{\text{oy}}} \hfill \\ \end{gathered} \right\} = \mu_{o} \Omega_{r} R_{o} L_{o} \left( {\frac{{R_{o} }}{{C_{2} }}} \right)^{2} \left( {\frac{{L_{o} }}{{2R_{o} }}} \right)^{2} \left\{ \begin{gathered} f_{{\text{ox}}} \hfill \\ f_{{\text{oy}}} \hfill \\ \end{gathered} \right\}$$

(12)

where f_ix, f_iy,andf_ox, f_oy are, respectively, the non-dimensional component forces on the journal and bearing in x and y directions. The detailed expression for these forces is shown in “appendix”.

2.2 Muszynska’s force model

Among different computing models, Muszynska’s sealing force model is widely employed because it is capable of explaining the nonlinear characteristics of the excitation force adequately. The nonlinear force expression is described as

$$\begin{aligned} \left\{ {\begin{array}{*{20}c} {F_{{\text{gx}}} } \\ {F_{{\text{gy}}} } \\ \end{array} } \right\} = & - \left[ {\begin{array}{*{20}c} {k_{{\text{g}}} - m_{{\text{g}}} \lambda^{2} \omega^{2} } & {\lambda \omega d_{{\text{g}}} } \\ { - \lambda \omega d_{{\text{g}}} } & {k_{{\text{g}}} - m_{{\text{g}}} \lambda^{2} \omega^{2} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} x \\ y \\ \end{array} } \right\} \\ & - \left[ {\begin{array}{*{20}c} {d_{{\text{g}}} } & {2\lambda \omega m_{{\text{g}}} } \\ { - 2\lambda \omega m_{{\text{g}}} } & {d_{{\text{g}}} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\dot{x}} \\ {\dot{y}} \\ \end{array} } \right\} - \left[ {\begin{array}{*{20}c} {m_{{\text{g}}} } & 0 \\ 0 & {m_{{\text{g}}} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\ddot{x}} \\ {\ddot{y}} \\ \end{array} } \right\} \\ \end{aligned}$$

(13)

The terms k_g, d_g, and m_g are, respectively, equivalent fluid stiffness, damping, and inertia coefficients. These are functions of radial displacements (x,y) of the rotor at the turbine node and can be expressed as:

$$k_{{\text{g}}} = k_{0} \left( {1 - \varepsilon^{2} } \right)^{{ - i_{1} }}$$

(14)

$$d_{{\text{g}}} = d_{0} \left( {1 - \varepsilon^{2} } \right)^{{ - i_{1} }}$$

(15)

where the exponent i₁ = 0.5 to 3, while $\lambda = \lambda_{0} \left( {1 - \varepsilon } \right)^{{i_{2} }}$, 0 < i₂ < 1 and λ < 0.5. Also, $\varepsilon = \frac{{\sqrt {x^{2} + y^{2} } }}{{C_{s} }}$ is relative eccentricity; C_s is the clearance. One of the major instability of system is due to rotation effect of the force. The symbol λ represent as average circumferential velocity ration of the fluid, and the λω represents the average velocity of the fluid in the sealing chamber.

From Child’s equation the characteristic factors k₀, d₀ and m_g are obtained [39].

2.3 Axial exhaust emission load model

The component of exhaust gas excitation in axial direction at the turbine side is treated as blade passing excitation. Because of the rotational symmetry of blade geometry and pressure distributions, only those harmonics which are multiples of the number of blades result in a non-cancelling thrust transmitted to the shaft. These are also called blade frequency loads. Under first blade frequency load excitation, the longitudinal primary resonance occurs. Here, the harmonic blade passing excitation force is

$$\tilde{g}_{{{\text{force}}}} = F_{0} \sin \left( {n_{{\text{b}}} \Omega t + \phi } \right)$$

(16)

where F₀ is the force magnitude, n_bΩ is blade passing frequency of rotor, ϕ is the phase angle and n_b is the number of blades on the turbine wheel.

2.4 Temperature-dependent bearing parameters

In practice, the oil film viscosity and clearances vary as a function of temperature. In this line, for both inner and outer films, the lubricant viscosity μ is evaluated as [40]:

$$\mu = \mu_{\infty } - \left[ {\frac{{\mu_{\infty } - Ke^{{\frac{c}{{\left( {d + T)} \right)}}}} }}{{\left( {{\raise0.7ex\hbox{${\dot{\zeta }}$} \!\mathord{\left/ {\vphantom {{\dot{\zeta }} {\dot{\zeta }_{{\text{i}}} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\dot{\zeta }_{{\text{i}}} }$}}} \right)}}} \right]$$

(17)

where T is temperature, $\mu_{\infty }$ denotes the reference viscosity at a null shear rate, while K, c, and d are Vogel’s viscosity fitting parameters selected from experimentally tabulated data. The symbols $\dot{\zeta }$ and $\dot{\zeta }_{{\text{i}}}$ are the shear rate and shear rate that produces a 50% reduction in reference viscosity, respectively.

3 Methodology and surrogate model

A detailed flowchart for the methodology used in the present work is shown in Fig. 3. Once after validating the finite element model, the frequency responses are predicted for different combinations of important bearing parameters. In order to develop the function approximation between inputs and frequency parameters, counter propagation neural network model is employed. The surrogate model of the system is developed via a counter propagation neural network. Finally, the optimum bearing parameters are identified by simultaneously minimizing the vibration amplitudes and enhancing the critical frequency of the system.

Fig. 3

Proposed methodology

3.1 Surrogate model

A surrogate model is employed when the output cannot be measured directly. To evaluate design objective and constraint functions, often a model or experiment is required. However, routine tasks are usually difficult, since they need several simulations to evaluate the objectives. By constructing approximate models mimicking the behaviour of simulators, the computational burden can be reduced to some extent. For such data-driven, bottom-up approaches, exact, simulation code is not required. The surrogate model, response surface method are few examples under such behavioural models. As the modal parameters are often influenced by rotor-bearing variables, a simplified model based on neural networks is employed for floating ring bearing case.

In the present task, counter propagation neural network is employed as a function estimator in the surrogate modelling to learn the relationship between the bearing parameters and the frequency response data. CPNN in its basic form has three layers [41]: (i) input, (ii) Kohonen, and (iii) Grossberg. It is a fully connected feed-forward neural network. Based on the winner-take-all, the input sets are categorized by the Kohonen layer. The Grossberg layer generates outputs for the category according to the target values. During the training, all weights Wⁱ and Vⁱ are initially assigned as random numbers and the winner node in the Kohonen (intermediate) layer correspond to each input pattern Xⁱ is predicted from maximum distance criterion max[$\left|{X}^{i}-{W}^{i}\right|$]. Then the weights of the winner node in the Kohonen layer are adjusted for every training pattern according to.

$$W^{{_{new} }} = W^{{_{old} }} + \alpha \left( {X - W^{{_{old} }} } \right)$$

(18)

Between the Kohonen and Grossberg layers, the weights are adjusted according to outstar or Grossberg learning rule, which can be written as.

$$V^{new} = V^{old} + \beta \left( {T - V^{old} } \right)$$

(19)

Here, T is the target or desired pattern and α and β refer to the adaptive learning parameters. The learning is quite simple and hybrid in nature.

3.2 Improved Cuckoo search optimization scheme

The Cuckoo search (CS) is one of the powerful metaheuristic stochastic global search optimization schemes. The method is inspired by the cuckoo’s behaviour. These birds are the “Brood parasites”. The cuckoo lays the eggs in another host bird nest because it does not build the nest. If the host bird identifies such eggs, it may throw the cuckoo’s egg or leave the nest and build a new one. The CS algorithm follows the three idealized rules [42]:

• (i) Cuckoo chose a random nest to dump the one egg at a time.

• (ii) The best nest with high quality of eggs carries to the next generation.

• (iii) The number of available host nests is fixed and if a host bird detects the cuckoo egg with the probability p_a ∈ (0,1) then the host bird can either throw them away or abandon them and build a new nest.

The initial positions of nests are identified by a set of randomly assigned values of control variables.

$$X_{m,n}^ {\text{{i}}} = X_{{\text{{n}}},\min } + {\text{rand}}(X_{{\text{{m}},{\text{Max}}}} - X_{{\text{{m}},{\text{min}}}} )$$

(20)

Here, $X_{m,n}^{\text{{i}}}$ denotes the initial values of mth variable for the nth nest and $X_{{\text{{m}},{\text{Max}}}}$,${{\text{{m}},{\text{min}}}}$ are the upper and lower bounds for the mth variable, respectively. Except for the best one, the entire nests are replaced by the new eggs of the cuckoo in the next step. From Levy distribution, the cuckoo moves from the present nest to the new one using a random step size. A random walk is a Markov chain whose next location depends only on the present location and the transition probability. Using Levy flights depending on their quality, the new nests (m = 1,2,..P)positions are determined as:

$$X_{m}^{i + 1} = X_{m}^{i} + \xi .G.(X_{m}^{i} - X_{{{\text{best}}}}^{i} ).t$$

(21)

where the superscript i (= 1,2,..N) denotes the generation (cycle) number, G denotes the step size, while $\xi$(> 0)is a step size scaling factor; t is a random number from the standard normal distribution and $X_{{{\text{best}}}}^{i}$ is the location of the best nest. The value of G can be evaluated from random walk using Levy flights and Mantegna’s algorithm according to:

$$G = \frac{c}{{\left| d \right|^{1/\beta } }}$$

(22)

where c and d are obtained from normal distribution as follows:

$$c \approx M(0,\gamma _{c}^{2} )\;and\;d \approx M(0,\gamma _{d}^{2} )$$

(23)

Also,

$$\gamma_{c} = \left| {\frac{{\Gamma \left( {1 + \beta } \right) \times \sin \left( {\pi \beta /2} \right)}}{{\Gamma \left( {\frac{1 + \beta }{2}} \right) \times \beta \times 2^{{\left[ {\frac{\beta - 1}{2}} \right]}} }}} \right|,\quad \gamma_{d} = 1,$$

(24)

Here, the Levy parameter β is in the range 1 to 2 and considered as 1.5 in the present work. Also, Γ is the standard Gamma function. If the value of scale parameter $\xi$ is kept constant, it is standard CS, while in improved CS method, the value of $\xi$ is selected as a function of iteration count i and maximum generations N as:

$$\xi \cdot {\text{t}} = \frac{1}{{i^{0.25} }}\exp \left[ {\frac{i}{N}\left( {\ln (\xi_{\min } ) - \ln (\xi_{\max } )} \right)} \right]$$

(25)

The values of $\xi_{\min }$ and $\xi_{\max }$ are, respectively, considered as 0.1 and 1.

4 Results and discussion

Initially, the dynamic model is validated with an experimental work conducted on a real-time turbocharger rotor system (supplied by EMTEX Engineering Pvt. Ltd. Delhi). In the test-rig, the turbine end of the rotor is coupled to an AC synchronous motor (0.25 hp ~ 0.186 kW) with a variable frequency drive and the outer casing of the rotor system is held fixed. The material for the turbine and compressor are, respectively, nickel–chromium–cobalt alloy and aluminium alloy, while the shaft is made of alloy steel. The geometric and material data considered are depicted in Table 1.

Table 1 Geometric parameters of turbocharger rotor

Figure 4 shows the experimental set-up, where the input motor with speed controller, the accelerometer mounting locations and recording oscilloscope arrangement are clearly illustrated.

Fig. 4

Experimental set-up for forced vibration test

Two accelerometers (PG 109 Mo, 1–10 kHz) with charge amplifiers are mounted near each bearing surface in lateral direction to measure the vibration responses. The signals are recorded in a digital storage oscilloscope (4-channel, Tektronix, model- DPO4034: 350 MHz bandwidth) at a sampling rate of 1 kHz. The experiment is performed at a rated rotor speed of 2500 rpm. The time-domain response signals are recorded at bearings and their fast Fourier transform (FFT) signals are calculated to identify the frequency content of the signal.

The solution is obtained by solving the resultant system of nonlinear equations with unbalance and bearing forces using an explicit Runge–Kutta (predictor–corrector) method with all zero initial conditions. Figure 5 shows the frequency spectra obtained from simulations and through the experimental response measured at the left bearing node.

Fig. 5

Dynamic response at left bearing node a FE Model b experimental

It is observed that the first two dominant frequencies in experimental work (29.9 Hz and 67 Hz) are matching with those obtained from the FE model (31.25 Hz and 67.38 Hz). The effect of radial external gas excitations on the rotor dynamic response at a rotor speed of 15,000 rpm is shown in Fig. 6.

Fig. 6

Frequency response at left bearing (15,000 rpm) a without radial gas forces b with radial gas forces

The amplitudes have increased rapidly with increase in speed and a sub-critical frequency at 72 Hz is noticed in comparison with the situation under no external radial load acting at the turbine.

4.1 Axial emission excitation force effects

The exhaust gas excitation in the axial direction is treated as periodic blade passing forces at the turbine. Here, the magnitude of force, its frequency Ω, phase angle ϕ and number of blades n_b can affect the dynamics. The unbalance responses of the system in dB scale at four different speed ratio (ω/Ω) values are shown in Fig. 7.

Fig. 7

Unbalance responses at right bearing node a ω/Ω = 0.1 b ω/Ω = 0.2, c ω/Ω = 1, d ω/Ω = 2

Here, the phase angle (ϕ) is taken as zero and room temperature conditions are considered. It is seen that there are three dominant peaks in all cases. At lower values of the frequency ratio (ω/Ω), more the sub-synchronous peaks are noticed. As the ratio increases, the critical frequency is decreasing and the amplitude is increasing. The influence of the amplitude (F₀) on the unbalance response of the system is studied. The response at the right bearing for different force amplitudes at a speed of 15,000 rpm is shown in Fig. 8.

Fig. 8

Unbalance responses at right bearing node a F₀ = 1 N b F₀ = 10 N

As the force amplitude increases, the response magnitudes also rise and the resonant frequencies remain the same in all the cases.

The influence of the phase angle ϕ on the response of the system is studied at a rotor speed of 15,000 rpm. Figure 9 shows the time response of two different values of the phase angle. It is observed that the system is periodic in nature at the two different values of the phase angle.

Fig. 9

Time histories at the right bearing nodea ϕ = 0^° b ϕ = 180⁰

The corresponding frequency responses at the two bearings at two different phase angles are shown in Fig. 10.

Fig. 10

Frequency response at bearings a left bearing b right bearing

The dominant peak amplitudes are comparatively more with phase angle ϕ = 180⁰_. Furthermore, the influence of the number of turbine blades on the dynamic response of the system is shown in Fig. 11. As the number of blades increases from 5 to 11, there is a uniform decrease in all the critical frequencies.

Fig. 11

Response at right bearing node a n = 5 b n = 7 c n = 9 d n = 11

4.2 Oil film clearances and viscosities

The influence of the bearing clearances on the response of the system is studied at a rotor speed of 15,000 rpm as shown in Fig. 12. Here, the outer oil film clearance (C₂ = 74 μm) is kept constant.

Fig. 12

Response at right bearing node a C₁ = 34 μm b C₁ = 54 μm c C₁ = 64 μm

It is observed that as the inner film clearance increases from 34 μm to 64 μm, the first two critical frequencies have reduced, while the third frequencies increased slightly. Further, the influence of the outer bearing clearance C₂ on the system response is shown at constant inner film radial clearance (C₁ = 34 μm) as depicted in Fig. 13.

Fig. 13

Response at right bearing node:a C₂ = 74 μm b C₂ = 94 μm c C₂ = 114 μm

It is observed a limited effect of the outer clearance on the critical frequencies.

The effect of lubricant viscosity on the dynamic response of the system is also considerable. In practice, the outer film lubricant viscosity effect is low on the response of the system. Figure 14 shows the frequency spectra at the right bearing node for three different values of inner film viscosity. In all cases, the outer film viscosity is maintained as 4.9 × 10^–3 Pa-s.

Fig. 14

Frequency spectra a μ₁ = 4.9 × 10^–3 Pa-s, b μ₁ = 6.9 × 10^–3 Pa-s c μ₁ = 8.9 × 10^–3 Pa-s

It is seen that as the inner film viscosity increases the first two critical frequencies only, while their amplitudes have reduced. The influence of the inner film lubricant viscosity on the response of the system is therefore considerable.

4.3 Bearing parameter estimation

With different parametric studies, it is observed that the oil film viscosity, bearing inner and outer clearances as well as the axial blade-passing force parameters including blade passing frequency ratio and the number of blades on the turbine have a significant effect on the overall dynamic response. These five input variables are considered in three levels each and the critical frequency and amplitude data are recorded in all 27 design of experiments. Table 2 shows the measured data from the simulations.

Table 2 The simulated input–output data

To generalize the floating ring bearing response analysis, an identification scheme based on the CPNN model is implemented. A training data consisting of blade passing frequency ratio, the number of turbine blades, bearing inner and outer clearances and inner oil film viscosity as inputs and the corresponding first critical frequency (f) and amplitudes (X) as the outputs. The set of connection weights between each layer are obtained after complete training, which is implemented with an in-house Matlab program using normalized input–output data. Learning rates of α = 0.4 and β = 0.01 are employed. After few trails, an optimum number of four hidden layer neurons are considered. Figure 15 shows the convergence trend as mean-square error versus number training cycles.

Fig. 15

CPNN error convergence

Table 3 illustrates the test results with the trained model. It is observed that the outputs are in good agreement with actual values.

Table 3 Results of identification

4.4 Optimization

Figure 16 shows the schematic of the present approach for finding the function minimum. For every population with five input variables, two function values are evaluated by CPNN model. These are used in improved CS method for evaluating the updated values of the next generation.

Fig. 16

Optimization schematic

The multi-objective optimization formulation can be written as a single objective f_eff with weighing factors w₁ and w₂ as:

$${\text{Maximize}}\;f_{{{\text{eff}}}} \left( X \right) = w_{1}^{{}} f_{1} \left( X \right) - w_{2} f_{2} \left( X \right)$$

(26)

Subjected to

$$X \in \left[ {X_{i}^{\min } ,\,X_{i}^{\max } } \right]$$

(27)

X is a vector of design variables defined as:

$$X \in \left[ {\frac{\omega }{\Omega }\begin{array}{*{20}c} {} & {\mu_{i} \begin{array}{*{20}c} {} & {C_{2} \begin{array}{*{20}c} {} & {C_{1} } & n \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]$$

(28)

The weighing factors taking care of uniformity in units. In the present case, these are considered as $w_{1} = \frac{1}{{f_{\max } }}$,$w_{2} = \frac{1}{{X_{\max } }}$ The lower and upper bounds of the variables are taken as $0.1 \le \frac{\omega }{\Omega } \le 2$, $5 \le n \le 11$, $30 \mu m \le C_{2} \le 74 \mu m$, $10 \mu m \le C_{1} \le 34 \mu m$ and $6.4 \times 10^{{ - 3}} {Pa} - {\text{s}} \le \mu _{i} \le 30.58 \times 10^{{ - 3}} {Pa} - {\text{s}}$.

Figure 17 shows the convergence of objective function values as a function of the number of generations in improved CS optimization. The swarm size is taken as 30.

Fig. 17

Convergence of effective objective function

The optimized parameters obtained are ω/Ω = 0.2, μ_i = 30.5 mPa-s, C₂ = 52.3 μm, C₁ = 34.7 μm and n = 9. Figure 18 shows the frequency response obtained with optimum parameters with all other previous conditions. An output response corresponding to one of the starting parameter set (ω/Ω = 0.1, μ_I = 6.4 mPa-s, C_o = 74 μm, C_i = 34 μm, n = 9) is also depicted for comparison.

Fig. 18

Frequency response at right bearing node with optimized parameters

It is observed that the first three peak frequencies of the optimized system as 51.88 Hz, 149.5 Hz, 252 Hz and the corresponding amplitudes to be  − 133.5 dB,  − 149.6 dB,  − 151 dB, respectively. It is also identified that with optimized parameters, the sub-synchronous peaks have reduced. The optimization program converges within 20 generations and the average time taken by the entire process is noticed as 140 s on X86 based PC with 3 GHz dual-core processor. The performance of the surrogate model is measured in terms of time taken and optimized data obtained with the use of regular FE model based function evaluations. It is further found that interestingly the optimization with regular FE model also resulted in the same set of optimum solution, but the average time taken is relatively more (240 s).

5 Conclusions

Dynamic analysis of turbocharger rotor under combined periodic and ideal nonlinear exhaust gas emission forces has been presented in this work. The finite element model of the system was implemented with consideration of oil film and floating ring lift forces at the bearings. On validation of the finite element model with an experimental procedure, the model was employed for the dynamic response studies under the exhaust gas emission forces in the radial and axial directions acting at the turbine node. Effects of different parameters on the response spectra were studied and the simulation findings were generalized by counter propagation neural network model. An optimization approach based on modified Cuckoo search scheme was adopted to predict the system parameters using the trained neural network model. Following are identified as some important observations.

• Drastic change in critical speeds is noticed with increase in rotor speed and the exhaust emission radial loads induce some sub-critical regions.

• An increase in the blade passing excitation frequency ratio resulted in the reduction in critical frequencies and increases the amplitudes. The effect of force amplitude is relatively small on the response changes. Likewise, the phase angle also has limited effect and with increase in the number of blades, the critical frequency values decrease.

• With an increase in inner film clearance, there is a drop in first two critical frequencies, while the third frequency has increased. The outer film clearance has relatively less effect on the critical frequencies.

• The temperature-dependent inner film oil viscosity increases the first two critical frequencies, while third frequency does not change.

• The counter propagation neural network with four hidden layer neurons perfectly generalizes the input–output relationship in present case.

The improved Cuckoo search optimization in-conjunction with the CPNN function approximation methodology was found to be relatively faster than the finite element model-based function evaluation approach without losing the accuracy.

Appendix

The component forces on the journal and bearing are expressed as:

$$\left\{ \begin{gathered} f_{ix} \hfill \\ f_{iy} \hfill \\ \end{gathered} \right\} = - \frac{{\sqrt {(y_{i} + 2\dot{x}_{i} ) + (x_{i} - 2\dot{y}_{i} )} }}{{(1 - x_{i} \cos \phi - y_{i} \sin \phi )}}\left\{ {\begin{array}{*{20}c} {3x_{i} V_{i} - \sin \alpha_{i} G_{i} - 2\cos \alpha_{i} F_{i} } \\ {3y_{i} V_{i} - \cos \alpha_{i} G_{i} - 2\sin \alpha_{i} F_{i} } \\ \end{array} } \right\}$$

(29)

where V, G, F, α are the lubricant force variants.

$$V_{i} = \frac{{2 + (y_{i} \cos \alpha_{i} - x_{i} \sin \alpha_{i} )G_{i} }}{{(1 - x_{i}^{2} - y_{i}^{2} )}}$$

(30)

$$G_{i} = \frac{\pi }{{\sqrt {1 - x_{i}^{2} - y_{i}^{2} } }} - \frac{2}{{\sqrt {1 - x_{i}^{2} - y_{i}^{2} } }}\tan^{ - 1} \left( {\frac{{y_{i} \cos \alpha_{i} - x_{i} \sin \alpha_{i} }}{{\sqrt {1 - x_{i}^{2} - y_{i}^{2} } }}} \right)$$

(31)

$$F_{i} = \frac{{(x_{i} \cos \alpha_{i} + y_{i} \sin \alpha_{i} )}}{{(1 - x_{i}^{2} - y_{i}^{2} )}}$$

(32)

$$\alpha_{i} = \tan^{ - 1} \left( {\frac{{y_{i} + 2\dot{x}_{i} }}{{x_{i} - \dot{y}_{i} }}} \right) - \frac{\pi }{2}{\text{sign}}\left( {\frac{{y_{i} + 2\dot{x}_{i} }}{{x_{i} - y_{i} }}} \right) - \frac{\pi }{2}{\text{sign}}(y_{i} + 2\dot{x}_{i} )$$

(33)

$$ \begin{aligned}\left\{ {\begin{array}{*{20}c} {f_{ox} } \\ {f_{oy} } \\ \end{array} } \right\} &= - \frac{{\sqrt {(y_{R} + 2\dot{x}_{R} ) + (x_{R} - 2\dot{y}_{R} )} }}{{(1 - x_{R} \cos \phi - y_{R} \sin \phi )}}\\ &\quad\left\{ {\begin{array}{*{20}c} {3x_{R} V_{0} - \sin \alpha_{0} G_{0} - 2\cos \alpha_{0} F_{0} } \\ {3y_{R} V_{0} - \cos \alpha_{0} G_{0} - 2\sin \alpha_{0} F_{0} } \\ \end{array} } \right\}\end{aligned} $$

(34)

$$V_{o} = \frac{{2 + (y_{R} \cos \alpha_{o} - x_{R} \sin \alpha_{o} )G_{o} }}{{(1 - x_{R}^{2} - y_{R}^{2} )}}$$

(35)

$$G_{o} = \frac{\pi }{{\sqrt {1 - x_{R}^{2} - y_{R}^{2} } }} - \frac{2}{{\sqrt {1 - x_{R}^{2} - y_{R}^{2} } }}\tan^{ - 1} \left( {\frac{{y_{R} \cos \alpha_{o} - x_{R} \sin \alpha_{o} }}{{\sqrt {1 - x_{R}^{2} - y_{R}^{2} } }}} \right)$$

(36)

$$F_{o} = \frac{{(x_{R} \cos \alpha_{o} + y_{R} \sin \alpha_{o} )}}{{(1 - x_{R}^{2} - y_{R}^{2} )}}$$

(37)

$$\alpha_{o} = \tan^{ - 1} \left( {\frac{{y_{R} + 2\dot{x}_{R} }}{{x_{R} - \dot{y}_{R} }}} \right) - \frac{\pi }{2}{\text{sign}}\left( {\frac{{y_{R} + 2\dot{x}_{R} }}{{x_{R} - y_{R} }}} \right) - \frac{\pi }{2}{\text{sign}}(y_{R} + 2\dot{x}_{R} )$$

(38)