Numerical simulation of the head-on collision of two drops in a vertical channel

Abstract

The head-on collision between two oil drops in a vertical channel is investigated numerically by using a volume-of-fluid method. Three-dimensional simulations are examined for laminar, fully developed, unsteady, and incompressible fluid flow. The effects of the Weber and Reynolds numbers and the density ratio on the collision dynamics are investigated before and after the drop coalescence. The results show that the deformation of drops increases and gap thickness decreases as the Weber and Reynolds numbers increase. The drops collide with each other faster for higher density ratios. It is found that the drops elongation has a sinusoidal behavior after collision due to the tendency of the drops to gain a spherical shape. Also, the results demonstrate that the elongation increases with increasing of the Weber and Reynolds numbers and decreasing of the density ratio.

1 Introduction

Interaction between two drops or bubbles in viscous flows is technologically important in a wide variety of practical processes. The flow of water and oil through pipelines, flow of slurries, polymeric flows, the motion of red blood cells, and fuel sprays are some such examples. Some industrial applications and processes include pharmaceutical manufacturing, geophysical systems, food and chemical processing, production of lubricant oils, paints, pharmaceutical, and cosmetic products. Numerical investigations on the collisional behavior of two drops have been performed in recent years. Initially, most experiments were accomplished for the case of the interaction between water drops. Recently, the collision of hydrocarbon drops has been performed. According to these studies, it is concluded that the size of drops, their properties, and environmental conditions affect on pairwise interaction of drops [1,2,3,4,5,6,7,8]. Bayareh and Mortazavi [2] studied the effects of geometry and viscosity ratio on the collision of two equal-sized drops at finite Reynolds numbers. They found that the angular velocity of drops decreases with the viscosity ratio during their collision. They also revealed that two drops reach a new steady state after separation, and the cross-flow separation decreases with the capillary number [3]. Jiang and James [4] studied the coalescence of two drops in a hyperbolic flow under the van der Waals forces. They developed two approaches to consider these forces and their effects on merging of drops. Goodarzi et al. [8] demonstrated that the velocity of two off-center drops before the coalescence is about twice of that after the coalescence. It should be mentioned that the drops are located in a laminar horizontal flow. Fortes et al. [9] investigated the fluid dynamics of fluidization of spherical particles in water experimentally. They observed the drafting, kissing, and tumbling phenomena between spheres and showed that the spheres alignment is unstable. The kissing spherical particles move toward relatively stable lines of particles in horizontal arrays. Inamuro et al. [10] simulated the collision of two drops with high density ratio by using a lattice Boltzmann method. They revealed that it is possible to observe the collision between two drops, coalescence, and separation in comparison with theoretical results. Dai and Schmidt [11] studied the effects of viscosity ratio on drop deformation using a finite volume method for a head‐on droplet collision. They showed that the deformation increases with increasing the Reynolds number, especially at low Reynolds numbers. Inamuro et al. [12] studied binary droplet collision with large density ratios by using a lattice Boltzmann method for various Weber numbers and impact parameters. They simulated the interaction and coalescence between two drops and observed two different types of separation between them: reflexive and stretching separations. Sun et al. [13] used an innovative technique to simulate the interaction between two central and non-central equal-sized droplets and found that low mixing effectiveness is obtained for higher collision velocity. Yoon et al. [14] studied experimentally the effect of viscosity ratio on the flow coalescence of two equal-sized drops.

Mortazavi and Tryggvason [15] studied the motion of a deformable drop in Poiseuille flow for finite Reynolds numbers. They showed that the migration of the drop depends on the viscosity ratio for Re < 1. Bayareh and Mortazavi [16, 17] investigated numerically the migration of a drop and the interaction of two drops in simple shear flow using a finite-difference/front-tracking method. They demonstrated that the interaction between drops raises the cross-flow separation of their centers. The drops deformation is minimum when they are separated from each other and maximum when the drops are pressed against each other. Roisman et al. [18] investigated experimentally and theoretically head-on collision of two immiscible liquid drops and compared the experimental results corresponding to the deformation and stability of drops with the theoretical ones. Ray et al. [19] simulated multiple liquid drop impacts on air–water free surface by using the coupled level-set and volume-of-fluid method. They showed that the drop coalescence depends on the time gap between two falling drops. Mortazavi and Tafreshi [20] investigated the behavior of suspension of drops on an inclined surface. They revealed that the suspended drops tend to stay away from the surface at small density ratios. In recent years, Amberg et al. [21] studied the deformation and degradation of spherical droplets in two different regimes. Their studies were carried out in a wide range of Reynolds numbers. They found that there are different drop shapes at different Weber numbers.

In the present work, collision of two head-on drops in a vertical channel is simulated for a laminar flow regime by using a volume-of-fluid (VOF) method. The results are presented for different densities and viscosity ratios and various Weber numbers. The effects of these parameters on the elongation, gap thickness, and deformation of drops are studied. Also, it is discussed that the Reynolds number and the relative size how to affect on stable drop configuration. The paper is organized as follows: In Sect. 2, the mathematical model is presented. Numerical method is presented in Sect. 3. In Sect. 4, the numerical results are compared with each other for different effective parameters. Finally in Sect. 5, the concluding remarks are presented.

2 Mathematical model

The continuity and Navier–Stokes equations are used to simulate the unsteady motion of liquid drops in a Newtonian fluid. The momentum equation includes the surface tension as a total body force concentrated at the interface. These equations are as follows [8]:

$$\frac{\partial \rho }{\partial t} + \nabla \cdot (\rho \varvec{u}) = 0$$

(1)

$$\frac{{\partial (\rho \varvec{u})}}{\partial t} + \nabla \cdot (\rho \varvec{uu} )= - \nabla p + \nabla \cdot \left[ {\mu \left( {\nabla \varvec{u} + \nabla \varvec{u}^{\text{T}} } \right)} \right] + \rho \varvec{g} + \varvec{F}_{\text{S}}$$

(2)

where u is the velocity filed, $\rho$ is the density and $\mu$ is dynamic viscosity. g is the acceleration due to the gravity, and $\varvec{F}_{\text{S}}$ indicates the surface tension force as follows:

$$\varvec{F}_{\text{S}} = \mathop \int \limits_{\Delta S}^{{}} \delta \sigma \kappa \varvec{n} \left( {\varvec{x} - \varvec{x^{\prime}}} \right){\text{d}}S$$

(3)

where $\kappa$ and $\varvec{n}$ are the curvature and normal unit vector, respectively. $\delta$ is Dirac delta function and $\varvec{x}$ and $\varvec{x^{\prime}}$ represent the position in Eulerian and Lagrangian coordinates.

The differential equations are solved using a control volume-based finite difference scheme. In this method, the computational domain is divided into several control volumes and each node is surrounded by a control volume. Also, the Semi-Implicit Method for Pressure-Linked Equations (SIMPLE) is used for pressure–velocity coupling.

The effective dimensionless parameters are the Weber number, We = ρ_f W ²_rel D₀/μ_f, the particle Reynolds number, Re_p = ρ_f W_rel D ²₀ /μ_f, the bulk Reynolds number, Re_b = ρ_fW_rel H/μ_f, the ratio of the viscosity, λ = μ_d/μ_f, and the density ratio, η = ρ_d/ρ_f. D₀ is the diameter of the undeformed drops. The viscosity and density of the drop liquid fluid are showed by μ_d and ρ_d, respectively, and the ambient fluid has viscosity μ_f and density ρ_f. The Reynolds and Weber numbers are defined based on W_rel and the channel height, H. Dimensionless time is defined as t* = t W_rel/H.

3 Numerical method

The volume-of-fluid (VOF) method is used to simulate the interaction between two drops in a vertical channel. This computational technique is efficient to capture the dynamics of the interaction of drops. It is a surface-capturing method that is useful to investigate the dynamic behavior of the interface between two immiscible fluids. A single set of momentum equations is divided by the fluids, and the volume fraction of each of the fluids in each computational cell is traced throughout the domain. The method exerts phase averaging to determine the amount of dispersed and continuous phase in each cell. The volume fraction, α, is determined as follows: when the cell is totally occupied by the dispersed phase, α = 0, when the cell is completely occupied by the continuous phase, α = 1, and when the cell includes the interface between the two phases, 0 < α < 1 (Fig. 1). In other words, the volume fraction is one inside the drops and zero inside the continuous phase. The interface is represented by other values of the volume fraction. The viscosity, μ, and the density, ρ, for the two phases are computed using a linear relation:

$$\rho = \alpha \rho_{1} + (1 - \alpha )\rho_{2}$$

(4)

$$\mu = \alpha \mu_{1} + (1 - \alpha )\mu_{2}$$

(5)

where 1 and 2 indicate the drop and the continuous phases, respectively. Since the fluid in the drops and in the ambient liquid is assumed as a whole, the governing equations are used for whole computational domain. It should be mentioned that the material derivative of the function α is zero; due to that, α is a constant property of the fluids:

$$\frac{D\alpha }{Dt} = \frac{\partial \alpha }{\partial t} + \left( {\varvec{u} \cdot \nabla } \right)\alpha = 0$$

(6)

Fig. 1

Distribution of function α

In other words, the volume fraction α moves with the fluids. The unit vector perpendicular to the interface is computed based on the fractional volume:

$$\varvec{n} = \frac{\nabla \alpha }{{\left\| {\nabla \alpha } \right\|}}$$

(7)

A Piecewise Linear Interface Calculation (PLIC) method that is a combination of dispersed phase volume fraction and the unit normal vector is employed to reconstruct the interface between two fluids.

4 Results and discussion

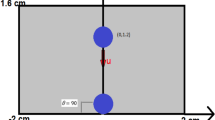
In this section, the head-on collision between two drops is considered, which their centerline is parallel to the parabolic flow in a vertical channel (Fig. 2). The center-to-center distance is initially equal to the diameter of the undeformed drops, $D_{0}$ for pairwise interaction of two identical drops. The computational domain has the dimensions of $h_{x} \times h_{y} \times h_{z}$. The domain includes two no-slip walls in the x-, and y-directions. Periodic boundary condition is applied in the z-direction. The ambient fluid has initially the parabolic velocity distribution. The physical properties of the drops and the ambient fluid are as follows:

$$\rho_{\text{d}} = 890\;{\text{kg/m}}^{3} ,\quad \rho_{\text{f}} = 1000\,{\text{kg/m}}^{3} ,\quad \mu_{\text{d}} = 0.005\,{\text{kg/m}}\,{\text{s}},\quad \mu_{\text{f}} = 0.001\,{\text{kg/m}}\,{\text{s}},\quad D_{0} = 0.004\,{\text{m}}$$

where d and f refer to the drop and ambient fluid, respectively.

Fig. 2

Computational domain for simulation of head-on collision of drops in a vertical channel

The drops are initially getting close to each other since they have a relative velocity W_rel (see Fig. 2). There are two regimes when the drops collide: coalescence or bouncing, depends on the Weber number. They bounce with a super-elasticity at low Weber numbers and coalesce at high ones. In the present simulations, the values of surface tension coefficient are relatively high leads to low Weber numbers. Hence, the drops collide and coalesce to create a larger drop.

4.1 Validation

To verify the present results, average velocity of drops is plotted in Fig. 3 as a function of non-dimensional time for a falling drop compared to the results of Mousavi et al. [22]. According to this reference, the channel width, w, is twice the diameter of the drop, the drop viscosity is 0.006 ${\text{kg/m}}\,{\text{s}}$, the ambient fluid viscosity is 0.006 ${\text{kg/m}}\,{\text{s}}$, the drop density is 1000 ${\text{kg/m}}^{3}$, and the ambient fluid density is 800 ${\text{kg/m}}^{3}$. Fluid and drop Ohnesorge numbers and Eotvos number are Oh_f = 0.053, Oh_d = 0.105 and Eo = 5, respectively. These dimensionless parameters are defined as follows:

$$Eo = \frac{{g\left( {\rho_{\text{d}} - \rho_{\text{f}} } \right)D_{0}^{2} }}{\sigma }\quad Oh = \frac{\mu }{{\left( {\rho D_{0} \sigma } \right)^{1/2} }}$$

(8)

Fig. 3

Average velocity of a falling drop versus dimensionless time: Oh_f = 0.053, Oh_d = 0.105 and Eo = 5

It is shown that the velocity of falling drop increases, reaches a maximum, and then drops rapidly. The drop gains its terminal velocity about t* ~ 3. Figure 3 indicates that the present simulation is in very good agreement with the one of Mousavi et al. [22].

4.2 Grid resolution tests

The grid study is also performed for a drop descending in a vertical channel by considering four grid resolutions of 40 × 40 × 80, 60 × 60 × 100, 80 × 80 × 120 and 100 × 100 × 140 grid points. Figure 4 shows the drop deformation versus dimensionless time for different grid resolutions at Weber and Reynolds numbers, $We = 11\;{\text{and}}\;Re = 50$, respectively. The density ratio for all cases is $\eta = 0.89$. The results show that 80 × 80 × 120 and 100 × 100 × 140 grid resolutions result in similar amount of drop deformation, so the coarser one, 80 × 80 × 120 grid points, is employed for further simulations.

Fig. 4

Drop deformation as a function of dimensionless time for different grid resolutions for $\eta = 0.89$, $We = 11\;{\text{and}}\;Re = 50$

4.3 Head-on collision of drops

In this section, the time-dependent central binary collision of drops is simulated. The gap thickness between two drops is defined as the shortest distance between two drop surfaces (Fig. 5):

$$dz^{*} = \frac{dz}{{D_{0} }}$$

(9)

where the drop initial diameter is $D_{0}$. In the present work, the Taylor deformation [12] is used to calculate the deformability of the drops and is defined as follows (Fig. 6):

$$d = \frac{l - b}{l + b}$$

(10)

where l and b are the major and minor semi-axes of the drop (defined by the largest and smallest distances of the surface from the center). Also, the drop elongation is defined according to Nikolopoulos et al. [23] for the cases that the drops coalesce and form a single larger drop (Fig. 7):

$$e^{*} = \frac{{L_{1} }}{{L_{0} }}$$

(11)

Fig. 5

Definition of the gap thickness between two drops in x–z plane

Fig. 6

The largest and smallest diameter of an oval drop in x–z plane

Fig. 7

The elongation of drops in x–z plane

4.3.1 Before the coalescence

Initially, two drops move toward each other with an initial velocity. Drop deformation is caused by two forces: surface tension that tends to maintain the spherical shape of the drops and shear force that causes the drops to deform. Also, each drop operates as a barrier against the flow. Figure 8 sows the time evolution of binary collision of drops for $\frac{{D_{1} }}{{D_{2} }} = 1$, $\eta = 0.89$, We = 11, and $Re = 50$. According to this figure, as the drops approach each other, fluid between them is squeezed. Hence, a fluid jet is generated in the gap jumping out toward the surrounding fluid results in flattening of the drop surfaces. When two drops approach each other, the ambient fluid is trapped between them and needs a time to spread out the gap. For this reason, the phenomenon of delayed coalescence occurs. The delayed coalescence takes place when the surface tension is relatively high (low Weber numbers). Weber number is a dimensionless parameter that is proper to evaluate drop surface tension effect. It is the ratio of deforming inertial forces to stabilizing cohesive forces for liquids flowing through a fluid medium. Here, it is expected that the required time for the coalescence is negligible because of high values of considered Weber numbers. The collision regimes include drop bouncing, stable and unstable drop coalescence, and drop separation depends on the Weber number magnitude [18]. In the present simulations, four different values of Weber number (We = 10, 14, 18, and 22) are considered to study the dynamics of the interaction between the drops. The Reynolds number, the viscosity, and the density ratios are Re = 50, λ = 1, and η = 0.89, respectively. Figure 9 illustrates the drop deformation of top drop as a function of dimensionless time. The drops have the same diameter initially. The figure shows that the deformation increases with the time for each Weber number due to larger effect of shear force in comparison with the surface tension. In other words, the Reynolds number is relatively high and the inertial force causes the drops to deform. Due to the small amount of surface tension, the spherical shape of the drops is not maintained. The less surface tension, the less elasticity of the droplets, and therefore, they exhibit larger deformation. On the other hand, the drop deformation enhances as the Weber number increases (the surface tension decreases). For example, the drop deformation is d = 0.128, 0.132, 0.144, and 0.17 for We = 10, 14, 18, and 22, respectively. It is worth noting that the rate of the deformation increases with the Weber number. This is confirmed by the variation of gap thickness for different Weber numbers (Fig. 10). This figure shows that dimensionless gap thickness $dz^{*}$ decreases with the dimensionless time for all Weber numbers. The approach velocity of drops is calculated for the time period of 0.2–0.3 s for different Weber numbers. The velocity is 1.32, 1.391, 1.447, and 1.673 m/s for We = 10, 14, 18, and 22, respectively. In other words, the drop moves faster by increasing the Weber number, and therefore, the coalescence time decreases. Figure 11 shows some snapshots related to the interaction between the drops at different non-dimensional times for different Weber numbers. It is observed that the deformation is completely different for top and bottom drops. The bottom drop moves in the flow direction with its relative velocity. In other words, the ascending velocity of the bottom drop is higher than the descending velocity of top drop. This effect leads to that the top drop becomes prolate and the bottom one remains almost spherical. It should be pointed out that as the Weber number increases the shape of top, drop becomes more prolate. It is worth nothing to evaluate the collision mechanism by taking into account the force due to the gravity. Hence, different Eotvos numbers are considered to simulate the motion of drops before collision. Eotvos number is the ratio of the gravitational force to the surface tension one (Eq. 8). Figure 12 illustrates the gap thickness of drops for different Eotvos numbers, $\eta = 0.89$ and $Re = 50$. The figure shows that the gap thickness decreases with the Eotvos number; however, the difference between the gap thickness values for various Eotvos numbers is larger than that for different Weber numbers. Since similar surface tensions are used to obtain the Eotvos and Weber numbers, it can be concluded that the gravitational force is dominant compared to the inertial force for the studied range of Reynolds numbers.

Fig. 8

Velocity vectors at different dimensionless times for $\frac{{D_{1} }}{{D_{2} }} = 1$, $\eta = 0.89$, $We$ = 11, and $Re = 50$

Fig. 9

Deformation of drops versus non-dimensional time for different Weber numbers, $\frac{{D_{1} }}{{D_{2} }} = 1$, $\eta = 0.89$, and $Re = 50$

Fig. 10

Gap thickness versus non-dimensional time for different Weber numbers, $\frac{{D_{1} }}{{D_{2} }} = 1$, $\eta = 0.89$, and $Re = 50$

Fig. 11

Snapshots of the interaction between the drops at different non-dimensional time for different Weber numbers, $\frac{{D_{1} }}{{D_{2} }} = 1$, $\eta = 0.89$, and $Re = 50$

Fig. 12

Gap thickness of drops versus non-dimensional time for different Eotvos numbers, $Re = 50,\; \frac{{D_{1} }}{{D_{2} }} = 1$, $\eta = 0.89$, and $We = 11$

Now, the effect of Reynolds number on the interaction between drops is considered. The Reynolds number is the ratio of inertial and viscous forces. In the present study, the Reynolds number is defined based on the average velocity of drops. At constant Weber number ($We = 11)$ and the density ratio ($\eta = 0.89)$, the effects of four different values of Reynolds number on pairwise interaction of drops are studied. The deformation of drops as a function of dimensionless time is plotted in Fig. 13 at different Reynolds numbers. It is demonstrated that the deformation decreases as the Reynolds number increases due to larger effect of inertial forces. It is also concluded that the gap thickness increases with the Reynolds number because of increasing the kinetic energy of drops (Fig. 14). The coalescence time decreases with the Reynolds number similar to the pervious case. Figure 15 shows some snapshots of the interaction between two drops at different Reynolds numbers. Even though the deformation of drops increases with the Reynolds number, however, the drop shapes are different from the previous case (different Weber numbers). It is observed that the bottom drop becomes almost oblate. As the Reynolds number enhances, the shape of top drop changes to hemi-spherical. This shape change is reported for the case of a sedimenting drop at the same range of Reynolds numbers [24]. It should be mentioned that the delayed coalescence decreases with the Reynolds number. This is due to that the required time for the ambient fluid to spread out the gap decreases at higher Reynolds numbers.

Fig. 13

Deformation of drops versus non-dimensional time for different Reynolds numbers with $\frac{{D_{1} }}{{D_{2} }} = 1$, $\eta = 0.89$, and $We = 11$

Fig. 14

Gap thickness of drops versus non-dimensional time for different Reynolds numbers, $\frac{{D_{1} }}{{D_{2} }} = 1$, $\eta = 0.89$, and $We = 11$

Fig. 15

Snapshots of the interaction between two drops at different non-dimensional times at different Reynolds numbers for $\frac{{D_{1} }}{{D_{2} }} = 1$, $\eta = 0.89$, and $We = 11$

Another parameter that impacts on the collision process is the density ratio. The density ratio is the ratio of the density of the drop fluid to the density of the suspending one. To evaluate the effect of the density ratio on drop coalescence, the interaction between ethanol drops is considered and compared to the case of oil ones. Figure 16 shows that the gap thickness increases with the density ratio. At constant Weber and Reynolds numbers, as the density ratio increases, the inertial force and the surface tension reduce. Therefore, the drops are more deformed. Hence, the drops move faster toward each other and the gap thickness increases. Figure 17 shows time evolution of the interaction between the drops for different density ratios.

Fig. 16

Gap thickness versus non-dimensional time for different density ratios at Re = 50 and $We = 11$

Fig. 17

Snapshots of the interaction between the drops at different non-dimensional times for different density ratios at $Re = 50\;{\text{and}}\;We = 11$

Since the drops deform before collision, the initial distance between them can be an effective parameters. Thus, an additional dimensionless number is used to evaluate the influence of the initial distance on the deformation and gap thickness of drops. This dimensionless number is the ratio of initial distance to the diameter $L/D_{o}$. In Fig. 18, the drop deformation is presented as a function of dimensionless time for different dimensionless initial distances between the drops. The figure reveals that the deformation decreases with the initial distance for a given time. In other words, the delayed coalescence decreases with the initial distance between the drops.

Fig. 18

Deformation of drops versus non-dimensional time for different values of initial distance between the drops,$Re = 50$, $\eta = 0.89$ and $We = 10$

4.3.2 After the coalescence

As mentioned in the previous section, two drops accelerate toward each other, approach, and collide. It should be pointed out that there are two possibilities for the binary collision of drops: bouncing and coalescence. The occurrence of former case is not realistic, but the latter one occurs for real drops. For the case of realistic collision, the film of ambient fluid is ruptured, results in the coalescence of drops. It was found that the constant force acting on drops is turned off when their center-to-center distance is equal to half a diameter of drops [25]. However, the drops have enough momentum to approach and collide. After collision, the kinetic energy is converted into surface tension energy. In the present simulations, the ambient fluid film is ruptured and two drops form a larger drop after collision. The larger drop continues to move downward to obtain its final shape.

The time in which the film is ruptured depends on the effective parameters. These parameters have a tremendous effect on physical behavior of drops after coalescence. Hence, initial drop diameter, initial impact velocity, the density and viscosity of two drops and ambient fluid, and also surface tension are effective parameters. Two drops obtain a stable equilibrium position after collision at relatively low Weber and Reynolds numbers. This is due to that the kinetic energy is less than the surface tension energy. The drop oscillates after collision to reach its equilibrium position. Oscillating motion is as a sinusoidal behavior, because the shear forces keep the spherical shape but surface tension deforms the drop. The oscillation magnitude decreases until eventually the drop attains a spherical shape.

Figure 19 shows drop elongation as a function of dimensionless time for different Weber numbers. It is found that the elongation increases with the Weber number due to a reduction in surface tension. Therefore, the inertial forces becomes more than the force of surface tension. Details of time evaluation of the mechanism of collision are presented in Fig. 20 for different Weber numbers. As the drops approach each other, they merge and continue to deform. Then, they form a dumbbell shape. There is a competition between the shear force and surface tension effect, so the dumbbell shape is converted to both oblate (flattened) and prolate (elongated) ellipsoids alternatively. As expected, the drop finally attains a spherical shape. It is found that the rate of conversion to spherical drop decreases with the Weber number.

Fig. 19

Elongation of drop versus non-dimensional time for different Weber numbers, $\frac{{D_{1} }}{{D_{2} }} = 1$, $\eta = 0.89$, and $Re = 50$

Fig. 20

Time evaluation of the formation of single drop for different Weber numbers, $\frac{{D_{1} }}{{D_{2} }} = 1$, $\eta = 0.89$, and $Re = 50$

Figure 21 demonstrates that the elongation decreases as the Reynolds number increases due to an increase in the inertia forces. Snapshots of the collision between two drops for different Reynolds numbers are presented in Fig. 21. The oscillation motion of the drop is obviously observable. The formation of merged drop occurs faster for larger Reynolds numbers. For example, it is observed that the conversion of dumbbell shape of merged drop to flattened ellipsoid takes place at smaller time for larger Reynolds numbers at dimensionless time, t* = 0.36. Larger elongation at lower Reynolds numbers (Fig. 22) confirms the previous conclusions.

Fig. 21

Elongation of drop versus non-dimensional time for different Reynolds numbers, $\frac{{D_{1} }}{{D_{2} }} = 1$, $\eta = 0.89$, and $We = 11$

Fig. 22

Time evaluation of the formation of single drop for different Reynolds numbers, $\frac{{D_{1} }}{{D_{2} }} = 1$, $\eta = 0.89$, and $We = 11$

Figure 23 shows the effect of the density ratio on the coalescence mechanism of drops. The elongation decreases with the Reynolds number because a reduction in the density ratio leads to a reduction in the surface tension at fixed Weber and Reynolds numbers. Details of time evaluation of the interaction are presented in Fig. 24 for two density ratios. It is revealed that the merged ethanol drop is more elongated and also more flattened during the coalescence process. Also, the maximal value of the elongation occurs at larger time for lighter drop. The results show that the surface tension is sufficiently enough to maintain the merged drop for two cases, so the stretching separation does not take place for the parameters of the present simulations.

Fig. 23

Elongation of drop versus non-dimensional time for different density ratios, Re = 50 and $We = 11$

Fig. 24

Time evaluation of the formation of single drop for different density ratios, Re = 50 and $We = 11$

5 Concluding remarks

In the present work, head-on collision of two drops inside a vertical channel was numerically studied by using a VOF method. The mechanism of the interaction between the drops was investigated for different governing non-dimensional parameters: Weber and Reynolds numbers and the density ratio. The results showed the following conclusions for the cases of before and after the coalescence:

Before the coalescence the drop deformation increases with the Weber and Reynolds numbers and decreases with the density ratio. It was concluded that the gap thickness increases and decreases with the Reynolds and Weber numbers, respectively. In addition, the results showed that the gap thickness increases with the density ratio. It was found that the variation of gap thickness of drops is higher for different Eotvos numbers than different Weber numbers due to that the Eotvos numbers include the gravitational force.

After the coalescence for the range of the Weber and Reynolds numbers, two drops collide with each other and obtain a stable equilibrium position. The drop stretching separation was not observed. The elongation curve has a sinusoidal behavior due to the tendency of the drop to achieve a spherical shape. The results demonstrated that the elongation increases with the Weber and Reynolds numbers and decreases with the density ratio.