Certain methods to solve bipolar fuzzy linear system of equations

Abstract

In this article, we present two different analytical methods based on embedding technique and bipolar fuzzy center to solve bipolar fuzzy linear system (BFLS) of equations. In the first method, to solve BFLS of equations, we replace BFLS of equations by a pair of positive$(*)$ and negative$(\bullet )$ two $n \times n$ crisp linear systems. We provide the necessary and sufficient conditions for the solution of BFLS of equations. In the second method, we use the graphical technique and apply bipolar fuzzy center to draw a graph at some specific end points to solve the BFLS of equations. Further, we develop a technique to solve the fully bipolar fuzzy linear system of equations. We present solutions of some numerical examples to show the effectiveness of the proposed techniques.

1 Introduction

The notion of fuzzy set was introduced by Zadeh (1965, (1975) to deal with uncertain information. Dubois and Prade (1978) discussed the basic arithmetic operations of fuzzy numbers. Zhang (1998, (1994) introduced the concept of bipolar fuzzy set in (1994) which is an extension of fuzzy set. A bipolar fuzzy set (BFS) is a powerful mathematical tool for expressing fuzziness and uncertainty. The simultaneous linear system of equations play an important role in different kinds of fields including mathematics, physics, statistics, networking and attribute decision-making. In many places, a system of fuzzy linear equation in bipolar form is used for linear optimization of system when system is represented in bipolar form. Firstly, the fuzzy linear system (FLS) of equations was examined by Friedman et al. (1998) and they used the embedding method to solve fuzzy system. They used the procedure in which $n \times n$ FLS of equations whose coefficient matrix is a crisp number matrix and right-side column vector is fuzzy number vector which is replaced by $2n \times 2n$ crisp linear systems. Abbasbandy and Alavi (2005) used another method to solve $n \times n$ FLS of equations whose coefficient matrix is a crisp number matrix and right-side column vector is fuzzy number vector. They used a procedure in which $n \times n$ FLS of equations is replaced by two $n \times n$ crisp linear systems. Allahviranloo (2019) proposed different methods to solve uncertain linear system of equations. Some numerical techniques, to solve FLS of equations are presented in Allahviranloo (2004, (2005a, (2005b) and Abbasbandy and Jafarian (2006). Recently new techniques are proposed by Akram et al. (2019a, (2019b, (2019c, (2019d) to solve BFLS of equations, fully bipolar fuzzy linear system FBFLS of equations and linear system of equations in m-polar fuzzy environment. Suparna and Chakraverty (2011) proposed a method to solve FLS and fully fuzzy linear system (FFLS) by using fuzzy interval.

In this article, we use two different techniques which are the extensions of Abbasbandy and Alavi (2005) method and fuzzy center method to solve $n \times n$ BFLS of equations whose coefficient matrix is a crisp matrix and right-hand side column vector is a parametric form of bipolar fuzzy number (BFN). In the first technique, to solve BFLS we replace $n \times n$ BFLS of equations by pair of positive$(*)$ and negative$(\bullet )$ of two $n \times n$ crisp linear systems. In the second technique, we apply the bipolar fuzzy center method to solve the preceding BFLS of equations by drawing a graph at some specific end points of the system. These two techniques are efficient for both asymmetric and symmetric BFLSs. Some numerical examples are discussed to describe the efficiency of the techniques. Further, we use the fuzzy interval method in bipolar fuzzy environment to solve the FBFL system of equations. In FBFL system, the coefficient matrix, unknown parameters and vector on right side are bipolar triangular fuzzy numbers (BTFNs). We utilize the current flow circuit which is represented by FBFL system of equations and use interval technique to find unknown current in the circuit in terms of BTFN.

2 Preliminaries

In this section, we present some basic definitions like BFN, parametric form of symmetric BFN and symmetric BFLS of equations.

Definition 2.1

Akram and Arshad (2019) A bipolar fuzzy number (BFN)

$$\begin{aligned} \xi = \prec M , N \succ = \prec [m_{1},m_{2},m_{3},m_{4}],[n_{1},n_{2},n_{3},n_{4}]\succ \end{aligned}$$

is a bipolar fuzzy set of the mapping $\sigma : R \longrightarrow [0,1]\times [-1,0]$, with satisfaction degree $\sigma _{M}$ and dissatisfaction degree $\sigma _{N}$ such that:

$$\begin{aligned} \sigma _{M}(\kappa )= & {} {\left\{ \begin{array}{ll} \begin{array}{ll} \sigma _{M}^{L}(\kappa ), &{} \mathrm{if}~ \kappa ~ \in ~ [m_{1},m_{2}],\\ 1, &{} \mathrm{if}~ \kappa ~ \in ~ [m_{2},m_{3}],\\ \sigma _{M}^{R}(\kappa ), &{} \mathrm{if}~ \kappa ~ \in ~ [m_{3},m_{4}],\\ 0, &{} \mathrm{otherwise}, \end{array} \end{array}\right. }\\ \sigma _{N}(\kappa )= & {} {\left\{ \begin{array}{ll} \begin{array}{ll} \sigma _{N}^{L}(\kappa ), &{} \mathrm{if}~ \kappa ~ \in ~ [n_{1},n_{2}],\\ -1, &{} \mathrm{if}~ \kappa ~ \in ~ [n_{2},n_{3}],\\ \sigma _{N}^{R}(\kappa ), &{} \mathrm{if}~ \kappa ~ \in ~ [n_{3},n_{4}],\\ 0, &{} \mathrm{otherwise}, \end{array} \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned}&\sigma _{M}^{L}(\kappa ):[m_{1},m_{2}]\rightarrow [0,1],~~\sigma _{M}^{R}(\kappa ):[m_{3},m_{4}]\rightarrow [0,1],\\&\sigma _{N}^{L}(\kappa ):[n_{1},n_{2}]\rightarrow [-1,0],~~\sigma _{N}^{R}(\kappa ):[n_{3},n_{4}]\rightarrow [-1,0], \end{aligned}$$

where $\sigma _{M}^{L}(\kappa )$ and $\sigma _{N}^{L}(\kappa )$ represent the left membership functions for $\sigma _{M}(\kappa )$ and $\sigma _{N}(\kappa )$, respectively. Similarly, $\sigma _{M}^{R}(\kappa )$ and $\sigma _{N}^{R}(\kappa )$ represent right membership functions for $\sigma _{M}(\kappa )$ and $\sigma _{N}(\kappa )$, respectively.

Definition 2.2

Akram et al. (2019e) A BFN  h in a parametric form is a quadruple $\prec [\underline{h}^{*}(r),\overline{h}^{*}(r)],[\underline{h}^{\bullet }(s),\overline{h}^{\bullet }(s)]\succ$ of the mappings $\underline{h}^{*}(r),\overline{h}^{*}(r),\underline{h}^{\bullet }(s),\overline{h}^{\bullet }(s);$$0 \le r \le 1,$$-1 \le s \le 0$ and fulfill the following restrictions:

• (i) $\underline{h}^{*}(r)$ is bounded left-continuous and monotonically non-decreasing mapping on a set (0, 1] and right-continuous at point 0,

• (ii) $\overline{h}^{*}(r)$ is bounded left-continuous and monotonically non-increasing mapping on a set (0, 1] and right-continuous at point 0,

• (iii) $\underline{h}^{\bullet }(r)$ is bounded left-continuous monotonically non-increasing mapping on a set $(-1,0]$ an right-continuous at point $-1$,

• (iv) $\overline{h}^{\bullet }(s)$ is bounded left-continuous monotonically non-decreasing mapping on a set $(-1,0]$ and right-continuous at point $-1$,

• (v) $\underline{h}^{*}(r) \le \overline{h}^{*}(r)$,

• (vi) $\underline{h}^{\bullet }(s) \le \overline{h}^{\bullet }(s)$.

On the basis of Ming et al. (1999), we use BFN $h=\prec [\underline{h}^{*}(r),\overline{h}^{*}(r)],[\underline{h}^{\bullet }(s),\overline{h}^{\bullet }(s)]\succ$ in symmetric form if

$$\begin{aligned} h^{c}(r) = \frac{\underline{h}^{*}(r)+\overline{h}^{*}(r)}{2}~~,~~ h^{c}(s) = \frac{\underline{h}^{\bullet }(s)+\overline{h}^{\bullet }(s)}{2}, \end{aligned}$$

is a real number for all $0 \le r \le 1, -1 \le s \le 0$.

Example 2.3

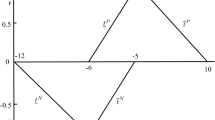
The graphical representation of a BFN $h =\prec [\underline{h}^{*}(r),\overline{h}^{*}(r)],[\underline{h}^{\bullet }(s),\overline{h}^{\bullet }(s)]\succ =\prec [4+2r,9-3r],[3-s,6+2s]\succ$ is given in Figs. 1 and 2.

Fig. 1

The graph of $\underline{h}^{*}(r)$, $\overline{h}^{*}(r)$ functions of bipolar fuzzy number

Fig. 2

The graph of $\underline{h}^{\bullet }(s)$, $\overline{h}^{\bullet }(s)$ functions of bipolar fuzzy number

It is easy to see that $\underline{h}^{*}(r)$ is a mapping that is bounded monotonically non-decreasing left-continuous over (0,1] and right-continuous at 0, $\overline{h}^{*}(r)$ is a mapping that is bounded monotonically non-increasing left-continuous over (0,1] and right-continuous at 0, $\underline{h}^{\bullet }(s)$ is a mapping that is bounded monotonically non-increasing left-continuous over(-1,0] and right-continuous at -1, $\overline{h}^{\bullet }(s)$ is mapping that is bounded monotonically non-decreasing left-continuous over (-1,0] and right-continuous at –1, also $\underline{h}^{*}(r) \le \overline{h}^{*}(r), \underline{h}^{\bullet }(s) \le \overline{h}^{\bullet }(s)$, where $0 \le r \le 1$ and $-1 \le s \le 0$.

In a similar way, $v =\prec [\underline{v}^{*}(r),\overline{v}^{*}(r)],[\underline{v}^{\bullet }(s),\overline{v}^{\bullet }(s)]\succ =\prec [-5+2r,-1-2r],[-6-s,-4+s]\succ$ is a parametric form of symmetric BFN.

Definition 2.4

Akram et al. (2019e) For arbitrary BFNs $h =\prec [\underline{h}^{*},\overline{h}^{*}],[\underline{h}^{\bullet }, \overline{h}^{\bullet }]\succ$, $g =\prec [\underline{g}^{*},\overline{g}^{*}],[\underline{g}^{\bullet }, \overline{g}^{\bullet }]\succ$ and c is arbitrary scalar number, we define $h+g=m=\prec [\underline{m}^{*},\overline{m}^{*}], [\underline{m}^{\bullet },\overline{m}^{\bullet }]\succ$, $h.g=n=\prec [\underline{n}^{*},\overline{n}^{*}], [\underline{n}^{\bullet },\overline{n}^{\bullet }]\succ$ and scalar multiplication by c as follows:

• (i) $\underline{m}^{*}(r)=\underline{h}^{*}(r)+\underline{g}^{*}(r),~~ \overline{m}^{*}(r)=\overline{h}^{*}(r)+\overline{g}^{*}(r),$

• (ii) $\underline{m}^{\bullet }(s)=\underline{h}^{\bullet }(s)+\underline{g}^{\bullet }(s),~~ \overline{m}^{\bullet }(s)=\overline{h}^{\bullet }(s)+\overline{g}^{\bullet }(s),$

• (iii) $\underline{n}^{*}(r)= \min \{\underline{h}^{*}.\underline{g}^{*},\underline{h}^{*}.\overline{g}^{*},\overline{h}^{*}.\underline{g}^{*},\overline{h}^{*}.\overline{g}^{*}\},$

• (iv) $\overline{n}^{*}(r)= \max \{\underline{h}^{*}.\underline{g}^{*},\underline{h}^{*}.\overline{g}^{*},\overline{h}^{*}.\underline{g}^{*},\overline{h}^{*}.\overline{g}^{*}\},$

• (v) $\underline{n}^{\bullet }(s)= \max \{\underline{h}^{\bullet }.\underline{g}^{\bullet },\underline{h}^{\bullet }.\overline{g}^{\bullet },\overline{h}^{\bullet }.\underline{g}^{\bullet },\overline{h}^{\bullet }.\overline{g}^{\bullet }\},$

• (vi) $\overline{n}^{\bullet }(s)= \min \{\underline{h}^{\bullet }.\underline{g}^{\bullet },\underline{h}^{\bullet }.\overline{g}^{\bullet },\overline{h}^{\bullet }.\underline{g}^{\bullet },\overline{h}^{\bullet }.\overline{g}^{\bullet }\},$

• (vii) If c is non-negative then, $ch = \prec [c(\underline{h}^{*}),c(\overline{h}^{*})],[c(\underline{h}^{\bullet }),c(\overline{h}^{\bullet })]\succ ,$ But if c is negative then, $ch = \prec [c(\overline{h}^{*}),c(\underline{h}^{*})],[c(\overline{h}^{\bullet }),c(\underline{h}^{\bullet })]\succ .$

The collection of all BFNs under the operation addition and scalar product, represented by $\Omega$ are concave and convex cones.

Definition 2.5

Akram et al. (2019e) Consider the $n \times n$ BFLS of equations is given by:

$$\begin{aligned} {\left\{ \begin{array}{ll} l_{11}h_{1} + l_{12}h_{2} + \cdots + l_{1n}h_{n}&{}= z_{1},\\ l_{21}h_{1} + l_{22}h_{2} + \cdots + l_{2n}h_{n}&{}= z_{2},\\ .\\ .\\ .\\ l_{n1}h_{1} + l_{n2}h_{2} + \cdots + l_{nn}h_{n}&{}= z_{n}, \end{array}\right. } \end{aligned}$$

(1)

where the coefficient elements $(l_{pq})$, $1 \le p,q \le n$ is a crisp matrix of order $n \times n$ and each $z_{q}$, $1 \le q \le n$ is a parametric form of BFN and each unknown $h_{p}$, where $1 \le p \le n$ is also parametric form of BFN, is known as the parametric form of BFLS of equations.

Definition 2.6

Akram et al. (2019e) A BFNs vector $H= (h_{1},h_{2},\ldots h_{n})^{T}$ is the form of $(H_{q})_{(r,s)}= \prec [\underline{h}_{q}^{*}(r),\overline{h}_{q}^{*}(r)],[\underline{h}_{q}^{\bullet }(s),\overline{h}_{q}^{\bullet }(s)]\succ$, where $1 \le q \le n,$$0 \le r \le 1$ and $-1 \le s \le 0$ is called the solution of BFLS of equations in (1) if

$$\begin{aligned} {\left\{ \begin{array}{ll} \underline{\sum _{q=1}^{n}l_{pq}h_{q}^{*}(r)} &{}= \sum _{q=1}^{n}{l_{pq}\underline{h_{q}^{*}(r)}} = \underline{z}_{p}^{*}(r),\\ \\ \overline{\sum _{q=1}^{n}l_{pq}h_{q}^{*}(r)} &{}= \sum _{q=1}^{n}{l_{pq}\overline{h_{q}^{*}(r)}} = \overline{z}_{p}^{*}(r), \\ \\ \underline{\sum _{q=1}^{n}l_{pq}h_{q}^{\bullet }(s)} &{}= \sum _{q=1}^{n}{l_{pq}\underline{h_{q}^{\bullet }(s)}} = \underline{z}_{p}^{\bullet }(s),\\ \\ \overline{\sum _{q=1}^{n}l_{pq}h_{q}^{\bullet }(s)} &{}= \sum _{q=1}^{n}{l_{pq}\overline{h_{q}^{\bullet }(s)}} = \overline{z}_{p}^{\bullet }(s). \\ \end{array}\right. } \end{aligned}$$

(2)

Definition 2.7

Abbasbandy and Alavi (2005) For any BFLS $LH=Z$, we define a matrix A obtained from non-negative entries of L and defined a matrix B obtained from absolute of the negative entries of L. Then $L=A-B$ and we define $L^{+}=A+B.$

Definition 2.8

Abbasbandy and Alavi (2005) A square matrix is known as permutation matrix in which every row and column contain exactly one unit element and all other entries in each row and column are zero.

Definition 2.9

Abbasbandy and Alavi (2005) A matrix L is known as absolutely permutation matrix if absolute of the entries of matrix L, i.e., $(L^{+})$ is a permutation matrix.

Remark 1

$L^{^-1}$ is an absolutely permutation matrix if L is an absolutely permutation matrix and $LL^{T}= I$.

Theorem 2.10

Minc (1988) The inverse of non-negative matrix L is non-negative if L is a permutation matrix.

3 Bipolar fuzzy solution

The $p^{th}$ positive$(*)$$n \times n$ crisp system of equations of (1) is written in the following form:

$$\begin{aligned} \sum _{l_{pq}\ge 0}l_{pq}\underline{h}_{q}^{*}(r) + \sum _{l_{pq}< 0}l_{pq}\overline{h}_{q}^{*}(r)=\underline{z}_{p}^{*}(r),~~ \sum _{l_{pq}\ge 0}l_{pq}\overline{h}_{q}^{*}(r) + \sum _{l_{pq}< 0}l_{pq}\underline{h}_{q}^{*}(r)=\overline{z}_{p}^{*}(r). \end{aligned}$$

(3)

From Eq. (3), we get

$$\begin{aligned} \sum _{l_{pq}\ge 0}l_{pq}(\overline{h}_{q}^{*}(r)-\underline{h}_{q}^{*}(r)) - \sum _{l_{pq}< 0}l_{pq}(\overline{h}_{q}^{*}(r)-\underline{h}_{q}^{*}(r))&= \overline{z}_{p}^{*}(r)-\underline{z}_{p}^{*}(r). \end{aligned}$$

(4)

If we assume $w_{q}^{*}(r)= \overline{h}_{q}^{*}(r)-\underline{h}_{q}^{*}(r)$ and $v_{p}^{*}(r)=\overline{z}_{p}^{*}(r)-\underline{z}_{p}^{*}(r)$, then Eq. (4) becomes

$$\begin{aligned} \sum _{l_{pq}\ge 0}l_{pq}w_{q}^{*}(r) - \sum _{l_{pq}< 0}l_{pq}w_{q}^{*}(r)&= v_{p}^{*}(r),~~ p= 1,2, \ldots n. \end{aligned}$$

In matrix form

$$\begin{aligned} (A + B)W^{*}(r) =V^{*}(r), \end{aligned}$$

where

$$\begin{aligned} W^{*}(r)= (w_{1}^{*}(r),w_{2}^{*}(r), \ldots ,w_{n}^{*}(r))^{T},~V^{*}(r)= (v_{1}^{*}(r),v_{2}^{*}(r), \ldots ,v_{n}^{*}(r))^{T}~\mathrm{and}~L= A - B. \end{aligned}$$

Similarly, the pth negative$(\bullet )$$n \times n$ crisp system of equations of (1) is written in the following form:

$$\begin{aligned} \sum _{l_{pq}\ge 0}l_{pq}\underline{h}_{q}^{\bullet }(s) + \sum _{l_{pq}< 0}l_{pq}\overline{h}_{q}^{\bullet }(s)=\underline{z}_{p}^{\bullet }(s),~ \sum _{l_{pq}\ge 0}l_{pq}\overline{h}_{q}^{\bullet }(s) + \sum _{l_{pq}< 0}l_{pq}\underline{h}_{q}^{\bullet }(s)=\overline{z}_{p}^{\bullet }(s). \end{aligned}$$

(5)

From Eq. (5) we get

$$\begin{aligned} \sum _{l_{pq}\ge 0}l_{pq}(\overline{h}_{q}^{\bullet }(s)-\underline{h}_{q}^{\bullet }(s)) - \sum _{l_{pq}< 0}l_{pq}(\overline{h}_{q}^{\bullet }(s)-\underline{h}_{q}^{\bullet }(s))&= \overline{z}_{p}^{\bullet }(s)-\underline{z}_{p}^{\bullet }(s). \end{aligned}$$

(6)

If we assume $u_{q}^{\bullet }(s)= \overline{h}_{q}^{\bullet }(s)-\underline{h}_{q}^{\bullet }(s)$ and $k_{p}^{\bullet }(s)=\overline{z}_{p}^{\bullet }(s)-\underline{z}_{p}^{\bullet }(s)$, then Eq. (6) has the form

$$\begin{aligned} \sum _{l_{pq}\ge 0}l_{pq}u_{q}^{\bullet }(s) - \sum _{l_{pq}< 0}l_{pq}u_{q}^{\bullet }(s)&= k_{p}^{\bullet }(s),~~ p= 1,2,\ldots n, \end{aligned}$$

and in the matrix form

$$\begin{aligned} (A + B)U^{\bullet }(s) =K^{\bullet }(s), \end{aligned}$$

where $U^{\bullet }(s)= (u_{1}^{\bullet }(s),u_{2}^{\bullet }(s), \ldots ,u_{n}^{\bullet }(s)^{T}$, $K^{\bullet }(s)= (k_{1}^{\bullet }(s),k_{2}^{\bullet }(s),\ldots ,k_{n}^{\bullet }(s))^{T}$ and $L= A - B$.

$$\begin{aligned} \mathrm{Let}~H^{c} = (h_{1}^{c},h_{2}^{c}, \ldots ,h_{n}^{c})~\mathrm{and}~Z^{c} = (z_{1}^{c},z_{2}^{c}, \ldots ,z_{n}^{c}), \end{aligned}$$

where

$$\begin{aligned} h_{p}^{c}(r)&= \frac{\underline{h}_{p}^{*}(r)+\overline{h}_{p}^{*}(r)}{2},~h_{p}^{c}(s) = \frac{\underline{h}_{p}^{\bullet }(s)+\overline{h}_{p}^{\bullet }(s)}{2},~z_{p}^{c}(r) = \frac{\underline{z}_{p}^{*}(r)+\overline{z}_{p}^{*}(r)}{2}~\mathrm{and}\\ z_{p}^{c}(s)&= \frac{\underline{z}_{p}^{\bullet }(s)+\overline{z}_{p}^{\bullet }(s)}{2}, \end{aligned}$$

for $1 \le p \le n$, $0 \le r \le 1$ and $-1 \le s \le 0$.

Remark 2

A system of non-linear equations can often be approximated by system of linear equations due to their complexity. The bipolar parameters r and s in BFLS of equations form the system more complex. To solve such a system, we have transformed the system in term of their parameters from $n \times n$ to pair of $2n \times 2n$ positive$(*)$ and negative$(\bullet )$ linear system of equations.

Theorem 3.1

Let H is a solution of BFLS of equations in (1), where coefficient matrix L is invertible matrix and Z is a BFN vector. Then $LH^{c}(r)=Z^{c}(r)$ and $LH^{c}(s)=Z^{c}(s)$.

Proof

First due to Eq. (3), we have for each p and q, $1 \le p,q \le n$

$$\begin{aligned} \sum _{l_{pq}\ge 0} \left( l_{pq}\frac{(\overline{h}_{q}^{*}(r)+\underline{h}_{q}^{*}(r))}{2}\right) + \sum _{l_{pq}< 0} \left( l_{pq}\frac{(\overline{h}_{q}^{*}(r)+\underline{h}_{q}^{*})}{2}\right)&= \frac{(\overline{z}_{p}^{*}(r)+\underline{z}_{p}^{*}(r))}{2}, \end{aligned}$$

and hence

$$\begin{aligned} \sum _{l_{pq}\ge 0}l_{pq}h_{q}^{c}(r)+\sum _{l_{pq}< 0}l_{pq}h_{q}^{c}(r)&= z_{p}^{c}(r), \end{aligned}$$

that is, $(A-B)H^{c}(r)=Z^{c}(r)$.

Similarly, due to Eq. (5), for each p and q, $1 \le p,q \le n$, we have

$$\begin{aligned} \sum _{l_{pq}\ge 0} \left( l_{pq}\frac{(\overline{h}_{q}^{\bullet }(s)+\underline{h}_{q}^{\bullet }(s))}{2} \right) + \sum _{l_{pq}< 0} \left( l_{pq}\frac{(\overline{h}_{q}^{\bullet }(s)+\underline{h}_{q}^{\bullet }(s))}{2} \right)&= \frac{(\overline{z}_{p}^{\bullet }(s)+\underline{z}_{p}^{\bullet }(s))}{2}, \end{aligned}$$

and hence

$$\begin{aligned} \sum _{l_{pq}\ge 0}l_{pq}h_{q}^{c}(s)+\sum _{l_{pq}< 0}l_{pq}h_{q}^{c}(s)&= z_{p}^{c}(s), \end{aligned}$$

that is, $(A-B)H^{c}(s)=Z^{c}(s)$, which completes the proof. $\square$

Remark 3

On the basis of the Theorem (3.1), if Z is bipolar fuzzy vector in symmetric form then H is also bipolar fuzzy vector in symmetric form.

Remark 4

We want to obtain the bipolar fuzzy solution of BFLS of equations in (1), then we have to solve the given crisp linear systems

$$\begin{aligned} {\left\{ \begin{array}{ll} (A+B)W^{*}(r) = V^{*}(r),\\ (A-B)H^{c}(r)= Z^{c}(r), \end{array}\right. } \end{aligned}$$

(7)

and

$$\begin{aligned} {\left\{ \begin{array}{ll} (A+B)U^{\bullet }(s) = K^{\bullet }(s),\\ (A-B)H^{c}(s)= Z^{c}(s). \end{array}\right. } \end{aligned}$$

(8)

After solving Eqs. (7) and (8), it is enough to take

$$\begin{aligned} \underline{h}_{p}^{*}(r)&= h_{p}^{c}(r) - \frac{1}{2}w_{p}^{*}(r),~~~~~~\overline{h}_{p}^{*}= h_{p}^{c}(r) + \frac{1}{2}w_{p}^{*}(r), \end{aligned}$$

and

$$\begin{aligned} \underline{h}_{p}^{\bullet }(s)&= h_{p}^{c}(s) - \frac{1}{2}u_{p}^{\bullet }(s),~~~~~~\overline{h}_{p}^{\bullet }= h_{p}^{c}(s) + \frac{1}{2}u_{p}^{\bullet }(s), \end{aligned}$$

for each $p, 1 \le p \le n$.

Theorem 3.2

For any arbitrary bipolar fuzzy vector Z the unique solution H is a bipolar fuzzy vector for BFLS of equations in (1) if and only if $(A+B)^{-1}$ and $(A-B)^{-1}$ exist and $(A+B)^{-1}$ is a non-negative matrix.

Example 3.3

Consider the $2 \times 2$ BFLS of equation in symmetric form

$$\begin{aligned} {\left\{ \begin{array}{ll} h_{1} - h_{2} &{}= {\prec [r, 2-r],[-1-3s, 5+3s]\succ },\\ h_{1} + 3h_{2} &{}= {\prec [4+2r, 8-2r],[-9-7s, 5+7s]\succ }. \end{array}\right. } \end{aligned}$$

To solve this bipolar fuzzy system, we convert this system in pair of positive$(*)$ and negative$(\bullet )$ of two $2 \times 2$ crisp system.

First, we consider positive$(*)$ two crisp systems,

$$\begin{aligned}&\underline{h}_{1}^{*}-\overline{h}_{2}^{*}= r~, ~\underline{h}_{1}^{*}+3\underline{h}_{2}^{*}=4+2r,~\\&\overline{h}_{1}^{*}-\underline{h}_{2}^{*}= 2-r~, ~\overline{h}_{1}^{*}+3\overline{h}_{2}^{*}=8-2r,~ \end{aligned}$$

the above equations can be written in the following form:

$$\begin{aligned} {\left\{ \begin{array}{ll} (\overline{h}_{1}^{*}-\underline{h}_{1}^{*}) + (\overline{h}_{2}^{*}-\underline{h}_{2}^{*}) = 2-2r,\\ (\overline{h}_{1}^{*}-\underline{h}_{1}^{*}) + 3(\overline{h}_{2}^{*}-\underline{h}_{2}^{*})= 4-4r. \end{array}\right. } \end{aligned}$$

This is equivalent to

$$\begin{aligned} {\left\{ \begin{array}{ll} w_{1}^{*}(r) + w_{2}^{*}(r) = v_{1}^{*}(r),\\ w_{1}^{*}(r) + 3w_{2}^{*}(r)= v_{2}^{*}(r), \end{array}\right. } \end{aligned}$$

(9)

where $v_{1}^{*}(r)= 2-2r, v_{2}^{*}(r)= 4-4r$. Another crisp system is

$$\begin{aligned} {\left\{ \begin{array}{ll} h_{1}^{c} - h_{2}^{c} = 1= y_{1}^{c},\\ h_{1}^{c} + h_{2}^{c} = 6= y_{2}^{c}. \end{array}\right. } \end{aligned}$$

(10)

By solving equations (9) and (10), we have $w_{1}^{*}(r)=1-r$, $w_{2}^{*}(r)=1-r$, $h_{1}^{c}(r)=\frac{9}{4}$, $h_{2}^{c}(r)=\frac{5}{4}$ and, therefore,

$$\begin{aligned} \underline{h}_{1}^{*}(r)&=\frac{9}{4} - \frac{1}{2}(1-r)~,~~~~\overline{h}_{1}^{*}(r)=\frac{9}{4} + \frac{1}{2}(1-r)~,\\ \underline{h}_{2}^{*}(r)&=\frac{5}{4} - \frac{1}{2}(1-r)~,~~~~\overline{h}_{2}^{*}(r)=\frac{5}{4} + \frac{1}{2}(1-r)~. \end{aligned}$$

Here $\underline{h}_{1}^{*}(r) \le \overline{h}_{1}^{*}(r)$, $\underline{h}_{2}^{*}(r) \le \overline{h}_{2}^{*}(r)$ and $\overline{h}_{1}^{*}(r)$, $\overline{h}_{2}^{*}(r)$ are monotonic decreasing and $\underline{h}_{1}^{*}(r)$, $\underline{h}_{2}^{*}(r)$ are monotonic increasing functions. Similarly, We consider negative$(\bullet )$ two crisp systems,

$$\begin{aligned}&\underline{h}_{1}^{\bullet }-\overline{h}_{2}^{\bullet }= -1-3s~, ~\underline{h}_{1}^{\bullet }+3\underline{h}_{2}^{\bullet }=-9-7s,~\\&\overline{h}_{1}^{\bullet }-\underline{h}_{2}^{\bullet }= 5+3s~, ~\overline{h}_{1}^{\bullet }+3\overline{h}_{2}^{\bullet }=5+7s.~ \end{aligned}$$

The above equations can be written in the following form:

$$\begin{aligned} {\left\{ \begin{array}{ll} (\overline{h}_{1}^{\bullet }-\underline{h}_{1}^{\bullet }) + (\overline{h}_{2}^{\bullet }-\underline{h}_{2}^{\bullet }) = 6+6s,\\ (\overline{h}_{1}^{\bullet }-\underline{h}_{1}^{\bullet }) + 3(\overline{h}_{2}^{\bullet }-\underline{h}_{2}^{\bullet })= 14+14s, \end{array}\right. } \end{aligned}$$

this is equivalent to

$$\begin{aligned} {\left\{ \begin{array}{ll} u_{1}^{\bullet }(s) + u_{2}^{\bullet }(s) = k_{1}^{\bullet }(s),\\ u_{1}^{\bullet }(s) + 3u_{2}^{\bullet }(s)= k_{2}^{\bullet }(s), \end{array}\right. } \end{aligned}$$

(11)

where $k_{1}^{\bullet }(s)= 6+6s,~ k_{2}^{\bullet }(s)= 14+14s$. Another crisp system is

$$\begin{aligned} {\left\{ \begin{array}{ll} h_{1}^{c} - h_{2}^{c} = 2= y_{1}^{c},\\ h_{1}^{c} + h_{2}^{c} = -2= y_{2}^{c}. \end{array}\right. } \end{aligned}$$

(12)

By solving Eqs. (11) and (12), we have $u_{1}^{\bullet }(s)=2+2s$, $u_{2}^{\bullet }(s)=4+4s$, $h_{1}^{c}(s)=1$, $h_{2}^{c}(s)=-1$ and, therefore,

$$\begin{aligned} \underline{h}_{1}^{\bullet }(s)&=-s~, ~\overline{h}_{1}^{\bullet }(s)=2+s~,\\ \underline{h}_{2}^{\bullet }(s)&=-3-2s~, ~\overline{h}_{2}^{\bullet }(s)=1+2s~. \end{aligned}$$

Here $\underline{h}_{1}^{\bullet }(s) \le \overline{h}_{1}^{\bullet }(s)$, $\underline{h}_{2}^{\bullet }(s) \le \overline{h}_{2}^{\bullet }(s)$ and $\overline{h}_{1}^{\bullet }(s)$, $\overline{h}_{2}^{\bullet }(s)$ are monotonic increasing and $\underline{h}_{1}^{\bullet }(s)$, $\underline{h}_{2}^{\bullet }(s)$ are monotonic decreasing functions.

Hence solution of bipolar fuzzy system in (3.3) is given as,

$$\begin{aligned} h_{1}&={\prec [\underline{h}_{1}^{*}(r),\overline{h}_{1}^{*}(r)], [\underline{h}_{1}^{\bullet }(s),\overline{h}_{1}^{\bullet }(s)]\succ =\prec \left[ \frac{7}{4} +\frac{1}{2}r,\frac{11}{4} - \frac{1}{2}r\right] ,[-s,2+s]\succ },\\ h_{2}&={\prec [\underline{h}_{2}^{*}(r),\overline{h}_{2}^{*}(r)], [\underline{h}_{2}^{\bullet }(s),\overline{h}_{2}^{\bullet }(s)]\succ =\prec \left[ \frac{3}{4} +\frac{1}{2}r,\frac{7}{4} -\frac{1}{2}r\right] ,[-3-2s,1+2s]\succ }. \end{aligned}$$

The graphical representation of $\underline{h}_{1}^{*}(r)$, $\overline{h}_{1}^{*}(r)$, $\underline{h}_{2}^{*}(r)$, $\overline{h}_{2}^{*}(r)$ is given below in Fig. 3.

The graphical representation of $\underline{h}_{1}^{\bullet }(r)$, $\overline{h}_{1}^{\bullet }(r)$, $\underline{h}_{2}^{\bullet }(r)$, $\overline{h}_{2}^{\bullet }(r)$ is given below in Fig. 4.

Fig. 3

The graph of $\underline{h}^{*}(r)$, $\overline{h}^{*}(r)$ functions of bipolar fuzzy number

Fig. 4

The graph of $\underline{h}^{\bullet }(s)$, $\overline{h}^{\bullet }(s)$ functions of bipolar fuzzy number

4 Weak bipolar fuzzy solution

We restrict our discussion to bipolar triangular fuzzy number(BTFN),i.e., $\underline{z}_{p}^{*}(r)$, $\overline{z}_{p}^{*}(r)$, $\underline{z}_{p}^{\bullet }(s)$, $\overline{z}_{p}^{\bullet }(s)$ and $\underline{h}_{p}^{*}(r)$, $\overline{h}_{p}^{*}(r)$, $\underline{h}_{p}^{\bullet }(s)$, $\overline{h}_{p}^{\bullet }(s)$ they all are linear functions of r and s, $\underline{z}_{p}^{*}(1)=\overline{z}_{p}^{*}(1)$, $\underline{z}_{p}^{\bullet }(-1)=\overline{z}_{p}^{\bullet }(-1)$ and $\underline{h}_{p}^{*}(1)=\overline{h}_{p}^{*}(1)$, $\underline{h}_{p}^{\bullet }(-1)=\overline{h}_{p}^{\bullet }(-1)$ for all $1\le p \le n$. By using Theorem (3.2) since $(A+B)$ is non-negative, $(A+B)^{-1}$ may be negative, so by this, $w_{p}^{*}(r)$, $u_{p}^{\bullet }(s)$ may be negative for some p and, therefore, $\overline{h}_{p}^{*}(r) - \underline{h}_{p}^{*}(r)< 0$ and $\overline{h}_{p}^{\bullet }(s) - \underline{h}_{p}^{\bullet }(s)< 0$. So, by this fact $h_{p}$ is not a BFN and we define a BFN vector

$$\begin{aligned} G=([\underline{g}_{1}^{*},\overline{g}_{1}^{*}] [\underline{g}_{1}^{\bullet },\overline{g}_{1}^{\bullet }],\ldots , [\underline{g}_{n}^{*},\overline{g}_{n}^{*}][\underline{g}_{n}^{\bullet }, \overline{g}_{n}^{\bullet }])^{T}, \end{aligned}$$

where

$$\begin{aligned} \underline{g}_{p}^{*}&=\min \{\underline{h}_{p}^{*}(r), \overline{h}_{p}^{*}(r),\underline{h}_{p}^{*}(1)\},\\ \overline{g}_{p}^{*}&=\max \{\underline{h}_{p}^{*}(r),\overline{h}_{p}^{*}(r), \underline{h}_{p}^{*}(1)\},\\ \underline{g}_{p}^{\bullet }&=\min \{\underline{h}_{p}^{\bullet }(s), \overline{h}_{p}^{\bullet }(s),\underline{h}_{p}^{\bullet }(-1)\},\\ \overline{g}_{p}^{\bullet }&=\max \{\underline{h}_{p}^{\bullet }(s), \overline{h}_{p}^{\bullet }(s),\underline{h}_{p}^{\bullet }(-1)\}. \end{aligned}$$

If $\prec [\underline{h}_{p}^{*}(r),\overline{h}_{p}^{*}(r)],[\underline{h}_{p}^{\bullet }(s),\overline{h}_{p}^{\bullet }(s)]\succ$, $1 \le p \le n$, are all fuzzy numbers then $\underline{h}_{p}^{*}(r)=\underline{g}_{p}^{*}(r)$, $\overline{h}_{p}^{*}(r)=\overline{g}_{p}^{*}(r)$, $\underline{h}_{p}^{\bullet }(s)=\underline{g}_{p}^{\bullet }(s)$ and $\overline{h}_{p}^{\bullet }(s)=\overline{g}_{p}^{\bullet }(s)$, $1 \le p \le n$, and then G is called the strong bipolar fuzzy solution. Otherwise, G is called the weak bipolar fuzzy solution. In example (3.3) the bipolar fuzzy solution was strong solution.

Example 4.1

Consider the $2 \times 2$ BFLS of equation in symmetric form

$$\begin{aligned} {\left\{ \begin{array}{ll} h_{1} - h_{2} = {\prec [-5+2r, -1-2r],[-6-s, -4+s]\succ },\\ h_{1} - 2h_{2} = {\prec [2+5r, 12-5r],[7-5s, 17+5s]\succ }. \end{array}\right. } \end{aligned}$$

To solve this bipolar fuzzy system, we convert this system into pair of positive$(*)$ and negative$(\bullet )$ of two $2 \times 2$ crisp system.

First, we consider positive$(*)$ two crisp systems,

$$\begin{aligned} \underline{h}_{1}^{*}-\overline{h}_{2}^{*}&= -5+2r,~ ~~~~\underline{h}_{1}^{*}-2\overline{h}_{2}^{*}=2+5r,~\\ \overline{h}_{1}^{*}-\underline{h}_{2}^{*}&= -1-2r,~ ~~~~\overline{h}_{1}^{*}-2\underline{h}_{2}^{*}=12-5r,~ \end{aligned}$$

and above equations can be written in the following form:

$$\begin{aligned} {\left\{ \begin{array}{ll} (\overline{h}_{1}^{*}-\underline{h}_{1}^{*}) + (\overline{h}_{2}^{*}-\underline{h}_{2}^{*}) = 4-4r,\\ (\overline{h}_{1}^{*}-\underline{h}_{1}^{*}) + 2(\overline{h}_{2}^{*}-\underline{h}_{2}^{*}) = 10-10r, \end{array}\right. } \end{aligned}$$

this is equivalent to

$$\begin{aligned} {\left\{ \begin{array}{ll} w_{1}^{*}(r) + w_{2}^{*}(r) =4-4r= v_{1}^{*}(r),\\ w_{1}^{*}(r) + 2w_{2}^{*}(r)=10-10r= v_{2}^{*}(r), \end{array}\right. } \end{aligned}$$

(13)

where $v_{1}^{*}(r)= 4-4r$, $v_{2}^{*}(r)= 10-10r$. Another crisp system is

$$\begin{aligned} {\left\{ \begin{array}{ll} h_{1}^{c} - h_{2}^{c} = -3= z_{1}^{c},\\ h_{1}^{c} - 2h_{2}^{c} = 7= z_{2}^{c}. \end{array}\right. } \end{aligned}$$

(14)

By solving Eqs. (13) and (14), we have $w_{1}^{*}(r)=-2+2r$, $w_{2}^{*}(r)=6-6r$, $h_{1}^{c}(r)=-13$, $h_{2}^{c}(r)=-10$ and, therefore,

$$\begin{aligned} ~\underline{h}_{1}^{*}(r)&=-12-r,~ ~~~~\overline{h}_{1}^{*}(r)=-14+r,~\\ ~\underline{h}_{2}^{*}(r)&=-13+3r,~ ~~~~\overline{h}_{2}^{*}(r)=-7-3r.~ \end{aligned}$$

Similarly, we consider negative$(\bullet )$ two crisp systems,

$$\begin{aligned} ~\underline{h}_{1}^{\bullet }-\overline{h}_{2}^{\bullet }&=-6-s,~ ~~~~\underline{h}_{1}^{\bullet }-2\overline{h}_{2}^{\bullet }=7-5s,~\\ ~\overline{h}_{1}^{\bullet }-\underline{h}_{2}^{\bullet }&=-4+s,~ ~~~~\overline{h}_{1}^{\bullet }-2\underline{h}_{2}^{\bullet }=17+5s~ \end{aligned}$$

and above equations can be written in the following form:

$$\begin{aligned} {\left\{ \begin{array}{ll} (\overline{h}_{1}^{\bullet }-\underline{h}_{1}^{\bullet }) + (\overline{h}_{2}^{\bullet }-\underline{h}_{2}^{\bullet }) = 2+2s,\\ (\overline{h}_{1}^{\bullet }-\underline{h}_{1}^{\bullet }) + 2(\overline{h}_{2}^{\bullet }-\underline{h}_{2}^{\bullet })= 10+10s, \end{array}\right. } \end{aligned}$$

this it is equivalent to

$$\begin{aligned} {\left\{ \begin{array}{ll} u_{1}^{\bullet }(s) + u_{2}^{\bullet }(s) =2+2s= k_{1}^{\bullet }(s),\\ u_{1}^{\bullet }(s) + 2u_{2}^{\bullet }(s) =10+10s= k_{2}^{\bullet }(s), \end{array}\right. } \end{aligned}$$

(15)

where $k_{1}^{\bullet }(s)= 2+2s$, $k_{2}^{\bullet }(s)= 10+10s$. Another crisp system is

$$\begin{aligned} {\left\{ \begin{array}{ll} h_{1}^{c} - h_{2}^{c} = -5= z_{1}^{c},\\ h_{1}^{c} - 2h_{2}^{c} = 12= z_{2}^{c}. \end{array}\right. } \end{aligned}$$

(16)

By solving Eqs. (15) and (16), we have $u_{1}^{\bullet }(s)=-6-6s$, $u_{2}^{\bullet }(s)=8+8s$, $h_{1}^{c}(s)=-22$, $h_{2}^{c}(s)=-17$ and, therefore,

$$\begin{aligned} ~\underline{h}_{1}^{\bullet }(s)&=-19+3s,~ ~~~~\overline{h}_{1}^{\bullet }(s)=-25-3s,~\\ ~\underline{h}_{2}^{\bullet }(s)&=-21-4s,~ ~~~~\overline{h}_{2}^{\bullet }(s)=-13+4s.~ \end{aligned}$$

The solution of BFLS in (4.1) is given as,

$$\begin{aligned} h_{1}&={\prec [\underline{h}_{1}^{*}(r),\overline{h}_{1}^{*}(r)], [\underline{h}_{1}^{\bullet }(s),\overline{h}_{1}^{\bullet }(s)]\succ =\prec [-12-r,-14+r],[-19+3s,-25-3s]\succ },\\ h_{2}&={\prec [\underline{h}_{2}^{*}(r),\overline{h}_{2}^{*}(r)], [\underline{h}_{2}^{\bullet }(s),\overline{h}_{2}^{\bullet }(s)]\succ =\prec [-13+3r,-7-3r],[-21-4s,-13+3s]\succ }. \end{aligned}$$

The graphical representation of $h_{1}$ and $h_{2}$ is given below in Figs. 5 and 6.

Fig. 5

The graph of $\underline{h}^{*}(r)$, $\overline{h}^{*}(r)$ functions of bipolar fuzzy number

Fig. 6

The graph of $\underline{h}^{\bullet }(s)$, $\overline{h}^{\bullet }(s)$ functions of bipolar fuzzy number

The fact is that $h_{1}$ is not a BFN, so that bipolar fuzzy solution is a weak and now strong solution given as

$$\begin{aligned} g_{1}&={\prec [-14+r,-12-r],[-25-3s,-19+3s]\succ },\\ g_{2}&={\prec [-13+3r,-7-3r],[-21-4s,-13+3s]\succ }. \end{aligned}$$

The graphical representation of the strong solution of $g_{1}$ and $g_{2}$ is given in Figs. 7 and 8.

Fig. 7

The graph of $\underline{g}^{*}(r)$, $\overline{g}^{*}(r)$ functions of bipolar fuzzy number

Fig. 8

The graph of $\underline{g}^{\bullet }(s)$, $\overline{g}^{\bullet }(s)$ functions of bipolar fuzzy number

5 Bipolar fuzzy solution by using bipolar fuzzy center

Senthilkumar and Rajendran (2009) suggested a new way to solve $n \times n$ linear fuzzy system used by Abbasbandy and Alavi (2005), and they used a method of fuzzy center to solve $n \times n$ linear fuzzy system. In this article, we extend the method of fuzzy center technique Senthilkumar and Rajendran (2009) in bipolar fuzzy center to solve BFLS of equations. This method depends on the method of drawing graphs to solve the system of bipolar n scattered equations with n bipolar fuzzy variables. In this method, we take some specific end points of the bipolar solution and use the straight-line equation to solve the BFLS of equations. The original bipolar system is replaced by a pair of positive$(*)$ and negative$(\bullet )$ two $n \times n$ linear fuzzy system and then draw the graph of solution at some specific points to solve it. This technique is use for both asymmetric and symmetric BFLS of equations. This technique is more effective to find the bipolar solution when the number of variables in the bipolar fuzzy linear system is large.

Remark 5

By using the Theorem (3.1), the bipolar fuzzy center $h_{p}^{c}(r)$ and $h_{p}^{c}(s)$ satisfies Eq. (1) and in the resultant, we can find $h_{p}^{c}(r)$ and $h_{p}^{c}(s)$ from Eq. (1) by using simplest method.

We can represent the $p^{th}$ positive$(*)$ and negative$(\bullet )$ crisp part of system in (1), which is given as

$$\begin{aligned}&{\left\{ \begin{array}{ll} \sum _{l_{pq}\ge 0}l_{pq}\underline{h}_{q}^{*}(r) + \sum _{l_{pq}< 0}l_{pq}\overline{h}_{q}^{*}(r) &{}= \underline{z}_{p}^{*}(r),\\ \sum _{l_{pq}\ge 0}l_{pq}\overline{h}_{q}^{*}(r) + \sum _{l_{pq}< 0}l_{pq}\underline{h}_{q}^{*}(r) &{}= \overline{z}_{p}^{*}(r), \end{array}\right. } \end{aligned}$$

(17)

$$\begin{aligned}&{\left\{ \begin{array}{ll} \sum _{l_{pq}\ge 0}l_{pq}\underline{h}_{q}^{\bullet }(s) + \sum _{l_{pq}< 0}l_{pq}\overline{h}_{q}^{\bullet }(s) &{}= \underline{z}_{p}^{\bullet }(s),\\ \sum _{l_{pq}\ge 0}l_{pq}\overline{h}_{q}^{\bullet }(s) + \sum _{l_{pq}< 0}l_{pq}\underline{h}_{q}^{\bullet }(s) &{}= \overline{z}_{p}^{\bullet }(s), \end{array}\right. } \end{aligned}$$

(18)

where $h_{q}^{c}(r) = \frac{\underline{h}_{q}^{*}(r)~+~\overline{h}_{q}^{*}(r)}{2}$, $h_{q}^{c}(s) = \frac{\underline{h}_{q}^{\bullet }(s)~+~\overline{h}_{q}^{\bullet }(s)}{2}$ and $z_{q}^{c}(r) = \frac{\underline{z}_{q}^{*}(r)~+~\overline{z}_{q}^{*}(r)}{2}$, $z_{q}^{c}(s) = \frac{\underline{z}_{q}^{\bullet }(s)~+~\overline{z}_{q}^{\bullet }(s)}{2}$ for $1 \le q \le n$, $0 \le r \le 1$ and $-1 \le s \le 0$.

Theorem 4.2

For the solution of BFLS of equations, following results hold:

• (a) End points in the monotonous non-increasing solution vector $(\overline{h}_{1}^{*}(r), \overline{h}_{2}^{*}(r), \ldots ,\overline{h}_{n}^{*}(r))$ are obtained by replacing $\underline{h}_{q}^{*}(r)$ in terms of $\overline{h}_{q}^{*}(r)$ by using the bipolar fuzzy center in (17) at $r = 1$ and $r = 0$.

• (b) End points in the monotonous non-decreasing solution vector $(\underline{h}_{1}^{*}(r),\underline{h}_{2}^{*}(r), \ldots ,\underline{h}_{n}^{*}(r))$ are obtained by replacing $\overline{h}_{q}^{*}(r)$ in terms of $\underline{h}_{q}^{*}(r)$ by using the bipolar fuzzy center in (17) at $r = 1$ and $r = 0$.

• (c) End points in the monotonous non-decreasing solution vector $(\overline{h}_{1}^{\bullet }(s), \overline{h}_{2}^{\bullet }(s), \ldots ,\overline{h}_{n}^{\bullet }(s))$ are obtained by replacing $\underline{h}_{q}^{\bullet }(s)$ in terms of $\overline{h}_{q}^{\bullet }(s)$ by using the bipolar fuzzy center in (18) at $s = 0$ and $s = -1$.

• (d) End points in the monotonous non-increasing solution vector $(\underline{h}_{1}^{\bullet }(s), \underline{h}_{2}^{\bullet }(s), \ldots ,\underline{h}_{n}^{\bullet }(s))$ are obtained by replacing $\overline{h}_{q}^{\bullet }(s)$ in terms of $\underline{h}_{q}^{\bullet }(s)$ by using the bipolar fuzzy center in (18) at $s = 0$ and $s = -1$.

Proof

(a). We know that $h_{q}^{c}(r) = \frac{\underline{h}_{q}^{*}(r)~ +~ \overline{h}_{q}^{*}(r)}{2}$, which yields $\underline{h}_{q}^{*}(r)=2h_{q}^{c}(r) - \overline{h}_{q}^{*}(r)$ replace $\underline{h}_{q}^{*}(r)$ by using the above result in Eq. (17), we get

$$\begin{aligned} \sum _{l_{pq}\ge 0}l_{pq}\overline{h}_{q}^{*}(r) + \sum _{l_{pq}< 0}l_{pq}(2h_{q}^{c}(r) - \overline{h}_{q}^{*}(r))=\overline{z}_{p}^{*}(r), ~~~~p,q=1,2,\ldots ,n. \end{aligned}$$

This gives

$$\begin{aligned} \sum _{l_{pq}\ge 0}l_{pq}\overline{h}_{q}^{*}(r) - \sum _{l_{pq}< 0}l_{pq}\overline{h}_{q}^{*}(r) = \overline{z}_{p}^{*}(r) -2\sum _{l_{pq}< 0}l_{pq}h_{q}^{c} , ~~~~~p,q=1,2,\ldots n. \end{aligned}$$

(19)

The above Eq. (19) represents a crisp linear system when $r = 1$ and $r = 0$.

The crisp linear system can be solved by using simplest method and thus we get the solution vector $(\overline{h}_{1}^{*}(r), \overline{h}_{2}^{*}(r), \ldots ,\overline{h}_{n}^{*}(r))$ at $r = 1$ and $r = 0$.

(b).    Similar to (a).

(c). We know that $h_{q}^{c}(s) = \frac{\underline{h}_{q}^{\bullet }(s)~+~\overline{h}_{q}^{\bullet }(s)}{2}$, which yields $\underline{h}_{q}^{\bullet }(s)=2h_{q}^{c}(s) - \overline{h}_{q}^{*}(s)$ replace $\underline{h}_{q}^{\bullet }(s)$ by using the above result in Eq. (18), we get

$$\begin{aligned} \sum _{l_{pq}\ge 0}l_{pq}\overline{h}_{q}^{\bullet }(s) + \sum _{l_{pq}< 0}l_{pq}(2h_{q}^{c}(s) - \overline{h}_{q}^{\bullet }(s))=\overline{z}_{p}^{\bullet }(s), ~~~~p,q=1,2,\ldots ,n. \end{aligned}$$

This gives

$$\begin{aligned} \sum _{l_{pq}\ge 0}l_{pq}\overline{h}_{q}^{\bullet }(s) - \sum _{l_{pq}< 0}l_{pq}\overline{h}_{q}^{\bullet }(s) = \overline{z}_{p}^{\bullet }(s) -2\sum _{l_{pq}< 0}l_{pq}h_{q}^{c} ,~~~~~p,q=1,2,\ldots n. \end{aligned}$$

(20)

The above Eq. (20) represents a crisp linear system at $s = 0$ and $s = -1$.

The crisp system can be solved by using simplest method, thus we get the solution vector $(\overline{h}_{1}^{\bullet }(s), \overline{h}_{2}^{\bullet }(s),\ldots ,\overline{h}_{n}^{\bullet }(s))$ at $s = 0$ and $s = -1$.

(d).    Similar to (c). $\square$

When we identify the points in the graph by using the previous theorem, then we use these end points to obtained the equation of solution of straight line joining the two end points by using linear spline interpolation formula, i.e., $y =y_{1}+\frac{y_{2}-y_{1}}{x_{2}-x_{1}} (x - x_{1})$. This will give the complete solution of the particular system.

The following example is use to explain the above technique.

Example 4.3

Consider the $2 \times 2$ BFLS of equation in symmetric form

$$\begin{aligned} {\left\{ \begin{array}{ll} h_{1} - h_{2} &{}= {\prec [r, 2-r],[-1-3s, 5+3s]\succ },\\ h_{1} + 3h_{2} &{}= {\prec [4+2r, 8-2r],[-9-7s, 5+7s]\succ }. \end{array}\right. } \end{aligned}$$

First, we solve positive part$(*)$ of bipolar system, for this.

By using the Theorem (3.1), we have

$$\begin{aligned} h_{1}^{c}(r) - h_{2}^{c}(r)&= 1,\\ h_{1}^{c}(r) + 3h_{2}^{c}(r)&= 6. \end{aligned}$$

Solving the above system, we get

$$\begin{aligned} h_{1}^{c}(r) = \frac{9}{4}~~~~ , ~~~~ h_{2}^{c}(r) = \frac{5}{4}. \end{aligned}$$

Now, by using Eq. (17), we write

$$\begin{aligned} {\left\{ \begin{array}{ll} \underline{h}_{1}^{*}(r)-\overline{h}_{2}^{*}(r)= r,\\ \underline{h}_{1}^{*}(r)+3\underline{h}_{2}^{*}(r)=4+2r. \end{array}\right. } \end{aligned}$$

By replacing $\overline{h}_{2}^{*}(r)$ by $2h_{2}^{c}(r)-\underline{h}_{2}^{*}$ in $\underline{h}_{1}^{*}(r)-\overline{h}_{2}^{*}(r)= r$, and also substituting the value of $h_{2}^{c}(r)= \frac{5}{4}$, we obtained

$$\begin{aligned} {\left\{ \begin{array}{ll} \underline{h}_{1}^{*}(r)+\underline{h}_{2}^{*}(r)=r+\frac{5}{2},\\ \underline{h}_{1}^{*}(r)+3\underline{h}_{2}^{*}(r)=2r+4. \end{array}\right. } \end{aligned}$$

Putting $r=0$ in the above equations, the above equations are reduced to a crisp system that can be solved to give

$$\begin{aligned} \underline{h}_{1}^{*}(r)~ \mathrm{at}~ r=0~ is~ \frac{7}{4}~~~\mathrm{and}~~~\underline{h}_{2}^{*}(r)~ \mathrm{at}~ r=0~ \mathrm{is}~ \frac{3}{4}. \end{aligned}$$

Now, putting $r=1$ in the above equations, the the above equations are reduced to a crisp system that gives

$$\begin{aligned} \underline{h}_{1}^{*}(r)~ \mathrm{at}~ r=1~ \mathrm{is}~ \frac{9}{4}~~~\mathrm{and}~~~\underline{h}_{2}^{*}(r)~ \mathrm{at}~ r=1~ is~ \frac{5}{4}. \end{aligned}$$

The solution equation is obtained by drawing the straight line using these two end points $(\frac{7}{4},0)$ and $(\frac{9}{4},1)$ in graph, we obtained the required solution for $\underline{h}_{1}^{*}(r)$,

$$\begin{aligned} \underline{h}_{1}^{*}(r) = \frac{7}{4}+\frac{1}{2}r. \end{aligned}$$

Similarly, the solution equation is obtained by drawing the straight line using these two end points $(\frac{3}{4},0)$ and $(\frac{5}{4},1)$ in graph, we obtained the required solution for $\underline{h}_{2}^{*}(r)$,

$$\begin{aligned} \underline{h}_{2}^{*}(r) = \frac{3}{4}+\frac{1}{2}r. \end{aligned}$$

In the similar way, using Eq. (17) we write

$$\begin{aligned} {\left\{ \begin{array}{ll} \overline{h}_{1}^{*}(r)-\underline{h}_{2}^{*}(r)= 2-r,\\ \overline{h}_{1}^{*}(r)+3\overline{h}_{2}^{*}(r)=8-2r. \end{array}\right. } \end{aligned}$$

By replacing $\underline{h}_{2}^{*}(r)$ by $2h_{2}^{c}(r)-\overline{h}_{2}^{*}(r)$ in $\overline{h}_{1}^{*}(r)-\underline{h}_{2}^{*}(r)= 2-r$, and also substituting the value of $h_{2}^{c}(r)= \frac{5}{4}$, we obtained

$$\begin{aligned} {\left\{ \begin{array}{ll} \overline{h}_{1}^{*}(r)+\overline{h}_{2}^{*}(r)=\frac{9}{2}-r,\\ \overline{h}_{1}^{*}(r)+3\overline{h}_{2}^{*}(r)=8-2r. \end{array}\right. } \end{aligned}$$

Putting $r=0$ in the above equations, the above equations are reduced to a crisp system that can be solved to give

$$\begin{aligned} \overline{h}_{1}^{*}(r)~ \mathrm{at}~ r=0~ \mathrm{is}~ \frac{11}{4}~~~\mathrm{and}~~~\overline{h}_{2}^{*}(r)~ \mathrm{at}~ r=0~ is~ \frac{7}{4}. \end{aligned}$$

Similarly, putting $r=1$ in the above equations, the above equations are reduced to a crisp system that gives

$$\begin{aligned} \overline{h}_{1}^{*}(r)~ \mathrm{at}~ r=1~ \mathrm{is}~ \frac{9}{4}~~~\mathrm{and}~~~\underline{h}_{2}^{*}(r)~ \mathrm{at}~ r=1~ is~ \frac{5}{4}. \end{aligned}$$

The solution equation is obtained by drawing the straight line using these two end points $(\frac{11}{4},0)$ and $(\frac{9}{4},1)$ in graph, we obtained the required solution for $\overline{h}_{1}^{*}(r)$,

$$\begin{aligned} \overline{h}_{1}^{*}(r) = \frac{11}{4}-\frac{1}{2}r. \end{aligned}$$

Similarly, the solution equation is obtained by drawing the straight line using these two end points $(\frac{7}{4},0)$ and $(\frac{9}{4},1)$ in graph, we obtained the required solution for $\overline{h}_{2}^{*}(r)$,

$$\begin{aligned} \overline{h}_{2}^{*}(r) = \frac{7}{4}-\frac{1}{2}r. \end{aligned}$$

The graphical solution for positive$(*)$ membership function of bipolar solution number is shown below in Fig. 9.

Fig. 9

The graphical representation of positive$(*)$ membership functions $\underline{h}^{*}(r)$, $\overline{h}^{*}(r)$ of bipolar fuzzy numbers

Secondly, we solve for negative$(\bullet )$ part of bipolar system, for this

By using the Theorem (3.1), we have

$$\begin{aligned} h_{1}^{c}(s) - h_{2}^{c}(s)&= 2,\\ h_{1}^{c}(s) + 3h_{2}^{c}(s)&= -2. \end{aligned}$$

Solving the above system, we get

$$\begin{aligned} h_{1}^{c}(s) = 1~~~~ , ~~~~ h_{2}^{c}(s) = -1. \end{aligned}$$

Now, by using Eq. (18), we write

$$\begin{aligned} {\left\{ \begin{array}{ll} \underline{h}_{1}^{\bullet }(s)-\overline{h}_{2}^{\bullet }(s)= -1-3s,\\ \underline{h}_{1}^{\bullet }(s)+3\underline{h}_{2}^{\bullet }(s)=-9-7s. \end{array}\right. } \end{aligned}$$

By replacing $\overline{h}_{2}^{\bullet }(s)$ by $2h_{2}^{c}(s)-\underline{h}_{2}^{\bullet }(s)$ in $\underline{h}_{1}^{\bullet }(s)-\overline{h}_{2}^{\bullet }(s)= -1-3s$, and also substituting the value of $h_{2}^{c}(s)= -1$ we obtained

$$\begin{aligned} {\left\{ \begin{array}{ll} \underline{h}_{1}^{\bullet }(s)+\underline{h}_{2}^{\bullet }(s)=-3-3s,\\ \underline{h}_{1}^{\bullet }(s)+3\underline{h}_{2}^{\bullet }(s)=-9-7s. \end{array}\right. } \end{aligned}$$

Putting $s=0$ in the above equations, the above equations are reduced to a crisp system that can be solved to give

$$\begin{aligned} \underline{h}_{1}^{\bullet }(s)~ \mathrm{at}~ s=0~ \mathrm{is}~ 0~~~\mathrm{and}~~~\underline{h}_{2}^{\bullet }(s)~ \mathrm{at}~ s=0~ \mathrm{is}~ -3. \end{aligned}$$

Similarly, putting $s=-1$ in the above equations, the above equations are reduced to a crisp system that gives

$$\begin{aligned} \underline{h}_{1}^{\bullet }(s)~ \mathrm{at}~ s=-1~ \mathrm{is}~ 1~~~\mathrm{and}~~~\underline{h}_{2}^{\bullet }(s)~ \mathrm{at}~ s=-1~ is~ -1. \end{aligned}$$

The solution equation is obtained by drawing the straight line using these two end points (0, 0) and $(1,-1)$ in graph, we obtained the required solution for $\underline{h}_{1}^{\bullet }(s)$.

$$\begin{aligned} \underline{h}_{1}^{\bullet }(s) = -s. \end{aligned}$$

Similarly, the solution equation is obtained by drawing the straight line using these two end points $(-3,0)$ and $(-1,-1)$ in graph, we obtained the required solution for $\underline{h}_{2}^{\bullet }(s)$,

$$\begin{aligned} \underline{h}_{2}^{\bullet }(s) = -3-2s. \end{aligned}$$

In the similar way, by using Eq. (18) we have

$$\begin{aligned} {\left\{ \begin{array}{ll} \overline{h}_{1}^{\bullet }(s)-\underline{h}_{2}^{\bullet }(s)= 5+3s,\\ \overline{h}_{1}^{\bullet }(s)+3\overline{h}_{2}^{\bullet }(s)=5+7s. \end{array}\right. } \end{aligned}$$

By replacing $\underline{h}_{2}^{\bullet }(s)$ by $2h_{2}^{c}(s)-\overline{h}_{2}^{\bullet }(s)$ in $\overline{h}_{1}^{\bullet }(s)-\underline{h}_{2}^{\bullet }(s)= 5+3s$, and also substituting the value of $h_{2}^{c}(s)= -1$ we obtained

$$\begin{aligned} {\left\{ \begin{array}{ll} \overline{h}_{1}^{\bullet }(s)+\overline{h}_{2}^{\bullet }(s)=3+3s,\\ \overline{h}_{1}^{\bullet }(s)+3\overline{h}_{2}^{\bullet }(s)=5+7s. \end{array}\right. } \end{aligned}$$

Putting $s=0$ in the above equations, the above equations are reduced to a crisp system that can be solved to give

$$\begin{aligned} \overline{h}_{1}^{\bullet }(s)~ \mathrm{at}~ s=0~ \mathrm{is}~ 2~~~\mathrm{and~}~~\overline{h}_{2}^{\bullet }(s)~ \mathrm{at}~ s=0~ \mathrm{is}~ 1. \end{aligned}$$

Similarly, putting $s=-1$ in the above equations, they are reduced to a crisp system that gives

$$\begin{aligned} \overline{h}_{1}^{*}(s)~ \mathrm{at}~ s=-1~ \mathrm{is}~ 1~~~\mathrm{and}~~~\underline{h}_{2}^{\bullet }(s)~ \mathrm{at}~ s=-1~ \mathrm{is}~ -1. \end{aligned}$$

The solution equation is obtained by drawing the straight line using these two end points (2, 0) and $(1,-1)$ in graph, we obtained the required solution for $\overline{h}_{1}^{\bullet }(s)$.

$$\begin{aligned} \overline{h}_{1}^{\bullet }(s) = 2+s. \end{aligned}$$

Similarly, the solution equation is obtained by drawing the straight line using these two end points (1, 0) and $(-1,-1)$ in graph, we obtained the required solution for $\overline{h}_{2}^{\bullet }(s)$,

$$\begin{aligned} \overline{h}_{2}^{\bullet }(s) = 1+2s. \end{aligned}$$

The graphical solution for negative$(\bullet )$ membership function of bipolar solution number is shown below in Fig.10.

Fig. 10

The graphical representation of negative$(\bullet )$ membership functions $\underline{h}^{\bullet }(s)$, $\overline{h}^{\bullet }(s)$ of bipolar fuzzy numbers

Thus, the solution of symmetric BFLS of equation in (4.3) is given as,

$$\begin{aligned} h_{1}&={\prec [\underline{h}_{1}^{*}(r),\overline{h}_{1}^{*}(r)],[\underline{h}_{1}^{\bullet }(s),\overline{h}_{1}^{\bullet }(s)]\succ =\prec [\frac{7}{4} + \frac{1}{2}r,\frac{11}{4} - \frac{1}{2}r],[-s,2+s]\succ },\\ h_{2}&={\prec [\underline{h}_{2}^{*}(r),\overline{h}_{2}^{*}(r)],[\underline{h}_{2}^{\bullet }(s),\overline{h}_{2}^{\bullet }(s)]\succ =\prec [\frac{3}{4} + \frac{1}{2}r,\frac{7}{4} - \frac{1}{2}r],[-3-2s,1+2s]\succ }. \end{aligned}$$

It is noted that, the solution of BFLS of equation in (4.3) is same as (3.3).

6 Fully bipolar fuzzy solution of linear system by using interval

In this section, we propose a method to solve FBFL system of equations in which unknown parameter, right-side vector are BFN and coefficients of unknown are BTFNs. Suparna and Chakraverty (2011) suggested a method to solve $n \times n$ fully fuzzy linear system in which coefficient matrix is a fuzzy matrix and unknown and right-side vector are fuzzy number. We extent the Chakraverty technique to solve fully fuzzy linear system in bipolar fuzzy environment. First, we will convert BTFNs in the form of interval using $\alpha$-cut, and then solve the FBFL system using the proposed method in this section. We use this technique to solve the example of circuit flow and find the current which is calculated in terms of BFN.

Definition 5.1

A BTFN is defined as $\widetilde{A}= (a_{1},a_{2},a_{3})(a_{4},a_{5},a_{6})$ with negative$(\bullet )$ and positive$(*)$ membership functions $\sigma _{\widetilde{A}}^{\bullet }$ and $\sigma _{\widetilde{A}}^{*}$ as follows:

$$\begin{aligned} \sigma _{\widetilde{A}}^{\bullet }= & {} {\left\{ \begin{array}{ll} \begin{array}{cc} \dfrac{(a_{1}-x)}{(a_{2}-a_{1})}, &{} \mathrm{if}~ x~ \in ~ [a_{1},a_{2}],\\ \\ \dfrac{(x-a_{3})}{(a_{3}-a_{2})}, &{} \mathrm{if}~ x~ \in ~ [a_{3},a_{2}],\\ 0, &{} \mathrm{otherwise}, \end{array} \end{array}\right. }\\ \sigma _{\widetilde{A}}^{*}= & {} {\left\{ \begin{array}{ll} \begin{array}{ll} \dfrac{(x-a_{4})}{(a_{5}-a_{4})}, &{} \mathrm{if}~ x~ \in ~ [a_{4},a_{5}],\\ \\ \dfrac{(a_{6}-x)}{(a_{6}-a_{5})}, &{} \mathrm{if}~ x~ \in ~ [a_{5},a_{6}],\\ 0, &{} \mathrm{otherwise}, \end{array} \end{array}\right. } \end{aligned}$$

where $\sigma _{\widetilde{A}}^{\bullet }$ and $\sigma _{\widetilde{A}}^{*}$ are the membership functions of negative and positive polars.

Conversion from BTFN to interval using alpha cut

Let, a BTFN defined as $\widetilde{H}= (h_{1},h_{2},h_{3})(h_{4},h_{5},h_{6})$ , to find $\alpha$-cut of $\widetilde{H}$ we set $\alpha$ equal to the negative and positive membership functions of $\widetilde{H}$. That is,

$$\begin{aligned} \alpha =\frac{(h_{1}-x)}{(h_{2}-h_{1})} ,~~ \alpha =\frac{(x-h_{3})}{(h_{3}-h_{2})}, \end{aligned}$$

and

$$\begin{aligned} \alpha =\frac{(x-h_{4})}{(h_{5}-h_{4})} ,~~ \alpha =\frac{(h_{6}-x)}{(h_{6}-h_{5})}. \end{aligned}$$

Expressing each x in terms of $\alpha$ we get, $x_{1}=h_{1}-\alpha (h_{2}-h_{1})$ , $x_{2}=h_{3}+\alpha (h_{3}-h_{2})$ and $x_{3}=h_{4}+\alpha (h_{5}-h_{4})$ , $x_{4}=h_{6}-\alpha (h_{6}-h_{5})$.

Therefore, we can write the BTFN in $\alpha$-cut interval as:

$$\begin{aligned} \widetilde{H}_{\alpha }= [h_{1}-\alpha (h_{2}-h_{1}),h_{3}+\alpha (h_{3}-h_{2})][h_{4}+\alpha (h_{5}-h_{4}),h_{6}-\alpha (h_{6}-h_{5})] \end{aligned}$$

Definition 5.2

An interval is a subset of $\mathfrak {R}$ is given as $H=[h_{1},h_{2}]$=$\{t|~h_{1} \le t \le h_{2},~where h_{1},h_{2}~ \epsilon ~ \mathfrak {R}\}$. For arbitrary $H=[h_{1},h_{2}]$ and $G=[g_{1},g_{2}]$ are two intervals, then we defined their addition, subtraction, product and division as follows:

• (i) $[h_{1},h_{2}]+[g_{1},g_{2}]=[h_{1} + g_{1},h_{2} + g_{2}],$

• (ii) $[h_{1},h_{2}]-[g_{1},g_{2}]=[h_{1} - g_{2},h_{2} - g_{1}],$

• (iii) $[h_{1},h_{2}]\bullet [g_{1},g_{2}]=[\min (h_{1}g_{1},h_{1}g_{2},h_{2}g_{1},h_{2}g_{2}),\max (h_{1}g_{1},h_{1}g_{2},h_{2}g_{1},h_{2}g_{2})],$

• (iv) $[h_{1},h_{2}]/[g_{1},g_{2}]=[\min (h_{1}/g_{1},h_{1}/g_{2},h_{2}/g_{1},h_{2}/g_{2}),\max (h_{1}/g_{1},h_{1}/g_{2},h_{2}/g_{1},h_{2}/g_{2})],$ where $g_{1}, g_{2} \ne 0.$

Definition 5.3

Consider a $n \times n$ system of linear equations given as,

$$\begin{aligned} {\left\{ \begin{array}{ll} l_{11}h_{1} + l_{12}h_{2} + \cdots + l_{1n}h_{n}&{}= z_{1},\\ l_{21}h_{1} + l_{22}h_{2} + \cdots + l_{2n}h_{n}&{}= z_{2},\\ \cdot \\ \cdot \\ \cdot \\ l_{n1}h_{1} + l_{n2}h_{2} + \cdots + l_{nn}h_{n}&{}= z_{n},\\ \end{array}\right. } \end{aligned}$$

(21)

where the coefficient elements $(l_{pq})$, $1 \le p,q \le n$ is a bipolar fuzzy matrix of order $n \times n$ and each $z_{q}$, $1 \le q \le n$ and unknown $h_{p}$, $1 \le p \le n$ are also BFN, is known as the FBFL system of equations.

Convert the BFNs in interval form using $\alpha$-cut in equation (21) and then we can write $n \times n$ FBFL system of equations as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} {[}\underline{l}_{11}^{*},\overline{l}_{11}^{*}][\underline{l}_{11}^{\bullet },\overline{l}_{11}^{\bullet }]h_{1}+[\underline{l}_{12}^{*},\overline{l}_{12}^{*}][\underline{l}_{12}^{\bullet },\overline{l}_{12}^{\bullet }]h_{2}+\cdots +[\underline{l}_{1n}^{*},\overline{l}_{1n}^{*}][\underline{l}_{1n}^{\bullet },\overline{l}_{1n}^{\bullet }]h_{n}=[\underline{z}_{1}^{*},\overline{z}_{1}^{*}][\underline{z}_{1}^{\bullet },\overline{z}_{1}^{\bullet }],\\ {[}\underline{l}_{21}^{*},\overline{l}_{21}^{*}][\underline{l}_{21}^{\bullet },\overline{l}_{21}^{\bullet }]h_{1}+[\underline{l}_{22}^{*},\overline{l}_{22}^{*}][\underline{l}_{22}^{\bullet },\overline{l}_{22}^{\bullet }]h_{2}+\cdots +[\underline{l}_{2n}^{*},\overline{l}_{2n}^{*}][\underline{l}_{2n}^{\bullet },\overline{l}_{2n}^{\bullet }]h_{n}=[\underline{z}_{2}^{*},\overline{z}_{2}^{*}][\underline{z}_{2}^{\bullet },\overline{z}_{2}^{\bullet }],\\ .\\ .\\ .\\ {[}\underline{l}_{n1}^{*},\overline{l}_{n1}^{*}][\underline{l}_{n1}^{\bullet },\overline{l}_{n1}^{\bullet }]h_{1}+[\underline{l}_{n2}^{*},\overline{l}_{n2}^{*}][\underline{l}_{n2}^{\bullet },\overline{l}_{n2}^{\bullet }]h_{2}+\cdots +[\underline{l}_{nn}^{*},\overline{l}_{nn}^{*}][\underline{l}_{nn}^{\bullet },\overline{l}_{nn}^{\bullet }]h_{n}=[\underline{z}_{n}^{*},\overline{z}_{n}^{*}][\underline{z}_{n}^{\bullet },\overline{z}_{n}^{\bullet }],\\ \end{array}\right. } \end{aligned}$$

(22)

where all $l_{pq}$, $1 \le p,q \le n$ are positive real numbers.

First, we take positive$(*)$ crisp interval system from equations (22) and written into the following form:

$$\begin{aligned} {\left\{ \begin{array}{ll} {[}\underline{l}_{11}^{*},\overline{l}_{11}^{*}][\underline{h}_{1}^{*},\overline{h}_{1}^{*}]+[\underline{l}_{12}^{*},\overline{l}_{12}^{*}][\underline{h}_{2}^{*},\overline{h}_{2}^{*}]+ \cdots +[\underline{l}_{1n}^{*},\overline{l}_{1n}^{*}][\underline{h}_{n}^{*},\overline{h}_{n}^{*}]=[\underline{z}_{1}^{*},\overline{z}_{1}^{*}],\\ {[}\underline{l}_{21}^{*},\overline{l}_{21}^{*}][\underline{h}_{1}^{*},\overline{h}_{1}^{*}]+[\underline{l}_{22}^{*},\overline{l}_{22}^{*}][\underline{h}_{2}^{*},\overline{h}_{2}^{*}]+ \cdots +[\underline{l}_{2n}^{*},\overline{l}_{2n}^{*}][\underline{h}_{n}^{*},\overline{h}_{n}^{*}]=[\underline{z}_{2}^{*},\overline{z}_{2}^{*}],\\ .\\ .\\ .\\ {[}\underline{l}_{n1}^{*},\overline{l}_{n1}^{*}][\underline{h}_{1}^{*},\overline{h}_{1}^{*}]+[\underline{l}_{n2}^{*},\overline{l}_{n2}^{*}][\underline{h}_{2}^{*},\overline{h}_{2}^{*}]+ \cdots +[\underline{l}_{nn}^{*},\overline{l}_{nn}^{*}][\underline{h}_{n}^{*},\overline{h}_{n}^{*}]=[\underline{z}_{n}^{*},\overline{z}_{n}^{*}]. \end{array}\right. } \end{aligned}$$

(23)

The system in (23) may be written in linear equations form as

$$\begin{aligned} \begin{array}{ccl} \underline{l}_{11}^{*}\underline{h}_{1}^{*}+\underline{l}_{12}^{*}\underline{h}_{2}^{*}+ \cdots +\underline{l}_{1n}^{*}\underline{h}_{n}^{*}=\underline{z}_{1}^{*},\\ \overline{1}_{11}^{*}\overline{h}_{1}^{*}+\overline{l}_{12}^{*}\overline{h}_{2}^{*}+ \cdots +\overline{l}_{1n}^{*}\overline{h}_{n}^{*}=\overline{z}_{1}^{*},\\ \underline{l}_{21}^{*}\underline{h}_{1}^{*}+\underline{l}_{22}^{*}\underline{h}_{2}^{*}+ \cdots +\underline{l}_{2n}^{*}\underline{h}_{n}^{*}=\underline{z}_{2}^{*},\\ \overline{1}_{21}^{*}\overline{h}_{1}^{*}+\overline{l}_{22}^{*}\overline{h}_{2}^{*}+ \cdots +\overline{l}_{2n}^{*}\overline{h}_{n}^{*}=\overline{z}_{2}^{*},\\ .\\ .\\ \underline{l}_{n1}^{*}\underline{h}_{1}^{*}+\underline{l}_{n2}^{*}\underline{h}_{2}^{*}+ \cdots +\underline{l}_{nn}^{*}\underline{h}_{n}^{*}=\underline{z}_{n}^{*},\\ \overline{1}_{n1}^{*}\overline{h}_{1}^{*}+\overline{l}_{n2}^{*}\overline{h}_{2}^{*}+ \cdots +\overline{l}_{nn}^{*}\overline{h}_{n}^{*}=\overline{z}_{n}^{*},\\ \end{array} \end{aligned}$$

(24)

and Eq. (24) can be written in matrix form as given:

$$\begin{aligned} \left( \begin{array}{cccccccccccc} \underline{l}_{11}^{*} &{} \underline{l}_{12}^{*} &{} . &{} . &{} . &{} \underline{l}_{1n}^{*} &{} 0 &{} 0 &{} . &{} . &{} . &{} 0 \\ 0 &{} 0 &{} . &{} . &{} . &{} 0 &{} \overline{l}_{11}^{*} &{} \overline{l}_{12}^{*} &{} . &{} . &{} . &{} \overline{l}_{1n}^{*} \\ \underline{l}_{21}^{*} &{} \underline{l}_{22}^{*} &{} . &{} . &{} . &{} \underline{l}_{2n}^{*} &{} 0 &{} 0 &{} . &{} . &{} . &{} 0 \\ 0 &{} 0 &{} . &{} . &{} . &{} 0 &{} \overline{l}_{21}^{*} &{} \overline{l}_{22}^{*} &{} . &{} . &{} . &{} \overline{l}_{2n}^{*} \\ . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . \\ \underline{l}_{n1}^{*} &{} \underline{l}_{2n}^{*} &{} . &{} . &{} . &{} \underline{l}_{nn}^{*} &{} 0 &{} 0 &{} . &{} . &{} . &{} 0 \\ 0 &{} 0 &{} . &{} . &{} . &{} 0 &{} \overline{l}_{n1}^{*} &{} \overline{l}_{n2}^{*} &{} . &{} . &{} . &{} \overline{l}_{nn}^{*} \\ \end{array} \right) \left( \begin{array}{c} \underline{h}_{1}^{*} \\ \underline{h}_{2}^{*} \\ . \\ . \\ . \\ \underline{h}_{n}^{*} \\ \overline{h}_{1}^{*} \\ \overline{h}_{2}^{*} \\ . \\ . \\ . \\ \overline{h}_{n}^{*} \\ \end{array} \right) = \left( \begin{array}{c} \underline{z}_{1}^{*} \\ \overline{z}_{1}^{*} \\ \underline{z}_{2}^{*} \\ \overline{z}_{2}^{*} \\ . \\ . \\ . \\ \underline{z}_{n}^{*} \\ \overline{z}_{n}^{*} \\ \end{array} \right) . \end{aligned}$$

(25)

Similarly, we take negative$(\bullet )$ crisp interval system from equations (22) and written into the following form:

$$\begin{aligned} {\left\{ \begin{array}{ll} {[}\underline{l}_{11}^{\bullet },\overline{l}_{11}^{\bullet }][\underline{h}_{1}^{\bullet },\overline{h}_{1}^{\bullet }]+[\underline{l}_{12}^{\bullet },\overline{l}_{12}^{\bullet }][\underline{h}_{2}^{\bullet },\overline{h}_{2}^{\bullet }]+ \cdots +[\underline{l}_{1n}^{\bullet },\overline{l}_{1n}^{\bullet }][\underline{h}_{n}^{\bullet },\overline{h}_{n}^{\bullet }]=[\underline{z}_{1}^{\bullet },\overline{z}_{1}^{\bullet }],\\ {[}\underline{l}_{21}^{\bullet },\overline{l}_{21}^{\bullet }][\underline{h}_{1}^{\bullet },\overline{h}_{1}^{\bullet }]+[\underline{l}_{22}^{\bullet },\overline{l}_{22}^{\bullet }][\underline{h}_{2}^{\bullet },\overline{h}_{2}^{\bullet }]+ \cdots +[\underline{l}_{2n}^{\bullet },\overline{l}_{2n}^{\bullet }][\underline{h}_{n}^{\bullet },\overline{h}_{n}^{\bullet }]=[\underline{z}_{2}^{\bullet },\overline{z}_{2}^{\bullet }],\\ .\\ .\\ .\\ {[}\underline{l}_{n1}^{\bullet },\overline{l}_{n1}^{\bullet }][\underline{h}_{1}^{\bullet },\overline{h}_{1}^{\bullet }]+[\underline{l}_{n2}^{\bullet },\overline{l}_{n2}^{\bullet }][\underline{h}_{2}^{\bullet },\overline{h}_{2}^{\bullet }]+ \cdots +[\underline{l}_{nn}^{\bullet },\overline{l}_{nn}^{\bullet }][\underline{h}_{n}^{\bullet },\overline{h}_{n}^{\bullet }]=[\underline{z}_{n}^{\bullet },\overline{z}_{n}^{\bullet }]. \end{array}\right. } \end{aligned}$$

(26)

The system in (26) may be written in linear equations form as

$$\begin{aligned} \begin{array}{ccl} \underline{l}_{11}^{\bullet }\underline{h}_{1}^{\bullet }+\underline{l}_{12}^{\bullet }\underline{h}_{2}^{\bullet }+ \cdots +\underline{l}_{1n}^{\bullet }\underline{h}_{n}^{\bullet }=\underline{z}_{1}^{\bullet },\\ \overline{1}_{11}^{\bullet }\overline{h}_{1}^{\bullet }+\overline{l}_{12}^{\bullet }\overline{h}_{2}^{\bullet }+ \cdots +\overline{l}_{1n}^{\bullet }\overline{h}_{n}^{\bullet }=\overline{z}_{1}^{\bullet },\\ \underline{l}_{21}^{\bullet }\underline{h}_{1}^{\bullet }+\underline{l}_{22}^{\bullet }\underline{h}_{2}^{\bullet }+ \cdots +\underline{l}_{2n}^{\bullet }\underline{h}_{n}^{\bullet }=\underline{z}_{2}^{\bullet },\\ \overline{1}_{21}^{\bullet }\overline{h}_{1}^{\bullet }+\overline{l}_{22}^{\bullet }\overline{h}_{2}^{\bullet }+ \cdots +\overline{l}_{2n}^{\bullet }\overline{h}_{n}^{\bullet }=\overline{z}_{2}^{\bullet },\\ .\\ .\\ \underline{l}_{n1}^{\bullet }\underline{h}_{1}^{\bullet }+\underline{l}_{n2}^{\bullet }\underline{h}_{2}^{\bullet }+ \cdots +\underline{l}_{nn}^{\bullet }\underline{h}_{n}^{\bullet }=\underline{z}_{n}^{\bullet },\\ \overline{1}_{n1}^{\bullet }\overline{h}_{1}^{\bullet }+\overline{l}_{n2}^{\bullet }\overline{h}_{2}^{\bullet }+ \cdots +\overline{l}_{nn}^{\bullet }\overline{h}_{n}^{\bullet }=\overline{z}_{n}^{\bullet },\\ \end{array} \end{aligned}$$

(27)

and Eq. (27) can be written in matrix form as given:

$$\begin{aligned} \left( \begin{array}{cccccccccccc} \underline{l}_{11}^{\bullet } &{} \underline{l}_{12}^{\bullet } &{} \cdot &{} \cdot &{} \cdot &{} \underline{l}_{1n}^{\bullet } &{} 0 &{} 0 &{} \cdot &{} \cdot &{} \cdot &{} 0 \\ 0 &{} 0 &{} \cdot &{} \cdot &{} \cdot &{} 0 &{} \overline{l}_{11}^{\bullet } &{} \overline{l}_{12}^{\bullet } &{} \cdot &{} \cdot &{} \cdot &{} \overline{l}_{1n}^{\bullet } \\ \underline{l}_{21}^{\bullet } &{} \underline{l}_{22}^{\bullet } &{} \cdot &{} \cdot &{} \cdot &{} \underline{l}_{2n}^{\bullet } &{} 0 &{} 0 &{} \cdot &{} \cdot &{} \cdot &{} 0 \\ 0 &{} 0 &{} \cdot &{} \cdot &{} \cdot &{} 0 &{} \overline{l}_{21}^{\bullet } &{} \overline{l}_{22}^{\bullet } &{} \cdot &{} \cdot &{} \cdot &{} \overline{l}_{2n}^{\bullet } \\ \cdot &{} \cdot &{} \cdot &{} \cdot &{} \cdot &{} \cdot &{} \cdot &{} \cdot &{} \cdot &{} \cdot &{} \cdot &{} \cdot \\ \cdot &{} \cdot &{} \cdot &{} \cdot &{} \cdot &{} \cdot &{} \cdot &{} \cdot &{} \cdot &{} \cdot &{} \cdot &{} \cdot \\ \cdot &{} \cdot &{} \cdot &{} \cdot &{} \cdot &{} \cdot &{} \cdot &{} \cdot &{} \cdot &{} \cdot &{} \cdot &{} \cdot \\ \underline{l}_{n1}^{\bullet } &{} \underline{l}_{2n}^{\bullet } &{} \cdot &{} \cdot &{} \cdot &{} \underline{l}_{nn}^{\bullet } &{} 0 &{} 0 &{} \cdot &{} \cdot &{} \cdot &{} 0 \\ 0 &{} 0 &{} \cdot &{} \cdot &{} \cdot &{} 0 &{} \overline{l}_{n1}^{\bullet } &{} \overline{l}_{n2}^{\bullet } &{} \cdot &{} \cdot &{} \cdot &{} \overline{l}_{nn}^{\bullet } \\ \end{array} \right) \left( \begin{array}{c} \underline{h}_{1}^{\bullet } \\ \underline{h}_{2}^{\bullet } \\ . \\ . \\ . \\ \underline{h}_{n}^{\bullet } \\ \overline{h}_{1}^{\bullet } \\ \overline{h}_{2}^{\bullet } \\ . \\ . \\ . \\ \overline{h}_{n}^{\bullet } \\ \end{array} \right) = \left( \begin{array}{c} \underline{z}_{1}^{\bullet } \\ \overline{z}_{1}^{\bullet } \\ \underline{z}_{2}^{\bullet } \\ \overline{z}_{2}^{\bullet } \\ . \\ . \\ . \\ \underline{z}_{n}^{\bullet } \\ \overline{z}_{n}^{\bullet } \\ \end{array} \right) . \end{aligned}$$

(28)

For the clear understanding, we consider the $2 \times 2$ FBFL system of equations,

$$\begin{aligned} {\left\{ \begin{array}{ll} {[}\underline{l}_{11}^{*},\overline{l}_{11}^{*}][\underline{l}_{11}^{\bullet },\overline{l}_{11}^{\bullet }][\underline{h}_{1}^{*},\overline{h}_{1}^{*}][\underline{h}_{1}^{\bullet },\overline{h}_{1}^{\bullet }]+[\underline{l}_{12}^{*},\overline{l}_{12}^{*}][\underline{l}_{12}^{\bullet },\overline{l}_{12}^{\bullet }][\underline{h}_{2}^{*},\overline{h}_{2}^{*}][\underline{h}_{2}^{\bullet },\overline{}_{2}^{\bullet }]=[\underline{z}_{1}^{*},\overline{z}_{1}^{*}][\underline{z}_{1}^{\bullet },\overline{z}_{1}^{\bullet }],\\ {[}\underline{l}_{21}^{*},\overline{l}_{21}^{*}][\underline{l}_{21}^{\bullet },\overline{l}_{21}^{\bullet }][\underline{h}_{1}^{*},\overline{h}_{1}^{*}][\underline{h}_{1}^{\bullet },\overline{h}_{1}^{\bullet }]+[\underline{l}_{22}^{*},\overline{l}_{22}^{*}][\underline{l}_{22}^{\bullet },\overline{l}_{22}^{\bullet }][\underline{h}_{2}^{*},\overline{h}_{2}^{*}][\underline{h}_{2}^{\bullet },\overline{}_{2}^{\bullet }]=[\underline{z}_{2}^{*},\overline{z}_{2}^{*}][\underline{z}_{2}^{\bullet },\overline{z}_{2}^{\bullet }].\\ \end{array}\right. } \end{aligned}$$

(29)

First, we take the positive$(*)$ crisp interval equations for the system (29),

$$\begin{aligned} {\left\{ \begin{array}{ll} {[}\underline{l}_{11}^{*},\overline{l}_{11}^{*}][\underline{h}_{1}^{*},\overline{h}_{1}^{*}]+[\underline{l}_{12}^{*},\overline{l}_{12}^{*}][\underline{h}_{2}^{*},\overline{h}_{2}^{*}]=[\underline{z}_{1}^{*},\overline{z}_{1}^{*}],\\ {[}\underline{l}_{21}^{*},\overline{l}_{21}^{*}][\underline{h}_{1}^{*},\overline{h}_{1}^{*}]+[\underline{l}_{22}^{*},\overline{l}_{22}^{*}][\underline{h}_{2}^{*},\overline{h}_{2}^{*}]=[\underline{z}_{2}^{*},\overline{z}_{2}^{*}],\\ \end{array}\right. } \end{aligned}$$

(30)

and the system of Eq. (30) can be written in matrix form as

$$\begin{aligned} \left( \begin{array}{cccc} \underline{l}_{11}^{*} &{} \underline{l}_{12}^{*} &{} 0 &{} 0 \\ 0 &{} 0 &{} \overline{l}_{11}^{*} &{} \overline{l}_{12}^{*} \\ \underline{l}_{21}^{*} &{} \underline{l}_{22}^{*} &{} 0 &{} 0 \\ 0 &{} 0 &{} \overline{l}_{21}^{*} &{} \overline{l}_{22}^{*} \\ \end{array} \right) \left( \begin{array}{c} \underline{h}_{1}^{*} \\ \underline{h}_{2}^{*} \\ \overline{h}_{1}^{*} \\ \overline{h}_{2}^{*} \\ \end{array} \right) = \left( \begin{array}{c} \underline{z}_{1}^{*} \\ \overline{z}_{1}^{*} \\ \underline{z}_{2}^{*} \\ \overline{z}_{2}^{*} \\ \end{array} \right) . \end{aligned}$$

This matrix equation may be easily solved and the solutions from this matrix equation are given as:

$$\begin{aligned} \underline{h}_{1}^{*}=\frac{\underline{l}_{22}^{*}\underline{z}_{1}^{*} -\underline{l}_{12}^{*}\underline{z}_{2}^{*}}{\underline{l}_{11}^{*}\underline{l}_{22}^{*}-\underline{l}_{12}^{*}\underline{l}_{21}^{*}}~~~,~~~~ \underline{h}_{2}^{*}=\frac{\underline{l}_{11}^{*}\underline{z}_{2}^{*} -\underline{l}_{21}^{*}\underline{z}_{1}^{*}}{\underline{l}_{11}^{*}\underline{l}_{22}^{*}-\underline{l}_{12}^{*}\underline{l}_{21}^{*}},\\ \overline{h}_{1}^{*}=\frac{\overline{l}_{22}^{*}\overline{z}_{1}^{*}-\overline{l}_{12}^{*}\overline{z}_{2}^{*}}{\overline{l}_{11}^{*}\overline{l}_{22}^{*}-\overline{l}_{12}^{*}\overline{l}_{21}^{*}}~~~,~~~ \overline{h}_{2}^{*}=\frac{\overline{l}_{11}^{*}\overline{z}_{2}^{*}-\overline{l}_{21}^{*}\overline{z}_{1}^{*}}{\overline{l}_{11}^{*}\overline{l}_{22}^{*}-\overline{l}_{12}^{*}\overline{l}_{21}^{*}}, \end{aligned}$$

where $\underline{l}_{11}^{*}\underline{l}_{22}^{*} -\underline{l}_{12}^{*}\underline{l}_{21}^{*}\ne 0$ and $\overline{l}_{11}^{*}\overline{l}_{22}^{*}-\overline{l}_{12}^{*}\overline{l}_{21}^{*}\ne 0$.

Otherwise, we may also write Eq. (30) as left and right as:

LEFT:

$$\begin{aligned}&\underline{l}_{11}^{*}\underline{h}_{1}^{*}+\underline{l}_{12}^{*}\underline{h}_{2}^{*}=\underline{z}_{1}^{*}, \end{aligned}$$

(31)

$$\begin{aligned}&\overline{l}_{11}^{*}\overline{h}_{1}^{*}+\overline{l}_{12}^{*}\overline{h}_{2}^{*}=\overline{z}_{1}^{*}. \end{aligned}$$

(32)

RIGHT:

$$\begin{aligned} \underline{l}_{21}^{*}\underline{h}_{1}^{*}+\underline{l}_{22}^{*}\underline{h}_{2}^{*}=\underline{z}_{2}^{*}, \end{aligned}$$

(33)

$$\begin{aligned} \overline{l}_{21}^{*}\overline{h}_{1}^{*}+\overline{l}_{22}^{*}\overline{h}_{2}^{*}=\overline{z}_{2}^{*}. \end{aligned}$$

(34)

Solving Eq. (31) with (33) and Eq. (32) with (34), we obtained

$$\begin{aligned}&\underline{h}_{1}^{*}=\frac{\underline{l}_{22}^{*}\underline{z}_{1}^{*}-\underline{l}_{12}^{*}\underline{z}_{2}^{*}}{\underline{l}_{11}^{*}\underline{l}_{22}^{*}-\underline{l}_{12}^{*}\underline{l}_{21}^{*}}~~~,~~~~ \underline{h}_{2}^{*}=\frac{\underline{l}_{11}^{*}\underline{z}_{2}^{*}-\underline{l}_{21}^{*}\underline{z}_{1}^{*}}{\underline{l}_{11}^{*}\underline{l}_{22}^{*}-\underline{l}_{12}^{*}\underline{l}_{21}^{*}},\\&\overline{h}_{1}^{*}=\frac{\overline{l}_{22}^{*}\overline{z}_{1}^{*}-\overline{l}_{12}^{*}\overline{z}_{2}^{*}}{\overline{l}_{11}^{*}\overline{l}_{22}^{*}-\overline{l}_{12}^{*}\overline{l}_{21}^{*}}~~~,~~~ \overline{h}_{2}^{*}=\frac{\overline{l}_{11}^{*}\overline{z}_{2}^{*}-\overline{l}_{21}^{*}\overline{z}_{1}^{*}}{\overline{l}_{11}^{*}\overline{l}_{22}^{*}-\overline{l}_{12}^{*}\overline{l}_{21}^{*}}, \end{aligned}$$

where $\underline{l}_{11}^{*}\underline{l}_{22}^{*} -\underline{l}_{12}^{*}\underline{l}_{21}^{*}\ne 0$ and $\overline{l}_{11}^{*}\overline{l}_{22}^{*}-\overline{l}_{12}^{*}\overline{l}_{21}^{*}\ne 0$.

Similarly, we used the system (29) for the negative$(\bullet )$ crisp interval equations,

$$\begin{aligned} {\left\{ \begin{array}{ll} {[}\underline{l}_{11}^{\bullet },\overline{l}_{11}^{\bullet }][\underline{h}_{1}^{\bullet },\overline{h}_{1}^{\bullet }]+[\underline{l}_{12}^{\bullet },\overline{l}_{12}^{\bullet }][\underline{h}_{2}^{\bullet },\overline{h}_{2}^{\bullet }]=[\underline{z}_{1}^{\bullet },\overline{z}_{1}^{\bullet }],\\ {[}\underline{l}_{21}^{\bullet },\overline{l}_{21}^{\bullet }][\underline{h}_{1}^{\bullet },\overline{h}_{1}^{\bullet }]+[\underline{l}_{22}^{\bullet },\overline{l}_{22}^{\bullet }][\underline{h}_{2}^{\bullet },\overline{h}_{2}^{\bullet }]=[\underline{z}_{2}^{\bullet },\overline{z}_{2}^{\bullet }],\\ \end{array}\right. } \end{aligned}$$

(35)

and the system of Eq. (35) can be written in matrix form as

$$\begin{aligned} \left( \begin{array}{cccc} \underline{l}_{11}^{\bullet } &{} \underline{l}_{12}^{\bullet } &{} 0 &{} 0 \\ 0 &{} 0 &{} \overline{l}_{11}^{\bullet } &{} \overline{l}_{12}^{\bullet } \\ \underline{l}_{21}^{\bullet } &{} \underline{l}_{22}^{\bullet } &{} 0 &{} 0 \\ 0 &{} 0 &{} \overline{l}_{21}^{\bullet } &{} \overline{l}_{22}^{\bullet } \\ \end{array} \right) \left( \begin{array}{c} \underline{h}_{1}^{\bullet } \\ \underline{h}_{2}^{\bullet } \\ \overline{h}_{1}^{\bullet } \\ \overline{h}_{2}^{\bullet } \\ \end{array} \right) = \left( \begin{array}{c} \underline{z}_{1}^{\bullet } \\ \overline{z}_{1}^{\bullet } \\ \underline{z}_{2}^{\bullet } \\ \overline{z}_{2}^{\bullet } \\ \end{array} \right) . \end{aligned}$$

This matrix equation may be easily solved and the solutions from this matrix equation are given as:

$$\begin{aligned}&\underline{h}_{1}^{\bullet }=\frac{\underline{l}_{22}^{\bullet }\underline{z}_{1}^{\bullet }-\underline{l}_{12}^{\bullet }\underline{z}_{2}^{\bullet }}{\underline{l}_{11}^{\bullet }\underline{l}_{22}^{\bullet }-\underline{l}_{12}^{\bullet }\underline{l}_{21}^{\bullet }}~~~,~~~~ \underline{h}_{2}^{\bullet }=\frac{\underline{l}_{11}^{\bullet }\underline{z}_{2}^{\bullet }-\underline{l}_{21}^{\bullet }\underline{z}_{1}^{\bullet }}{\underline{l}_{11}^{\bullet }\underline{l}_{22}^{\bullet }-\underline{l}_{12}^{\bullet }\underline{l}_{21}^{\bullet }},\\&\overline{h}_{1}^{\bullet }=\frac{\overline{l}_{22}^{\bullet }\overline{z}_{1}^{\bullet }-\overline{l}_{12}^{\bullet }\overline{z}_{2}^{\bullet }}{\overline{l}_{11}^{\bullet }\overline{l}_{22}^{\bullet }-\overline{l}_{12}^{\bullet }\overline{l}_{21}^{\bullet }}~~~,~~~ \overline{h}_{2}^{\bullet }=\frac{\overline{l}_{11}^{\bullet }\overline{z}_{2}^{\bullet }-\overline{l}_{21}^{\bullet }\overline{z}_{1}^{\bullet }}{\overline{l}_{11}^{\bullet }\overline{l}_{22}^{\bullet }-\overline{l}_{12}^{\bullet }\overline{l}_{21}^{\bullet }}, \end{aligned}$$

where $\underline{l}_{11}^{\bullet }\underline{l}_{22}^{\bullet }-\underline{l}_{12}^{\bullet }\underline{l}_{21}^{\bullet } \ne 0$ and $\overline{l}_{11}^{\bullet }\overline{l}_{22}^{\bullet }-\overline{l}_{12}^{\bullet }\overline{l}_{21}^{\bullet }\ne 0.$

Otherwise, we may also write Eq. (35) as left and right as:

LEFT:

$$\begin{aligned}&\underline{l}_{11}^{\bullet }\underline{h}_{1}^{\bullet }+\underline{l}_{12}^{\bullet }\underline{h}_{2}^{\bullet }=\underline{z}_{1}^{\bullet }, \end{aligned}$$

(36)

$$\begin{aligned}&\overline{l}_{11}^{\bullet }\overline{h}_{1}^{\bullet }+\overline{l}_{12}^{\bullet }\overline{h}_{2}^{\bullet }=\overline{z}_{1}^{\bullet }. \end{aligned}$$

(37)

RIGHT:

$$\begin{aligned}&\underline{l}_{21}^{\bullet }\underline{h}_{1}^{\bullet }+\underline{l}_{22}^{\bullet }\underline{h}_{2}^{\bullet }=\underline{z}_{2}^{\bullet }, \end{aligned}$$

(38)

$$\begin{aligned}&\overline{l}_{21}^{\bullet }\overline{h}_{1}^{\bullet }+\overline{l}_{22}^{\bullet }\overline{h}_{2}^{\bullet }=\overline{z}_{2}^{\bullet }. \end{aligned}$$

(39)

Solving Eq. (36) with (38) and Eq. (37) with (39), we obtained

$$\begin{aligned}&\underline{h}_{1}^{\bullet }=\frac{\underline{l}_{22}^{\bullet }\underline{z}_{1}^{\bullet }-\underline{l}_{12}^{\bullet }\underline{z}_{2}^{\bullet }}{\underline{l}_{11}^{\bullet }\underline{l}_{22}^{\bullet }-\underline{l}_{12}^{\bullet }\underline{l}_{21}^{\bullet }}~~~,~~~~ \underline{h}_{2}^{\bullet }=\frac{\underline{l}_{11}^{\bullet }\underline{z}_{2}^{\bullet }-\underline{l}_{21}^{\bullet }\underline{z}_{1}^{\bullet }}{\underline{l}_{11}^{\bullet }\underline{l}_{22}^{\bullet }-\underline{l}_{12}^{\bullet }\underline{l}_{21}^{\bullet }},\\&\overline{h}_{1}^{\bullet }=\frac{\overline{l}_{22}^{\bullet }\overline{z}_{1}^{\bullet }-\overline{l}_{12}^{\bullet }\overline{z}_{2}^{\bullet }}{\overline{l}_{11}^{\bullet }\overline{l}_{22}^{\bullet }-\overline{l}_{12}^{\bullet }\overline{l}_{21}^{\bullet }}~~~,~~~ \overline{h}_{2}^{\bullet }=\frac{\overline{l}_{11}^{\bullet }\overline{z}_{2}^{\bullet }-\overline{l}_{21}^{\bullet }\overline{z}_{1}^{\bullet }}{\overline{l}_{11}^{\bullet }\overline{l}_{22}^{\bullet }-\overline{l}_{12}^{\bullet }\overline{l}_{21}^{\bullet }}, \end{aligned}$$

where $\underline{l}_{11}^{\bullet }\underline{l}_{22}^{\bullet }-\underline{l}_{12}^{\bullet }\underline{l}_{21}^{\bullet } \ne 0$ and $\overline{l}_{11}^{\bullet }\overline{l}_{22}^{\bullet }-\overline{l}_{12}^{\bullet }\overline{l}_{21}^{\bullet }\ne 0.$

The methods shown above are used to solve the FBFL system of equations. We may solve FBFL system by using left and right equations as shown above be solved by an ordinary method to solve linear equations or also solve the FBFL equations in (25) and (28) by taking the inverse of the coefficient matrix (if exists). Both techniques are efficient in solving FBFL system of equations.

We consider an example to show the efficiency of the techniques as given above.

Example 5.4

We consider a RLC circuit Suparna and Chakraverty (2011) in which source current and resistance all are in terms of BTFN. Related circuit is shown in Fig. 11.

Fig. 11

A circuit with bipolar fuzzy current, source and resistance

From the above circuit we use, Kirchhoff’s second law and write the linear equations for first and second loop,

$$\begin{aligned}&(5.9,6,6.1)(5.8,5.9,6)I_{1} + (3.9,4,4.1)(3.8,3.9,4)(I_{1}-I_{2})\\&\quad =(39,40,42)(38,39,41)-(11,12,13)(9,10,11),\\&\qquad -(3.9,4,4.1)(3.8,3.9,4)(I_{1}-I_{2}) + (11.9,12,12.1)(11.8,11.9,12)(I_{2})\\&\quad =(11,12,13)(9,10,11)+(23,24,25)(20,21,22). \end{aligned}$$

In the above system of equations source current and resistance are in BTFN, so we use the $\alpha$-cut at positive$(*)$ and negative $(\bullet )$ part of BTFNs to convert into the intervals and replace r and s in $\alpha$-cut intervals of positive$(*)$ and negative $(\bullet )$ parts, respectively. The above system is simplified and given as,

$$\begin{aligned}&[(5.9+0.1r,6.1-0.1r)(5.8-0.1s,6+0.1s)][(\underline{I}_{1}^{*}, \overline{I}_{1}^{*})(\underline{I}_{1}^{\bullet },\overline{I}_{1}^{\bullet })]\\&\qquad +[(3.9+0.1r,4.1-0.1r)(3.8-0.1s,4+0.1s)][(\underline{I}_{1}^{*}, \overline{I}_{1}^{*})(\underline{I}_{1}^{\bullet },\overline{I}_{1}^{\bullet })-(\underline{I}_{2}^{*},\overline{I}_{2}^{*})(\underline{I}_{2}^{\bullet }, \overline{I}_{2}^{\bullet })]\\&\quad =(39+r,42-2r)(38-s,41+2s)-(11+r,13-r)(9-s,11+s),\\&\qquad -[(3.9+0.1r,4.1-0.1r)(3.8-0.1s,4+0.1s)][(\underline{I}_{1}^{*}, \overline{I}_{1}^{*})(\underline{I}_{1}^{\bullet }, \overline{I}_{1}^{\bullet })-(\underline{I}_{2}^{*},\overline{I}_{2}^{*}) (\underline{I}_{2}^{\bullet },\overline{I}_{2}^{\bullet })]\\&\qquad +[(11.9+0.1r,12.1-0.1r) (11.8-0.1s,12+0.1s)][(\underline{I}_{2}^{*},\overline{I}_{2}^{*}) (\underline{I}_{2}^{\bullet },\overline{I}_{2}^{\bullet })]\\&\quad =(11+r,13-r)(9-s,11+s)+(23+r,25-r)(20-s,22+s). \end{aligned}$$

First, we take the positive $(*)$ crisp interval equation of the above system, we get

$$\begin{aligned}&(5.9+0.1r,6.1-0.1r)(\underline{I}_{1}^{*},\overline{I}_{1}^{*}) +(3.9+0.1r,4.1-0.1r)(\underline{I}_{1}^{*}-\overline{I}_{2}^{*}, \overline{I}_{1}^{*}-\underline{I}_{2}^{*})\nonumber \\&\quad =(26+2r,31-3r), \end{aligned}$$

(40)

$$\begin{aligned}&\qquad -(3.9+0.1r,4.1-0.1r)(\underline{I}_{1}^{*}-\overline{I}_{2}^{*}, \overline{I}_{1}^{*}-\underline{I}_{2}^{*})+(11.9+0.1r,12.1-0.1r) (\underline{I}_{2}^{*},\overline{I}_{2}^{*})\nonumber \\&\quad =(34+2r,38-2r), \end{aligned}$$

(41)

and above system can be written as,

$$\begin{aligned}&(9.8+0.2r)\underline{I}_{1}^{*} - (3.9+0.1r)\overline{I}_{2}^{*}=26+2r,\\&(10.2-0.2r)\overline{I}_{1}^{*} - (4.1-0.1r)\underline{I}_{2}^{*}=31-3r,\\&\quad -(4.1-0.1r)\overline{I}_{1}^{*} + 16\underline{I}_{2}^{*}=34+2r,\\&\quad -(3.9+0.1r)\underline{I}_{1}^{*} + 16\overline{I}_{2}^{*}=38-2r. \end{aligned}$$

Above system can be written in matrix form as

$$\begin{aligned} \left( \begin{array}{cccc} (9.8+0.2r) &{} -(3.9+0.1r) &{} 0 &{} 0 \\ 0 &{} 0 &{} (10.2-0.2r) &{} -(4.1-0.1r) \\ 0 &{} 0 &{} -(4.1-0.1r) &{} 16 \\ -(3.9+0.1r) &{} 16 &{} 0 &{} 0 \\ \end{array} \right) \left( \begin{array}{c} \underline{I}_{1}^{*} \\ \overline{I}_{2}^{*} \\ \overline{I}_{1}^{*} \\ \underline{I}_{2}^{*} \\ \end{array} \right) = \left( \begin{array}{c} 26+2r \\ 31-3r \\ 34+2r \\ 38-2r \\ \end{array} \right) . \end{aligned}$$

Solving the above equations, solution of system is given as,

$$\begin{aligned}&(\underline{I}_{1}^{*},\overline{I}_{1}^{*}) =\left( \frac{20r^{2}-2800r-56420}{r^{2}-242r-14159}~~,~~ \frac{20r^{2}+4320r-63540}{r^{2}+238r-14639}\right) ,\\&(\underline{I}_{2}^{*},\overline{I}_{2}^{*}) =\left( \frac{10r^{2}+180r-47390}{r^{2}+238r-14639}~~,~~ \frac{20r^{2}+160r-47380}{r^{2}-242r-14159}\right) . \end{aligned}$$

The graphical representation of positive$(*)$ solution of FBFL system is shown in Fig. 12.

Fig. 12

The graphical representation of positive$(*)$ membership functions $\underline{I}^{*}(r)$, $\overline{I}^{*}(r)$ of bipolar fuzzy numbers

Similarly, we can take the negative $(\bullet )$ crisp interval part of the FBFL system we get,

$$\begin{aligned}&(5.8-0.1s,6+0.1s)(\underline{I}_{1}^{\bullet },\overline{I}_{1}^{\bullet }) +(3.8-0.1s,4+0.1s)(\underline{I}_{1}^{\bullet }-\overline{I}_{2}^{\bullet }, \overline{I}_{1}^{\bullet }-\underline{I}_{2}^{\bullet })\nonumber \\&\quad =(27-2s,32+3s), \end{aligned}$$

(42)

$$\begin{aligned}&\qquad -(3.8-0.1s,4+0.1s)(\underline{I}_{1}^{\bullet }-\overline{I}_{2}^{\bullet }, \overline{I}_{1}^{\bullet }-\underline{I}_{2}^{\bullet })+(11.8-0.1s,12+0.1s) (\underline{I}_{2}^{\bullet },\overline{I}_{2}^{\bullet })\nonumber \\&\quad =(29-2s,33+2s), \end{aligned}$$

(43)

and above system can be written as,

$$\begin{aligned}&(9.6-0.2s)\underline{I}_{1}^{\bullet } - (3.8-0.1s)\overline{I}_{2}^{\bullet }=27-2s, (10+0.2s)\overline{I}_{1}^{\bullet } - (4+0.1s)\underline{I}_{2}^{\bullet }=32-+3s,\\&\qquad -(4+0.1s)\overline{I}_{1}^{\bullet } + 15.8\underline{I}_{2}^{\bullet }=29-2s, -(3.8-0.1s)\underline{I}_{1}^{*} + 15.8\overline{I}_{2}^{\bullet }=33+2s. \end{aligned}$$

Above system can be written in matrix form as

$$\begin{aligned} \left( \begin{array}{cccc} (9.6-0.2s) &{} -(3.8-0.1s) &{} 0 &{} 0 \\ 0 &{} 0 &{} (10+0.2s) &{} -(4+0.1s) \\ 0 &{} 0 &{} -(4+0.1s) &{} 15.8 \\ -(3.8-0.1s) &{} 15.8 &{} 0 &{} 0 \\ \end{array} \right) \left( \begin{array}{c} \underline{I}_{1}^{\bullet } \\ \overline{I}_{2}^{\bullet } \\ \overline{I}_{1}^{\bullet } \\ \underline{I}_{2}^{\bullet } \\ \end{array} \right) = \left( \begin{array}{c} 27-2s \\ 32+3s \\ 29-2s \\ 33+2s \\ \end{array} \right) . \end{aligned}$$

Solving the above equations, the solution of system is given as,

$$\begin{aligned}&(\underline{I}_{1}^{\bullet },\overline{I}_{1}^{\bullet }) =\left( \frac{20s^{2}+2730s-55200}{s^{2}+240s-13724}~~,~~\frac{20s^{2}-4230s-62160}{s^{2}-236s-14200}\right) ,\\&(\underline{I}_{2}^{\bullet },\overline{I}_{2}^{\bullet }) =\left( \frac{10s^{2}-100s-41800}{s^{2}-236s-14200}~~,~~\frac{20s^{2}-230s-41940}{s^{2}+240s-13724}\right) . \end{aligned}$$

The graphical representation of negative$(\bullet )$ solution of FBFL system is shown in Fig. 13.

Fig. 13

The graphical representation of negative$(\bullet )$ membership functions $\underline{I}^{\bullet }(s)$, $\overline{I}^{\bullet }(s)$ of bipolar fuzzy numbers

The solution of the system in BTFN form is given as,

$$\begin{aligned}&I_{1}=(3.985,4.112,4.340)(4.022,4.147,4.378),\\&I_{2}=(3.237,3.278,3.346)(2.944,2.986,3.056). \end{aligned}$$

7 Conclusions

In many real-world problems, linear system of equations plays a vital role in physics, economics, networking and intelligence systems involving uncertainty in unknown parameters in terms of BFNs. The present paper discussed the different techniques to find out the solution of BFLS and FBFL system of equations. In the first method, we have presented an effective technique for solving a bipolar fuzzy linear system of n equations for a bipolar system of n variables. The original bipolar system with matrix L can be replaced by a pair of positive$(*)$ and negative$(\bullet )$ of two $n \times n$ linear fuzzy systems. In the second method, we have used the same BFLS of equations and have solved this system by using bipolar fuzzy center technique. In this technique, we first drew a graph by using some specific end points and then used this graph to find the solution of BFLS of equations. The solution vector will be the symmetric solution if the column vector on the right side is symmetric. In third method, we presented a technique to solve FBFL system of equations. First, we convert the coefficients of right-side vector and unknowns which are in terms of BTFNs to $\alpha$-cut interval and then we used interval technique to solve the system. Our proposed methods may be used to solve artificial intelligence problem and engineering models. In future, we are trying to extend our methods to solve complex bipolar fuzzy linear systems.