A Simple Optimization Method for Tuning the Gains of PID Controllers for the Autopilot of Cessna 182 Aircraft Using Model-in-the-Loop Platform

Abstract

Currently, there is a growing demand for automatic control systems for unmanned aerial vehicles due to the numerous civil and military applications. An unmanned aerial vehicle has sophisticated and complex controllers that are used to stabilize it, which composes the autopilot. In autopilots, PID controllers are commonly used, and various techniques are applied to tune their gains. In this paper are proposed optimization procedures of gains for the designed PID controllers from the transfer functions simulated in the Matlab/Simulink software, establishing a model-in-the-loop system, for the autopilot of the Cessna 182 aircraft. In this context, results of simulations are obtained to prove the effectiveness of using these proposals for optimization. They offer a simple, effective, systematic and replicable way to obtain the gains and dispense the use of classical methods of determination of gains for control loops, as well as the trial and error method.

1 Introduction

Autopilot systems play an important role in the development of aviation, since they contribute to the improvement of navigation procedures, flight management and stability and control of the aircraft (Nelson 1998). Studies involving the autopilot design are increasingly being developed due to its possibility of being employed in almost all aircraft models (Santos and de Oliveira 2011). The use of autopilot systems can also provide increased artificial stability of the aircraft, which in turn contributes to improving the quality of flight (Ribeiro and Oliveira 2010).

In recent years, extensive research involving the development of algorithms in automatic pilot designs using modern control theory has been investigated (Kada and Ghazzawi 2011). Many of these control algorithms involving nonlinear terms, scalable systems and optimization techniques have succeeded, though a small number of implementations were reported due to their complexity and computational costs. On the other hand, PID (proportional-integral-derivative) control algorithms have been successfully used due to their simplicity, ease of implementation and the good performance achieved in many cases (Kada and Ghazzawi 2011).

Typically, in the synthesis of classical control laws, simulations involving closed-loop systems, which use mathematical models of the real plant, are applied to estimate the transient responses of the designed controllers (Pedroni and Cova 2013). Techniques such as the root locus method may be used to locate the gains of the control loops and assist in the tuning of the PID controllers (Franklin et al. 2015; Ogata 2011; Thums et al. 2012).

In Splendor et al. (2015), the design of an autopilot system is presented, based on PID controllers for the Cessna 182 aircraft using transfer functions (TFs). The autopilot proposed consists of a longitudinal control system, responsible for the maintenance of the altitude and the pitch angle, and a system of lateral-directional control, which will contribute to the maintenance of roll and yaw angles. The developed controllers are tested in X-Plane flight simulator (Research 2016) for the Cessna 172SP aircraft.

In this paper are proposed optimization procedures of the developed PID controllers, from the TFs simulated in the Matlab/Simulink software, establishing a model-in-the-loop system (MIL), for the automatic pilot of the Cessna 182 aircraft. However, without pretending to enter into the eternal discussion about which methodology is best, this paper presents the advantages of using the optimization procedures of gains of the PID controllers. Among the advantages, the optimization can considerably minimize the demand for in-flight tuning and substantially reduce the risks and costs involved in flight-testing. Moreover, other benefits of optimization procedures are: the controllers are reasonably tuned now for desired response, i.e., the gains of the controllers are optimized successfully in accordance with trade-off between acceptable errors and control efforts as well in attendance with the restrictions of the design specifications, with the purpose of achieving a satisfactory command-responsiveness and guaranteeing a longer lifetime of the actuators; and the overhead associated with the tuning methods treated in this section and literature as well as avoiding manual fine adjustment (trial and error) of the gains can be significantly reduced for future tuning requirements of all longitudinal and lateral-directional PID controllers of autopilot. In this context, the results of simulations are obtained to prove the effectiveness of using these proposals of optimization.

2 Preliminary

In this section, the longitudinal and lateral-directional controls for the autopilot of the Cessna 182 aircraft developed in Splendor et al. (2015) are briefly described, which are implemented and simulated in the Matlab/Simulink software, in order to enable the completion of the analysis of results from the gains obtained from the proposals for the optimization of gains of these controllers. The mathematical model (geometric, mass, inertial, stability, control and hinge moment data) of the Cessna 182 is given in Roskam (2001). More details can be found in Splendor et al. (2015).

2.1 Aircraft and Automatic Control

A fixed-wing aircraft is a type of aircraft capable of moving into the atmosphere through its driving force, using a propeller or turbine to maintain equilibrium in relation to aerodynamic forces that act on its structure. The aircrafts are designed for different purposes; however, they have basically the same components with operational characteristics and differentiated dimensions according to their purpose (Rodrigues 2013). In addition, the aircrafts have sophisticated and complex controllers that are used to stabilize them, which constitute the autopilot. The longitudinal and the lateral-directional are among these controllers, and they are described below, regarding the autopilot of the Cessna 182.

2.1.1 Longitudinal Control

The longitudinal autopilot system aims at controlling the variables related to the pitch angle, the attack angle and the vertical and horizontal velocities (Santos and de Oliveira 2011). The longitudinal autopilot for the Cessna 182 is composed of an internal control loop that controls the pitch angle and an outer control loop responsible for controlling the altitude of the aircraft.

Dynamic longitudinal stability of an aircraft is divided into two modes: short-period and long-period. These modes are generated in situations where the aircraft suffers a disturbance in its state of balance (Cook 2007).

Table 1 presents the specifications used in the longitudinal control loop for the response to an unit-step-type input.

Table 1 Design specifications for the longitudinal controller

Fig. 1

Pitch angle control loop

Fig. 2

Altitude control loop

As reference for the pitch angle control loop, the desired pitch angle $\theta _\mathrm{ref}$ is compared to the value measured by a vertical gyroscope, generating an error signal $\theta _\mathrm{e}$. Usually, the gyro signal must be amplified ($K_\mathrm{a}$) before it is sent to the control surface, generating an elevator deflection ($\delta _\mathrm{e}$). The movement caused by this deflection provides a change in the pitch angle, causing changes in the forces and moments acting on the aircraft in relation to its gravity center (Nelson 1998).

To improve the performance of the pitch angle control system, an internal control loop can be added in order to change the damping coefficient of the short-period mode (Nelson 1998). The difference between the pitch angle error $e_\mathrm{a}$ and the pitch rate error $e_\mathrm{rg}$ leads in the relation $e_{\delta a}$, thus resulting in the full control loop for the pitch angle. With the gain parameters $K_\mathrm{a}$ e $K_\mathrm{rg}$, it is possible to adjust the damping coefficient, the rise time, the maximum overshoot and, consequently, to adjust the stability of the aircraft.

Figure 1 shows the pitch angle control loop obtained and implemented in Matlab/Simulink software. The internal control loop is represented by the following open-loop TFs,

• for the elevator servo gain, in radian, Blakelock (1991):

  $$\begin{aligned} G_\mathrm{ser}=\frac{\delta _\mathrm{e}(s)}{e_{\delta a}}=\frac{-10}{s+10} \end{aligned}$$

  (1)

• for the pitch angle gain, in radian:

  $$\begin{aligned} G_{{{\dot{\theta }}}}=\frac{{{\dot{\theta }}}(s)}{\delta _\mathrm{e}(s)}=\frac{-5.0297s^3-10.3466s^2-0.5920s}{s^4+8.94s^3+28.2s^2+1.49s+0.813} \nonumber \\ \end{aligned}$$

  (2)

• for the external gain shown in Fig. 1, in radian:

  $$\begin{aligned} G_\mathrm{ext}=\frac{1}{s}G_\mathrm{int} \end{aligned}$$

  (3)

The root locus method is used to determine the values of the gains related to this control loop (Franklin et al. 2015; Ogata 2011). First, the gain $K_\mathrm{rg}=1.18$ the internal control loop is determined using Eqs. 1 and 2. With the damping coefficient $\zeta =0.7$, and using Eq. 3, the gain $K_\mathrm{a}=14.3$ is obtained.

The altitude control loop aims at maintaining the aircraft altitude h, minimizing the error $h_\mathrm{e}$ between the current h and the desired $h_\mathrm{ref}$ altitudes. Considering that the horizontal speed is controlled by another control loop, and knowing the dynamic equation that relates the change in altitude caused by the elevator deflection, it is possible to obtain the transfer function (TF) for the altitude controller (Santos and de Oliveira 2011). The TF that relates the altitude to an elevator deflection, in feet per radian, is given by:

$$\begin{aligned} \frac{h(s)}{\delta _\mathrm{e}(s)}=\frac{402.858s^3+68698.5s^2+902.567s+2831.2}{s^5+8.943s^4+28.2s^3+1.49s^2+0.813s} \nonumber \\ \end{aligned}$$

(4)

The relation between variation in altitude and elevator deflection in flight conditions can be converted to $h(s)/\theta (s)$, when the pitch angle of the aircraft becomes the input, i.e.,

$$\begin{aligned} \frac{h(s)}{\theta (s)}=\frac{h(s)}{\delta _\mathrm{e}(s)}\frac{\delta _\mathrm{e}(s)}{\theta (s)} \end{aligned}$$

(5)

Using Eq. 5, the TF applied in the altitude control of the aircraft, in feet per radian, is obtained as:

$$\begin{aligned} \frac{h(s)}{\theta (s)}=\frac{-1.2837s^3-2.3295s^2+442.6304s+16.469}{s^3+2.0571s^2+0.1176s} \nonumber \\ \end{aligned}$$

(6)

A PID controller was chosen for the altitude control loop, as shown in Fig. 2, being this choice due to its practical applicability in most control systems and the various tuning methods available in the literature (Franklin et al. 2015; Ogata 2011). Among these methods, the second rule of Ziegler-Nichols stands out, proposing the use of critical gain $K_\mathrm{cr}$ and critical period $P_\mathrm{cr}$ of the loop to be controlled to determine the gains $K_\mathrm{p}$, $K_\mathrm{i}$ and $K_\mathrm{d}$ of the PID controller.

With the root locus method and the open-loop TF, given by Eq. 6, it is possible to find the critical gain $K_\mathrm{cr}$ and the imaginary portion $S_\mathrm{i}$ that correspond to the value of the point of intersection of the imaginary axis and the root locus curve (Santos and de Oliveira 2011).

Table 2 Design specifications for lateral-directional controller

Fig. 3

Roll angle control loop

Thus, the values obtained are $K_\mathrm{cr}=0.0246$ and $S_\mathrm{i}=2.9$, from which it is possible to determine the gains of the PID controller as follows:

$$\begin{aligned} P_\mathrm{cr}= & {} 2\pi /S_\mathrm{i}=2.17s \end{aligned}$$

(7)

$$\begin{aligned} K_\mathrm{p}= & {} 0.6\times K_\mathrm{cr}=0.0148 \end{aligned}$$

(8)

$$\begin{aligned} K_\mathrm{i}= & {} 0.6\times K_\mathrm{cr}/0.5\times P_\mathrm{cr}=0.0136 \end{aligned}$$

(9)

$$\begin{aligned} K_\mathrm{d}= & {} 0.6\times K_\mathrm{cr}\times 0.125\times P_\mathrm{cr}=0.0040 \end{aligned}$$

(10)

Since the tuning method used provides an estimate for gain values of the controller, it is possible to perform a manual fine adjustment to get a response with significant improvement. For this reason, the values used for the gains are $K_\mathrm{p}=0.0112$, $K_\mathrm{i}=0.00038$ and $K_\mathrm{d}=0.0032$.

2.1.2 Lateral-Directional Control

The lateral-directional autopilot system is related to the roll, yaw and sideslip angles (Ribeiro and Oliveira 2010). The control loops for the roll and yaw angles are presented to simplify the study of lateral-directional controllers for the Cessna 182, in order to provide a greater stability of the aircraft.

The specifications used in the lateral-directional control loop for a response to an unit-step-type input are presented in Table 2.

The value obtained by a gyroscope is used as reference for the control of the roll angle $\varphi$. The value provided by the gyroscope is compared to a reference value $\varphi _\mathrm{ref}$, generating an error signal $\varphi _\mathrm{e}$ that acts in the servo control, causing a deflection $\delta _\mathrm{a}$ in the ailerons. Ailerons are mobile equipment installed on the trailing edge of the wing, moving up and down oppositely to each other, whose main purpose is to tilt the plane to one side. By maintaining this inclination, the aircraft can turn toward the direction of the lowered wing, resulting in a rolling motion. The deflection $\delta _\mathrm{a}$ changes the roll angle, so it is maintained in the desired value.

For the roll angle control loop to achieve a good performance, it is necessary to include an internal feedback loop in the control system in order to increase the value of the damping coefficient (McLean 1991).

The difference between the roll angle error $e_\mathrm{pid}$ and the roll angle rate error $e_\mathrm{rg}$ results in the relation $e_{\delta pid}$, thus providing the full internal control loop for the roll angle. It should be noted here that ${{\dot{\varphi }}}$ is the derivative of the roll angle $\varphi$.

Figure 3 presents the roll angle control loop obtained.

The open-loop TFs for the roll angle, regarding the full internal control loop, in radian, are given as:

$$\begin{aligned} G_\mathrm{ser}= & {} \frac{\delta _\mathrm{a}(s)}{e_{\delta pid}}=\frac{5}{s+5} \end{aligned}$$

(11)

$$\begin{aligned} G_{{\dot{\varphi }}}= & {} \frac{{\dot{\varphi }}}{\delta _\mathrm{a}}=\frac{246.26s^2+320.315s+1986.232}{s^4+14.37s^3+28.2s^2+137.5s+2.452} \nonumber \\ \end{aligned}$$

(12)

$$\begin{aligned} G_\mathrm{ext}= & {} \frac{1}{s}G_\mathrm{int} \end{aligned}$$

(13)

With the full internal control loop for the roll angle, it is possible to use a PID controller for the control of the roll angle $\varphi$. The values of the gains $K_\mathrm{rg}$, $K_\mathrm{p}$, $K_\mathrm{i}$ and $K_\mathrm{d}$, related to the control loop, are determined by the application of the root locus method. Thus, the gain $K_\mathrm{rg}=0.0803$ of the internal loop is determined using the open-loop TFs given by Eqs. 11 and 12 (Splendor et al. 2015). In addition, through Eq. 13 the values of $K_\mathrm{cr}=2.42$ and $S_\mathrm{i}=12.9$ are obtained.

Using the values $K_\mathrm{cr}$ and $S_\mathrm{i}$, it is possible to calculate the values for the gains of the PID controller using the second tuning method of Ziegler-Nichols, which are $K_\mathrm{p}=2.6430$, $K_\mathrm{i}=1.6498$ and $K_\mathrm{d}=1.1090$, after a manual fine adjustment.

Fig. 4

Yaw rate control loop

In the yaw rate control, the yaw damper will try to drive any perceived yaw rate to zero. It will work fine if the airplane is intended to be in straight line flight. However, the yaw damper will tend to oppose the roll angle control when it is trying to set up a constant bank angle turn and this is not acceptable. In such a turn, the airplane has a constant (non-zero) yaw rate. A low-cost solution is to use a washout circuit, that has the following TF:

$$\begin{aligned} H_\mathrm{washout}=\frac{\tau s}{\tau s+1} \end{aligned}$$

(14)

where $\tau$ is the washout circuit time constant. It is seen that a washout circuit drives a given input signal to zero at a pace determined by the magnitude of the time constant, $\tau$.

When in a turn, the washout circuit will stop opposing yaw rate in any significant manner after a little more than $\tau$ seconds have elapsed. If $\tau$ is very small, the yaw damper will not work at all. If $\tau$ is very large, the yaw damper will oppose the roll angle control in setting up a turn. A compromise is required. Typical of such a compromise is $\tau = 4s$ (Roskam 2001).

Another problem with the yaw rate control is that the sensitive axis of the yaw rate gyroscope is aligned with vertical axis at the center of gravity at only a single flight condition. For all other flight conditions, the yaw rate gyroscope senses a combination of stability axis roll and yaw rates. The output signal may be denoted as McLean (1991):

$$\begin{aligned} {\dot{\psi }}=K_\mathrm{yrg} \times \{p\times \sin (\alpha +\alpha _R)+r\times \cos (\alpha +\alpha _R)\} \end{aligned}$$

(15)

where $K_\mathrm{yrg}$ is the yaw rate gyro gain which was considered equal to 1 in this work, p is the derivative of the roll angle $\varphi$, r is the derivative of the yaw angle $\psi$, $\alpha$ is the angle of attack, and $\alpha _R$ is the tilt angle of a rate gyro.

Figure 4 presents the yaw rate control loop obtained, in which it can be seen that variable angle represents the inclination angle $(\alpha +\alpha _R)$ given in radians. The control loop, considering the inclination angle, is represented by the following TFs:

$$\begin{aligned} \frac{\delta _r(s)}{e_{\delta pid}}= & {} \frac{5}{s+5} \end{aligned}$$

(16)

$$\begin{aligned} H_\mathrm{was}= & {} \frac{s}{s+0.25} \end{aligned}$$

(17)

$$\begin{aligned} \frac{r(s)}{\delta _r(s)}= & {} \frac{9.2717s+131.1518}{s^2+14.1843s+16.4729} \end{aligned}$$

(18)

$$\begin{aligned} \frac{p(s)}{\delta _r(s)}= & {} \frac{-30.2497s-16.7841}{s^2+14.1843s+16.4729} \end{aligned}$$

(19)

By using the inclination angle $(\alpha +\alpha _R)$ in the yaw rate control loop, it is possible to increase the dynamic performance of its damping coefficient. With the full control loop, it is possible to determine the value of the gains $K_\mathrm{rg}$, $K_\mathrm{p}$, $K_\mathrm{i}$ and $K_\mathrm{d}$ using the root locus method. In this case, the gain $K_\mathrm{rg}$ of the control loop must be determined using the TFs given by Eqs. 16–19 considering the inclination angle $(\alpha +\alpha _R)=0$. Moreover, with the application of the same equations considering the inclination angle $(\alpha +\alpha _R)=1$ the values $K_\mathrm{rg}=0.1$, $K_\mathrm{cr}=1.13$ and $S_\mathrm{i}=3.85$ are provided, which enable the calculation of the values of gains of the PID controller for the yaw rate control loops. The values obtained after a manual fine adjustment are $K_\mathrm{p}=0.2143$, $K_\mathrm{i}=0.5698$ and $K_\mathrm{d}=0.0089$.

3 Simulation Results with Optimization of Gains from the TFs

The objectives of the proposed optimization are to minimize the error between the reference value and the current value obtained by each controller as well as the control efforts in attendance with the restrictions of the design specifications, thus achieving a satisfactory command-responsiveness and guaranteeing a longer lifetime of the actuators. Besides, the optimization tries to make the results obtained even more satisfactory (with significant improvement) than those of Splendor et al. (2015), but beforehand prioritizing the trade-off between acceptable errors and control efforts. The optimization of the gains of the controllers is performed using the tools Simulink Design Optimization and Response Optimization of Matlab/Simulink software (Mathworks.com 2016). To do so, the blocks Check Step Response Characteristics and Check Against Reference, from Simulink Design Optimization, are inserted in the output of the control loop, as shown in Fig. 5. The block Check Step Response Characteristics provides the criteria for the design, as rise time, % rise, settling time, % settling, % overshoot and % undershoot, required by the gain optimization of each controller, based on restrictions of the design specifications defined by Splendor et al. (2015) and presented in Tables 1 and 2. The block Check Against Reference determines a smooth reference response. In the optimization, the response obtained tends to approximate this reference.

Fig. 5

Optimization blocks in conjunction with a control loop

The % rise and rise time specify that the response to an unit-step-type input reaches a percentage greater than or equal to the one given by the % rise in a time less than or equal to the one determined by the rise time. The block Check Against Reference specifies a reference signal, which the response provided (current value obtained) by the controller must approach or match. This signal is defined to a unit-step-type input by the function:

$$\begin{aligned} f(x)=1-e^{(-a.x)} \end{aligned}$$

(20)

where a is defined by equation:

$$\begin{aligned} 0.02=e^{(-t_\mathrm{s}.a)} \end{aligned}$$

(21)

where $t_\mathrm{s}$ is from Tables 1 and 2.

In addition, to perform the optimization, the same gains obtained in Sect. 2 are used as initial gains of the controllers, as well as the same TFs of the longitudinal and lateral-directional control loops described in Sect. 2.

To achieve the objectives of the proposed optimization, the following performance indexes are used in the evaluation of the control loops. In statistics, the mean-squared error (MSE) measures the average of the squares of the errors (Lehmann and Casella 2006). It is defined by

$$\begin{aligned} MSE=\frac{\sum _{i=1}^n(y(i)-y_\mathrm{ref})^2}{n} \end{aligned}$$

(22)

The mean control effort (MCE) measures the average of the squares of the controller outputs (Vale 2007), which is defined as

$$\begin{aligned} MCE=\frac{\sum _{i=1}^n(u(i))^2}{n} \end{aligned}$$

(23)

The control signal variance (CSV) measures the average of the squares of the difference between the average controller output and actual output (do Carmo et al. 2012). This performance requirement is given by

$$\begin{aligned} CSV=\frac{\sum _{i=1}^n(u(i)-{\bar{u}})^2}{n} \end{aligned}$$

(24)

where

$$\begin{aligned} {\bar{u}}=\frac{\sum _{i=1}^nu(i)}{n} \end{aligned}$$

(25)

In the optimization using TFs (MIL platform), the control loops are totally independent of each other, that is, the response of one has no influence over the other, there is no coupling between them. For all simulations, the sampling time is 0.1s and the total computation time is 50s.

3.1 Optimization with MIL Platform Using TFs

In this section are utilized the same transfers functions from the longitudinal and lateral-directional control loops described in Sect. 2 for the optimization in Matlab/Simulink software.

3.1.1 Longitudinal Control—Pitch Angle

The proportional controller for the pitch angle has been replaced by a PID controller to enable an even better response and eliminate the steady-state error. Then, the $K_\mathrm{a}$ gain was replaced by $K_\mathrm{p}$ and the $K_\mathrm{i}$ and $K_\mathrm{d}$ gains were added, both initialized with zero, as shown in Fig. 5 (Thums et al. 2012). Table 1 does not specify a value for the settling time, $t_\mathrm{s}$, in the pitch angle control, so it was defined as $t_\mathrm{s}=10s$. The peak time $t_\mathrm{p}$ was disregarded because it was not possible to obtain a realistic response smoothly meeting this criterion. Therefore, it was only prioritized to minimize the settling time and the maximum overshoot. After some tests, it was verified that the optimization, without $K_\mathrm{p}$, $K_\mathrm{d}$ and $K_\mathrm{rg}$ maximum values, converged to gains very close to the stability limits. So, after some more tests, a range was defined. Minimum values have been set to zero to open the possibility of using a PI or PD controller. Negatives values wouldn’t make sense. This was done for all control loops. The value of $K_\mathrm{p}$ was limited to a maximum of 18.59 (14.3 * 130%), $K_\mathrm{i}$ without maximum, and $K_\mathrm{d}$ and $K_\mathrm{rg}$ 1.18 (1.18 * 100%).

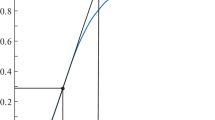
Figure 6 shows the response to a unit-step-type input of the pitch angle control loop with the gains defined before optimization, in the red dashed line, and with the gains $K_\mathrm{p}=7.1278$, $K_\mathrm{i}=2.0630$, $K_\mathrm{d}=0.0$, and $K_\mathrm{rg}=1.18$ obtained from the optimization, in the blue line. It can be seen that the response is smoother and now it settle. The design specifications obtained are shown in Table 3.

Fig. 6

Response to an unit-step-type input of the pitch angle control loop with optimization of gains in MIL platform

Table 3 Comparison of design specifications obtained in the pitch angle control loop

3.1.2 Longitudinal Control—Altitude

Fig. 7

Response to an unit-step-type input of the altitude control loop with optimization of gains in MIL platform

For the altitude control loop, the value of $K_\mathrm{p}$ was limited to a maximum of 0.0146 (0.0112 * 130%), $K_\mathrm{i}$ without maximum, and $K_\mathrm{d}$ maximum of 0.0032 (0.0032 * 100%). Minimum values have been set to zero.

Figure 7 shows the response to a unit-step-type input of the altitude control loop with the gains defined before optimization, in the red dashed line, and with the gains $K_\mathrm{p}=0.0058$, $K_\mathrm{i}=0.00006$ and $K_\mathrm{d}=0.0032$ obtained from the optimization, in the blue line. The design specifications obtained are shown in Table 4.

Table 4 Comparison of design specifications obtained in the altitude control loop

3.1.3 Lateral-Directional Control—Roll Angle

In the roll angle control loop, the value of $K_\mathrm{p}$ was limited to a maximum of 3.4359 (2.6430 * 130%), $K_\mathrm{i}$ without maximum, $K_\mathrm{d}$ maximum of 1.1090 (1.1090 * 100%) and $K_\mathrm{rg}$ maximum of 0.0803 (0.0803 * 100%). Minimum values have been set to zero.

Figure 8 shows the response to a unit-step-type input of the roll angle control loop with the gains defined before optimization, in the red dashed line, and with the gains $K_\mathrm{p}=0.5915$, $K_\mathrm{i}=0.2574$, $K_\mathrm{d}=0.0662$, $K_\mathrm{rg}=0.0803$ obtained from the optimization, in the blue line. The design specifications obtained are shown in Table 5.

Fig. 8

Response to an unit-step-type input of the roll angle control loop with optimization of gains in MIL platform

Table 5 Comparison of design specifications obtained in the roll angle control loop

3.1.4 Lateral-Directional Control—Yaw Rate

The value of $K_\mathrm{p}$ was limited to a maximum of 0.2786 (0.2143 * 130%), $K_\mathrm{i}$ without maximum, $K_\mathrm{d}$ maximum of 0.0089 (0.0089 * 100%) and $K_\mathrm{rg}$ maximum of 0.1 (0.1 * 100%). Minimum values have been set to zero.

Figure 9 shows the response to a unit-step-type input of the yaw rate control loop with the gains defined before optimization, in the red dashed line, and with the gains $K_\mathrm{p}=0.2786$, $K_\mathrm{i}=0.4322$, $K_\mathrm{d}=0.0089$ and $K_\mathrm{rg}=0.0562$ obtained from the optimization, in the blue line. The design specifications obtained are shown in Table 6.

Fig. 9

Response to a unit-step-type input of the yaw rate control loop with optimization of gains in MIL platform

Table 6 Comparison of design specifications obtained in the yaw rate control loop

3.2 Discussion

Table 7 shows the comparison of performance indexes obtained before and after optimization in MIL platform. With the optimization, the pitch angle control had a performance worsening of 21% in the MSE, but significant performance improvements of 42% in MCE and 67% in CSV. This is because, with optimized gains, the response has been slightly slower but much smoother and without steady-state error. This was reflected in the altitude control response with a performance worsening of 38% in the MSE, but both MCE and CSV had performance improvements of 11%. In the roll angle control, besides a good performance improvement of 42% in MSE, there was a great performance improvement, i.e., of 100%, in both MCE and CSV. This indicates that before performing the optimization, there was a high-frequency oscillation in the control, that can be seen in the magnification made in Fig. 8. Also in the yaw rate control, it is possible to see performance improvement in all indexes: 10% in MSE, 11% in MCE, and in 33% CSV. It should be emphasized that the design specifications obtained with the optimized gains of the controllers for the control loops, via simulations, on the MIL platform have also been improved over design specifications obtained in Splendor et al. (2015).

Table 7 Comparison of performance indexes in MIL platform

3.3 Final Considerations

In the optimizations, smooth responses were priority in all control loops. The second priority was the elimination of steady-state errors, especially in the pitch angle control loop, with the use of a PID controller, instead of the proportional controller used in Splendor et al. (2015). Third, the minimization of overshoots and settling times. All this were done in hope to find a good compromise between errors and control efforts and, at the same time, meet the design specifications. It should be emphasized that there are situations in which there is an inverse relationship between performance indexes, i.e., forcing the improvement of one of them implies worsening others.

Another important point to be noted is that, in the optimizations using the MIL platform, the control loops are completely decoupled. However, in a real flight situation, it is expected that the tightly coupling of the control loops will reflect in the results.

4 Conclusions

This paper presented proposals for the optimization of controller gains of an automatic pilot system for the Cessna 182 aircraft. The reason for the use of the Cessna 182 in the development of the TFs is due to the availability of aerodynamic derivatives in the reference literature

In the study performed previously, the gains of the control loops were obtained by the root locus method and the tuning by means of Ziegler-Nichols. Later, those gains underwent a manual fine adjustment, featuring as a method of trial and error, from which the simulations were conducted. On the other hand, the proposals for optimization presented in this study offer a simple, effective, systematic and replicable way to obtain the gains, providing a improvement of the results in relation to those obtained in the study by Splendor et al. (2015) for the unit-step-type input responses. Besides, the proposals for optimization dispense the use of classical methods of determination of gains for control loops, as well as the trial and error method. Therefore, the Simulink Design Optimization, through its optimization blocks Check Step Response Characteristics and Check Against Reference, is a good alternative to tune gains of the controllers.

Based on the results obtained in this study, a comparative analysis of the simulations results is being carried out using design specifications (optimization block Check Step Response Characteristics) and reference responses (optimization block Check Against Reference) common to the proposed approaches for the optimization of controller gains by the use of MIL platform, using TFs. Regarding future studies, it is deemed necessary to develop robust and adaptive controllers for the autopilot system when the aircraft is under the influence of uncertainties and disturbances. Moreover, other advantages of the use of optimization method are the considerable minimization of the requirement of in-flight tuning, substantial reduction in the risks and costs involved in flight-testing, which have been verified in software-in-the-loop and hardware-in-the-loop platforms.