1 Introduction

Multifunctional materials with coexistence of ferroelectric, ferromagnetic and ferroelastic behaviors have attracted considerable attention among the scientific community in recent years and owing to this kind of materials offer very interesting applications. Multiferroics have emerged as good candidates to be used in electrically controllable microwave elements, magnetic field sensors and even in spintronics. These potential applications dramatically increase if these materials exhibit magnetoelectric effect (coupling between the magnetic and electric parameters) [1]. However, the electronic structures are required for ferromagnetism and ferroelectricity [2]. Perovskites (ABO3) can exhibit a wide diversity of behaviors. The most common examples are high dielectric constant, piezoelectricity, ferroelectricity, magnetoresistance, charge ordering and spin-dependent transport. Nowadays, one of the most promising multiferroic materials is the perovskite BiFeO3 (BFO) which is detected for the first time as early as the 1960s [3–6]. This oxide shows a rhombohedral structure (Space Group: R3c), with lattice parameter a = 0.3965 nm and angle α = 89.3° at room temperature. This material exhibits ferroelectric (T C = 825 °C) and antiferromagnetic (T N = 370 °C) behavior [7–17]. The (BiFeO3) x –(PbTiO3)1−x solid solution series was first reported in 1960 by Venevstev et al. [18]. They observed that the tetragonal phase persists in the series from the PT end member up to 70 wt% BFO and remarked upon the large c/a ratio present in the tetragonal structure at 60 wt% BFO. Wang et al. [19] reported an enhancement of ME properties in the (1 − x)BiFeO3-xPbTiO3 solid solutions. Zhu et al. [20] proposed a phase diagram for the (1− x)BFO-xPT. Their results reveal the existence of a morphotropic phase boundary (MPB) in this system, at which rhombohedral (x ≤ 0.20), orthorhombic (0.20 ≤ x ≤ 0.28) and tetragonal (x ≥ 0.31) phases exist with a large tetragonality in the tetragonal phase region. Cotica et al. [21] investigated the relationship between ferroic states and the physicochemical mechanism which governs the (Bi/Pb/La)–O bonds in polycrystalline La-doped 0.6BFO–0.4PT compounds. A solid solution can be formed between BFO and PT with a tetragonally distorted ferroelectric perovskite with space group P4 mm and T c~490 °C [22]. Mishra et al. [23] investigated phonons and magnetic and ferroelectric ordering in La-substituted (Bi1−x La x )0.5Pb0.5Fe0.5Ti0.5O3 for samples with 0.0 ≤ x ≤ 0.5 using Raman, magnetization and polarization measurements as a function of temperature. As per our knowledge, the electrical properties (impedance, modulus, relaxation time, AC conductivity and DC conductivity) have not been investigated so far at elevated temperatures. In this work, we have reported the structural, impedance, modulus and conductivity properties of 0.5(BiLa x Fe1−x O3)–0.5(PbTiO3) (x = 0.05, 0.10, 0.15, 0.20) multiferroic composites.

2 Experimental

Lanthanum (La)-doped BFO-PT with the formula 0.5BiLa x Fe1−x O3–0.5(PbTiO3) (x = 0.05, 0.10, 0.15, 0.20) was prepared by the conventional solid oxide processing route. The high-purity precursors: Bi2O3 and La2O3 (99.99%, Spectrochem Pvt. Ltd., India), Fe2O3 (≥99%, M/s Loba Chemicals, Pvt. Ltd., India), PbO (≥95%, Spectrochem Pvt. Ltd., India) and TiO2 (≥99% Merck Specialties Pvt. Ltd., India) were carefully weighed in a suitable stoichiometric proportion and mixed thoroughly in an agate mortar for 2 h and in methanol for another 2 h. The mixed powders were calcined in a high-purity closed alumina crucible at an optimized temperature of 800 °C for 6 h in an air atmosphere. The process of grinding and calcinations was repeated several times till the formation of the compounds was confirmed. Then, calcined powders were mixed with polyvinyl alcohol (PVA), which acts as a binder to reduce the brittleness of the pellet and burnt out during high-temperature sintering. The calcined powders were pressed into cylindrical pellets using KBr hydraulic press at pressure of 4 × 106 Pa and sintered at 800 °C for 6 h. The pellets were about 12 mm in diameter and 1–2 mm thickness. The sintered pellets were polished by fine emery paper to make both the surfaces flat and parallel. To study the electrical properties of the compounds, both flat surfaces of the pellets were electroded with air-drying conducting silver paste. After electroding, the pellets were dried at 150 °C for 4 h to remove moisture, if any, and then cooled to room temperature before taking any electrical measurement. The formation and quality of the compounds were studied by an X-ray diffraction (XRD) technique at room temperature with a powder diffractometer (D8 advanced, Bruker, Karmsruhe, Germany) using CuK α radiation (\( \lambda = 0.15405\, {\text{nm}} \)) in a wide range of Bragg’s angles 2θ (20° ≤ 2θ ≤ 80°) with a scanning rate of 3°/min. The electrical parameters (impedance and capacitance) of the compounds were measured by using an LCR meter (HIOKI, Model-3532) in the frequency range of 102–106 Hz and the temperature range 25–450 °C.

3 Results and Discussion

3.1 Structural Analysis

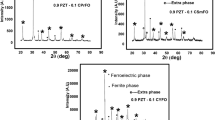
Solid solutions of BL x F1−x -PT for x = 0.05, 0.10, 0.15 and 0.20 were prepared by the mixed oxide method. Figure 1 shows the XRD patterns of La-doped BL x F1−x -PT composites at room temperature. The X-ray diffraction data of BL x F1−x -PT (0.05 ≤ x ≤ 0.20) at room temperature confirmed the tetragonal structure, which is in good agreement with the reported materials 0.45(Bi1−x La x FeO3)–0.55(PbTiO3) [24] and 0.50(BiFeO3)–0.50(PbTiO3) [25]. The multiferroic composites BL x F1−x -PT showed the tetragonal perovskite structure of which the c/a ratio decreases with increasing of La x (x = 0.05–0.20) content. A good agreement between observed and calculated interplanar spacing was observed. The extra peak observed at around 2θ∼25° may be due to presence of La2O3 (JCPDS file no 22-0641) as indicated in Fig. 1 (inset). The lattice parameters of the selected unit cells were refined using the least-squares sub-routine of a standard computer program package “POWD” [26], and the refined lattice parameters of the composites are shown in Table 1. The lattice parameter and c/a ratio found to be very close as reported for BiFeO3–PbTiO3 by taking 55% of PbTiO3 and doping of La on Bi site [24]. The crystallite sizes (P) of BL x F1−x -PT (x = 0.05–0.20) were roughly estimated from the broadening of XRD peaks (in a wide 2θ range) using the Scherrer’s equation: \( P = K\lambda /\left( {\beta_{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} \cos \theta_{hkl} } \right) \) [27] (where K = 0.89 is a constant, λ = 0.15405 nm and β 1/2 is the peak width of the reflection at half intensity). The average crystal size (P) of the composites is found to be 13 nm for all concentration.

Fig. 1
figure 1

X-ray diffraction patterns of 0.5BiLa x Fe1−x O3–0.5PbTiO3 (BL x F1−x -PT) (x = 0.05–0.20) at room temperature

Full size image
Table 1 Values of lattice parameters (10−1 nm) of 0.5BiLa x Fe1−x O3–0.5PbTiO3 (x = 0.05–0.20)
Full size table

3.2 Impedance Properties

Complex impedance spectroscopy (CIS) [28] is a unique and powerful technique to characterize the electrical behavior of a system such as grain, grain boundary and interface properties. This formalism includes the determination of capacitance (bulk and grain boundary), relaxation frequency and electronic conductivity. A polycrystalline material usually gives grain and grain boundary properties with different time constants leading to two successive semicircles. Generally, the data in the complex plane are represented in any of the four basic formalisms. These are complex impedance (Z*), complex admittance (Y*), complex permittivity (ε*) and complex electric modulus (M*), which are related to each other: \( Z^{*} = Z^{\prime } - jZ^{\prime \prime } ,M^{*} = M^{\prime } + jM^{\prime \prime } ,Y^{{^{*} }} = Y^{\prime } + jY^{\prime \prime } ,\varepsilon^{*} = \varepsilon^{\prime } - j\varepsilon^{\prime \prime } \) and \( \tan \delta = \varepsilon^{\prime \prime } /\varepsilon^{\prime } = M^{\prime \prime } /M^{\prime } = Z^{\prime } /Z^{\prime \prime } \), where \( j = \left( { - 1} \right)^{\frac{1}{2}} \) is the imaginary factor, and the symbols (\( Z^{\prime } , M^{\prime } , Y^{\prime } ,\varepsilon^{\prime } \)) and (Z″, M″, Y″, ε″) are real and imaginary components of impedance, electrical modulus, admittance and permittivity, respectively. The complex impedance of “electrode/sample/electrode” configuration can be explained as the sum of a single with a parallel combination of RC (R is resistance, C is capacitance) circuit. Thus, the impedance analysis is an unambiguous and provides a true picture of the electrical behavior of the materials.

Figure 2a–d shows the complex impedance spectrum (\( Z^{\prime } \;vs.\;Z^{\prime \prime } \)) of BL x F1−x -PT with x = 0.05, 0.10, 0.15, 0.20 at various temperatures with an equivalent circuit (inset). Single semicircular arcs have been observed for all the compositions in a wide temperature (200–300 °C) region. The semicircles are found to be depressed with their centers below the real axis (not shown), which confirms the existence of non-Debye type relaxation. The angle, by which the semicircle is depressed below the real axis, is related to the width of the relaxation time distribution and confirms the presence of grain effect in the materials even in increasing the percentage of La concentration. It is also observed that the intercept point on the real axis shifts toward the origin with the increase in temperature which indicates decrease in the resistive property, i.e., called bulk resistance (\( R_{\text{b}} \)) of the materials like a semiconductor [29, 30]. The impedance data fit well with equivalent circuits, R[CR(QR)] given in the Fig. 2a–d (inset) at 200 °C for x = 0.05–0.20, where R, C and Q are resistance, capacitance and constant phase element (CPE). The fitting parameters of the circuit are shown in Table 2.

Fig. 2
figure 2

Complex impedance plot (Z′ vs. Z″) in the temperature range 200–300 °C: a x = 0.05, b x = 0.10, c x = 0.15, d x = 0.20

Full size image
Table 2 Summarizing of fitting parameters corresponding to equivalent circuit R[CR(QR)] at 200 °C of Fig. 2a–d
Full size table

Figure 3a–d shows the variation of Z ′ with frequency (102–106 Hz) of BL x F1−x -PT with x = 0.05, 0.10, 0.15 and 0.20 at different temperatures (200–300 °C). It is observed that the magnitude of Z ′ decreases with rise in temperature in the low-frequency region and appears to merge in the high-frequency region. This may be due to the release of space charge with rise in temperature [31, 32]. On increasing the La concentration, the occurrence of space charge shifted to higher frequency side. This may be due to the reduction in barrier properties of the materials with rise in temperature and responsible for the enhancement of conductivity [33, 34]. At a particular frequency, Z ′ becomes independent of frequency. This type behavior is similar to the other material reported by Singh et al. [35]. The loss spectrum (Z″ vs. frequency) at different temperatures was shown in the Fig. 3a–d (inset), which is broader than the ideal Debye curve and asymmetric. As the temperature increases, the peak position frequency shifts toward higher frequency side and exists a strong dispersion of Z″. The peak width of loss spectrum exhibits the distribution of relaxation times. The relaxation effect and asymmetric spectrum (observed above 200 °C) suggest that non-Debye type of relaxation process occurs in these materials. Generally, the impedance data were used to evaluate the relaxation time (τ) of the electrical phenomena in the materials using the relation: \( \tau = 1/\omega = 1/2\pi f_{\text{r}} \), \( f_{\text{r}} \) is the relaxation frequency. The variation of τ as a function of inverse of absolute temperature was shown in the Fig. 4. It appears to be linear and follows the Arrhenius relation, τ = τ 0 exp (−E a/K B T), where τ0 is the pre-exponential factor, E a is the activation energy, \( K_{\text{B}} \) is the Boltzmann constant and T is the absolute temperature. The activation energy calculated from impedance plot for BL x F1−x -PT composites decreases with the increase in Lanthanum (La) contents and found to be 1.06, 0.77, 0.73 and 0.66 eV for x = 0.05, 0.10, 0.15 and 0.20, respectively.

Fig. 3
figure 3

Variation of Z ′ and Z″ (inset) with frequency at different temperatures: a x = 0.05, b x = 0.10, c x = 0.15, d x = 0.20

Full size image
Fig. 4
figure 4

Variation of relaxation time (τ) with inverse of temperature (103/T ′) calculated from impedance plot

Full size image

3.3 Modulus Properties

The complex modulus spectroscopy is a very important and convenient tool to determine, analyze and interpret the dynamical aspects of electrical transport process in the material, such as the parameters (carrier/ion hopping rate and conductivity relaxation time) with the smallest capacitance occurs in a dielectric system. Modulus spectroscopy plots are particularly useful for separating spectral components of the materials having similar resistances but different capacitances. The other advantage of the electric modulus formula is that the electrode effect is suppressed. The electric modulus M *(ω) is expressed by the complex modulus formula [36, 37]:

\( M^{*} \left( \omega \right) = j\left( {\omega C_{0} } \right)Z^{*} = M^{\prime } + jM^{\prime \prime } \), where \( M^{\prime } = \omega C_{0} Z^{\prime \prime } \; {\text{and}}\;M^{\prime \prime } = \omega C_{0} Z^{\prime } \), where the symbols have their usual meanings.

Figure 5a–d shows the complex modulus spectra (\( M^{\prime } \; {\text{vs}} .\;M^{\prime \prime } \)) of BL x F1−x -PT with x = 0.05–0.20 at different temperatures. In order to avoid the ambiguity arising out of the presence of grain/grain boundary effect [38] at different temperatures, the impedance data were re-plotted in the modulus formula. The intercept on the real axis indicates that the grain and grain boundary effects contribute the total capacitance. Further, the modulus spectra show a change in its shape with rise in temperature and suggest a probable change in the values of the capacitance as a function of the temperature. Complex impedance spectra give more emphasis to elements with larger resistance, whereas complex electric modulus plots highlight those with smaller capacitance. The variation of M ′ as a function of frequency for BL x F1−x -PT with x = 0.05–0.20 at selected temperatures (200–300 °C) is shown in Fig. 5a–d (inset). At lower frequencies, M ′ tends to be very small value (approximately zero). There is a continuous dispersion with increase in frequency. This may be due to the short-range mobility of charge carriers [39], which confirms the negligibly small contribution of electrode effect. In this figure, M′ reaches a constant value (M ∞) at high frequencies for all the temperatures and shows relaxation process, which occurs in the materials. The variation of M′′ with frequency at different temperatures is shown in Fig. 6a–d. The maxima M′′max shifts toward higher frequencies side with rise in temperature as well as La concentration which shows the correlation between motions of mobile ions [40]. This suggests that the dielectric relaxation is a thermally activated process. This type of effect has been reported in the modulus spectrum of some ionic conductors [41]. The asymmetric peak broadening indicates the spread of relaxation times with different time constants, and hence, relaxation is of non-Debye type. The nature of modulus spectrum suggests the existence of hopping mechanism of electrical conduction in the materials [39]. The variation of relaxation time (τ) as a function of reciprocal of temperature 1/T of BL x F1−x -PT (x = 0.05–0.20) at high-temperature region is shown in Fig. 7 (calculated from modulus spectrum). This graph follows the Arrhenius relation: \( \tau = \tau_{0} \exp \left( { - E_{\text{a}} /K_{\text{B}} T} \right) \), where the symbols have their usual meanings and thermally activated process. The values of the activation energy of the composites are found to be 0.75, 0.68, 0.70 and 0.70 eV for all compositions of La.

Fig. 5
figure 5

Complex modulus spectrum (M′ vs. M ″) and variation of M ′ as a function of frequency (inset) for BLxF1−x-PT with x = 0.05–0.20 at different temperatures: a x = 0.05, b x = 0.10, c x = 0.15, d x = 0.20

Full size image
Fig. 6
figure 6

Variation of imaginary part of electric modulus with frequency for BL x F1−x -PT (x = 0.05–0.20) at selected temperatures: a x = 0.05, b x = 0.10, c x = 0.15, d x = 0.20

Full size image
Fig. 7
figure 7

Variation of relaxation time (τ) as a function of reciprocal of temperature (103/T) of BL x F1−x -PT (x = 0.05–0.20) at different temperature region calculated from modulus spectrum

Full size image

4 Electrical Conductivity

The conductivity study is a most prominent example to relate the macroscopic measurement with the microscopic movement of the ions. The frequency-dependent conductivity spectrum is shown in Fig. 8a–d at selected temperatures (200–300 °C) of BL x F1−x -PT, which displays a low-frequency plateau and high-frequency dispersive regions. The frequency-independent conductivity characterizes the dc conductivity may be due to the random diffusion of the ionic charge carriers via activated hopping. However, power-law dispersion indicates a nonrandom process, wherein the ions perform correlated forward–backward motion [42]. At low temperature, i.e., 200–225 °C, the \( \sigma_{\text{ac}} \left( \omega \right) \) increases with increasing frequency, which is a characteristic of ω n (n is the frequency exponent related to the degree of correlation among moving ions). At high temperatures, i.e., at 250–300 °C and low frequencies, \( \sigma_{\text{ac}} \left( \omega \right) \) shows flat (plateau) response while it depends on ω n dependence at higher frequency. The nature of the conductivity dispersion in solids is generally analyzed using Jonscher’s power law [43]; σ ac(ω) = σ(0) + Aω n, where ω(0) is the frequency independent (electronic or dc) part of ac conductivity, n (0 ≤ n ≤ 1) is the index, ω is angular frequency of applied ac field and A = [πN 2 e 2/6K B T(2α)] is a constant, e is the electronic charge, T is the temperature, α is the polarizability of a pair of sites, and N is the number of sites per unit volume among which hopping takes place. The term Aωn can often be explained on the basis of two distinct mechanisms for carrier conduction: quantum mechanical tunneling (QMT) through the barrier separating the localized sites and correlated barrier hopping (CBH) over the same barrier. In these models, the exponent n is found to have two different trends with temperature and frequency. If the ac conductivity is assumed to originate from QMT, n is predicted to be temperature independent but expected to show a decreasing trend with ω, while for CBH the value of n should show a decreasing trend with an increase in temperature. According to Funke [44], the values of n have a physical meaning, i.e., n ≤ 1 means that the hopping motion involves a translational motion with a sudden hopping, whereas n > 1 means that the motion involves localized hopping without the species leaving the neighborhood. The recent literature also endorsed that the exponent n is not limited to values below 1 [45]. Further, hopping conduction mechanism is generally consistent with the existence of a high density of states in the materials having band gap like that of a semiconductor. Due to localization of charge carriers, formation of polarons takes place and the hopping conduction may occur between the nearest neighboring sites [46]. This suggests that the electrical conduction in BL x F1−x -PT is a thermally activated process. The nonlinear curve fit to Jonscher’s power law for all the composites at different temperatures (200–300 °C) is shown in the Fig. 8a–d. The fitting parameters \( A, n,\sigma \left( 0 \right) \) are calculated from the nonlinear fitting (given in Table 3). Figure 9 shows the variation of n with temperature (200–300 °C). It is observed that the value of n increases linearly with the increase in the temperatures. This may be the result of the rise of the electrode polarization contribution with temperatures [47], which lead to decreasing amount of ac conductivity data available to perform the least-squares fitting. Figure 8a shows that the value of n varies from 0.8 to 1, whereas in Fig. 8b–c the value of n (0.8–1.9) increases with the increase in La x (x = 0.10–0.20) concentration of the composites. This type of behavior may be associated with the small polaron (SP) tunneling models. The exponent n is a temperature-dependent factor in correlated barrier hopping (CBH) models, overlapping large polarons (OVL) models and small polarons (SP) tunneling models [48].

Fig. 8
figure 8

Variation of ac conductivity with frequency at different temperatures: a x = 0.05, b x = 0.10, c x = 0.15, d x = 0.20

Full size image
Table 3 Fitting parameters obtained from the Jonscher’s power law at different temperatures (200–300 °C) of 0.5BiLa x Fe1−x O3–0.5PbTiO3 (x = 0.05–0.20)
Full size table
Fig. 9
figure 9

Variation of n with different temperatures (200–300 °C)

Full size image

Figure 10 shows the variation of \( \sigma_{\text{dc}} \) (bulk) with inverse of absolute temperature (103/T). The bulk conductivity (σ) of the material was evaluated from the complex impedance plots of the sample at selected temperatures using the relation ρ = l/R b A, where l is the thickness, \( R_{\text{b}} \) is the bulk resistance and A is the area of cross section of the sample. The nature of variation of the composites is following the Arrhenius relation: σ dc = σ 0 exp (−E a/K B T) where σ 0 is the pre-exponential factor. It is observed that the dc conductivity increases (i.e., bulk resistivity decrease) with rise in the temperature, and hence, the material shows negative temperature coefficient of resistance (NTCR) behavior like a semiconductor [49]. The temperature dependence of dc conductivity indicates that the electrical conduction in the material is a thermally activated process. The activation energy E a due to bulk of the composites was calculated as 0.81, 0.77, 0.76 and 0.74 eV for x = 0.05, 0.10, 0.15, 0.20 in the temperature region (225–300 °C). The activation energy of the composites is found to be very close for Nd-doped 0.5BiFeO3–0.5PbTiO3 [31]. This small amount of the energy required for the conduction process in the composites may be due to the singly ionized oxygen vacancies at higher temperatures.

Fig. 10
figure 10

Variation of dc conductivity with inverse of temperature

Full size image

5 Conclusions

The polycrystalline sample of BL x F1−x -PT (x = 0.05–0.20) was prepared by a high-temperature solid-state reaction technique. The structural analysis shows tetragonal structure at room temperature for all compositions. The crystal sizes of the composites are roughly estimated as 13 nm for all concentration. Complex impedance spectroscopy was used to characterize the electrical properties of the materials. Modulus analysis confirmed the presence of hopping mechanism in the materials. The electrical conduction of the samples is due to bulk effect only. The bulk resistance decreases with rise in the temperature indicating a typical NTCR behavior of the composites. The temperature dependence of relaxation phenomena occurs in the composites. The ac conductivity spectrum was found to obey Jonscher’s universal power law, whereas dc conductivity shows a typical Arrhenius type of electrical conductivity. The values of activation energy of the composites were found to be 0.81, 0.77, 0.76 and 0.74 eV for x = 0.05, 0.10, 0.15 and 0.20, respectively.