1 Introduction

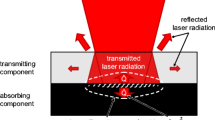
Laser transmission welding (LTW) has grown into a viable industrial tool, in the last two decades, for welding thermoplastic components in a variety of sectors, including aerospace [1], electrical [2], electronics [3], medical devices [4, 5], microfluidic devices [6], and automotive [7]. The potential advantage of laser as a concentrated and high-intensity light source for heating and melting of materials makes this process a contactless, highly precise, and flexible welding process [8, 9]. In LTW, a laser beam irradiates the overlapping polymer parts, where the upper polymer part is laser-transparent, and the lower polymer part is the laser-absorbing part, as shown in Fig. 1. The laser beam, which has penetrated through the transparent part, strikes the absorbing polymer part at the joint interface. The laser radiation absorbed by the laser-absorbing polymer causes the part to heat up. A part of the heat generated in the absorbing polymer is transferred to the transparent upper polymer part, which is in intimate contact at the interface. The temperature rise at interface causes the polymers to melt or soften as and when it reaches to the melting range or glass transition temperature of the polymers. After solidification and molecular diffusion, a firm weld is formed between the mating parts [10, 11]. Most of the polymers are highly transparent to the radiation of Nd:YAG, diode, and fiber lasers, and thus these laser are widely used to perform LTW of polymers [10, 12].

Fig. 1
figure 1

Working principle of laser transmission welding of polymers

Full size image

A decent number of academic and industrial research and development works are carried out to investigate the materials [13] and parametric aspects [14] of LTW, to develop new irradiation strategies [15], to identify new application areas [14], and to optimize the process [16, 17]. It has been discovered that the polymer compositions (additives, reinforcements, filler, etc.) and conditions (part thickness, crystallinity, moisture content, etc.) influence laser energy transmission, reflection, and absorption, as well as the quality and performance of the welded parts [18, 19]. The major LTW parameters are laser power, welding speed, and beam size, which control the energy input and, as a result, the temperature field during LTW, as well as the weld strength and quality [20, 21]. Continued research and development in the field of LTW leads in the creation of innovative laser irradiation strategies such as absorber-free LTW [22], TWIST (transmission laser welding using incremental scanning technique) [23], and hybrid LTW [24] of polymers. LTW is not only used to weld polymers and polymer composites, but it is also employed to join hybrid structures, such as polymer-metal joints [25].

Numerical modeling is a widely used and well accepted technique for systematic investigation of manufacturing processes and for prediction of process variables and responses without much experimental efforts [26]. Several scientific publications on LTW attempted to investigate the heat transfer phenomena, the evolution of the weld pool, and the effect of various process variables on the temperature field during LTW by developing thermal models [26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43]. Potente et al. [27] studied the thermal cycle in LTW of nylon 6 using an analytical model and, after considering a correction factor, the model reliably predicts the outputs. Kurosaki et al. [28] developed a numerical model for LTW of low-density polyethylene by solving a simplified 1-D transient heat-transfer equation. Russek et al. [29] developed 2-D thermal models of contour and simultaneous LTW to determine the distribution of energy density and the temperature field by solving the energy conservation equation for different steps of approximation. The temperature distribution is revealed to be impacted by the combination of laser power and welding speed at constant line energy, and the limiting link is discovered to be thermal conductivity. Hadriche et al. [30] studied the effect of LTW parameters on weld morphology using a 2-D finite difference model (FDM), supported by the experimental data. A differential equation derived from the Avrami equation is used to describe the evolution of relative crystallinity. The modelling findings revealed that the welded sections’ thermal cycle entailed isotherm cooling, which causes morphological changes owing to inhomogeneous crystallinity. Hopmann and Kreimeier [31] developed a 2-D FE (finite element) model of simultaneous welding variant of LTW of semi-crystalline polymers to predict the welding temperature and weld dimensions. The heating simulation accounts for temperature-dependent material properties as well as the influence of crystallinity on optical properties. Aden [32] constructed a 2-D FE model to study the effect of laser energy distribution on LTW seam properties, considering Gaussian- and M-shaped laser beams. It is observed that Gaussian- and M-shape beams create distinct temperature fields for LTW of amorphous and semi-crystalline polymers.

Mayboudi et al. [33] developed a 3-D FE model of LTW of polyamide 6 exposed to a stationary laser beam, and further expanded this model to the application of LTW with a moving laser beam [34]. Ilie et al. [35] evaluated the laser weldability of ABS using a 3-D transient thermal FE model and experimental data. The first principle of heat transfer is utilized to compute the temperature field within the materials and at the interface, considering perfect interfacial contact between the mating parts. Acherjee et al. [26] developed a 3-D transient thermal FE model to investigate the effect of carbon black on temperature field and weld profile during LTW of polymers. The model is created parametrically by solving a 3-D heat diffusion equation while taking temperature-dependent material properties into account. This FE model is designed to simulate the contour welding variant of LTW with a moving laser beam. As an extension of the early model, Acherjee et al. [36] constructed a 3-D transient thermal FE model for simultaneous welding variant of LTW considering a stationary Gaussian laser beam. The FE responses are incorporated into RSM (response surface model) to investigate the influence of process parameters on the temperature field and weld dimensions and to determine the optimal process zone for a satisfactory weld. Wang et al. [37] developed a 3-D axisymmetric FE model of contour LTW for polymer to metal welding by considering a moving super-Gaussian laser beam. The FE model outputs are integrated with RSM and GA (genetic algorithm) to improve model prediction efficiency. In continuation of their work, Wang et al. [38] built a 3-D FE model to investigate the temperature field and melt-pool geometry for LTW of polymers. The model is used to investigate the correlations between process parameters, molten pool shape, and shear strength in LTW of polyethylene terephthalate and polypropylene. Liu et al. [39] built a 3-D FE model of LTW that includes the effect of interfacial contact status along with the volumetric absorption of laser radiation. The proposed thermal contact model is used to evaluate and predict weld temperature contours and weld profiles when there is no interface gap and when there is an interface gap. Chen et al. [40] developed a 3-D FE model of LTW to estimate the welding temperature and the size of weld pool by considering a composite heat source by integrating the rotary-Gauss heat source with a Gaussian heat source. Acherjee et al. [41] designed a 3-D FE model of quasi-simultaneous LTW process to simulate the transient temperature field and to study the parametric effects. Later, Acherjee et al. [42] proposed a 3-D FE model of LTW of dissimilar polymers that incorporates the dilution factor with a volumetric heat source model to predict thermal responses and weld pool dimensions. Xu et al. [43] developed a 3-D transient FVM (finite volume method)-based LTW model to simulate the formation of molten pools during LTW between polymer and stainless steel.

A few publications are available in open literature where couple field models are used to study the thermo-mechanical phenomena during LTW [44,45,46,47,48,49,50,51]. Thermo-mechanical models are used to evaluate process conditions for bridging part gaps by producing adequate thermal expansions and to study the stress field developed during heating and cooling phases of the LTW. The stresses that would exist in the welded component after cooling, when all external loads have been removed, are called residual stresses. Residual stresses are developed due to the deformation gradients in the material by the development of thermal gradients, volumetric changes arising during solidification, or from solid state transformations. Tensile residual stress adversely affects the performance of the weld and can cause premature failure of the component. This can accelerate the extent of damage caused by fatigue, creeping, or environmental decays. Compressive residual stress is usually advantageous; however, it reduces the buckling resistance.

Potente and Fiegler [44] created a 2-D thermo-mechanical FE model of LTW that incorporates the impact of welding pressure to analyze flow and temperature profiles with a stationary heat source. The intensity distribution is modelled using the Bouguer-Lambert equation, and the pressure effect is realized using thermo-elasticity and plasticity theory. Ven and Erdman [45] designed a 2-D thermo-mechanical FE model to select process parameters to produce necessary thermal expansion to bridge the part gaps and to shape the weld during LTW. Internal pressure and gap-bridging capabilities are determined by knowing the unconstrained volumetric change of a specified mass of material due to heating. Shaban et al. [46] developed a 2-D thermo-mechanical FE model of LTW to analyze the evolution of the stress field with the temperature cycle during the heating and cooling phases. The model considers the viscoplastic behavior of the polymer while simplifying the thermal model by focusing on surface heat flow rather than volumetric heat generation. Lakemeyer and Schöppner [47] developed a 2-D thermo-mechanical FE model to explore the effects of welding temperature and energy input. The thermo-elasticity and plasticity model is used to represent the squeezing flow of the material during welding, as the entire weld seam is plasticized during quasi-simultaneous welding. It is found that the welding temperature has a greater impact on weld strength than the energy input.

Schmailzl et al. [48] built a 3-D FE model to analyze the effect of temperature distribution on thermal expansion to bridge the parts gap during LTW. The thermo-mechanical model employs one-way coupling because the thermal simulation is done in small time steps with time-dependent effects, and the thermal field is then incorporated in the mechanical simulation to determine thermal expansion. Casalino and Ghorbel [49] proposed a 3-D thermo-mechanical FE model of LTW to estimate polymer decomposition and residual stress. The effect of the clamping pressure is neglected, and the estimated residual stress is found to be negligible. Sooriyapiragasam and Hopmann [50] developed a 3-D thermo-mechanical FE model to quantify the spatial temperature distribution during simultaneous LTW and estimate the residual stress distribution. A couple field model that combines a heat conduction-based thermal model with an elasto-plastic mechanical model with mechanical boundary constraints imposed on displacement of horizontal exterior surfaces is used to estimate the thermally induced stress field. Hopmann et al. [51] developed a 3-D FE thermo-mechanical model of LTW to simulate temperature and residual stress while using a stationary laser beam. The thermomechanical model is built that takes into account elastic, elastoplastic, and viscoelastic material behavior to predict thermally induced stress filed during simultaneous LTW of polymers.

In this work, a 3-D thermo-mechanical FE model is developed to simulate the LTW process for contour laser welding of polycarbonate with a moving laser beam. The FE model incorporates all major thermo-mechanical phenomena associated with LTW process including volumetric absorption of radiation, heat generation, 3-D transient heat transfer, and rate-dependent elasto-plasticity. The viscoplastic effect of polymer is included in the thermo-mechanical model by implementing Perzyna’s rate-dependent plasticity model in ANSYS®. This model is utilized to study the temperature field and the evolution of stress field during heating and cooling phases of LTW process. This model is designed parametrically using APDL (ANSYS® parametric design language), which allows flexibility in the use of this model with different part geometries, thermoplastic materials, process conditions, and parameter values.

2 Mathematical formulations

Simulation of complex thermo-mechanical phenomena of LTW requires many physical aspects to be considered during modeling, and thus few simplification assumptions are made during model development, which are as follows:

  1. i.

    symmetric boundary condition is used to reduce model size due to presence of geometric and loading symmetries,

  2. ii.

    there is sufficient contact between mating parts at joint interface,

  3. iii.

    the laser intensity follows the Gaussian distribution,

  4. iv.

    the isotropic thermo-mechanical characteristics of the work-piece material, and

  5. v.

    the effect of creep is neglected because the time scale is small.

The objective of this research is to simulate the temperature and stress field during the heating and cooling phases of the LTW process. As a result, any pre-stress induced in the specimens because of the production process of polycarbonate plaques is ignored. In this study, the development of the stress field is attributed to the application of clamping pressure and the internal pressure generated due the confinement of the thermal expansion of the polymers during LTW.

2.1 Heat transfer model

The mathematical expression for thermal simulation of LTW is derived by combining the Fourier’s law of heat transfer with law of conservation of energy, and is given by the following [52]:

$$\rho c\left(\frac{\delta T}{\delta t}\right)={\left\{L\right\}}^{T}\left(\left[D\right]\left\{L\right\}T\right)+{q}_{v}$$
(1)

where ρ is density, c is specific heat, T is temperature that depends on location and time, t is time, {L} is a vector operator, and [D] is the conductivity matrix:

$$\left\{L\right\}=\left\{\begin{array}{c}\frac{\partial }{\partial x}\\ \frac{\partial }{\partial y}\\ \frac{\partial }{\partial z}\end{array}\right\};\left[D\right]=\left[\begin{array}{c}\begin{array}{ccc}{k}_{xx}& 0& 0\end{array}\\ \begin{array}{ccc}0& {k}_{yy}& 0\end{array}\\ \begin{array}{ccc}0& 0& {k}_{zz}\end{array}\end{array}\right]$$
(2)

where Kxx, Kyy, Kzz are the thermal conductivity of elements along three dimensional coordinates. The variable \({q}_{v}\) of Eq. (1) denotes the rate of internal heat generation per unit volume. Beer Lambert equation, which denotes that the intensity of monochromatic light decays exponentially with the degree of penetration inside an absorbent medium, is coupled with Gaussian expression and is used to calculate the nodal values of \({q}_{v}\) at each node [53]:

$$q_v=\left\{\begin{array}{l}\begin{array}{cc}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0&\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;,for\;transparent\;part\end{array}\\\begin{array}{cc}\frac P{\pi r_0^2}exp\left(-\frac{r^2}{r_0^2}\right)exp\left(-Kz_a\right)&,for\;absorbing\;part\end{array}\end{array}\right.$$
(3)

where K is the coefficient of absorption and za is the distance within the absorbent polymer in the direction of depth, P is laser power and r0 is beam radius, r = √(x2 + y2) is the distance between the node and the center of the beam on joint interface, computed radially using x, y Cartesian coordinates. At the wavelength range employed in LTW (0.8–1.1 μm), polycarbonates, a glasslike polymer, transmits about 90 ± 2% [8] and specularly reflects only about 7% of the incident beam energy [54]. At that wavelength, polycarbonates absorb a tiny amount of beam energy [55]. Because the absorption of laser energy by the transparent part is negligible, it is assumed to be zero in the computation of the rate of internal heat generation, \({q}_{v},\) to reduce simulation time.

Natural convection and radiation heat losses from the outer surfaces of the workpiece to the environment are considered as boundary conditions [41]:

$${\left\{q\right\}}^{T}\left\{\eta \right\}=h\left({T}_{S}-{T}_{B}\right)+\sigma \varepsilon \left({T}_{S}^{4}-{T}_{B}^{4}\right)$$
(4)

where, {η} is unit outward normal vector, h is coefficient of convective heat transfer, \({T}_{S}\) is the temperature of the sample surfaces, \({T}_{B}\) is the temperature of the surrounding fluid, ε is emissivity, and σ is the Stefan Boltzmann constant. The convective-radiative heat transfer is realized in a single unified boundary condition as follows [53]:

$${\left\{q\right\}}^{T}\left\{\eta \right\}={h}_{r}\left({T}_{S}-{T}_{B}\right)$$
(5)

where hr is the coefficient of combined heat transfer,

$${h}_{r}=h+\varepsilon \sigma \left({T}_{S}+{T}_{B}\right)\left({T}_{S}^{2}+{T}_{B}^{2}\right)$$
(6)

Furthermore, combination of Eq. (6) with Fourier’s law results in the following:

$${\left\{\eta \right\}}^{T}\left[D\right]\left\{L\right\}T={h}_{r}\left({T}_{B}-T\right)$$
(7)

Multiplying Eq. (1) by a virtual temperature change, and integrating this over volume of the element, and coupling with Eq. (7) with a few manipulations yield the governing equation for temperature field simulation used for the present study as given below:

$$\underset{vol}{\int }\left(\rho c\left(\frac{\partial T}{\partial t}\right)\delta T+{\left\{L\right\}}^{T}\delta T\left(\left[D\right]\left\{L\right\}T\right)\right)d\left(vol\right)=\underset{S}{\int }\delta T{h}_{r}\left({T}_{B}-T\right)dS+\underset{vol}{\int }\delta T{q}_{v} d(\mathrm{vol})$$
(8)

where, vol is the volume of the element and δT is a virtual temperature dependent on the x, y, z, and t [52].

2.2 Plasticity model

The nonlinearity of materials is attributed to the nonlinear interaction of stress and strain. The stress–strain relationship can be expressed as follows:

$$\left\{\sigma \right\}=D\left\{\varepsilon \right\}$$
(9)

where {σ} and {ε} are stress and strain vectors, respectively, and D is stiffness matrix. Again,

$$\left\{\varepsilon \right\}=\left\{{\varepsilon }^{el}\right\}+\left\{{\varepsilon }^{pl}\right\}+\left\{{\varepsilon }^{th}\right\}+\left\{{\varepsilon }^{cr}\right\}+\left\{{\varepsilon }^{sw}\right\}$$
(10)

where {εel}, {εpl}, {εth}, {εcr}, and {εsw} are elastic, plastic, thermal, creep, and swelling strain vectors, respectively [52].

Based on the assumptions made during the LTW simulation, the total strain vector {ε} is defined as follows:

$$\left\{\varepsilon \right\}=\left\{{\varepsilon }^{el}\right\}+\left\{{\varepsilon }^{pl}\right\}+\left\{{\varepsilon }^{th}\right\}$$
(11)

The elastic strain vector is defined by the relation between stress and elastic strain.

$$\left\{{\varepsilon }^{el}\right\}={D}^{-1}\left\{\sigma \right\}$$
(12)

where, D−1 is the compliance matrix.

$${D}^{-1}=\left[\begin{array}{ccc}1/E& -\nu /E& 0\\ -\nu /E& 1/E& 0\\ 0& 0& 1/G\end{array}\right]$$
(13)

where, E, G, and ν are Young’s modulus, shear modulus, and Poisson’s ratio, respectively.

Plastic deformation occurs as induced stresses go past the material’s yield point. The thermal strain vector is governed by a temperature-dependent thermal expansion coefficient.

$$\left\{{\varepsilon }^{th}\right\}=\Delta T{\left[{\alpha }^{se}(T)\right]}^{T}$$
(14)

where [αse(T)] is temperature-dependent secant coefficient of thermal expansion, and

$$\Delta T=T-{T}_{ref}$$

where, T and Tref are the present and the reference (strain free) temperatures, respectively.

The plasticity model integrates the von Mises yield criteria, the associative flow rule, and the isotropic hardening law. The von Mises stress is used to estimate the yielding of materials under multiaxial loading using the uniaxial tensile test results as model input. The isotropic hardening model ensures the uniform yielding of the entire yield area. The measure of the yield area varies with the magnitude of the plastic strains.

3 Thermo-mechanical modeling using ANSYS

Figure 2 illustrates the steps involved in thermo-mechanical FE modeling of LTW using ANSYS®. Figure 3a shows the polymer parts in lap joint geometry used for present investigation with their dimensions. Model size is reduced using symmetric boundary conditions, and only one half of the model is considered due to the presence of geometric and loading symmetries (Fig. 3b). The conductive solid element, SOLID70, is used for meshing of the model for thermal analysis. SOLID70 element supports input heat flux, convection and radiation as surface loads, and input heat generation rates as body loads. For subsequent structural analysis, SOLID70 elements are substituted by equivalent structural element, SOLID45. This structural element supports temperatures and fluences as element body loads at nodes, and pressures on element faces as surface loads [56]. A selective meshing is used to ensure a denser mesh pattern at the irradiation zone and a coarser mesh pattern at the remaining part (Fig. 3c). A node density sensitivity analysis is performed to determine optimum grid spacing at irradiation zone. The moving laser beam is realized using a subroutine executed in ANSYS® parametric design language [26]. Thermo-mechanical simulation of LTW requires coupled field analysis. In this study, the sequentially coupled analysis is used where temperature distributions are first calculated in a nonlinear transient thermal analysis step, then the temperatures are imported and applied as body loads for the subsequent mechanical analysis.

Fig. 2
figure 2

Flowchart showing steps involved in thermo-mechanical FE modeling of LTW

Full size image
Fig. 3
figure 3

Schematic of a the sample, b the reduced geometric model, and c the FE mesh pattern of geometric model

Full size image

Thermo-elasto-viscoplastic modeling entails the modeling and integration of thermal, elasto-plastic, and viscoplastic attributes. The following sub-Sects. (3.1, 3.2, and 3.3) present the simulation of the temperature field and thermal expansion, and development of elasto-plastic and viscoplastic models in details. Subsection 3.1 provides a step-by-step discussion of the material data, modelling strategy, and parameters used for simulation of temperature field and thermal expansion. Subsection 3.2 provides a detailed explanation of the material data, modelling strategy, and parameters used in elasto-plastic simulation. Subsection 3.3 explains how the viscoplastic effect of the polymer is accounted for in the thermo-mechanical FE simulation.

3.1 Temperature field and thermal expansion

A heat conduction-based FE model is developed to simulate the temperature field during LTW. The temperature response in the material involved in high heat fluxes is determined by the thermal properties, namely, thermal conductivity, specific heat, and density, which are dependent on temperatures. Therefore, the thermo-physical properties of polycarbonate varying with temperature, viz., density, thermal conductivity, and specific heat are used in heat transfer simulation [26].

For thermal modelling, the convective and radiative heat transfer boundary conditions are merged to form a single boundary condition as shown in Eq. 5. The values of the combined heat transfer coefficient, hr, are computed at different temperatures and recorded in a look-up table. The coefficient of convective heat transfer, h, is considered as 5 W/m2K [57]. Emissivity of polycarbonate is known to be 0.95 [58].

Thermal expansion during welding depends on the coefficient of thermal expansion of the work material. Temperature-dependent coefficient of thermal expansion of polycarbonate is determined from the pvT curve of Makrolon® 2605–generic polycarbonate [59] at 0.1 MPa atmospheric pressure condition. Figure 4 presents the temperature-dependent coefficient of thermal expansion of polycarbonate.

Fig. 4
figure 4

Temperature-dependent linear thermal expansion coefficients of polycarbonate

Full size image

The thermal model predictions are compared with the experimental results in terms of weld pool dimensions in Fig. 5 and found to be in close agreement.

Fig. 5
figure 5

Comparison of weld width results predicted by the FE model and measured experimentally at different operational conditions

Full size image

3.2 Elasto-plastic model

Plasticity is the non-reversible deformation of a substance in relation to the forces applied. The stress–strain relationship of the substance beyond yield point is of key significance for elasto-plastic simulation. Though, there is a slight difference between limit of proportionality and the yield point of material, ANSYS® FE code considers that those points are the same for plasticity modeling [60].

The FE model requires temperature-dependent mechanical properties of the material including Young’s modulus, Poisson’s ratio, and uniaxial true stress–strain relationship for elasto-plastic analysis. Temperature-dependent Young’s modulus of polycarbonate is determined from temperature-dependent stress–strain relationship of Makrolon® 2605–generic polycarbonate [59], and plotted in Fig. 6. For describing the softening/melting of polycarbonate beyond its glass transition temperature, a constant and very low Young’s modulus value of 5 MPa is assumed above 150 °C. Poisson’s ratio of polycarbonate is 0.38 [61].

Fig. 6
figure 6

Temperature-dependent Young’s modulus of polycarbonate

Full size image

A multilinear isotropic option (MISO in ANSYS®) is used to add true stress–strain results to the plasticity model. The MISO curve is represented by a piece-wise linear stress–strain curve, beginning from the origin, in which the slope of the first curve segment correlates with the Young’s modulus of the material. Temperature-dependent true stress–strain data of polycarbonate [62] is used to feed the MISO material property table. The MISO model implements the von Mises yield criteria, the associative flow rule, and the isotropic hardening [52].

3.3 Viscoplastic model

The viscoplastic effect of the polymer is included in the thermo-mechanical FE simulation. Viscoplasticity is a time-dependent mechanical behavior of materials in which the evolution of plastic strains depends on the loading rate. Many materials behave in way that their strength improves with the rate of loading (Fig. 7), since the viscous effect is induced in the substrate at high strain rates that bears a portion of the load. Integrating the viscous effect into the plasticity model, a viscoplastic model is developed that simultaneously addresses the viscous and plastic behaviors of the materials. In the case of amorphous polymers, such as polycarbonate, the plasticity of the material is typically viscoplastic [63].

Fig. 7
figure 7

Effect of a temperature and b strain rate on deformation characteristics of materials

Full size image

The rate-dependent uniaxial stress–strain data of polycarbonate [64] is used in viscoplastic model. The yield stress value of polycarbonate under dynamic loading is considerably higher than that of static loading. This effect can be successfully incorporated in plasticity model in ANSYS® using Perzyna viscoplastic model [60].

In this work, Perzyna model in combination with the MISO model is implemented for elasto-viscoplastic modeling of LTW process. The Perzyna model can be stated as follows:

$$\sigma =\left[1+{\left(\frac{{\dot{\varepsilon }}^{pl}}{\gamma }\right)}^{m}\right]{\sigma }_{0}$$
(16)

where σ and σ0 are the dynamic and static yield stress of the material, \({\dot{\varepsilon }}^{pl}\) is the equivalent plastic strain rate, and m and γ are the strain rate hardening and material viscosity parameters, respectively. If γ tends to ∞ or \({\dot{\varepsilon }}^{pl}\) tends to zero, the equation is converging into a static solution (rate-independent). The parameters m (0 ≤ m ≤ 1) and γ (0 ≤ γ ≤ ∞) are computed from uniaxial stress–strain results at varying strain rates. In order to calculate these parameters, it is required to evaluate the values of σ, σ0, and \({\dot{\varepsilon }}^{pl}\) directly from the tensile test results at these strain rates. The values of parameters m and γ are determined as 0.192 and 6742 s−1, respectively. Figure 8 shows that the experimentally measured yield strength and that from model prediction are in good agreement, within the range of strain rate considered in this study.

Fig. 8
figure 8

Strain rate sensitivity of yield stress

Full size image

4 Results and discussion

Temperature field induced by moving heat source is shown in Fig. 9. The process parameters used in the present simulation are 5-W laser power, 20-mm/s welding speed, 1.5-mm beam diameter, and 1-MPa clamp pressure. The temperature contours show that LTW causes an intense localized heating of the joining polymers. The glass transition temperature (Tg) of polycarbonate is 150 °C, so it softens steadily beyond this temperature. The weld pool is recognizable by the zone shown in the contours plot with a temperature above 150 °C. The contours plot indicates that the temperature attains a peak of 314 °C during LTW, and that the heat produced at the irradiation zone is eventually transmitted to the adjacent material through heat conduction. Due to the volumetric absorption of laser radiation by the absorbing polymer, the peak temperature is reached inside the absorbing polymer part which creates an asymmetric welding pool configuration. The temperature profile within joining polymers change rapidly with time and distance as the laser beam travels. The temperature gradient in front of the laser beam is found to be steeper than that in the back. By plotting the temperature results against distance along x and y axes, weld width and depth of penetration can be determined by taking 150 °C as the reference point for melting [65].

Fig. 9
figure 9

Temperature distribution along the weld line at t = 0.76 s

Full size image

The temperature field in the weld zone is found to be non-uniform, resulting in differential thermal expansion of the polymers in the weld region. Thermally induced residual stresses are largely attributed to differential expansion and contraction during heating or cooling of the material. Thermal treatment (heating cycle, temperature gradient, cooling rate, etc.) and physical restraints (clamping, stiffening, etc.) are the two key factors that govern the evolution of residual stresses. Stress field during welding is influenced by multiple factors, such as welding parameters and procedures, process conditions, material characteristics, part design, weld geometry, and restraint conditions.

Figure 10a, b and c show the contours of X-, Y-, and Z- components of the normal stresses during LTW heating phase at t = 0.76 s. Positive stress values represent tensile stress, while negative stress values imply compressive stress. It is observed that the patterns of stress distribution are similar to temperature distributions and that the maximum stress occurs just behind the beam position. The higher stress concentration exists at the neighboring zone around the molten pool. These stresses are caused by the containment of the expansion of the hot material under the beam by the cooler surrounding materials. Figure 10d shows 3-D contour plot of von Mises equivalent stress during heating phase at t = 0.76 s. Figure 11 presents the cross-sectional view of thermal stress distribution in the weld pool and the adjacent region, during heating phase at t = 0.76 s. It is noticed from Fig. 11a–c that the maximum compressive normal stress of the order of 30.6 MPa occurs at heat-affected zone during heating phase, while the maximum tensile normal stress of the order of 10.5 MPa is observed to act longitudinally. It is seen from Fig. 11d that the heat-affected zone experiences the maximum equivalent tensile stress of 16.1 MPa during heating phase.

Fig. 10
figure 10

3-D stress distribution during LTW. a Normal stresses in transverse direction, SX. b Normal stresses in longitudinal direction, SY. c Normal stresses in depth direction, SZ. d von Mises equivalent stress, SEQV

Full size image
Fig. 11
figure 11

Stress contours across the weld cross-section during LTW. a Normal stresses in transverse direction, SX. b Normal stresses in longitudinal direction, SY. c Normal stresses in depth direction, SZ. d von Mises equivalent stress, SEQV

Full size image

The history of stress evolution over time at different specified locations (A, B, C, D, and E) over a time period of 0.76 s is shown in Fig. 12. It is observed from this figure that the normal stresses (SX and SY) at specified locations along the y-axis, i.e., the direction along the beam path (A, E) and along the x-axis, i.e., the direction transverse to the beam path (A, B) rapidly changes to higher compressive stresses values during heating and subsequent melting/softening. When the beam moves forward and leaves that zone, the compressive stress gradually transforms into tensile stresses with subsequent cooling. This effect is attributed to the contraction of the weld zone during cooling. It is also found that the maximum stress is developed along the y-axis, i.e., along the direction of the laser path. The normal stress (SZ) at specified locations along the y-axis (A, E) and z-axis (C, D) changes into compressive stresses with heating and afterward starts to drop with cooling. However, at location B (along the x-axis), tensile normal stress (SZ) is seen to evolve during heating phase, which implies that this location is outside of the heat-affected zone. During the heating phase, the thermal expansion may result in the formation of a compressive stress field in the heat-affected region. At all the specified locations, von Mises equivalent tensile stresses are developed during the heating and cooling phase, as shown in Fig. 12d. However, the magnitude varies with time and location.

Fig. 12
figure 12

Stress histories at different specified locations. a Normal stresses in transverse direction, SX. b Normal stresses in longitudinal direction, SY. c Normal stresses in depth direction, SZ. d von Mises equivalent stress, SEQV

Full size image

Figure 13 shows the normal and equivalent stress distributions along the depth of the material. Three specific conditions are chosen to study the evolution of thermally induced stresses during welding and the evolution of residual stresses: (a) at the beginning of the welding, where the stress development is only due to the applied clamp pressure, (b) during welding, where stress development is due to thermal expansion, welding pressure, and restraint conditions, and (c) after welding and cooling, where the remaining stress after removal of all external loads is the residual stress. The maximum equivalent residual stress developed for the stated parametric combination is around 18.1 MPa which is substantially lower than the yield strength of polycarbonate (63 MPa). This indicates a safer joint with the possibility of good mechanical performance and longer lifespan.

Fig. 13
figure 13

Stress distribution along line AA. a Normal stresses in transverse direction, SX. b Normal stresses in longitudinal direction, SY. c Normal stresses in depth direction, SZ. d von Mises equivalent stress, SEQV

Full size image

5 Conclusion

The temperature field and the evolution of stress field during heating and cooling phase of LTW are studied using a 3-D thermo-elasto-viscoplastic FE model. The developed model includes all major thermo-mechanical phenomena associated with the LTW. This model is capable of predicting transient temperature and stress field. The amount of residual stress is estimated after the cooling phase, when all external thermal and mechanical loads are removed.

  1. 1.

    The temperature field within the joining polymers is observed to change rapidly with time and distance as the laser beam travels.

  2. 2.

    The stress distribution pattern is found to be similar to the temperature distribution, and the maximum stress occurs just behind the beam position. Higher stress concentration occurs in the adjacent zone around the weld pool.

  3. 3.

    The heat-affected zone undergoes compressive stress during heating and subsequent melting/softening. This compressive stress is gradually transformed into a tensile stress with subsequent cooling.

  4. 4.

    The maximum stress is found to evolve in the direction of the laser path.

  5. 5.

    The maximum equivalent residual stress developed, for the welding parameters used in this study, is significantly lower than the yield strength of the work-piece material, suggesting a safer joint.

The magnitude and distribution of residual stress vary with the welding parameters, process conditions, materials, part design, welding geometry, restraint conditions, etc. Numerical investigation of the effects of these variables on stress field distribution and the resulting residual stresses will provide the space for future research using the developed FE model. The incorporation of pre-stressed material conditions in the FE model, such as residual stresses induced in specimens due to the manufacturing process of working material, would be considered for future study on LTW of polymers.