A 2nd−order SCF solution for modeling distortion effects on fatigue of lightweight structures

Abstract

This paper focuses on a series of new developments on analytical treatment of secondary stress concentration effects caused by the presence of angular and buckling distortions in thin plate structures. The distortion profiles are idealized through a simple mechanics treatment upon which the analytical solution to the stress concentration factor (SCF) induced by secondary bending is further derived. With such approach, the distortion effects on fatigue behaviors can be captured without the need for performing detailed finite element calculations incorporating measured distortions. The applications of these analytical solutions incorporating secondary bending caused by distortions and remote loading are demonstrated by analyzing existing test data obtained on small-scale thin plate butt joints containing local and global angular distortions. By considering the fatigue test data as well as measured distortion data, the use of so calculated SCFs not only enable an effective correlation among simple butt-welded specimens with various forms of angular and axial misalignments, but also between the tested specimens and the 2007 ASME master S-N curve scatter band which contain large-scale fatigue test data with plate thicknesses ranging from 5 mm up to over 100 mm.

1 Introduction

It has been well established that welding-induced distortions have been a major issue in the construction of lightweight ship structures [1,2,3]. In addition to developing effective mitigation techniques for reducing such distortions, existing distortion tolerances such as those given by class societies such as ABS [4] which were based on data for thick-section structures, and those dated back many decades ago (e.g., MIL-STD-1698 [5]) may need to be revisited for their applicability in lightweight structures. As discussed in by Huang et al. [6], in lightweight steel shipboard structures, plate thicknesses of equal or less than five mm have become increasingly dominant and post a major challenge in accuracy control in ship construction processes.

Effects of weld residual stresses on structural integrity have been extensively addressed in the context of fitness for service in the literature as recently summarized by Dong and Brust [7] and Dong et al. [8], Song and Dong [9], and Dong [1, 10]. However, how welding-induced distortions impact the structural integrity of lightweight structures has not been adequately addressed. Some of the early publications on this subject are scarce, e.g., by Antoniou [11] and Carlsen and Czujko [12] focused on limited experimental observations on specific types of distortions in ship construction environment. These studies had a narrow focus on effects of some observed welding distortions on structural buckling strength under compressive loading with plate thicknesses being above 10 mm and did not address how distortions affect fatigue behaviors of welded structures. In existing fatigue assessment and fitness-for-service (FFS) procedures, there are virtually no treatment of distortion effects except for one equation provided by BS7910 [13] for treating angular misalignment effect in butt-welded joints; however, this equation does not consider the distortion curvature effect which may become a significant source of secondary bending stress in thin-section structures.

Recognizing the prevalence of distortions in thin plate structures, recent investigations into fatigue behaviors in thin plate structures include those by Lillemäe et al. [14, 15] on distortion effects on fatigue strength in butt-welded joints, Xing, Dong, and Threstha [16] on fatigue failure mode transition behaviors in thin plate cruciform joints, Xing, Dong, and Wang [17] on quantitative fillet weld sizing criteria for preventing weld throat cracking in load-carrying fillet welds, and Xing and Dong [18] on analytical treatment of joint misalignments and application in fatigue test data interpretation. In the latter studies, the importance of proper treatment of joint misalignments in thin plate structures is clearly demonstrated by means of a series of new analytical stress concentration factor solutions. Both these experimental and finite element studies along this line have shown that fatigue behaviors in thin plate structures tend to show a great deal of scattering, much more so than thick plate structures joint.

Eggert et al. [19], Fricke and Feltz [20], and Lillemäe et al. [21] recently performed finite element (FE)-based stress concentration analyses by incorporating detailed distortion measurements of full-scale panel specimens and showed that distortions in both longitudinal and transverse directions, referred to as 3D distortions, can have significant effects on stress concentration at weld locations. Lillemäe et al. [21, 22] and Eggert et al. [19] further pointed out that both the distorted shape in the longitudinal direction and the magnitude of distortions can have a dominant effect on stress concentration factors (SCF) which cannot be properly captured using the existing axial and misalignment formulae given in [23] without considering second-order effects.

To clarify some of the dominant effects of welding-induced distortions on fatigue, a fundamental approach is needed for separating distortion characteristics that are intrinsic to certain lightweight structural forms, which can be quantitatively related to fatigue performance from those distortion features that may exhibit a great deal of variability, whose effects on fatigue may not be either readily quantifiable or deemed as being secondary.

As a sequel to the study by Dong et al. [24], Dong, Zhou, and Xing [25], this paper focus on the analytical treatment of distortion-load interaction considering geometric nonlinearity and its applications on interpretation of some of the recent test data available in literature (e.g., by Lillemäe et al., [14]). These fatigue tests involved thin plate butt-welded specimens containing complex angular distortions as well as axial misalignments. Based on the simple distortion type as studied in [24, 25], a simple mechanics treatment is used and a unique approach to solving imperfect beam problems is developed subsequently. Using this developed approach, both test load conditions and angular distortions in butt seam-welded specimens are analytically treated. In this process, the angular misalignment equation given by BS 7910 incorporating nonlinear geometry effects is recovered by the present solution scheme. By introducing a decomposition-assembly scheme incorporating local and global distortions as well as axial misalignments documented in [14], the test data can be satisfactorily correlated with the 2007 ASME master S-N curve scatter band which contain large-scale fatigue test data with plate thicknesses ranging from 5 mm up to over 100 mm.

2 Analytical model for distortion-induced secondary bending stress

The analytical derivation presented in this section is based on the following assumptions which will be validated by finite element analysis solution at the end of this section:

• a. The material is linear elastic and the deformation is small.

• b. The magnitude of distortion is small compared with the structural members’ dimension in length.

• c. The contribution from transverse shear is negligible.

2.1 Mechanics idealization of distortion

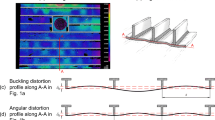
As discussed in Dong [1, 10] and Yang and Dong [3], welding-induced distortion thin section plate structures tend to exhibit buckling distortions due to structural instability triggered by compressive residual stress distributions, often accompanied by angular distortions. Both distortion types are described in Fig. 1, in which Fig. 1a shows a LIDAR scan image of a 16′ by 20′ stiffened panel indicating a checker-board pattern, particularly on the lower half of the panel. A stiffened panel exhibiting angular distortion is illustrated in Fig. 1b. The corresponding deformation profiles of both cases are illustrated in Fig. 1c and d respectively. As such, the buckling distortion profile can be characterized as a sinusoidal wave form in which rotation at stiffener location is unrestricted (see Fig. 1c) while angular distortion profile has one-half cosine shape with no rotation at stiffener fillet weld locations. Note that such an idealization for representing angular distortions is consistent with classical definitions of angular distortions in stiffened panels involving multiple stiffeners. If only one single stiffener fillet weld is considered, i.e., a T fillet weld, the corresponding angular distortion is typically represented as two plate rotation in straight line form resulted from the local curvature at weld location. In both cases shown in Fig. 1, stiffener spacing is represented by l and out of plane distortion peak value by δ₀. In this study, we ignore the variation of distortion in transverse direction (in-plane, normal to the loading direction) so that the strip beam theory can be applied, and unless otherwise stated, the beams mentioned in this paper are unit width beams.

Fig. 1

Two major distortion types in thin plate structures [24]

As a first-order approximation, the angular distortion profile between two stiffeners is idealized as the deflection of an equivalent linear beam model with clamped ends and loaded with a concentrated dummy force F₀ in the middle, as shown in Fig. 2. The dummy force on the beam represents the equivalent driving force (e.g., residual stresses) of the distortion, but it is not an actual external force on the structure. By matching the peak deflection of the beam with the measured peak distortion value δ₀, the magnitude of F₀ can be readily obtained using classic beam theory. Similarly, the buckling distortion profile between two stiffeners is idealized as the deflection of an equivalent linear beam model with pinned ends loaded with a concentrated dummy force in the middle, as shown in Fig. 3. With such mechanics idealization of the distortion profile, we are also able to acquire the distortion field along the horizontal axis v₀(z), which will be used for solving the secondary bending stress in the next section. For simplicity, the dummy loads applied in this study are limited to concentrated force and moments.

Fig. 2

Linear beam model idealization of angular distortion

Fig. 3

Linear beam model idealization of buckling distortion

2.2 Formulation and solution

In structural mechanics, the pre-existing distortion and its interaction with lateral loading can be best modeled by an imperfect beam model under axial loading. For example, the corresponding imperfect beam models for angular distortion are given in Fig. 4, where P represents the axial force which is remotely applied to the neutral axis of the beam, v₀ is the given pre-existing distortion field obtained in the previous section, and v₁ is the unknown vertical deflection of the beam under axial load P. We refer to such imperfect beam models as distortion modes. The model in Fig. 4 is referred to as the angular distortion mode.

Fig. 4

Equivalent imperfect beam model—angular distortion mode

The governing equation for the imperfect beam problem considering geometric nonlinearity is

$$ EI{v}_1^{(4)}-P{\left({v}_0+{v}_1\right)}^{\prime \prime }=0 $$

(1)

where E is the Young’s modulus and I is the section moment of inertia. And the secondary bending moment M₁ caused by the initial distortion is proven to be

$$ {M}_1=- EI{v}_1^{{\prime\prime} } $$

(2)

Therefore, by solving Eq. (1) for v₁, we can acquire the secondary bending moment sought from Eq. (2). However, the nonhomogeneous Eq. (1) could sometimes be hard and lengthy to be solved directly, and traditional approximation method such as Rayleigh-Ritz method involving infinite series cannot give out a close form solution. But if we take advantage of the mechanics idealization of distortion discussed in the previous section, we can form an intuitive geometric nonlinear perfect beam problem to solve for v₁ by combining the imperfect beam problem and the geometric linear perfect beam problem from the mechanics idealization.

Because v₀ is the deflection of a linear perfect beam, it is the solution to the following governing differential equation:

$$ EI{v}_0^{(4)}=0 $$

(3)

Then, by the superposition principle of linear systems, we can superimpose Eq. (1) and Eq. (3) (as well as the boundary conditions) and obtain the following:

$$ EI{\left({v}_0+{v}_1\right)}^{(4)}-P{\left({v}_0+{v}_1\right)}^{\prime \prime }=0 $$

(4)

The solution to Eq. (4) is the sum of v₀ and v₁. By denoting v = v₀ + v₁, Eq. (4) becomes

$$ EI{v}^{(4)}-P{v}^{\prime \prime }=0 $$

(5)

Equation (5) is the governing equation of a geometric nonlinear perfect beam problem (as shown in Fig. 5 for angular distortion) subject to same dummy loads on the linear perfect beam and axial loading P. Therefore, the displacement sought v₁ can be obtained by solving Eq. (5) for v and then through v₁ = v − v₀. And the secondary bending moment can be calculated using Eq. (2) subsequently.

Fig. 5

Nonlinear perfect beam model—angular distortion mode

Based on this method, the secondary bending induced by distortion for the angular distortion mode can be expressed as, in terms of normalized bending stress (normalized by P/t) or bending stress concentration factor (SCF_b) generated at fillet weld toe location (e.g., z = 0, y = t/2):

$$ SC{F}_{\mathrm{b}}=\Big\{{\displaystyle \begin{array}{cc}-\frac{144}{{\left(\lambda l\right)}^2}\frac{\delta_0}{t}\left(\frac{4}{\lambda l}\frac{\cosh \frac{\lambda l}{2}-1}{\sinh \frac{\lambda l}{2}}-1\right)& P>0,\lambda =\sqrt{\frac{P}{EI}}\\ {}-\frac{144}{{\left(\lambda l\right)}^2}\frac{\delta_0}{t}\left(\frac{4}{\lambda l}\frac{\cos \frac{\lambda l}{2}-1}{\sin \frac{\lambda l}{2}}+1\right)& P<0,\lambda =\sqrt{\frac{-P}{EI}}\end{array}} $$

(6)

Note that in the rest of this paper, all SCF_b solutions are related to the top surface (e.g., y = t/2).

Following the similar procedure, the imperfect beam model of buckling distortion mode can be established as illustrated in Fig. 6. The corresponding nonlinear perfect beam model is given in Fig. 7 by imposing the boundary conditions of the imperfect beam problem (Fig. 6) and the dummy loads from the linear perfect beam problem (Fig. 3) onto a straight beam. The SCF_b due to secondary bending for the buckling distortion mode with respect to the fillet weld toe location (z = 0) can be then obtained:

$$ SC{F}_{\mathrm{b}}=\Big\{{\displaystyle \begin{array}{cc}18\left[\frac{\delta_0}{t}\frac{\cosh \frac{\lambda l}{2}}{\lambda l\sinh \frac{\lambda l}{2}}-\frac{8}{{\left(\lambda l\right)}^2}\frac{\delta_0}{t}\left(\frac{\cosh \frac{\lambda l}{2}-1}{\lambda l\sinh \frac{\lambda l}{2}}\right)\right]& P>0,\lambda =\sqrt{\frac{P}{EI}}\\ {}-18\left[\frac{\delta_0}{t}\frac{\cos \frac{\lambda l}{2}}{\lambda l\sin \frac{\lambda l}{2}}+\frac{8}{{\left(\lambda l\right)}^2}\frac{\delta_0}{t}\left(\frac{\cos \frac{\lambda l}{2}-1}{\lambda l\sin \frac{\lambda l}{2}}\right)\right]& P<0,\lambda =\sqrt{\frac{-P}{EI}}\end{array}} $$

(7)

Fig. 6

Equivalent imperfect beam model—buckling distortion mode

Fig. 7

Nonlinear perfect beam model—buckling distortion mode

2.3 Validation with finite element solutions

To prove that the assumptions made and the analytical solutions in previous sections are valid, two finite element (FE) imperfect beam models corresponding to the angular distortion mode and the buckling distortion mode are created using the distortion profiles obtained in Sec. 2.1 with a given measured distortion peak value of δ₀ = 3.175 mm (1/8"), as shown in Fig. 8. The same boundary conditions in Fig. 4 and Fig. 6 are applied to the FE model and nonlinear geometry is considered in the FE calculation. Both beam models have unit width and same Young’s modulus of E = 210000 MPa. The axial loading varies from P = − 317.5 N (σ_n =  − 50 MPa) to P = 1587.5 N (σ_n = 250 MPa). The SCF is calculated at weld location (z = 0). The FE and analytical solutions are compared in Fig. 9 and a perfect agreement is achieved for the calculated axial loading range.

Fig. 8

Finite element beam models used for validation of assumptions and analytical solutions of angular distortion mode (a) and buckling distortion mode (b)

Fig. 9

Comparison of SCF_b calculated by FE and analytical solutions. a Angular distortion mode. b Buckling distortion mode

2.4 Treatment of angular distortions in butt-welded specimens

Some interesting fatigue tests on thin plate-welded specimens were reported by Lillemäe et al. [14], which were shown difficult to interpret with either finite element-based hot spot stress or notch stress method. These are butt seam-welded plate specimens with distortions characterized as shown in Fig. 10 (based on Lillemäe et al. [14]). The specimens are allowed to rotate freely during clamping but were fixed during cyclic tensile axial loading in fatigue testing. In addition to axial misalignment e, angular distortion measurements of α_{L, 1}, α_{L, 2}, and α_G are given as illustrated in Fig. 10.

Fig. 10

Distortion definitions associated with butt-welded thin plate specimens (based on Lillemäe et al. [14])

To facilitate the analytical treatment of such conditions, the axial misalignment is considered separately using the analytical solutions derived by Xing and Dong [18]. Then, the distortion is assumed to be symmetric about the weld and thus only one-half of the specimen with greater distortion needs to be considered, as depicted in Fig. 11, where k₁ = α_{L, 1}/2, k₂ = α_{L, 2}, and k_g = α_G/2 due to symmetry. Considering the fixed-end boundary conditions and symmetry, an equivalent imperfect beam model featuring fixed rotation condition at loaded end is established for secondary bending analysis as shown in Fig. 12. To study the contribution of distortion curvature effect, the distortion is further decomposed into two basic distortion modes to calculate the SCF due to secondary bending: the global angular distortion and the local angular distortion. The beam model for both modes has same E, I and is subject to the same axial loading P.

Fig. 11

Distortion definition under symmetric assumption

Fig. 12

Equivalent imperfect beam model—global and local angular distortion of butt-weld

2.4.1 Global angular distortion

The global angular distortion and its corresponding nonlinear beam model are shown in Fig. 13. Because the beams are straight by definition, the problem is already a nonlinear perfect beam problem. By solving this problem, we can get the SCF_b solution at butt-weld location (z = 0) as follows:

$$ SC{F}_{\mathrm{b}}=\Big\{{\displaystyle \begin{array}{cc}6{k}_g\frac{l}{t}\left(\frac{\cosh \lambda l-1}{\lambda l\sinh \lambda l}\right)& P>0,\lambda =\sqrt{\frac{P}{EI}}\\ {}-6{k}_g\frac{l}{t}\left(\frac{\cos \lambda l-1}{\lambda l\sin \lambda l}\right)& P<0,\lambda =\sqrt{\frac{-P}{EI}}\end{array}} $$

(8)

Fig. 13

Equivalent nonlinear beam model—global angular distortion

The global angular distortion is same as the angular misalignment in BS7910. Note that

$$ \lambda =\sqrt{\frac{P}{EI}}=2\sqrt{\frac{3P}{E{t}^3}}=\frac{2}{t}\sqrt{\frac{3{\sigma}_m}{E}} $$

(9)

where σ_m = P/t. And by substituting y = αl/2 = k_gl, t = B, β = λl, Eq. (8) can be rewritten as follows:

$$ SC{F}_b=\Big\{{\displaystyle \begin{array}{cc}\frac{6y}{B}\left\{\frac{\cosh \beta -1}{\beta \sinh \beta}\right\}=\frac{3y}{B}\left\{\frac{\tanh \left(\beta /2\right)}{\beta /2}\right\}& P>0\\ {}-\frac{6y}{B}\left\{\frac{\cos \beta -1}{\beta \sin \beta}\right\}=\frac{3y}{B}\left\{\frac{\tan \left(\beta /2\right)}{\beta /2}\right\}& P<0\end{array}} $$

(10)

Equation (10) is exactly the same as the one for fixed-end condition given in BS7910 of which the reference containing its derivation is not available. Same conclusion can also be obtained for pinned-end condition using similar procedure. This confirms the validity of the equations in BS7910 for angular misalignment in butt joints.

2.4.2 Local angular distortion

The local angular distortion is obtained by subtracting the global angular distortion from the total distortion. It contains the distortion curvature of the specimen. As shown in Fig. 14, the local angular distortion is defined by the slope k_A, k_B at either ends. For this distortion case, we use a tilted cantilever beam loaded with a concentrated dummy force F₀ and a concentrated dummy moment m₀ as shown in Fig. 15a to model its distortion field v₀. Then, based on the corresponding nonlinear perfect beam problem Fig. 15b, the secondary bending-induced SCF_b generated at weld location can be expressed as follows:

$$ SC{F}_{\mathrm{b}}=\Big\{{\displaystyle \begin{array}{cc}6\left\{\begin{array}{l}{k}_{\mathrm{A}}\frac{l}{t}\frac{\cosh \lambda l}{\lambda l\sinh \lambda l}-{k}_{\mathrm{B}}\frac{l}{t}\frac{1}{\lambda l\sinh \lambda l}\\ {}+\frac{2}{{\left(\lambda l\right)}^2}\frac{l}{t}\left({k}_{\mathrm{A}}+2{k}_{\mathrm{B}}\right)+\frac{6}{{\left(\lambda l\right)}^2}\frac{l}{t}\left({k}_{\mathrm{A}}+{k}_{\mathrm{B}}\right)\left(\frac{\cosh \lambda l-1}{\lambda l\sinh \lambda l}-1\right)\end{array}\right\}& P>0,\lambda =\sqrt{\frac{P}{EI}}\\ {}6\left\{\begin{array}{l}-{k}_{\mathrm{A}}\frac{l}{t}\frac{\cos \lambda l}{\lambda l\sin \lambda l}+{k}_{\mathrm{B}}\frac{l}{t}\frac{1}{\lambda l\sin \lambda l}\\ {}-\frac{2}{{\left(\lambda l\right)}^2}\frac{l}{t}\left({k}_{\mathrm{A}}+2{k}_{\mathrm{B}}\right)+\frac{6}{{\left(\lambda l\right)}^2}\frac{l}{t}\left({k}_{\mathrm{A}}+{k}_{\mathrm{B}}\right)\left(\frac{\cos \lambda l-1}{\lambda l\sin \lambda l}+1\right)\end{array}\right\}& P<0,\lambda =\sqrt{\frac{-P}{EI}}\end{array}} $$

(11)

Fig. 14

Equivalent imperfect beam model—local angular distortion

Fig. 15

Models for local angular distortion. a Linear beam model idealization. b Nonlinear beam model

Note that for cases with the slope at supported end k_B not available, we can set m₀ = 0 in the linear beam model Fig. 15a and thus k_B =  − k_A/2.

2.4.3 Analytical solution to the angular distortions in butt-welded specimen and justification

From the decomposition of the distortion profile in Fig. 12, we know that k_A = k₁ − k_g, k_B = k₂ − k_g in Eq. (11). Then, by summing up Eq. (8) and Eq. (11), we can achieve the SCF_b at weld location. To justify this result is exact, we compare this summation with the result derived directly from the model containing both global angular distortion and local angular distortion (as shown in Fig. 12):

$$ SC{F}_{\mathrm{b}}=\Big\{{\displaystyle \begin{array}{cc}6\left\{\begin{array}{l}{k}_1\frac{l}{t}\frac{\cosh \lambda l}{\lambda l\sinh \lambda l}-{k}_2\frac{l}{t}\frac{1}{\lambda l\sinh \lambda l}\\ {}-\frac{2}{{\left(\lambda l\right)}^2}\frac{l}{t}\left[3\left({k}_g-{k}_1\right)-2\left({k}_2-{k}_1\right)\right]\\ {}-\frac{12}{{\left(\lambda l\right)}^2}\frac{l}{t}\left[\left({k}_g-{k}_1\right)-\frac{1}{2}\left({k}_2-{k}_1\right)\right]\left(\frac{\cosh \lambda l-1}{\lambda l\sinh \lambda l}-1\right)\end{array}\right\}& P>0,\lambda =\sqrt{\frac{P}{EI}}\\ {}6\left\{\begin{array}{l}-{k}_1\cdot \frac{l}{t}\cdot \frac{\cos \lambda l}{\lambda l\sin \lambda l}+{k}_2\frac{l}{t}\frac{1}{\lambda l\sin \lambda l}\\ {}+\frac{2}{{\left(\lambda l\right)}^2}\frac{l}{t}\left[3\left({k}_g-{k}_1\right)-2\left({k}_2-{k}_1\right)\right]\\ {}-\frac{12}{{\left(\lambda l\right)}^2}\cdot \frac{l}{t}\cdot \left[\left({k}_g-{k}_1\right)-\frac{1}{2}\left({k}_2-{k}_1\right)\right]\left(\frac{\cos \lambda l-1}{\lambda l\sin \lambda l}+1\right)\end{array}\right\}& P<0,\lambda =\sqrt{\frac{-P}{EI}}\end{array}} $$

(12)

It can be easily seen that Eq. (12) is exactly the same as the sum of Eq. (8) and Eq. (11).

3 Applications in fatigue test data analysis

The fatigue test results on thin plate butt-welded specimens (3 mm in thickness) were reported in [14], who also performed detailed finite element analysis (FEA) of these specimens with measured distortions. With geometric nonlinearity considerations, they evaluated the feasibility of using either surface extrapolated hot spot stress or local notch stress method recommended by IIW (Hobbacher, [23]). The results are shown in Fig. 16, indicating that neither method provides a satisfactory correlation of the test data in that these data spread within a factor of 10 in fatigue lives at a rather similar stress range level in terms of either hot spot stress (Fig. 16a) or local notch stress (Fig. 16b), especially for arc-welded specimens which are subject to more significant distortions.

Fig. 16

Test data correlation using nonlinear geometry FEA–calculated stress (taken from [14]). a IIW’s surface extrapolated hot spot stress method. b IIW’s effective notch stress method

With the developments presented in Sec. 2, treatment of measured misalignments (e) which is given in [18] under various boundary conditions, measured global angular distortion (α_G = 2k_g) and local angular distortion (α_L = 2k₁, and k₂ is available for some specimens from collaboration), the results are summarized in Fig. 17. In Fig. 17, the equivalent structural stress range is defined as according to the 2007 ASME Div 2 Code as (see Dong [26,27,28]):

$$ \varDelta {S}_s=\frac{\varDelta {\sigma}_s}{t^{\frac{2-m}{2m}}I{(r)}^{\frac{1}{m}}} $$

(13)

where Δσ_s in the current case (with load ratio R = 0) is calculated as follows:

$$ \varDelta {\sigma}_s=\left(1+ SC{F}_e+ SC{F}_{\mathrm{b},\mathrm{distortion}}\right)\times \varDelta {\sigma}_n $$

(14)

in which SCF_{b, distortion} is the bending stress concentrated factor caused by welding-induced distortions, calculated by previously derived equations in Sec. 2; and SCF_e = 3e/t is the normalized bending stresses contributed by axial misalignment e according to [18]. Note that m is 3.6 as given in 2007 ASME Boiler and Pressure Vessel Code, Section VIII, Div. 2 [29] and I(r)^1/m is a dimensional function of bending stress ratio r = |Δσ_b|/(|Δσ_m| + |Δσ_b|), which is also given in ASME BPVC.

Fig. 17

Data correlation using the equivalent structural range parameter given in 2007 ASME master S-N curve incorporating analytically calculated SCF_b due to axial misalignments, global and local angular distortions. a Nominal stress range. b Equivalent structural stress range

For comparison purpose, nominal stress range-based plot is given in Fig. 17a and master S-N curve scatter band based on mean ± 2 × STD is also given as dashed lines in Fig. 17b. It can be seen in Fig. 17b, the thin plate butt-welded specimen tests correlate reasonably well not only within themselves by forming a well-defined scatter band with standard deviation of 0.202, but also within 2007 ASME’s master S-N curve scatter band which represents about 1000 large-scale fatigue tests with plate thickness varies from 5 mm up to over 100 mm. This shows that the ASME master S-N curve is applicable in fatigue life prediction of butt-welded joints in thin section structures as long as the distortion-induced secondary bending is correctly calculated with the developed approach.

4 Discussion

From the validation result in Sec. 2.3, we can see that the SCF_b caused by secondary bending has the order of magnitude of 1 in thin plates with the distortion peak value of t/2, showing that such secondary bending cannot be ignored. Especially in compression axial loading condition, the SCF_b ramps up very quickly as the load increases, which will result in a larger stress range than expected. With the developed tool for calculating the secondary bending stress, we may analytically evaluate the effect of distortion magnitude and develop the distortion allowance criteria for thin-section structures.

In the application of developed method to calculate the secondary bending due to distortion reported in [14], we found that some distortion profiles may not be well modeled with merely two measurements (α_G and α_L); therefore, extra distortion measurements are provided by the Aalto University to better calculate the secondary bending. Moreover, in a larger scale, e.g., in structure level, the distortion may be even more complex as reported in [15]. Modeling of such complex distortion profiles is hard using the any single model developed in this paper, but as an extension of this study, a comprehensive approach based on the idea of decomposition discussed in the Sec. 2.4 to model complex distortion and find the secondary bending stress generated is under development and will be presented in the future.

5 Summary

In this paper, three typical welding-induced distortion types observed in lightweight structures, i.e., the angular distortion and buckling distortions and the global and local angular distortion related to butt welds prevalent in lightweight shipboard structures today, are idealized using Euler-Bernoulli beam models with dummy loads. To quantitatively examine the distortion effects on fatigue under remote fatigue loading conditions in service, the imperfect beam models considering geometric nonlinearity are used for solving the secondary bending stress caused by pre-existing distortion. Using the distortion idealization model, the imperfect beam problem is converted into a nonlinear perfect beam problem and the analytical SCF_b solutions are solved for each basic distortion mode. As far as the global angular distortions are concerned, the angular misalignment equation given by BS7910 is covered by the presented method. By incorporating SCF_b from global and local angular distortion as well as axial misalignments into the equivalent structural stress range parameter given by the 2007 ASME Div 2 Code, the test data documented in [14, 15] can be correlated reasonably well among themselves in forming a narrow band with a clearly defined slope. Furthermore, all these test data points but one fall within the 2007 ASME master S-N curve scatter band which contains about 1000 large-scale fatigue tests with plate thicknesses ranging from 5 mm up to over 100 mm, indicating that if the distortion-induced secondary bending is correctly computed with the developed method, the 2007 ASME master S-N curve can be used for predicting fatigue life of welded joints in thin plate structures with distortions.