Introduction

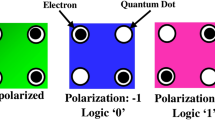
Formerly, complementary metal–oxide–semiconductor (CMOS) technology has been the leading technology to design Very Large Scale Integrated circuits or nano-electronic circuits. But currently, CMOS technology is impending to its physical limitations [1, 2]. One of the best alternatives to carry forward nano-level design is the emerging quantum-dot cellular automata (QCA). It was introduced by Lent et al. [1, 2]. This QCA technology is mainly based on tunneling two electrons inside four quantum dots QCA cell [2]. A cell, as shown in Fig. 1, is the smallest unit of QCA technology. Two electrons inside a cell may choose any of the four dots located at each corner of the square. However, due to Coulombic interaction, those two electrons always elect diagonal positions [1, 2]. Therefore, as shown in Fig. 1, two arrangements are possible: polarization ‘− 1’ or logic 0 and polarization ‘ + 1’ or logic 1. QCA was first fabricated in 1997 [3].

Fig. 1
figure 1

QCA cell

Full size image

The fundamental blocks of QCA are majority voter, wire, and inverter, which can be used to design different logic circuits. A majority voter has three inputs and one output, as shown in Fig. 2 [4]. The middle cell of the majority voter is called the driver cell. Among three inputs, one of them may be fixed at polarization ‘ − 1’ then it works as AND gate, and if one of the inputs is set at polarization ‘ + 1’, it acts as OR gate [4]. As shown in Fig. 2, it follows the equation AB + BC + CA for three inputs A, B, and C. As shown in Fig. 3, when few cells are positioned back to back, they form a chain, called wire and the input polarization reaches at the output without alteration [5]. As shown in Fig. 4, when two cells are located diagonally, it acts as a NOT gate, called QCA inverter [4].

Fig. 2
figure 2

QCA Majority voters or majority gate

Full size image
Fig. 3
figure 3

QCA Wire

Full size image
Fig. 4
figure 4

QCA Inverter

Full size image

No separate supply of bias voltage is necessary for these circuit operations; instead, QCA can perform processes using four internal clocks, which assured low power depletion [5]. There are four phases of each clock as shown in Fig. 5, and they are known as the switch phase, the hold phase, the release phase, and the relax phase [6].

Fig. 5
figure 5

QCA clocking

Full size image

In the QCA field, extensive research work has been done yet, primarily in the design and simulation of digital circuits. Logic gates [7, 8], adders [9, 10], subtractors [11, 12], Adder–subtractors [13, 14], flip-flops and memories [15, 16], registers [17,18,19], counters [20, 21], Arithmetic Logic Units [22, 23] etc. already been reported. Recently researchers are focusing on nano communication, where multiplexer and demultiplexer are the unavoidable design units. One simple multiplexer [24] and one simple demultiplexer [25] are the experimental objects of this article. It should be mentioned that both the experimental entities, i.e., multiplexer and demultiplexer, are elementary as they occupied a minimal area, and their complexity is low too. This multiplexer has a complexity of 17, cell area of 0.005508 μm2 and a total area of 0.01 μm2; whereas, demultiplexer has the complexity of 21, cell area 0.006804 μm2, and total area of 0.02 μm2 [24, 25]. The calculation of energy dissipation and the cost of simple circuits are the recent trends of QCA technology, which accelerate us to do this research work. Most semiconductor and electronics industries that work on quantum computation, nano-computation, and nano-communication, for example, are active in the development and implementation of QCA-based circuits. It is worth mentioning that QCA multiplexer and demultiplexer have devoted applications in nano communication and nano computation, like nanoswitch, nano router, reversible computing circuits, etc.

Former works and gaps

The QCA literature is clogged with multiplexers and demultiplexers. There have been a few good designs in the last few years that have been mentioned. Roohi et al. (2011) used three clocks with a complexity of twenty-seven to create a 2:1 multiplexer [26]. Kianpour et al. (2013) offered a basic multiplexer with twenty-two cells and three clocks [27], whereas, Chabi et al. (2014) proposed a similar multiplexer with twenty-three cells and the same three clock zones [28]. Similarly, Sen et al. (2015) used twenty-three cells but just two clocks to construct an efficient 2:1 multiplexer [29]. Rashidi et al. [30] developed a fifteen-cell multiplexer with a cell area of 0.01 µm2. Das et al. used three majority voters and one inverter to demonstrate a 2:1 multiplexer. They calculated that 47.22% of the available area was used [31]. Rashidi et al. used two AND gates, one OR gate, and one NOT gate to create a multiplexer [32]. Asfestani et al. created an efficient QCA multiplexer structure without utilizing majority votes [33]. Khosroshahy et al. looked at a different method of lowering the number of external inputs in multiplexers [34]. Ahmad proposed an n-bits multiplexer design strategy, while Ahmadpour et al. built fault-tolerant multiplexers employing four clocks with a complexity of 36 [35, 36]. Mosleh [37] discusses a multilayer design method based on the new majority voter (MV32) concept. Xingjun et al. reported a 2:1 multiplexer with only 22 cells and a 0.03 µm2 surface area [38]. AlKaldy et al. recently constructed an optimal multiplexer with only 11 cells and no majority voters [39]. Similarly, there are many more design examples of QCA multiplexers in the literature, leading to a lengthy discussion. It is not, however, valid for the QCA demultiplexer unit. There is a dearth of contributions to demultiplexer design despite the abundance of multiplexers in the QCA literature. To keep the flow of this part going, we're bringing up a few good demultiplexers here. For higher-order circuit design, Shah et al. presented a modular demultiplexer with 56 cells [40]. Iqbal et al. [41] suggested another modular 1:2 demultiplexer with a complexity of 27. A demultiplexer for nano communication applications was designed by Sardinha et al. [42]. Safoev et al. contributed to a multilayer layout of a 1: 2 demultiplexer [43], which used two clocks and 21 cells. Ahmad presented a 21-cell demultiplexer, while Das et al. recommended a 32-cell demultiplexer [35, 44]. Except for the QCA demultiplexers listed above, there are few designs and analyses of demultiplexers in the literature. The number of research papers with demultiplexers, on the other hand, is never more remarkable than the research of the QCA multiplexer.

It is worth mentioning that the experimental multiplexer architecture was reported at [24], and the energy dissipation was computed using the QDE Coherence vector mode applying the Euler technique at [45]. The energy dissipation using the Ranga Kutta approximation, on the other hand, has yet to be done. Similarly, an exhaustive cost analysis for this multiplexer is still unavailable. On the other hand, the experimental demultiplexer was proposed in [25], and the energy dissipation was estimated using the Euler technique in the same study [25]. Nonetheless, thorough cost analysis and energy dissipation in a QDE context applying the Ranga Kutta approximation are still needed for the demultiplexer.

As a result, the energy analysis of basic multiplexer/demultiplexer adopting Ranga Kutta approximation using QCADesigner-E (QDE) is still vacant in the QCA literature. None of the research fully described the several forms of costs associated with QCA circuits for a more precise analysis.

This study addressed all of the aforementioned gaps in the literature by examining one primary multiplexer and one simple demultiplexer. The originality of this work includes the energy estimation by QDE in Coherence vector mode employing Ranga Kutta approximation. In addition, different cost functions and other design elements have been incorporated for a higher evaluation.

Projected experimental objects

This article's experimental entities are a QCA multiplexer [24] and a QCA demultiplexer [25]. Using the QCA methodology, the arrangement of both units is simple to design. In a 2:1 multiplexer, the select line is ‘S’ the inputs are ‘M’ and ‘N’ and the output is ‘O’ In a 1:2 demultiplexer, the select line is ‘S’ the input data is ‘O’ and the outputs are ‘M’ and ‘N’ The relevant truth table is shown in Table 1, and the projected experimental objects are Figs. 6 and 7 [24, 25]. The multiplexer has a complexity of 17, and the demultiplexer has a complexity of 21, which is relatively low in terms of design perspective. The multiplexer's cell area is 5508 nm2, while the demultiplexer's cell area is 6804 nm2, indicating the minimal area requirements [24, 25]. Figures 8 and 9 illustrate the simulation output of the multiplexer and demultiplexer, respectively.

Table 1 Truth table of 2:1 multiplexer and 1:2 demultiplexer
Full size table
Fig. 6
figure 6

Simple QCA multiplexer unit [24]

Full size image
Fig. 7
figure 7

Simple QCA demultiplexer unit [25]

Full size image
Fig. 8
figure 8

Simulation output of QCA multiplexer [24]

Full size image
Fig. 9
figure 9

Simulation output of QCA demultiplexer [25]

Full size image

Parameters analysis of projected items

The decisive variables for measuring the performance of QCA circuits include cell complexity or cell count, area needed for designing the circuit, percentage of cell area used from the total area, delay or latency, number of gates used to design the circuit, and number of employed crossovers. This sub-section goes over all of the critical parameters for the present experimental objects.

This 2:1 multiplexer's cell complexity, or the number of employed cells, is 17, while this 1:2 demultiplexer's cell-complexity is 21.

The multiplexer requires 0.005508 μm2 of cell area, whereas, the demultiplexer requires 0.006804 μm2. The projected multiplexer requires 0.01 μm2 of total space, while the demultiplexer requires 0.02 μm2. Therefore, the area usage of the projected multiplexer is 55.08%, and the area usage of the demultiplexer is 34.02%.

Latency, often known as delay, is the time difference between the output and the input. The input-to-output latency is what it's known as. The number of clocks used for successful simulation of the multiplexer and the demultiplexer is three and two. Therefore, the latency for both of the experimental items is 0.5 clock-cycle. It's worth noting that one clock cycle is equal to four clock zones or clock phases.

The number of majority voters or majority gates and the number of inverters utilized in the multiplexer architecture is 3 and 1, respectively. The number of majority voters and inverters used in the demultiplexer are 2 and 1, respectively.

There was no crossover employed in the construction of the QCA arrangement for both experimental items.

Current experiments and evaluations

This work is unique in that it performs extensive energy calculations and calculates the cost of the projected items. The energy calculation methods for 2:1 MUX and 1:2 DeMUX are described in this section.

Energy calculations

Energy estimation has been popular in QCA circuit analysis recently. QCAPro [46] is a standard energy calculation tool. It is a widely used and well-known energy computation tool. It would not work with any newer versions of QCADesigner, unfortunately. QCAPro works with an older version of QCADesigner, which the proprietor has discontinued. As a result, QCADesigner 2.0.3 does not currently support QCAPro on top of it.

QCADesigner-E, or QDE, on the other hand, is a relatively new tool that is fast gaining traction. Using this program, we computed the energy dissipation of the multiplexer and demultiplexer. To compute energy dissipation using QDE, both approximations (the Euler technique or the Ranga–Kutta approach) can be utilized. The energy was previously computed using the Euler approach in [25, 45]. However, the same has yet to be reported using the Ranga–Kutta approximation.

To maintain the continuity of the discussion, a little amount of discussion on QCAPro is required. Using the QCAPro tool, we can evaluate the non-adiabatic power loss or energy dissipation of QCA circuits. It is based on the popular Hartree–Fock approximation [46, 48, 49]. The overall energy of the QCA cell is determined using the following Hamiltonian matrix [46] as described in Eq. (1), which represents the Coulombic interaction between cells:

$$\widehat{{\user2{H}_{\user2{i}} }} = ~\left[ {\begin{array}{*{20}c} {\frac{{ - E_{k} }}{2}\mathop \sum \limits_{i} C_{j} f_{{i,j}} } & { - \gamma } \\ { - \gamma } & {\frac{{ + E_{k} }}{2}\mathop \sum \limits_{i} C_{j} f_{{i,j}} } \\ \end{array} } \right].$$
(1)

Here Ci indicates the polarization of ith adjacent cell, fi,j is the geometrical factor related to electrostatic interaction between ith cell and jth cell and γ is tunneling energy between two cell states [46, 48, 49]. For every clock cycle, the expectation energy value of the cell is derived from Eq. (2) below:

$$\mathbf{E} = ~\mathbf{H} = ~\frac{{\hbar} }{2}~ \times ~{\Gamma }~ \times ~{\uplambda }.$$
(2)

The instantaneous power of a QCA cell is given as:

$$P_{{to}} = \frac{{{{\rm d}}E}}{{{{\rm d}}t}} = \frac{{\hbar} }{2}~\left[ {\frac{{{{{\rm d}\Gamma }}}}{{{{{\rm d}}}t}}. \lambda } \right] + \frac{{\hbar}}{2} \left[ {\Gamma .\frac{{{{\rm d}}\lambda }}{{{{\rm d}}t}}} \right],$$
(3)

where λ is the coherence vector, Γ is the energy vector (three-dimensional), and \({\hbar}\) is the reduced Planck’s constant.

The first term of Eq. (3) is \(\frac{{\hbar} }{2} \left[ \frac{ {\rm d}\Gamma } {{\rm d}t.\lambda } \right]\). It is the combination of the cell-to-cell power and clock-in–out power [50].

The second term of the Eq. (3) is \(\frac{{\hbar} }{2}\left[ {\Gamma .\frac{{{\text{d}}\lambda }}{{{\text{d}}t}}} \right]\) and it is our interest as it is instantaneous dissipated power [50]. For a time interval [− T, + T], the energy dissipation is expressed as:

$$E_{d} = \frac{{\hbar} }{2}\mathop \smallint \limits_{{ - T}}^{{ + T}} \left[ {\Gamma .\frac{{{\text{d}}\lambda }}{{{\text{d}}t}}} \right]{\text{d}}t.$$
(4)

Using a similar fashion, we can calculate the leakage energy dissipation and switching energy dissipation using Eqs. (5) and (6), respectively [50]:

$$P_{{{\text{leakage}}}} = ~\frac{1}{{2^{r} }}\mathop \sum \limits_{{i = 1}}^{{N - r}} P_{{i,n \to m}}^{{{\text{leakage}}}}$$
(5)
$$P_{{{\text{switch}}}} = ~\frac{1}{{2^{r} }}\mathop \sum \limits_{{i = 1}}^{{N - r}} P_{{i,n \to m}}^{{{\text{switch}}}}$$
(6)

The power dissipation may be determined in different tunneling energy levels (e.g., γ = 0.5EK, γ = 1.0EK, γ = 1.5EK, etc.) at fixed temperature using QCAPro. However, this work explored the energy dissipations exclusively for two tunneling levels, γ = 0.5EK, γ = 1.0EK and temperature kept fixed at 2 K. At 2 K temperature and 0.5EK tunneling level, the total energy dissipation of the multiplexer and demultiplexer is 21.67 meV, and 32.86 meV, respectively. At 1.0EK, the same is 28.70 meV and 41.41 meV, respectively. The leakage energy dissipations and switching energy dissipations can also be calculated using a similar method; however, this article only looked at the overall energy dissipations.

QCADesigner-E, often known as QDE [47], is a new energy estimation tool that is based on the famous QCADesigner [51]. The energy dissipation was computed using the Runge–Kutta approach [47]. The QCA circuit can be thought of as an array of cells, with coordinate numbers assigned to each cell. During operation, the cell can be considered an energy bath. Let, E_BATH is the sum of all energy transfers to the ‘bath’ of all QCA cells separated for each clock cycle, and the total energy dissipation is \(\sum _{\mathrm{a}\mathrm{l}\mathrm{l}}E\_\mathrm{B}\mathrm{A}\mathrm{T}\mathrm{H}\) [52, 53]. \(\sum _{\mathrm{a}\mathrm{l}\mathrm{l}}E\_\mathrm{B}\mathrm{A}\mathrm{T}\mathrm{H}\) is the addition of three components of energy dissipation, and it is expressed as \(\sum _{\mathrm{a}\mathrm{l}\mathrm{l}}E\_\mathrm{B}\mathrm{A}\mathrm{T}\mathrm{H}={E}_{\mathrm{C}\mathrm{K}}+{E}_{\mathrm{E}\mathrm{V}}+{E}_{\mathrm{I}\mathrm{O}}\), where ECK is the sum of all energy transfers between QCA cells and the clock separated for each clock cycle, EEV is the energy that transfers QCA cells to the environment, and EIO is the energy transfer amongst QCA cells [52, 53]. Note that EIO = EIN – EOUT for QCA wire, where EIN = energy entering in the QCA cell and EOUT = energy leaving the QCA cell. ERR is the sum of all QCA cell’s energy analysis errors for each clock cycle, ERR = EEV − (ECK + EIO) [52, 53]. The positive energy value indicates that energy has been transferred to EEV, EIO, and ECK. The energy has been calculated using ‘array coordinates’ as introduced QDE, and we have used the Runge–Kutta approximation [52, 53]. The array coordinates are assigned as ‘[column number] [row number]’. At the coherence vector energy simulation mode, the simulation was performed on 500,000 samples. For the QCA multiplexer, the total energy dissipation is 13 meV with a slight error of − 0.639 meV. The average energy dissipation of the multiplexer per cycle is 1.18 meV with a minor error of − 0.0581 meV. In contrast, the total energy consumption of the demultiplexer is 10.40 meV, including a minor error of − 0.382 meV, and the average energy dissipation per cycle is 0.948 meV with a slight error of − 0.0348 meV.

Cost calculations

The cost of a QCA circuit is an important parameter to consider while evaluating its performance. It is also one of the recent QCA research trends to determine the cost of a circuit for a better performance evaluation.

Area-delay cost

It is the general cost of QCA circuits, and it is the metric that most researchers seek to find. It is determined by the overall area used to build the QCA layout as well as the output delay. This delay is also referred to as latency, the output delay in relation to the input. This latency or delay is expressed in the number of clocks. The latency of our experimental multiplexer and demultiplexer are the same, and it is 0.5 clock-cycle or 0.5 cc, which means half of a clock cycle. The area delay cost is expressed as (Area) × (latency)2 [50]. For our multiplexer the total area is 0.01 μm2 and the latency is 0.5 cc; therefore, the area-delay cost is ((0.01 × 10−12) × (0.5)2) = 0.002 × 10−12 m2-cc. Hence the calculated area-delay cost (× 1012) for the multiplexer is 0.002 m2-cc. Now the total area of our demultiplexer is 0.02 μm2 and the latency is 0.5 cc; thus, the area-delay cost is ((0.02 × 10−12) × (0.5)2) = 0.005 × 10−12 m2-cc. So, the area-delay cost (× 1012) of our demultiplexer is 0.005 m2-cc.

QCA-specific cost

This cost is primarily considered for QCA circuits. The figure of Merit (FoM) is another name for it [54, 55]. To build a QCA architecture, the number of utilized majority voters (MV), used inverters (IN), used clocks (CK), and used crossover (CV) are taken into account. The formula to calculate the QCA-specific cost or FoM is = ((MVm + IN + CVn) × CKp) [50, 54]. Here, m, n, and p are the experimental weightings for majority voter, crossover, and clock count (number of clock phase). In general, m = n = p = 2 considered as standard value [50, 54]. Because the number of majority voters, inverters, and crossovers are unit-less, QCA-specific cost is represented in square clock phases (scp). For our multiplexer, the QCA-specific cost is (32 + 1 + 0) × 32 = 90 scp and the QCA-specific cost of our demultiplexer is (22 + 1 + 0) × 22 = 20 scp. It’s important to know that one clock cycle means four clock phases (or four clock zones).

Energy-delay cost

We calculated the energy dissipation using QDE, but we also used QCAPro to determine the energy-delay cost based solely on the energy dissipation (eV) at the 1.0 EK tunneling level. It is worth noting that the same calculations can be applied to two more tunneling levels 0.5 EK and 1.5 EK. The energy-delay cost is calculated as (Ex × Dy), where E is the dissipated energy, D is the delay or latency, x = y = experimental weightings [49, 53]. The standard value of x = y = 2 is taken for our calculation [49, 53]. The unit of energy-delay cost is square eV–square clock cycles, or seV–scc, if energy dissipation is measured in eV and delay is measured in clock cycles (cc). Total energy dissipation of our multiplexer and demultiplexer at 2 K temperature with tunneling level 1.0 EK is 28.70 meV and 41.41 meV, respectively. The latency of the multiplexer and the demultiplexer is 0.5 cc. Therefore, the energy-delay cost of multiplexer is (28.70 × 10−3)2 × (0.5)2 = 2.06 × 10−4 seV–scc. Similarly, the energy-delay cost of demultiplexer is (41.41 × 10−3)2 × (0.5)2 = 4.29 × 10−4 seV–scc. Hence, the energy-delay cost (× 103) is 0.206 seV–scc and 0.429 seV–scc for multiplexer and demultiplexer, respectively.

Comparisons and discussion

For comparisons, we selected a few good designs from the QCA literature over the last five years (2016–2010). The computation of energy dissipation is one of the parameters that may be used to make better comparisons. However, most previously published studies did not account for the dissipated energy of the multiplexer or demultiplexer. Only Alkaldy et al. [36] and Ahmad [35] used QCAPro to calculate the multiplexer's dissipated energy. Furthermore, none of the previous work included an energy calculation for the demultiplexer. Interestingly, one of the key benefits of our work is that we employed Ranga–Kutta approximation using QDE to find the dissipated energy.

Another essential factor to consider is the cost. This parameter has been extensively discussed. We investigated three different forms of costs, but none of the previous work addressed them. According to area-delay cost (m2-cc), our multiplexer and demultiplexer are excellent designs as its area delay cost (× 1012) is 0.002 and 0.005, respectively. Similarly, the calculated QCA-specific cost or FoM (scp) of our multiplexer and demultiplexer are 90 and 20; these are also moderately good values. The energy-delay cost (× 103) in seV–scc of our multiplexer and demultiplexer are 0.206 and 0.429. It is worth noting that no previous research has estimated all of the cost parameters for multiplexers and demultiplexers. A detail of these values is presented in Table 2. Several graphical representations have been utilized to explain the results better; Figs. 10, 11, and 12 are pictorial views of comparisons for multiplexers, and Figs. 13, 14, and 15 are graphical views of comparisons for demultiplexers. Table 2 also includes a few generic metrics such as complexity, size, area consumption, clocks count, latency, and gate count to help comparisons. If all of the discussed parameters are measuring, we can conclude that our experimental items are efficient designs.

Table 2 Comparisons of all important parameters of current works with existing works
Full size table
Fig. 10
figure 10

Graphical view of comparisons of QCA specific cost for multiplexer

Full size image
Fig. 11
figure 11

Graphical view of comparisons of area-delay cost for multiplexer

Full size image
Fig. 12
figure 12

Graphical view of comparisons of energy-delay cost for multiplexer

Full size image
Fig. 13
figure 13

Graphical view of comparisons of QCA specific cost for demultiplexer

Full size image
Fig. 14
figure 14

Graphical view of comparisons of area-delay cost for demultiplexer

Full size image
Fig. 15
figure 15

Graphical view of comparisons of energy-delay cost for demultiplexer

Full size image

Conclusion and future scope

The QCA layouts of multiplexer and demultiplexer used in this experiment were made as small as possible in terms of circuit complexity, area requirements, and cost. The experimental research on energy estimation using QCAPro and QDE tools revealed that both circuits have low energy dissipation. This article is extremely important in today's QCA technology because it completely follows current design trends. This article measures three different sorts of costs. The basic multiplexer and simple demultiplexer's area-delay, QCA-specific, and energy-delay costs are addressed, proving that the objects are efficient enough. As a result, these little blocks devised a means for creating higher-order nano computational circuits, notably nano-communication devices such as nano-routers, where multiplexer and demultiplexer are unavoidable blocks.