1 Introduction

Studies of non-Newtonian fluid flows are major advances in the area of fluid dynamics. Non-Newtonian fluid is further divided into six major categories and one of them is visco-elastic fluid [1]. During the motion of visco-elastic fluid, viscosity signifies energy dissipation and elasticity indicates accumulation of energy. Walters [2] proposed a theoretical model for visco-elastic fluid and it is named as Walters liquid (Model \( B^{\prime } \)) for short relaxation memories. It resists shear flow and strains linearly with time under the application of applied stress but when the stress is removed it quickly returns to its original position. Walters liquid (Model \( B^{\prime } \)) exhibits both visco-elastic and viscous properties.

The constitutive equation for Walters liquid (Model \( B^{\prime } \)) is

$$ \sigma_{ik} = - pg_{ik} + \sigma_{ik}^{'} ,\quad \sigma^{\prime ik} = 2\eta \varepsilon^{ik} - 2k\varepsilon^{'ik} $$
(1.1)

where \( \sigma^{ik} \) is the stress tensor, \( \sigma^{'ik} \) is the viscous stress tensor, p is isotropic pressure, g ik is the metric tensor of a fixed co-ordinate system x i, v i is the velocity vector, the contravarient form of \( \varepsilon^{{'{\text{ik}}}} \) (derivative of \( \varepsilon^{\text{ik}} \)) is given by

$$ \varepsilon^{'ik} = \frac{{\partial \varepsilon^{ik} }}{\partial t} + v^{m} \varepsilon_{,m}^{ik} - v_{,m }^{k} \varepsilon^{im} - v_{,m}^{i} \varepsilon^{mk} , $$
(1.2)

The deformation rate tensor \( \varepsilon^{ik} \) defined by

$$ 2\varepsilon^{ik} = v_{i,k} + v_{k,i} $$
(1.3)

Here η is the limiting viscosity at the small rate of shear which is given by

$$ \eta = \int_{0}^{\infty } {{\mathbf{\aleph }}(\tau )d\tau } \quad {\text{and}}\quad k = \int_{0}^{\infty } {\tau N(\tau )d\tau } $$
(1.4)

\( {\mathbf{\aleph }}(\tau ) \) being the relaxation spectrum. This idealized model is a valid approximation of Walters liquid (Model \( B^{\prime } \)) taking very short memories into account so that terms involving

$$ \int_{0}^{\infty }\tau^\gimel {{\mathbf{\aleph }}(\tau )d\tau } \quad \gimel \ge 2 $$
(1.5)

have been neglected.

The mixture of polymethyl methacrylate and pyridine at 25 °C containing 30.5 g of polymer per litre and having density 0.98 g/ml fits very nearly to the above model [3]. Polymers are used in the manufacture of space crafts, aeroplanes, tyres, belt conveyers, ropes, cushions, seats, foams, plastic, engineering equipments, contact lens etc.

Motion of viscous fluid flow containing immiscible fine solid particles has attracted many researchers because of its uses in nuclear reactor cooling, powder technology, acoustics, sedimentation, aerosol and pain spraying, aircraft icing etc. Saffman [4] studied the stability of laminar flow of dusty gas by neglecting the volume fraction of dust particles. Michael and Miller [5] have investigated the behaviour of plane parallel flow of a dusty gas. For high fluid densities or high particle mass fraction, the volume fraction should be considered. So, Rudinger [6], in his work has discussed the dynamics of gas-particle mixture in presence of volume fraction. Nayfeh [7] also, formulated the equations of motion of fluid particles in presence of volume fraction of dust particles. The mechanics of viscous fluid flow embedded with Stokesian solid particles in presence of various physical configurations has been studied by Gupta and Gupta [8], Singh [9], Singh and Ram [10], Prasad and Ramacharyulu [11], Ajadi [12], Alle et al. [13], Attia et al. [14] and Kalita [15]. Non-Newtonian fluid embedded with non-conducting, solid, spherical dust particles has many applications such as in the production of products like rayon, nylon etc., in purification of crude oil and rain water, in pulp, paper and textile industry. Gupta and Gupta [16] have investigated the unsteady flow of a dusty visco-elastic fluid through channel with volume fraction.

Nowadays, researchers have given a special attention to the area of stratified fluid flows due its applications in the dynamics of ocean and atmospheric science and also in various industries. In stratified fluid flow, motion is characterized by density, viscosity variations along the axis of gravity. Rayleigh [17] has demonstrated the character of an incompressible heavy fluid of variable density. Channabasappa and Rangana [18], Gupta and Sharma [19] have investigated the problem of viscous stratified fluid flow past a porous bed in presence of various physical configurations. Effects of heat and mass transfer on stratified viscous fluid flow past a vertical porous plate have been analysed by Agarwal et al. [20] and Sharma et al. [21]. In this study, the physical properties like density, viscosity, visco-elasticity, number density of dust particles, electrical conductivity are assumed to be vary along the axis of gravity. Application of visco-elastic stratification along with density and viscosity variation may be seen in case of multilayer polymer extrusion. MHD flow and heat transfer of a dusty visco-elastic stratified fluid flow past an inclined porous medium under variable viscosity has been studied by Chakraborty [22]. The effect of stratified Rivlin–Ericksen fluid on MHD free convective flow past a vertical porous plate with heat and mass transfer has been investigated by Dharmendra and Varshney [23]. Prakash et al. [24] have investigated the heat transfer in MHD flow of dusty viscoelastic (Walters’ liquid model \( B^{\prime } \)) stratified fluid in porous medium under variable viscosity.

The objective of this study is to bring out the effects of visco-elasticity, volume fraction of dust particles and stratification on hydro-magnetic Couette flow of dusty stratified Walters liquid (Model \( B^{\prime } \)) through horizontal porous medium. Also, the study is carried out to investigate the difference in flow pattern between Newtonian fluid and non-Newtonian fluid. The physical properties like density, viscosity, visco-elasticity, electrical conductivity and number density of dust particles are assumed to vary along the axis of gravity of the channel.

2 Mathematical Formulation

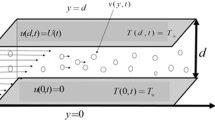
A two dimensional unsteady Couette flow of non-Newtonian (Walters liquid, Model \( B^{\prime } \)) dusty stratified fluid through a porous medium bounded by two infinite parallel plates separated by distance 2h has been investigated. A magnetic field of strength B 0 is applied along the direction perpendicular to the plate. The central line of the channel coincides with the \( x^{{\prime }} \)-axis and \( y^{{\prime }} \)-axis is taken perpendicular to it (Fig. 1). Equations of two horizontal plates are considered as \( y^{\prime } = \pm h \), the lower one is kept fixed and the upper one is moving with a velocity. The following assumptions are made for analysing the governing fluid motion:

Fig. 1
figure 1

Geometry of the problem

Full size image
  1. (a)

    The fluid is containing immiscible and suspended dust particles known as Stokesian solid particles.

  2. (b)

    These dust particles are assumed to be electrically non-conducting and spherical in shape. They are also supposed to be dilute, so particle–particle interaction may be neglected [25].

  3. (c)

    Effects due to pressure, gravity, Darcy’s force and magnetic field on dust particles are small and so are ignored.

  4. (d)

    The induced magnetic field is neglected by assuming very small values of magnetic Reynolds number.

  5. (e)

    Intensity of the electric field is neglected in comparison to Lorentz force generated by transverse magnetic field.

  6. (f)

    Chemical reaction, mass transfer and radiation between the particles are not considered.

  7. (g)

    Effect of Buoyancy force is neglected for the governing fluid flow in the horizontal channel.

  8. (h)

    Temperature is assumed to be uniform within the system.

  9. (i)

    As the speed of fluid flow is considerably small for visco-elastic fluid, so energy dissipation due to viscosity is neglected.

  10. (j)

    For the motion of fluid having smaller electrical conductivity, the Joule heating effect may be neglected.

  11. (k)

    The channel is assumed to be infinite in length along the direction of \( x^{{\prime }} \)-axis. So, all physical properties except the pressure function are independent of the variable \( x^{{\prime }} \).

  12. (l)

    The fluidic properties like density (ρ), limiting viscosity (η), visco-elasticity (k), particle number density (N) and electrical conductivity (σ) under consideration are varying along \( y^{\prime } \)-axis throughout the channel and are considered as

    $$ \begin{aligned} \rho & = \rho_{0} e^{{ - n\left( {\frac{{y^{\prime } }}{h} + 1} \right)}} , \quad \eta = \eta_{0} e^{{ - n\left( {\frac{{y^{\prime } }}{h} + 1} \right)}} , \quad k = k_{0} e^{{ - n\left( {\frac{{y^{\prime } }}{h} + 1} \right)}} , \\ N & = N_{0} e^{{ - n\left( {\frac{{y^{\prime } }}{h} + 1} \right)}} ,\quad \sigma = \sigma_{0} e^{{ - n\left( {\frac{{y^{\prime } }}{h} + 1} \right)}} \\ \end{aligned} $$

    where, n is the stratification factor of the fluid and for stable stratification, n > 0. Also, ρ 0, η 0, k 0, N 0 and σ 0 are the respective fluid properties at lower plate \( {\text{y}}^{\prime } \) = −h. The negative sign present in the exponentials indicate that density and other physical properties have maximum values in the neighbourhood of lower plate.

  13. (m)

    The volume occupied by dust particles per unit volume of the mixture (volume fraction of dust particle, ϕ) is taken into consideration but smaller values of volume fraction have been used in order to maintain the Saffman model [16].

The equations of governing fluid motion are:

Using the assumptions (k) and (l), equations of continuity for the stratified fluid flow having density varies along \( y^{\prime } \) axis is [26, 27]:

$$ \frac{\partial }{{\partial y^{\prime } }}(\rho v^{\prime } ) = 0 $$
(2.1)

where, \( v^{{\prime }} \) be velocity of fluid motion along the direction of \( y^{{\prime }} \) axis. Substituting the expression of ρ and integrating, we get

$$ v^{\prime } = A_{1} {\text{e}}^{{\rho_{0} \frac{n}{h}y^{\prime } }} $$

where, A 1 is constant of integration.

Since, in absence of suction at the plate i.e. \( v^{{\prime }} = 0\;\;{\text{at}}\;\;y^{{\prime }} = - h \) gives A 1 = 0 and hence \( v^{{\prime }} = 0. \)

Similarly the equation of continuity for dust particles is given by

$$ \frac{\partial }{{\partial y^{{\prime }} }}\left( {V_{t}^{{\prime }} N} \right) = 0 $$
(2.2)

where, \( V_{t}^{\prime } \) be velocity of dust particles along the direction of \( y^{{\prime }} \) axis. Substituting the expression of N and integrating, we get

$$ V_{t}^{'} = A_{2} {\text{e}}^{{N_{0} \frac{n}{h}y^{{\prime }} }} $$

where, A 2 is constant of integration.

Again, in absence of suction at the plate i.e. \( V_{t}^{'} = 0 \;\;{\text{at}}\;\;y^{\prime } = - h \) gives A 2 = 0 and hence \( V_{t}^{'} = 0. \)

The equation of motion is based on conservation of linear momentum and the forces acting on the motion are:

  1. 1.

    The net effect of the dust particles on fluid is equivalent to an extra force \( KN\left( {V^{\prime } - u^{\prime } } \right) \) appears in Eq. (2.3).

  2. 2.

    Lorentz force becomes \( - \sigma B_{0}^{2} u^{\prime } \), B 0 is the strength of the magnetic field appears in Eq. (2.3).

  3. 3.

    By Newton’s 3rd law of motion, the effect of fluid particles on dust is \( - KN\left( {V^{\prime } - u^{\prime } } \right) \) appears in Eq. (2.4).

  4. 4.

    Effect of permeability of porous medium is exhibited through \( - \frac{{\eta u^{{\prime }} }}{{K_{p}^{{\prime }} }} \) appears in Eq. (2.3).

Using all assumptions (a)–(m) and above mentioned forces along with pressure gradient, viscous and visco-elastic properties, equations of motion for fluid particles and dust particles are given as follows:

$$ \begin{aligned} \left( {1 - \phi } \right)\left( {\rho \frac{{\partial u^{{\prime }} }}{{\partial t^{{\prime }} }}} \right) & = \left( {1 - \phi } \right)\left\{ { - \frac{{\partial p^{{\prime }} }}{{\partial x^{{\prime }} }} + \frac{\partial }{{\partial y^{{\prime }} }}\left( {\eta \frac{{\partial u^{{\prime }} }}{{\partial y^{{\prime }} }}} \right)} \right. \\ & \left. {\quad - \frac{\partial }{{\partial y^{{\prime }} }}\left( {k\frac{{\partial^{2} u^{{\prime }} }}{{\partial y^{{\prime }} \partial t^{{\prime }} }}} \right)} \right\} - \frac{{\eta u^{{\prime }} }}{{K_{p}^{{\prime }} }} \\ & \quad + KN\left( {V^{{\prime }} - u^{{\prime }} } \right) - \sigma B_{0}^{2} u^{{\prime }} \\ \end{aligned} $$
(2.3)
$$ \begin{aligned} mN\frac{{\partial V^{{\prime }} }}{{\partial t^{{\prime }} }} & = \phi \left\{ { - \frac{{\partial p^{{\prime }} }}{{\partial x^{{\prime }} }} + \frac{\partial }{{\partial y^{{\prime }} }}\left( {\eta \frac{{\partial u^{{\prime }} }}{{\partial y^{{\prime }} }}} \right)} \right. \\ & \quad \left. { - \frac{\partial }{{\partial y^{{\prime }} }}\left( {k\frac{{\partial^{2} u^{{\prime }} }}{{\partial y^{{\prime }} \partial t^{{\prime }} }}} \right)} \right\} - KN\left( {V^{{\prime }} - u^{{\prime }} } \right) \\ \end{aligned} $$
(2.4)

The boundary conditions of the problem are:

$$ \left. {\begin{array}{*{20}c} {u^{{\prime }} = 0, \quad V^{{\prime }} = 0,\quad v^{{\prime }} = V_{t}^{{\prime }} = 0; \quad y^{{\prime }} = - h} \\ {u^{{\prime }} = U_{0} {\text{e}}^{{ - nt^{{\prime }} \frac{{U_{0} }}{h}}} , \quad V = V_{o} {\text{e}}^{{ - nt^{{\prime }} \frac{{V_{0} }}{h}}} ,\quad v^{{\prime }} = V_{t}^{{\prime }} = 0; \quad y^{{\prime }} = h} \\ \end{array} } \right\} $$
(2.5)

The boundary conditions reveal that the lower surface is at rest and by using the no-slip condition, the velocities of fluid and dust particles at the lower surface are zero. The upper surface is moving with a velocity which is a function of time. \( x^{{\prime }} \) and \( {\text{y}}^{{\prime }} \) are displacement variables, \( t^{{\prime }} \) is the time, \( u^{{\prime }} \) and \( V^{{\prime }} \) represent velocities of fluid and dust particles respectively, \( p^{{\prime }} \) be the pressure, ρ be the density, σ be the electrical conductivity of the fluid, N be the number of dust particles per unit volume of the mixture, \( K_{p}^{{\prime }} \) be the permeability of porous medium, K be the Stokes resistance coefficient and is derived from Stokes drag formula (K = \( 6\pi \eta_{0} r \), r be the average radius of the dust particles), m be the average mass of dust particle.

The pressure gradient is taken as \( {-}\frac{{\partial p^{{\prime }} }}{{\partial x^{{\prime }} }} = a^{{\prime }} (t) \)Let us define the following non-dimensional parameters:

$$ \begin{aligned} u & = \frac{{u^{\prime } }}{{U_{0} }}, \;V = \frac{{V^{\prime } }}{{V_{0} }}, \;y = \frac{{y^{\prime } }}{h}, \\ t & = \frac{{t^{\prime } U_{0} }}{h}, \;a = \frac{{a^{\prime } h}}{{U_{0}^{2} }}, \;K_{p} = \frac{h}{{\sqrt {K_{p}^{\prime } } }}, \\ \lambda & = \frac{{U_{0} }}{{V_{0} }}, \;R = \frac{{\rho_{0} U_{0} h}}{{\eta_{0} }}, \;K_{e} = \frac{{k_{0} }}{{\rho_{0} h^{2} }}, \\ \end{aligned} $$
$$ M = \frac{{\sigma_{0} B_{0}^{2} h^{2} }}{{\eta_{0} }}, \;f_{0} = \frac{{N_{0} m}}{{\rho_{0} }}, \;\gamma = \frac{Kh}{{mU_{0} }} $$

where y is dimensionless displacement variable, u and V are dimensionless velocities, t be the dimensionless time, K p be the permeability parameter in non-dimensional form, λ be the ratio of velocities of fluid particle and dust particle respectively, R be the Reynolds number, K e be the dimensionless visco-elastic parameter, M be the Hartmann number, f 0 be the mass concentration of dust particles, \( \frac{1}{\gamma } \) be the dimensionless relaxation time of dust particles.

Simplifying Eqs. (2.3) and (2.4) by using the expressions of density (ρ), limiting viscosity (η), visco-elasticity (k), particle number density (N) and electrical conductivity (σ) given in assumption (l) and introducing the non-dimensional parameters, we get the following set of differential equations:

$$ \begin{aligned} \frac{\partial u}{\partial t} & = \bar{a}(t){\text{e}}^{ - ny} - \frac{n}{R}\frac{\partial u}{\partial y} + \frac{1}{R}\frac{{\partial^{2} u}}{{\partial y^{2} }} \\ & \quad - K_{e} \frac{{\partial^{3} u}}{{\partial y^{2} \partial t}} + K_{e} n\frac{{\partial^{2} u}}{\partial y\partial t} - \frac{{K_{p}^{2} }}{R}\epsilon_{1} u \\ & \quad + \left( {\frac{V}{\lambda } - U} \right)\epsilon_{1} f_{0} \gamma - \frac{M}{R}\epsilon_{1} u \\ \end{aligned} $$
(2.6)
$$ \begin{aligned} \frac{\partial V}{\partial t} & = \phi \frac{\lambda }{{f_{0} }}\left[ {\bar{a}{\text{e}}^{ - n} {\text{e}}^{ - ny} - \frac{n}{R}\frac{\partial u}{\partial y} + \frac{1}{R}\frac{{\partial^{2} u}}{{\partial y^{2} }}} \right. \\ & \quad \left. { - K_{e} \frac{{\partial^{3} u}}{{\partial y^{2} \partial t}} + K_{e} n\frac{{\partial^{2} u}}{\partial y\partial t}} \right] - \gamma \left( {V - \lambda_{1} U} \right) \\ \end{aligned} $$
(2.7)

where, \( \bar{a} = \frac{a}{{\rho_{0} }} \) and \( \epsilon_{1} = \frac{1}{1 - \phi } \).

The relevant boundary conditions of the problem are:

$$ \left. {\begin{array}{*{20}l} {u = V = 0\qquad{\text{at}}\;y = - 1} \\ {u = V = {\text{e}}^{ - nt} \quad{\text{at}}\; y = 1} \\ \end{array} } \right\} $$
(2.8)

3 Method of Solution

Equations (2.6) and (2.7) have been solved analytically by using separation of variable technique, where the solution is expressed as a product of functions of two variables. Subject to the boundary conditions (2.8), the solutions are assumed to be of the form

$$ u = f(y){\text{e}}^{ - nt} ,\; V = g(y){\text{e}}^{ - nt} ,\; \bar{a} = \bar{a}_{0} {\text{e}}^{ - nt} $$
(3.1)

Using Eq. (3.1) in the above two dimensionless Eqs. (2.6) and (2.7), we get

$$ \begin{aligned} & \left( {1 + K_{e} n} \right)\frac{{d^{2} f}}{{dy^{2} }} + \left( {K_{e} nR - n} \right)\frac{df}{dy} \\ & \quad + \left( {nR - K_{p}^{2} \epsilon_{1} - \epsilon_{1} f_{0} \gamma R - M\epsilon_{1} } \right)f \\ & \quad + R\bar{a}_{0} e^{n} e^{ny} + \frac{R}{\lambda }\epsilon_{1} f_{0} \gamma g = 0 \\ \end{aligned} $$
(3.2)
$$ \begin{aligned} & \left( {\frac{\phi \lambda }{{f_{0} R}} + \frac{{K_{e} n\phi \lambda }}{{f_{0} }}} \right)\frac{{d^{2} f}}{{dy^{2} }} + \left( { - \frac{\phi \lambda n}{{f_{0} R}} - \frac{{K_{e} n^{2} \phi \lambda }}{{f_{0} }}} \right)\frac{df}{dy} \\ & \quad + \gamma \lambda f + \left( {\frac{\phi \lambda }{{f_{0} }}\bar{a}_{0} e^{n} } \right)e^{ny} + \left( {\gamma - n} \right)g = 0 \\ \end{aligned} $$
(3.3)

Eliminating g from Eqs. (3.2) and (3.3), we get

$$ A_{1} \frac{{d^{2} f}}{{dy^{2} }} + A_{2} \frac{df}{dy} + A_{3} f + A_{4} {\text{e}}^{ny} = 0 $$
(3.4)

The constants are given by

$$ \begin{aligned} A_{1} & = \left( {1 + K_{e} n} \right)\left( {\gamma - n} \right) - \left( {\frac{\phi \lambda }{{f_{0} R}} + \frac{{K_{e} n\phi \lambda }}{{f_{0} }}} \right)\frac{R}{\lambda }\epsilon_{1} f_{0} \gamma , \\ A_{2} & = \left( {K_{e} nR - n} \right)\left( {\gamma - n} \right) - \left( { - \frac{\phi \lambda n}{{f_{0} R}} - \frac{{K_{e} n^{2} \phi \lambda }}{{f_{0} }}} \right)\frac{R}{\lambda }\epsilon_{1} f_{0} \gamma \\ A_{3} & = \left( {nR - K_{p}^{2} \epsilon_{1} - \epsilon_{1} f_{0} \gamma R - M\epsilon_{1} } \right)\left( {\gamma - n} \right) - \gamma R\epsilon_{1} f_{0} \gamma , \\ A_{4} & = \bar{a}_{0} {\text{e}}^{n} R\left( {\gamma - n} \right) - \frac{\phi }{{f_{0} }}\bar{a}_{0} {\text{e}}^{n} R\epsilon_{1} f_{0} \gamma \\ \end{aligned} $$

The relevant boundary conditions of the problem are:

$$ \begin{aligned} f(y) & = 0 = g(y)\quad {\text{at}}\;\;{\text{y}} = - 1; \\ f(y) & = g(y) = 1\quad {\text{at}}\;\;{\text{y}} = 1 \\ \end{aligned} $$
(3.5)

Solving the differential Eq. (3.4) with the above mentioned boundary conditions, the solutions are obtained as:

$$ f(y) = C_{1} {\text{e}}^{{\alpha_{1} y}} + C_{2} {\text{e}}^{{\alpha_{2} y}} + C_{3} {\text{e}}^{ny} $$
(3.6)

Then from Eq. (3.3), we get

$$ g(y) = C_{4} {\text{e}}^{{\alpha_{1} y}} + C_{5} {\text{e}}^{{\alpha_{2} y}} + C_{6} {\text{e}}^{ny} $$
(3.7)

where,

$$ \begin{aligned} \alpha_{1} & = \frac{{ - A_{2} + \sqrt {A_{2}^{2} - 4A_{2} A_{3} } }}{{2A_{1} }}, \;\alpha_{2} = \frac{{ - A_{2} - \sqrt {A_{2}^{2} - 4A_{2} A_{3} } }}{{2A_{1} }}, \\ C_{1} & = C_{3} {\text{e}}^{{\alpha_{1} - n}} - C_{2} {\text{e}}^{{\alpha_{1} - \alpha_{2} }} , \;C_{2} = \frac{{C_{3} \left( {{\text{e}}^{{\alpha_{1} - n}} - {\text{e}}^{{n - \alpha_{1} }} } \right)}}{{\left( {{\text{e}}^{{\alpha_{2} - \alpha_{1} }} - {\text{e}}^{{\alpha_{1} - \alpha_{2} }} } \right)}}, \\ C_{3} & = \frac{{A_{4} }}{{A_{1} n^{2} + A_{2} n + A_{3} }}, \\ C_{4} & = \frac{1}{n - \gamma }\left[ {\left( {\frac{\phi \lambda }{{f_{0} R}} + \frac{{K_{e} n\phi \lambda }}{{f_{0} }}} \right)C_{1} \alpha_{1}^{2} } \right. \\ & \quad \left. { + \left( { - \frac{\phi \lambda n}{{f_{0} R}} - \frac{{K_{e} n^{2} \phi \lambda }}{{f_{0} }}} \right)C_{1} \alpha_{1} + \gamma \lambda C_{1} } \right] \\ C_{5} & = \frac{1}{n - \gamma }\left[ {\left( {\frac{\phi \lambda }{{f_{0} R}} + \frac{{K_{e} n\phi \lambda }}{{f_{0} }}} \right)C_{2} \alpha_{2}^{2} } \right. \\ & \quad \left. { + \left( { - \frac{\phi \lambda n}{{f_{0} R}} - \frac{{K_{e} n^{2} \phi \lambda }}{{f_{0} }}} \right)C_{2} \alpha_{2} + \gamma \lambda C_{2} } \right] \\ C_{6} & = \frac{1}{n - \gamma }\left[ {\left( {\frac{\phi \lambda }{{f_{0} R}} + \frac{{K_{e} n\phi \lambda }}{{f_{0} }}} \right)C_{3} n^{2} } \right. \\ & \quad \left. { + \left( { - \frac{\phi \lambda n}{{f_{0} R}} - \frac{{K_{e} n^{2} \phi \lambda }}{{f_{0} }}} \right)C_{3} n + \gamma \lambda C_{3} + \frac{\phi \lambda }{{f_{0} }}\bar{a}_{0} {\text{e}}^{n} } \right] \\ \end{aligned} $$

4 Results and Discussions

The dimensionless velocities of fluid and dust particles are given by

$$ u = \left( {C_{1} {\text{e}}^{{\alpha_{1} y}} + C_{2} {\text{e}}^{{\alpha_{2} y}} + C_{3} {\text{e}}^{ny} } \right){\text{e}}^{ - nt} $$
(4.1)
$$ V = \left( {C_{4} {\text{e}}^{{\alpha_{1} y}} + C_{5} {\text{e}}^{{\alpha_{2} y}} + C_{6} {\text{e}}^{ny} } \right){\text{e}}^{ - nt} $$
(4.2)

The dimensionless flow flux for fluid (f f ) and dust particles (f d ) are given by

$$ \begin{aligned} f_{f} & = \mathop \smallint \limits_{ - 1}^{1} udy = {\text{e}}^{ - nt} \left[ {\frac{{C_{1} }}{{\alpha_{1} }}\left( {{\text{e}}^{{\alpha_{1} }} - {\text{e}}^{{ - \alpha_{1} }} } \right)} \right. \\ & \quad \left. { + \frac{{C_{2} }}{{\alpha_{2} }}\left( {{\text{e}}^{{\alpha_{2} }} - {\text{e}}^{{ - \alpha_{2} }} } \right) + \frac{{C_{3} }}{n}\left( {{\text{e}}^{n} - {\text{e}}^{ - n} } \right)} \right] \\ \end{aligned} $$
(4.3)
$$ \begin{aligned} f_{d} & = \mathop \smallint \limits_{ - 1}^{1} Vdy = {\text{e}}^{ - nt} \left[ {\frac{{C_{4} }}{{\alpha_{1} }}\left( {{\text{e}}^{{\alpha_{1} }} - {\text{e}}^{{ - \alpha_{1} }} } \right)} \right. \\ & \quad \left. { + \frac{{C_{5} }}{{\alpha_{2} }}\left( {{\text{e}}^{{\alpha_{2} }} - {\text{e}}^{{\alpha_{2} }} } \right) + \frac{{C_{6} }}{n}\left( {{\text{e}}^{n} - {\text{e}}^{ - n} } \right)} \right] \\ \end{aligned} $$
(4.4)

Non-dimensional shearing stress at both the plates are given by

$$ \sigma = \left[ {\left\{ {\frac{1}{R}\frac{\partial u}{\partial y} - K_{e} \frac{{\partial^{2} u}}{\partial y\partial t}} \right\}{\text{e}}^{{ - \left( {n + 1} \right)y}} } \right]_{y = \pm 1} $$
(4.5)

The effects of volume fraction and stratification on dusty visco-elastic electrically conducting fluid flow through a porous medium bounded by two parallel plates have been analyzed graphically for various values of flow parameters involved in the solution. The elastico-viscous effect is exhibited through the non-dimensional parameter K e . For short relaxation memories, the energies required for the visco-elastic response are very small, so during this study, the visco-elastic parameter is taken to be a smaller order of magnitude. The nonzero value of the parameter K e  = 0.2 characterizes the visco-elastic fluid and K e  = 0 represents the Newtonian fluid flow phenomenon.

Figures 2, 3, 4, and 5 illustrate the nature of velocity profiles of both Newtonian and non-Newtonian fluids against the displacement variable y for various values of flow parameters involved in the solution. These figures also indicate the difference of flow patterns in the fluid motions of Newtonian and non-Newtonian fluid. It is seen that fluid has least speed in the vicinity of the lower fixed plate and then some acceleration is noticed but finally, because of friction of the boundary layer formed in the neighbourhood of the upper plate, flow experiences a decelerating trend. In the constitutive equation of Walters liquid (Model \( B^{\prime } \)), we see that the lesser values of visco-elasticity subdues the values of resistivity present in the fluid. Thus from all these figures, we can conclude that if the energies required for visco-elastic responses become higher, then the speed of the Walters liquid [governed by constitutive Eq. (1.1)] will be enhanced in comparison to the simple Newtonian fluid (K e  = 0).

Fig. 2
figure 2

Velocity profile u against y for R = 1, n = 0.1, λ = 0.8, ϕ = 0.02, f 0 = 0.2, \( \gamma = \frac{1}{0.6} \), K p  = 0.8 at t = 0.5

Full size image
Fig. 3
figure 3

Velocity profile u against y for R = 1, λ = 0.8, M = 2, f 0 = 0.2, ϕ = 0.02, \( \gamma = \frac{1}{0.6} \), K p  = 0.8 at t = 0.5

Full size image
Fig. 4
figure 4

Velocity profile u against y for R = 1, λ = 0.8, M = 2, f 0 = 0.2, n = 0.1, \( \gamma = \frac{1}{0.6} \), K p  = 0.8 at t = 0.5

Full size image
Fig. 5
figure 5

Velocity profile u against y for R = 1, λ = 0.8, f 0 = 0.2, n = 0.1, \( \gamma = \frac{1}{0.6} \), K p  = 0.8 at t = 0.5

Full size image

Figure 2 represents the behaviour of velocity profiles against y for various values of Hartmann number (M). Application of transverse magnetic field produces Lorentz force and this force might control the weak turbulent motion present in the system. It is observed that this Lorentz force has a retarding effect on the fluid motion as it increases the resistance of the fluid. As a result, increasing values of Hartmann number decelerate the fluid motion. Same phenomenon is also experienced in case of Newtonian fluid.

The effects of stratification on dusty visco-elastic fluid flow are represented by Fig. 3. Stratification parameter is taken of the order 10−1 because higher value of stratification might cease its stability. Growth in stratification parameter (n) reduces the strength of fluidic properties and for n = 0.5, the fluid experiences a back flow in the neighbourhood of lower plate. In the region [0.5, 0.6], the curves traced for n = 0.1 and n = 0.5 have a common magnitude of speed in velocity-displacement graph. The difference in flow pattern between Newtonian and non-Newtonian fluids is also prominent due to the presence of stratification in visco-elasticity for n = 0.5 than in comparison to n = 0.1.

Figure 4 explains the effect of volume fraction (ϕ) of dust particles in the governing fluid motion. Motion of dust particles is governed by parameters (1) mass concentration parameter f 0, (2) relaxation time for the adjustment of dust particles during its motion \( \frac{1}{\gamma } \) and (3) the volume fraction ϕ. In this paper, all these parameters are considered to be of lesser order of magnitude because very high values of f 0 and ϕ are examples for the case of no motion and for spherical sized fine dust particles, \( \frac{1}{\gamma } \) ≪ 1 [3]. If the amount of dust particles (volume fraction) rises then both Newtonian and non-Newtonian fluid motions will experience more and more disturbances and as a result the speed will slow down. Maximum effect of the presence of dust particles on fluid motion is noticed in the neighbourhood of upper plate.

We study the combined effect of Hartmann number and volume fraction on stratified dusty fluid flow (Fig. 5). Both the Hartmann number (Fig. 2) and volume fraction (Fig. 3) have retarding effects on the fluid flow, so, their combination also subdues the speed of Newtonian as well as non-Newtonian fluid motions.

Figures 6 and 7 give emphasis on the velocity profile of dust particles present in the system. The visco-elasticity present in Walters liquid also affects the motion of dust particles and it is seen that the presence of visco-elastic parameter increases the speed of dust particles. The application of transverse magnetic field produces a Lorentz force and the force thickens the fluid flow and as a consequence it affects the motion of dust particles present in the fluid i.e., growth in Hartmann number reduces the speed of dust particles and these dust particles experience a back flow in the neighbourhood of the lower plate (Fig. 6). The ascending nature of stratification parameter generalizes the adverse pressure gradient and as a result a back flow is formed in the neighbourhood of the lower plate and later it is observed that due to stratification, the dust particles decelerate along the upward vertical direction (Fig. 7).

Fig. 6
figure 6

Velocity profile V against y for R = 1, λ = 0.8, f 0 = 0.2, n = 0.1, \( \gamma = \frac{1}{0.6} \), ϕ = 0.02, K p  = 0.8 at t = 0.5

Full size image
Fig. 7
figure 7

Velocity profile V against y for R = 1, λ = 0.8, f 0 = 0.2, M = 2, \( \gamma = \frac{1}{0.6} \), ϕ = 0.02, K p  = 0.8 at t = 0.5

Full size image

The impact of fluid motion on the boundary surfaces are to be measured in the form of shearing stress or viscous drag. Effects of flow parameters on shearing stress at the plates are analysed by Figs. 8, 9 and 10. Figure 8 shows the effect of Hartmann number on skin friction and it is observed that if the strength of applied magnetic field (Hartmann number) is improved, then the resistivity or friction will increase and as a result, the shearing stress or frictional force rises for both Newtonian and non-Newtonian fluid motions on lower and upper surfaces respectively. The volume occupied by the dust particles per unit volume of the mixture also affects the viscous drag and it is seen in Fig. 9. The presence of more and more dust particles also enhances the viscous drags, but this is experienced only at the lower surface. The upper surface is moving and skin friction formed there declines with the rise of volume fraction. The effect of stratification parameter on the shearing stress is shown in Fig. 10. Rise of stratification magnifies the strength of the shearing stress at the lower plate, but an opposite trend is seen at the upper surface. The maximum effect of stratification on shearing stress is seen for n ≫ 0.6.

Fig. 8
figure 8

Shearing stress (σ) against M for R = 1, λ = 0.8, f 0 = 0.2, n = 0.1, \( \gamma = \frac{1}{0.6} \), ϕ = 0.02, K p  = 0.8 at t = 0.5

Full size image
Fig. 9
figure 9

Shearing stress (σ) against ϕ for R = 1, λ = 0.8, f 0 = 0.2, n = 0.1, \( \gamma = \frac{1}{0.6} \), M = 2, K p  = 0.8 at t = 0.5

Full size image
Fig. 10
figure 10

Shearing stress (σ) against n for R = 1, λ = 0.8, f 0 = 0.2, ϕ = 0.02, \( \gamma = \frac{1}{0.6} \), M = 2, K p  = 0.8 at t = 0.5

Full size image

The nature of flow flux of fluid particles (f f ) and flow flux of dust particles (f d ) against time (t) are shown in Figs. 11 and 12. The flow fluxes of both Newtonian and non-Newtonian fluids are following a decreasing pattern (Fig. 11) i.e., it states that as time passes, the amounts of fluid flow (both Newtonian and non-Newtonian fluids) through the horizontal porous channel are diminishing. Flow flux of dust particle also follows the same pattern (Fig. 12) but the magnitude of flux of dust particles over the time interval [0, 4] less than the flux of fluid particle.

Fig. 11
figure 11

Flow flux of fluid particles (f f ) against time t for R = 1, n = 0.1, λ = 0.8, ϕ = 0.02, f 0 = 0.2, \( \gamma = \frac{1}{0.6} \), M = 2, K p  = 0.8

Full size image
Fig. 12
figure 12

Flow flux of dust particles (f d ) against time t for R = 1, n = 0.1, λ = 0.8, ϕ = 0.02, f 0 = 0.2, \( \gamma = \frac{1}{0.6} \), M = 2, K p  = 0.8

Full size image

5 Conclusions

Some of the points from the study of non-Newtonian stratified dusty fluid through horizontal porous medium in presence of transverse magnetic field and volume fraction are listed as below:

  1. (a)

    The speed of both Newtonian and non-Newtonian fluids enhances steadily in the neighbourhood of the lower plate but in the neighbourhood of the upper plate, a declined nature of speed is noticed.

  2. (b)

    Enhanced volume fraction present in both Newtonian and non-Newtonian fluid flows accelerates the fluid flow but a deceleration is noticed in the neighbourhood of upper plate.

  3. (c)

    The presence of visco-elasticity raises the speed of non-Newtonian fluid in comparison to the Newtonian fluid. Effect of visco-elasticity is seen prominent in the neighbourhood of upper plate.

  4. (d)

    Combination of Hartmann number and volume fraction of dusty electrically conducting fluid diminishes the speed of both Newtonian and non-Newtonian fluid motions.

  5. (e)

    A significant effect of visco-elasticity of fluid is observed during the back flow of dust particles in the neighbourhood of the lower plate.

  6. (f)

    The Lorentz force has shown an accelerating effect on the magnitude of viscous drag formed by the governing motion of Newtonian and non-Newtonian fluids at both the plates.

  7. (g)

    The increasing values of volume fraction raise the shearing stress at the lower plate but a reverse behaviour is seen in case of formation of shearing stress at the upper plate.