Introduction

One of the most important routes for production of polyolefins (i.e., polyethylene, polypropylene and their copolymer with α-olefins) is accomplished by heterogeneous catalysts. In these processes, the reaction begins when small catalyst particles (20–100 µm in diameter) are injected into the reactor. The continuous phase of the reactor contains monomer(s) either in the form of gas or liquid which must diffuse through both the boundary layer around each catalyst particle and its pores to reach the active sites, where the polymerization takes place. The produced polymer deposits on the pores and the catalyst surface, then the monomer(s) must also diffuse through this polymer layer to reach the active sites. As the reaction proceeds, the catalyst particles grow to form a pseudo-homogeneous polymer particle with about 500–2500 µm in diameter. Typical heterogeneous catalysts currently used in polyolefin industry are single site silica-supported metallocene catalysts and multiple site MgCl2/silica-supported Zeigler–Natta (ZN) catalysts.

A significant number of articles have been published to model the growth of catalyst particles in heterogeneous polymerization [1–3]. The two popular models most widely used in single particle modeling are the polymeric flow model (PFM) [4–6] and the multigrain model (MGM) [7–9]. Both models are considered to have reasonable approximations of the actual physical and chemical phenomena taking place in a polymer particle and can estimate the overall particle polymerization rate, particle temperature and molecular properties of the produced polymer. The PFM assumes that growing polymer chain and catalyst fragments form a continuum and the mass transfer in particle follows a Fickian diffusion mechanism through the pseudo-homogeneous polymer phase. The MGM model provides a more detailed look into the growing polymer particle and considers the diffusion phenomena within micro- and macro-particle levels. With the extended versions of MGM, such as polymeric multigrain model (PMGM) [10, 11] and polymeric multilayer model (PMLM) [12–14], the former does neglect the diffusion resistance at the micro-particle level and the latter ignores the micro-particle to improve the initial MGM model. These models have shown success with low active catalyst. When the more active generations of heterogeneous catalyst emerged, the models failed to predict the high rate of polymerization. If the transport properties such as diffusion increases, then the broad molecular weight of the polymer cannot be justified by transport limitation and the multiple sites assumption can be used to justify the breath of molecular weight. While the molecular weight broadness can be modeled by multiple sites assumption, there is no justification for high rates of polymerization in the presence of transport limitation [1, 15]. To justify the high rates of polymerization, in some studies on single particle modeling, it is assumed that the mass transfer inside the particle occurs not only by diffusion, but also by the convection of the monomer through the particle. Therefore, some models were developed by introducing convective terms into the particle model [16–18].

Previously, some research groups focused on the modeling of the catalyst/polymer fragmentation and morphological development in olefin polymerization. Kittelsen et al. [19] introduced a viscoelastic model based on the magnitude and the generation rate of the mechanical stresses due to the produced polymer. Kosek et al. [20, 21] treated the polymer particle as an agglomeration of a large number of micro-elements and used a force balance between the neighboring micro-elements to predict the different morphology patterns of polyolefin particles. Recently, Parvazinia et al. [22–24] have introduced a two-dimensional PFM and considered the fragment patterns that affect the average molecular weight properties, the polymerization rate and the particle overheating in heterogeneous Ziegler–Natta olefin polymerization.

Machado et al. [25] have analyzed the very early development of particle morphology and polymer properties for three different Ziegler–Natta and supported metallocene commercial catalyst systems using stopped flow reactor. It is declared that, depending on the operating conditions, distinct non-uniform catalyst fragmentation patterns can develop. In addition, it is shown experimentally that the polydispersity of polymer at the initial moments of the polymerization is very high, suggesting the existence of significant concentration or temperature gradients. Although at very low degree of polymerization, multigrain structure is detected in SEM and TEM photographs of a nascent polymer [1, 26, 27], but micrograins merge into larger structures and form agglomerations when the reaction advances. These agglomerates would contain several fragments and could make larger structures in fully grown particles [28]. Cecchin et al. [29] have declared that a spherical particle of nascent polymer produced on MgCl2/TiCl4 catalyst comprises many polymer globules with diameter of around 1–2 µm and consists of microparticles which can be assimilated to the PFM. As well, the major portion of the porosity of the catalyst macro-particles is due to the spaces between sub-particles. According to this double grain morphology, they have named the whole system as a double grain model. Skomorokhov et al. [30] have for the first time used this name for their model, by assuming that polymer granules consist of some sub-particles with 10 % of the scale of the whole particle and each of them in turn consists of some microparticles having diameter of about 0.5 µm. It has been concluded that the size of sub-particles has a decisive effect on the yield of polymerization. Kittilsen et al. [31] have also proposed a three level model, micro- meso- and macro-level and included the fragments (meso-scale) in the model. The introduced meso-scale has about 10–40 % of the scale of the whole particle.

In this work, to justify the higher rates of polymerization in heterogeneous olefin polymerization, it is assumed that the particle consists of a number of fragments and in this respect the effect of fragment size and size distribution on the reaction rate, polymer yield and molecular weight distribution is studied. It is assumed that the catalyst particle is fully fragmented at the beginning of polymerization and no more fragmentation occurs during the reaction. This means that the number of fragments is taken to be constant, but the fragments are growing as polymerization proceeds. A polymeric flow model is used to model the growth of fragments and it is assumed that all fragments are spherical. The monomer concentration inside the cracks is assumed to be equal to monomer bulk concentration. Catalysts with single and double active sites are studied.

Model development

Kinetic model

In the present study, the kinetic mechanism for olefin homo-polymerization over heterogeneous catalysts includes chain initiation, propagation, site transformation and deactivation (Table 1). \(P_{n}^{k}\) and \(D_{n}^{k}\) are living and dead polymer chain of length n on kth type of active site, respectively. \(C^{*k}\) and \(C_{d}^{k}\) are the concentrations of active and deactive kth type of catalyst sites. It is assumed that the chain transfer to hydrogen forms the same site type \(C^{*k}\) and the rate constant for all steps is independent of the chain length [32]. Based on above kinetic mechanism, \(\lambda_{i}^{k}\) and \(\mu_{i}^{k}\) are ith moments for living and dead polymer chains of the kth active site accordingly:

$$\lambda_{i}^{k} = \mathop \sum \limits_{n = 1}^{\infty } n^{i} P_{n}^{k}$$
(1)
$$\mu_{i}^{k} = \mathop \sum \limits_{n = 2}^{\infty } n^{i} D_{n}^{k}$$
(2)
Table 1 Kinetic mechanism of heterogeneous catalytic olefin polymerization
Full size table

The reaction rate equations of all molecular species are reported in Table 2. In Table 3, the numerical values of the kinetic rate constants of the heterogeneous catalytic systems are reported. These numerical values are in the range of commonly reported values in the literature [22, 33, 34].

Table 2 Net production–consumption rates of the leading moments of living and dead polymer chains
Full size table
Table 3 Kinetic rate constants used for single-type-site and two-type-site catalysts [22, 33, 34]
Full size table

Particle growth model

To predict the spatial evolution of monomer concentration and the polymerization rate in a single catalyst/polymer particle in olefin polymerization, the modified polymeric flow model [17] is used. The growing polymer particle and fragments are assumed to be spherical and pseudo-homogeneous with constant density. The particle is isothermal and there is no external boundary transfer resistance. The mass transport of monomer is by diffusion only and the mass transfer resistance of all the other species (Table 2) is assumed to be negligible. The monomer diffusion and consumption is included in the unsteady-state mass balances for growing polymer substructures.

The governing equation for the monomer concentration, M, in a growing polymer particle is described as follows:

$$\frac{\partial M}{\partial t} = \frac{1}{r}\frac{\partial }{\partial r}\left( {Dr^{2} \frac{\partial M}{\partial r}} \right) - R_{pf}$$
(3)

The boundary and initial conditions are:

$$M = M_{\text{bulk}} \quad r = R$$
(4)
$$\frac{\partial M}{\partial r} = 0\quad r = 0$$
(5)
$$R = R_{0} \quad t = 0$$
(6)

In which D, R 0 and M bulk are the monomer diffusion coefficient, the radius of the initial catalyst/substructures and the monomer concentration, respectively. The system of governing differential equations is solved using the Runge–Kutta method.

Assuming that the all other molecular species in the growing polymer particle are not diffusion limited, the following dynamic conservation equation to describe the distribution of the molecular species (\(X: C^{*k}\), \(\lambda_{\nu }^{k}\) and \(\mu_{\nu }^{k}\), \(\nu = 0,\; 1 {\text{ and 2}}\) and \(k = 1,{ 2}\)) in the growing particle can be derived.

$$\frac{\partial X}{\partial t} = \frac{1}{{r^{2} }}\frac{\partial }{\partial r}\left( {r^{2} uX} \right) + R_{X}$$
(7)

The boundary and initial conditions are:

$$\frac{\partial X}{\partial r} = 0\;\quad r = 0$$
(8)
$$X = X_{0} \,\quad t = 0$$
(9)

where \(R_{X}\) is the net production/consumption rate of species X (Table 2). At time zero, the concentrations of \(\lambda_{\nu ,0}^{k}\) and \(\mu_{\nu ,0}^{k}\) are equal to zero, while the concentration of the catalyst active sites at time t = 0, \(C_{0}^{*k}\) is equal to a selected value (Table 4).

Table 4 Catalyst characteristics and physical and transport properties
Full size table

Due to the polymer formation, the initial catalyst particle volume will grow with time. Assuming that the polymer phase behaves as an incompressible medium, the following pseudo-steady state mass conservation equation is derived to describe the particle volume change with time:

$$4/3\pi r^{2} \frac{{{\text{d}}r}}{{{\text{d}}t}} = 4\pi \mathop \int \limits_{0}^{r} \frac{{M_{\text{m}} R_{\text{p}} }}{{\rho_{\text{p}} }}r^{2} {\text{d}}r$$
(10)

where \(\frac{{{\text{d}}r}}{{{\text{d}}t}} = u\) (in m3/(s m)) denotes the flux volumetric flow rate of the growing polymer phase.

Equations (1)–(10) are used to calculate the monomer and other species concentrations for each catalyst fragment.

For each fragment, to calculate the number and the weight average chain lengths (\(\overline{X}_{nf}\) and \(\overline{X}_{wf}\)) of the polymer chains produced over the two-type-site catalyst, the following equations are employed:

$$\overline{X}_{nf} = \frac{{\mathop \sum \nolimits_{k = 1}^{2} \left( {\lambda_{1}^{k} + \mu_{1}^{k} } \right)}}{{\mathop \sum \nolimits_{k = 1}^{2} \left( {\lambda_{0}^{k} + \mu_{0}^{k} } \right)}}$$
(11)
$$\overline{X}_{wf} = \frac{{\mathop \sum \nolimits_{k = 1}^{2} \left( {\lambda_{2}^{k} + \mu_{2}^{k} } \right)}}{{\mathop \sum \nolimits_{k = 1}^{2} \left( {\lambda_{1}^{k} + \mu_{1}^{k} } \right)}}$$
(12)

To calculate the polymerization rate of whole particle at any moment, the following equation is used:

$$R_{P} = \mathop \sum \limits_{i = 1}^{m} w_{i} R_{{pf_{i} }}$$
(13)

where m is the total number of fragments in the particle and w is the weight fraction of the polymer produced by fragment i at a time.

Equations (14) and (15) are used to calculate the number and the weight average chain lengths of whole particle, respectively.

$$\overline{X}_{n} = \frac{{\mathop \sum \nolimits_{i = 1 }^{m} W_{i} }}{{\mathop \sum \nolimits_{i = 1}^{m} \left( {\frac{{W_{i} }}{{\overline{X}_{{nf_{i} }} }}} \right)}}$$
(14)
$$\overline{X}_{w} = \frac{{\mathop \sum \nolimits_{i = 1}^{m} \overline{X}_{{nf_{i} }} W_{i} }}{{\mathop \sum \nolimits_{i = 1}^{m} W_{i} }}$$
(15)

Model validation

To assess the accuracy of the numerical approach, simulation results can be compared with the results obtained from the approximated analytical solution. If we assume a pseudo-steady-state approximation for the monomer concentration in the growing polymer particle and also assuming that the “living” polymer chains and catalyst active sites are uniformly distributed in a growing particle, Eq. (3) can be written as follows:

$$0 = \frac{1}{r}\frac{\partial }{\partial r}\left( {Dr^{2} \frac{\partial M}{\partial r}} \right) - K_{p} MC_{t}^{*}$$
(16)

where \(C_{t}^{*}\) (in mol/m3) denotes the total concentration of “living” polymer chains and catalyst active sites in the particle. The solution to Eq. (16) is given by Kosek et al. [20]:

$$\frac{M(r,t)}{M} = \frac{{R_{t} }}{r}\frac{{\sin h(\theta r/R_{t} )}}{\sin h(\theta )}$$
(17)

where R t is the particle radius at time t and θ, the Thiele modulus is equal to:

$$\theta = \sqrt {{{R_{t}^{2} K_{p} C_{t}^{*} } \mathord{\left/ {\vphantom {{R_{t}^{2} K_{p} C_{t}^{*} } D}} \right. \kern-0pt} D}}$$
(18)

\(\theta_{0}\) is the Thiele modulus value at time t = 0, defined by:

$$\theta_{0} = \sqrt {{{R_{0}^{2} K_{p} C_{0}^{*} } \mathord{\left/ {\vphantom {{R_{0}^{2} K_{p} C_{0}^{*} } D}} \right. \kern-0pt} D}}$$
(19)

where \(C_{0}^{*}\) denotes the initial concentration of catalyst active sites in the particle and R 0 is the radius of the initial catalyst/substructures.

The time-varying particle radius, R t , depends on the overall particle polymerization rate and is given by:

$$R_{t}^{2} \frac{{{\text{d}}R_{t} }}{{{\text{d}}t}} = \mathop \int \limits_{0}^{{R_{t} }} \frac{{K_{p} C_{t}^{*} M(r,t)M_{\text{m}} }}{{\rho_{\text{p}} }}r^{2} {\text{d}}r$$
(20)

By substituting Eq. (17) into Eq. (20) and integrating the resulting equation, R t as function of time is obtained as follows:

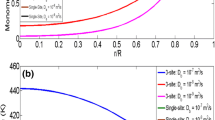
$$\int\limits_{{R_{0} }}^{{R_{t} }} {\frac{{R_{t}^{2} {\text{d}}r}}{{\left( {\frac{\cot h\left( \theta \right)}{\theta } - \frac{1}{{\theta^{2} }}} \right)}} = \frac{{K_{p} C_{0}^{*} MM_{\text{m}} R_{0}^{3} }}{{\rho_{\text{p}} }}t}$$
(21)

In Fig. 1, simulation results obtained from the numerical solution are compared with the analytical solution for three different values of Thiele modulus. In the analytical solution K p  = 2.64 (m3/(mol s)), K d  = 0 (1/s) and other properties are listed in Table 4. As Fig. 1 shows, in the absence of monomer diffusion limitations (i.e., for low values of the Thiele modulus \(\theta \, = \sqrt {9.4}\)), the agreement between the approximate analytical solution and the numerical results is obtained. However, when the system is diffusion limited, the assumption of analytical solution is not true anymore and the analytical solution overestimates the rate of particle growth.

Fig. 1
figure 1

Comparison of analytical and numerical results of particle growth. (a) \(\theta \, = \sqrt {9.4}\), (b) \(\theta = \sqrt {85}\) and (c) \(\theta \, = \sqrt {150}\)

Full size image

Result and discussion

In this study, the growth evolution of a fragmented catalyst particle is modeled to investigate the effect of fragment size distribution and the mass transfer resistance on the molecular weight distribution and particularly on the reaction rate and yield of polymerization. The broadness of molecular weight distribution is explained by multi-active site assumption, while the high rate of polymerization for active catalysts is still a question. It is assumed that the polymer particle is made up of seven different size fragments from 0.5 to 3.5 µm and the number of fragments is constant, but they grow in the course of polymerization. The fragments are separated from each other by interconnected cracks, and the monomer concentration inside the cracks is assumed to be equal to the bulk concentration. PFM is used to model the polymerization process inside the fragments and in fragment level the polymerization is diffusion controlled. The effect of intra-particle mass transfer will be the most pronounced in a semi-crystalline polymer, while the polymer surrounding the active sites becomes thicker and the diffusion coefficient in the dense polymer zone in the particle is about 10−12 (m2/s) [8, 9, 11].

Five different fragment size distributions of a non-uniform fragmented catalyst based on the weight fractions used in this study are shown in Fig. 2 and each contains seven different size fragments from 0.5 to 3.5 µm. Scheme 1 shows the schematic picture of a non-uniform fragmented catalyst and the fragment size distributions in the polymer particle after 3600 s of polymerization time. The schematic picture of a uniform fragmented catalyst, in which the initial radius of all fragments is 0.5 µm, is illustrated in Scheme 2 and the polymer particle after 3600 s of polymerization time is still uniformly fragmented.

Fig. 2
figure 2

Different fragment size distribution of a non-uniform fragmented catalyst

Full size image
Scheme1
scheme 1

Schematic picture of a non-uniform fragmented catalyst

Full size image
Scheme2
scheme 2

Schematic picture of a uniform fragmented catalyst

Full size image

Figure 3 presents the dynamic evolution of the rate of polymerization, yield and PDI for a uniform fragmented catalyst with three different monomer diffusion coefficients. It can be seen that using a two-site kinetic assumption (curves D) while the yield is nearly the same, the PDI would be considerably higher. The inclusion of fragments generates a higher reaction rate and yield, while a two-site assumption generates a higher molecular weight distribution.

Fig. 3
figure 3

Dynamic evolution of the R p (a) yield (b) and PDI (c) for a uniform fragmented catalyst. (A), (B) and (C) correspond to a single-type-site catalyst with D = 1 × 10−11 (m2/s), D = 2 × 10−12 (m2/s) and D = 5 × 10−13 (m2/s), respectively. D corresponds to a two-type-site catalyst with D = 2 × 10−12 (m2/s)

Full size image

For non-uniform fragmented catalysts, Figs. 4, 5 and 6 show the weight fractions of different fragment size categories at the first moment of the reaction and after 3600 s of the polymerization time for three different monomer diffusion coefficients of 1 × 10−11, 2 × 10−12 and 5 × 10−13 m2/s, respectively. All cases show that the smaller fragments grow faster and the weight fractions of the fragments with larger initial sizes are found to be larger; but it does not mean that they are larger than the fragments with a larger initial size. For example, when the diffusion coefficient inside the fragments is 1 × 10−11 m2/s, the weight fraction of the first fragment size category in the distribution type 1 is increased from 14.7 wt% to about 22 wt%. By decreasing the diffusion coefficient to 5 × 10−13 m2/s, the fragments with smaller initial size grow even faster and their weight fractions are found to be larger (about 75 wt%). The exact value of the initial radius (R 0f) and the radius after 3600 s (R f) of polymerization time for each fragment size category in the three different diffusion are reported in Table 5. Fragment size distribution in a growing particle is strongly affected by mass transfer resistance. By increasing the mass transfer resistance, the impact of initial fragment size distribution is reduced. For instance, if the diffusion coefficient inside the fragments set is 5 × 10−13 m2/s (Fig. 6), then after 3600 s, the fragment size distribution is nearly identical for all initial distributions.

Fig. 4
figure 4

Fragment size distribution in t = 0 s and t = 3600 s of polymerization time if D = 1 × 10−11 (m2/s)

Full size image
Fig. 5
figure 5

Fragment size distribution in t = 0 s and t = 3600 s of polymerization time if D = 2 × 10−12 (m2/s)

Full size image
Fig. 6
figure 6

Fragment size distribution in t = 0 s and t = 3600 s of polymerization time if D = 5 × 10−13 (m2/s)

Full size image
Table 5 Initial radiuses and final radiuses for each fragment size
Full size table

The reaction rate, polymer yield and PDI of different fragment size distributions in the single-type-site catalyst with 1 × 10−11 m2/s monomer diffusion are shown in Fig. 7. Larger weight fractions of the smaller fragments (case V) result in an increase in the yield and reaction rate but the weight fractions of larger fragments show no significant effect on the reaction rate and polymer yield (cases III and IV). As the weight fraction of the smaller fragments increases, the PDI decreases accordingly. In smaller fragments, the monomer concentration gradient decreases and it is the main reason for the reduction in PDI. It is generally accepted that, the PDI of the polymer produced by single-type-site catalyst is about 2 when there is no mass transfer resistance [32].

Fig. 7
figure 7

Dynamic evolution of the R p (a), yield (b) and PDI (c) for different fragment size distribution of a single-type-site catalyst with D = 1 × 10−11 (m2/s)

Full size image

In all cases of different fragment size distributions, by reducing the monomer diffusivity to 2 × 10−12 m2/s, the yield decreases and the PDI increases accordingly (Fig. 8). These observations are consistent with the results of uniform fragmented catalysts illustrated in Fig. 3. In cases I and V where the weight fractions of the smaller fragments are higher, the polymerization rate and yield, in the higher rates (for instance Fig. 8) take a considerable distance from the other cases. By further decreasing to 5 × 10−13 m2/s (Fig. 9), the differences between the two cases of I and V become even smaller.

Fig. 8
figure 8

Dynamic evolution of the R p (a), yield (b) and PDI (c) for different fragment size distribution of a single-type-site catalyst with D = 2 × 10−12 (m2/s)

Full size image
Fig. 9
figure 9

Dynamic evolution of the R p (a), yield (b) and PDI (c) for different fragment size distribution of a single-type-site catalyst with D = 5 × 10−13 (m2/s)

Full size image

The main objective of this work is to study the effect of fragment size distribution on polymer yield and molecular weight. Since the multiple sites assumption is widely accepted to justify the broadness of molecular weight distribution, the catalyst with two-type active sites is studied. The same concentration of active sites and mean propagation rate for the single-type-site catalyst are considered (Table 3). As can be seen in Fig. 10, the reaction rate and polymer yield display the same trend as is usual in a single-type-site catalyst. According to Fig. 10, by applying the multiple sites assumption, the PDI can also be increased while there are a relatively high rate and yield as mentioned before in discussing Fig. 3.

Fig. 10
figure 10

Dynamic evolution of the R p (a), yield (b) and PDI (c) for different fragment size distribution of two-type-site catalyst with D = 2 × 10−12 (m2/s)

Full size image

Finally, for comparison with a normal PFM model of a single particle with no fragmentation, the reaction rate, polymer yield and PDI of the non-fragmented single-type-site catalyst with 1 × 10−11 and 2 × 10−12 m2/s monomer diffusion are represented in Fig. 11. As it can be seen, the yield is very low, but the PDI is higher than the fragmented cases. It shows that the fragments play an essential role in reaction yield while PDI can mainly be generated by a multiple sites assumption.

Fig. 11
figure 11

Dynamic evolution of the R p (a), yield (b) and PDI (c) for a non-fragmented single-type-site catalyst. (A) and (B), respectively, correspond to D = 1 × 10−11 (m2/s) and D = 2 × 10−12 (m2/s)

Full size image

Conclusion

In this paper, the modeling of a single particle heterogeneous catalyst at fragment level (sub-particle level) is carried out and the effect of fragment size and size distribution on the reaction rate, polymer yield and polydispersity index is examined. It was assumed that the catalyst particle is fully fragmented in different fragment sizes and different fragment size distributions at the beginning of polymerization and the number of fragments was taken to be constant, but the fragments were grown based on the polymeric flow model assumptions as polymerization proceeded. The interconnected cracks separated fragments and the monomer concentration at the surface of fragments was assumed to be equal to the bulk concentration. The main purpose of the research was to justify the high rates of polymerization in spite of diffusional limitations. As the results show, by introducing fragment size and size distribution in the particle model, much higher yields of polymerization could be achieved. The results indicate that the smaller fragments inside the particle make a strong impact on the increase of reaction yield.