Introduction

The mixing process of polymers has attracted a lot of attention in the recent decades because of both technical and economic advantages [1]. It is possible to achieve new and unique properties by mixing two or more polymers; however, properties of a blend are related to its final morphological structure, which is affected by variation of volume fraction of constituents and process parameters [2]. It is essential to acquire a mechanical model, which would wrap the whole morphological structure of the blend which is strongly affected by the variation of volume fractions of constituents.

Considering immiscibility for majority of polymers, mixing process chiefly results in droplet-matrix structure at low contents of dispersed phase (lower than percolation threshold) [2]. Knotting and interconnecting of droplets form locally fiber/rod structure, which could be interpreted as co-continuous sectors. The higher content of dispersed phase results in more interconnection, which consequently leads to co-continuous structure to be formed at phase inversion point. However, it should be noted that the co-continuous morphology of a blend has a drastic effect on most physical properties, e.g., modulus, electrical conduction and insulation properties [1, 3]. Displacement of phases at phase inversion changes the properties of blend completely, which is attributed to the effects of the major phase on blend properties.

So far, many models have been investigated to predict physical and mechanical properties of polymeric blends [3, 4]. It has been always desirable to search for models which can cover whole morphological variations of blend. Kolarik [5] has presented a cross-orthogonal skeleton (COS), which characterizes a three-dimensional symmetric structure with interchangeable components. Based on percolation theory, he has adopted a two-component equivalent box model (EBM) to calculate the volume fraction variation of the continuous phase. However, the EBM cannot be consistent with the COS model at the expected symmetrical continuous point. Furthermore, this model does not take droplet-matrix component into account, which exists at the intervals between critical volume fractions (percolation thresholds) and phase inversion point [6]. In another study, Kolarik [5] tried to enhance the accuracy of the model and eliminate the errors emerged by the above inconsistency. Though, the weakness of EBM model to incorporate the structural details into the modulus calculation process of polymer blend still holds the results somewhat dubious. A three-dimensional model consisting of three orthogonal bars, same as Kolarik’s model was introduced by Nijhof [7] and Veenstra et al. [2]. Wang et al. [8] have proposed another way for modeling of polymer blends, which relies on removing the weaknesses of COS model and combines it with Maxwell–Eucken (ME) model. They have introduced symmetric interconnected skeleton structure (SISS) model, which is a reformed Kolarik’s COS model, under consideration of eliminating EBM model from calculation process. At the next step, combination of SISS and ME models results in knotted and interconnected skeleton structure (KISS), which is a generalized model and wraps the entire range of volume fraction of dispersed phase between 0 and 1. Although KISS model is in good accordance with experimental results, the complicated mathematical calculation procedures make this model somewhat difficult to use. Our work is focused on making whole calculation processes, e.g., mathematical, geometrical, etc., easier compared to the previous approaches and it proposes a generalized model which is capable of being used with any validated dispersed and co-continuous models as its basis. Zhao et al. [9] have investigated the effects of blend composition and microphase structure on the mechanical behavior of A/B polymer blend film by coupling the Monte Carlo (MC) simulation of morphology with the lattice spring model (LSM) of micro mechanics of materials. Deng et al. [10] used the dynamic density functional theory approach embodied in MesoDyn method to investigate the mechanical behavior of binary polymer blends polystyrene/polypropylene by continuous mesoscopic simulation method. Yousef et al. [11] have used the artificial neural network to predict the tensile curves and mechanical properties of pure polyethylene (PE) pure propylene (PP) and their blends of different proportions. They also have indicated that a multi-layered artificial neural network can simulate the effect of the polymer blending ratio on the mechanical behavior and properties to a high degree of accuracy.

In this article, direct and independent approximation model (DIA) is proposed which covers the entire range of volume fraction of dispersed phase. Based on percolation theory, a consistency parameter is introduced which unifies two fundamentally different models (one signifies on droplet-matrix structure and the other signifies on co-continuous structure). The model is checked using our experimental data for PA/POE blend and some other published data in the literature.

Experimental

Materials and sample preparation

The polymers employed were polyamide (PA, Akulon F223D) and polyolefin elastomer (POE, Tafmer DF740). PA was dried at 80 °C for 12 h before processing. The volume ratios of PA/POE were 100/0, 90/10, 80/20, 60/40, 40/60, 20/80, 10/90 and 0/100. The blend samples were prepared using a twin-screw extruder (ZSK 25, Coperion Werner Pfleiderer, 2002 Germany, L/D = 40) after three repetitions. The screw speed was 250 rpm, and the temperature profile was 220, 230, 240, 235, 225 and 210 °C, respectively. The extrudates were injected (Aslanian, EM80) at 230 °C to obtain dumb-bell for tensile test.

Tensile test

Tensile measurements were performed in accordance with D638 at room temperature on a Santam STM-20 tensile tester with crosshead speed of 50 mm min−1. The Young’s moduli are determined by the initial slope of stress–strain curves, and the results are reported as the average of five runs.

Results and discussion

A brief discussion on DIA model

The main assumptions of DIA model are to consider a blend comprising two components, which are both pure and isotropic in macroscopic scale and the interface is strong enough to transfer stress from one phase to another. Due to good accordance with experimental data, ME and SISS models are chosen as base models.

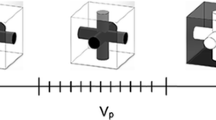
The most important point to deal with in DIA model is to correlate the two above fundamental models. In order to unify KISS and ME models, a consistency parameter called F(D) is used, which is directly elicited from percolation theory. The volume fraction range of dispersed phase between 0 and 1 could be divided into four sub-intervals plus phase inversion point (Fig. 1) as follows:

Fig. 1
figure 1

Variation of blend morphology in different assumed intervals and phase inversion point (crossed line indicates the phase inversion point)

Full size image
  1. 1)

    First interval: (\(0 \le \vartheta_{2} \le \vartheta_{\text{cr2}}\))

  2. 2)

    Second interval: (\(\vartheta_{\text{cr2}} \le \vartheta_{2} < \vartheta_{\text{p}}\))

  3. 3)

    Phase inversion point: \(\vartheta_{\text{p}}\)

  4. 4)

    Third interval: (\(\vartheta_{\text{p}} < \vartheta_{2} \le 1 - \vartheta_{\text{cr1}}\))

  5. 5)

    Forth interval: (\(1 - \vartheta_{\text{cr1}} < \vartheta_{2} \le 1\))

Percolation thresholds of phases 1 and 2 are indicated as \(\vartheta_{\text{cr1}}\) and \(\vartheta_{\text{cr2}}\), respectively, and \(\vartheta_{\text{p}}\) expresses the phase inversion point at which co-continuous symmetric structure is formed. Therefore, when \(0 \le \vartheta_{2} \le \vartheta_{\text{cr2}}\), a droplet-matrix structure is the dominated morphology; and when \(\vartheta_{\text{cr2}} < \vartheta_{2} < \vartheta_{\text{p}}\), both droplet-matrix and co-continuous structures exist and at phase inversion point \(\vartheta_{\text{p}}\) co-continuous structure is the dominant structure of the blend. The structure at the third and fourth intervals is the same as the second and first intervals, respectively.

A mathematical approach to F(D)

In order to find an appropriate and meaningful mathematical term to describe F(D), percolation theory is adopted, in which modulus of the blend in vicinity of percolation threshold is given as follows [12, 13]:

$$E = E_{0} \left( {\vartheta - \vartheta_{\text{cr}} } \right)^{T}$$
(1)

where E 0 is constant, \(\vartheta_{\text{cr}}\) is percolation threshold and T is critical universal exponent which is about 2 [14, 15]. However, some other recent research works show that the percolation relationship is still valid at volume fractions up to 0.66 [14]. Despite De Gennes proposed 11.6 for T, for the sake of simplicity, in this work T is considered as 2 [14]. Since phase 2 is the dispersed phase, Eq. 1 can be rearranged as below:

$$E_{\text{P}} = E_{0} \left( {\vartheta_{\text{p}} - \vartheta_{\text{cr2}} } \right)^{2}$$
(2)

And at \(\vartheta_{2} = \,\vartheta_{\text{p}}\):

$$E_{\text{p}} = E_{0} \left( {\vartheta_{\text{p}} - \vartheta_{\text{cr2}} } \right)^{2}$$
(3)

where E p is the modulus of blend at phase inversion point according to the percolation theory (which could be interpreted as modulus at co-continuous state of blend); however, it is different from the predicted modulus by SISS model at inversion point. Some research works show that the phase inversion point is often formed at intermediate blend content [3, 4]. Dividing Eq. 2 to Eq. 3, yields:

$$\frac{E}{{E_{\text{P}} }} = \frac{{E_{0} \left( {\vartheta_{2} - \vartheta_{\text{cr2}} } \right)^{2} }}{{E_{0} \left( {\vartheta_{\text{P}} - \vartheta_{\text{cr2}} } \right)^{2} }}$$
(4)

Therefore F(D) is given:

$$F\left( D \right) = \left( {\frac{{\vartheta_{2} - \vartheta_{\text{cr2}} }}{{\vartheta_{\text{P}} - \vartheta_{\text{cr2}} }}} \right)^{2}$$
(5)

where E is the variable modulus of blend as a function of \(\vartheta_{2}\).Considering same procedure at third phase yields:

$$F\left( D \right) = \left( {\frac{{\vartheta_{1} - \vartheta_{\text{cr1}} }}{{\vartheta_{\text{P}} - \vartheta_{\text{cr1}} }}} \right)^{2} = \left( {\frac{{\vartheta_{2} - \left( {1 - \vartheta_{\text{cr1}} } \right)}}{{\vartheta_{\text{p}} - \left( {1 - \vartheta_{\text{cr1}} } \right)}}} \right)^{2} = \frac{E}{{E_{\text{P}} }}$$
(6)

where E is the variable modulus of blend as a function of \(\vartheta_{1}\).

Therefore, based on Eqs. 5 and 6, the variation of F(D) corresponding to the increasing of volume fraction of phase 2 (dispersed phase) is illustrated in Fig. 2. It is clear that in the range of 0–\(\vartheta_{\text{cr2}}\), value of F(D) is zero, which is interpreted as droplet-matrix dominant structure. At next interval of higher values between \(\vartheta_{\text{cr2}}\) and \(\vartheta_{\text{p}}\), F(D) increases exponentially to 1, which is due to existence of both droplet-matrix and co-continuous structures. At \(\vartheta_{\text{p}}\), for totally co-continuous structure of blend, F(D) is equal to 1. Nevertheless, at third and fourth intervals, displacement of minor and major phase is likely, and the variation of F(D) is exactly inverse of that of second and first intervals, respectively. F(D) exponentially decreases from 1 to 0 at the third interval, which is attributed to the increase in droplet-matrix sectors of dispersed phase; probably being the phase 1. Finally, at the last interval, the blend structure consists of a matrix of phase 2 including droplets of phase 1.

Fig. 2
figure 2

Variation of F(D) as a function of dispersed phase volume fraction. At second interval, after percolation threshold a little increase in content of dispersed phase transforms a small part of droplet-matrix structure into co-continuous structure, which proceeds since \(\vartheta_{2} = \vartheta_{{_{\text{p}} }}\)

Full size image

Percolation threshold volume fractions are determined by evaluating the geometrical shape of the dispersed particles. By considering a spherical shape, the percolation critical volume fraction would be 0.15–0.2 [12].

Characterizing the DIA model

In order to unify SISS and ME models, F(D) was used and consequently applied to predict the mechanical properties, e.g., modulus of blend. The final equations of ME and SISS models are presented below:

The ME model is able to predict the mechanical properties of a blend in which spherical particles of one phase are dispersed into another phase [8]:

$$E_{\text{m}} = \frac{{E_{1} \vartheta_{1} + E_{2} \vartheta_{2} \frac{{3E_{1} }}{{2E_{1} + E_{2} }}}}{{\vartheta_{1} + \vartheta_{2} \frac{{3E_{1} }}{{2E_{1} + E_{2} }}}}$$
(7)

where E m is modulus of blend, E i and \(\vartheta_{i}\) are the modulus and volume fractions of phase i, respectively. It is clear that by considering the replacement of subscripts 1 and 2, after phase inversion point, the ME model could be used as well.

The SISS model is chiefly used to predict the modulus of a blend in co-continuous morphological state:

$$E_{\text{SISS}} = \left( {E_{1} \vartheta_{1p} + E_{2} \vartheta_{2p} } \right) + \frac{{\left( {\vartheta_{1s} + \vartheta_{2s} } \right)^{2} }}{{\frac{{\vartheta_{1s} }}{{E_{1} }} + \frac{{\vartheta_{2s} }}{{E_{2} }}}}$$
(8)

where subscripts s and p denote the parallel and series cross sections of SISS model. Interchanging subscripts 1 and 2 makes no change in the main equation, which reveals the symmetrical nature of this model. Since, we have adopted SISS and ME models, DIA model would be proposed as following:

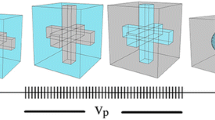
$$E_{\text{DIA}} = F\left( D \right)E_{\text{SISS}} + \left( {1 - F\left( D \right)} \right)E_{\text{ME}}$$
(9)

Figure 3 illustrates two assumed different parts of the blend at second and third intervals. As it is mentioned earlier, after percolation threshold, an interconnection between the spherical particles of dispersed phase occurs (Fig. 3a) and continues since volume fraction is equal to \(\vartheta_{\text{p}}\). This process constructs a co-continuous sector, which is shown in Fig. 3b.

Fig. 3
figure 3

a Droplet-matrix sector after percolation threshold which decreases with the content of dispersed phase, and b co-continuous sector after percolation threshold which increases with the content of dispersed phase

Full size image

Assuming the phase inversion at \(\vartheta_{\text{p}}\), Table 1 shows the formulas for DIA model at different intervals.

Table 1 DIA model at different indicated intervals
Full size table

Young’s modulus of PA/POE blend as a function of POE volume fractions (10, 20, 40, 60, 80 and 90) is demonstrated in Fig. 4a. Furthermore, to check the model in other cases, the modulus of some other blends (which are prepared from Refs. [16] and [17]) are also shown in Fig. 4b, c.

Fig. 4
figure 4

a Comparison of Young’s modulus for PA/POE system (prepared in ZSK twin-screw extruder at 250 rpm) using the predictions of DIA model and experimental data, b comparison of Young’s modulus for PC/ABS system using the predictions of DIA model and experimental data [16] and c comparison of Young’s modulus for PCL/PLA system using the predictions of DIA model and experimental data [17]

Full size image

Furthermore, F(D) can be considered as a ratio R(D), which implies that the volume fraction of dispersed phase is higher than that corresponding to the percolation threshold:

$$R\left( D \right) = \sqrt {\frac{E}{{E_{\text{P}} }}} = \frac{{\vartheta_{2} - \vartheta_{\text{cr2}} }}{{\vartheta_{\text{p}} - \vartheta_{\text{cr2}} }} = \frac{{V_{2} - V_{\text{cr2}} }}{{V_{\text{P}} - V_{\text{cr2}} }} = \sqrt {F\left( D \right)}$$
(10)

where V 2 is the volume of dispersed phase after percolation threshold, V cr2 is the volume of dispersed phase at percolation threshold and V P is the volume of dispersed phase at phase inversion point.

When V 2 reaches V cr2, there are still no co-continuous sectors in the blend, which means no interconnection has occurred between the droplets, but with increasing the volume of dispersed phase the co-continuous sectors gradually start to appear. Therefore, a difference between V 2 and V cr2 \(\left( {V_{2} - V_{\text{cr2}} } \right)\) indicates a residual volume of dispersed phase which can partly turn droplet-matrix structure into co-continuous structure, while \(V_{\text{p}} - V_{\text{cr2}}\) indicates the residual volume of dispersed phase which turns the whole structure of blend system into co-continuous structure. As a result, while R(D) is equal to zero, no co-continuous structure is constructed in the blend, and when it is equal to 1, the structure is totally in co-continuous state (Fig. 5). It can be concluded that after percolation threshold, R(D) indicates the ratio of co-continuous sector, while 1-R(D) indicates the ratio of droplet-matrix sector in the blend system.

Fig. 5
figure 5

Variation of R(D) with the content of dispersed phase

Full size image

The calculation process of DIA model is entirely programmed by MATLAB software, and the results are illustrated in Fig. 4.

Conclusion

In this paper, DIA model is proposed as a new approach to predict the modulus of polymeric blends. Based on percolation theory, a consistency parameter is introduced to unify two fundamentally different models, one predicts the modulus of droplet-matrix structure and the other indicates the modulus of co-continuous structure. After percolation threshold, the knotting and interconnecting of droplets divide the blend structure into two co-continuous and droplet-matrix sectors, each being characterized by its corresponding model. Considering F(D) as a consistency parameter, based on percolation theory, a correlation between two models is formed. At first and last intervals, the value of F(D) is zero which is interpreted as “dominant droplet matrix structure”. At second and third intervals, the quota of each sector is indicated by the value of F(D). While the residual volume, \(V_{2} - V_{\text{cr2}}\), describes the volume which induces interconnection between the droplets of dispersed phase, the fraction of each sector at second and third intervals could be calculated by parameter R(D). However, the variation of R(D) at second and third intervals is somewhat different from F(D), but it is also based on percolation threshold. Nonetheless, both F(D) and R(D) are functions of minor phase volume fraction which forms the major phase after phase inversion point. A significant coincidence of experimental data and DIA predictions is observed due to the accuracy and appropriate presumptions of our model.